Dry powder injection on chip

Abstract

To match the current speed of drug development there is a serious requirement for the pharmaceutical industry to upgrade powder handling processes. Miniaturisation is a key concept especially in the early stages of drug development when only small amounts of the drug compound are available. This paper shows for the first time the application of miniaturisation through chip technology for dry powder handling. Two methods to separate and transport minute amounts of dry powder particles on chip are described. Both techniques could be employed in small scale mixing devices, which depend on reliable particle feeding systems to substitute balances and the time consuming weighing process.

---

Introduction

Drug development in the pharmaceutical industry

The development process of new drugs is slow and also very expensive. Dry powder handling is commonly required during drug development, since the majority of dosage forms contain solids (tablets, capsules, powders). While unquestioned safety reasons prohibit a significant shortening of the period of clinical trials it is aimed to reduce the time and cost of the exploratory development phase.¹ However, during these stages of the development process the availability of new drug candidates is very often limited to a few grams of the synthesised powder. Analysis and characterisation is hampered since available instruments are generally oversized to cope with these small amounts of material. Consequently the application of miniaturised processes is needed.² Small-scale formulation techniques, which are needed when only a few tablets have to be produced for testing purposes, are also inadequately developed. Rowe pointed out that producing an oral dosage form using small quantities of an expensive and scarce new drug is the perennial problem of drug formulation.³ Several approaches of downsizing powder handling equipment have been published.^4–7 However, the problem of accurately weighing and mixing a small amount of dry powder has not been solved so far. In this context, automation of the time consuming weighing step is highly desirable.

Miniaturisation in chemical analysis—the concept of micro total analysis systems (μ-TAS)

Traditional chemical analysis comprises sampling, sample pretreatment, separation, detection, signal evaluation and interpretation. All these processes require transport steps between each of them, which can be time consuming and poses sources for possible errors. In the early 1990's researchers started to combine some of these procedures on small microstructured devices gaining advantages such as low sample consumption, faster reactions or highly efficient separations. Manz et al. proposed the concept of Miniaturised Total Chemical Analysis Systems for the first time in 1990.⁸ Since then the field of microfluidics and µ-TAS has been growing rapidly and many researchers have contributed to its development which has been reviewed by Reyes et al.,⁹ Auroux et al.¹⁰ and recently by Vilkner et al.¹¹ Microfluidic devices are nowadays applied in almost all areas of chemical analysis and other biosciences. While the current research deals mainly with fluids and their problems of mixing, diffusing or pumping, particulate matter has only been treated in liquid suspension. Solutions containing monodisperse beads of several sizes are commonly used. Dittrich and Schwille fabricated a microfluidic system for detecting and sorting fluorescent beads with diameters of 2.5 µm.¹² Pamme et al. developed a system for counting and sizing 2–9 µm small particles.¹³ Microfluidic reactors have been utilised to synthesise particulate matter. Recent research focussed on semiconductor nanoparticles.¹⁴ The synthesis of colloidal silica particles in a microfluidic chemical reactors was achieved by Khan et al.¹⁵ However, particle sizes never exceed 1 µm. These are only a few examples of particles that were handled on chip in solution, but to our knowledge there has been no dry powder handling on chip so far.

Fluidisation of dry particles

When a fluid or a gas is pumped upward through a bed of solid particles, the drag generated by this flow counterbalances the weight of the particle bed at a certain flow velocity. The dry particle bed expands and suddenly takes on properties of a fluid. It is therefore called a fluidised bed. Depending on the particle size, density and shape, the fluidisation medium, bed dimensions and gas or fluid velocity, different types of fluidised beds can be distinguished. Fixed, moving, bubbling/turbulent or fast fluidised beds are the most common types.¹⁶ Fluidised beds are a very popular means of contacting solids with liquids or gases. Rapid mixing and the resulting high heat transfer and high mass transfer rates are advantages that lead to numerous applications including: drying operations, carbonisations, calcinations, heat exchange and granulation. However, not all materials can be fluidised and beds of fine particles are sometimes very difficult to predict. Geldart introduced a classification for gas fluidised beds characterised by density and mean size of the particles.¹⁷ He concluded that fine and cohesive powders (Geldart group C) are difficult to fluidise because of their high interparticulate forces and small particle sizes.

Here we show two techniques to separate and transport minute amounts of dry powders in glass and plastic chips using the technology known from microfluidics and Micro Total Analysis Systems (µ-TAS). Both techniques could be integrated in a chip-based micro mixing system for dry powders.

Materials and methods

Materials

Fujicalin (Fuji Chemical Industry, Japan), a free flowing preparation of Dibasic Calcium Phosphate Anhydrous (DCPA)¹⁸ was chosen as sample excipient for the injection experiments. Improved flow properties compared to standard DCPA's¹⁹ are due to the spherical shape and the narrow size distribution of the particles (mean particle size 113 ± 2.7 µm). Nitrogen gas was utilised as transport and fluidisation medium.

Chip fabrication, chip designs and injection setups

The two different injection methods will be referred to as “fluidised bed injection” and “pulsed injection” in the following paragraphs.

Fluidised bed injection

Here a small side channel with the powder inlet is connected perpendicularly to the main channel with gas inlet and outlet. The injection principle is based on generating and collapsing a fluidised bed of powder and thus injecting small amounts of particles into the microchannel.

The chips for the fluidised bed injection consisted of two layers of glass with wet-etched channels and inlet holes for the gas (diameter 1 mm) and the particles (diameter 7 mm) on the top side of the chip as well as one outlet hole for gas and the injected powder (diameter 1.5 mm) on the bottom side. Commercially available soda lime glass substrates (Nanofilm, Westlake Village, CA, USA) precoated with a 530 nm thick layer of positive photoresist (AZ 1518) on top of a 100 nm chromium layer were used. The design was drawn in AutoCAD^® 2000 and transferred onto the photoresist via a direct writing laser system (DWL) (Heidelberg Instruments, Heidelberg, Germany). It featured a T-shaped channel with a gas inlet, a powder inlet and an outlet (Fig. 1, bottom). The distance between gas inlet and outlet was 32.5 mm and between powder inlet and the channel 7 mm for design A and 4 mm for design B. The latter was also characterised by the conical shape of the connecting channel, which was intended to facilitate the particle introduction into the main channel. All channels had a width of 1 mm and were wet-etched to a depth of 450 µm (design A) and 300 µm (design B) using a diluted HF solution (HF 1.25%, NH₄F 8.75%, HCl 20% and H₂O 70%). Two glass plates with mirrored designs were aligned to form a channel with an ellipsoidal cross-section and a height of 900 µm and 600 µm respectively (Fig. 1, top). The glass chip was thermally bonded at 605 °C using a Model K114 oven (Heraeus, Hanau, Germany).

Fig. 1 Different channel designs that were used for the fluidised bed injection and the respective channel cross-sections. (Top) Cross sectional view of the channel dimension in chip design A and B. (Bottom) Top view of design A and B.

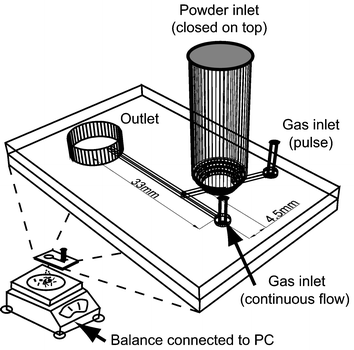
Gas pressure was supplied via Teflon tubing that was glued into the gas inlet hole of the chip. The flow rate was regulated using a mass flow controller (Tylan FC260, Mykrolis Corp., Billerica, US). On/off switching of the gas flow was carried out through a solenoid valve (VJ114, SMC Ltd., MiltonKeynes, UK) that was digitally regulated by a control board (Microrobotics K4 Control Computer, Cambridge, UK) connected to a PC. The powder particles were introduced via a cylindrical hopper (4 ml volume, cut from a 10 ml glass pipette) with an inner diameter of 8.5 mm. The whole chip was fixed directly above a balance such that the particles leaving the chip via the outlet fell into a dish on the balance (Fig. 2). The mass values were digitally transferred to a PC. After filling the hopper with powder the minimum fluidisation velocity was chosen experimentally. The gas flow was slowly increased until the first bubbles appeared. The flow was then increased by 10% to obtain a thorough fluidisation of the bed. Prior to every injection experiment the particles were fluidised in the hopper on the chip for 2 min at this rate to prevent any effects of moisture content or cluster formation that might have occurred during storage. One injection cycle took 15 s and started with switching off the gas flow using the solenoid valve for 2 s. The refluidisation time was 13 s. Injection cycles were repeated until no more particles were injected into the system. The mass value from the balance was digitally recorded after 14 s of each cycle.

Fig. 2 Schematic of the experimental setup for the fluidised bed injection.

Pulsed injection

In this device there were two gas streams applied, a continuous stream from the gas inlet towards the outlet and a pulsed stream through a side channel as well as the bottom of the powder bed which moved particles into the main channel.

The chips for the pulsed injection were made of two layers of PMMA. The channel design was manufactured in the bottom side of the top layer using CNC machining. The circular outlet hole was drilled into the bottom plate. Seven metal screws tightly connected both layers. The design was characterised by channels of 1 mm width and 700 µm height with a rectangular cross-section. A continuous gas flow of 1 ml s⁻¹ was applied to the straight channel (Fig. 3). A second channel merged with the straight channel 10 mm downstream from the continuous gas inlet. This second channel passed through the bottom of the powder hopper and featured a gas inlet for pulsed gas flow. With the intention of facilitating the movement of particle plugs through the channels the angle between the two was chosen to be smaller than 90°. The value of 68° was selected for practical reasons to prevent any interference between powder inlet and tubing connections on top of the chip due to the conical inlet design.

Fig. 3 Schematic of the chip for the pulsed injection.

Cylindrical plastic vials with a volume of 15 ml were utilised as powder hoppers for the pulsed injection. Their outer diameter fitted a notch, which was CNC machined on the top surface of the chip, such that a smooth and airtight connection was established by simple plugging of the vial. The vial was filled with particles and was then closed with a screw cap. For a defined time between 20 ms and 300 ms a pressure pulse with a flow rate of 60 ml s⁻¹ was applied through the pulse gas inlet. This forced particles into the channel. Fluidisation did not occur as the powder hopper was closed. After a break of 15 s the next pressure pulse was applied. The mass values of injected particles were digitally transferred from the balance to a PC every 15 s. A series of 20 injections was carried out for every pressure pulse time value. In a second experiment, injections (t_pulse = 100 ms) were conducted until the powder hopper was completely emptied. Thus the pulsed injection could be compared with the fluidised bed injection, where injection cycles were always repeated until no more material was injected.

Data analysis and evaluation

The initial bed height in the hopper for the fluidised bed injection was calculated from the mass of the powder that was filled into the hopper (ρ = 0.4 g cm⁻³ and A_hopper = πr² = 0.57 cm², eqn. (1)).

The actual bed heights were obtained through subtraction of the height of the preceding injection masses (calculated through eqn. (1)) from the initial bed height. Microcal Origin was then used for data analysis.

Results and discussion

Our aim was to investigate the feasibility of the fluidised bed and the pulsed injection approach to introduce dry powder particles into small channels in glass and plastic chips. Both methods were found to be able to achieve this goal.

As evident from Fig. 4 dry particles could be introduced into and transported within the channel on the chip for the fluidised bed injection. The powder in the inlet hopper became fluidised through the application of a certain gas pressure from the gas inlet. At lower flow velocities the gas escaped straight through the outlet without affecting the particle bed. When the upward gas velocity inside the particle bed and its gravity became equivalent the powder started behaving like a fluid (Fig. 4a). After switching off the gas flow gravity overcame the other forces and the bed collapsed. This downward movement of flowing particles was utilised to introduce small amounts of powder into the channel between gas inlet and outlet (Fig. 4B–D). Reapplying the gas pressure injected the powder plug that was in the channel and fluidised the powder bed again for the next injection (Fig. 4E–F).

Fig. 4 Sequence of a fluidised bed injection of Dibasic Calcium Phosphate particles using chip design A. (A) Nitrogen gas fluidises dry particles in the powder hopper. (B) The gas pressure has just been turned off. Free flowing particles are being introduced into the main channel. (C, D) A particle plug was introduced into the channel. The gas pressure was turned off for 300 ms in this experiment. (E–F) The gas flow has just been reapplied and the powder plug is transported towards the outlet. The powder bed in the hopper becomes fluidised again for the next injection.

In order to investigate the mass of powder injected into the channel, we repeated the injection cycle until no more particles were introduced into the straight channel, as described in the materials and methods. A typical result is shown in Fig. 5. It was observed that the mass of particles per injection decreased continuously with the number of injections.

Fig. 5 Mass of injected particles (accumulated and per injection) over the number of injections for fluidised bed injection (design A). This general behaviour was observed during all experiments with designs A and B.

While fluidisation of dry particles is affected by many parameters such as gas velocity, powder density, bed diameter or particle size distribution, the bed height was the only parameter in our experiments that changed. A graph of the mass of injected particles over the bed height is plotted in Fig. 6. Evidently, the mass of a single injection is linearly related to the fill height of the hopper.

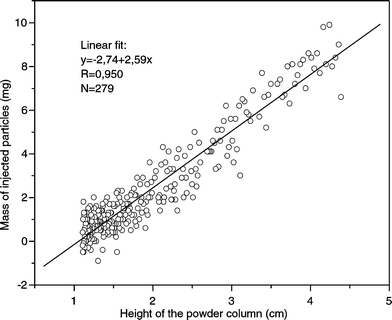Fig. 6 Height dependence of the mass of injected particles (fluidised bed injection, design A).

If we compare the fluidised particle bed to a fluid, the injection process can be described with the equation for the continuous discharge of a vessel through a perpendicular horizontal pipe (Hagen–Poiseuille's law, eqn. (2)).

The flow (i) is proportional to the pressure difference (Δp). The pressure at the base of a fluid arises from the static component of Bernoulli's equation and is given by the product of density (ρ), gravity force (g) and height (h, eqn. (3)).

p_static = ρgh (3)

Since density and gravity force are constant in our system the static pressure and therefore also the flow through the horizontal pipe are linearly dependent on the bed height. This is exactly what we also found experimentally (Fig. 6). Interestingly the straight line of the linear fit intersects the y-axis at −2.74 mg and not at 0 mg. It can be assumed that the channel, which connected powder inlet with the main channel, might have been a dead volume in the system. Flowing particles filled this part of the channel every time the powder bed collapsed but were pushed back and fluidised when the gas flow was applied again (Fig. 4). The absolute value of the negative number of the intersection with the y-axis might be the mass that was retained during every injection in the small connecting channel.

In order to verify this theory additional experiments with a different channel design (B) were conducted. Table 1 shows the results obtained from the experiments with both channel designs.

Table 1 Results of fluidised bed injection experiments with the designs A and B (Fig. 1). The values a and b are parameters of the linear regression (Fig. 6) with y = a + bx, where a is the intercept value and b the slope value of the regression graph. R is the regression coefficient and N the number of data points

Design	Powder mass/g	Gas flow/ml min^−1	a	Error of a	b	Error of b	R	N
A	1.05	800	−2.65	0.13	2.62	0.05	0.961	212
A	1.12	758	−2.45	0.07	2.53	0.04	0.963	406
A	1.00	950	−2.74	0.11	2.59	0.05	0.950	279
B	1.00	370	−2.07	0.07	1.45	0.03	0.936	389
B	1.00	370	−2.32	0.08	1.58	0.03	0.933	384
B	1.00	450	−2.10	0.12	1.52	0.05	0.829	402

---

Several differences between the two designs could be observed. Surprisingly a much higher gas flow rate was needed to fluidise the powder bed on the chip with design A. This must be attributed to the larger cross-section of the channel in design A due to the deeper etching. Practically our chip system featured two parallel branches of channels, the direct inlet–outlet connection and the flow through the powder bed, each of them providing a certain resistance to the applied gas flow. The resistance of the powder bed branch was mainly determined by the permeability of the powder bed and its height. Since similar amounts (≈ 1 g) of the same sample excipient were used in an identical hopper, the flow resistances given by the particle beds were almost equal during all the experiments. Hagen–Poiseuille's law was used to calculate the resistance of the direct inlet–outlet channel. Eqn. (2) can be written as

Δp = Ri (4)

with the flow resistance (R)

The cross-sectional area of the ellipsoidal channels (Fig. 1) relate to cross-sectional areas of circular tubes with radii of 0.69 mm for design A and 0.53 mm for design B, respectively. Since the resistance is inversely proportional to r⁴ the flow resistance of the straight channel for design A was three times lower than that for design B. Subtracting the flow rate, which was required to just fluidise the bed when the other channel was closed (≈50 ml min⁻¹), from the overall flow rate, gives a gas flow through the straight channel in design A that is three times greater that that in design B. This goes in line with the lower resistance.

Table 1 shows that there were also differences in the slope (b) of the graphs and in the value for the intersection (a) with the y-axis. The slope of a graph such as in Fig. 6 is a measure of the average mass of a single shot at a certain bed height. The observed differences cannot be attributed to the applied gas flow as the overall gas flows were caused by the different resistances of the direct inlet–outlet channels as explained before. It is however more likely that only those particles, which directly hit the opening of the small connecting channel when the bed collapsed, could actually enter the channel. While a liquid would streamline to pass through, the dry powder particles probably lost their kinetic energy on impacting the walls around the channel opening or other stationary particles and thus stopped moving. In such a case the mass of a single shot should be directly related to the cross-sectional area of the channel that connected the powder hopper with the direct inlet–outlet channel. This theory is supported as the ratios of the slope of the graph to the cross-sectional area of the channel are virtually equal for both designs (1.69 and 1.73). The conical shape of the channel as it was used in design B might not have an influence on the amount of injected particles as these data show, but further experiments would be needed for final conclusions.

As mentioned before it also appeared that the small connecting channel between powder inlet and main channel retained an equal amount of particles during every injection. The average values for the intercept with the y-axis for design A and B in Table 1 however do not correspond directly to the volumes available (2.61 mg in 10.7 mm³ for design A and 2.16 mg in 5.5 mm³ for design B). The value for design B is larger than expected. Interestingly the particle bulk densities in these connecting channels were almost identical to the bulk density of Fujicalin particles (0.4 g cm⁻³) for design B (≈0.4 g cm⁻³) while they were lower for design A (≈0.26 g cm⁻³). It can therefore be speculated that the smaller cross-sectional area of the channel in design B leads to a denser fraction of retained particles here. Since fewer particles passed through the channel more particles impacted on others that had stopped moving already and pushed them closer together. Unfortunately this area of the channel could not be observed with the microscope, as it was not transparent due to either the glue or the powder hopper itself.

The method we referred to as pulsed injection was also able to transport minute amounts of dry particles through the channels. However, the injection behaviour of this method was different to the fluidised bed injection. A short pressure pulse moved particles from the bottom of the powder bed via the main channel towards the outlet. At the end of each pulse the continuous gas stream from the other gas inlet ensured that the injected plug was completely dragged towards the outlet. The injected masses during the course of one experiment of 400 injections are shown in Fig. 7. The powder hopper was empty after approximately 315 injections. It is noticeable that the mass for one injection did not change considerably during the first 315 injections. There was obviously no dependence on the fill height of the powder hopper as it was inferred for the fluidised bed injection. Nevertheless, the amount of injected particles could be controlled by the time the gas pulse was applied. We investigated injection pulses between 20 ms and 300 ms (Fig. 8). The data show that the mass of injected powder increases linearly with pulse time.

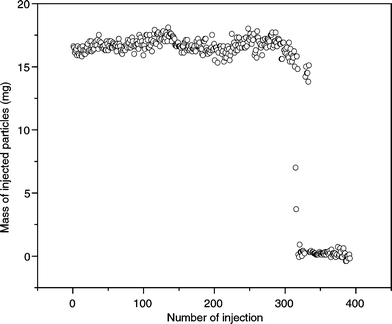Fig. 7 Mass of injected particles over the number of injections (pulsed injection, t_pulse = 100 ms). The powder hopper was empty after 315 injections.

Fig. 8 Time dependence of the injection mass (pulsed injection, 20 injections per time value).

The independence of the bed height and the simple adjustment of the injection mass by the length of the gas pulse are advantageous for this method. However, smaller amounts of particles could be introduced using the fluidised bed injection. For application in a mixing chip the injection method to be used must therefore be chosen depending on the particular needs for the mixture.

Conclusion

Producing an oral dosage form from small amounts of an expensive and scarce drug is one of the biggest problems and a limiting step in drug development. Small-scale equipment is needed to overcome this problem. Here we have demonstrated two powerful methods for injecting and transporting small amounts of a dry, non-cohesive powder in a glass and a plastic chip. The described powder handling methods could be employed as an automated alternative to the time consuming manual weighing and thus comprise a first step towards automated formulation and mixing of small amounts of dry powders. Most industrial excipients, however, are cohesive powders that feature strong interparticulate forces. Such powders could not be handled with the fluidised bed approach. The aim of our future work will be to find and investigate alternative approaches that will allow for handling of cohesive and non-cohesive powders.

Acknowledgements

This research was carried out with financial support of Pfizer Ltd. Torsten Vilkner acknowledges Dr. Robin Fortt for technical support.

References

1. O. J. Bjerrum, Nature Reviews Drug Discovery, 2002, 1, 395.
2. S. Balbach and C. Korn, Int. J. Pharm., 2004, 275, 1.
3. R. C. Rowe, Pharm. Sci. Technol. Today, 2000, 3, 187.
4. M. Landin, P. York, M. J. Cliff, R. C. Rowe and A. J. Wigmore, Int. J. Pharm., 1996, 133, 127.
5. A. Faure, I. M. Grimsey, R. C. Rowe, P. York and M. J. Cliff, Eur. J. Pharm. Sci., 1999, 8, 85.
6. E. Rasanen, J. Rantanen, J. P. Mannermaa, J. Yliruusi and H. Vuorela, J. Pharm. Sci., 2003, 92, 2074.
7. M. Murtomaa, E. Rasanen, J. Rantanen, A. Bailey, E. Laine, J. P. Mannermaa and J. Yliruusi, J. Electrostat., 2003, 57, 91.
8. A. Manz, N. Graber and H. M. Widmer, Sens. Actuators, B, 1990, 1, 244.
9. D. R. Reyes, D. Iossifidis, P. A. Auroux and A. Manz, Anal. Chem., 2002, 74, 2623.
10. P. A. Auroux, D. Iossifidis, D. R. Reyes and A. Manz, Anal. Chem., 2002, 74, 2637.
11. T. Vilkner, D. Janasek and A. Manz, Anal. Chem., 2004, 76, 3373.
12. P. S. Dittrich and P. Schwille, Anal. Chem., 2003, 75, 5767.
13. N. Pamme, R. Koyama and A. Manz, Lab Chip, 2003, 3, 187.
14. J. B. Edel, R. Fortt, J. C. deMello and A. J. deMello, Chem. Commun., 2002, 1136.
15. S. A. Khan, A. Gunther, M. A. Schmidt and K. F. Jensen, Langmuir, 2004, 20, 8604.
16. D. Kunii and O. Levenspiel, Fluidization engineering, Butterworth–Heinemann, 1991.
17. D. Geldart, Powder Technol., 1973, 7, 285.
18. K. Takami, H. Machimura, K. Takado, M. Inagaki and Y. Kawashima, Chem. Pharm. Bull., 1996, 44.
19. H. Schlack, A. Bauer-Brandl, R. Schubert and D. Becker, Drug Dev. Ind. Pharm., 2001, 27, 789.

---

Footnote

† Electronic supplementary information (ESI) available: Video showing injection of Dibasic Calcium Phosphate particles. See http://www.rsc.org/suppdata/lc/b4/b412566p/

---