Temperature dependent setting kinetics and mechanical properties of β-TCP–pyrophosphoric acid bone cement
Liam M. Grover*a, Uwe Gbureckb, Anne M. Youngc, Adrian J. Wrightd and Jake E. Barraleta
aFaculty of Dentistry, McGill University, Montréal, Québec, H3A 2B2, Canada. E-mail: liam.grover@mcgill.ca; Fax: +1 (514) 398 8900; Tel: +1 (514) 398 7203 ext. 3908
bDepartment of Functional Materials in Medicine and Dentistry, University of Würzburg, Würzburg, D-97070, Germany
cEastman Dental Institute, UCL, London, UK WC1X 8LD
dSchool of Chemistry, University of Birmingham, Birmingham, UK B15 2TT
First published on 10th October 2005
Abstract
Brushite (CaHPO4·2H2O) is the product of acidic calcium phosphate cement forming reactions. It has a higher solubility than hydroxyapatite under physiological conditions and is a promising resorbable bone cement candidate. It reacts extremely fast so dilute mixes are required to form cements having setting times with surgical utility, which in turn compromises strength and produces a highly porous material. Pyrophosphate ions have a strong affinity for calcium orthophosphate surfaces, can inhibit their mineralisation and are thought to hydrolyze, forming orthophosphate during bone formation. The effect of replacing the acid orthophosphate component of a brushite cement with pyrophosphoric acid on the cement setting reaction time at temperatures of between 24 °C and 70 °C was determined. The substitution of pyrophosphate for orthophosphate retarded setting and improved mechanical performance of the cement. Pyrophosphate did not inhibit the extent of reaction but did influence microstructure of the brushite crystals. Temperature was found to have a significant (p < 0.01) influence on mechanical performance, and this was attributed to the formation of monetite (CaHPO4) rather than brushite at temperatures of ≥55 °C.
Introduction
Calcium phosphate cements are currently employed in both medical and dental surgery. They are most frequently used in non-load bearing applications such as maxillofacial augmentation,1 although several orthopaedic applications have been proposed, including the repair of the tibial plateau2 and the distal radius.3 Many of the currently available calcium phosphate cement formulations set following the mixture of a calcium phosphate powder with an aqueous solution to form a matrix of apatite.4–7 Hardening occurs as a result of a dissolution/precipitation reaction similar to that of gypsum; an example of such a setting reaction is shown in eqn (1).| 3-Ca3(PO4)2 + H2O → Ca9(HPO4)(PO4)5OH | (1) |
Apatite cements set with little or no exotherm and at near-neutral pH. They may therefore be used for the delivery of heat sensitive molecules such as drugs or proteins.8,9 Recent advances have resulted in the production of apatite cements that exhibit compressive strengths in the same range as cortical bone.10 Despite these highly attractive properties, a major limitation of apatite cements is that hydroxyapatite is practically insoluble (−logKsp = 58.6 at 37 °C) at physiological pH. The cements are also generally micro-porous and usually resorbed by cell mediated phagocytosis from the surface of the graft material.11 This means that hydroxyapatite cements are typically only slowly resorbed in vivo.
Calcium phosphate cement formulations produced from the mixture of either β-tricalcium phosphate (β-TCP)12 or nanocrystalline hydroxyapatite13 and an acidic source of orthophosphate ions such as monocalcium phosphate monohydrate set to form a matrix consisting predominantly of brushite in accordance with eqn. (2).
| β-Ca3(PO4)2 + Ca(H2PO4)2·H2O + 7H2O → 4CaHPO4·2H2O | (2) |
Brushite is sparingly soluble at physiological pH (−logKsp = 6.63 at 37 °C). Resorption can potentially therefore occur by phagocytosis and dissolution such that following implantation, brushite cements may be either completely or largely resorbed in 16 to 18 weeks.14,15 Despite this, the widespread use of brushite cements is limited; they are typically weaker than the majority of apatite cements.16 One reason for the comparatively low compressive strength is that due to an extremely rapid setting reaction, they are usually mixed at a low powder to liquid ratio compared with stoichiometric proportions. This results in high porosity and consequently a weak cement. Several additives have been used to retard the setting reaction of brushite cements including citrate, sulfate and pyrophosphate ions.17 Of these ions, pyrophosphate is the most effective setting retardant, Bohner et al.17 showed that the addition of tetra-sodium pyrophosphate at a concentration as low as 23 mM caused a six-fold increase in setting time when compared with an un-retarded cement mix. It is thought that pyrophosphates may function as retarding agents by bonding to the surface of newly forming crystals thereby inhibiting crystallization.18 Recently it was shown that when significant (>10 wt%) amounts of pyrophosphoric acid solution were added to a calcium orthophosphate cement, it behaved as a reactant to form up to 28 wt% of calcium pyrophosphate in the set cement matrix.19
Temperature may affect the setting and mechanical properties of calcium phosphate cement systems. Operating theatre temperature has been reported to vary between 18 and 27 °C and orthopaedic cement setting reaction will proceed at 37 °C once the cement is implanted. Such variation can have a marked effect on the setting times. One apatite cement system, for example, was shown to require ∼30 min to set at 20 °C but only 10 min at 37 °C.20 The effect of temperature on brushite cements is perhaps even more significant. At low pH values, such as those reported within the matrix of set brushite cements, and at temperatures of >40 °C, monetite has been shown to be formed.21 The presence of monetite has been attributed to the dehydration of the brushite crystals.21 Since monetite is considerably denser than brushite (2.8 compared with 2.32 g cm−3), the dehydration of brushite resulted in shrinkage of the cement matrix and the formation of considerable additional porosity, markedly reducing compressive strength.22 Furthermore, the dehydration of brushite results in the evolution of hydrogen ions, which may elicit an adverse biological reaction in vivo.22
The aim of this study was to determine the setting reaction mechanism of an aqueous β-TCP–pyrophosphoric acid cement at 37 °C using real-time X-ray diffraction and scanning electron microscopy of embedded and sectioned cement samples. The results are compared with data for a previously reported aqueous β-TCP–orthophosphoric acid solution brushite cement.17 Since temperature was shown to have a significant effect on the physicochemical properties of the earlier brushite cement,21 we also determined its effect on the setting reaction of the aqueous β-TCP–pyrophosphoric acid cement. As phase changes are known to influence the mechanical properties exhibited by brushite cements,22 the effects of storage temperature on the compressive strength and relative porosities of both cements were additionally investigated.
Experimental
The β-TCP–pyrophosphoric acid cement was formed by combining a 2 M pyrophosphoric acid solution (Rhodia, West Midlands, UK) with β-TCP (Plasma-Biotal, Derbyshire, UK). The β-TCP–orthophosphoric acid solution cement was produced by mixing 2 M orthophosphoric acid (Sigma, Dorset, UK) containing trisodium citrate (Sigma, Dorset, UK) at a concentration of 50 mM with the β-TCP. The cements were both mixed in a powder to liquid ratio of 1.50 g ml−1. For both cements, the β-TCP was divided into four piles of equal mass, which were combined one at a time with the acid solution. Following the inclusion of each quarter of powder, the slurry was mixed using a stainless steel spatula for 5 s. Once all of the β-TCP was combined with the liquid phase, the cement slurry was kneaded with the spatula for a further 20 s.Monitoring the setting reaction
The microstructural development of β-TCP–pyrophosphoric acid and β-TCP–orthophosphoric acid cements at 37 ± 1 °C (temperatures throughout the paper are shown ± the maximum variation measured during the experiments) was observed by examination of sections through the cement paste 5, 15, 45, 90 and 180 min after mixing. The cement was mixed at ambient temperature (24 °C) and stored at 37 ± 1 °C. After periods of 5, 15, 45, 90 and 180 min the cement paste was immersed in absolute ethanol (Sigma, Dorset, UK) for 1 min. The paste was then removed from the absolute ethanol and dried at 37 ± 1 °C for 24 h, after which the cement was embedded under vacuum (Epovac, Struers, Glasgow, UK) in cold setting epoxy resin (Epofix, Struers, Glasgow, UK). Once set, sections were made through the cement using a low speed diamond saw (Isomet, Buehler, Il, USA) lubricated with a non-aqueous lubricant (DP Blue, Struers, Glasgow, UK). The sections were ground using a series of silicon carbide papers (Struers, Glasgow, UK) of 500, 1000, 2400 and 4000 grit. Ground samples were polished using a 1 µm diamond suspension (Struers, Glasgow, UK). Once polished, the samples were mounted on an aluminium stub and prepared for examination using a scanning electron microscope (JSM 5300 LV, JEOL, Tokyo, Japan) in high vacuum mode.X-Ray powder diffraction data were collected using Cu Kα radiation from an X-ray powder diffractometer fitted with a Gobel mirror (D5005, Siemens, Karlsruhe, Germany). Data were collected from 2θ = 20–40° with a step size of 0.02° and a normalized count time of 1 s per step. The presence of brushite, monetite and β-TCP in the partially set β-TCP–pyrophosphoric acid solution cement was confirmed by comparing the complete patterns with published data.
X-Ray diffraction was used to monitor the rate of brushite formation and β-TCP reaction in the cement pastes at temperatures of 24, 37, 55 and 70 ± 1 °C. Prior to measurement, the controlled temperature chamber (HTK 1200 variable temperature stage, Anton Paar, Graz, Austria) in the X-ray diffractometer was set at the desired temperature. β-TCP–pyrophosphoric acid and β-TCP–orthophosphoric acid cement pastes were mixed and placed, using a spatula, into a stainless steel sample cup of depth 2 mm and diameter 12 mm. The sample cup was mounted in the X-ray diffractometer in an enclosed chamber. The detector scanned between 27° and 33° 2θ for 90 s every 600 s for the slower setting cements and lower two temperatures or every 250 s for the more rapid setting cements and/or higher temperatures. At each time-point the peak areas at 29° and 31° 2θ, characteristic of the 1, 4, −1 of brushite and the 0, 2, 10 of β-TCP reflection were determined using the EVA programme (Bruker, Karlsruhe, Germany).
Since the samples were not removed from the instrument during the course of a given kinetic experiment it is reasonable to assume that any reduction or increase in the peak areas are proportional to changes in the weight fractions of the reactant or product to which the peak corresponds. Extending concepts in basic reaction kinetic methods23,24 we can define the fractional reaction extent for this study (ξ) as the change in concentration of a component in a reaction mixture divided by the total change at equilibrium. Combining this assumption and definition leads to eqn. (3), and a quantitative method of data analysis.
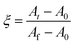 | (3) |
At, A0 and Af are the peak areas at time t, initially and at equilibrium respectively. Expressing data as these fractional reaction extents is a useful method of analysing kinetic results because for simple chemical processes with no reactive intermediates it will have the same value irrespective of which reactant or product peak (or concentration from any other technique) is used to calculate it. In more complex reactions, however, any delay between reactant loss and product gain due to formation of reactive intermediates can be detected by none overlap of reaction extent plots. Additionally, multiplying the percentage of reactant remaining at equilibrium, ϕ, by ξ gives the percentage of reactant reacted in the cement at any given time point during the setting process. Assuming the area under the 31° 2θ peak is zero with 100% reaction (i.e., that there is no reactant/product peak overlap) the percentage of β-TCP reacted at equilibrium is given by eqn. (4).
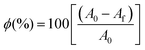 | (4) |
A further parameter of use in the interpretation of the kinetic data is the ratio, χ, of product (P) and reactant (R) maximum area change (see eqn. (5)).
 | (5) |
Any variation in this ratio with temperature would be consistent with the formation of more than one product in differing ratios.
Since the area at zero time (A0) is not directly measured in this experiment it was calculated by linear extrapolation of the first four or five data points to zero time. For some samples a delay was observed before any reaction. In this case an inhibition time, I, was calculated by linear extrapolation of data, where maximum area change with time was observed, to zero reaction extent. Additionally, experiments were performed until changes in area with time had decreased for at least ten data points to approximately one hundred times the maximum rate of change. Using data at the end of the experiment (last ten time points) Af was obtained from the intercept of area plotted versus inverse time (equivalent to an extrapolation to infinite time). Finally, reaction rates were calculated from the gradient of reaction extent as a function of time using Excel (Microsoft, Redmond, USA). The average maximum value at each temperature calculated using both the product and reactant data is quoted in the following.
Mechanical characterisation
Nominally identical cement cylinders of diameter 6 mm and height 12 mm were formed by placing freshly manipulated cement paste into a PTFE split mould. The mould was stored in a container at temperatures of 4, 24, 37, 55 and 70 ± 1 °C for a period of 24 h. The cement samples were removed from the mould after 24 h, and geometrical measurements made in triplicate using digital callipers (RS Electronic, Northamptonshire, UK). For compression testing, each cement cylinder was mounted on the lower anvil of a Universal testing machine (5544, Instron, Buckinghamshire, UK) with its long axis perpendicular to the anvil's surface. It was then loaded to failure from the upper surface by a second anvil at a constant displacement rate of 1 mm min−1. The applied load was detected by a 2 kN load cell (Instron, Buckinghamshire, UK). The compressive strength of the cement was the mean of at least ten measurements. Multiple comparisons of the data were performed using a one-way analysis of variance (ANOVA) within a statistical analysis package (SPSS for Windows, SPSS, IL, USA). A Tukey multiple range post hoc test was used to compare paired groups of data.After testing in compression, the cement fragments were collected and dried in a desiccator at a temperature of 37 ± 1 °C until no further mass-loss was noted. The samples were then ground to powder using a pestle and mortar. The true density of the cement powder was determined using a helium pycnometer (Accupyc 1330, Micromeritics, Bedfordshire, UK). The sample chamber was purged with helium a total of ten times before ten consecutive measurements of volume were performed. For each sample set, the true density of four different cement fragments was determined so that values were the mean of 40 measurements. Apparent density was calculated using mass and dimensional measurements of the cement cylinders made before testing. The relative porosity of the cements was calculated from the values for true and apparent density. The microstructures of gold sputtered set cement fragments were examined using a scanning electron microscope (JSM 5300 LV, JEOL, Tokyo, Japan) set in high vacuum mode.
Results
Cement setting mechanism
Scanning electron microscopy revealed that five minutes after manipulation, the microstructure of the β-TCP–pyrophosphoric acid cement consisted predominantly of loosely packed rounded particles of the same morphology as the β-TCP (diameter ∼50 µm) (Fig. 1a). At 15 and 45 min dissolution of the β-TCP particles was apparent (micrographs not shown), which was associated with the formation of material in the interstices between the particles. Appreciably more cementitous product was observed at 90 min (Fig. 1b), since little porosity could be observed between the reactant particles. At 180 min after mixing (Fig. 1c), the number of rounded particles in the cement matrix had reduced significantly but rounded pores of comparable diameter could be detected. Matrix development in the β-TCP–orthophosphoric acid cement occurred comparatively more rapidly (Figs. 1d, e and f). In this case, cement formation was detectable in the matrix phase by 5 min (Fig. 1d) and there was little further change after this time (Fig. 1e and f). | ||
| Fig. 1 Scanning electron micrographs of resin sections through β-TCP–pyrophosphoric acid solution cement (a) 5 min, (b) 90 min, and (c) 180 min after mixing, and β-TCP–orthophosphoric acid solution cement (d) 5 min, (e) 90 min and (f) 180 min after mixing. | ||
Diffraction patterns of the β-TCP–pyrophosphoric acid cement at temperatures of 24, 37, 55 and 70 °C are shown in Fig. 2. At temperatures of 24 and 37 °C a peak at 21° 2θ was apparent indicating the presence of brushite. When the cement was stored at temperatures of 55 and 70 °C, however, the peak at 21° 2θ reduced in intensity and peaks at 26° 2θ and 30° 2θ were evident, indicating the presence of monetite. In all cases all intensity was attributed to the major peaks for brushite, monetite and β-TCP.
 | ||
| Fig. 2 X-Ray diffraction patterns of cements formed from the mixture of β-TCP with pyrophosphoric acid solution stored at temperatures of 24, 37, 55 and 70 ± 1 °C. Marked on the patterns are the positions of the peaks for brushite (△), monetite (□) and β-TCP (○). All intensity could be attributed to presence of these phases confirming the presence of no additional crystalline materials. | ||
X-Ray diffraction kinetic data showed that when β-TCP was combined with the aqueous pyrophosphoric acid the reaction between 24 and 37 °C occurred more slowly than when the β-TCP was combined with the orthophosphoric acid solution (see for example Fig. 3). For the pyrophosphoric acid cements at 24 ± 1 °C there was a delay of 23 min before a reduction in the area under the peak representative of β-TCP (Table 1). There was then an additional further delay of 28 min before an increase in the area under the peak representative of brushite was noted (Table 1). At 37 ± 1 °C reaction extent calculated from reactant and product peaks overlapped better (see Fig. 3) and indicated inhibition times of 30 and 51 min (see Table 1) respectively. The X-ray diffraction patterns confirmed, however, that when the β-TCP was mixed with the orthophosphoric acid solution the setting reaction proceeded rapidly at both 24 and 37 ± 1 °C and was approximately 60% complete after only 10 min (Fig. 3). A reduction in the area under the peak representative of the β-TCP was observed from the first measurements as was an increase in the area under the peak that was representative of brushite.
 | ||
| Fig. 3 The extent of the cement setting reaction as indicated by the area under the peak representative of brushite (29° 2θ) and β-TCP (31° 2θ) with time for cement formed from the mixture of β-TCP with either pyrophosphoric acid or orthophosphoric acid solution during storage at 37 ± 1 °C. | ||
| Temperature/°C | Inhibition times, I/min | β-TCP reacted ϕ (%) | Equilibrium brushite/β-TCP area change χ | Max reaction rate dξ/dt | |
|---|---|---|---|---|---|
| Reactant | Product | (%/s) | |||
| 24 | 23 | 51 | 97 | 4.4 | 0.012 |
| 37 | 30 | 51 | 100 | 4.8 | 0.013 |
| 55 | 1 | 1 | 49 | 1.2 | 0.024 |
| 70 | 0 | 0 | 36 | 2.1 | 0.040 |
Increasing the temperature at which the cement was stored to ≥55 °C resulted in an increase in the rate at which both the β-TCP–orthophosphoric acid and β-TCP–pyrophosphoric acid cements set. In the case of the β-TCP–orthophosphoric acid cement this meant that the setting reaction was almost complete by the time the first X-ray diffraction measurement was made. In the case of the β-TCP–pyrophosphoric acid cement, an increase in temperature to ≥55 °C caused a marked reduction in the delay between cement mixing and the time at which β-TCP consumption and brushite formation were detected (Table 1). At both 55 and 70 ± 1 °C differences between the calculated reaction extents for the products and reactants were small and suggested no measurable delay between β-TCP reaction and brushite formation.
The final percentages of β-TCP reaction (eqn. (4)), χ values (eqn. (5)) and maximum reaction rates at different temperatures are shown in Table 1. These results indicate that at both 24 and 37 ± 1 °C practically all the β-TCP reacts and comparable levels of brushite per gram of reactant are produced. At higher temperatures, the reaction rates are increased but the equilibrium levels of β-TCP reacted reduced (Table 1). There is also a significant reduction in χ at 55 and 70 ± 1 °C (see Table 1) and an abrupt change in reaction rate (dξ/dt) both of which are consistent with a change in the type of reaction and β-TCP forming largely monetite instead of brushite.
A rise in temperature also resulted in an increase in the true density of the set cement formed from the mixture of β-TCP with either orthophosphoric acid or pyrophosphoric acid solution (Fig. 4). For example, the true density of the β-TCP–pyrophosphoric acid solution cement increased from 2.41 ± 0.03 g cm−3 when stored at a temperature of 24 ± 1 °C to 2.75 ± 0.06 g cm−3 at 70 ± 1 °C. This is consistent with precipitation of a higher density calcium phosphate compound than brushite combined with less reaction of the β-TCP at higher temperatures.
 | ||
| Fig. 4 The effect of temperature on the true density of the cement formed from the mixture of β-TCP and either pyrophosphoric acid or orthophosphoric acid solution. Also marked on the graph are lines showing the theoretical density of β-TCP, monetite and brushite. | ||
Mechanical properties
The temperature at which the β-TCP–orthophosphoric acid cement specimens were stored prior to testing had little effect on the compressive strength exhibited by the set cement (Fig. 5). They varied between 2.0 ± 0.3 MPa (4 ± 1 °C) and 2.1 ± 0.8 MPa (24 ± 1 °C). When stored for 24 h at 4 ± 1 °C, the β-TCP–pyrophosphoric acid solution cement hardened fully and exhibited a compressive strength of 2.8 ± 0.7 MPa. Notably, when storage temperature was increased to 37 ± 1 °C, the β-TCP–pyrophosphoric acid solution cement exhibited a compressive strength of 8.7 ± 2.4 MPa, which was significantly stronger (p < 0.01) than either the β-TCP–orthophosphoric acid solution cement or the β-TCP–pyrophosphoric acid solution cement stored at any other temperature investigated. At all storage temperatures except 4 ± 1 °C, the β-TCP–pyrophosphoric acid cement exhibited significantly higher (p < 0.05) compressive strengths than the β-TCP–orthophosphoric acid cements stored in like conditions. | ||
| Fig. 5 The compressive strengths exhibited by the cements formed from the mixture of β-TCP with either pyrophosphoric acid or orthophosphoric acid solutions following storage for 24 h at 4, 24, 37, 55 and 70 ± 1 °C. * indicates that the mean value for the β-TCP–pyrophosphoric acid cement made at that temperature is significantly (p < 0.05) higher than the β-TCP–orthophosphoric acid cement made at the corresponding temperature. ‡ indicates that the β-TCP–pyrophosphoric acid cement stored at 37 ± 1 °C is significantly (p < 0.01) stronger than both cement formulations stored at all temperatures investigated. | ||
The relative porosities of the β-TCP–orthophosphoric acid and β-TCP–pyrophosphoric acid solution cement samples stored at temperatures of 24, 37, 55 and 70 ± 1 °C are shown in Fig. 6. At all temperatures except 70 ± 1 °C, the β-TCP–pyrophosphoric acid solution cement was of significantly (p < 0.05) higher density than the β-TCP–orthophosphoric acid solution cement. The relative porosities of the β-TCP–pyrophosphoric acid solution cement increased with an increase in temperature from 32 ± 1% (24 ± 1 °C) to 53 ±1% (70 ± 1 °C). A similar trend was apparent for the β-TCP–orthophosphoric acid cement, the relative porosity of which increased from 44 ± 1% (24 ± 1 °C) to 54 ± 1% (70 ± 1 °C).
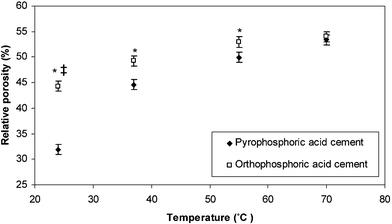 | ||
| Fig. 6 The relative porosities of cements formed from the mixture of β-TCP and either pyrophosphoric acid or orthophosphoric acid solutions when stored at temperatures of 24, 37, 55 and 70 ± 1 °C. * indicates storage temperatures where the β-TCP–pyrophosphoric acid cement was significantly denser (p < 0.05) than the β-TCP–orthophosphoric acid cement stored at like temperatures. ‡ indicates that the cement formed from the combination of β-TCP and pyrophosphoric acid and stored at 24 ± 1 °C was significantly denser (p < 0.05) than all other cement formulations stored at the temperatures investigated. | ||
Although the β-TCP–pyrophosphoric acid cement and β-TCP–orthophosphoric acid cements both set to form a matrix consisting predominantly of brushite, the microstructures of the cements were markedly different. The cement that was formed from the combination of β-TCP with orthophosphoric acid (Fig. 7a) consisted of blade-like crystals of 10–20 µm in length, similar to those previously reported in the literature.12 The β-TCP–pyrophosphoric acid cement consisted of more densely packed irregularly shaped particles (Fig. 7b).
 | ||
| Fig. 7 Scanning electron micrographs showing the microstructure of the cement formed from the combination of (a) β-TCP with orthophosphoric acid solution and (b) β-TCP with pyrophosphoric acid solution. The microstructures of the two cements were markedly different despite the fact that they both set to form a matrix of predominantly brushite. | ||
Discussion
The most striking consequence of using pyrophosphoric acid solution in the cement mix rather than orthophosphoric acid solution was the inhibitory effect that it had on the cement setting reaction. This type of inhibition can be useful clinically because it provides the clinician with a longer working period and enables higher levels of powder to be incorporated into the cement. When cement was formed from the mixture of orthophosphoric acid solution and β-TCP the cement setting reaction was 60% complete within 10 min (Fig. 3). In the case of the cement formed using the pyrophosphoric acid solution, the cement set more slowly and between 90 min and 180 min after mixture, there was a notable change in microstructure (Fig. 1b and c). Pyrophosphate ions are well documented to have an inhibitory effect on crystallization.25 They function by binding to the nuclei of calcium salts in solution and preventing the incorporation of ions into the crystal lattice, stopping the crystals from attaining a critical size to allow crystal growth and aggregation.26 The inhibitory effect of pyrophosphates on crystallization has resulted in them being used as setting retardants in brushite calcium phosphate cements.17 In this study, we demonstrated that pyrophosphate ions controlled the rate of cement setting not only by inhibiting brushite crystallization but also by slowing the rate at which the β-TCP was consumed. Studies investigating the inhibitory effect of pyrophosphate ions on calcium phosphate crystallization are frequently performed in a system where there are few or no calcium phosphate crystals present and so the pyrophosphate ions may remain free in solution.27,28 In the case of cements, there is typically a large volume fraction of solids (in this study 33 vol%) and it would be likely that much of the pyrophosphate would bind to the surface of the solid component before reactant dissolution. The presence of a surface layer of pyrophosphate ions on hydroxyapatite crystals has previously been shown to reduce the rate at which they may be dissolved29 and it is possible that the pyrophosphate ions in this study had a similar effect on the β-TCP, which may explain why, when the cement paste contained pyrophosphoric acid, β-TCP consumption required longer to initiate than in its absence (Fig. 3). Since dissolution of the β-TCP would be expected to cause an increase in the pH value of the cement paste, if pyrophosphate did slow the rate of β-TCP dissolution, it would be expected that the cement paste would remain at a pH minimum for longer period of time than in the absence of pyrophosphoric acid. Bohner et al.30 demonstrated that the presence of pyrophosphate ions in a cement mix increased the period of time for which the pH value remained at a minimum and this time period increased with an increase in pyrophosphate concentration. To minimize the time period for which the pH value of a brushite cement remains at its minimum, it may be desirable to use a sparingly soluble pyrophosphate salt which would dissolve in the liquid component at a similar rate to the β-TCP thereby inhibiting the crystallization of brushite without slowing β-TCP dissolution.As the temperature at which the β-TCP–pyrophosphoric acid solution cement was stored was increased to ≥55 °C there was a reduction in the mass of brushite formed per gram of β-TCP consumed and β-TCP reacted at equilibrium (Table 1). The increase in true density with temperature (Fig. 4) also indicated less β-TCP reaction and/or an alternative product of higher density than brushite (2.32 g cm−3) being formed at higher temperatures. X-Ray diffraction patterns confirmed this higher density product was monetite (density 2.8 g cm−3) (Fig. 2). Monetite has previously been shown to form in powders containing β-TCP and monocalcium phosphate monohydrate (MCPM) when aged in ambient conditions (relative humidity 60%, temperature 22 °C) for a period of seven days31 and also in the matrices of set brushite cement formed from the mixture of β-TCP with a orthophosphoric acid solution incubated in distilled water.21 When stored in distilled water the formation of monetite in the set cement was shown to be favoured at temperatures of 60 °C and when the pH value of the ageing solution was low. Fulmer and Brown32 demonstrated that in a tetracalcium phosphate–MCPM cement that above a temperature of 45 °C that monetite was formed as an intermediate product in the setting of the cement. However, Bohner et al.,21 suggested that the formation of monetite in cement could only result from the dehydration of the brushite crystals. If monetite formation occurred as a consequence of the dehydration of the brushite phase in the β-TCP–pyrophosphoric acid solution cements, it would have been expected that as time proceeded the area under the peak representative of brushite would have reached a plateau and then reduced as the brushite dehydrated, however, in the present study this was not the case, suggesting that in the β-TCP–pyrophosphoric acid cement, monetite was formed directly by the cement setting reaction. A possible mechanism is shown in eqn. (6).
| 2Ca3(PO4)2 + H4P2O7 + 2H2O → 4CaHPO4 + Ca2P2O7·2H2O | (6) |
Despite being less soluble than brushite at all pH values, monetite is relatively infrequently encountered in vivo and this is thought to be because its crystal growth rate is slower than brushite. Increasing the temperature at which the cement set may have increased the crystal growth rate of monetite and therefore favoured its precipitation over brushite. Since at a temperature of ≤37 °C no monetite was detected in the β-TCP–pyrophosphoric acid cement, it is unlikely that its formation would occur in the β-TCP–pyrophosphoric acid solution cement in vivo.
The precipitation of monetite in the matrices of brushite cements has previously been shown to cause a reduction in the strength exhibited by the set cement.22 This was explained by the formation of a larger volume of porosity due to the shrinkage of the cement matrix.22 Such an increase in relative porosity with temperature was shown here for both the β-TCP–orthophosphoric acid solution and β-TCP–pyrophosphoric acid solution cements (Fig. 6). The increase in relative porosity, however, was only shown in this study to have a detrimental effect on the β-TCP–pyrophosphoric acid solution cement. It is possible that, since the strength of a ceramic material is related to relative porosity by an inverse exponential relationship,33 the relative porosity of the β-TCP–orthophosphoric acid solution cement stored at a temperature of 24 ± 1 °C (44 ± 1%) was such that a further increase in porosity gave only a negligible reduction in compressive strength. A particularly interesting finding was that the cement formed from the mixture of β-TCP and pyrophosphoric acid solution exhibited a compressive strength when stored at 37 ± 1 °C significantly (p < 0.05) higher than when stored at any other temperature investigated. This increase in compressive strength could not be attributed to a reduction the relative porosity of the cement matrix (Fig. 6), but was as a result of an increase in the degree of conversion of the β-TCP to brushite (Fig. 2). The disparity between the degree of conversion of the cement when monitored using real-time XRD (Table 1) and following storage for testing in compression (Fig. 2) may have been as a result of a number of factors. These include sample geometry, differences in evaporation rate from the cements or small differences in composition between the surface and the bulk of the cement and this warrants further study. At all temperatures the cement formed from β-TCP and pyrophosphoric acid was considerably more dense than that formed from β-TCP and orthophosphoric acid (45% compared with 50% at a temperature of 37 °C). The higher compressive strength exhibited by the β-TCP–pyrophosphoric acid cement may be attributed to its higher density when compared with the β-TCP–orthophosphoric acid cement. The comparatively high density of the β-TCP–pyrophosphoric acid cement may be as a consequence of the change that was observed in the crystals precipitated in the cement matrices. The presence of pyrophosphates reduced the size of the brushite crystals and this allowed them to pack closely together (Fig. 7b), thus forming a cement microstructure of high density when compared with the large brushite crystals formed in the matrix of the β-TCP–orthophosphoric acid cement (Fig. 7a). Such changes in crystal structure have been observed for calcium carbonate crystals following precipitation from a solution containing pyrophosphate ions34 and may be attributed to the binding of pyrophosphate ions to the brushite crystals surfaces upon precipitation.
Conclusion
The setting reaction and mechanical properties of a new β-TCP–pyrophosphoric acid solution cement have been compared with those of a similar cement produced from the mixture of β-TCP and orthophosphoric acid solution. The presence of the pyrophosphate ion in the β-TCP–pyrophosphoric acid solution cement resulted in a considerable increase in the length of time required for the formation of the cement matrix when compared with the cement containing no orthophosphate ions. The inhibitory mechanism was shown to arise not only from the well-documented ability of pyrophosphate ions to inhibit calcium orthophosphate crystallization, but also because of a reduction in the rate at which the β-TCP was dissolved. At temperatures of ≥55 °C, the β-TCP–pyrophosphoric acid solution cement set to form monetite via a one-step process, rather than the dehydration of brushite as previously thought.Acknowledgements
We would like to acknowledge the EPSRC for the provision of a studentship (L. M. Grover) and Smith and Nephew Research Centre for a CASE award.References
- C. D. Friedman, P. D. Costantino, C. H. Snyderman, L. C. Chow and S. Takagi, Arch. Facial Plast. Surg., 2000, 58, 124–129 Search PubMed.
- P. Lobenhoffer, T. Gerich, F. Witte and H. Tscherne, J. Orthop. Trauma, 2002, 16, 143–149 CrossRef CAS.
- J. Sanchez-Sotelo, L. Munuera and R. Madero, J. Bone Jt. Surg. Br. Vol., 2000, 82B, 856–863 Search PubMed.
- W. E. Brown and L. C. Chow, in Cements Research Progress, ed. P.W. Brown, American Ceramic Society, Ohio, 1986, pp. 352–379 Search PubMed.
- E. Fernandez, M. G. Boltong, M. P. Ginebra, O. Bermudez, F. C. M. Driessens and J. A. Planell, Clin. Mater., 1994, 16, 99–103 Search PubMed.
- A. Tofighi, S. Mounic, P. Chakravarthy, C. Rey and D. Lee, Key Eng. Mater., 2000, 192–1, 769–772.
- B. R. Constantz, I. C. Ison, M. T. Fulmer, R. D. Poser, S. T. Smith, M. Van Wagoner, J. Ross, S. A. Goldstein, J. B. Jupiter and D. I. Rosenthal, Science, 1995, 267, 1796–1799 CrossRef.
- E. J. Blom, J. Klein-Nulend, J. G. C. Wolke, K. Kurashina, M. A. J. van Waas and E. H. Burger, Biomaterials, 2002, 23, 1261–1268 CrossRef CAS.
- M. P. Ginebra, A. Rilliard, E. Fernandez, C. Elvira, J. San Roman and J. A. Planell, J. Biomed. Mater. Res., 2001, 57, 113–118 CrossRef CAS.
- J. E. Barralet, M. Hofmann, L. M. Grover and U. Gbureck, Adv. Mater., 2003, 15, 2091–2094 CrossRef CAS.
- E. M. Ooms, J. G. C. Wolke, M. T. van de Heuvel, B. Jenschke and J. A. Jansen, Biomaterials, 2003, 24, 989–1000 CrossRef CAS.
- A. A. Mirtchi, J. Lemaitre and N. Terao, Biomaterials, 1989, 10, 475–480 CrossRef CAS.
- J. E. Barralet, K. J. Lilley, L. M. Grover, D. F. Farrar, C. Ansell and U. Gbureck, J. Mater. Sci.: Mater. Med., 2004, 15, 407–411 CrossRef CAS.
- K. Ohura, M. Bohner, P. Hardouin, J. Lemaitre, G. Pasquier and B. Flautre, J. Biomed. Mater. Res., 1996, 30, 193–200 CrossRef CAS.
- P. Fraysinnet, L. Gineste, P. Conte, J. Fages and N. Rouquet, Biomaterials, 1998, 19, 971–977 CrossRef.
- E. Charriere, S. Terrazzoni, C. Pittet, P. Mordasini, M. Dutoit, J. Lemaitre and P. Zysset, Biomaterials, 2001, 22, 2937–2945 CrossRef CAS.
- M. Bohner, J. Lemaitre and T. A. Ring, J. Am. Ceram. Soc., 1996, 79, 1427–1434 CrossRef CAS.
- J. L. Meyer, Arch. Biochem. Biophys., 1984, 231, 1–8 CrossRef CAS.
- L. M. Grover, U. Gbureck, A. J. Wright and J. E. Barralet, J. Am. Ceram. Soc., 2005 DOI:10.1111/j.1551-2916.2005.00558x.
- F. C. M. Driessens, M. G. Boltong, E. A. P. De Maeyer, R. M. H. Verbeek and R. Wenz, J. Mater. Sci.: Mater. Med., 2000, 11, 453–457 CrossRef CAS.
- M. Bohner, H. P. Merkle and J. Lemaitre, J. Mater. Sci.: Mater. Med., 2000, 11, 155–162 CrossRef CAS.
- M. Bohner, J. Lemaitre and T. A. Ring, in Third Euro Ceramics, ed. J. Duran and J.A. Fernandez, Faenza Editrice Iberica, Castellon de la Plana, 1995, pp. 95–100 Search PubMed.
- K. J. Laidler, in Chemical Kinetics, Harper Collins, New York, 3rd edn., 1987, ch. 1, pp. 1–17 Search PubMed.
- M. J. Pilling and P. W. Seakins, in Reaction Kinetics, Oxford Science Publications, New York, 1995, ch. 1, pp.3–26 Search PubMed.
- R. G. G. Russell, S. Bisaz, A. Donath, D. B. Morgan and H. Fleisch, J. Clin. Invest., 1971, 50, 961–969 CrossRef CAS.
- R. L. Ryall, R. M. Harnett and V. R. Marshall, Clin. Chim. Acta, 1981, 112, 349–356 CrossRef CAS.
- F. Grases, M. Ramis and A. Costa-Bauza, Urol. Res., 2000, 28, 136–141 CrossRef CAS.
- P. K. Cheng and K. P. H. Pritzker, J. Rheumatol., 1983, 10, 769–777 Search PubMed.
- H. Fleisch, J. Maerki and R. G. G. Russell, Proc. Soc. Exp. Biol. Med., 1966, 122, 317–320 Search PubMed.
- M. Bohner, P. van Landuyt, H. P. Merkle and J. Lemaitre, J. Mater. Sci.: Mater. Med., 1997, 8, 675–681 CrossRef CAS.
- U. Gbureck, S. Dembski, R. Thull and J. E. Barralet, Biomaterials, 2005, 26, 3691–3697 CrossRef CAS.
- M. T. Fulmer and P. W. Brown, J. Mater. Res., 1993, 8, 1687–1696 CrossRef CAS.
- E. Ryshkewitch, J. Am. Ceram. Soc., 1953, 36, 65–68.
- J. R. Van Wazer, in Phosphorous and its Compounds, Vol I: Chemistry, Interscience Publishers, London, 1958 Search PubMed.
| This journal is © The Royal Society of Chemistry 2005 |
