The structure of a bioactive calcia–silica sol–gel glass

Abstract

We have used neutron diffraction with isotopic substitution to gain new insights into the nature of the atomic scale calcium environment in bioactive sol–gel glasses, and also used high energy X-ray total diffraction to probe the nature of the processes initiated when bioactive glass is immersed in vitro in simulated body fluid (SBF). Recent work has highlighted the potential of sol–gel derived calcium silicate glasses for the regeneration or replacement of damaged bone tissue. The mechanism of bioactivity and the requirements for optimisation of the properties of these materials are as yet only partially understood but have been strongly linked to calcium dissolution from the glass matrix. The data obtained point to a complex calcium environment in which calcium is loosely bound within the glass network and may therefore be regarded as facile. Complex multi-stage dissolution and mineral growth phases were observed as a function of reaction time between 1 min and 30 days, leading eventually to the formation of a disordered hydroxyapatite (HA) layer on the glass surface, which is similar to the polycrystalline bone mineral hydroxyapatite. This methodology provides insight into the structure of key sites in these materials and key stages involved in their reactions, and thereby more generally into the behaviour of bone-regenerative materials that may facilitate improvements in tissue engineering applications.

---

Introduction

Average life expectancy in the Western world has increased significantly; to allow people to remain active and to contribute to society for longer, the need for new materials to replace and repair worn out and damaged tissues becomes ever more important.^1–4 Conventionally, melt-quenched silicate glasses containing calcium and phosphorus, and often alkali metals, have been much studied for their applications to promote bone regeneration and to fuse to living bone, creating strong implants with less danger of interfacial instability than previous materials. More recent work has focused on the use of the relatively low temperature sol–gel route for generating bioactive glasses, by which fewer components are required and a wider spectrum of compositions and glass porosities may be achieved. Samples of the general formula (CaO)_x(SiO₂)_1−x have been shown to possess significant potential as bioactive bone-regenerative materials since they exhibit Class A bioactivity.^3–7 The exact mechanism by which these materials promote bone growth and the requirements for optimisation of their properties are still as yet only partially understood but have been strongly linked to evidence that gene activation necessary for tissue regeneration is linked to the release of soluble silica and calcium ions from the bioactive glass.^6,8 A great deal of interest in the structure of these materials has therefore been engendered, particularly in the relationship between structure and bioactivity, and especially the nature and the role of the Ca sites within the glass network.

The local calcium environment in crystalline calcium silicate minerals and apatites is extremely diverse; in most minerals there are several crystallographically distinct Ca environments. This diversity, and thus the complexity, of environments is associated with a wide range of possible calcium–oxygen coordination numbers. Amorphous materials are intrinsically even more structurally complex in the sense that the long-ranged order of the crystalline form is lost. Analysis of the short-range environment in calcium silicate glasses has been attempted using X-ray absorption fine structure and near edge structure (EXAFS and XANES) and X-ray powder diffraction,^9–11 however the complexity of the calcium environment limits the useful information available from these techniques. For instance, conventional diffraction measurements show the Ca–O correlations as a broad feature centred around 2.35 Å, but this feature is overlapped by the strong O–O correlation making a quantitative measure of Ca environment impossible based solely on such data.

Neutron diffraction with isotopic substitution (NDIS)

This technique offers the potential for the nature of the calcium environment to be probed in great detail, as studies of melt–quench derived silicate glasses have shown.^12–14 In principle, it is possible with care to extract information on both short and medium-range order in such glassy materials using samples prepared with stable isotopes. However, there has hitherto been no such work published on the more subtle structures associated with the novel modified amorphous networks generated by the sol–gel method.

High energy X-ray diffraction (XRD)

Although our work is underpinned by a broad-based characterisation approach, combining complementary advanced physical probe techniques including neutron diffraction, X-ray absorption spectroscopy and multinuclear (²⁹Si, ¹⁷O, ⁴³Ca) MAS NMR,¹⁵ the results reported herein are derived from X-ray diffraction (XRD) using the relatively short wavelengths and high fluxes available only from a synchrotron source. Electron diffraction has provided some evidence for there being a precursor to the deposition of hydroxyapatite on such bioactive glasses,¹⁶ but both electron diffraction and conventional laboratory-based XRD are limited by the dynamic range of the data (i.e. the Q-range, where Q = 4πsinθ/λ, with 2θ being the scattering angle and λ the wavelength) in that hydroxyapatite can be mis-identified as octacalcium phosphate given their similar peak positions in the Q-range accessible. Previous work has not been able to offer a definitive statement regarding whether the structure is actually hydroxyapatite or a related calcium phosphate. Further, these studies have focused on a conventional search for identifiable Bragg diffraction peaks only: i.e. the amorphous component, which is often large, tends to be ignored. The overall nature of the structure and the precise definition of any intermediate stages in the growth of hydroxyapatite remain important open questions.

Experimental

Sample preparation for NDIS

The isotopically enriched sample was synthesised from ⁴⁴CaCO₃ (96 atom% enriched, Chemgas): this was converted to ⁴⁴Ca(NO₃)₂ by titration with 2 M nitric acid, the resulting hygroscopic solid was dried at 130 °C until no further weight loss was observed. Calcium nitrate containing a natural mixture of Ca isotopes is available commercially (99% pure Ca(NO₃)₂·4H₂O, Fisher Chemicals). The two sol–gel samples were prepared following previously published procedures.¹⁷ Crucially, both samples were shown to be structurally equivalent using X-ray diffraction (Station 9.1, Synchrotron Radiation Source, UK); given that X-rays scatter from the electrons in a material and not the nucleus, the diffraction pattern is unaffected by the particular isotopic mixture present. Further characterisation was performed by X-ray fluorescence using a Bruker S4 spectrometer to provide the CaO : SiO₂ ratio, and a measurement of the residual C, H and N concentrations was performed using a Carlo Verba 1106 elemental analyser. Sample densities were determined by helium pycnometry using a Quantachrome multipycnometer.

Sample preparation for XRD

Samples of composition (CaO)_0.3(SiO₂)_0.7 were synthesised according to the method described in detail elsewhere.¹⁷ Specimens were immersed in SBF, prepared using existing literature methods,⁵ and incubated at 36.5 °C according to published procedures.¹⁸ Incubation periods were varied from 1 min to 30 days. After immersion, samples were washed with water and then acetone, and dried at 100 °C. Sample characterization was again performed, both before and after SBF immersion. After they had been reacted with SBF, selected (CaO)_0.3(SiO₂)_0.7 samples were annealed in a Lenton 12/65/300 tube furnace at 650 °C in air for 12 h in order better to reveal the nature of mineral deposits.

Neutron diffraction with isotopic substitution

The GEM diffractometer allows data to be collected over an exceptionally wide dynamic range, with Q_max ≈ 60 Å⁻¹. Given that the resolution in real space may be expressed as Δr ∼ 2π/Q_max, this ensures the very best chance of being able to differentiate between distinct but close bond lengths. Finely powdered samples were held in 8 mm diameter cylindrical vanadium containers. The ATLAS suite of programs was used for data reduction and correction, which includes the subtraction of container and background scattering and the effects of absorption, multiple scattering and inelastic scattering events; the spectra are normalised to an absolute scale using the scattering profile from a cylindrical sample of vanadium.¹⁹ Vanadium is used as the preferred material for the sample containers and as the normalising calibrant because its cross section for neutron scattering is almost entirely incoherent.

The Q-space simulation of the structure factor is generated using the following equation (eqn. 1):

p(Q)_ij = (N_ijω_ij/C_j)(sinQR_ij/QR_ij)exp(−Q²σ²/2) (1)

where p(Q)_ij is the pair function in reciprocal space (i.e. derived from the real-space model by Fourier transformation); N_ij, R_ij and σ_ij are the coordination number, atomic separation and disorder parameter respectively of atom i with respect to atom j; c_j is the concentration of atom j, and ω_ij is a weighting factor calculated from the relevant concentration and neutron scattering length data.

X-Ray diffraction

X-Ray diffraction data were collected on station 9.1 at the SRS Daresbury Laboratory, UK, using a two circle diffractometer. Data were collected in θ/2θ scans from 2θ = 1.6 to 125° in steps of 0.2° at ambient temperature. The wavelength was calibrated using the K-edge of a silver foil and thereby set to λ = 0.4858 Å. This wavelength was low enough to provide data to a value of wavevector transfer (Q ∼ 22 Å⁻¹) that is higher than would be achievable using a conventional laboratory-based source. Finely powdered samples were packed into the hole in the centre of a circular plate, of 1 mm depth, and covered with thin polyimide windows. Data for the sub-set of SBF-treated samples that were subsequently annealed was collected on a Bruker D8 powder diffractometer. In this case, the samples were run as powders in a thin layer on a silicon wafer over a range 2θ = 10 to 70° at 0.2° steps, collecting for 1 s per point at ambient temperature.

The analysis of the data to provide an interference function, i(Q), follows the method outlined by Warren²⁰ and implemented by Pickup et al.²¹ The data were normalised to the measured incident beam intensity, corrected for X-ray beam polarisation, and the small contribution of the empty sample cell was subtracted. Further corrections were made to account for absorption of the incident beam by the sample and for Compton (inelastic) scattering—noting that this could only be carried out approximately in the case of those samples reacted with SBF, which were necessarily inhomogeneous as a result. Real-space pairwise atomic correlations may be generated by Fourier transformation of the interference function using the following generic relationship (eqn. 2):

D(r) = 2/π ∫Qi(Q) sinQr dr (2)

It is important to note that, due to the inhomogeneous nature of the reacted samples and the fact that the correlation function represents an average over all pairwise terms, weighted by concentration and element-dependent X-ray form factors, the D(r) may only be analysed quantitatively in the case of an unreacted sample; relative trends are however more easily derived.

Results and discussion

Neutron diffraction with isotopic substitution

Two samples of (CaO)_0.3(SiO₂)_0.7 were prepared,¹⁷ one containing natural Ca and the other ⁴⁴Ca (having cross sections for coherent neutron scattering of σ_coh = 278 fm² and σ_coh = 25 fm² respectively). The NDIS experiment relies upon the samples being absolutely identical in composition and structure, i.e. with the only difference between the samples being the isotopes of Ca present. Thus, both sample preparation and subsequent characterisation must be carried out with rigorous care to ensure that this condition has been met.

The two neutron diffraction patterns were collected on the GEM diffractometer at the ISIS spallation neutron source at the Rutherford Appleton Laboratory, UK. The resultant interference function, the structure factor i(Q), can reveal real-space structural information by Fourier transformation to give the corresponding total pair correlation function (eqn. 3):¹⁸

T(r) = T⁰(r) + 2/π∫Q_i(Q)M(Q)sin(Qr)dQ (3)

where T⁰(r) = 4πrρ⁰(Σ_ic_ib_i)² is the average density contribution (ρ⁰ is the atomic number density, c_i is the fraction of element i and b_i = (σ_coh/4π)^1/2 is its associated coherent scattering length for neutron scattering) and M(Q) is a Lorch modification function used to take into account the finite maximum experimentally attainable value of Q. Structural information is obtained from the neutron diffraction data by an iterative fitting of the i(Q) using trial values for the real-space pair correlations.²²

Hence, if two experiments are performed in which the scattering length of element A is varied by isotopic substitution, the difference between the experimental correlation functions is of the form (eqn. 4):²³

ΔT(r) = T(r) − T′(r) = c²_A(b²_A − b²_A′)t′_AA′ + 2Σc_Ac_jb_j(b_A − b_A′)t′_Aj(r) (4)

where t′_AX(r) represents the partial pair correlation function for elements A and X. Thus, the structural environment of element A may be isolated using this method: in other words, in the present case, the result of taking the difference is that one is left with only the correlations involving Ca, all the other pairwise terms (e.g. Si–O) having been cancelled out. This powerful method therefore facilitates the quantitative study of the local atomic environment around the minority calcium species and thereby offers a unique insight into the structural role of the key element in these bioactive materials.

The i(Q) of the ^natCa and ⁴⁴Ca-enriched (CaO)_0.3(SiO₂)_0.7 samples are shown in Fig. 1, together with the corresponding weighted difference between the two. The structural parameters derived from fitting to the difference function are provided in Table 1 with additional information on the ‘host’ silica network derived from the original diffraction data and from complementary X-ray diffraction. The Fourier transform of the difference function, and the associated numerical fit using the parameters presented in Table 1, are shown in Fig. 2; this provides information exclusively on the Ca–X pair correlations present in the material. The slight ripple through the data is a residual artefact of the data analysis process.

Fig. 1 i(Q) data for ^natCa (top) and ⁴⁴Ca (middle) (CaO)_0.3(SiO₂)_0.7 and difference between i(Q) functions from the ⁴⁴Ca and ^natCa samples. ^natCa and difference have been offset by +0.2 and −0.2 respectively for clarity.

Fig. 2 Difference correlation function, t_Ca–X(r), obtained by Fourier transformation of the difference between i(Q) functions from the ⁴⁴Ca and ^natCa samples (solid line) and simulation of the t_Ca–X(r) function (dotted line).

Table 1 Fitting parameters obtained from simulation of neutron diffraction data

Correlation	R/Å (±0.01)	N (±0.25)	S/Å (±0.01)
D–D	1.28	1.02	0.05
Si–O	1.61	3.8	0.05
Si–D	2.20	0.7	0.15
Ca–O	2.32	2.3	0.08
Ca–O	2.51	1.65	0.07
O–O	2.64	4.64	0.09
Ca–O	2.75	1.05	0.08
Ca–D	2.95	0.6	0.08

---

The parameters obtained for Si–O and O–O are as one would expect for porous sol–gel derived silica²¹ and this lends confidence to the fitting of the other correlations observed. In a fully condensed silica network the O–O coordination number would be 6, in these materials it is reduced to ∼4.6 due to the presence of non-bridging oxygen atoms (NBO) which are abundant in high surface area materials. It is important also to note that the parameters obtained from the fit to the difference correlation function, t_Ca–X(r), may be carried over to the fitting of the original datasets unchanged: we take this as further evidence that the fits generated to t_Ca–X(r) are robust.

The fit parameters obtained uniquely from the NDIS results show clearly that the Ca–O environment actually consists of distinct, but partially overlapping, correlation shells centred at 2.3 Å, 2.5 Å and 2.75 Å. This is the first time a Ca–O environment of this complexity has been discerned in the context of contemporary bioactive glass materials: it is a key observation given the central role that Ca dissolution plays in the material's ability to promote bone growth.

It is helpful at this point to draw comparisons with crystalline calcium silicate materials where Ca–O distances ranging from 2.3 to 2.8 Å have been observed, indicating that the values obtained here are certainly physically reasonable per se. In theory it should be possible to extract information from the NDIS data relating to higher correlations such as those from Ca–Si and Ca–Ca. However in practice, even using this method, the residual overlaps between the large range of possible correlations above ∼3 Å renders this unreliable as a quantitative exercise. What the NDIS results do offer is the uniquely detailed quantitative data required for computer simulation studies of bioactive glasses, and in particular towards the full understanding of the Ca dissolution and subsequent mineral deposition processes.

X-Ray diffraction

The nature of the variation in overall composition of samples immersed in SBF is shown in Fig. 3, measured using X-ray fluorescence, via CaO and P₂O₅ relative molar percentages: approximately 75% of the initial calcium content is lost from the sample within 30 min of reaction time, after which a gradual increase in Ca content occurs. The phosphorus content mirrors the calcium level, as might be anticipated given the expectation of hydroxyapatite formation, and again one observes the largest change in the phosphorus content within the first 30 min of the glass's exposure to SBF; the silicon content decreases gradually with the dissolution of the glass. A key observation here is that the Ca content undergoes a series of oscillations during the initial reaction period, before entering a long period of more monotonic increase thereafter. Analogous fluctuations in the calcium concentration within the SBF as a function of time have previously been observed for similar glasses immersed in SBF,^24–25 along with corresponding fluctuations in the pH of the solution, but the fluctuations have not been explained. Although not on identical samples, there are published results derived from the measurement of the zeta potential (which relates to the surface charge present on the solid bioactive material) that also reveal fluctuations over similar time periods.²⁵ One is drawn inexorably to the conclusion that the fluctuations must be due to continual release of calcium from the glass and the growth of calcium phosphate on the glass surface. The dissolution of the bioactive glass, and the growth in its place of hydroxyapatite, cannot therefore be a monotonic process—and thus understanding the precise details of this process at the atomic scale will be helpful in optimising these materials.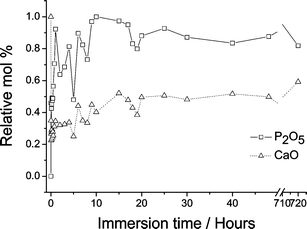

Fig. 3 Relative mol% of P₂O₅ and CaO calculated from XRF measurements of (CaO)_0.3(SiO₂)_0.7 before and after exposure to SBF. (Corroborative evidence regarding calcium content measured using X-ray absorbance has been previously reported.¹⁰)

Conventional powder diffraction experiments typically focus on the observed Bragg peaks (in Q-space), and the analogous studies of amorphous materials focus on the diffuse pair correlation function (in real-, r-, space). Here, a total diffraction strategy is adopted²⁶ in which Bragg analysis in Q-space and Fourier analysis of the r-space pair distribution, to provide both crystallographic and local order information, are combined. The experimentally determined interference functions, i(Q), for the unreacted and reacted samples are shown in Fig. 4. It is immediately apparent that, after only 30 min, the shape of the i(Q) has altered significantly, most noticeably on the high-Q side of the first principal diffraction peak at ∼2.1 Å⁻¹; our earlier published work on the structure of these glasses as a function of calcium content enables it to be concluded that this change is associated with the initial rapid dissolution of Ca.⁵ After 1 h, whilst the underlying amorphous pattern remains, there is clear evidence for the formation of Bragg diffraction peaks: i.e. of the growth of crystallites within the sample. The peaks observed at 5 happear very strong (although the intensity may in part be the result of an inhomogeneity of crystallite concentration within the powder sample) and may be attributed to the presence of calcium phosphate. In particular, the two peaks at 2.8 and 9.4 Å⁻¹, seen only in the 1 and the 5 h spectra, are associated with the (412) and (200) reflections from octacalcium phosphate respectively (and not with hydroxyapatite).¹⁶ However, by 10 h the polycrystalline calcium phosphate appears to have been largely replaced by a more dominant disordered phase which, in its turn becomes increasingly prominent and well-defined thereafter. By 25 h, and even more clearly by 72 h, the i(Q) has the appearance of a poorly crystalline hydroxyapatite overlaying a (Ca-depleted) silicate glass interference pattern. Given that hydroxyapatite recrystallises at ∼600 °C, the 7 day sample was annealed in order to help verify its presence: the diffraction features seen in Fig. 4 readily sharpened to reveal the presence of polycrystalline hydroxyapatite.

Fig. 4 i(Q) data for SBF treated samples: from top to bottom, 7 days, 72 h, 25 h, 10 h, 5 h, 1 h, 30 min, unreacted.

The corresponding real-space pair correlation function, D(r), allows us to consider the amorphous (short-range) component in more detail. Fig. 5 shows the D(r) curves for the untreated and the reacted samples. In order to bring out the important qualitative changes taking place, we have chosen to scale the various D(r) such that the area of the Si–O first neighbour correlation, at 1.61 Å, is made the same for each. It is possible to discern four distinct changes that occurred with increasing exposure to SBF solution. The correlation at 2.02 Å, labelled as peak (a) in Fig. 5, was found as a major feature only in the SBF-reacted (CaO)_0.3(SiO₂)_0.7 sol–gel glasses and corresponds to the second neighbour O–H bond lengths found in hydrated calcium phosphates.²⁷ The correlation labelled peak (b) at 2.3 Å appears only in the unreacted sample: after exposure to SBF it disappears. Peak (c), at 2.54 Å, begins to change position on exposure to SBF, reaching a maximum correlation distance of 2.63 Å after 5 h, labelled peak (d). Similarly, peaks (e) and (f), at 3.6 and 3.75 Å respectively, also show a shift in their position; the peak at shorter r being replaced on SBF treatment by a feature at a longer correlation distance. Peak (g) at 4.08 Å narrows as the SBF reaction progresses. From a comparison with distances observed in calcium silicate minerals,^28–30 peaks (b) and (c) may be assigned as Ca–O, and peak (e) with the corresponding higher order Ca–O, Ca–Ca and Ca–Si correlations. Peak (d) is within the range reported in the literature for the Ca–O bond in both calcium phosphates and hydroxyapatite³¹ whereas (f) is most probably due to a combination of Ca–O–Ca, inter-tetrahedral P–O and intra-tetrahedral P–O–P peaks in hydroxyapatite. The decrease in intensity of peaks (b), (c) and (e) in the D(r), and the associated increase in the intensity of peaks (d), (f) and (g), mirror in real-space the changes already identified in the interference patterns, i(Q): that is to say the removal of Ca from the glass network and the growth of a calcium phosphate layer followed by an increasingly ordered form of hydroxyapatite. Given that the pair correlation function, D(r), is an average over the volume of the sample in the X-ray beam—in contrast to the Bragg features observed in the i(Q), which may derive from small crystallites at the glass surface—we surmise that the real-space data reveal a change in the underlying glass network structure, which may be correlated with the measured changes in the overall sample composition discussed above and shown in Fig. 3. The XRF analysis also revealed a decrease in phosphorus content at ∼5 h, to a value less than that observed at 30 min, which is reflected in the relative intensities of the inter-tetrahedral P–O and intra-tetrahedral P–O–P correlations observed at ∼3.7 Å. This provides additional supportive evidence for a dynamic reaction mechanism driven by the interplay between the pH of the SBF and the surface charge of the glass.

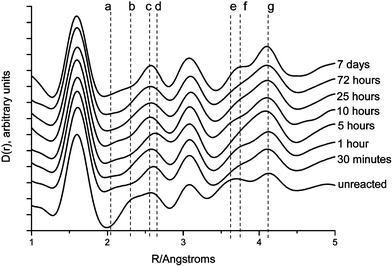Fig. 5 D(r) data for SBF treated samples: from top to bottom, 7 days, 72 h, 25 h, 10 h, 5 h, 1 h, 30 min, unreacted. In all cases the correlation functions have been normalised to the Si–O first-neighbour peak as it appears in the unreacted sample.

Conclusions

In summary, by using neutron diffraction with isotopic substitution we have for the first time directly observed three Ca–O distances in a bioactive (CaO)_x(SiO₂)_1−x sol–gel glass and quantified their respective contributions to the bonding of Ca within the silica network. The data obtained point to a complex calcium environment in which the calcium is loosely bound at the surface of the network. This data provides a direct atomic-scale explanation for the empirical observation that calcium loss from these materials is facile and can be achieved by simple ion exchange with body fluid.

We have also demonstrated the nature of the principal stages to the generation of HA on the surface of a bioactive glass. Further, a link has been demonstrated between these distinct structural stages and the macroscopically determined elemental analysis of the glass as a function of time; that is to say, the atomic-scale structure to the surface charge- and pH-driven dissolution/growth processes have been related. Following immersion of a sol–gel derived bioactive glass in body fluid there is rapid initial dissolution of Ca, there is a growth of an amorphous, or very poorly crystalline, calcium phosphate layer within 1 h of immersion, which becomes increasingly evident and/or ordered by 5 h. However, by 10 h this polycrystalline layer is apparently replaced by a predominantly disordered material, now more akin to an amorphous hydroxyapatite; it is this layer that then develops steadily into a more ordered, bone mineral-like, hydroxyapatite.

Although these observations pertain to a particular bioactive material, it is reasonable to suggest that the underlying mechanisms may have a high degree of commonality with those associated with other bioactive, tissue-regenerative, solids—and certainly that the experimental methodology for their investigation requires the generic breadth employed here. It is only by such a detailed knowledge of the sites of importance in complex materials that systematic improvements in their application to tissue engineering applications can be achieved.

Acknowledgements

We are grateful to V. FitzGerald for her help in the collection of the neutron data. We acknowledge the support of the EPSRC (awards GR/R57492 and GR/R59298) and of the CCLRC (SRS and ISIS facilities, and their instrument scientists), the University of Kent Hyatt–Wolff fund for a studentship (LJS) and also the EPSRC/ESRF for a studentship (KOD).

References

1. L. L. Hench and J. Wilson, Introduction to Bioceramics, World Scientific, Singapore, 1993.
2. L. L. Hench, Biomaterials, 1998, 19, 1419.
3. R. Li, A. E. Clark and L. L. Hench, Chemical Processing of Advanced Materials, Wiley, New York. 1992.
4. M. M. Pereira, A. E. Clark and L. L. Hench, J. Mater. Synth. Proc., 1994, 2, 189.
5. P. Saravanapavan, J. R. Jones, R. S. Pryce and L. L. Hench, J. Biomed. Mater. Res. A., 2003, 66A, 110.
6. P. Saravanapavan, S. Verrier, J. R. Jones, R. Beilby, V. J. Shirtliff, L. L. Hench and J. M. Polak, Bio-Med. Mater. Eng., 2004, 14(4), 467.
7. M. Cerruti, G. Magnacca, V. Bolis and C. Morterra, J. Mater. Chem., 2003, 13, 1279.
8. I. D. Xynos, A. J. Edgar, L. D. K. Buttery, L. L. Hench and J. M. Polak, J. Biomed. Mater. Res., 2000, 155(2), 151.
9. F. E. Sowrey, L. J. Skipper, D. M. Pickup, K. O. Drake, Z. Lin, M. E. Smith and R. J. Newport, Phys. Chem. Chem. Phys., 2004, 6, 188.
10. L. J. Skipper, F. E. Sowrey, D. M. Pickup, V. Fitzgerald, R. Rashid, K. O. Drake, Z. Lin, P. Saravanapavan, L. L. Hench, M. E. Smith and R. J. Newport, J. Biomed. Mater. Res., 2004, 70A, 354.
11. L. J. Skipper, F. E. Sowrey, D. M. Pickup, R. J. Newport, K. O. Drake, Z. Lin, M. E. Smith, P. Saravanapavan and L. L. Hench, Mater. Sci. Forum., 2004, 480–481, 21.
12. M. C. Eckersley, P. H. Gaskell, A. C. Barnes and P. Chieux, Nature., 1988, 335, 525527.
13. P. H. Gaskell, M. C. Eckersley, A. C. Barnes and P. Chieux, Nature., 1991, 350, 675677.
14. L. Cormier, G. Calas and P. H. Gaskell, Chem. Geo.l., 2001, 174, 349.
15. Z. Lin, M. E. Smith, F. E. Sowrey and R. J. Newport, Phys. Rev. B., 2004, 69, 224107.
16. Y. Leng, X. Lu and J. Chen, Key Eng. Mater., 2004, 254–256, 339.
17. P. Saravanapavan and L. L. Hench, J. Non-Cryst. Solids, 2003, 318, 1.
18. P. Saravanapavan and L. L. Hench, J. Biomed. Mater. Res., 2001, 54, 608.
19. A. C. Hannon, W. S. Howells and A. K. Soper, in Proceedings of the Second Workshop on Neutron Scattering Data Analysis, ed. M. W. Johnson, IOP Conference Series, Institute of Physics, Bristol, 1990, vol. 107, p. 193.
20. B. E. Warren, X-Ray Diffraction, Dover Publications Inc., New York, 1990.
21. D. M. Pickup, G. Mountjoy, M. A. Roberts, G. W. Wallidge, R. J. Newport and M. E. Smith, J. Phys.: Condens. Matter, 2000, 12, 3521.
22. P. H. Gaskell, Materials Science and Technology, VCH, Weinhaim, 1991, vol. 9.
23. C. A. Yarker, P. A. V. Johnson, A. C. Wright, J. Wong, R. B. Greegor, F. W. Lytle and R. N. Sinclair, J. Non-Cryst. Solids., 1986, 79, 117.
24. Z. Gou and J. Chang, J. Eur. Ceram. Soc., 2004, 24, 93.
25. T. Kokubo, H.-M. Kim and M. Kawashita, Biomaterials, 2003, 24, 2161.
26. S. J. Hibble, A. C. Hannon and I. D. Fawcett, J. Phys: Condens. Matter, 1999, 11, 9203.
27. N. S. Mandel, Acta Crystallogr., Sect. B: Struct. Sci., 1973, B31, 1730.
28. K. S. Mamedov and N. V. Belov, Dokl. Akad. Nauk, 1956, 107, 465.
29. T. Ito, R. Sadanaga, Y. Takeuchi and M. Tokonami, Proc. Jpn. Acad., 1969, 45, 913.
30. Y. Ohashi, Phys. Chem. Miner., 1984, 10, 217.
31. R. M. Wilson, J. C. Elliot and S. E. P. Dowker, Am. Mineral., 1999, 84, 1406.

---