Factors determining the effect of Co(II) in the ordered double perovskite structure: Sr₂CoTeO₆

Abstract

Double perovskites are of interest due to their diverse properties that are of potential use in technological applications. In order to determine the effect of Co(II) in the double perovskite structure in the absence of other paramagnetic species, mixed valency or mis-site disorder, we have studied the ordered perovskite Sr₂CoTeO₆ synthesised by the freeze-drying method. The room temperature monoclinic P2₁/n symmetry (a = 5.6437(2) Å, b = 5.6096(2) Å, c = 7.9271(2) Å, β = 90.059(2)°) is maintained down to 4 K with structural transitions to I2/m then Fm3̄m at 373 K (100 °C) and 773 K (500 °C). Below T_N = 18 K, the Type I antiferromagnetic structure is observed with magnetic moments of magnitude 2.25(3) μ_B rotated 58° out of the ab plane. AC magnetic susceptibility and specific heat data show maxima at 19 K, associated with long-range antiferromagnetic order. EPR and diffuse reflectance spectroscopies confirm that Co is in the +2 oxidation state, in highly regular octahedral coordination and is highly ionic. A small magnetic irreversibility, with H_c and M_r of 36 Oe and 0.5 emu mol⁻¹, is observed at low temperature but this is not due to conventional spin glass or cluster glass behaviour. Calculations from specific heat give a magnetic entropy of 4.2 J mol⁻¹ K⁻¹, close to the theoretical value for the S′ = ½ state of the Co²⁺ cation at low temperature. Distortions of the structure, demonstrated to be primarily rotations of highly regular octahedra, change the geometry of the magnetic exchange pathways but are insufficient to explain the variation in ordering temperatures and magnetic structure types observed, with orbital energies within the exchange pathways having a significant influence on the properties of these and similar technologically important materials.

---

Introduction

Complex oxides with the perovskite type structure of general formula AB_0.5B′_0.5O₃ (A being alkaline, alkaline-earth or rare earth cations and B transition metals) have often served as reference materials for the study of several physical properties.¹ Among these oxides, ordered perovskites, A₂BB′O₆, became of technological interest in the early 1950s when the search for ferroelectric and piezoelectric materials, to be used mainly as capacitors, was extended from the common perovskite oxides, ABO₃, to more complex systems such as the ordered perovskites.² These materials continue to receive a large amount of academic interest and have potential applications in catalysis, magnetic media, electrical conductors and gas sensors, with both the content and the structural distortions of the B/B′O₆ octahedra being important factors in determining their physical behaviour.³

From the structural point of view, in an ABO₃ simple cubic perovskite described by the Pm3̄m space group with a primitive cell parameter, a_p, distortions arise from three mechanisms: cation displacements within the BO₆ octahedra and distortions and tiltings of these octahedra. Glazer⁴ classified the resulting structures considering that the most important factors determining the crystal structure of a perovskite oxide were the tilts of the rigid octahedra. Woodward⁵ extended that scheme to the A₂BB′O₆ ordered double perovskites (described by the Fm3̄m space group and a 2a_p cell parameter when ideal cubic). Since Woodward, many authors have published similar and sometimes more complicated schemes, such as a recent scheme of Howard et al.⁶

The magnetic properties, and how the different magnetic behaviours depend on the constituent cations, have become one of the most important topics of research in ordered double perovskites after the discovery by Kobayashi et al., in 1998, of room temperature magnetoresistance in Sr₂FeMoO₆⁷ in which ferrimagnetic, half metallic behaviour is due to the mixed valencies of Fe and Mo. Conversely, Sr₂CoB′O₆, where B′ = Mo, W are in the +6 oxidation state, leaving Co as the only paramagnetic cation, are antiferromagnetic with Néel temperatures ∼30 K.^8,9 Recently Blackstead et al.¹⁰ found high temperature superconductivity by replacing a 15% of Ru cations by Cu in the Sr₂YRuO₆ phase re-opening the interest in high temperature superconductors.

We have chosen to study the Sr₂CoTeO₆ ordered perovskite oxide for several reasons. Firstly, detailed determination of the structural transitions and systematic crystallographic studies of ordered double perovskite type oxides is a relatively new field of study.^11–14 A perovskite which is significantly distorted at room temperature therefore offers the possibility to study structural phase transitions at high temperature. Secondly, the absence of any further paramagnetic ions within the structure, that may interact with those of Co²⁺, can provide a clear view of the magnetic interactions between the cobalt ions. Thirdly, due to the particular characteristics of the cobalt(II) cation as a d⁷ ion which presents an effective spin state change in octahedral symmetry between high and low temperatures and shows an important orbital contribution to the magnetic moment, materials such as Sr₂CoTeO₆ offer a wide variety of phenomena that can be explored in detail both from magnetic and spectroscopic points of view.

Experimental

Polycrystalline Sr₂CoTeO₆ and Sr₂(Mg_0.99Co_0.01)TeO₆ were synthesised by the freeze-drying method. Stoichiometric quantities of SrCO₃, Co(C₂H₃O₂)₂, Mg(C₂H₃O₂)₂ and TeO₂ were dissolved in dilute aqueous nitric acid. The solutions were drop-by-drop frozen under liquid nitrogen. The frozen solutions were subsequently freeze-dried and the powders obtained were ground and calcined at 900 °C for 6 hours. The samples were ground, pelleted and calcined four times for 8 hours at 1000 °C. Phase purity was confirmed by X-ray powder diffraction and the expected content of Sr, Co and Te in Sr₂CoTeO₆ by inductively coupled plasma atomic emission spectroscopy (ICP-AES) performed with an ARL Fisons 3410 spectrometer (content in %: observed Sr, 35(1), Co, 11.9(1) and Te, 27(1); calculated Sr 38.3, Co 12.9, Te 27.9).

Neutron powder diffraction data were collected at 4, 30 and 298 K on Instrument D2B at the Institut Laue Langevin (ILL), Grenoble, France. Thermal neutrons of wavelength 1.594 Å were incident on 6 g of polycrystalline Sr₂CoTeO₆, packed in an 8 mm diameter vanadium can. Data were collected in the angular range 5 ≤ 2θ ≤ 162° in steps of 0.05° with an integration time of 50000 monitor counts per step and with each point in the diffraction pattern being recorded by 6 independent detectors for subsequent normalisation and summation, giving an overall collection time of approximately 3 hours for the entire data set.

Temperature dependent neutron powder diffraction data were collected on Instrument D1B at the ILL. Neutrons of wavelength 2.52 Å were incident on 6 g of Sr₂CoTeO₆, contained in an 8 mm diameter vanadium can held in a liquid helium cryostat. Data were collected every 2 K from 2 to 34 K over the angular range 10 ≤ 2θ ≤ 90°. Sequential refinement was carried out in FullProf¹⁵ from the initial structural model refined from D2B data at 4 K and the evolution of lattice parameters and magnetic moments (M_x and M_z) with temperature was refined.

Room temperature X-ray powder diffraction data were collected in the range 17 ≤ 2θ ≤ 105° in steps of 0.02° with an integration time of 17 seconds per step using a Philips X′Pert-MPD X-ray diffractometer with secondary beam graphite monochromated Cu-Kα radiation. The room temperature crystal structure was refined simultaneously from X-ray and high resolution neutron diffraction data by the Rietveld method¹⁶ using the GSAS software package.¹⁷

Temperature resolved X-ray diffraction data were collected using an Anton Paar HTK16 temperature chamber with a platinum stage mounted in the same diffractometer. The sample for high temperature measurement was mixed with acetone and a high temperature resin and applied to the Pt stage. In order to monitor the evolution of several characteristic peaks, data were collected every 10 °C from 30 to 600 °C in the angular ranges 72 ≤ 2θ ≤ 78° and 91 ≤ 2θ ≤ 95°. Higher quality, temperature dependent X-ray diffraction data for subsequent Rietveld refinement were collected in the range 17 ≤ 2θ ≤ 95° in steps of 0.05° with an integration time of 12 seconds per step between 25 and 600 °C every 25 °C.

Spectroscopic measurements were made by both Diffuse Reflectance and Electron Paramagnetic Resonance. The diffuse reflectance spectrum was collected on a Cary 2415 spectrometer and registered at room temperature in the 5000–50000 cm⁻¹ range. X-Band EPR spectra of the 1% Co substituted sample, Sr₂(Mg_0.99Co_0.01)TeO₆, were recorded between 0 and 7 kOe from 300 to 5 K on a Bruker ESP 300 spectrometer. The temperature was controlled by an Oxford Instruments (ITC4) regulator. The magnetic field was measured with a Bruker BNM 200 gaussmeter and the frequency inside the cavity was determined using a Hewlett Packard 5352B microwave frequency counter.

DC magnetic susceptibility measurements were performed using a Quantum Design MPMS-7 SQUID magnetometer whilst heating from 5 to 300 K in an applied field of 1 kOe, after cooling either in the presence (field cooling, FC) or absence (zero field cooling, ZFC) of the applied field.

Magnetisation as a function of applied field (H) was measured using the same MPMS-7 SQUID magnetometer at 5 K after cooling the sample in zero field. During the measurement, the field was swept between 70 and −70 kOe. Magnetisation was also measured as a function of temperature between 5 and 40 K.

AC magnetic susceptibility measurements were made using a standard QD PPMS system with an alternate excitation field (H_ac) of 1 Oe. Data were recorded from 4 to 100 K as a function of both frequency and applied DC magnetic field. Frequencies from 100 to 10000 Hz were measured in the absence of an applied magnetic field and field dependent data were collected at a fixed frequency of 1000 Hz with applied fields from 0 to 40 kOe.

Heat capacity measurements were carried out by a relaxation method using the same PPMS system. The sample was a plate of ≈0.3 mm thickness and 11 mg weight obtained by compressing the polycrystalline powder. Data were collected with zero field and under an applied field of 90 kOe from 1.8 to 300 K. The phonon contribution, modelled by two independent Debye¹⁸ spectra, was subtracted to give the magnetic specific heat, Cp_mag, from which the magnetic entropy S_mag was calculated.

Results

Room temperature crystal structure

The X-ray and neutron diffraction data show a large number of weak reflections which indicate a significant distortion of the cubic perovskite structure. The resolution of the ‘characteristic’ (4 0 4) peak (given with respect to a cell of approximate dimensions √2a_p × √2a_p × 2a_p, where a_p is the primitive cubic perovskite parameter, which corresponds to the unique (444) in the 2a_p × 2a_p × 2a_p cubic Fm3̄m lattice) into (404), (4̄04) and (044) peaks and the observed weak diffraction maxima with Miller indices that violate the I-centring condition on hkl, h + k + l = 2n are consistent with monoclinic P12₁/n1 symmetry.

Peak profiles and background were fitted as previously reported for the isostructural Sr₂MnTeO₆ oxide.¹⁹ The contrast provided between Co and Te when refining X-ray and neutron diffraction data simultaneously (the ratio of scattering factors for X-rays and neutrons, Te : Co, being 3.7 : 1 and 0.7 : 1,²⁰ respectively) allowed the free refinement of Co and Te fractions over the B and B′ sites. No evidence for mis-site disorder or vacancy formation was observed. Three independent oxygen fractions were also allowed to refine but all remained close to unity. In the final model, Co, Te and all oxygen fractions were fixed at unity. The isotropic thermal parameters of all atoms were allowed to refine freely. Final refined parameters and statistics are given in Table 1 and selected bond distances and angles in Table 2. Rietveld fits to the room temperature X-ray and neutron diffraction data are shown in Fig. 1(a) and (b), respectively.

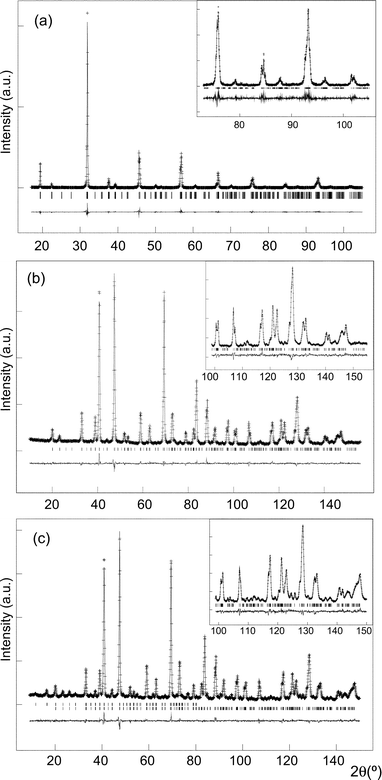Fig. 1 Rietveld fit of Sr₂CoTeO₆ in space group P12₁/n1 showing observed, calculated and difference curves to (a) the room temperature X-ray diffraction data, (b) the room temperature D2B neutron data and (c) the fit to the 4 K D2B neutron data, with the upper and lower reflection markers corresponding to the magnetic and nuclear phases, respectively. In each case, the fit to the high angle data is inset.

Table 1 Refined parameters and R factors for Sr₂CoTeO₆ in space group P12₁/n1 at various temperatures from X-ray (XPD) and D2B neutron (NPD) data

	T/K
	298 (XPD)	298 (NPD)	40	4
a μMx = 1.18(6); μMy= 0; μMz= 1.91(4).
Symmetry	Monoclinic		Monoclinic	Monoclinic
Space group	P21/n		P21/n	P21/n
a/Å	5.6437(2)		5.6324(1)	5.6319(1)
b/Å	5.6096(2)		5.5983(1)	5.5976(1)
c/Å	7.9271(2)		7.9187(2)	7.9197(2)
β/°	90.059(2)		90.052(3)	90.055(3)
V/Å^3	250.96(2)		249.69(1)	249.67(1)
Sr x	0.4999(3)		0.5016(3)	0.5016(3)
Sr y	0.0066(3)		0.0134(3)	0.0135(3)
Sr z	0.2493(3)		0.2507(5)	0.2505(5)
U iso/×100 Å^2	0.81(2)		0.39(2)	0.38(2)
Co x = y = z	0		0	0
U iso/×100 Å^2	0.67(6)		1.0(2)	0.8(2)
Te x = y	0		0	0
Te z	0.5		0.5	0.5
U iso/×100 Å^2	0.44(3)		0.48(6)	0.50(6)
O1 x	0.9499(3)		0.9481(3)	0.9477(3)
O1 y	0.0028(8)		0.0046(4)	0.0051(4)
O1 z	0.7376(4)		0.7379(4)	0.7381(4)
U iso/×100 Å^2	0.66(5)		0.53(5)	0.51(5)
O2 x	0.2751(6)		0.2838(4)	0.2839(4)
O2 y	0.2452(6)		0.2376(5)	0.2377(5)
O2 z	0.9721(6)		0.9724(4)	0.9720(4)
U iso/×100 Å^2	1.1(1)		0.76(6)	0.56(7)
O3 x	0.7536(6)		0.7589(4)	0.7582(4)
O3 y	0.2727(6)		0.2798(5)	0.2805(5)
O3 z	0.0224(6)		0.0263(5)	0.0259(5)
U iso/×100 Å^2	1.3(1)		0.76(6)	0.72(6)
μ eff (Co)^a	—		—	2.25(3)
R wp (%)	15.6	4.0	4.3	4.3
R p (%)	9.2	3.2	3.3	3.4
χ ^2	1.5		1.0	1.0
R calc	6.0	2.4	2.0	1.7
R mag	—		—	4.6

---

Table 2 Selected bond distances and angles of Sr₂CoTeO₆ at various temperatures

	T/K
	298	40	4
a Value calculated considering the following ionic radii (in Å) and coordination numbers, CN: Co^2+CN=6 = 0.745, Te^6+CN=6 = 0.56 and O^2−CN=2 = 1.35.^21
Co–O1/Å (×2)	2.099(4)	2.096(3)	2.095(3)
Co–O2/Å (×2)	2.086(3)	2.091(2)	2.092(2)
Co–O3/Å (×2)	2.075(3)	2.084(3)	2.089(3)
Mean	2.087	2.090	2.092
Calculated^a	2.095
O1–Co–O2	90.6(1)	90.3(1)	90.4(1)
O1–Co–O3	90.6(2)	90.0(1)	90.2(1)
O2–Co–O3	91.2(2)	91.7(1)	91.8(1)
Te–O1/Å (×2)	1.905(4)	1.907(3)	1.909(3)
Te–O2/Å (×2)	1.924(3)	1.920(2)	1.920(2)
Te–O3/Å (×2)	1.925(4)	1.921(3)	1.915(3)
Mean	1.918	1.916	1.915
Calculated^a	1.910
O1–Te–O2	90.5(2)	90.3(1)	90.3(1)
O1–Te–O3	90.8(2)	90.1(1)	90.1(1)
O2–Te–O3	90.5(2)	90.2(2)	90.2(1)
Co–O1–Te	163.7(1)	163.10(9)	163.01(9)
Co–O2–Te	165.6(3)	163.6(2)	163.5(2)
Co–O3–Te	168.1(3)	165.1(2)	165.3(2)

---

The crystal structure is characterised by the tilting of the CoO₆ and TeO₆ octahedra along the three axes of the primitive perovskite (Fig. 2). Rotations around the c axis are in phase (+) and rotations normal to the c axis are anti-phase (−). It is also worth mentioning the negligible distortion of both octahedra with statistical variances in the M–O distances of only 0.004 and 0.002 Å within the CoO₆ and TeO₆ octahedra, respectively, and internal angles very close to 90°, as shown in Table 2.

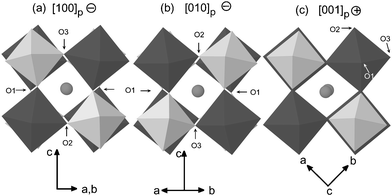Fig. 2 Projections of the room temperature structure of Sr₂CoTeO₆ along the three primitive axes of the cubic perovskite showing in-phase (+) and out-of-phase (−) rotations. Structural transitions at higher temperatures correspond to the disappearance of rotations about one or two of these primitive axes. Dark octahedra represent CoO₆ and light octahedra TeO₆. Spheres are Sr atoms.

Low temperature crystal structure

Rietveld refinement of the low temperature crystal structure from high resolution D2B neutron powder diffraction data recorded at 4 and 40 K, showed that the P12₁/n1 symmetry is maintained down to 4 K. The structural model was as previously deduced at 298 K with all atomic positions and isotropic thermal factors freely refined. No mis-site disorder or vacancy formation was observed at 298 K and so was not refined at low temperature. Refined structural parameters are shown in Table 1 and selected bond distances and angles in Table 2 and the fit to the 4 K data is shown in Fig. 1(c). As expected, the magnitudes of the octahedral rotations increase and the cell volume reduces on lowering the temperature. Mean bond distances of 1.918 and 2.087 Å for Te–O and Co–O are virtually invariable with temperature, yielding a mean through-bond superexchange path length of 8.010 Å. The 4 K neutron data also show the presence of several additional peaks which arise from long range magnetic order in the sample, as explained below.

Temperature dependent X-ray diffraction

Temperature dependent X-ray diffraction data, from 25 to 600 °C measured in the range 17 ≤ 2θ ≤ 95°, were fitted by the Rietveld method using the GSAS program. Atomic positions for all atoms not fixed by symmetry and all isotropic thermal factors were allowed to refine but with all oxygens constrained to have equal thermal factors. A surface roughness absorption correction²² was refined to compensate for a slightly uneven surface arising from application of the sample to the Pt stage. Peak profile and background were modelled using the same functions used previously. As all sites have been shown to be fully occupied by refinement from ambient temperature X-ray and neutron diffraction data, no attempt was made to refine any atomic fractions.

Fig. 3 shows the temperature resolved X-ray data of ‘characteristic’ reflections in the angular ranges 74.2 ≤ 2θ ≤ 76.6° and 91.2 ≤ 2θ ≤ 94.0° from 30 to 600 °C. The structural model in space group P12₁/n1, deduced for this phase at room temperature, was fitted up to 100 °C. At 100 °C, discontinuities in the refined lattice parameters a and c (see Fig. 4) accompany a transition to I12/m1 symmetry with the disappearance of the in phase (+) rotations around the c axis. At 500 °C, simultaneous disappearance of both out of phase rotations perpendicular to c yield the cubic Fm3̄m structure. It is worth noting that there is no evidence for any single-rotation intermediary typically observed in similar systems.⁶

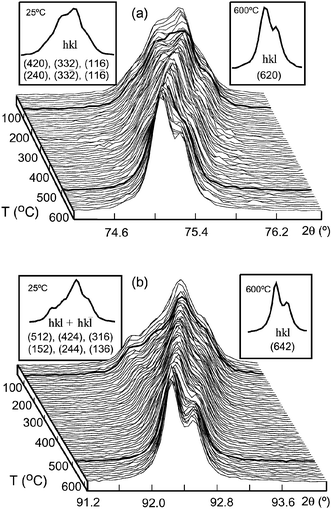Fig. 3 Evolution of selected ‘characteristic peaks’ of Sr₂CoTeO₆ with temperature in the angular ranges (a) 74.2 ≤ 2θ ≤ 76.6 and (b) 91.2 ≤ 2θ ≤ 94.0. Bold curves show the structural transitions. Maxima indexed in P12₁/n1 at 25 °C and Fm3̄m at 600 °C are inset.

Fig. 4 Evolution of reduced refined lattice parameters and monoclinic angle, β, of Sr₂CoTeO₆ from temperature dependent X-ray diffraction data. Assigned space group symmetries, the transitions between these symmetries and the associated rotation senses (0, + or −) around the three primitive axes are also shown. Reduced lattice parameters were calculated as follows for the various space group symmetries: monoclinic (P12₁/n1 and I12/m1): a_m = a/√2, b_m = b/√2; c_m = c/2; cubic (Fm3̄m): a_c = a/2.

Magnetic structure

Neutron diffraction data collected at 4 K show the presence of additional peaks not coincident with those of the nuclear structure which arise from long range antiferromagnetic order in the sample (see Fig. 1(c)). These peaks were indexed considering a magnetic cell with the same dimensions as that of the nuclear cell (with parameters √2a_p × √2a_p × 2a_p, where a_p is the primitive cubic perovskite parameter) in the P1 space group. The first two sharp magnetic peaks are, consequently, the unique (001) reflection and the unresolved doublet composed of the (010) and (100) reflections indicating that there are significant components of the magnetic moment both parallel and perpendicular to the c direction.

Free refinement of the magnetic moments gave significant components (M_z = 1.91(4) μ_B) in the c-direction and in the ab plane (M_xy = 1.18(6) μ_B), yielding an overall magnitude, |M|, of 2.25(3) μ_B. Due to coincidence of the (010) and (100) reflections, no information could be obtained about the orientation of the component perpendicular to c. In the final model, magnetic moments were fixed to be zero in the b-direction and refined along a (and −a) and c (and −c) in alternating planes in the c-direction, i.e. the Type I antiferromagnetic structure shown in Fig. 5. Frustration in this magnetic structure is minimised as the strength of both the 90° and 180° superexchange interactions via diamagnetic –O²⁻–Te⁶⁺–O²⁻– bridges approach zero with the M–O²⁻⋯O²⁻–M interactions, via O²⁻ pπ, the dominant interactions responsible for the observed magnetic arrangement.²³

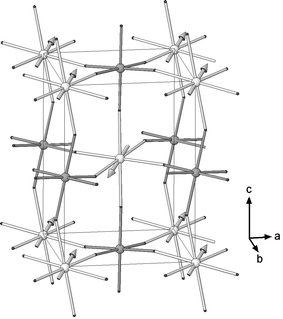Fig. 5 Type I antiferromagnetic structure of Sr₂CoTeO₆ (lighter spheres are Co and darker spheres are Te. Sr atoms are omitted for clarity).

Fig. 6 shows the temperature dependent D1B diffraction data. The thermal dependence of the magnitude of the magnetic moment is represented in Fig. 7. It can be observed that the three-dimensional magnetic order begins on cooling through 20 K. The magnitude of the Co²⁺ moments rapidly increases below 20 K, reaching saturation at around 10 K. At 4 K the effective moment per cobalt ion is μ_eff = 2.25(3) μ_B. This antiferromagnetic ordering is not accompanied, however, by any discontinuity in the lattice parameters or unit cell volume as shown in Fig. 8.

Fig. 6 Temperature dependent D1B neutron diffraction data from 2 to 35 K. Magnetic peaks are marked by arrows.

Fig. 7 Temperature dependence of the magnitude of the magnetic moment refined from D1B neutron diffraction data from 2 to 35 K, with the Néel temperature, T_N = 18 K, marked.

Fig. 8 Temperature dependence of the cell parameters and volume refined from D1B neutron diffraction data from 2 to 30 K. Reduced lattice parameters were calculated as follows: a_m = a/√2, b_m = b/√2; c_m = c/2.

Spectroscopic measurements

The diffuse reflectance spectrum of Sr₂CoTeO₆ in the visible region shows the spin allowed transitions of the CoO₆ octahedral chromophore, ⁴T_1g (⁴F) ← ⁴T_2g(⁴F), ⁴T_1g (⁴F) ← ⁴A_2g(⁴F) and ⁴T_1g (⁴F) ← ⁴T_1g(⁴P), at the frequencies 6450, 13200 and 17200 cm⁻¹, respectively. The Dq and the B Racah parameters, calculated by fitting the experimental frequencies to an energy level diagram for an octahedral d⁷ system,²⁴ are 675 and 820 cm⁻¹, respectively. No further bands were observed, confirming the octahedral environment of the Co atom in the perovskite structure.

The EPR spectrum of the Co²⁺ ion in this type of structure was evaluated measuring the spectra at 4.2 K (see Fig. 9) of the Co²⁺-doped Sr₂MgTeO₆ double perovskite (1% of Co²⁺ in the site of the Mg²⁺). It can be described in terms of a spin doublet S = ½ interacting with a single ⁵⁹Co nucleus (I = 7/2) yielding the theoretical EPR spectrum in Fig. 9. This effective spin doublet arises from the splitting of the ⁴T₁ term through spin–orbit coupling and local distortion of the octahedral sites.²⁵ The g values obtained are g₁ = 4.60, g₂ = 4.33 and g₃ = 4.14. The observed value for the sum of the three orthogonal g-values (g_sum = 13.07) is in excellent agreement with the theoretical value of 13 proposed by Abragam and Pryce.²⁶ The hyperfine splitting parameters, A₁ = 140(5) × 10⁻⁴ cm⁻¹, A₂ = 120(5) × 10⁻⁴ cm⁻¹ and A₃ = 100(5) × 10⁻⁴ cm⁻¹ are similar to those observed in other cobalt(II) compounds in which Co²⁺ is in octahedral coordination to O²⁻. The g factor and hyperfine coupling constant are unusually isotropic for Co²⁺ ions, consistent with the highly regular octahedral environment.

Fig. 9 Experimental (solid line) and simulated (dashed line) EPR powder spectra of the 1% Co²⁺ substituted Sr₂(Mg_0.99Co_0.01)TeO₆ at 4 K.

Magnetic properties

The temperature dependences of the magnetic and reciprocal susceptibilities measured at 1 kOe are shown in Fig. 10. The molar magnetic susceptibility increases with decreasing temperature and reaches a maximum at ca. 18 K (T_N), indicating that long range antiferromagnetic order is established below this temperature. At high temperature, T > 150 K, the thermal evolution of χ_m follows the classical Curie–Weiss law, χ = C_m/(T − θ), with C_m = 3.8 cm³ K mol⁻¹ and θ = −140 K. The effective magnetic moment (μ_eff) calculated for the paramagnetic region well above the Néel temperature as μ_eff = 2.828√C_m gave the value of 5.4 μ_B whereas at room temperature, calculated as μ_eff = 2.828√(χ_mT) resulted in 4.6 μ_B. Detail of the low temperature susceptibility, measured warming under 1 kOe after cooling down from room temperature firstly without applied field (ZFC) and subsequently under applied field (FC), is inset in Fig. 10. This low-temperature behaviour is characterised by a clear maximum in both ZFC and FC signals at 18 K and a slight divergence between both curves, indicating the possible presence of weak ferromagnetic interactions or spin-glass behaviour.

Fig. 10 Temperature dependences of the magnetic and reciprocal susceptibilities measured at 1 kOe. Detail of the low temperature field cooled (FC) and zero field cooled (ZFC) susceptibilities is inset.

The magnetisation vs. applied field at 5 K (see Fig. 11) shows a small hysteresis loop in which the H_c and M_r values are 36 Oe and 0.5 emu mol⁻¹, respectively. The evolution with temperature of low temperature magnetisation, obtained at H_dc = 0 after cooling from T > T_N under a magnetic field of 100 Oe, is inset in Fig. 11. Canting of the antiferromagnetically aligned moments has been previously observed, often showing significantly larger spontaneous magnetisations. Saturation of the magnetisation at 5 K is not reached up to 70 kOe, and from the M²vs.H/M Arrott plots²⁷ no low temperature spontaneous magnetisation could be estimated. This result is not surprising in the light of the magnitude of the magnetisation.

Fig. 11 Magnetisation vs. applied field at 5 K. Inset are (a) detail of −0.04 ≤ H ≤ 0.04 region showing magnetic irreversibility and (b) remnant magnetisation vs. temperature.

In order to determine the possible existence of spin-glass behaviour, AC magnetic susceptibility measurements were carried out. The real (or in-phase, χ′) and imaginary (or out-of-phase, χ″) components of the AC magnetic susceptibility at different frequencies are given in Fig. 12. The maximum observed at 19 K in χ′ is associated with long-range magnetic order, as previously described. The lack of absorption in out-of-phase AC susceptibility in this temperature region indicates the absence of a significant ferromagnetic component, in good agreement with the results obtained from χ_mvs.T. The rounded maximum, centred at 19 K, does not shift in temperature with increasing frequency, indicating that the sample does not demonstrate conventional spin glass or cluster glass behaviour.²⁸

Fig. 12 Real (χ′) and imaginary (χ″) components of the AC magnetic susceptibility as a function of (a) frequency and (b) applied DC field. In both cases, detail of the maximum susceptibility is inset.

The influence of a superimposed DC field in χ′ and χ″ is also shown in Fig. 12. The AC susceptibility shows a negligible dependence with magnetic field, even up to 40 kOe, which is an indication of both a large magnetocrystalline anisotropy and that the antiferromagnetic interactions are strong enough to resist the effect of the applied field.

The specific heat data between 1.8 and 50 K are shown in Fig. 13. The heat-capacity measurements exhibit a three-dimensional magnetic ordering peak at 15 K. The temperature at which this λ-type peak appears is consistent with that obtained from the magnetic susceptibility measurements (T_N ≈ 18 K). At temperatures higher than 30 K, the strong increase of Cp is due to the lattice (or phonon) contribution (Cp_pho). Below this temperature the magnetic contribution (Cp_mag) is relatively important compared with the phonon one. The contribution of the lattice vibrations to the specific heat capacity was fitted to the high temperature data by a Debye model,¹⁸ by considering the existence of two phonon spectra. For the unit cell containing N atoms, n₁ were assigned a Debye temperature θ₁ and n₂, constrained such that n₂ = N − n₁, a Debye temperature θ₂, yielding three independent variables to be refined, namely θ₁, θ₂ and n₁. Refined values indicate that, of the 10 atoms in the unit cell, 4.12 (n₁) have a Debye temperature of 252.3 K and 5.88 (n₂ = N − n₁) have 655.8 K. This result not only produces an excellent fit to the experimental data (see Fig. 13) but is also in good agreement with the unit cell contents of 4 heavy atoms and 6 light atoms with a higher Debye temperature. The magnetic contribution can then be calculated as Cp_mag = Cp − Cp_pho. The effect of the magnetic field on the heat capacity is inset in Fig. 13. Under an applied magnetic field of 90 kOe, the λ-type peak is slightly displaced to lower temperatures and its intensity is reduced. Both effects are as expected for a three-dimensional transition to an antiferromagnetically ordered state. In addition, the small magnitude of the change reflects the robustness of the antiferromagnetic structure under an applied magnetic field, as was previously observed in the AC susceptibility measurements.

Fig. 13 (a) Specific heat vs. temperature of Sr₂CoTe O₆ from 1.8 to 50 K showing total specific heat, Cp, the calculated phonon contribution, Cp_pho, and the resultant magnetic contribution, Cp_mag. Inset shows the total specific heat in the presence and absence of a 9 T magnetic field.

The thermal evolution of the magnetic entropy, S_mag, for this phase is shown in Fig. 14. The total magnetic entropy, calculated from

was found to be ≈4.2 J mol⁻¹ K⁻¹ above 35 K. This value is 73% of the theoretical value, Rln(2S + 1) = 5.76 J mol⁻¹ K⁻¹, expected for the S′ = ½ state of the Co²⁺ cation at low temperatures.

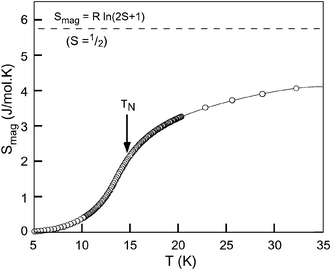Fig. 14 Calculated magnetic entropy, S_mag. The theoretical value for S = ½ is also shown.

Discussion and conclusions

The perovskite structure in which two distinct B cations order, due to significant differences in their nominal oxidation states and ionic radii, is known to display a varied structural chemistry with a wide range of physical properties.^3,29 The study of the double perovskite Sr₂CoTeO₆ and comparison with compositions from the literature has allowed us to obtain useful information about the factors which determine them. In the current study, attention is focused on the complete ordering of paramagnetic cobalt 2+ with a diamagnetic cation to get information about the behaviour of Co(II) and its magnetic interactions within the double perovskite structure.

The high temperature phase transitions in Sr₂CoTeO₆ show the evolution, at 100 °C, from the room temperature P12₁/n1 structure to I12/m1. Above 500 °C, the ‘ideal’ cubic, Fm3̄m ordered double perovskite structure is observed, with no evidence for a single rotation intermediary. Despite the appearance of what is nominally a low symmetry for the double perovskite structure at room temperature, the octahedra themselves remain virtually undistorted even down to low temperature. Within the octahedra, the six, or more accurately three pairs of two, bond distances are virtually equal. At 4 K, internal distances, as shown in Table 2, have mean values of 2.092 and 1.914 Å for the CoO₆ and TeO₆ octahedra with statistical variances of only 0.004 and 0.002, respectively, with internal angles barely varying from 90°. The regularity of these octahedra will be of importance when considering the spectroscopy and magnetic behaviour of Co.

The highly regular octahedral environment of the Co²⁺ ion offers a good opportunity to explore in detail its spectroscopic properties. The free cobalt(II) ion has a 3d⁷ configuration with a ⁴F term as the ground state. In an octahedral crystal field the ground state splits into two orbital triplets ⁴T_1g, ⁴T_2g and one singlet ⁴A_2g. Strong spin–orbit coupling effects split the ⁴T_1g triplet into a set of three levels the lowest in energy being a Kramer's doublet, meaning that only a magnetic field can split this energy level, usually denoted in the literature as Γ₆ subspace.³⁰ This doubly degenerate level is an effective S′ = ½ state at low temperatures and is characterised by unusual features, the explanation of which was developed by Abragam and Pryce.²⁶ In the weak field limit the orbital contribution of the nearby components of the ⁴T_1g ground state causes the ground doublet to have an isotropic g = 4.33, but large anisotropy in the g value is expected as the crystal field becomes more distorted. The three resultant orthogonal values (g_x, g_y and g_z) are expected to sum in the first order to the value of 13.²⁹ Under the effect of an applied magnetic field the S′= ½ ground state loses its degeneracy and interacts with the I = 7/2 nuclear spin of ⁵⁹Co (100% isotopic abundance). The allowed transitions between the resulting energy levels produce a set of octets of resonance lines in the EPR spectrum which can be completely resolved if the Co²⁺ ions are well diluted in the host compound.

In order to obtain insight into the octahedral environment of cobalt ions in Sr₂CoTeO₆, a 1% Co substituted Sr₂(Mg_0.99Co_0.01)TeO₆ sample was studied by EPR spectroscopy. Sr₂MgTeO₆ is a similarly distorted double perovskite, described by space group I12/m1, with Mg²⁺ having comparable ionic radius to that of Co²⁺.²¹ As a generally accepted rule,⁶ originally pointed out by Glazer,⁴ we can consider these octahedra as rigid entities the tilts of which around the axes of the primitive cubic perovskite are the most important factors that determine the distortion of the compound from that of the ideal cubic perovskite. Consequently, Sr₂(Mg_0.99Co_0.01)TeO₆ represents an analogous picture of the octahedral environment of Co²⁺ in the parent compound, Sr₂CoTeO₆.

The observed values of the three orthogonal g factors of g₁ = 4.60, g₂ = 4.33 and g₃ = 4.14 and Σg = 13.07 in the partially resolved EPR spectrum at 4 K in this compound (see Fig. 9), give an average value of g = 4.36, indicating that the octahedral environment of the Co²⁺ ion is highly regular. These results are consistent with the three almost equal Co–O distances of 2.095(3), 2.092(2), 2.089(3) Å, refined from neutron powder diffraction data at the same temperature which are very close to the calculated expected value of 2.095 Å.²¹ This confirms the rigidity of the CoO₆ octahedral units despite the high degree of distortion from the ideal cubic perovskite allowed by the P12₁/n1 space group.

Combining the parameters obtained from EPR measurements and those obtained from diffuse reflectance spectroscopy, it is possible to extract qualitative information of the degree of covalency between Co²⁺ cations and the neighbouring O²⁻ anions. In order to obtain this information the Racah parameter B, the crystal-field parameter Dq and the average g of the compound are needed, with values of 675 cm⁻¹, 820 cm⁻¹ and 4.36, respectively, in the present case.

Detailed theoretical considerations are not the subject of this paper and can be found elsewhere^30–32 so will be treated briefly. For an undistorted octahedron, it can be considered that the Co²⁺ ions are in cubic symmetry. It has also been proven that the crystal field of lower symmetry produced by slightly distorting these octahedra does not invalidate this approximation with the g values in the lower order environment being obtained from the matrix elements of the Zeeman term in the Γ₆ subspace of the ⁴T₁ ground triplet. The matrix elements of the orbital angular momentum L within a T₁ subspace are proportional to those of a P term, but one should note that the excited term ⁴P is also of the ⁴T₁ symmetry, and is mixed by the cubic field with the ⁴T₁ of the ground ⁴F term. If we indicate two states of ⁴F and ⁴P with ϕ_i and ϕ′_i, respectively, such that they transform in the same way under the cubic group, the states of the ground ⁴T₁ will be of the form aϕ_i + bϕ′_i. The values of the constants a and b can be obtained from the Racah parameter B and the crystal-field parameter Dq. With the values obtained for Sr₂CoTeO₆ one obtains a = 0.98731 and b = −0.15882, and the proportionality constant of the angular momentum is α = −1.5a² + b² = −1.43694. Two further effects should be considered in the calculation of the isotropic g tensor. One is the second-order contribution of the ⁴T₂ states, that are separated by Δ′ = −15B − 6Dq = 5834 cm⁻¹ from the ground ⁴T₁ states, and the other is the covalency between the Co and the neighbouring O, described by several covalence factors, that reduce the matrix elements of the orbital angular momentum and of the spin–orbit interaction. Using a single k_o for all these factors one obtains the expression for the g factor in a cubic field:

where λ = −180 cm⁻¹ is the Co²⁺ spin–orbit coupling constant. With the parameters employed, the isotropic g tensor coincides with the trace of the experimental one when k_o = 0.91. When one employs the parameters of Co : MgO³³viz.B = 815 cm⁻¹ and Dq = 905 cm⁻¹, the following values are obtained: a = 0.9811, b = −0.1933, α = −1.4063, Δ′ = 7953 cm⁻¹, and k_o = 0.86. This degree of covalency is similar to that of MgO, confirming that, in the Sr₂CoTeO₆ ordered perovskite, Co is a highly ionic species with an oxidation state very close to the nominal value of +2.

With respect to the magnetic behaviour, this sample shows a completely unquenched magnetic moment in the paramagnetic region. The experimental μ_eff = 5.46(3) μ_B is close to the theoretical 5.20 μ_B and agrees well with the values obtained for similar ordered double perovskites and related compounds in which cobalt(II) is the only paramagnetic ion as shown in Table 3. At 4 K, when three-dimensional antiferromagnetic ordering is observed, the effective magnetic moment has been obtained from Rietveld refinement of neutron powder diffraction data. The value of μ_eff = 2.25(3) μ_B is in good agreement with that of 2.17 μ_B obtained from the expression μ_eff = gS, taking into account that at low temperatures the cobalt(II) ion has an effective S′ = ½ state and an average g tensor of 4.36 obtained from ESR spectroscopy. As shown in Table 3, this value for μ_eff at low temperatures is also in good agreement with related oxides.

Table 3 Observed low temperature magnetic moments in several Co²⁺ containing ordered perovskites obtained above and below the Néel temperature, T_N, from magnetic susceptibility and neutron data, respectively

Sample	T N	Type	μ eff/μB (T ≫ TN)	μ eff/μB (T ∼ 4 K)^b	Ref.
a Note that this perovskite contains 75% Co^2+ and 25% Co^3+. b From neutron diffraction.
Ba2CoWO6	17	II	5.24	2.0(3)	34, 35
Ba2CoMoO6	20	II	5.58	2.0(1)	35
Ba2CoTeO6	19	—	5.42	—	36
Sr2CoWO6	32	II	5.20	2.35(3)	8
Sr2CoMoO6	34	—	5.03, 5.23	—	9, 37
Sr2CoSbO5.63^a	14	—	4.85	—	38
Sr2CoTeO6	18	I	5.46	2.25(3)	This work

---

Specific heat measurements provide further evidence for the S′ = ½ effective spin state of cobalt(II) at low temperatures. It is known that for a solid, the magnetic entropy associated with a magnetic transition can be theoretically calculated as S_mag = Rln(2S + 1). In the present case, an S = 3/2 spin state ought to give a total magnetic entropy of ≈11.5 J mol⁻¹ K⁻¹, which is far higher than the observed 4.2 J mol⁻¹ K⁻¹ around 35 K (see Fig. 14). This value, however, agrees with the 73% of the theoretical value of 5.76 J mol⁻¹ K⁻¹, expected for the S′ = ½ state of the Co²⁺ cation at low temperatures. As pointed out previously, the method to extract S_mag from the specific heat (which involves two steps, firstly to obtain Cp_mag using an estimated Cp_pho and secondly to extract S_mag from Cp_mag) usually yields approximate values, which are typically lower than the theoretical values for the entropy corresponding to the spin state of the magnetic ion involved.

In order to obtain insight into the magneto-structural correlations in double perovskites in which Co(II) and a diamagnetic cation order, we must take into consideration that interactions between the paramagnetic cations occur via two different mechanisms. Strong Co–O–X–O–Co superexchange interactions, approximately equal in strength for both 90 and 180° interactions, are frequently seen in the double perovskite structure, yielding a magnetic propagation vector k = (½ ½ ½), producing the familiar Type II antiferromagnetic structure in which moments aligned in [1 1 1] planes are parallel to one another with adjacent planes aligned antiparallel. However, Sr₂CoTeO₆ exhibits the Type I structure in which moments in the [0 0 1] plane are aligned parallel to one another with consecutive planes in the (0 0 1) direction antiparallel. This structure is a consequence of the weakening of the Co–O–X–O–Co exchange interactions and the Co–O⋯O–Co, pπ interactions becoming increasingly important. This reduction in strength can be partially explained by a longer Co–O–X–O–Co exchange pathway but is also likely to be influenced by other factors such as the relative energies of the overlapping orbitals. It is worth noting that the superexchange interactions, if not totally absent, lead to frustration in the Type I structure which can in turn produce spin-glass type behaviour or small ferromagnetic interactions leading to canting of the antiferromagnetic spins, as previously discussed.

Table 3 shows the Néel temperatures, magnetic structure types and effective magnetic moments both from fits to data above the Néel temperature and, where available, from low temperature neutron diffraction. The tabulated A₂CoB′O₆ double perovskites fall into two broad families. For A = Ba, cubic symmetry is maintained down to 4 K for both B′ = Mo and W. Both have Néel temperatures of approximately 18 K and the Type II magnetic structure. In the case of Ba₂CoTeO₆,³⁶ though a similar Néel temperature of 19 K is observed, the crystal structure is 6H hexagonal and no comparison can therefore be made between structural features. Sr₂CoSbO_5.63 also shows a lower Néel temperature of 14 K and a reduced magnetic moment with respect to other Sr containing A₂CoB′O₆ double perovskites. Comparison is again complicated, this time by the presence of a nominally +5 diamagnetic B′ cation and the presence of mixed valence Co(II)/Co(III). Sr₂CoB′O₆ for both B′ = Mo and W has higher Néel temperatures of approximately 30 K, despite the deviation of angles from 180° within the Co–O–B′–O–Co exchange pathways in these P12₁/n1 monoclinically distorted low temperature structures. Sr₂CoWO₆ again has the Type II magnetic structure, produced by strong superexchange interactions, perhaps due to shortening of the mean through-bond exchange path length (7.981 and 8.108 Å, for A = Sr and Ba, respectively). In the case of Sr₂CoTeO₆, with a mean exchange path length of 8.010 Å, the T_N value of 18 K is more comparable to those of Ba than of Sr and the magnetic structure is of Type I. The structural differences between this and the other Sr containing double perovskites in which the diamagnetic cation is Mo or W are not sufficient to explain these differences and some other factor, such as the relative energies of orbitals within the exchange pathways, must also play a significant role.

In summary, a detailed study of the Sr₂CoTeO₆ and comparison with several similar A₂CoBO₆ (A = Sr, Ba; B = W, Mo, Sb) containing structures from the literature have enabled us to deduce information about the factors affecting the physical behaviour in the double perovskite structure. The structure is described by the three rotation (− − +) P2₁/n space group from 4 K to 373 K (100 °C) where a transition occurs to I2/m symmetry, with a further transition to cubic, Fm3̄m at 773 K (500 °C). Below the Néel temperature of 18 K, Type I antiferromagnetic order is observed with moments of 2.25(2) μ_B rotated 58° out of the ab plane. A slight divergence of field cooled and zero field cooled susceptibility and a small ferromagnetic moment and irreversibility at 4 K, are not due to spin-glass behaviour and may be due to a minute canting of the antiferromagnetically aligned moments. The magnetic behaviour of Co, in particular the effective magnetic moments observed, has been shown to be dependent on the isotropy of the CoO₆ octahedral environment. Distortions of the structure, demonstrated to be primarily rotations of these regular octahedra, change the geometry of the magnetic exchange pathways but are insufficient to explain the variation in ordering temperatures and magnetic structure types observed, with orbital energies within the exchange pathways having a significant influence on the properties of these and similar technologically important materials.

Acknowledgements

This work has been funded by the ‘Ministerio de Ciencia y Tecnología’ (MCyT). L. Ortega-San Martin acknowledges MCyT for a Doctoral Fellowship. Dr J. P. Chapman thanks MCyT for funding (MAT 2001-0064). The authors gratefully acknowledge Dr G. Cuello for assistance with data collection and the ILL, Grenoble, France for provision of beam-time on Instruments D2B and D1B. F. Guillen and R. Olazcuaga of the ICMCB, Bordeaux, France are acknowledged for providing the diffuse reflectance data. Finally we thank Profs. M. E. Foglio and G. E. Barberis of the ‘Instituto de Física Gleb Wataghin’, Sao Paulo, Brazil for their assistance with combined EPR and diffuse reflectance data treatment.

References

1. A. S. Bhalla, R. Guo and R. Roy, Mater. Res. Innov., 2000, 4, 3.
2. F. Galasso, Perovskites and High Tc superconductors, Gordon & Breach, New York, 1990.
3. Properties and applications of perovskite-type oxides, ed. L. G. Tejuca and J. L. G. Fierro, Marcel Dekker, New York, 1993.
4. A. M. Glazer, Acta Crystallogr., Sect. A, 1975, 31, 756; A. M. Glazer, Acta Crystallogr., Sect. B, 1972, 28, 3384.
5. P. M. Woodward, Acta Crystallogr., Sect. B, 1997, 43, 32.
6. C. J. Howard, B. Kennedy and P. M. Woodward, Acta Crystallogr., Sect. B, 2003, 59, 463 and references therein.
7. K.-I. Kobayashi, T. Kimura, H. Sawada, K. Terakura and Y. Tokura, Nature, 1998, 395, 677.
8. M. C. Viola, M. J. Martínez-Lope, J. A. Alonso, J. L. Martínez, S. Pagola, J. M. Depaoli, J. C. Pedregosa, M. T. Fernández-Díaz and M. E. Carbonio, Chem. Mater., 2003, 15, 1655.
9. M. Itoh, I. Ohta and Y. Inaguma, Mater. Sci. Eng. B, 1996, B41, 55.
10. H. A. Blackstead, J. D. Dow, D. R. Harshman, W. B. Yelon, M. X. Chen, M. K. Wu, D. Y. Chen, F. Z. Chien and D. B. Pulling, Phys. Rev. B, 2001, 61, 214412–1.
11. I. Levin, L. A. Bendersky, J. P. Cline, R. S. Rot and T. A. Vanderah, J. Solid State Chem., 2000, 150, 43.
12. M. Gateshki, J. M. Igartua and E. Hernández-Bocanegra, J. Phys.: Condens. Matter, 2003, 15, 6199.
13. G. Baldinozzi, D. Grebille, Ph. Sciau, J.-M. Kiat, J. Moret and J. F. Berar, J. Phys.: Condens. Matter, 1998, 10, 6461.
14. S. Pei, J. D. Jorgensen, B. Dabrovski, D. G. Hinks, D. R. Richards, A. W. Mitchel, J. M. Newsam, S. K. Sinha, D. Vaknin and A. J. Jacobson, Phys. Rev. B, 1990, 41, 4126.
15. J. Rodriguez-Carvajal, FULLPROF: A Program for Rietveld Refinement and Pattern Matching Analysis, Abstracts of the Satellite Meeting on Powder Diffraction of the XV Congress of the IUCr, Toulouse, France, 1990, p. 127.
16. H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65.
17. A. C. Larson and R. B. Von Dreele, GSAS: General Structure Analysis System, LAUR 86-748, 1994.
18. P. Debye, Ann. Phys., 1912, 39, 789.
19. L. Ortega-San Martín, J. P. Chapman, E. Hernández-Bocanegra, M. Insausti, M. I. Arriortua and T. Rojo, J. Phys.: Condens. Matter, 2004, 16, 3879–88.
20. V. F. Sears, Neutron News, 1992, 3, 29.
21. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751.
22. P. Suortti, J. Appl. Crystallogr., 1972, 5, 325.
23. P. D. Battle and S. Kim, J. Solid State Chem., 1995, 114, 174 and references therein.
24. A. B. P. Lever, Inorganic Electronic Spectroscopy, Elsevier Publishing Company, London, 1984.
25. R. L. Carlin, Magnetochemistry, Springer, Berlin, 1986.
26. A. Abragam and M. H. L. Pryce, Proc. R. Soc. London A, 1951, 206, 173.
27. A. Arrott, Phys. Rev., 1957, 108, 1394.
28. J. A. Mydosh, Spin glasses: an experimental introduction, Taylor and Francis, London, 1993.
29. M. T. Anderson, K. B. Greenwood, G. A. Taylor and K. R. Poeppelmeier, Prog. Solid State Chem., 1993, 22, 197.
30. A. Goñi, L. Lezama, T. Rojo, M. E. Foglio, J. A. Valdivia and G. E. Barberis, Phys. Rev. B, 1998, 57, 246.
31. L. T. Peixoto and M. E. Foglio, Rev. Bras. Fis., 1983, 13, 564.
32. M. Tinckham, Proc. R. Soc. London, Ser. A, 1956, 236, 549.
33. A. Abragam and B. Bleaney, Electron Paramagnetic Resonance of Transition Ions, Clarendon, Oxford, 1970.
34. D. E. Cox, G. Shirane and B. C. Frazer, J. Appl. Phys., 1967, 38, 1459.
35. M. J. Martínez-Lope, J. A. Alonso, M. T. Casais and M. T. Fernández-Díaz, Eur. J. Inorg. Chem., 2002, 9, 2463–2469.
36. L. Ortega-San Martín et al., to be published.
37. Y. Moritomo, Sh. Xu, A. Machida, T. Akimoto, E. Nishibori, M. Takata and M. Sakata, Phys. Rev. B, 2000, 61, R7827.
38. V. Primo-Martín and M. Jansen, J. Solid State Chem., 2001, 157, 76.

---