Introductory Lecture

Strategies for controlling intra- and intermicellar packing in block copolymer solutions: Illustrating the flexibility of the self-assembly toolbox

Abstract

Block copolymers constitute a class of self-assembling macromolecules that offer remarkable flexibility for controlling nanostructure, both in discrete objects and in bulk materials. Block copolymer micelles may be formed with multiple compartments by judicious choice of ingredients in an ABC triblock copolymer. For example, we have shown that a poly(ethylene oxide–b–styrene–b–fluorinated butadiene) triblock assembles in dilute aqueous solution into large, flat core/shell/corona disks, with the fluorine containing block forming the core. In contrast, the unfluorinated precursor generates large spherical micelles. A numerical analysis suggests that the disk-like motif is characteristic of the so-called superstrong segregation regime, whereby the interfacial tension becomes so large as to overwhelm the conformational entropy of the core blocks. For ABC miktoarm stars comprising polyethylene oxide, polyethylethylene, and polyhexafluoropropylene oxide arms, a much richer variety of micellar structures are observed. Prominent amongst these is a “segmented worm”, in which alternating layers (5–7 nm thick) of hydrocarbon and fluorocarbon blocks form disks (6–10 nm in radius) that stack into cylindrical aggregates. The disk radii suggest almost fully stretched blocks, again consistent with the superstrong segregation regime. These structures are rationalized in terms of the constraints imposed by the star architecture, combined with the extremely strong interfacial tensions. In contrast, for lipids, surfactants, and aqueous diblock copolymers, increasing the interfacial tension can induce a transition from spheres to cylinders to flat bilayers; the disk-like motif is not usually seen. Interestingly, in aqueous diblocks both worm-like micelles and vesicles have been well-documented, whereas in “simple” organic systems they have not. We have shown that by suitable choice of block composition and solvent selectivity, the curvature sequence sphere/cylinder/vesicle can also be observed in poly(styrene–b–isoprene) diblocks in dialkyl phthalates. In more concentrated solutions such spherical micelles assemble onto body-centered or face-centered cubic lattices. In some cases a thermoreversible fcc/bcc transition has been noted. We have recently demonstrated that this transition corresponds to a particular aggregation number; higher aggregation numbers, found at lower temperatures, favor the “hard-sphere-like” fcc packing. All of these results are based on a combination of dynamic light scattering, small angle X-ray and neutron scattering, and cryogenic transmission electron microscopy.

---

Introduction

A central goal of nanoscience is to exert control over the structure of materials, and thus over their function, over the range of about 5–200 nm. One general strategy that is enjoying tremendous attention in the research community is self-assembly, whereby the component molecules within some material spontaneously select a structure with a predictable degree and type of ordering. Such structures might comprise discrete objects (e.g., micelles, vesicles, nanoparticles, etc.), or they might correspond to materials that are continuous in either two (e.g., thin films) or three dimensions. Self-assembly is often considered the epitome of “bottom-up” engineering, as the processing of nanostructures may be very economical in terms of labor or energy input. Within the realm of self-assembly, an emerging paradigm is that of hierarchical structure, i.e., materials with designed organization on at least two distinct length scales. Success in this endeavor would presumably enable many more, relatively sophisticated applications.

Among the various classes of molecules that undergo self-assembly, block copolymers are particularly versatile and rich in promise.^1,2 Consider the simplest case of an AB diblock copolymer, in the bulk state. Fig. 1 illustrates the seven known structures (four symmetries) that such materials adopt.³ The periodicities of the structures are dictated primarily by molecular weight, and as such are naturally in the 5–50 nm range. They may also be tuned continuously, by blending, dilution, and temperature, for example. The self-assembly process itself is usually quite tolerant of component heterogeneity, so that commercially viable materials are perfectly acceptable. Furthermore, different functional groups or additives may be selectively incorporated into one domain. The four symmetries shown in Fig. 1 span the range of possible domain connectivities, i.e. the minor component microdomains are connected in zero (spheres), one (cylinders), two (lamellae) or three (double gyroid) dimensions. As these various morphologies are equilibrium phases, it is reasonable to expect, and indeed found, that theory can predict the relative free energies of possible structures rather reliably.^3,4 If a greater wealth of possible structures are sought, then straightforward extension to 3 component systems, such as ABC triblock copolymers, offers morphological richness that has only begun to be explored.¹

Fig. 1 Schematic illustration of the nanostructures formed by an AB diblock copolymer in the bulk. The various phases are S (bcc spheres), C (hexagonally-packed cylinders), G (double gyroid), and L (lamellae). The white and grey domains represent the A and B blocks, respectively, as the fraction of A in the copolymer increases from left to right.

Block copolymers are but one class of structured-directing materials, but they can also illustrate the great design flexibility that self-assembly affords. It is perhaps helpful to consider four general ways in which the experimenter has access to control over structure. First is the choice of molecules themselves. For block copolymers, the design variables include number and chemical identity of ingredients, molecular weight, composition, and architecture (i.e., linear versus star versus branched, diblock versus triblock versus multiblock, etc.). The chemical ingredients may be chosen on the basis of the dominant interactions (ionic, dipolar, hydrogen-bonding, dispersive, etc.), because they are responsive to some external trigger, or because they have a particular structure-directing character (mesogens, helix formers, crystallizable blocks, etc.) Second, we may consider the composition of the mixture. Here important variables include the selectivity of an added solvent or diluent, the miscibility or immiscibility of different polymeric components, the use of complementary groups such as hydrogen bond donors and acceptors, or particular recognition elements. Third, external stimuli such as temperature, pressure, pH, and ionic strength may be used to tune structure. Finally we may consider the use of external fields to produce the desired organization, particularly for anisotropic structures. Examples include shear and extensional flow, electric and magnetic fields, and even gradients in temperature. In short, there are many dials that may be turned to affect the final structure, and the papers in this volume illustrate many of the examples just listed.

In this introductory paper, we provide four examples of block copolymer self-assembly from our recent work that highlight some of the important issues and possibilities. In the first, we demonstrate that the sequence of interfacial curvature sphere/cylinder/vesicle, which is well documented in lipids, surfactants and aqueous block copolymers, can also be achieved in a rational and systematic way in standard nonaqueous block copolymer solutions.⁵ Second, we show how a linear ABC triblock copolymer, with suitably chosen block lengths and mutual interaction strengths, can form core/shell/corona micelles in water.⁶ Furthermore, we argue that the formation in one case of a flattened oblate disk-like micelle is indicative of a new arena in block copolymer assembly,⁷ the so-called superstrong segregation regime.^8,9 In the third example, the introduction of an ABC “miktoarm” star architecture¹⁰ leads to a fascinating variety of multicompartment micelles, in which separate fluoropolymer and hydrocarbon blocks form multiple distinct nanodomains within a micellar core.^11,12 Finally, we discuss recent progress in understanding the packing of spherical micelles onto superlattices at higher concentrations,^13–19 and in particular identify the control variable that dictates whether the chosen cubic lattice is body-centered or face-centered.

Experimental section

Polymers

Poly(styrene–b–isoprene) diblock copolymers were prepared by sequential living anionic polymerization, following standard protocols as previously described.¹⁹ Molecular weights and polydispersity indices were determined by size exclusion chromatography (SEC) with light scattering detection, and compositions were determined by ¹H NMR spectroscopy. Samples are designated SI(x-y), where x and y denote the styrene and isoprene block molecular weights in kDa.

A poly(ethylene oxide–b–styrene–b–1,2-butadiene) linear triblock terpolymer was synthesized by anionic polymerization, as previously described.⁶ The styrene block was initiated with a tert-butyldimethylsiloxylithium protected initiator, and polymerized in cyclohexane. The butadiene block was then polymerized, with addition of THF as a polar modifier to produce almost complete 1,2 addition; the resulting SB diblock was terminated with isopropanol. The protected initiator was cleaved off with tetrabutyl ammonium fluoride, followed by acid treatment. The resulting hydroxyl group was used to initiate polymerization of the ethylene oxide, using potassium naphthalenide in THF. The resulting “OSB” triblock had block molecular weights of 13,200, 4700, and 1300 Da, respectively. The butadiene block was reacted with perfluorohexyliodide in the presence of triethylborane and air as previously described,²⁰ to produce a fluorinated butadiene derivative in an “OSF” triblock. The molecular weight of the resulting “F” block was 4600 Da, and the O and S blocks were essentially unaffected by this free radical chemistry.

ABC triblock miktoarm stars were prepared as follows.¹² Butadiene was polymerized in THF at low temperature, and terminated with a protected bifunctional terminator 2-methoxymethoxymethyloxirane. The functional 1,2 polybutadiene was fully hydrogenated over Pd/CaCO₃ to produce polyethylethylene, without compromising the functional groups. The terminal hydroxyl group was then used to initiate ethylene oxide polymerization, using diphenyl methylpotassium in THF. The resulting midfunctional EO diblock was terminated with bromoethane. The methoxymethyl protecting group was cleaved off with HCl, to provide a pendant hydroxyl group at the EO junction. Acid chloride terminal poly(perfluoropropylene oxide) (Krytox® from DuPont) was then conjugated to the EO diblock in a mixture of fluorinated solvents, to produce the desired triblock miktoarm stars, designated μ-EOF(x-y-z).

Solutions

Aqueous solutions were prepared by direct dissolution of OSB, OSF, and various μ-EOF terpolymers, assisted by stirring and, in some cases, mild sonication. All solutions appeared clear to the eye. Solutions were filtered through 0.2 μm filters prior to dynamic light scattering analysis. Solutions of SI copolymers in various dialkyl phthalates (dimethyl phthalate, DMP; diethyl phthalate, DEP; di-n-butyl phthalate, DBP) and tetradecane were prepared by codissolution in methylene chloride, which was subsequently stripped off under flowing nitrogen.

Dynamic light scattering

DLS measurements were taken on a homebuilt goniometer in the homodyne mode, using a BI-9000 correlator. Temperatures were controlled to within ±0.2 °C using a flow-through heater immersed in the silicon oil index-matching fluid. Correlation functions were obtained at several scattering angles to confirm the diffusive character of the decay modes. Individual correlation functions were analyzed with single exponential, double exponential, cumulant expansion, or Laplace inversion techniques, as appropriate.

Small angle X-ray scattering

SAXS measurements were performed either at the University of Minnesota Characterization Facility, or at the Argonne National Laboratory at the DND-CAT beamline 5-D-ID. Scattered X-rays were incident on area detectors, and the (isotropic) intensities were azimuthally averaged to give intensity, I, versus scattering wave vector, q (= (4π/λ) sin (θ/2)). No attempt was made to place the intensities on an absolute scale, but background/solvent subtractions were performed in those cases where I(q) was fitted to specific form factor expressions.

Small angle neutron scattering

Measurements were performed at the National Institute of Standards and Technology NSF/ExxonMobil/University of Minnesota beamline NG7. A neutron wavelength of 6 Å with spread Δλ/λ = 0.1 was selected, and various detector positions employed to achieve a suitable q range. Scattering patterns were corrected for transmission, background, empty cell, and incoherent contributions, and placed on an absolute scale using the direct beam method.

Cryotransmission electron microscopy

A small droplet of each solution was placed on a lacey carbon film supported on microperforated cryoTEM grid. Careful blotting produced thin films (typical thickness 200 ± 100 nm) within the pores of the film. The aqueous solutions were vitrified by rapid immersion in liquid ethane. Solutions in dialkyl phthalates were frozen in liquid nitrogen. All samples were examined using low dose conditions on a JEOL 1210 at 120 kV. The high resolution cryoTEM of μ-EOF(2-7-2), μ-EOF(2-13-2),and μ-EOF(2-13-3) aqueous solutions was performed at the Hannah and George Krumholz Advanced Microscopy Laboratory of the Technion Project on Complex Fluids, Microstructure and Macromolecules. The other measurements were performed in the IT Characterization Facility at the University of Minnesota.

Results and discussion

1. Sphere/cylinder/vesicle sequence in a non-aqueous diblock copolymer/solvent system

In small molecule surfactants, the observed micellar shape can often be well correlated with a packing parameter that balances the effective size of the headgroup with that of the hydrophobic tail.²¹ The larger the former, the larger the spontaneous curvature, and spherical micelles result. As the tail size increases, the curvature changes to form first cylinders, or worm-like micelles, and then flat bilayer sheets, which usually wrap around to form closed vesicles or liposomes. The same curvature sequence, i.e. spheres/cylinders/bilayers, has been recently documented in aqueous solutions of both nonionic^22–25 and ionic block copolymers.^26–29 To the best of our knowledge, the equivalent sequence has not been clearly established in a particular system for non-aqueous block copolymers, which is perhaps surprising, given that micellization in such systems (e.g., PS–PI, PS–PB, PS–PMMA) has been studied for over 40 years. There have been some intriguing precedents, however. Canham et al. found long, worm-like micelles in PS–PB–PS triblocks dissolved in ethyl acetate.³⁰ Pedersen et al. found PS–PI and PS–PI–PS copolymers that formed prolate ellipsoidal micelles, with an aspect ratio of about 3.³¹ Most recently, LaRue et al. observed long worm-like micelles in PS–PI in heptane.³² Clear evidence of vesicles is described in a paper in this volume, where Borsali and coworkers found both worms and vesicles in solutions of cyclic PS–PI diblocks.^33,34

There are at least three variables that one might tune in order to induce this curvature sequence: relative block length, solvent, and temperature. The latter two are more convenient, and are qualitatively equivalent in that they both act through the interfacial tension. In our study we selected SI(13-71) in a series of styrene-selective solvents.⁵ The larger isoprene core block accesses the “crew-cut” micelle regime, where the penalty for compressing the relatively short corona blocks as the curvature decreases is mitigated. The dialkyl phthalates form a well-studied homologous series of styrene-selective solvents, which may be blended as desired to tune the selectivity. For example, for SI(15-13), which forms spherical micelles exclusively, the critical micelle temperature was found to be well below room temperature, 83 °C, and 156 °C for 1% solutions in DBP, DEP, and DMP, respectively.³⁵ We examined 1% solutions of SI(13-71) in DBP, DEP, and DMP, and in 3∶1, 1∶1, and 1∶3 mixtures of DBP∶DEP and DEP∶DMP, all at room temperature.⁵ We found spherical micelles in DBP and 3∶1 DBP∶DEP; short cylindrical micelles in 1∶1 and 1∶3 DBP∶DEP; vesicles in DEP, 3∶1 DEP∶DMP, and 1∶1 DEP∶DMP. Solutions in 1∶3 DEP∶DMP and pure DMP phase separated. Evidence for these structural assignments is presented in Figs. 2 and 3.⁵ The former shows typical SAXS form factors, along with the minima associated with the assigned structures. The relative spacings of the minima are consistent with the assigned structures, and the values of the core dimensions thus extracted agree well with both cryoTEM and full fits of the SAXS data. Further discussion of the form factors, and the full fits to the appropriate mathematical functions,^36,37 will be provided elsewhere.⁵Fig. 3 provides representative cryoTEM images of the three structures. It is worth noting that the cryoTEM images are rather overexposed, but when underexposed, the micelles appear lighter than the solvent, due to the relative electron densities. The glass-forming nature of the dialkyl phthalates is actually an advantage for cryoTEM, as crystallization does not compete with vitrification. The sequence of curvatures is completely consistent with expectation, namely as the solvent selectivity increases, the interfacial tension goes up. This is accommodated by the change in curvature, which reduces the area per chain (from roughly 13 to 11 to 8 nm² chain⁻¹ in this case). These results confirm the universality of this curvature sequence in nonaqueous block copolymer systems.

Fig. 2 Typical SAXS form factors for SI(13-71) showing spheres (in 3∶1 DBP∶DEP), cylinders (in 1∶1 DBP∶DEP), and vesicles (in 1∶1 DMP∶DEP). The vertical arrows indicate the positions of the characteristic minima of the associated form factors, from which the core dimensions (spheres: radius 28 ± 1 nm; cylinders: radius 25 ± 2 nm; vesicles: half-layer thickness 17 ± 1 nm) may be obtained.

Fig. 3 CryoTEM images of SI(13-71) micelles; the scale bars are 200 nm. (a) spherical micelles in 3∶1 DBP∶DEP; (b) short cylinders in 1∶1 DBP∶DEP; (c) vesicles in 1∶1 DEP∶DMP. Larger fields of view, and further images of these solutions, may be found elsewhere.⁵

2. Transformation from sphere to flat core/shell/corona disk

As a first example of micelles formed by ABC triblock terpolymers, we examined 1% aqueous solutions of linear OSB and OSF by a variety of techniques.⁶ In the case of OSB, the relatively short S and B blocks, combined with the relatively weak interaction parameter χ_SB, meant that these two blocks could be mixed within an overall hydrophobic micelle core. In block copolymer language, the product χN for this pair of blocks is on the order of 5, well short of the critical value needed for microphase separation in the bulk (χ_SBN > 10). The small angle scattering curves could be well described by a spherical form factor, containing a single S/B core, with a core radius about 20 nm.⁶ This is actually a rather large value, given the low molecular weights, implying that the core SB chains are significantly stretched. This is consistent with the notion that the interfacial tension in this system is very high, driving the micelles to adopt a large radius and therefore a large aggregation number (ca. 3000 in this case). Dynamic light scattering on this system also indicated very large micelles, with a hydrodynamic radius of about 55 nm, and the ability of single exponential decays to fit the correlation functions indicates a narrow distribution of micellar sizes.⁶

Dynamic light scattering on the OSF system gave similar results, namely a narrow distribution of sizes and a mean hydrodynamic radius of 52 nm.⁶ However, the more detailed characterization experiments revealed a much more interesting micellar morphology. Both SAXS and SANS curves were well described by a flattened disk (oblate ellipsoid) core/shell corona structure, whereby the F block was segregated into a core with principal radii of 25, 25, and 5 nm, and the S block formed a shell approximately 5 nm thick.⁶ Definitive confirmation of this unique morphology was obtained via cryoTEM;⁷ an example is shown in Fig. 4. Most of the micellar cores appear circular in the image, but with a uniform optical density suggesting a disk-like structure. The invisible O corona chains are nevertheless evidenced by the empty halo surrounding each micelle. Fortuitously, some of the micelles were captured standing on edge in the field of view (see inset for an expanded image), in which the electron rich F core is clearly resolved from the lighter gray S shell.

Fig. 4 CryoTEM images of OSF core/shell/corona disk-like micelles. The circles correspond to disks exposed along the short axis, and the arrow heads indicate the extent of the (almost invisible) PEO corona. The inset shows an expanded view of a micellar core viewed edge-on; the dark F core and the grey S shell are clearly resolved. Another image from this system has been presented elsewhere;⁷ the inset is reproduced with permission. The label ‘S’ denotes the perforated support film.

The question of immediate interest is why this micelle is a flattened disk. The fact that the F and S blocks are segregated is not a surprise per se; the S/F interaction is expected to be significantly stronger than the S/B case.³⁸ Similarly, the S and F blocks occupy about the same volume, so that all other things being equal a flat interface would be preferred. However, the interfacial tension at the shell/corona interface cannot be significantly different from the OSB case. Furthermore, the O block is still significantly larger than the combined S and F blocks. Accordingly, a spherical micelle might have been expected, or, perhaps, a cylindrical structure in order to acknowledge the increase in the size of the core block. Instead, a flat disk is seen. This is therefore in contrast to the curvature sequence discussed in the previous section. A schematic illustration of the situation is given in Fig. 5. For “typical” micelle systems, increasing the interfacial tension and/or increasing the size of the core block induces transitions from spheres to cylinders to flat sheets; in the OSB to OSF case, the intermediate structure is a flattened disk.

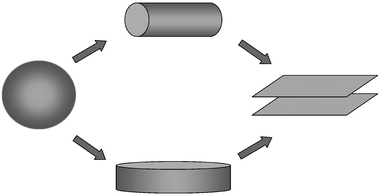Fig. 5 Schematic illustration of the curvature sequence sphere/cylinder/flat bilayer (top) adopted by typical surfactants and AB diblock copolymers, compared with sphere/disk/flat bilayer (bottom), adopted by superstrongly segregated ABC triblocks.

We propose that the difference resides in the fact that the OSF system reflects a new regime of block copolymer phase behavior, designated the superstrong segregation regime (SSSR).⁷ The SSSR was proposed and analyzed theoretically by Semenov et al. a decade ago,⁸ but as yet we are unaware of any nonionic chemical system that appears to satisfy the necessary criteria. The underlying physical concept is straightforward. In a normal “hairy” micellar system, i.e., a diblock in which the corona block is longer than the core block, an increase in interfacial tension will lead to an increase in aggregation number and core radius, at the price of increased crowding of the corona chains.³⁹ Depending on conditions, this will either just increase the size of a spherical micelle, or induce the transition to a cylinder. However, if the system is very strongly segregated, yet the corona block is long enough to suppress the transition to a cylinder, the sphere will increase in size until the core blocks are essentially fully extended. This, in fact, is apparently the case for OSB. Any further increases in interfacial tension must be accommodated by a change in structure, but as the core block is fully stretched, the dominant parameter is the interfacial area per chain. This quantity is minimized by a flattened disk, rather than by a cylindrical shape. We have recently made numerical estimates of the various contributions to the free energy, after extending the analysis of Semenov et al.⁸ to the triblock case, and find that indeed the OSB system is on the brink of accessing the SSSR, and the OSF system achieves it.⁷ An important aspect of the problem is the fact that the presence of two interfaces in an ABC copolymer micelle significantly enhances the interfacial tension contributions to the free energy balance.⁷

3. Multicomponent micelles: constraint of star architecture

Dilute solutions of several EOF miktoarm stars were examined by dynamic light scattering, and cryoTEM.¹¹ In all cases the DLS correlation functions could be reasonably well fit with the sum of two exponential decays, suggesting the presence of two (or more) distinct micellar species. However, it should be noted that because the ratio of the decay constants for the faster and slower modes was typically only 3–5, we cannot discount a distribution of particle sizes centered about these two modes. Both modes were diffusive, and hydrodynamic radii were extracted via the Stokes–Einstein relation. The values of R_h are reproduced in Table 1. The smaller values (typically ca. 20–30 nm) are much too large for single chains, and can be assigned to discrete micelles. The larger values are too big for spherical micelles, given the estimated radii of gyration of the various blocks (also listed in Table 1).

Table 1 Dimensions of micelles formed by μ-EOF polymers in water by dynamic light scattering¹¹

Sample	^aRg/nm (PEE)	^aRg/nm (PEO)	^aRg/nm (PFPO)	Rh/nm (small)	Rh/nm (large)
μ-EOF(2-6-2)	1.3	2.8	0.9	34	97
μ-EOF(2-7-2)	1.3	2.9	0.9	24	111
μ-EOF(2-9-2)	1.3	3.4	0.9	17	68
μ-EOF(2-9-3)	1.3	3.4	1.0	27	98
μ-EOF(2-9-5)	1.3	3.4	1.3	33	118
μ-EOF(2-13-2)	1.3	4.1	0.9	19	81
μ-EOF(2-13-3)	1.3	4.1	1.0	19	82

---

Identical or equivalent solutions were examined by cryoTEM,¹¹ and representative images are presented in Figs. 6a–c. In Fig. 6a, micelles formed by μ-EOF(2-13-3) are shown. In this case there are discrete cores, approximately 15 nm in diameter. The cores are roughly uniformly distributed in space, with the distance of closest approach reflecting the invisible O corona chains. The cores themselves have a speckled appearance, which we attribute to the segregation of small F domains within an E matrix. In Fig. 6b, discrete micelles and strings of micelles are both visible for μ-EOF(2-7-2). These results are initially rather surprising, in that one might expect the O corona to provide steric stabilization for the individual micelles, and thus a repulsive intermicellar potential. The image shows, however, that there is some kind of attraction between the cores, and furthermore that this attraction is not spherically symmetric. Finally, in Fig. 6c, one can see that μ-EOF(2-9-3) forms long, segmented worms. In this case the dark stripes reflect the F domains, which are separated by E layers. Again the O coronas are not directly visible.

Fig. 6 CryoTEM images of micelles formed from (a) μ-EOF(2-13-3); (b) μ-EOF(2-7-2); (c) μ-EOF(2-9-3); these images are reprinted with permission from a larger series which have been reported elsewhere.¹¹ The scale bar is 100 nm.

These images, and many others on the μ-EOF series,¹¹ may be understood at least qualitatively in the following terms. First, all three blocks are extremely strongly segregated from one another, and as the E and F blocks are very hydrophobic, the micellar cores all involve separate compartments of E and F. The very strong segregation causes very high interfacial tensions, which encourages flat interfaces. At the same time, the O block is the longest of the three in all cases, and thus osmotic crowding in the corona favors higher curvature. This interplay is illustrated by the fact that in Fig. 6a the stars with the longest O blocks form discrete micelles, whereas the micelles in Figs. 6b and c show more aggregation of multiple core domains. Although E and F are both hydrophobic, the latter is presumably much more so, so that within the μ-EOF(2-13-3) cores the F nanodomains are surrounded by an E matrix. Note, however, that the star architecture requires the E and F domains to intersect on the outer surface of the core, in contact with the O corona; the F blocks cannot form a separate inner core as was observed in linear triblocks.⁶ The formation of multiple small domains of such a strongly segregating group within an overall hydrophobic core has been anticipated theoretically.⁴⁰

In the case of μ-EOF(2-7-2), the attraction between micelles is proposed to arise as follows. The F blocks aggregate as an ellipsoidal layer, with the E blocks on top and bottom, somewhat in the manner of a hamburger, where E chains constitute the buns.¹¹ The O corona chains are anchored at the E/F interface, and must then wrap around the top and bottom of the buns. The origin of the attraction between micelles is therefore clear: the O corona can fluctuate and expose the hydrophobic domains, so that when two micelles aggregate, the E blocks come into contact and the O chains can relax and stabilize a roughly cylindrical aggregate. The same packing motif is apparent in Fig. 6c, except that in this case the E and F domains have each segregated into flat disks. The diameters of these “segmented worm” micelles are comparable to the fully extended contour lengths of the E and F blocks, once again suggesting that the system is in the superstrong segregation regime.⁸

4. Lattice transition in ordered spherical micelles

It is well established that spherical micelles will order on a lattice at sufficiently high concentrations (typically above 10–20% polymer). At still higher concentrations the spheres may transform to cylinders, and then possibly also to gyroid or to lamellae, depending on the copolymer composition and temperature. Detailed phase diagrams have recently been presented for a variety of SI diblocks, in a range of solvents of varying selectivity.^19,41,42 An interesting observation is that the spherical micelles can pack onto either an fcc or a bcc lattice, depending on conditions. This should be contrasted with the bulk, where only the bcc phase is reported.³ Furthermore, in several solutions a thermoreversible fcc/bcc transition is found. This experimentally convenient order–order transition offers a means to ascertain the control parameter that dictates the choice of lattice symmetry. Examples of the location of the fcc, bcc, and cylinder phases are shown in Fig. 7, in the temperature–composition plane.¹⁹

Fig. 7 Phase behavior of SI diblocks as a function of composition in DEP at the indicated polymer concentrations; figure updated with permission from ref. 19.

The pioneering work of McConnell and Gast,^13,14 and the extensive studies of Hamley, et al.,^15,43 provide some experimental guidance as to the location of the fcc/bcc boundary in SI and in aqueous PEO–PPO and PEO–PBO systems, respectively. The former authors related the micellar results to previous studies on charged colloids, and computer simulations, in which the range and steepness of the intermicellar potential is the key factor. Qualitatively, steeper, shorter-ranged interactions favor fcc, whereas softer, longer ranged potentials favor bcc. The authors did not study the effect of temperature, and thus the phase boundary was crossed by changing polymer composition. The authors proposed that the boundary corresponded to a value of ca. 1.5 for the ratio of the corona block to core block dimensions.

Here we take the following experimental approach.^17,44,45 An SI(16-15) copolymer with a perdeuterated styrene block was dissolved in a mixture of normal and perdeuterated tetradecane, an isoprene selective solvent, to mask out the SANS from the corona block. Similarly, SI(15-14) with a perdeuterated isoprene block was dissolved in the styrene-selective solvent DEP. Low concentrations (0.5, 1, and 2%) were examined as a function of temperature, from room temperature up to the critical micelle temperature.^44,45 The resulting scattering intensities were placed on an absolute basis, and the angular dependence fit to the appropriate spherical form factor.³⁷ The higher concentration solutions also required a term accounting for the structure factor, as previously described.^44,45 In this way it was possible to quantify the temperature dependence of the micellar characteristics, including the aggregation number, the core radius, the fraction of solvent in the core, and the associated equivalent hard-sphere radius. The results between the two systems were very similar, in that at room temperature and up to about 40 °C, the core was devoid of solvent, and the aggregation number and micellar size remained almost constant. However, at higher temperatures the diminishing solvent selectivity led to appreciable solvent uptake in the core. This was actually accompanied by a decrease in mean aggregation number and in micellar dimensions, and an associated increase in the number density of micelles. These changes are a direct consequence of the lowering of the interfacial tension at the core/corona interface, an effect that is completely consistent with the results for SI(13-71) referred to above.⁵

Solutions of the same polymers in tetradecane and DEP were examined by SAXS at higher concentrations, in the ordered state.⁴⁵ Both systems adopted the fcc phase at room temperature, but converted to bcc at a higher temperature (but below the dilute solution CMT). The position of the principal scattering peak, q*, and therefore the lattice parameter, were independent of temperature up to the point where the dilute solution micelles began to shrink. Above that temperature the lattice parameter began to decrease, consistent with a denser packing of progressively smaller but more numerous objects. On the assumption that the temperature dependence of the spherical micellar dimensions is essentially the same in both dilute and concentrated solutions, an assumption that is justified at greater length elsewhere,⁴⁵ it is possible to assign a particular aggregation number as the critical value for the fcc/bcc transition. Then, direct comparison can be made to recent simulations and density functional theory calculations for highly branched star polymers.⁴⁶ The agreement between our micellar data and the predictions for stars is remarkable. Experimentally, aggregation numbers of about 90–100 correspond to the transition, whereas in the simulations the critical number of arms is about 60–70. This small difference is actually consistent with the presence of some loose chains, which in this case act to further stabilize the bcc phase.⁴⁷ Qualitatively, these results are in accord with the previous interpretation in terms of the steepness of the potential.¹⁴ Specifically the lower the aggregation number, the lower the penalty for the overlap of corona chains; this overlap is required in the less efficiently packed bcc lattice. However, we do find that the corona/core length ratio at the transition may vary by up to a factor of two from system to system, but is independent of temperature for a given system, thereby indicating that this is not a reliable parameterization.

Summary

The self-assembly of block copolymers represents a versatile platform for producing nanostructures in the bulk, in thin films, and as discrete objects. In this paper we have illustrated several interesting aspects of micelle formation in block copolymer systems. First, we have demonstrated that the curvature sequence sphere/cylinder/flat bilayer may be observed in “conventional” styrene–isoprene diblock copolymer micelles dispersed in organic solvents, confirming the universality of this phenomenon. The key step in this case is to find a sufficiently selective solvent system, given the rather similar solubility parameters of the two blocks, and furthermore to adjust the composition of the copolymer to minimize osmotic crowding in the corona. Second, the self-assembly of a linear ABC terpolymer leads to an interesting new morphology, a core/shell/corona flattened disk in water. This was achieved by combining a hydrophilic block, a lipophilic block, and a hydrophobic/lipophobic fluorocarbon block. We propose that the observation of a flattened disk, as opposed to a spherical or cylindrical core/shell/corona structure, reflects entry into the superstrong segregation regime. Third, when the architecture of the ABC terpolymer is changed from linear to a miktoarm star, the core/shell/corona motif is suppressed in favor of multicompartment micelles. A fascinating array of micellar structures is observed in cryoTEM, depending on the relative lengths of the three blocks. Finally, we discuss how the thermoreversible fcc/bcc transition observed in higher concentration solutions of spherical micelles may be directly related to changes in the mean aggregation number of the micelles.

Acknowledgements

This work was supported primarily by the MRSEC Program of the National Science Foundation under Award Number DMR-0212302.

References

1. F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38.
2. T. P. Lodge, Macromol. Chem. Phys., 2003, 204, 265–273.
3. I. W. Hamley, The Physics of Block Copolymers, Oxford University Press, Oxford, 1998.
4. M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 1091–1098.
5. J. Bang, S. Jain, Z. Li, T. P. Lodge, J. S. Pedersen, E. Kesselman and Y. Talmon, in preparation.
6. Z. L. Zhou, Z. B. Li, Y. Ren, M. A. Hillmyer and T. P. Lodge, J. Am. Chem. Soc., 2003, 125, 10182–10183.
7. T. P. Lodge, M. A. Hillmyer, Z. L. Zhou and Y. Talmon, Macromolecules, 2004, 37, 6680–6682.
8. A. N. Semenov, I. A. Nyrkova and A. R. Khokhlov, Macromolecules, 1995, 28, 7491–7500.
9. I. A. Nyrkova, A. R. Khokhlov and M. Doi, Macromolecules, 1993, 26, 3601–3610.
10. H. Iatrou and N. Hadjichristidis, Macromolecules, 1992, 25, 4649–4651.
11. Z. Li, E. Kesselman, Y. Talmon, M. A. Hillmyer and T. P. Lodge, Science (Washington, D. C.), 2004, 306, 98–101.
12. Z. Li, M. A. Hillmyer and T. P. Lodge, Macromolecules, 2004 , in press.
13. G. A. McConnell, A. P. Gast, J. S. Huang and S. D. Smith, Phys. Rev. Lett., 1993, 71, 2102–2105.
14. G. A. McConnell and A. P. Gast, Macromolecules, 1997, 30, 435.
15. I. W. Hamley, C. Daniel, W. Mingvanish, S.-M. Mai, C. Booth, L. Messe and A. J. Ryan, Langmuir, 2000, 16, 2508–2514.
16. I. W. Hamley, J. A. Pople and O. Diat, Colloid Polym. Sci., 1998, 276, 446.
17. J. Bang, T. P. Lodge, X. H. Wang, K. L. Brinker and W. R. Burghardt, Phys. Rev. Lett., 2002, 8921, 18.
18. J. Bang and T. P. Lodge, J. Phys. Chem. B, 2003, 107, 12071–12081.
19. T. P. Lodge, B. Pudil and K. J. Hanley, Macromolecules, 2002, 35, 4707–4717.
20. Y. Ren, T. P. Lodge and M. A. Hillmyer, Macromolecules, 2001, 34, 4780–4787.
21. J. N. Israelachvili, Intermolecular and Surface Forces, 1991.
22. Y.-Y. Won, A. K. Brannan, H. T. Davis and F. S. Bates, J. Phys. Chem. B, 2002, 106, 3354–3364.
23. Y.-Y. Won, H. T. Davis and F. S. Bates, Science (Washington, D. C.), 1999, 283, 960–963.
24. S. Jain and F. S. Bates, Science (Washington, D. C.), 2003, 300, 460–464.
25. S. Jain and F. S. Bates, Macromolecules, 2004, 37, 1511–1523.
26. H. Shen and A. Eisenberg, Macromolecules, 2000, 33, 2561–2572.
27. H. Shen and A. Eisenberg, J. Phys. Chem. B, 1999, 103, 9473–9487.
28. L. Zhang and A. Eisenberg, Science (Washington, D. C.), 1995, 268, 1728–1731.
29. L. Zhang and A. Eisenberg, Macromolecules, 1999, 32, 2239–2249.
30. P. A. Canham, T. P. Lally, C. Price and R. B. Stubbersfield, J. Chem. Soc., Faraday Trans. I., 1980, 76, 1857–1867.
31. J. S. Pedersen, I. W. Hamley, C. Y. Ryu and T. P. Lodge, Macromolecules, 2000, 33, 542–550.
32. I. LaRue, M. Adam, M. da Silva, S. S. Sheiko and M. Rubinstein, Macromolecules, 2004, 37, 5002–5005.
33. R. Borsali, E. Minatti, J.-L. Putaux, M. Schappacher, A. Deffieux, P. Viville, R. Lazzaroni and T. Narayanan, Langmuir, 2003, 19, 6–9.
34. J.-L. Putaux, E. Minatti, C. Lefebvre, R. Borsali, M. Schappacher and A. Deffieux, Faraday Discuss., 2004, 128 10.1039/b403157a.
35. K. J. Hanley, PhD Thesis, University of Minnesota, 2001.
36. J. S. Pedersen and M. C. Gerstenberg, Macromolecules, 1996, 29, 1363.
37. J. S. Pedersen, J. Appl. Crystallogr., 2000, 33, 637–640.
38. Y. Ren, T. P. Lodge and M. A. Hillmyer, Macromolecules, 2002, 35, 3889–3894.
39. A. Halperin, M. Tirrell and T. P. Lodge, Adv. Polym. Sci., 1991, 100, 33.
40. E. E. Dormidontova and A. R. Khokhlov, Macromolecules, 1997, 30, 1980–1991.
41. T. P. Lodge, K. J. Hanley, B. Pudil and V. Alahapperuma, Macromolecules, 2003, 36, 816–822.
42. K. J. Hanley, T. P. Lodge and C.-I. Huang, Macromolecules, 2000, 33, 5918.
43. I. W. Hamley, J. A. Pople and O. Diat, Colloid Polym. Sci, 1998, 276, 446.
44. J. Bang, K. Viswanathan, T. P. Lodge, M. J. Park and K. Char, J. Chem. Phys., 2004 , in press.
45. T. P. Lodge, J. Bang, M. J. Park and K. Char, Phys. Rev. Lett., 2004, 92, 145501.
46. M. Watzlawek, C. N. Likos and H. Löwen, Phys. Rev. Lett., 1999, 82, 5289.
47. E. Stiakakis, D. Vlassopoulos, C. N. Likos, J. Roovers and G. Meier, Phys. Rev. Lett., 2002, 89, 208302.

---