The simultaneous modelling of metal ion and humic substance transport in column experiments

Abstract

Pulsed column experiments using Co, fulvic acid and porous sediment packing, along with up/down-flooding experiments using Eu, humic acid and intact sandstone blocks have been performed. The elution of metal and humic and their distribution along the sandstone columns have been measured. A mixed equilibrium and kinetic coupled chemical transport model has been used to simulate the results. In both cases, one exchangeable and one non-exchangeable component have been used to simulate the interaction of metal and humic substance. For the pulsed experiments, a simple equilibrium approach was used to model humic sorption, while a two component, kinetic model was required for the sandstone columns.

---

1 Introduction

Humic substances have a high affinity for most cations, and have long been suspected as possible vectors for the movement of heavy metals and radionuclides in the environment.¹ As a result, their interactions with metals have been heavily studied. Most of this work has been experimental, but there have also been a significant number of modelling studies, which have taken a wide variety of approaches.¹ The majority of models have addressed the rapid uptake of metal ions by solution phase humic substances (for example refs. 2 and 3). However, it has become clear that, although the initial uptake of metals is rapid, not all of the metal loading may be removed instantaneously by a stronger competing sink. Rather, a fraction of the metal becomes ‘non-exchangeably’ bound, the size of the fraction depending upon the contact time.⁴ This slowly desorbing component is the most likely to be responsible for the humate-mediated transport of metals in the environment.^5,6 A coupled chemical transport model, k1-D, has been developed,^6,7 which incorporates simple 1-D transport, and allows chemical processes to be described with both equilibrium and rate constants simultaneously. It has been used successfully to model the migration of metals, Eu⁶ and Am,⁷ through porous columns. However, in both cases, the transport of the humic itself was not determined during the experiments, and was not treated explicitly in the modelling. Most transport modelling has naturally focussed upon simulating the behaviour of the metal, rather than the humic substance itself. In some cases, where the solid phase has been pre-equilibrated with the humic, it has been found that there is no significant retardation of metal–humic complexes. For example, Warwick et al.⁶ were able to simulate Eu transport, by assuming that the Eu–humate complex moved as a conservative tracer, whilst Schussler et al.⁷ found that Am–humate complex moved slightly faster than a conservative tracer, presumably because of exclusion effects. In many cases, it is impossible to treat explicitly the behaviour of the humic, because in a pre-equilibrated system, it is often impossible to track the movement of fresh humic. However, this work concerns the simultaneous modelling of both metal and humate transport in column experiments. The object of this work is not to investigate the mechanisms of the interactions between metal ions, humic substances and surfaces. Rather, the aim is to test whether a simple chemical model may be used to predict metal ion and humate transport in laboratory column experiments. Field scale models of metal ion transport are required, for example, in the long-term radiological performance assessment of radioactive disposal sites. In order for such models to be used routinely, they must be as numerically efficient as possible, and hence, simplicity is essential. Column effluent, or breakthrough, data are routinely used on their own to calibrate transport models, but in the field scale predictions, it is the distribution of pollutant with distance from the source (the profile) that is of greatest interest. Another aim of this work is to determine whether a model calibrated with effluent data alone is able to predict the distribution of metal ions along the length of a column.

The uptake of humic substances by surfaces has been studied previously, mostly via batch experiments. A number of studies (for example refs. 8, 9 and 10) have found that the adsorption step may be simulated with Langmuir isotherms, although the derived parameters may be conditional. There are two distinct aspects to this reaction, sorption and desorption. Both are complex, but the sorption step appears, at least superficially, easier to model. It has been characterised as fast, whilst desorption is described as slow.¹¹ Most studies have addressed only the sorption step, and have not addressed kinetic effects.¹² As a result, most transport models consider humate sorption to be reversible.¹² However, the desorption step is crucial in the transport of humate borne contaminants.¹²

A number of mechanisms have been suggested for the binding of humic substances to inorganic surfaces. These include:¹³ ligand exchange; cation/anion exchange; cation bridging; ‘entropy-driven’ physical sorption; hydrogen bonding and van der Waals/hydrophobic interactions. Experiments using NMR/FTIR have suggested that the ligand exchange mechanism does take place.¹⁴ In the case of that mechanism, the oxygen donors from humic acid, probably hydroxyl –O, replace surface –OH groups, and a covalent bond forms between the humic and the surface.¹⁴ However, the evidence that ligand exchange occurs does not preclude that the others also take place. Indeed, Juhna et al.¹⁵ have suggested that different fractions may have predominantly physical or chemical interactions with the surface.

Although the nature of the interaction is uncertain, most recent authors agree that it is not possible to treat humic substances as single, simple ligands (for example ref. 13). Even for the sorption step alone, it is necessary to define more than one reaction, or to treat the sample as a mixture of ligands in order to reproduce the experimental data. Lenhart and Honeyman¹³ use a multi-ligand, equilibrium approach. They define 5 components, each with a distinct interaction. On the other hand, Gu et al.¹⁴ adopt a modified Langmuir approach, which uses a single (total) humic acid concentration, but where the affinity changes with surface coverage. Although superficially these two approaches are quite different, the net result is the same: a single humic acid–surface affinity constant does not describe the sorption of humic substances.

It is accepted that these systems show considerable hysteresis, or irreversibility. That is, the desorption isotherm is not the same as the sorption isotherm.¹⁶ It has been shown that if surfaces are coated with competing ligands, then humate sorption may be prevented,¹⁷ but that if the same concentration of ligand is introduced to a surface already coated with humate, then only a fraction of the humic will be desorbed.¹⁸ A number of studies have shown that at least some fraction of sorbed humic material only desorbs very slowly,¹⁴ and that as long as 60 d may be required to re-establish equilibrium,¹² although there are a number of possible explanations for this behaviour. Avena and Koopal¹⁶ found that desorption as a result of pH change was rapid, but as a result of a change in humic concentration was slow, requiring months to be complete. These results suggested that electrostatic interactions are crucial to the binding mechanism. Some fraction of the humic material may form a stronger interaction with the surface; for example, Gu et al.¹⁴ have suggested that species with ortho functional groups might form strong chelate interactions with the surface. They also suggest that the slow desorption kinetics may be due to the fact that multiple strong bonds are formed between the humic and the surface, which must all be broken, resulting in a large activation energy. Beyond any specific chemical effect, high weight species should be preferentially sorbed, because they lose less translational entropy in doing so.¹⁹ Hence, the differences between sorption and desorption isotherms could be due to the fact that the two experiments have different fraction populations. In the adsorption step, higher molecular weight fractions are preferentially absorbed, leaving less favoured species in solution. During desorption, when the solution is replaced with electrolyte, the majority of species in the system have high affinities, and so for a given humic surface loading, a lower solution concentration is observed.¹⁶ In this model, the hysteresis is only apparent, an artefact caused by treating the humic substance as uniform with a single concentration. Gu et al.¹² provide some support for this approach, since they found that higher weight fractions were bound more strongly, and had higher capacities. Similar effects were observed for more hydrophobic fractions, and it was suggested that the inherent polydispersity of humic substances could be the key to understanding hysteresis. However, there is experimental evidence that desorption is a slow process. It has been suggested that slow transfer between the bulk solution and the adsorbed layer (involving some sort of activation barrier) on top of this mechanism is responsible for the slow reactions.^16,20 Most authors suggest that the complex behaviour is due to some property of the humic (for example ref. 14). In contrast, other authors have suggested that the hysteresis is the result of available reversible and (pseudo)-irreversible sorption sites on the surface itself.²¹

There have been a number of attempts to predict humic desorption quantitatively, but only a few humate desorption rate constants have been published. McCarthy et al.^22,23 used a two site model to match the adsorption stage of humic transport. Gu et al.¹⁴ had to adapt their modified Langmuir model, which they used to describe the sorption step. An extra hysteresis parameter was added, which had the effect of increasing the amount of humic sorbed onto the surface relative to a system with the same free solution humic concentration during the sorption step. Munch et al.²⁴ used column experiments to measure humate desorption from soil. They found that as flow rate decreased, the humate concentration in the effluent increased, a clear indication of kinetic control. By fitting, they determined a first order desorption rate of 4.5 × 10⁻⁷ s⁻¹. The NOMADS model of Van de Weerd et al.²⁵ has proved to be most promising. Selectivity by mass fraction forms the basis of the approach. It is assumed that the number of surface binding sites covered by a given species will be variable, and may change with time, but that on average the number covered will increase with molecular weight and size. Each mass fraction has its own ‘local’ competitive kinetic adsorption isotherm, but all fractions compete for the same surface sites. Applying their model to the data of Gu et al.,¹⁴ they derived first order desorption rates for 3 mass fractions: 3 × 10⁻⁴ s⁻¹ (M < 10³); 9 × 10⁻⁶ s⁻¹ (10³ < M < 10⁵); 9 × 10⁻⁷ s⁻¹ (M > 10⁵). Even for the adsorption step, the model predicts that true equilibrium over all fractions may take hundreds of hours, depending upon the humic concentration (∼170 h at [HA] = 2 ppm and ∼720 h at 14 ppm). More recently, the model has been incorporated within a transport code,²⁶ and used to model lab and field scale humic transport experiments. Six fractions were defined to simulate the lab column experiments with first order desorption rates ranging from 6 × 10⁻³ s⁻¹ to 1 × 10⁻⁶ s⁻¹, and 3 fractions to model the field transport experiments (5 × 10⁻³ s⁻¹ to 1 × 10⁻⁵ s⁻¹). The results are very impressive, and the model is able to predict the transport of the humic substances, although it does not include metal ion transport.

2 Materials and methods

Two separate sets of column experiments were performed: (1) short, pulsed experiments with cobalt (Co) and using columns packed with porous sediment; (2) up/down-flooding experiments with europium (Eu) and using intact sandstone blocks. The k1-D transport code was used. Its operation and testing have been reported previously.^6,7

2.1 Pulsed column experiments

These experiments involved short columns (6–20 cm), packed with sand from a site in Cumbria, UK. The packing was fully equilibrated with groundwater taken from the same site. The groundwater contained humic substances, at a relatively low concentration (2.8 ppm). All injection solutions were made up with groundwater. The metal, ⁵⁷Co, and fulvic acid, isolated from the Broubster site in Scotland, UK, were injected as a pulse of metal–fulvate complex ([fulvic] = 32.5 ppm; [Co_TOTAL] = 1.3 × 10⁻⁸ M) in a continuous stream of groundwater. The metal–fulvate complex was allowed to equilibrate for a known period of time, of the order of a few days, prior to injection. The porosity and dispersivity were determined at the same time by injection of inert ³⁶Cl. The breakthrough of the ⁵⁷Co and ³⁶Cl were determined radiometrically, and the humic via UV/Vis absorption spectroscopy.

2.2 Up/down-flooding column experiments

These experiments used intact cylindrical columns cut from sandstone blocks. The sides of the columns were coated with impermeable resin, such that solutions could only pass into or out of the column via the ends. Iodinated (¹²⁵I) humic acid was prepared from Aldrich humic acid, using the method of Lassen et al.²⁷ Previous work has shown that the behaviour of the ¹²⁵I-humic is identical to that of the starting material.²⁸ Prior to the experiments, each sandstone column was equilibrated with the humic acid (non-radiolabelled) and inert electrolyte concentrations used in the experiments. All the columns had radii of 2.5 cm, but the lengths varied between 10 and 30 cm. The flow rates ranged from 5 ml h⁻¹ to 15 ml h⁻¹.

These experiments had two distinct parts: ‘up-flooding’ and ‘down-flooding’. In the up-flooding section, Eu–¹²⁵I-humate complex in 0.3 M NaCl, pH 6.5 electrolyte was injected into the column ([HA] = 40 ppm, [Eu_TOTAL] = 5 × 10⁻⁸ M, [¹²⁵I] = 360 kBq dm⁻³, [¹⁵²Eu] = 2.4 MBq dm⁻³). After a known volume (between 0.5 and 2 dm³) had been injected, the feed solution was changed to one that contained 40 ppm HA (not labelled with ¹²⁵I), but no Eu. This was the down-flooding section. The breakthrough of the Eu and ¹²⁵I-humic were determined radiometrically. At regular intervals, the distribution of the ¹⁵²Eu and ¹²⁵I along the column were determined using a collimated detector, which was tracked along the length of the column. The porosities and dispersivities were determined by injection of tritiated water.

2.3 Modelling

For both sets of experiments, one parameter set was used to describe the interaction of the metal with the humic substance, regardless of whether the humic colloid was sorbed or in solution.

The set of equations and parameters for the pulsed column experiments are shown in Table 1. HA_S and HA_FREE represent humic substance bound to the sediment surface and in solution, respectively, and Eq is the humic exchangeable binding site. Co_(aq) and Co_S represent free Co and Co bound to the surface, while Co_Eq and Co_FIX represent Co bound in the humic exchangeable and non-exchangeable fractions, respectively. Square brackets [*] represent concentrations, ↔ equilibria and ⇆ kinetic (slow) reactions. A single surface site was defined for both metal and humic sorption, which was present in vast excess, and hence had a virtually constant concentration ([S] = 0.1 mol dm⁻³ effective volume concentration). However, this does not suggest that the species are actually bound at a single, ‘real’ common site. The ‘correct’ surface site concentration for humic and Co sorption is unknown, and cannot be determined from the experimental data, since saturation was not even approached in either case. An arbitrary value has been used. However, this will not affect the goodness of fit, since the surface concentration is acting as a scaling constant: if the true value of [S] were lower, then K_S and K_HA would alter proportionately, but the fit would not change. In other words, the experimental data provide us with only the two products, K_S[S] = 1 × 10⁶ and K_HA[S] = 1, but not the absolute values of equilibrium constants and surface site concentrations.

Table 1 Reaction, equation and parameter set used to model the pulsed, Co columns

Chemical reaction	Mathematical equation	Parameter values
Co(aq) + S ↔ CoS		K S = 1.0 × 10^7 dm^3 mol^−1
Co(aq) + Eq ↔ CoEq		K Eq = 5.0 × 10^8 dm^3 mol^−1
HAFREE + S ↔ HAS		K HA = 10.0 dm^3 mol^−1
CoEq ⇄ CoFIX		k f = 2.9 × 10^−7 s^−1
		k b = 1.3 × 10^−6 s^−1

---

In the case of the sandstone columns, a more complex series of reactions and equations was required (Table 2): two surface bound humic fractions were required, HA_S1 and HA_S2, whose formation required a kinetic description. The sorption of both metal and humic was described by simple first order relationships. For these columns, the model parameters were obtained by fitting the elution profiles, and these parameters were then used ‘blind’ to predict the profile. It was found that the precise values of the k_f and k_b parameters (Table 2) were not well defined by the data, provided that the rates were sufficiently small that there was no significant desorption on the scale of the column residence time. Hence, values for k_f and k_b were taken from a previous batch desorption study.²⁹ The interaction of the Eu with the sandstone surface was modelled with a kinetic equation. This is in agreement with previous modelling of up/down-flooding experiments.⁶

Table 2 Reaction, equation and parameter set used to model the sandstone, Eu columns

Chemical reaction	Mathematical equation	Parameter values
Eu(aq) + Eq ↔ EuEq		K Eq = 2.0 × 10^5 dm^3 mol^−1
EuEq ⇄ EuFIX		k f = 2.4 × 10^−7 s^−1
		k b = 5.0 × 10^−7 s^−1
Eu(aq) ⇄ EuS		k EuSf = 2.0 × 10^−4 s^−1
		k EuSb = 1.0 × 10^−6 s^−1
HAFREE ⇄ HAS1		k HAS1f = 1.7 × 10^−5 s^−1
		k HAS1b = 1.5 × 10^−5 s^−1
HAFREE ⇄ HAS2		k HAS2f = 6.0 × 10^−6 s^−1
		k HAS2b = 1.0 × 10^−7 s^−1

---

Column experiments with humic substances have been modelled before, but this is the first time that the behaviour of metal ion and humic have been modelled simultaneously. The treatment of the profile data is also novel.

3 Results

All elution data (Figs. 1–4) are displayed as C/C₀, where C is the concentration of metal or humic eluting, and C₀ is the initial, injection concentration. For the profile data, Figs. 5 and 6, the experimental technique provides only relative concentrations of ¹⁵²Eu and ¹²⁵I. Therefore, the concentrations (y-axes) in these figures are relative only.

Figs. 1 and 2 show typical experimental and modelling results obtained with the pulsed columns. The experimental results show elution profiles typical of short, pulsed columns: a short lag time, followed by a steady rise to a maximum, and then a steady fall off. Both species were retarded by the columns, Co to a greater extent than the humic. The interaction of the humic with the packing is relatively weak (K_HA = 10 dm³ mol⁻¹, Table 1), whereas the interaction of the Co is very strong. In fact, in the absence of humate, there was no Co breakthrough (data not shown). Therefore, only humate-associated Co emerges in the effluent. Note the correlation between the Co and humic breakthrough in Fig. 2. In all of these experiments, the Co and humic breakthrough maxima always coincide. The model achieves a reasonable fit to both the humic and Co effluent plots. Only two columns are shown here, although similar results were obtained for a number of different column experiments. It was essential to have a mixed kinetic and equilibrium description of the metal–humate interaction, i.e., exchangeable and non-exchangeable binding. For the interaction of the humate with the packing, it was found that the use of a kinetic approach did not improve the fit.

Fig. 1 Experimental elution data for 6.4 cm pulsed column (flow rate = 0.5 ml h⁻¹, diameter = 1 cm; ○ = humic) and model prediction (line).

Fig. 2 Experimental elution data for 6 cm pulsed column (flow rate = 0.5 ml h⁻¹, diameter = 1 cm; ◆ = humic, + = Eu) and model predictions (lines).

Figs. 3 and 4 show typical elution profiles and modelling results for the sandstone column experiments. The general shapes of the plots are similar to those of Eu in previous up/down-flooding experiments using columns packed with sediment.⁶ That study demonstrated that plots of this shape may only be simulated using an approach that includes chemical kinetics. It is significant that, although the relative amount of the humic breaking through is different to that of the Eu, the shape of the elution plot is the same. Again, a kinetic description was required to simulate the behaviour correctly. The shapes and positions of the Eu and humic plots are indicative of a multi-component system. In each case, there is a fairly rapid breakthrough followed by a decrease in gradient to give a relatively steady outflow concentration. Since the steady value (C/C₀) is less than 1, there must be at least 2 chemical reactions involved: the exchangeable and non-exchangeable components in the case of Eu, and the two humic sorption sites in the case of the humic.

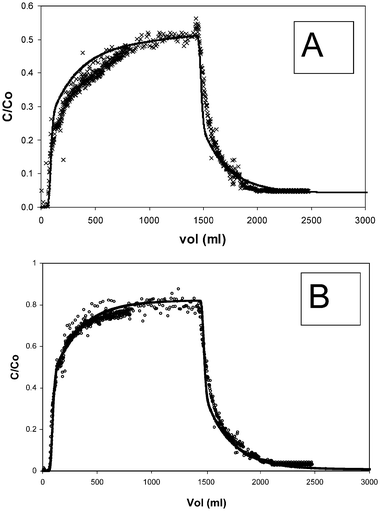Fig. 3 Experimental elution data for 30 cm sandstone column (flow rate = 10 ml h⁻¹; (A) × = Eu, (B) ○ = humic) and model predictions (lines).

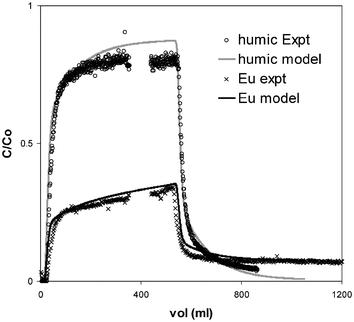Fig. 4 Experimental elution data for 10 cm sandstone column (flow rate = 15 ml h⁻¹; × = Eu, ○ = humic) and model predictions (lines).

Fig. 5 shows the distribution of ¹⁵²Eu and ¹²⁵I activity along a 30 cm column as a function of elution time for 6 equally spaced segments along the length of the column. During the up-flooding stage, as Eu sorbs to the sandstone, its activity in all 6 segments increases steadily with time. The maximum for each segment marks the start of down-flooding. As down-flooding proceeds, the Eu activity at the start (injection end) of the column eventually decreases as the humic acid, now not radiolabelled, pulls the sorbed metal into solution. In the middle and at the outflow end of the column the Eu activity actually increases slightly, because Eu released from further up the column is replacing that removed by the humic acid. Eventually, the activities in these segments would also start to decrease. In the case of the humic profile (Fig. 5B), the activity in all 6 segments starts to decrease immediately with the onset of down-flooding. This difference is indicative of the weaker interaction between the humic acid and the sandstone, compared to the Eu. Fig. 6 shows Eu column profiles for 10 cm columns and two different flow rates. Because of the short length of the columns, experimental data for only a single segment were recorded. Three model predicted profiles have been produced for each column, for the start, middle and outflow end.

Fig. 5 (A) Experimental Eu profile (×) and model prediction (lines) for 6 segments, plotted as relative concentration vs. elution time; (B) corresponding experimental humic profile (○) and model predictions (lines). 30 cm column, flow rate = 10 ml h⁻¹.

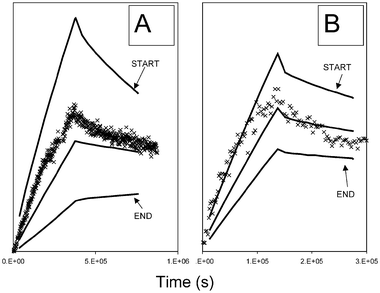Fig. 6 Experimental Eu profiles (×) plotted as relative concentration vs. elution time for 10 cm columns and model predicted profiles for start, middle and outflow ends of the columns: (A) flow rate = 5 ml h⁻¹; (B) flow rate = 15 ml h⁻¹.

4 Discussion

The experimental data on their own demonstrate that metal transport is dominated by humic interactions. In Figs. 1–4, there is a strong correlation between the elution of the metals and the humics. Indeed, for both sets of experiments, metal transport was negligible in the absence of humic material, which is in agreement with previous studies (for example refs. 5 and 7). The correlation between the Co and humic elution plots in the pulsed columns (Fig. 2) is significant. Firstly, it clearly demonstrates the role of the humic in promoting migration. It also demonstrates the importance of understanding the sorption behaviour of the humic. The Co and humate maxima are coincident, because the only Co emerging from the column is associated with the humic, and so has assumed the sorption characteristics of the humic itself. Any Co not bound to the humic does not make it past the very beginning of the column. When predicting the migration of metals in the geosphere, this relatively rapidly moving humic associated fraction will be of greatest interest. Therefore, it is crucial to know how the humic itself will behave.

In agreement with previous studies,^6,7 a mixed approach, with one kinetic and one equilibrium reaction, was used to simulate the interaction of both Co and Eu with humic substances. In those previous studies, this one non-exchangeable component approach was able to provide a decent fit to observation, and once again, it has worked here. Batch kinetic studies have found evidence for the existence of a spectrum of desorption rates, ranging from instantaneously exchangeable to very slow (for example refs. 4 and 29). However, amongst the continuum there appears to be a distinct, most slowly desorbing component, which may be described with a single definite rate constant. This fraction accounts for a significant proportion of bound metal, typically 20–50% for Eu–humic acid (depending upon solution conditions, pH, ionic strength etc.). It is the kinetic parameters for this fraction (determined by batch experiments) that have been used here (k_f and k_b, Table 2). It seems that, although the spectrum of desorption rates does exist, it is only necessary to consider the distinct, slow fraction in order to predict metal transport. There are small differences between experiment and model (Figs. 1–4). Small improvements could be achieved by the addition of extra non-exchangeable components to the model. However, any such extension would increase the complexity of the model for little return. In order to be useful on the field scale, chemical models need to be as simple as possible; otherwise, the calculations become prohibitively expensive.

The model fit for the sandstone profiles (Figs. 5 and 6) is less close than for the elution data (Figs. 3 and 4), because these profiles were blind modelled (i.e., profile data were not included in the parameter fitting process). This was deliberate, since transport models are used on the field scale to predict distributions even though they are typically calibrated with elution (breakthrough) data from column experiments. The object was to test whether the model was at least able to predict the profiles of the columns used to calibrate it. The 30 cm humic profile fit (Fig. 5B) is closer than the corresponding Eu profile (Fig. 5A): the model occupies the correct region of the plot, but the shape in the down-flooding section is not perfect. For the Eu profile (Fig. 5A), again the up-flooding section is quite good. During down-flooding the model performs less well, but the fit at the outflow end of the column is much better than at the start. This is not surprising, since the model parameters were determined by analysis of the elution (outflow) data, and hence, the model is bound to be better at predicting the conditions at the outflow end. This result shows the importance of considering elution and profile data. Elution (breakthrough) data are more common than profile data; and it is certainly possible to define transport parameters using only these data (for example ref. 6). However, when transport parameters are used to make field scale predictions, it is the predicted profile that is of most interest. This work suggests that profile predictions made using parameters derived from elution data will not always be as good as reproductions of the effluent data themselves. Therefore, with humic substances some care should be exercised when applying parameters to simulations outside of the scope of the data used to obtain them. The origin of the profile discrepancy is unclear. It could be a problem with the prediction of the behaviour of the humic, although the humic profile is better. Therefore, the error may lie in the description of the interaction of the Eu with the sandstone. The fit to the 10 cm columns (Fig. 6) seems better, although with only one segment, it is harder to make a comparison.

This study differs from our previous work in the treatment of humic substance sorption. There, it was not necessary to take account of humic sorption explicitly.^6,7 In this study, two different approaches are used to model humic sorption. In the case of the pulsed columns, a simple equilibrium, ‘K_d’ approach is sufficient, whereas for the sandstone columns, an equilibrium approach would not work, and a two component kinetic model was required. In the experiment shown in Fig. 2, the column residence time is ≈4 h, compared to 9 h for the experiment in Fig. 3. Hence, it is unlikely that the difference is due to this. However, the total experiment times are very different: ≈10 h, Fig. 2; 250 h, Fig. 3. In the case of the pulsed experiment, there may be insufficient time for significant desorption to take place. Hence, only the sorption step need be accounted for, and a ‘K_d’ approach works. In the sandstone experiments, there is sufficient time for desorption, and a full kinetic description is required. Of course, in such complex systems alternative explanations are possible. For example, the pulsed columns used fulvic acid and packing material not equilibrated with the fulvic concentration used in the experiments, while the sandstone experiments used humic acid and fully equilibrated columns. In many ways the sandstone experiments represent a more realistic approximation of the real system: at a contaminated site, the surfaces will be in equilibrium with the ambient concentration of humic substances, and short pulses of high concentration would not be expected. Alternatively, the different column media may be responsible. Humic sorption has been observed in the sandstone columns, but the modelling has shown that neither desorption nor exchange between sorbed and solution phase humic acid take place instantaneously. On the other hand, no evidence for so called ‘irreversible’ sorption was found, and given sufficient time, one would expect complete exchange to take place.

In the case of the metal–humic interaction, it has been found that a single description may describe a wide variety of systems, including fulvic and humic acids.^6,7,29 It seems that the mineral surface–humic interaction is more complex. A variety of approaches have been adopted.^23,25 Although the precise formulation of this model is different to others, we may compare the humic desorption rate constants, because they are first order. The rates found here, 1.5 × 10⁻⁵ and 1 × 10⁻⁷ s⁻¹ (sandstone columns), are in the same range as those quoted by Munch et al.,²⁴ 4.5 × 10⁻⁷ s⁻¹, and Van de Weerd et al.,²⁵ 3 × 10⁻⁴ s⁻¹ (M < 10³); 9 × 10⁻⁶ s⁻¹ (10³ < M < 10⁵); 9 × 10⁻⁷ s⁻¹ (M > 10⁵). Tentatively, one might suggest that our faster and more slowly desorbing fractions represent lower and higher mass material, respectively. This work does not imply that there are only two distinct fractions, only that a minimum of two are required to simulate the sandstone data adequately. Hence, this work seems to agree with those previous studies, although this approach is more simplistic. Of course, this model provides no information on the mechanism(s) of sorption. It is consistent with either inherent chemical heterogeneity and slow diffusion to the bulk, or the presence of different surface sites with varying sorption/desorption rates.

This model is a gross simplification of a very complex system, and there are many ways in which it might be considered unrealistic. For example, we have treated humic acid as a single entity with one concentration. This does not imply that there really is only one fraction. This model is the simplest possible description of a complex system that provides an adequate prediction. The ultimate aim of studies such as this is to provide information that will be useful in field scale predictions of humate mediated transport. We now have a better understanding of the transport of humic substances and metal ions in column experiments under these particular laboratory conditions. However, this understanding must be treated with care. Although models and parameters have been developed to describe lab experiments, it would be wrong to assume that they could be applied ‘blind’ to field-scale problems. In particular, models calibrated with elution data may not always provide the best predictions of profiles. This work has shown that even with a very simple chemical model, it is possible to obtain reasonable estimates of metal ion migration, at least on the column scale. However, we are not yet at the stage where models calibrated by column experiments alone may be applied with complete confidence to the field scale. The difference in the modelling between the pulsed and sandstone columns illustrates this point: the initial pulsed columns indicated that an equilibrium approach could model humic sorption, but such an approach failed to simulate the sandstone columns. The differences between column and field scales are likely to be at least as significant. Hence, more work is required, ideally on the field scale itself, before long range predictions of metal ion transport may be made with confidence.

5 Conclusions

It is now clear that a mixed equilibrium and kinetic approach is essential to describe the humate-mediated transport of metal ions. However, the precise definition of the model may vary.

In agreement with previous work, a single non-exchangeable component model has been used to describe the interaction of metals with humic substances, and although such a model can go a long way to explain the observed transport behaviour, it is still a gross simplification of a very complex system.

The evidence suggests that humic sorption may well be as complex as the interaction with metals, and that, although an equilibrium approach may suffice for some systems, a multi-component, kinetic approach is needed for many others. No evidence has been found for ‘irreversibility’ in these experiments. However, further work is required before predictions may be made on the field-scale with confidence.

This simple chemical model is sufficiently simple that it could conceivably be used to make field scale predictions, whilst still providing an adequate approximation of the surface/humic/metal ion system. However, the differences between the approach to humic sorption in the two sets of experiments and the poorer fits to the profiles shows that care should be taken when extrapolating beyond the range of calibration, and that these models should ideally be calibrated under the same conditions as their predictions.

Acknowledgements

The authors would like to thank the European Commission for funding this work as part of the 4th framework HUMICS and 5th framework HUPA projects.

References

1. M. N. Jones and N. D. Bryan, Adv. Colloid Interface Sci., 1998, 78, 1–48.
2. E. Tipping and M. A. Hurley, Geochim. Cosmochim. Acta, 1992, 56, 3627–3641.
3. D. G. Kinniburgh, C. J. Milne, M. F. Benedetti, J. P. Pinheiro, J. Filius, L. K. Koopal and W. H. van Riemsdijk, Environ. Sci. Technol., 1996, 30, 1687–1698.
4. G. R. Choppin and S. B. Clark, Mar. Chem., 1991, 36, 27–28.
5. J. F. McCarthy, K. R. Czerwinski, W. E. Sanford, P. M. Jardine and J. D. Marsh, J. Contam. Hydrol., 1998, 30, 49–77.
6. P. Warwick, A. Hall, V. Pashley, N. D. Bryan and D. Griffin, J. Contam. Hydrol., 2000, 42, 19–34.
7. W. Schussler, R. Artinger, J. I. Kim, N. D. Bryan and D. Griffin, J. Contam. Hydrol., 2001, 47, 311–322.
8. E. Tipping, Humic substances and the surface properties of iron oxides in freshwaters, in Transfer Processes in Cohesive Sediment Systems, ed. W. R. Parker and J. Kinsman, Plenum, 1984.
9. M. A. Schlautman and J. J. Morgan, Geochim. Cosmochim. Acta, 1994, 58, 4293–4303.
10. A. Tessier, D. Fortin, N. Belzile, R. R. De Vitre and G. G. Leppard, Geochim. Cosmochim. Acta, 1996, 60, 387–404.
11. M. Ochs, B. Cosovic and W. Stumm, Geochim. Cosmochim. Acta, 1994, 58, 639–650.
12. B. Gu, J. Schmitt, Z. Chen, L. Liang and J. F. McCarthy, Geochim. Cosmochim. Acta, 1995, 59, 219–229.
13. J. J. Lenhart and B. D. Honeyman, Geochim. Cosmochim. Acta, 1999, 63, 2891–2901.
14. B. Gu, J. Schmitt, Z. Chen, L. Liang and J. F. McCarthy, Environ. Sci. Technol., 1994, 28, 38–46.
15. T. Juhna, M. Klavins and L. Eglite, Chemosphere, 2003, 51, 861–868.
16. M. J. Avena and L. K. Koopal, Environ. Sci. Technol., 1999, 32, 2572–2577.
17. B. Gu, T. L. Melhorn, L. Liang and J. F. McCarthy, Geochim. Cosmochim. Acta, 1996, 60, 1943–1950.
18. B. Gu, T. L. Melhorn, L. Liang and J. F. McCarthy, Geochim. Cosmochim. Acta, 1996, 60, 2977–2992.
19. A. W. P. Vermeer and L. K. Koopal, Langmuir, 1998, 14, 4210–4216.
20. J. C. Dijt, M. A. Cohen Stuart and G. J. Fleer, in Colloid-Polymer Interactions, ed. P. L. Dublin and P. Tong, ACS Symposium Series No. 532, American Chemical Society, Washington DC, 1993, pp. 14–22.
21. D. A. Vaccari and M. Kaouris, J. Environ. Sci. Health, Part A, 1988, 23, 797–822.
22. J. F. McCarthy, T. M. Williams, L. Y. Liang, P. M. Jardine, L. W. Jolley, D. L. Taylor, A. V. Palumbo and L. W. Cooper, Environ. Sci. Technol., 1993, 27, 667–676.
23. J. F. McCarthy, B. Gu, L. Liang, J. Mas-Pla, T. M. Williams and T. C. J. Yeh, Water Resour. Res., 1996, 32, 1223–1238.
24. J. M. Munch, K. U. Totsche and K. Kaiser, Eur. J. Soil Sci., 2002, 53, 311–320.
25. H. Van de Weerd, W. H. Van Riemsdijk and A. Leijnse, Environ. Sci. Technol., 1999, 33, 1675–1681.
26. H. Van de Weerd, W. H. Van Riemsdijk and A. Leijnse, Water Resour. Res., 2002, 38 , No. 8 – article 33.
27. P. Lassen, L. Carlsen, P. Warwick, A. Randall and R. Zhao, Environ. Int., 1994, 20, 127–134.
28. A. Dierckx, A. Hall, P. De Canniere, P. Warwick and M. Put, Radiochim. Acta, 1998, 82, 379–384.
29. S. J. King, P. Warwick, A. Hall and N. D. Bryan, Phys. Chem. Chem. Phys., 2001, 3, 2080–2085.

---