DOI:
10.1039/B512307K
(Communication)
Phys. Chem. Chem. Phys., 2005,
7, 3677-3679
The effect of torsion angle on the rate of intramolecular triplet energy transfer
Received
31st August 2005
, Accepted 14th September 2005
First published on 23rd September 2005
Abstract
The magnitude of electronic coupling between the terminal chromophores shows a precise dependence on the dihedral angle around a bridging biphenyl group.
Long-range, triplet energy transfer along a well-defined molecular-scale wire offers one of the more promising routes by which to construct miniaturized communications systems.1 Furthermore, the super-exchange mechanism2 seems to provide the best approach for achieving proper control of the flux of information transfer along a molecular axis. This mechanism involves through-bond electronic coupling, the strength of which depends markedly on the nature of the wire.3 It has long-been argued that the relevant electronic coupling matrix element, this being a direct measure of electronic communication between donor and acceptor units, should depend on the geometry of the connector. Proving this concept by experiment, however, has proved to be extremely difficult, although several notable attempts have been made.4,5 In principle, it should be possible to regulate electron flow by controlling the central torsion angle of a bridging biphenyl group.6 We have previously used a variant on this approach to provide an estimate of how the efficacy of intervalence charge transfer depends on the geometry of the bridge.7 We now show that for a much expanded data set, the rate of triplet energy transfer depends precisely on the torsion angle of the lowest-energy conformation of the bridge.
Intramolecular triplet energy transfer between remote reactants connected through an organic spacer usually occurs via Dexter-type electron exchange.4 This process involves simultaneous transfer of an electron, through the bridging LUMO, and a positive hole, through the bridging HOMO, from donor to acceptor.4 Properties of the spacer, notably the length,8 connectivity9 and conductivity,10 combine to control the rate of energy transfer. For a spacer of fixed length and composition, it is likely that the rate will depend on the mutual orientation of subunits comprising the spacer,3,4 especially for a poly(phenylene)-based bridge.10 In order to test this long-standing hypothesis, a set of ruthenium(II)/osmium(II) bis (2,2′:6′,2″-terpyridine) binuclear complexes was synthesized†
(Fig. 1). The terminal metal complexes are linked by an ethynylene-substituted biphenyl bridge that itself is equipped with a constraining tether.11 These terminals are well known to display intramolecular triplet energy transfer from RuII donor to OsII acceptor.8,10 Clearly, the strap is intended to function as a ratchet and fix the dihedral angle around the biphenyl unit.12 This angle is further controlled by binding cations to the crown ether strap.13 The entire data set comprises 11 torsion angles, ranging from 37° to 130°. To prevent undue rotation, the system was studied in a glassy matrix.
 |
| | Fig. 1 Structural formulae for the binuclear complexes studied here. | |
Illumination into the ruthenium(II) bis (2,2′:6′,2″-terpyridine)
(Ru-terpy) terminal at 480 nm, where the corresponding Os-terpy unit absorbs ca. 40% of the incident photons, generates the excited triplet state. This species emits weakly at 660 nm in a butyronitrile glass. The emission quantum yield (ΦLUM) and lifetime (τLUM) increase with decreasing temperature but both values remain much less than those measured for the analogous binuclear Ru-terpy complex.11 The yield and lifetime measured for emission from the Os-terpy terminal at 770 nm remain similar to those recorded for reference compounds14 and following excitation at 650 nm where only Os-terpy absorbs. Thus, the presence of the Ru-terpy unit has no obvious effect on the photophysical properties of the Os-terpy terminal but emission from Ru-terpy is quenched. Comparison of ΦLUM and τLUM recorded for the Ru-terpy units of the various Ru-Os compounds with those for the corresponding Ru–Ru complexes indicates that quenching lies in the range 55–95% at 150 K. Close examination of time-resolved emission profiles recorded for the Os-terpy units indicates that more than 50% of the emission grows-in on the time scale of a few hundred nanoseconds (Fig. 2). This confirms that quenching of the Ru-terpy emission is due to intramolecular triplet energy transfer. The triplet lifetimes were measured also by laser flash photolysis following excitation at 480 nm.
 |
| | Fig. 2 Time-resolved luminescence decay profiles recorded following laser excitation of C1 in butyronitrile at 150 K. The decay records refer to emission from the Ru-terpy unit at 660 nm and emission from the corresponding Os-terpy unit at 760 nm. The sharp profile is the instrument response function (IRF). | |
The rate constant for intramolecular triplet energy transfer (kTT) was derived‡ for each compound by comparing triplet lifetimes measured for the Ru-terpy terminal (τCMP) in the mixed-metal complex with that found for the corresponding Ru–Ru complex (τREF). All emission decay profiles were mono-exponential.
| |  | (1) |
These first-order rate constants were measured over the temperature range 77–150 K where the
solvent remains frozen in a glassy matrix. For each compound, the derived
kTT value was found to follow a modified Arrhenius behaviour of the type expressed by
eqn (2).
| |  | (2) |
Here,
kF refers to an activationless rate constant for energy transfer whilst
kD is the rate constant for the activated process. The derived
kF values converge to a common rate constant of 2.2 ± 0.3 × 10
6 s
−1. In contrast, the derived
kD values span a wide range and are clearly sensitive to the length of the tether (
Table 1). The
activation energy, Δ
G‡, remains independent of strap length and corresponds to an average value of 2.8 ± 0.4 kJ mol
−1.
Table 1 The effect of torsion angle on the efficiency of triplet energy transfer in a glassy butyronitrile matrix
| Cmpd |
Angle/°
a |
10−6kF/s−1b |
10−7kD/s−1b |
ΔG‡/kJ mol−1c |
V
DA/cm−1d |
|
Central torsion angle calculated by MDS for the lowest-energy conformation.
From eqn (2).
From eqn (4).
From eqn (5).
|
| C1 |
37 |
2.1 |
15.5 |
3.05 |
0.31 |
| C2 |
55 |
1.8 |
5.0 |
2.93 |
0.17 |
| C3 |
67 |
2.0 |
2.1 |
2.45 |
0.11 |
| C4 |
94 |
2.1 |
0.30 |
2.86 |
0.04 |
| CE4 |
122 |
2.0 |
1.5 |
2.78 |
0.09 |
| CE5 |
125 |
1.7 |
4.0 |
3.00 |
0.16 |
| CE5 + Na |
83 |
1.8 |
0.49 |
2.90 |
0.05 |
| CE5 + K |
113 |
1.6 |
2.6 |
2.45 |
0.13 |
| CE6 |
130 |
1.9 |
8.8 |
2.75 |
0.22 |
| CE6 + Na |
58 |
2.0 |
2.8 |
3.02 |
0.13 |
| CE6 + K |
62 |
1.9 |
4.1 |
2.75 |
0.15 |
The activationless step, corresponding to kF, can be attributed to Förster-type dipole–dipole energy transfer.15 The calculated rate constant, determined using spectroscopic properties measured for the Ru–Ru complexes, is 2.5 × 106 s−1, which is in good agreement with the averaged kF value. As such, the activated process, corresponding to kD, can be assigned to Dexter-type electron exchange.4,5 This involves long-range, through-bond interactions and, therefore, is expected to depend on the geometry of the bridge. The activation energy for Dexter-type electron exchange corresponds to eqn. (3).16
| |  | (3) |
Here, Δ
ETT
(=1430 cm
−1) is the difference in triplet energies between Ru-terpy and Os-terpy
chromophores and
λTT
(=670 cm
−1) is the total reorganization energy accompanying deactivation of the two triplet excited states. This value can be calculated from a Franck–Condon analysis of the respective emission spectra.
17 The derived values are independent of strap length and give rise to an averaged activation energy for electron exchange of 2.6 ± 0.2 kJ mol
−1. This is in excellent agreement with the experimental Δ
G‡ values, thereby confirming that triplet energy transfer involves a mixture of Förster and Dexter mechanisms. Except at very low temperature, Dexter electron exchange dominates.
The variation in kD must be associated, in some way, with the geometry of the biphenyl bridge. Molecular dynamics simulations made in a reservoir of acetonitrile molecules showed the torsion angle around the central biphenyl group to be sensitive to the length of the strap (Table 1). Although there is considerable fluctuation about the mean value at high temperature, it was found that the strap constrains the geometry around the biphenyl group and imposes a preferred dihedral angle on the lowest-energy conformation. We suppose that the lowest-energy structure will predominate in the glassy matrix and that the measured kD value refers to electron exchange across that particular geometry. Additional angular variations are possible for the crown ether derived straps by incorporating selected cations into the central cavity.13
On the premise that kD refers to electron exchange across a certain torsion angle, we can relate the kinetic data to the electronic coupling matrix element (VDA) for long-range interaction between donor and acceptor. This can be done by way of eqn (4), which allows determination of VDA from the intercept of the appropriate Arrhenius-type expression4
(Fig. 3).
| |  | (4) |
The derived coupling elements are collected in
Table 1, together with the activation energies Δ
G‡, and vary over an eightfold range for the various bridges. Small torsion angles give higher coupling whilst there is a clear minimum in
VDA as the
phenylene rings become orthogonal. Coupling does not decrease to zero but follows the form of
eqn (5) where
ϑ refers to the torsion angle (
Fig. 4). A non-linear, least-squares fit to the derived values indicates that
VDA at 0° has a value of 0.400 ± 0.005 cm
−1 but this falls to only 0.046 ± 0.002 cm
−1 at 90°.
The term
VN in
eqn (5) describes the extent of the inherent electronic coupling when the
phenylene rings are orthogonal. The derived value (
VN
= 0.046 cm
−1) is about 12% that found for a coplanar arrangement of the bridge. This inherent coupling could be associated with internal rotation of the
biphenyl unit giving rise to a multitude of conformers at any given moment. However, given that the molecule is resident in a glassy matrix this structural variation should be kept modest. The experimental conditions (
e.g., low temperature and electron exchange occurring in the Marcus “inverted” region), however, do favour nuclear tunnelling.
18 This latter process involves tunnelling through the barrier separating donor from acceptor. Presumably, this barrier is presented by a single σ bond. In this case, electron exchange is promoted by specific vibrations associated with the reactants or the surrounding
solvent and the rate will be weakly temperature dependent.
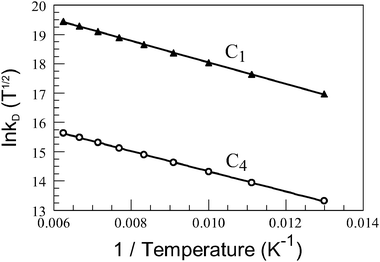 |
| | Fig. 3 Arrhenius-type plot constructed for intramolecular triplet energy transfer in C1 and C4 dissolved in a glassy butyronitrile matrix. The solid line drawn through the data points corresponds to a non-linear, least-squares fit to eqn (4). | |
 |
| | Fig. 4 Effect of torsion angle on the size of the electronic coupling matrix element measured for a glassy matrix. The solid line drawn through the data points corresponds to a best fit to eqn (5) with the parameters given in the text. | |
In summary, this research has established how the rate of electron exchange depends on the conformation of the biphenyl-based bridge. Triplet energy transfer occurs across an orthogonal geometry by way of nuclear tunnelling and/or coupling through the connecting σ bond but is accentuated by more favourable orientations of the bridge. The systems under investigation do not allow adoption of a coplanar arrangement but extrapolation of the data given in Fig. 4 implies that there is an 80-fold variation in rate between phenylene rings held at 0° and 90°. The methodology adapted here provides for the first detailed examination of how the torsion angle affects the extent of long-range electronic coupling.
Acknowledgements
We thank EPSRC (GR/R23305/01) and the University of Newcastle for financial support.
References
-
K. Horie, H. Ushiki and F. M. Winnik, Molecular Photonics: Fundamentals and Practical Aspects, Wiley-VCH, Weinheim, 2000 Search PubMed.
- C. Joachim and M. A. Ratner, Nanotechnology, 2004, 15, 1065 CrossRef CAS.
- S. Hayashi and S. Kato, J. Phys. Chem. A, 1998, 102, 2878 CrossRef CAS.
- G. L. Closs, P. Piotrowiak, J. M. MacInnis and G. R. Fleming, J. Am. Chem. Soc., 1988, 110, 2652 CrossRef CAS.
- H. Oevering, J. Verhoeven, M. N. Paddon-Row, E. Cotsaris and N. S. Hush, Chem. Phys. Lett., 1998, 143, 488.
- A. Helms, D. Heiler and G. McLendon, J. Am. Chem. Soc., 1991, 113, 4325 CrossRef CAS.
- A. C. Benniston, A. Harriman, P. Li, C. A. Sams and M. D. Ward, J. Am. Chem. Soc., 2004, 126, 13630 CrossRef CAS.
- A. Harriman, A. Khatyr, R. Ziessel and A. C. Benniston, Angew. Chem., Int. Ed., 2000, 39, 4287 CrossRef CAS.
- P. J. Wagner and P. Klan, J. Am. Chem. Soc., 1999, 121, 9626 CrossRef CAS.
- F. Barigelletti and L. Flamigni, Chem. Soc. Rev., 2000, 29, 1 RSC.
- A. C. Benniston, A. Harriman, P. Li and C. A. Sams, Phys. Chem. Chem. Phys., 2004, 6, 875 RSC.
- A. C. Benniston, A. Harriman, P. Li and C. A. Sams, Tetrahedron Lett., 2003, 44, 4167 CrossRef CAS.
- A. C. Benniston, A. Harriman, P. Li, P. Patel and C. A. Sams, Eur. J. Org. Chem., 2005 Search PubMed , in press.
- R. S. Lumpkin, E. M. Kober, L. A. Worl, Z. Murtaza and T. J. Meyer, J. Phys. Chem., 1990, 94, 239 CrossRef CAS.
- V. Grosshenny, A. Harriman, M. Hissler and R. Ziessel, Faraday Trans., 1996, 92, 2223 RSC.
- J. A. Schmidt, A. R. McIntosh, A. C. Weedon, J. R. Bolton, J. S. Connolly, J. K. Hurley and M. R. Wasielewski, J. Am. Chem. Soc., 1988, 110, 1733 CrossRef CAS.
- Z. Murtaza, D. K. Graff, A. P. Zipp, L. A. Worl, W. E. Jones, W. D. Bates and T. J. Meyer, J. Phys. Chem., 1994, 98, 10504 CrossRef CAS.
- H. Ohkita, H. Benten, A. Anada, H. Noguchi, N. Kido, S. Ito and M. Yamamoto, Phys. Chem. Chem. Phys., 2004, 6, 3977 RSC.
- A. C. Benniston, P. Li and C. A. Sams, Tetrahedron Lett., 2003, 44, 3947 CrossRef CAS.
- H. T. Uyeda, Y. Zhao, K. Wostyn, I. Asselberghs, K. Clays, A. Persoons and M. J. Therien, J. Am. Chem. Soc., 2002, 124, 13806 CrossRef CAS.
Footnotes |
| † The starting materials 4,4′-diiodobiphenyl-2,2′-diol19 and [M(terpy)(4′-ethynyl-2,2′:6′,2″-terpyridine)](PF6)2
(M
= Ru2+ or Os2+)20 were prepared by literature methods. The synthetic procedure used to isolate the required target compounds will be reported elsewhere. In brief, the two oxygen atoms of the bridge were linked via alkyl or alkoxy chains to create the desired tethered molecules. These compounds were coupled in sequential reactions, using the Sonogashira method,11 to the relevant synthons so as to afford the mixed-metal complexes. |
| ‡ Time-resolved luminescence measurements were made after excitation of the sample with a 4-ns laser pulse delivered at 480 nm and with a repetition rate of 1 kHz. Data analysis was made after deconvolution of the instrument response function. Temperature-dependent studies were made with an Oxford Instruments Optistat DN cryostat. Transient absorption studies were made by conventional methods after excitation with a 5 ns laser pulse delivered at either 532 or 480 nm from a Q-switched Nd:YAG laser. In the latter case the laser beam was focussed through a 1 m cell filled with deuterium and the required excitation line was isolated with a prism coupled to a narrow bandpass filter. The sample was deoxygenated by purging with N2. Other studies used a frequency-doubled, mode-locked Nd:YAG laser as excitation source. Some 200 individual laser shots were averaged at each delay time. |
|
| This journal is © the Owner Societies 2005 |
Click here to see how this site uses Cookies. View our privacy policy here. 







