Water molecule clusters measured at water/air interfaces using atomic force microscopy
O.
Teschke
a and
E. F.
de Souza
b
aLaboratorio de NanoEstruturas e Interfaces, Instituto de Física, Universidade Estadual de Campinas, 13083-970, Campinas, SP, Brazil
bFaculdade de Química, Centro de Ciências Exatas, Ambientais e de Tecnologia, Pontifícia Universidade Católica de Campinas, 13086-900, Campinas, SP, Brazil
First published on 20th September 2005
Abstract
During the tip approach to hydrophobic surfaces like the water/air interface, the measured interaction force reveals a strong attraction with a range of ∼250 nm at some points along the interface. The range of this force is ∼100 times larger than the measured for gold (∼3 nm) and 10 times larger than the one for hydrophobic silicon surfaces (∼25 nm). At other points the interface exerts a medium range repulsive force growing stepwise as the tip approaches the interface plane, consequently the hydrophobic force is a strong function of position. To explain these results we propose a model where the force on the tip is associated with the exchange of a small volume of the interface with a dielectric permittivity εint by the tip with a dielectric permittivity εtip. By assuming a oscillatory spatial dependence for the dielectric permittivity it is possible to fit the measured force profiles. This dielectric spatial variation was associated with the orientation of the water molecules arrangement in the interfacial region. Small nanosized hydrogen-bond connected cages of water molecules present in bulk water at the interface are oriented by the interfacial electric field generated by the water molecules broken bonds, one broken hydrogen bond out of every four. This interfacial field orients small clusters formed by ∼100 water molecules into larger clusters (∼100 nm). In the limit of small (less than 5 nm thick) water molecule cages we have modeled the static dielectric permittivity (ε) as the average response of those cages. In these regions the dielectric permittivity for water/air interfaces decreases monotonically from the bulk value ε ∼80 to ∼2 at the interface. For regions filled with medium size cages, the tip senses the structure of each cage and the static dielectric permittivity is matched to the geometrical features of these cages sized ∼25 to 40 nm. Interfacial electric energy density values were calculated using the electric field intensity and the dielectric permittivity obtained by the fitting of the experimental points. The integration of the electric energy density along the interfacial region gives a value of 0.072 J m−2 for interfacial energy density for points where the hydrophobic force has a range of ∼250 nm. Regions formed by various clusters result in lower values of the interfacial energy density.
1. Introduction
The statistical physics of liquid surfaces has been the subject of extensive theoretical studies, however, experiments capable of providing relevant data have only recently become available.1–7 One interesting development has been the interpretation of atomic force microscopy (AFM) force vs. distance measurements in terms of a variable dielectric permittivity layer of the liquid–vapor interface.8,9The nature of the interaction between air bubbles and particles has been the focus of research for over forty years simply because this interaction is central to the froth flotation process, used extensively for mineral concentration10 and water treatment.11 Hydrodynamic aspects of bubble-particle interactions, the stability of attachment, and the nature of the surface forces which dictate the stability of the liquid film between a particle and an air bubble have been considered in detail.12,13 Ducker et al.14 measured forces across water between a silica particle (∼10 nm diameter) attached the AFM cantilever and an air bubble. Fielden et al.15 and Preuss and Butt16 reported similar experiments. Here we have used ∼1 mm radii air bubbles in water working with a surface free of rugosities and with homogeneous composition and nanosized (radius ∼5 nm) AFM neutral tips.
The hydrophobic surface exhibits a long-range and strong attractive force in aqueous solutions. Although this strong force has been confirmed by a large number of experimental data,17–27 the mechanism for the attractive force has been a debated issue for almost 20 years. Recent studies suggested that the phenomena may be attributable to nanoscopic bubbles attached on the hydrophobic surface. Several researchers28–30 assumed that the origin is the bridge formation due to the coalescence between bubbles on the approaching surfaces assuming bubbles on both interactive surfaces. However, the lifetime of the bubbles and the bridge must be extremely short from the thermodynamic point of view, because the internal gas pressure in such small bubbles is so high that the gas is rapidly dissolved into the bulk solution.31 Ljunggren and Eriksson32 calculated their lifetime to be microseconds to milliseconds.
Recently the authors33–37 have modeled the force acting on uncharged tips when immersed in the interfacial double layer of ionic charged hydrophilic surfaces, which interact strongly with water molecules, using the dielectric exchange force. This force, which is repulsive at long distances to the interface and is followed by an attraction in the region close to it, is associated with the ionic surface charges effect on the alignment of water molecules within in the double layer region. However it has been observed that, the forces acting on uncharged tips immersed in hydration layers associated with hydrophobic surfaces are of the same order of magnitude of the ones measured for ionic charged hydrophilic surfaces.37 The study of this force profile by the authors has indicated8 that the origin of the strong long range hydrophobic field may be the dipolar distribution of broken hydrogen bonds at the air/water interface and the hydrogen bonding force in the bulk. Du et al.38,39 measured this interfacial dipolar distribution.
Here we describe force vs. separation curves when neutral tips with ∼5 nm radius of curvature probe ∼1 mm radius air bubbles surfaces in water. Different points along hydrophobic surfaces, like air bubble interfaces in water, when probed by atomic force microscope tips, reveal distinct behaviors. A spatially variable dielectric permittivity profile is used to model the measured curves.
2. Experimental
2.1. Atomic force microscope measurements in water
The AFM is the most adequate equipment available for measuring interfacial forces with a spatial resolution of few angstroms in the scanned plane and 0.01 nm in the normal direction. If we use soft cantilevers with a spring constant of 0.03 N m−1 the force resolution in the normal direction to the scanned plane is 0.03 N m−1 × 0.1 × 10−10 m = 30 pN.In our experiments a TopoMetrix TMX2000 AFM (ThermoMicroscopes, Veeco) instrument was used where the movement of the cantilever was detected by the conventional deflection sensor using a four-quadrant detector enabling vertical as well as lateral force measurements. A special cell was built in order to perform observations in liquid media.40,41 The cell was made of Teflon™ and the sample is fixed at its bottom and it is moved in the x-, y- and z-directions with respect to a stationary tip. The laser beam enters and leaves the cell through a glass plate and thus does not cross the air/liquid interface, which is usually curved. The top-confining surface of the solution in the cell is far removed from the cantilever beam. In this geometry the displaced liquid follows a path that is perpendicular to the cantilever beam.
2.2 Preparation of aqueous solutions
Deionized water (Milli-Q Plus quality, resistivity ∼15 MΩ cm−1) was used into the cell and was distilled once, then passed through a commercial Milli-Q system containing ion-exchange and charcoal stages. The experiments were performed at a temperature of 20 °C. Each curve presented was registered using at least five different samples of each interface and three different tips with various approach velocities averaged using measurements at different points of the sample. Preparing samples in a compact laminar flow cabinet and scanning samples in a clean air hood minimize airborne contamination.2.3 Tips
We have obtained best results in measurements with very soft cantilevers with silicon nitride tips, typically ∼0.03 N m−1 and 0.1 N m−1 (Microlever™, type B, ThermoMicroscopes). Verifications of the spring constants of the cantilever by the method of Sader42 and by the slope of force vs. distance curves during the tip jump to the substrate surface gave values not statistically different from the manufacturer’s values.Forces were measured between a commercial silicon nitride (εtip = 7.4) and mica immersed in water for 1 h and up to 5 h of immersion in water. Identical force vs. separation curves was registered showing that there was no evidence of tip aging during this time period.35
The surface of a silicon nitride tip in aqueous solution is composed of amphoteric silanol and basic silylamine [secondary (silazane, –Si2NH2) and possibly primary (silylamine, –SiNH3) amines though the latter is rapidly hydrolyzed] surface groups43,44 at pH ∼6; with no added electrolyte the silicon nitride surface is either zwitterionic (zero net charge) or slightly negatively charged.45 The commercial silicon nitride tip surface has been found to be close to electrically neutral over a wide pH range (from at least pH 6 to 8.5), thus indicating equal densities of silanol and silylamine surface groups. To verify the surface charging behavior of the tips, force vs. separation curves in solutions with pH between ∼5.2 and 6.8 were measured, and the isocharging point (i.c.p.) for silicon nitride was determined to be pHi.c.p. ≈ 6.3.
2.4. Tip radius of curvature estimative
The radius of the tip was characterized by the observation of porous silicon structures and by comparing the size of the measured silicon particles by transmission electron microscopy (TEM) and AFM.33 This comparison allows us to estimate the distortion of the AFM images due to the finite size of the tip radius. The estimation of the tip radius is obtained by the deconvolution of the measured profile curve and the comparison with the particle diameter measured by TEM. The determined values are in agreement with the value given by ThermoMicroscopes technical information sheets. The selected Si3N4 supertips have a 3.5–5.0 nm radius of curvature.All force vs. separation curves were obtained using sharpened conical tips with an apex angle of ∼18° and ∼200 nm height etched at the end of ∼3 mm height tips as schematically shown in Fig. 1. Only the lower part of tip (sharpened cone) is involved in the interaction with the water/air interface.
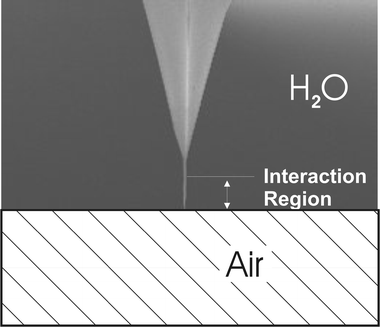 | ||
| Fig. 1 Schematic diagram of the super tip used in this work. | ||
2.5. Hydrophobic surfaces—preparation of the air bubble
The probed hydrophobic surface was an air bubble surface in water. A bubble was injected into the solution using a microsyringe and photos of bubbles attached on the polytetrafluoroethylene (PTFE) surface shows that the contact angle of the bubble is >90°. Air bubbles of radii r ≈ 1 mm were formed from clean air and attached to a thermal treated PTFE surface used in order to prevent the three-phase line from moving laterally. The PTFE surface was modified by heating the sample in air at 380 °C and its topography was imaged using AFM. After this PTFE surface was placed in water, a small air bubble was transferred from a microsyringe onto the hydrophobic surface where it remained attached. Air bubbles trapped in this way were stable for many hours except for its slow radius increased.2.6. Tip approach and separation curves
Usually when the tip and the probed surface are engaged at cycles of approach and separation the force curves are given for approach only. Tip approach mechanism control is not more precise than the tip diameter however the pattern measured in this work has a larger spatial period than the tip position mechanism and repetitive curves are obtained for points in region separated by ∼10 nm. Here we only show patterns of repetitive and reproducible curves for periods of approximately two hours.Only the top of the ∼1 mm radius of curvature air bubbles is selected for probing. Some times the tip is immersed in the air bubble; in this case the AFM does not register the force vs. separation curve.
The air bubble surface has low stiffness in comparison to the mica stiffness however this low value is large when compared to the cantilever stiffness (k = 0.03 N m−1). Fig. 2 shows a schematic force vs. separation curve where the tip/substrate interaction region starts at A and for large forces, indicated by B, the slope of the force curve is 0.03 which corresponds to the deflection of the cantilever when pressed against a hard substrate (mica). The cantilever spring constant has been previously determined using mica substrates. The reference line is then obtained by extending the region with a ∼0.03 slope (full line with ∼ 45° slope) and the reference coordinate is determined by the intersection with the zero-force line. In Fig. 2, for tip/substrate separations much larger than the width of the interaction region, there are no forces acting on the cantilever associated with the tip/interface interaction and the horizontal line observed is the zero-force line.
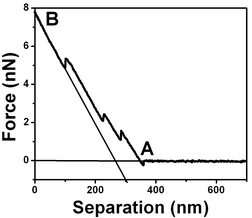 | ||
| Fig. 2 Schematic force vs. separation curve for air bubble/water interfaces with a 0.03 N m−1 spring constant cantilever. The curve shows a region where there is no force acting on the tip (horizontal line ending at A) and a region where the slope is the cantilever spring constant 0.03 N m−1 (indicated by B) which corresponds to the tip deflection when pressed against a hard surface like mica. | ||
2.7. Hydrophobic gold and silicon films
〈100〉 silicon wafers with a 10 Ω cm−1 resistivity from Virginia Semiconductor, Inc (VA, USA) were used. Previously to use ∼1 × 1 cm2 pieces were etched in 50/50% HF solutions for a few minutes and then rinsed with water. Electronic grade gold wire was evaporated onto mica substrates forming a polycrystalline gold film.3. Experimental results
3.1. Tip/bubble forces in water
The starting point was to measure the force–distance profile. Fig. 3 shows the measured force between a neutral tip and a hydrophobic surface within water at pH 6 plotted against surface separation (D) averaged 5 to 10 min after tip immersion. Attraction was observed starting at very large separations, D ≈ 250 nm and there was not one point of instability at which the force gradient exceeded the spring constant of the force-measuring device.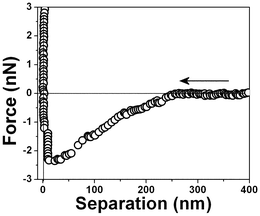 | ||
| Fig. 3 Typical force vs. separation curve for an air bubble/water interface measured with a 0.03 N m−1 spring constant cantilever 10 minutes after the bubble attachment to the PTFE substrate. | ||
Probing various regions of the air bubble/water interface of various bubbles using different tips we have obtained the following force vs. separation patterns shown in Fig. 4 to 9.
 | ||
| Fig. 4 Force vs. separation curve measured in an air bubble trapped within water at pH 6, curve □ with a 0.03 N m−1 and curve ● with a 0.1 N m−1 spring constant cantilever. | ||
 | ||
| Fig. 5 Force vs. separation curve measured in an air bubble trapped within water at pH 6. | ||
 | ||
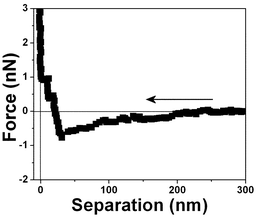
| Fig. 6 Force vs. separation curve measured in an air bubble trapped within water at pH 6. | ||
 | ||
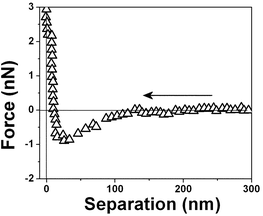
| Fig. 7 Force vs. separation curve measured in an air bubble trapped within water for the same interface shown in Fig. 6 at a different position. | ||
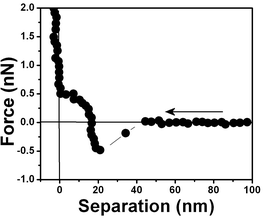
 | ||
| Fig. 8 Force vs. separation curve measured in an air bubble trapped within water for the same interface shown in Fig. 6 at another position. The differences in the force separation curves shown in Fig. 6, 7 and 8 are associated with spatial variation at the same air/water interface. | ||
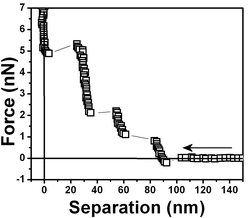 | ||
| Fig. 9 Another water/air interface was prepared and the measured force vs. separation curves shows three steps. | ||
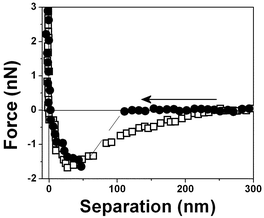
Fig. 4 shows the measured force for two different tips (curve □, cantilever spring constant k ≈ 0.03 N m−1 and curve ●, k ≈ 0.1 N m−1) and an air bubble trapped within water at pH 6. Both force curves have two repulsive steps close to the origin. The force curves are very similar to those for hydrophobic surfaces shown in Fig. 3 except for the longer range of the repulsive forces close to the origin. A repulsive step appears at D ∼ 25 nm in the approaching curve using a cantilever with k ≈ 0.03 N m−1 (curve □) and at D ∼50 nm with a cantilever with k ≈ 0.1 N m−1 (curve ●). For the tip with the larger spring constant there is an instability associated with the slope of the curve. At large distances, D > 250 nm, the force is negligible. At ∼220 nm from the interface, there is an attraction of the tip (curve □) to the bubble until a net repulsive force is experienced (∼25 nm). It is noteworthy to observe that the attraction force is much stronger and longer-ranged than the van der Waals attractive force.8 And since the cantilever deflection when pushed against the bubble and the bubble translation are equal, as shown in the force vs. distance curves, we have concluded that the bubble is undeformed for the set point force specified in these experiments; also no long range electrostatic repulsive force was detected.
Fig. 5 shows a force vs. separation curve with a larger repulsive component at the origin than shown in Fig. 4 and 6 where there is a force vs. separation curve with an even larger repulsive component at the origin. The repulsive component extending further into distances far away from the interface is depicted in Fig. 7. A curve showing only large repulsive behavior starting at ∼60 nm from the interface is depicted in Fig. 8 and 9 shows three repulsions followed by attraction steps; finally Fig. 10 shows one repulsive step and two attractive steps. Observe that most of the experimental curves previously shown start with an attractive component at a long distances from the interface followed by repulsive components.
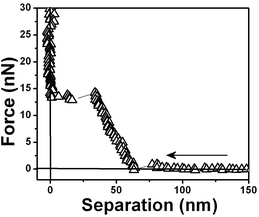 | ||
| Fig. 10 Force vs. separation curves showing one repulsive step measured for a water/air interface. | ||
The interaction forces were measured not only between the approaching surfaces but also between the separating surfaces (see Fig. 11). In the approaching force curves (Fig. 3–10), discontinuous steps appear at various separation values. The attractive force increases monotonically with the decrease of D and reaches the maximum attraction of about −2.5 nN (see Fig. 3). In the case of the separating force curve, the force curves are completely different from those shown in Fig. 3 to 9. In the approaching force curve, a long-range attractive force appears and the cantilever does not jump on the surface not even when the tip and surface are very close. In the separating force curve, the cantilever jumps out at a ∼50 nm separation distance, although a ∼8 nN strong adhesive force is present.
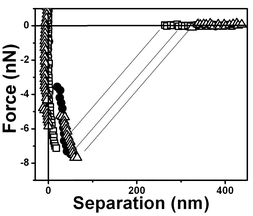 | ||
| Fig. 11 Typical force vs. separation curves for an air bubble/water interface for three retrace curves. The arrow indicates that the tip is receding from the interface. | ||
3.2. Silicon and polycrystalline gold film
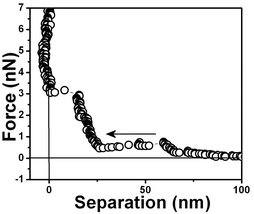
The range of the hydrophobic force measured for the air bubble/water interface is extremely long when compared to other hydrophobic surfaces. In order to make a comparison we have included in this work force vs. separation curves measured for other hydrophobic surfaces, polycrystalline gold surfaces and optically polished 〈100〉 silicon surfaces previously immersed in 50% HF solution.A silicon surface force vs. separation curve is shown in Fig. 12. Observe the much shorter range of the force when compared to one shown in Fig. 3. Next gold surfaces were probed. The probed substrates were polycrystalline gold films deposited on mica. The surface structure of polycrystalline gold is highly complicated. A polycrystalline gold electrode is composed of mainly the 〈111〉 and the 〈110〉 orientations and a complete understanding of polycrystalline surfaces is still missing.46
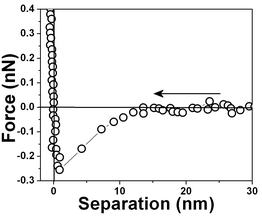 | ||
| Fig. 12 Force vs. separation curve for hydrophobic silicon surfaces measured ∼15 min after silicon immersion in water, measured with 0.03 N m−1 spring constant cantilever. | ||
The force vs. separation curve for gold is shown in Fig. 13. An image of the gold surface is shown in Fig. 14 and its profile in Fig. 15. Observe that the range of the repulsive force is ∼3 nm, which is ∼100 times smaller than the range of hydrophobic air/water interface and the silicon surface force range is ten times smaller.
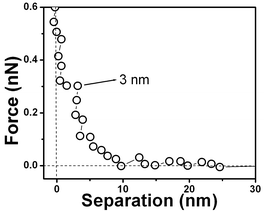 | ||
| Fig. 13 Force vs. separation curve for a polycrystalline gold substrate immersed in water showing its hydrophobic nature. | ||
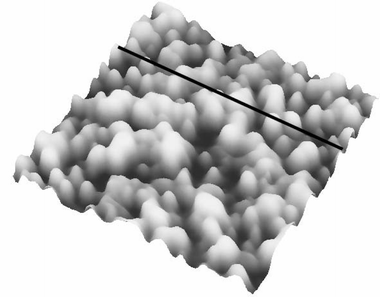 | ||
| Fig. 14 AFM image of the same gold film used in the measured force vs. the separation curve shown in Fig. 13. | ||
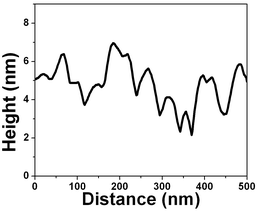 | ||
| Fig. 15 Vertical profile image of the image shown in Fig. 14. | ||
3.3. Water methanol/air interface
Recently Shen et al.47 showed that for a 11% mixture of methanol and water the hydrogen dangling bonds at the interface disappeared. In order to check the nature of the attractive force followed by repulsions we did the force vs. separation measurement for an air/bubble 11% methanol–water interface (Fig. 16 curve ●). For comparison the hydrophobic water/air interface force profile displayed in Fig. 3 is added to this figure (curve ○). Note that the attractive behavior of the force vs. separation curve for the methanol/water mixture has almost completely disappeared.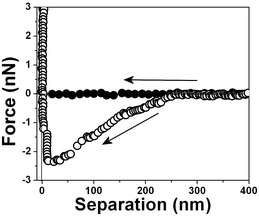 | ||
| Fig. 16 Typical force vs. separation curves ● for an air bubble from a 11% mixture of methanol and water, curve ○ is from Fig. 3. | ||
4. Results discussion and analysis
4.1. Analyses of the shape of force curves
Initially we would like to discuss the large variation in the shape of force curves. In previous works, large radius of curvature tips (∼1 mm) that averages spatial variations were used and the water/air interface appears as homogeneous. Here by using nanosized diameter tips we measure spatial variations in a nanometre scale. Typical forces curves include various steps in regions close the aqueous/air interface. These steps have been measured by various authors48,49 in hydrophobic surfaces and attributed to interfacial nanobubbles.Measured forces do not show a constant gradient but discontinuities and cannot be associated with the deformation of the bubble from its equilibrium configuration when in contact with the tip. Since with air bubbles the interface is very deformable the set point of the applied force is conveniently chosen, so that, after tip/air bubble contact the tip displacement (x) is equal to the piezo transducer (z) i.e., force vs. separation curves have slopes of ∼45° which means that only the cantilever is deformed. For higher values of the set point force the tip in the interfacial region would compress the bubble and deform it resulting in a force vs. separation slope given by k = kcant/((Δz/Δx) − 1). Force vs. separation curves in TopoMetrix TMX 2000 are performed as follows: A set point force is chosen and the tip approaches the surface until there is contact with the interface. The tip is then withdrawn from the interface and then brought closer. If the tip is immersed in the air bubble there is no force vs. separation curves measured because the tip and the tip support structure is hydrophobic and all the cantilever is immersed in the air bubble.
Impurities in solution are monitored as follows: We have used a fabricated liquid cell made of PTFE, which is washed with HF solutions. The contact angle of the bottom part of the container is observed. Only for an angle larger than ∼100° is the cell considered clean. The cell is then filled with water and an air bubble is injected in the water/PTFE interface. There is no contamination in the internal surface. Contamination of the surface would imply a substantial decrease in the PTFE/air contact angle, which would decrease the measured height of the bubble that would be detected by the AFM. Surfactant impurities may also affect the results. Artifacts like surfactants may play a role on the measurements. For a low concentration of surfactant up to 10−4 M (impurities are in a level lower than 10−6 M) only monolayers or bilayers are adsorbed; in this case thicknesses of ∼5 nm (SDS, CTAB, etc.) are measured. The steps in force vs. separation measured values are 20 times longer, implying an adsorption of ∼20 bilayers. If the solution is contaminated by the surfactant, the textured PTFE surface would show a contact angle much lower than 100°, which was not the case.
Similar investigations of force vs. separation curves of hydrophobic surface discover that impurities are responsible for decrease of the hydrophobic force range or even the disappearance of the force.
4.2. Gold/water interface
Water dipole ordering on metal electrodes can be described by the solution dipole potential, ϕS(M)(dip), and ionic potential, ϕS(M)(ion), contributions to the thermodynamic electrode potential U. It is assumed that ϕS(M)(dip) ≈ 0 at metals with complete d-shells, such as gold, and ϕS(M)(dip) ≈ 0 suggests a hydrophobic surface. Polycrystalline gold substrates were probed in water using force vs. separation curves. The result is shown in Fig. 13; observe a repulsion of the tip at ∼3 nm. This measurement indicates that the interaction between water and gold results in so-called boundary effects, i.e. higher molecular order and viscosity in the first water molecule layers as compared to the liquid bulk.50 It was suggested that the small polar water molecules form ordered patched structures at the solid–liquid interface due to oriented dipoles. Molecular dynamics simulations without consideration of potential changes suggest that water adopts an ordered structure similar to ice over a thickness of about 1 nm of platinum.50Fig. 13 shows a layer with an alignment of ∼7 water molecules (∼3 nm) for gold. The number of aligned water molecules layer is calculated assuming that at the water/gold interface there is an hexagonal lattice similar to the ice/air interface (lattice constant 4.52 Å). The gold surface is depicted in Fig. 14 and the vertical profile image in Fig. 15. It is possible to observe that the gold islands have a diameter of ∼40 nm and a height of 4 nm. The irregular arrangement of the gold surface maybe be responsible for the short range of water dipole alignment.4.3. Tip/bubble forces in water
Measurements in pure water show that the attraction and repulsion in the force curve frequently occurred at different separations (compare Fig. 3–10). It is difficult to understand how any force law could exist where the gradient of the force changes so abruptly from negative to positive at such small separations. It is also difficult to understand why the attractive force varies so greatly.The following observations resume our experimental results:
(i) the discontinuous step appears in the approaching and separating force curves (Fig. 4–11),
(ii) the force curve depends greatly on the measuring position on the interface and
(iii) distinct shapes of the repulsion component were measured.
All these results suggest that the long-range attraction followed by a variable patterns of the repulsive component is attributable to the liquid structure at the air/water interface.
4.4. Water methanol/air interface
In order to understand the origin of the interfacial structure, force vs. separation curves, were measured for methanol/water solutions. To estimate the interfacial polarization field at the air/water interface we must know how many dangling OH bonds exist at the interface. This has been achieved in the experiment previously performed using second harmonic generation at the air/water interface by Hu et al. 51 It is also known from the surface tension measurement of methanol/water solutions that 11% of methanol in bulk water leads to 25% of methanol at the air/water interface.45 Knowing that each methanol molecule at the surface could suppress one dangling OH bond, the result indicates that one out of every four water molecules in the surface monolayer must have contributed to one dangling OH bond at the vapor/water interface. This suggests that the surface water structure is ice-like and that at the surface, each molecule in the top submonolayer must have one of its four connecting hydrogen bonds broken. We can then conclude that the surface water structure at the vapor/water interface is ice-like although it is certainly not as ordered as the ice, as evidenced by the presence of the hydration force at larger distances from the interface (see Fig. 3). A recent theoretical calculation of Benjamin reproduces the observed spectrum and supports the above picture.52 The results displayed in Fig. 16 agree with the previous paragraph because in methanol/water case the hydrophobic attraction is practically absent in the force vs. separation curve. Without OH-dangling bonds the hydrophobic force is absent, thus indicating that interfacial polarization charges associated with OH-dangling bonds are the source of the hydrophobic force at air bubble/water interfaces.4.5. Air/bubble interface
Liquid water is held together by a random, fluctuating, three-dimensional network of hydrogen bonds. This unique liquid-state structure is responsible for many of water’s particular properties, and it has long been thought to play a role in the hydrophobic interaction.Close to the air/water interface (which acts like a hydrophobic surface) the hydrogen bonding pattern of water is disrupted without the compensatory interactions associated with the presence of ionic charges that might operate at hydrophilic surfaces. How does water cope with this loss of stability?
The driving force behind these processes is the interfacial water structure which is usually explained as an enhanced structuring of water in the immediate vicinity of hydrophobic surfaces. Experimental measurements that provide a molecular-level view of interfacial water structure and hydrogen bonding at these interfaces have proven to be problematic because of the difficulty in selectively examining interfacial water molecules. Here we report surface force vs. separation profiles at the air/water and air/water–methanol interfaces, which provide detailed information on the structure of the interfaces (see Fig. 3 to 13).
4.6. Tip/air/water interface interaction model
The properties of pure water in interfacial regions often exhibit notable anomalies in the force vs. separation as shown in Fig. 3 to 9 and these anomalies are interpreted as manifestations of structural transitions. They constitute detected evidence of a cooperative action through and within the structured units. With as many different “phases” (phases in the sense of different water molecular arrangement) as are involved here, it is obvious that a large number of adjustable parameters must be invoked. Here however we use only the dielectric permittivity profile as an adjustable parameter.Let us then apply our model to a hydration layer attached to a hydrophobic air/water interface [see appendix]. In the absence of ions the simple theory we are presenting assumes that the surface introduces a “symmetry breaking” in water dipole distribution. We can not assume a homogeneous bulk medium, instead a variable dielectric permittivity as a function of the dimension perpendicular to the surface was assumed generated by an interfacial electric field associated with the dangling bonds at the interface.
As in our previous work8 we have proposed that the polarization charge associated with the interfacial structure of broken hydrogen bonds generates in the bulk an electric field that aligns the water molecules. This polarization field is calculated as follows: since we have one of the four possible connecting hydrogen-bonds broken the polarization charge associated with this broken bond distribution generates for an infinite plane of charges an electric field |Ē| given by |Ē∼ σ/ε0|, where σ is surface polarization charge density arising from the single hydrogen bond broken per the unit cell and given by q (electron charge) divided by the water molecules separation square (4.9 Å)2. If we use the value of 6.18 × 10−30 C m−1 for the water molecule dipole moment the orientational energy of this field W = |μE| is ∼5.5 × 10−19 J. The energy associated with the hydrogen bonding is ca. 7 kT at room temperature8 while the orientational energy of water molecules associated with the interfacial polarization charges is then ∼140 kT. Consequently a hydrogen-bonded mediated structural reorganization in the substrate/water interfacial region may be observed up to ∼250 nm away from the interface as measured in this work.
To estimate the size of the force acting on the tip we assumed that the energy change involved in the immersion of the tip inside the polarization layer, is given by the product of the immersed tip volume times the dielectric permittivity variation and times the square of the electric field vector. The tip was defined to have a sharpened conical shape with one flat end with an area of πR2. The volume element (dv) of the tip immersed in the interaction region is given by dv = π[R + (tan α)z]2dz, where z is the integration variable of the conical volume and d is the distance between the surface and the end of the tip. The change in the electric energy involved in the exchange of the dielectric permittivity of the polarization layer by that of the tip is calculated by integrating the energy expression over the tip immersed volume in the polarization layer region. The force is obtained by the gradient of the energy expression, i.e., Fz = −(∂/∂z)ΔW, where
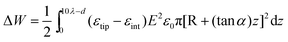 | (1) |
In order to account for the sudden and variable attractions and repulsions shown in the experimental curves (Fig. 4 to 9) an oscillation behavior for the dielectric permittivity will be assumed inside the polarization layer.
4.7. Other proposed mechanisms for steps on the force vs. separation curves
It was previously suggested that these steps at the onset of the force vs. separation curves are due to the bridging of submicroscopic bubbles or cavities that cause the long-range attraction between hydrophobic surfaces.28–30 However, this hypothesis was formulated for irregular substrate surfaces were nanobubbles could be attached. Here we have a millimetre air bubble which has a smooth surface and a homogeneous composition and the presence of the nanobubbles at the surface of this large bubble can not be possible because the nanobubbles would have a lifetime smaller than microseconds due to their high internal pressure when compared to that of the large air bubble.32One may think that the tip surface might be wetted by air bubbles. If that is the case, the adhesive force in Fig. 11 is due mainly to the air bridge between the bubbles on the tip which results in the immersion of most of the tip in the 1 mm bubble. This is not observed in our experimental conditions. Hence, we consider that air bubbles do not wet the tip surface after an immersion period (>10 min) of the tip in water. Further evidence for the absence of bubbles at the tip end comes from the following observation: at some points of interface, when we approach the water/air interface, a force vs. separation curve like the one shown in Fig. 3 is obtained. Then with the same tip we probe other points in a region close to the original point and now we measure various repulsive steps like the ones shown in Fig. 9. According to the previous theory, the steps would correspond to three bubbles in the region between the tip and the millimetric air bubble. Since there were no bubbles attached to the tip, registered by the absence of repulsion in the force vs. separation curves at some points of the interface and since there are not nanobubbles attached to a millimetric air bubble, the repulsive behavior has to be generated by some other mechanism.
4.8. Experimental curves fitting
Based on our previous work we have propose a model that assigns the attractive or repulsive force acting on the tip when immersed in the interaction region to a new variable dielectric profile where oscillations in the value of ε are present generated by alignment of water dipoles that have some likeness to domains in ferromagnetic materials. The evidence for the presence of the polarization domains comes from the fitting of the dielectric permittivity profile necessary to obtain a repulsive followed by an attractive behavior since the model predicts an attraction for a region where the medium dielectric permittivity is lower than that of the tip (εmedia < εtip) and a repulsion for a region where εmedia > εtip.The polarization profile was first determined by fitting eqn (1) to the experimental points shown in Fig. 3 which describes the water behavior near a hydrophobic surface. The calculated dielectric permittivity profile obtained by the best fitting to the experimental curve is shown in the inset of Fig. 17.
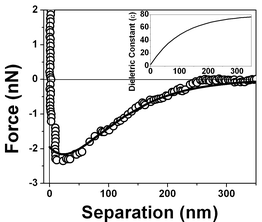 | ||
| Fig. 17 Measured force vs. separation curve from Fig. 3 and the fitting of eqn (1) to the experimental points (full line). Inset: values of the dielectric permittivity ε(z) as a function of the distance to the solid/liquid interface that resulted in the best fitting. | ||
Fig. 18 presents the force vs. separation curves shown in Fig. 9 for water at an air/water interface and the curve calculated (full line) using eqn (1). The curve shown in the inset corresponds to the dielectric permittivity spatial variation that results in the best fitting to the oscillation in the force vs. separation profile. Finally Fig. 19 and 20 show the corresponding fitting to the experimental points shown in Fig. 8 and 10 respectively.
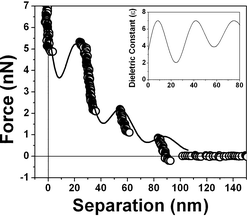 | ||
| Fig. 18 Measured force vs. separation curve from Fig. 9 and the fitting of eqn (1) to the experimental points (full line). Inset: values of the dielectric permittivity ε(z) as a function of the distance to the solid/liquid interface that resulted in the best fitting. | ||
 | ||
| Fig. 19 Measured force vs. separation curve from Fig. 8 and the fitting of eqn (1) to the experimental points (full line). Inset: values of the dielectric permittivity ε(z) as a function of the distance to the solid/liquid interface that resulted in the best fitting. | ||
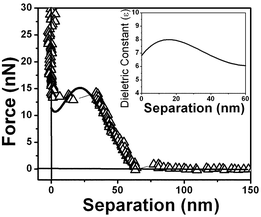 | ||
| Fig. 20 Measured force vs. separation curve from Fig. 10 and the fitting of eqn (1) to the experimental points (full line). Inset: values of the dielectric permittivity ε(z) as a function of the distance to the solid/liquid interface that resulted in the best fitting. | ||
4.9. Water structure as determined by the dielectric exchange force
The best fitting of the experimental data shown in Fig. 3 using eqn (1) results in the dielectric permittivity profile shown in the inset of Fig. 17. The calculated dielectric permittivity profile shows a value of ε ≈ 2 at the interface and ε ≈ 80 for a distance ∼300 nm away from the interface which corresponds to the water bulk value. This means that only at few nm close to the surface water is rigid as ice. This profile indicates a strong stiffness of the water molecules at the interface evidenced by the value of ε ≈ 2 and a decrease in a molecular orientational rigidity for regions far from the interface. Water molecules are almost rigid because they do not response to an external electric field (observe ε ≈ 1 corresponds to vacuum or air). We do not have means of determining the molecular structure of interfacial water but only determine the orientation invariant to an external electric field.Fig. 18, 19 and 20 show different scenarios with various attractions and repulsions. Insets show the corresponding dielectric permittivity spatial variation that results in the best fitting to the experimental points. We propose, based on this fitting, that the water presents a spatially oscillating polarization layer formed by a hydrogen-bonded network of water dipoles. This network is formed by cages of molecules with a central region surrounded by a layer with a more rigid arrangement of molecules, as indicated by the measured dielectric permittivity profile at the interface (see insets in Fig. 18, 19 and 20). The evidence for the presence of the polarization domains comes from the fitting of the dielectric permittivity profile necessary to obtain a repulsion followed by an attractive behavior.
For regions where the dielectric permittivity decreases monotonically from the bulk value ε ≈ 80 to ε ≈ 2 at the interface the water molecule cages are probably smaller than the tip diameter and measurements do not detect discontinuities. For regions, as those corresponding to the ones described by Fig. 18, 19 and 20, the cage arrangement is such that the effective oscillatory behavior of the dielectric permittivity is detected. The measured thicknesses of the domains varies from ∼20 nm to ∼40 nm and each domain is formed by a inner network delimited by walls typically 10 nm thick with a smaller values of ε, as indicated in Fig. 18, 19 and 20. These regions correspond therefore to domains with spatially oscillating dielectric permittivity profiles and do not have a structure with a gradual decrease in alignment away from the interface.
The interfacial electric energy density against distance to the interface is depicted in Fig. 21, and clearly shows the reason for the presence of this structure. The electric energy density values were calculated using the electric field intensity and the dielectric permittivity obtained by the fitting of the experimental points. Curve (a) in Fig. 21 corresponds to the curve shown in Fig. 17 and the integration of this curve gives a value of 0.072 J m−2 for interfacial energy density of the air/water interface. Curves (b) and (c) results in lower energy values and correspond to the force vs. separation curves displayed in Fig. 18 and 19, respectively. The most frequent measured curves are similar to that one displayed in Fig. 17 and the distribution profile is shown in Fig. 21.
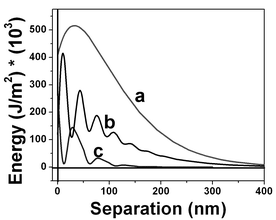 | ||
| Fig. 21 Electric energy density at the interfacial regions corresponding to values shown in Fig. 17 (curve a), 18 (curve b) and 19 (curve c). The interfacial energy obtained by the integration of the interfacial electric energy density shown in Fig. 17 is 0.072 J cm−2. Regions with lower electric energy density are shown by curves b and c. Curve c is the most frequently measured curve along the interfacial region. | ||
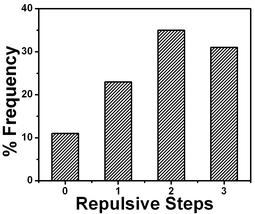 | ||
| Fig. 22 Comparison of number of repulsive steps obtained from force profiles measured using cantilevers with 0.03 N m−1 spring constant. | ||
The long range ordered structure near the water/air interface, which extends into the bulk liquid for a considerable distance (say, up to two tenths of a micrometre) would necessarily have to disappear with distance from surface because of the effects of thermal motion in randomizing the structure of water dipoles; this is apparent in Fig. 3.
If separate layers of ordered (or disordered) structures exist adjacent to a surface, the question that becomes important is related to the nature of the “transition region” over which one structure changes into another. It is important to detect how abrupt are the changes at the boundary. Indeed, the region near the air/water interface is characterized by a structure that shows an ε profile that oscillates indicating that there are variations in the organization within the structure and that the boundary between structures may be quite sharp. It is commonly thought that the orientation of the molecules of a liquid should disappear gradually in passing from the surface to the bulk. Here we show with the force vs. separation AFM measurements with a resolution of a few tenths of nanometres in normal plane to the surface that is possible to determine the structure of the molecular water arrangement.
All these results consistently indicate that the domains represent the water oriented regions attached on or near a hydrophobic surface. But one may ask whether these domains are attached on the hydrophobized surface from the beginning or generated during the tip approach to the surface. In the latter case for identical tip approaches we should obtain identical domains, which is not the case, we consider then that domains exist from the beginning.
The strong tendency for apolar solutes to associate in aqueous solution is formally attributed to the “hydrophobic interaction”. For small solutes, the magnitude has been carefully quantified both experimentally53 and via simulations54–56 but it has proven difficult to obtain an approximate analytical theory describing the phenomenon. Here we show that water molecules will bind to other water molecules except when there is a strong interfacial electric field generated by another solvent or interface that will align water molecules away from the originate cage distribution. Some hydrophobic units are then not able to form hydrogen bonds with water and consequently they associated in water.
5. Conclusions
There are no adsorbed ionic charges on a hydrophobic surface, but we have measured forces acting on a neutral tip immersed in its hydration layer that are of the same order of magnitude of the ones measured for ionic charged hydrophilic surfaces,35 which interact strongly with water molecules. Recently it was claimed8 that the origin of the strong long range hydrophobic field is the dipolar distribution of hydrogen broken bonds at the air/water interface. This statement is based on recent experimental results that suggest that at the water surface, each molecule in the top submonolayer has one of its four connecting hydrogen bonds broken.47Our force vs. separation AFM measurements with a few tenths of nanometres resolution in normal plane to the surface are used to measure in some detail the interfacial dielectric permittivity profile associated with the structure of the molecular water arrangement and consistently indicate that there are water domains attached on or near a hydrophobic surface. Indeed, the region near the air/water interface is characterized by a structure where the degree of the local molecular orientation rigidity is increased and decreased, generating an ε profile that oscillates and indicates not only the variations in the organization within the structure but also that the boundary between the ordered (or disordered) structures may be quite sharp.
The water/air interfaces presented here have decidedly complex local electric fields. Moreover, the surface free energy of an air/water interface is ∼70 mJ m−2 at room temperature and it is possible to account for such a high surface tension on the basis of interfacial electric field generated by the charge associated with one broken bond of the four possible connecting hydrogen bond.
7. Appendix
Water dielectric polarization model of an open system
Double-layer forces are associated with the colloidal particle interaction. Typically such particles will contain ionizable groups at their surfaces, so that the surfaces are charged. The charged surfaces create an inhomogeneous profile of cationic and anionic density. For an isolated surface at the simplest level of approximation the distribution follows from the Gauss equation, if we imagine that the water retains its bulk properties up to the surface:∇·![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) =
ρ(z,x)
=
ρ(z,x) | (A1) |
![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) is the density electric vector, ρ the charge density and the boundary conditions are |
is the density electric vector, ρ the charge density and the boundary conditions are |![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) 1|
−
|
1|
−
|![[D with combining macron]](https://www.rsc.org/images/entities/i_char_0044_0304.gif) 2|
=
σ, where σ is the surface charge density. The charge density profile ρ(x) is described by a Boltzmann distribution.
2|
=
σ, where σ is the surface charge density. The charge density profile ρ(x) is described by a Boltzmann distribution.
The second type is the force for an interface formed by pure water. Here we will propose that the liquid structure induced by the surface causes the force. In general, a surface will always induce re-ordering of water hydrogen bonds resulting in dipole orientations which extend over a number of layers. These are called “hydration” or “solvation forces”. In this case the electric field distribution will be calculated using ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) the polarization vector.57,58 A volume distribution of dipoles can be represented by a vector function
the polarization vector.57,58 A volume distribution of dipoles can be represented by a vector function ![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) , which gives the dipole moment per unit volume,
, which gives the dipole moment per unit volume,
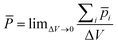 | (A2) |
![[p with combining macron]](https://www.rsc.org/images/entities/i_char_0070_0304.gif) i is the vector sum of dipole moments in the volume ΔV. If the volume is not taken to include the surface, the potential produced by a polarizing body is given by
i is the vector sum of dipole moments in the volume ΔV. If the volume is not taken to include the surface, the potential produced by a polarizing body is given by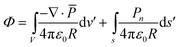 | (A3) |
The results expressed by eqn (A3) can be understood on a purely physical basis: where ∇·![[P with combining macron]](https://www.rsc.org/images/entities/i_char_0050_0304.gif) ≠ 0, means a net creation of dipole moments per unit volume, hence an incomplete cancellation of charge density from adjacent dipoles. Similarly, the surface charge density Pn occurs because the water dipoles ending on the surface cannot be neutralized for an adjacent dipole layer. Volume and surface polarization charge are therefore present because of incomplete cancellation of charges between adjacent dipoles both on the volume and at the surface.
≠ 0, means a net creation of dipole moments per unit volume, hence an incomplete cancellation of charge density from adjacent dipoles. Similarly, the surface charge density Pn occurs because the water dipoles ending on the surface cannot be neutralized for an adjacent dipole layer. Volume and surface polarization charge are therefore present because of incomplete cancellation of charges between adjacent dipoles both on the volume and at the surface.
Acknowledgements
The authors are grateful to J. R. Castro and L. O. Bonugli for technical assistance, the CNPq 523.268/95-5 for funding support in grant and FAPESP 03/12529-4 for financial support.References
- B. Windom, Faraday Symp. R. Soc. Chem., 1981, 20, 16 Search PubMed.
- C. A. Croxton, Statistical Mechanics of Liquid Surfaces, New York, 1980 Search PubMed.
- A. Rice, Proc. Natl. Acad. Sci., 1987, 84, 4709.
- J. Daillant, L. Bosio, I. J. Benattar and J. Meunier, Europhys. Lett., 1989, 8, 453 CrossRef CAS.
- A. Braslau, M. Deutsch, P. S. Pershan, A. H. Weiss, J. Als-Nielsen and J. Bohr, Phys. Rev. Lett., 1985, 54, 114 CrossRef CAS.
- S. K. Sinha, E. B. Sirota, S. Garoff and H. B. Stanley, Phys. Rev. B, 1988, 38, 2297 CrossRef.
- D. Beaglehole, Phys. Rev. Lett., 1987, 58, 1434 CrossRef CAS.
- O. Teschke and E. F. de Souza, Langmuir, 2003, 19, 5357 CrossRef CAS.
- O. Teschke, G. Ceotto and G. E. F. de Souza, Phys. Rev. E, 2003, 68, 31401-1.
- K. L. Sutherland and I. W. Wark, Principles of Flotation, Australasian Institute of Mining and Metallurgy, Melbourne, 1952 Search PubMed.
- F. Sebba, Ion Flotation, Elsevier, New York, 1962 Search PubMed.
- H. J. Schulze, Miner. Process. Extr. Metall. Rev., 1989, 5, 43 Search PubMed.
- R. Pashley and J. A. Kitchener, J. Colloid Interface Sci., 1979, 71, 491 CrossRef CAS.
- W. A. Ducker, Z. Xu and J. N. Israelachvili, Langmuir, 1994, 10, 3279 CrossRef CAS.
- M. L. Fielden, R. A. Hayes and J. Ralston, Langmuir, 1996, 12, 3721 CrossRef CAS.
- M. Preuss and H. J. Butt, Langmuir, 1998, 14, 3164 CrossRef CAS.
- J. N. Israelachvili and R. M. Pashley, Nature, 1982, 300, 341 CAS.
- J. L. Parker, V. V. Yaminsky and P. M. Claesson, J. Phys. Chem., 1993, 97, 7706 CrossRef CAS.
- P. Kekicheff and O. Spalla, Phys. Rev. Lett., 1995, 75, 1851 CrossRef CAS.
- V. S. J. Craig, B. W. Ninham and R. M. Pashley, Langmuir, 1998, 14, 3326 CrossRef CAS.
- Y. H. Tsao, D. F. Evans and H. Wennerstrom, Science, 1993, 262, 547 CrossRef CAS.
- J. Wood and R. Sharma, Langmuir, 1995, 11, 4797 CrossRef CAS.
- Y. I. Ravinovich and R. H. Yoon, Langmuir, 1994, 10, 1903 CrossRef.
- L. Meagher and V. S. J. Craig, Langmuir, 1994, 10, 2736 CrossRef CAS.
- N. Ishida, N. Kinoshita, M. Miyahara and K. Higashitani, J. Colloid Interface Sci., 1999, 216, 387 CrossRef CAS.
- J. Eriksson, S. Ljunggren and P. M. Claesson, J. Chem. Soc., Faraday Trans. 2, 1989, 85, 163 RSC.
- V. V. Yaminsky and B. W. Ninham, Langmuir, 1993, 9, 3618 CrossRef CAS.
- J. L. Parker, P. M. Claesson and P. Attard, J. Phys. Chem., 1994, 98, 8468 CrossRef CAS.
- N. Ishida, M. Sakamoto, M. Miyahara and K. Higashitani, Langmuir, 2000, 16, 5681 CrossRef CAS.
- R. F. Considine, R. A. Hays and R. G. Horn, Langmuir, 1999, 15, 1657 CrossRef CAS.
- P. S. Epstein and M. S. Plesset, J. Chem. Phys., 1950, 18, 1505 CrossRef CAS.
- S. Ljunggren and J. C. Eriksson, Colloids Surf. A, 1997, 129, 151 CrossRef.
- O. Teschke and E. F. de Souza, Appl. Phys. Lett., 1999, 74, 1755 CrossRef CAS.
- O. Teschke, G. Ceotto and E. F. de Souza, Chem. Phys. Lett., 2000, 326, 328 CrossRef CAS.
- O. Teschke, G. Ceotto and E. F. de Souza, Phys. Chem. Chem. Phys., 2001, 3, 3761 RSC.
- O. Teschke, G. Ceotto and E. F. de Souza, Phys. Rev. E, 2001, 64, 11605-01.
- O. Teschke and E. F. de Souza, Appl. Phys. Lett., 2003, 82, 1126 CrossRef CAS.
- Q. Du, E. Freysz and Y. R. Shen, Science, 1994, 264, 826 CrossRef CAS.
- Q. Du, E. Freysz and Y. R. Shen, Phys. Rev. Lett., 1994, 72, 238 CrossRef CAS.
- O. Teschke, R. A. Douglas and T. A. Prolla, Appl. Phys. Lett., 1997, 70, 1977 CrossRef CAS.
- R. M. Sassaki, R. A. Douglas, M. U. Kleinke and O. Teschke, J. Vac. Sci. Technol. B, 1996, 14, 2432 CrossRef CAS.
- J. E. Sader, I. Larson, P. Mulvaney and L. R. White, Rev. Sci. Instrum., 1995, 66, 3789 CrossRef CAS.
- L. Bergström and E. Bostedt, Coll. Surf. A, 1990, 49, 183 CrossRef.
- D. Harame, L. Bousse, J. Shott and J. D. Meindl, IEEE Trans. Electron Devices, 1987, 34, 1700 CrossRef.
- O. Teschke, G. Ceotto and E. F. de Souza, J. Vac. Sci. Technol. B, 2000, 18, 1144 CrossRef CAS.
- R. W. Zurilla, R. K. Sen and E. Yeager, J. Electrochem. Soc., 1978, 125, 1103 CAS.
- Y. R. Shen, Solid State Commun., 1998, 108, 399 CrossRef CAS.
- Y. H. Tsao, D. F. Evans and H. Wennerstrom, Langmuir, 1993, 9, 779 CrossRef CAS.
- O. I. Vinogradova, Langmuir, 1995, 11, 2213 CrossRef CAS.
- K. Raghavan, K. Foster, K. Motakabbir and M. Berkowitz, J. Chem. Phys., 1991, 94, 2110 CrossRef CAS.
- J. Hu, X-d. Xiao, D. F. Ogletree and M. Salmeron, Science, 1995, 268, 267 CrossRef CAS.
- I. Benjamin, Phys. Rev. Lett., 1994, 73, 2083 CrossRef CAS.
- C. Tanford, The Hydrophobic Effect, John Wiley, New York, 1980 Search PubMed.
- C. Pangali, M. Rao and B. J. Berne, J. Chem. Phys., 1979, 71, 2975 CrossRef CAS.
- D. E. Smith and A. D. Haymet, J. Chem. Phys., 1993, 98, 6445 CrossRef CAS.
- J. Forsman and B. Jonsson, J. Chem. Phys., 1994, 101, 5116 CrossRef CAS.
- R. Becker, Electromagnetic Fields and Interactions, Dover Publications Inc., New York, 1964, ch. BII Search PubMed.
- R. F. W. Bader, Mol. Phys., 2002, 100, 3333 CrossRef CAS.
| This journal is © the Owner Societies 2005 |
