O(¹D₂) orbital orientation in the ultraviolet photodissociation of ozone

Abstract

We present the absolute velocity-dependent orbital orientation for O(¹D₂) atoms produced from the photodissociation of ozone in the 248–285 nm region obtained using the DC slice imaging method. The results are analyzed in terms of laboratory frame anisotropy parameters describing distinct excitation and dissociation mechanisms possessing characteristic angular distributions. The results show negligible orbital orientation produced in dissociation by circularly polarized light, but strong recoil speed-dependent orientation following photolysis by linearly polarized light at all wavelengths studied. The origin of this polarization is ascribed to nonadiabatic transitions at avoided crossings and at long range.

---

1. Introduction

Despite its celebrated importance to life on earth, ozone photochemistry still remains a subject of surprising enigma. Although the dominant features of the photoabsorption in the ultraviolet spectral region and the ensuing chemistry have long been understood, there remain puzzles that elude definitive explanation: The mass independent heavy isotope enrichment in the stratosphere;^1,2 the vibrational structure seen in the Hartley and Huggins bands;^3,4 the varying bimodal vibrational distributions seen in the ground electronic state photolysis products;⁵ and the variation in the vibrational distributions in the dominant excited state products throughout the UV.⁶ Further investigations and alternative approaches are clearly needed. The use of ion imaging techniques to probe atomic orbital polarization in photodissociation^7–13 has recently emerged as once such alternative approach. These studies deliver fundamentally new insight into photochemical problems because they probe both the underlying features of the photoexcitation process as well as the subsequent dissociation dynamics across multiple electronic states. As such, these methods are ideally suited to for studying ozone photochemistry, a system notorious for its electronic complexity. In this paper we present application of the DC slice imaging method as a probe of atomic orbital orientation following ozone dissociation at a series of wavelengths within the Hartley absorption band. The Hartley band extends from about 200–310 nm and across most of this region photodissociation proceeds primarily via two pathways:and

The initial excitation is believed to take place directly to the 1¹B₂ (B̃)-state with about 90% of the population then dissociating on this surface to produce the O(¹D₂) products.^6,14–16 Nonadiabatic crossing to the nearby R̃-state results in roughly 10% yield of O(³P_J) atomic fragments.¹⁷ This is illustrated schematically in Fig. 1.

Fig. 1 Schematic diagram of the O₃ potential curves relevant to the UV absorption region.

The power of ion imaging and related methods in these applications lies in their ability to probe the nature of the angular momentum polarization as a function of photofragment recoil direction. This is an example of v–J vector correlation, and studies of this phenomenon can afford great insight into the dissociation dynamics by allowing one to examine the polarization in terms of more fundamental contributions.⁹ The polarization is conveniently expanded in a series of multipole moments ρ_KQ of rank K and component Q. The zeroth order multipole moment corresponds to the population, while higher order odd moments describe the angular momentum orientation, and even moments describe the alignment. The orientation can only be probed with circularly polarized light, while alignment can be probed either with linearly, or circularly polarized light. The polarization can be referred either to the laboratory, or to the body-fixed frame, in the latter case m_J is a projection of the total angular momentum J onto the breaking bond. Within the theoretical treatment which will be outlined here, it is assumed that the characteristic dissociation time is significantly smaller than the molecular rotation period: this approximation is called the axial recoil limit.

In general, K = 1 and 2 orientation and alignment are the leading contributions to the angular momentum polarization, but higher rank multipoles up to K = 2J exist, and may be needed to fully characterize the system. However, by carefully choosing a suitable probe scheme their contribution to the experimental signal may often be neglected,⁹ as will be discussed in more detail in Section 3. A fully quantum mechanical treatment has been developed for the K = 1 and K = 2 moments,^8,9 and very recently extended to include rank K = 4, the hexadecapole moment.¹⁸ For the case of O(¹D₂) fragments being considered here, all moments up to K = 4 are necessary for a complete description of the angular momentum polarization; however, for our present purposes we will largely be confined to a detailed investigation of the K = 1 contribution.

Atomic orbital polarization in photodissociation has lately been the subject of considerable interest, especially for diatomic^8,10,19,20 and triatomic^13,21–24 systems. Imaging methods now dominate over alternative probe methods such as Doppler or ion time-of-flight as the most convenient means of studying these phenomena. A significant recent advance has been the development of slice imaging methods^25–28 that allow the angular momentum polarization to be measured directly over a large spread of photofragment recoil velocities, without needing to apply any form of forward convolution to the experimental data. Our first application of this approach was to characterize alignment in the S(¹D₂) photofragment from ethylene sulfide photodissociation,²⁹ a polyatomic system with a broad trimodal speed distribution and alignment that varied significantly with recoil speed. Although most studies to date have focused on rank K = 2 polarization, rank K = 1 orbital orientation has also been shown to afford deep insight into molecular photophysics,³⁰ including the demonstration of matter wave interference in ICl, Cl₂ and OCS.^11,31–35 Finally, as mentioned above, theory has recently been extended to include the rank K = 4 case for photofragment alignment and applied to the experimental case of O(¹D₂) atoms from N₂O photodissociation.¹⁸

Imaging studies of vector correlations in ozone photodissociation have a long history, largely in studies from the Houston group.^5,24,36–38 Dylewski et al. studied alignment effects in ozone across a significant portion of the Hartley band, applying both a “diagonal” treatment, in which coherences between different electronic states are neglected, and a fully quantum mechanical approach (only considering the rank K = 2 moment explicitly) where off-diagonal elements of the density matrix representing the photofragment alignment describe any coherent phenomena.²⁴ They concluded that at dissociation wavelengths of 255 and 298 nm, an incoherent parallel excitation mechanism dominates the alignment. This was consistent with previous assertions, based on theory, that the initial absorption and subsequent dissociation largely take place on the 1¹B₂ surface. Their data also clearly revealed the contribution of a higher order K = 4 moment however, suggesting additional contributions from other excitation or dissociation pathways. More recently, Hancock and co-workers^39,40 have reported significant alignment and orientation in the molecular O₂(a¹Δ_g) fragment produced in conjunction with O(¹D₂) atoms, and this is seen to fluctuate with product rotational state, perhaps a manifestation of the fascinating rotational-state dependent curve crossing reported by Valentini et al.¹⁶ This observation of substantial rotational orientation is surprising and, to-date, lacking explanation.

In the following pages, we present a detailed slice imaging study of O(¹D₂) orbital orientation in ozone photodissociation from 248 to 285 nm. The paper is organized as follows: Section 2 presents the experimental background; Section 3 details the theoretical approach for extracting quantitative orientation data from slice imaging measurements; Section 4 introduces the experimental results; finally, Section 5 provides discussion and interpretation of the results.

2. Experimental

The key aspects of the experimental set-up employed in the DC slice imaging approach have been described in detail elsewhere.^27,29 Only the points specific to this particular study will be summarized here. Ozone was initially produced using a commercial generator (OREC) and retained in a silica gel trap held at −78 °C in a dry ice–acetone bath. A molecular beam was then formed by raising the trap temperature to −40 °C, flowing argon at about 730 Torr over the silica gel and expanding the resulting mixture through a 1 mm diameter pulsed nozzle. After passing through a skimmer and a second collimating aperture, the beam entered into a velocity mapping electrode assembly optimized for DC slice imaging and was intersected at right angles by two counter-propagating laser beams. The photolysis laser light was generated using several different strategies: 266 nm was provided by the fourth harmonic of a Nd:YAG laser (Quanta Ray DCR-2A) operating at 10 Hz; 248 nm was produced by pumping a dye laser (Quanta Ray PDL 3, DCM dye) with the 532 nm output of the same YAG laser and then sum-frequency mixing with the residual 1064 nm fundamental; Longer wavelengths (275 nm) were simply generated directly from the doubled output of the 532 nm pumped dye laser (Rhodamine 560 dye). In all cases the power of the resulting beam was attenuated to approximately 1 mJ pulse⁻¹ and then loosely focused into the interaction region using a 30 cm lens. Control over the polarization was achieved using either a fused silica Soleil–Babinet compensator (Special Optics) for cases where circular polarization was required or a double Fresnel rhomb in cases where linear polarization was required at 45°, as will be discussed in Section 3. The probe laser was provided by frequency tripling the output of a dye laser (Continuum Jaguar, Rhodamine 640 dye) pumped by the 532 nm harmonic of a second Nd:YAG laser (Quanta Ray GCR-5). A magnesium fluoride Soleil–Babinet compensator (Karl Lambrecht) was used to produce the required circular polarization. The probe beam (∼0.7 mJ pulse⁻¹) was then focused through a second 30 cm lens. The O(¹D₂) atomic photofragments produced in the dissociation event were probed using the following (2 + 1) REMPI scheme:Following ionization, the oxygen ions were accelerated through the multi-lens velocity mapping assembly and impacted upon a dual microchannel plate array of 120 mm diameter, which was coupled to a P-47 phosphor screen. In this particular instance a repeller electrode held at +700 V was used in conjunction with three additional focusing lenses in the velocity-mapping scheme to stretch the photofragment ion cloud along the time-of-flight axis to around 400 ns. The overall flight path from the laser interaction region to the detector was 120 cm. Application of a narrow (∼40 ns) time gate at the detector was then used to sample the central section of the distribution. The resulting image was recorded using a CCD camera (Mintron 2821e, 512 × 480 pixels) in conjunction with PC acquisition software (McLaren Research) that enabled real time event counting of the data. A more detailed description of this approach may be found in a previous discussion.²⁷

3. Theory and analysis

As shown by Kummel and co-workers,^41,42 the general expression describing the absorption intensity of polarized light by photofragments via a two-photon transition can be expressed in terms of the series of the state multipoles ρ_KQ with ranks K = 0,…,4 and projections Q = −K,…,K. The zeroth-rank state multipole ρ₀₀ is proportional to the total population of the photofragment magnetic sublevels and the multipoles with rank K > 0 describe the anisotropy of the photofragment angular momenta. In the case of photodissociation, the state multipoles are a function of (θ,ϕ) which are the polar and azimuthal angles of the photofragment recoil direction vector v. Usually, the spatial modulations in an ion image which result from photofragment orientation and alignment represent a relatively small fraction of the total signal. For this reason, it is useful to isolate these contributions by taking linear combinations of the signal recorded under different experimental geometries of the photolysis and probe laser polarizations, in such a way that the population term ρ₀₀ cancels.

The co-ordinate system originally used by Vasyutinskii and co-workers^8,9 for considering the angular distribution of photofragment state multipoles is displayed in Fig. 2. Specifically, for the case of probing photofragment orientation the following combination of signals can be used for isolating the rank K = 1,3 state multipoles from the rank K = 0, 2, and 4 ones:

where I^X_R(θ,ϕ) and I^X_L(θ,ϕ) are three-dimensional absorption intensities which are related to right- and left-handed circularly polarized probe light, while I_Y(θ,ϕ) and I_Z(θ,ϕ) are absorption intensities related to linearly polarized light with polarization vectors directed along the Y and Z axes, respectively. The probe light is assumed to propagate along the −X-axis.

Fig. 2 Laboratory frame co-ordinate system.

The factors P^c_K in eqn. (3.4) are linestrength factors which in the case of a (2 + 1) REMPI probe scheme may be simply evaluated from the following expression:⁴³

Here j_i and j_f are the initial and final total angular momenta of the detected atom and s indicates a cyclic projection of the electronic transition moment onto the direction of the probe beam, takes a value of 0 for a linearly polarized probe, +1 for right hand circular polarization and −1 for left hand circular polarization. Therefore, eqns. (3.5)–(3.8) are calculated using the s = +1 value. Substituting j_i = 2, j_f = 1, and s = +1 into eqn. (3.5), in accordance with the REMPI scheme shown in eqn. (2.3), one can easily obtain P^c₁/P₀ = −1.179 and P^c₃/P₀ = 0. Thus, the rank K = 3 state multipole gives zero contribution to the signal in this particular instance and can be neglected.

The denominator on the right hand side of eqn. (3.4) is a normalization factor which is proportional to the total population of all magnetic sublevels⁹ and the angular brackets denote an averaging of the corresponding absorption intensities over all recoil angles. As discussed in more detail in a previous publication, the slice imaging technique used in this study allows us to monitor only the narrow central part of the total three-dimensional absorption signal described by eqn. (3.4), which, within our coordinate scheme, corresponds to fixing θ to a value of π/2.²⁹ Note that several alternative approaches for normalization of the slice imaging data introduced in our previous study were limited to cases where the extent of the photofragment orbital polarization was small. This drawback can be completely removed by using the normalization factor in the denominator of eqn. (3.4), where the angular brackets now represent integration over the azimuthal angle ϕ at the polar angle θ = π/2. From eqn. (3.4), the explicit expressions for the state multipole⁹ρ₁₁ for the case of sliced images recorded under two different polarizations of the photolysis laser can be presented as:

Case I: The photolysis (right circularly polarized) and probe light (right or left circularly polarized) propagate along X and −X respectively:

Case II: The photolysis and probe light counterpropagate along the X-axis, with the photolysis light linearly polarized at 45° to the detector plane and the probe light circularly polarized:

The three first-rank orientation anisotropy parameters, α₁, γ₁, and γ^′₁ each characterize the extent to which a distinct physical mechanism plays a role in the overall dissociation dynamics. The parameters α₁ and γ₁ in eqn. (3.6) describe contributions to the fragment orientation from incoherent perpendicular excitation and a coherent superposition of a parallel/perpendicular excitation, respectively. The former contribution arises from photofragment electronic angular momentum which is parallel to the recoil velocity direction v, while the latter case comes from angular momentum that is perpendicular to the recoil direction and lies in the plane defined by the recoil vector v and the propagation direction of the photolysis laser beam (Fig. 3). The parameter γ^′₁ in eqn. (3.7) describes the contribution to the orientation from a coherent superposition of a parallel and a perpendicular excitation where the photofragment angular momentum is perpendicular both to the recoil velocity vector v and to the photolysis light polarization vector e. Only the last mechanism can be induced by linearly polarized light.

Fig. 3 Cartoon showing orientation of angular momentum vectors corresponding to each orientation anisotropy parameter relative to transition moment μ and recoil direction v.

Although photofragment orbital orientation can be produced either with circularly or linearly polarized dissociation light, in cases where the photolysis beam is linearly polarized along either the Y- or Z-axis (as would be common in a typical imaging experiment), an angular momentum distribution is produced that is antisymmetric with respect to reflection in the plane of the detector, and this results in zero observable orientation effect. However, when the linear polarization is rotated out of the YZ-plane, any non-zero γ^′₁ orientation effect that is present becomes observable and will, in fact, show a maximum value when the polarization is set at an angle of 45° with respect to both the Y and Z-axes.⁹

For any given photofragment recoil velocity, the orientation parameter described above may be extracted from the experimental data using a simple linear fitting algorithm, and a complete picture of the mechanism in the photodissociation event inferred directly from the result. Additionally, it should be noted that in the case of γ^′₁, the orientation parameter can be directly obtained without any fitting process by integrating the numerator of eqn. (3.7) over the azimuthal angle ϕ at any given recoil velocity. The resulting expression is written as:

A fully detailed description of the derivation of the rank K = 1 orientation basis functions presented in eqn. (3.6) and eqn. (3.7) will follow in a future publication.

4. Results

Experimental images obtained at a photolysis wavelength of 266 nm using left and right circularly polarized probe light are shown in Fig. 4. The dissociation laser was polarized either circularly or linearly at 45° with respect to the YZ-plane, as indicated, in order to investigate the three possible atomic orientation effects, as described fully in Section 3. The four rings in each image correspond to ν = 0–3 in the O₂ (a¹Δ_g) co-fragment. We see from the difference images, and from integration of the images (not shown) that the values of the orientation anisotropy parameters (α₁,γ₁), obtained using circularly polarized photolysis light, are negligible within the statistical error. For the case of 45° linearly polarized light however, there is a significant orientation effect arising from a coherent parallel/perpendicular excitation (γ^′₁) that is strongly dependent upon the photofragment recoil speed. A particularly striking feature is the change in sign of the innermost ring relative to the other three, which is confirmed by switching the direction of the photolysis polarization from +45° to −45°, as shown.

Fig. 4 DC sliced images and difference images of O(¹D₂) from 266 nm dissociation of ozone for indicated combination of photolysis-probe laser polarization. Red and blue correspond to positive and negative intensities, respectively.

In order to investigate the recoil speed dependence of γ^′₁ more closely, additional orientation measurements (using linear polarization at +45°) were carried out at various dissociation wavelengths ranging from 248 to 285 nm. The results are presented in Fig. 5. In general, we consistently note a change of sign in the difference images for the slower fragments. This suggests that the sign and magnitude of γ^′₁ correlates most strongly with the O-atom recoil speed rather than the specific vibrational level of O₂ co-fragment. In addition, some cases exhibit a change of sign of γ^′₁ within one ring (see Fig. 5, e.g. the v = 0 ring at 285 nm, the v = 1 ring at 280 nm and the innermost ring at 248 nm). This observation suggests that the correlation of γ^′₁ with co-fragment rotational level may be an additional aspect of the dependence of the orientation effect on recoil speed.

Fig. 5 DC sliced difference images for the photodissociation of ozone at from 248 nm to 266 nm. Red and blue correspond to positive and negative intensities, respectively.

Fig. 6 Orientation anisotropy parameter, γ^′₁, as a function of O-atom recoil speed following the photodissociation of ozone at 248, 266, and 285 nm. Circles (○) denote γ^′₁. The solid and dashed lines correspond to the total population, (〈I_Z〉 + 〈I_Y〉 − 1/3[〈I^X_R〉 + 〈I^X_L〉]) and the difference signal, (I^X_R − I^X_L), respectively. These values have been arbitrarily scaled.

The absolute K = 1 orientation anisotropy parameters can be obtained by fitting the difference images to the relevant eqn. (3.6) and eqn. (3.7), which include the correct normalization factor weighted by the recoil-dependent β for the sliced image. As described earlier, for the γ^′₁ case, it is also possible to measure directly the orientation parameter by just integrating the total intensity of the difference image at each recoil speed (eqn. (3.8)). With the latter approach, γ^′₁ may be determined directly from the experimental difference images and plotted as a function of O atom recoil speed, as shown in Fig. 6 for dissociation wavelengths of 248, 266, and 285 nm. Speed-dependent values for the recoil anisotropy parameter, β, were obtained by fitting the vertical–vertical (photolysis-probe polarization) image recorded using the O(¹D₂) → O(¹F₃) → O⁺ REMPI probe transition at 203.7 nm, and neglecting the K = 4 contribution (which, as may be deduced from eqn. (3.5), is small in this instance). Peak γ^′₁ values for each vibrational level of the O₂ co-fragment are presented in Table 1 for all dissociation wavelengths studied.

Table 1 Variation in orientation anisotropy parameter, γ^′₁ with O₂ co-fragment vibrational level following the photodissociation of ozone in the region 248–266 nm

Wavelength/nm	ν = 0	ν =1	ν =2	ν =3	ν = 4	ν = 5
248	−0.123	−0.167	−0.124	−0.148	−0.176	0.052
266	−0.139	−0.151	−0.105	0.051
278	−0.090	0.006	0.015
280	−0.137	−0.009	−0.029
282	−0.102	−0.013
285	−0.073	0.054

---

From the speed-dependent orientation distributions plotted in Fig. 6, it can be seen that the peak of the orientation parameter does not generally occur at the peak of the population for each vibrational level. Instead, the maximum occurs at the slow side (corresponding to higher rotational states of the co-fragment) at each vibrational level except for the innermost ring. For the inner ring, where γ^′₁ changes sign, this dependence on co-fragment rotational level is also inverted. That is, for the inner ring it is the lower rotational levels that have the largest magnitude of the orientation, and this occurs for rotational levels that are lower than the most probable levels for the given vibration. This behavior is consistently observed for other photolysis wavelengths even though it is not as clear at 248 nm, perhaps due to a complex overlapping in rotational structures.

5. Discussion

We have measured all three first-rank orientation anisotropy parameters in the 266 nm photodissociation of ozone. The α₁ and γ₁ parameters, corresponding to incoherent perpendicular and coherent parallel/perpendicular excitation/dissociation mechanisms, respectively are zero within the experimental uncertainties, while the dissociation mechanism represented by γ^′₁ shows a strong effect. Although γ^′₁ also reflects the coherent excitation of a parallel and a perpendicular transition, it is quite different in origin from γ₁. The α₁ and γ₁ parameters arise, in effect, from propagation of the photon helicity into the product. The origin of γ^′₁ however may simply reflect simultaneous excitation of different components of the transition moment in the molecular frame. Therefore, it should not be surprising that the values of γ^′₁ and γ₁ are very different.

For the moment, we have no complete quantum mechanical theory of these phenomena and cannot give a fully quantitative analysis; however, a qualitative explanation can be put forward based upon the following arguments. As already mentioned, the α₁ and γ₁ parameters directly reflect a mapping of the photon helicity E₁₀(e)⁴⁴ into the angular momentum distribution of the O-atom products. The components of the fragment angular momenta j_‖ and j_⊥ lie in the molecular plane parallel and perpendicular to the recoil axis, respectively (see Fig. 3). In fact, the condition for this orientation mechanism is preservation of the quantum number Ω (helicity) in the molecular excited state during dissociation. For a planar triatomic molecule this condition usually cannot be fulfilled. Let us consider the following expansion of the electronic molecular wavefunction over the basis set |Ω〉:

where Ω is the component of the total angular momentum projected onto the recoil axis.

The wavefunction Ψ_mol is either symmetric or antisymmetric under reflection of the electron coordinates in the molecular plane. Interaction between the basis states |Ω〉 and |−Ω〉 within the stationary wavefunction Ψ_mol in eqn. (5.9) results in destruction of the orientation due to population exchange between these states. Qualitatively, the rate of this interaction is proportional to the energy separation between the excited state and the nearest electronic states of the same symmetry, ΔE_e. Therefore, if ΔE_e/ħ is large compared with the inverse dissociation time τ⁻¹_diss, the quantum number Ω is not preserved and the orientation effect of the considered type (α₁ and γ₁), in general, cannot exist in planar molecules. An opposite case is met in diatomic molecules, where interaction between |Ω〉 and |−Ω〉 basis states is usually caused by a rather weak Λ-doubling interaction. As a result, for fast dissociation ΔE_e/ħ ≪ τ⁻¹_diss and the fragment orientation due to the above mechanism is close to its maximum possible value, as reported elsewhere.^12,45,46

The photofragment state multipole ρ₁₁(k) described by the γ^′₁ parameter arises in completely different way. As shown by Siebbeles and co-workers,⁴⁷ this state multipole arises as a direct tensor product of two alignments: ρ₁₁(k) ∝ [Y₂(k) ⊗ E₂(e)]₁₁, where Y_2q1(k) is the fragment recoil spherical harmonic and E_2q2(e) is the photolysis photon alignment. Note that the interaction between the basis states |Ω〉 and |−Ω〉, discussed above, does not affect the molecular alignment. The corresponding component of the fragment angular momenta j′_⊥is perpendicular to the molecular plane. Therefore, the orientation characterized by the parameter γ^′₁ should be expected for the polyatomic molecules in the absence of the Coriolis nonadiabatic interactions and in case if the molecular planes possess alignment due to photodissociation.

The appearance of this coherent parallel/perpendicular contribution even in dissociation initiated on a single surface can be understood in light of related observations previously reported in NO₂.²¹ In ozone excitation to the B̃-state, the transition moment has B₂ symmetry within the C_2v point group and lies in the molecular plane at an angle θ = 31.6° with respect to the recoil axis. This gives rise to non-limiting β values even within the axial recoil approximation, and the transition moment possesses both parallel and perpendicular components in the recoil frame. This is a “static” coherence effect because the two “pathways” are degenerate and the initial phase difference between them is locked at a certain value during the initial excitation. In NO₂ a similar coherent dissociation mechanism gave contributions to the alignment described by the γ₂ anisotropy parameter. In the case of orientation, the three anisotropy parameters described above should be considered in general. The parameter γ₁ is proportional to cos Δϕ, while the parameter γ^′₁ is proportional to sin Δϕ, where Δϕ is the phase shift between the “parallel” and the “perpendicular” axes to the recoil direction.^32,46 In general, the phase shift contains a contribution from the nuclear movement which can be qualitatively associated with the elastic scattering phase shift and a “dynamical phase” (or Stokes phase, see ref. 48) contribution which is due to the optical electron excitation and the nonadiabatic interactions. The former contribution is known to give rise to the oscillation of the magnitudes of anisotropy parameters with photon wavelength;³² it can likely be neglected in the “static” coherent case. However, the “dynamical” phase shift is nonzero and in our experiment, results in the significant value of the γ^′₁ parameter.

Although this “static” coherence could account for the large γ^′₁ we observe, it cannot simply account for the profound speed dependence. This speed dependence is shown clearly in Fig. 7 in which we have plotted the maximum magnitude of the γ^′₁ for each peak at all dissociation wavelengths. Regardless of the photolysis wavelength or cofragment vibrational level, the value of γ^′₁ is generally small and positive for the slow fragments, and abruptly changes to large and negative for O atom recoil speeds of 1300 m s⁻¹ or greater. Schinke has recently argued that photoexcitation in the Hartley–Huggins band system is exclusively to the B̃-state, but that curve crossings with the Ã-state occur both at very short range (not likely to be important in this case), and at longer range (see Fig. 1).¹⁷ Both the B̃ and the Ã-state encounter the R̃-state subsequently, and there is additional opportunity for recrossing back. Furthermore, the à and B̃-states correlate asymptotically to the same electronic states of the products, so coherences created in the initial excitation may well be preserved and give rise to interference following these curve crossings. In fact, the abrupt change we see in Fig. 7 as a function of recoil speed is likely a consequence of “diabatic” dissociation on the B̃-state giving rise to large magnitude orientation effects for higher recoil speeds, with adiabatic dissociation (i.e., crossing to the Ã-state) quenching this effect at lower recoil speeds.

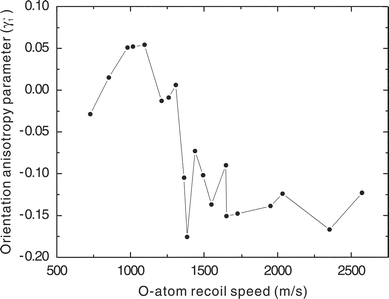Fig. 7 Recoil speed dependence of γ^′₁ for all O₂ co-fragment vibrational levels and all photolysis wavelengths.

The change in sign of γ^′₁ for the slowest fragments and the related observation of the shift in the orientation peak from the population peak for each vibrational level provide further clues to the origin of the orientation. Since the latter observation persists in some form for all recoil speeds, to understand the effect we must look for a mechanism that would give a correlation between co-fragment rotational level and atomic orientation. The static coherence mentioned above might exhibit this behavior, since dissociation from more acute bond angles would be associated with greater perpendicular contributions and thus a larger parallel/perpendicular coherence, and at the same time with greater product rotational excitation. But if this were the principal mechanism, the coherence should closely track the β value since they both would find their origin in the deviation from the parallel limit. It does not. An alternative explanation may be found by considering the dependence of the long-range potentials on the bond angle. Alignment measurements of O(¹D₂) in N₂O photodissociation by Teule et al. showed that the atomic polarization is correlated with the rotational state of the N₂ co-fragment. They developed a semiclassical model taking into account the long-range quadrupole-quadrupole interaction that could account for this correlation.²³ A similar argument could account for the rotational correlation we see in ozone: i.e., it is a manifestation of the O–O–O bond angle mediating the long-range interactions.

In summary, the gross features of the speed-dependent orientation are likely a consequence of the static coherence persisting or being quenched at the avoided crossing between the B̃ and à states. Superimposed upon these large effects are smaller modulations, correlated with co-fragment rotational level, that are induced by the long-range interactions and by other nonadiabatic processes. Although the system begins on a single excited potential surface and ends in a single atomic state, the angular momentum polarization reveals the distinct paths followed. Additional theoretical investigation will be necessary to frame this interpretation in quantitative terms.

Acknowledgements

This work was supported by the Director, Office of Science, Office of Basic Energy Sciences, Division of Chemical Sciences, Geosciences and Biosciences, of the US Department of Energy under contract number DE-FG02-04ER15593, by the National Science Foundation under grant number CHE-0415393, and by a Cooperative Grant from the Civilian Research and Development Foundation, CRDF Award No. RC2-2570-ST-03.

References

1. D. Babikov, B. K. Kendrick, R. B. Walker, R. Schinke and R. T. Pack, Chem. Phys. Lett., 2003, 372, 686.
2. Y. Q. Gao and R. A. Marcus, Science, 2001, 293, 259.
3. L. T. Molina and M. J. Molina, J. Geophys. Res., 1986, 91, 14501.
4. J. Malicet, D. Daumont, J. Charbonnier, C. Parisse, A. Chakir and J. Brion, J. Atmos. Chem., 1995, 21, 263.
5. J. D. Geiser, S. M. Dylewski, J. A. Mueller, R. J. Wilson, R. Toumi and P. L. Houston, J. Chem. Phys., 2000, 112, 1279.
6. M. A. Thelen, T. Gejo, J. A. Harrison and J. R. Huber, J. Chem. Phys., 1995, 103, 7946.
7. Y. Mo, H. Katayanagi, M. C. Heaven and T. Suzuki, Phys. Rev. Lett., 1996, 77, 830.
8. A. S. Bracker, E. R. Wouters, A. G. Suits and O. S. Vasyutinskii, J. Chem. Phys., 1999, 110, 6749.
9. E. R. Wouters, M. Ahmed, D. S. Peterka, A. S. Bracker, A. G. Suits and O. S. Vasyutinskii, in Imaging in Chemical Dynamics, ed. R. E. Continetti and A. G. Suits, American Chemical Society, Washington, 2000, p. 238.
10. E. R. Wouters, M. Beckert, L. J. Russell, K. N. Rosser, A. J. Orr-Ewing, M. N. R. Ashfold and O. S. Vasyutinskii, J. Chem. Phys., 2002, 117, 2087.
11. T. P. Rakitzis and T. N. Kitsopoulos, J. Chem. Phys., 2002, 116, 9228.
12. T. P. Rakitzis, P. C. Samartzis, R. L. Toomes, T. N. Kitsopoulos, A. Brown, G. G. Balint-Kurti, O. S. Vasyntinskii and J. A. Beswick, Science, 2003, 300, 1936.
13. M. Brouard, R. Cireasa, A. P. Clark, T. J. Preston, C. Vallance, G. C. Groenenboom and O. S. Vasyutinskii, J. Phys. Chem. A, 2004, 108, 7965.
14. C. E. Fairchild, E. J. Stone and G. M. Lawrence, J. Chem. Phys., 1978, 69, 3632.
15. R. K. Sparks, L. R. Carlson, K. Shobatake, M. L. Kowalczyk and Y. T. Lee, J. Chem. Phys., 1980, 72, 1401.
16. J. J. Valentini, D. P. Gerrity, J.-C. N. Phillips and K. D. Tabor, J. Chem. Phys., 1987, 86, 6745.
17. Z.-W. Qu, H. Zhu and R. Schinke, Chem. Phys. Lett., 2003, 377, 359.
18. A. G. Smolin, O. S. Vasyutinskii, E. R. Wouters and A. G. Suits, J. Chem. Phys., 2004, 121, 6759.
19. T. P. Rakitzis, R. L. Toomes, L. Tsigaridas, M. Coriou, D. Chestakov, A. T. J. B. Eppink, D. H. Parker and T. N. Kitsopoulos, Chem. Phys. Lett., 2002, 364, 115.
20. M. J. Bass, M. Brouard, A. P. Clark, C. Vallance and B. Martinez-Haya, Phys. Chem. Chem. Phys., 2003, 5, 856.
21. M. Ahmed, D. S. Peterka, A. S. Bracker, O. S. Vasyutinskii and A. G. Suits, J. Chem. Phys., 1999, 110, 4115.
22. M. Ahmed, E. R. Wouters, D. S. Peterka, O. S. Vasyutinskii and A. G. Suits, Faraday Discuss., 1999, 113, 425.
23. T. M. Teule, G. C. Groenenboom, D. W. Neyer, D. W. Chandler and M. H. M. Janssen, Chem. Phys. Lett., 2000, 320, 177.
24. S. M. Dylewski, J. D. Geiser and P. L. Houston, J. Chem. Phys., 2001, 115, 7460.
25. C. R. Gebhardt, T. P. Rakitzis, P. C. Samartzis, V. Ladopoulos and T. N. Kitsopoulos, Rev. Sci. Instrum., 2001, 72, 3848.
26. J. J. Lin, J. Zhou, W. Shiu and K. Liu, Rev. Sci. Instrum., 2003, 74, 2495.
27. D. Townsend, M. P. Minitti and A. G. Suits, Rev. Sci. Instrum., 2003, 74, 2530.
28. D. Chestakov, S.-M. Wu, G. Wu, D. H. Parker, A. T. J. B. Eppink and T. N. Kitsopoulos, J. Phys. Chem. A, 2004, 108, 8100.
29. D. Townsend, S. K. Lee and A. G. Suits, Chem. Phys., 2004, 301, 197.
30. A. J. Alexander and R. N. Zare, Acc. Chem. Res., 2000, 33, 199.
31. T. P. Rakitzis, S. A. Kandel and R. N. Zare, J. Chem. Phys., 1998, 108, 8291.
32. T. P. Rakitzis, S. A. Kandel, A. J. Alexander, Z. H. Kim and R. N. Zare, Science, 1998, 281, 1346.
33. Z. H. Kim, A. J. Alexander, S. A. Kandel, T. P. Rakitzis and R. N. Zare, Faraday Discuss., 1999, 113, 27.
34. Z. H. Kim, A. J. Alexander and R. N. Zare, J. Phys. Chem. A, 1999, 103, 10144.
35. T. P. Rakitzis, P. C. Samartzis and T. N. Kitsopoulos, J. Chem. Phys., 1999, 111, 10415.
36. A. G. Suits, R. L. Miller, L. S. Bontuyan and P. L. Houston, J. Chem. Soc., Faraday Trans. 2, 1993, 89, 1443.
37. R. J. Wilson, J. A. Mueller and P. L. Houston, J. Phys. Chem. A, 1997, 101, 7593.
38. N. Taniguchi, K. Takahashi, Y. Matsumi, S. M. Dylewski, J. D. Geiser and P. L. Houston, J. Chem. Phys., 1999, 111, 6350.
39. G. Hancock, P. J. Pearson, G. A. D. Ritchie and D. F. Tibbetts, Phys. Chem. Chem. Phys., 2003, 5, 5386.
40. G. Hancock, P. J. Pearson, G. A. D. Ritchie and D. F. Tibbetts, Chem. Phys. Lett., 2004, 393, 425.
41. A. C. Kummel, G. O. Sitz and R. N. Zare, J. Chem. Phys., 1986, 85, 6874.
42. A. C. Kummel, G. O. Sitz and R. N. Zare, J. Chem. Phys., 1987, 88, 6707.
43. Y. Mo and T. Suzuki, J. Chem. Phys., 1998, 109, 4691.
44. R. N. Zare, Angular Momentum, Wiley, New York, 1988.
45. K. O. Korovin, B. V. Picheyev, O. S. Vasyutinskii, H. Valipour and D. Zimmermann, J. Chem. Phys., 2000, 112, 2059.
46. G. G. Balint-Kurti, A. J. Orr-Ewing, J. A. Beswick, A. Brown and O. S. Vasyutinskii, Phys. Chem. Chem. Phys., 2002, 116, 10760.
47. L. D. A. Siebbeles, M. Glass-Maujean, O. S. Vasyutinskii, J. A. Beswick and O. Roncero, J. Chem. Phys., 1994, 100, 3610.
48. H. Naramura, Nonadiabatic Transitions: Beyond Born–Oppenheimer Dynamics of Molecules and Chemical Reactions, Marcel Dekker, New York, 1996.

---