State of water at 136 K determined by its relaxation time
G. P.
Johari
*
Department of Materials Science and Engineering, McMaster University, Hamilton, Ontario, Canada L8S 4L7. E-mail: joharig@mcmaster.ca
First published on 21st February 2005
Abstract
Dielectric relaxation time of pure bulk water has been determined from the dielectric loss tangent scans against temperature at two frequencies. After calculating the frequency-independent background loss, the relaxation loss was obtained, and the relaxation time determined. The dielectric relaxation time of water is 35 ± 13 s at 136 ± 1 K, which is comparable with its structural relaxation time of ca. 33 s estimated from its Tg endotherm (G. P. Johari, A. Hallbrucker and E. Mayer, Nature, 1987, 330, 552). Therefore, water is an ultraviscous liquid at 136 K, and this removes the basis for a comparison-based inference that water is a rigid glass up to a temperature of 165 K or higher (Y. Yue and C. A. Angell, Nature, 2004, 427, 717). The method yields satisfactory values for the relaxation time of stable glasses at their known calorimetric Tg.
1. Introduction
Amorphous solid water is believed to be abundant in the universe, particularly as thin film deposits and as particles in interstellar space, and yet liquid water is difficult to vitrify. Therefore amorphous solid water has been produced either by depositing its vapours on a substrate kept at ca. 77 K, or by hyperquenching (cooling at rates of higher than 106 K s−1) its less than 2 μm size droplets on a substrate kept at a temperature below 100 K.1,2 Both its glass softening temperature, Tg, and viscosity are important for a variety of technologies, and for understanding water’s role in several scientific disciplines.Amorphs produced by vapour-deposition and hyperquenching have an unusually large frozen-in enthalpy and entropy and therefore they crystallizes rapidly on heating. This was partly prevented by developing an anneal-and-scan technique, which allowed most of the enthalpy of an amorph to relax at a temperature sufficiently low that crystallization did not occur.1,2 The technique was used to determine Tg, a temperature at which an ultraviscous liquid’s viscosity is 1012–1013 Poise, of water by using differential scanning calorimetry (DSC). For heating rate of 30 K/min, this Tg was found to be 136 K for both the vapor-deposited amorphous solid water2 (ASW) and hyperquenched glassy water (HGW).1 Further studies of ASW and HGW intended for other purposes performed repeatedly over a period of several years had confirmed their Tg of 136 K, and no study of water has put this value in question. However, in a series of recent papers, its calorimetric behavior has been unjustifiably compared with those of o-terphenyl, basalt composition and metal alloy glasses (for review see refs. 3–5), and its dielectric behavior compared with those of glycerol, propylene carbonate and, more recently, with concentrated aqueous solutions.6 From this comparison, it has been inferred that water remains a rigid glass up to a temperature of ∼165 K or higher. These inferences have been reviewed and subjected to scrutiny in several recent papers.3–5,7 It has been found that the basis of these inferences violates the precepts of both calorimetry and dielectrics.3–5,7
Glass-softening is a relaxation phenomenon, related to the onset of molecular diffusion. Therefore, if the relaxation time of water could be determined at a temperature near 136 K by a familiar technique, comparison-based inferences on its Tg would no longer be needed. Here we determine its value by dielectric loss scans and show that water’s relaxation time is 35 ± 13 s at 136 ± 1 K, which is consistent with the structural relaxation time of ca. 33 s, as estimated from the Tg endotherm (i.e., a sigmoid shape rise in the heat capacity in a DSC scan measured on heating). Therefore, water is an ultraviscous liquid of viscosity on the order of 1012 poise at 136 K, and remains a viscous liquid until it crystallizes to cubic ice rapidly in the 146–150 K range.1,2 It is not a rigid glass up to a temperature of 165 K or 180 K. The method for ascertaining Tg by determining the relaxation time may be used also for clarifying the state of other high-enthalpy amorphs that rapidly crystallize on heating through their Tg, and show little indication of their glass-softening in a DSC scan.5
The dielectric loss tangent, tan δ (= ε″/ε′, the ratio of dielectric loss to permittivity) of ASW had been measured at different temperatures at two fixed frequencies by Johari et al.9 In these studies, as in the preceding ones,1,2 cubic ice (contaminant) grains grew and nucleation–crystallization occurred when ASW was heated from 130 K to 165 K at a relatively slow rate of ca. 0.5 K min−1. It had been noted,9 “Therefore, the unusual exothermic effects on crystallization of highly viscous water observed by both DSC and DTA and by dielectric measurements are associated with the micro-structural state of ASW whose conversion on heating into a highly viscous liquid allows at least two occurrences, namely (i) growth of the already existing nuclei or crystallites at the expense of the liquid phase, and (ii) formation of nuclei and their growth within the liquid phase.”9 This, initially slow and then rapid cubic ice formation caused tan δ of the sample to decrease with time and therefore, as in the earlier studies of molecular glasses,10 only the tan δ scans against the temperature for fixed frequencies of 1 kHz and 10 kHz (i.e., isochrones) were reported. The tan δ values are taken here from their9 Fig. 2 and are plotted for two ASW samples in Fig. 1. For convenience, the temperature ranges of grain-growth, and nucleation-crystallization are indicated in Fig. 1.
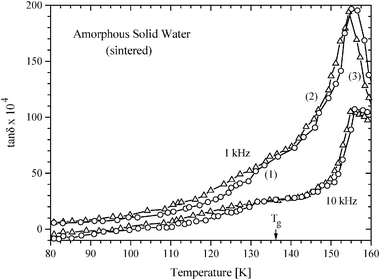 | ||
| Fig. 1 The dielectric loss tangent of vapor-deposited amorphous solid water (ASW) measured for 1 kHz and 10 kHz frequencies is plotted against the temperature. Triangles are for sample 1, and circles for sample 2. Note that structural relaxation and grain-growth tend to decrease tan δ in region (1) but increase in relaxational and background loss dominates d(tan δmeas)/dT. Nucleation and crystal growth tend to decrease tan δ in region (2) but relaxational increase dominates. Finally, decrease in tan δ as a result of crystallization to cubic ice dominates in region (3) and tan δ decreases. | ||
Because of the unavoidable time- and temperature-dependent grain-growth and nucleation–crystallization, which decreases the dielectric loss continuously on heating above 136 K, the tan δ peak due to molecular relaxation in ultraviscous water is not observed. Nevertheless, one observes a relatively rapid rise in tan δ on heating from 115 K to 128 K in Fig. 1, which is gradually attenuated first by the grain-growth and thereafter by nucleation-crystallization as the temperature is increased. Thus a progressive rise of tan δ in the 115 K to 128 K range turns into a sigmoid-shape curve in the 130 K to 140 K range, as seen in Fig. 1. During the period of the study9 in 1990, we made no effort to determine water’s relaxation time because we did not believe that glassy water would be compared with unrelated materials for the sole purpose of inferring that its Tg is higher than 165 K,6 and for suggesting that a glass can crystallize rapidly at T far below its Tg. Now, fifteen years later, we use those data and precepts of dielectrics11 to determine its relaxation time by a new method, with sufficient accuracy to ascertain water’s Tg.
2. Determining the relaxation time of unstable liquids from isochrones
Dielectric relaxation of viscous liquids occurs with a distribution of times given by the Davidson–Cole equation,11,12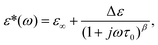 | (1) |
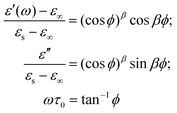 | (2) |
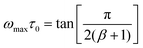 | (3) |
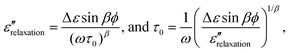 | (4) |
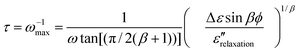 | (5) |
The measured dielectric quantities, ε″meas and tan δmeas, of dipolar liquids and crystalline and amorphous solids contain a non-relaxational loss, called the frequency-independent background loss.13–24 Therefore, ε″meas is the sum of the relaxation and background losses,
| ε″meas = ε″relaxation + ε″background | (6) |
 | (7) |
3. Relaxation time of water at 136 K
We use eqns. (5)–(7), to determine τ for water at ca. 136 K. From the plot for sintered ASW’s sample 1 (shown by triangles) in Fig. 1, tan δmeas(1 kHz) = 66 × 10−4 and tan δmeas (10 kHz) = 26.5 × 10−4 at 136 ± 1 K, with an accuracy9 of ±5 × 10−4. As was stressed earlier9 there was an impedance mismatch between the dielectric cell–connector assembly and the Digibridge, which varied from one cell assembly to another. Consequently, tan δmeas(10 kHz) appeared as a negative reading of −4.5 × 10−4 for sample 1 at 80 K and −8.4 × 10−4 for sample 2, instead of a value less than ∼1 × 10−4 (∼1/10th of the tan δmeas(1 kHz) at 80 K; the lowest value that this equipment could measure was 1 × 10−4). After this correction, tan δmeas(10 kHz) = 31 × 10−4 (= 26.5 × 10−4 from Fig. 1 plus 4.5 × 10−4) at 136 ± 1 K.The distribution parameter, β, for the ultraviscous liquids has been generally found to be in the range of 0.6 to 0.9.25–27 With respect to water, Hasted,34 has discussed this subject and concluded that there is a small distribution of dielectric relaxation times in water at 293 K (see p. 47, ref. 34). Since β for ultraviscous water has not been experimentally determined, we use an average value of 0.75 for β for our purpose of determining an approximate value of τ for water at 136 K. (It will later become evident that other values for 0.6 < β < 1 have little consequence for ascertaining water’s Tg.) By substituting β = 0.75, and the above given tan δmeas(1 kHz) of 66 × 10−4 and tan δmeas(10 kHz) = 31 × 10−4 in eqn. (7) we calculate tan δbackground as 23 × 10−4. According to eqn. (6), tan δrelaxation(1 kHz) would be 43 × 10−4.
We now consider the possibility of a contribution to tan δmeas from the so-called Johari–Goldstein (J-G) relaxation in glasses.19,22,23,25–33 Unsintered ASW had shown a small J-G relaxation peak in tan δmeas in the vicinity of 95 K.9 This peak was not observed after sintering the sample,9 and therefore its origin was attributed to the motion of dangling water molecules on the inside surface of its microporous state. Its contribution to tan δmeas at 1 kHz and 10 kHz frequencies would be negligible in the vicinity of 136 K, and therefore tan δrelaxation(1 kHz) of 43 × 10−4, as determined above is for the α-relaxation process that determines the viscosity of ultraviscous water.
Hasted34 has summarized the dielectric properties of water. At 293 K, εs of water is 91.3,34 and ε∞ is 4.46,34 or Δε = 86.8. Since Δε increases on cooling in proportion to 1/T, which also follows from statistical mechanical theories of dielectric polarization (see monograph, ref. 11), Δε for ultraviscous water at 136 K would be ca. 187 (= 86.8 × 293/136). Since molecular vibrational contributions to ε∞ decrease with decrease in T,11ε∞ will be less than 4.46 at 136 K, and we use ε∞ = 4 for our purpose. Since ε″ = ε∞ tan δ at 136 K for such high frequencies, multiplying the different tan δ values by ε∞ of 4.0 yields the corresponding ε″meas at 1 kHz and 10 kHz frequencies, ε″background and ε″relaxation(1 kHz). These values are listed in Table 1, where ε″relaxation(1 kHz) of 0.017 is ca. 64% of ε″meas(1 kHz) of 0.0264.
| Substance | T g/K | β | Δε | 103ε″ | 103ε″ | 103ε″background | 103ε″relaxation | τ/s |
|---|---|---|---|---|---|---|---|---|
| a From ref. 31. Δε and β are the average values taken from the figures in ref. 37. b From ref. 6, tan δmeas read from Fig. 4, ε″ = ε∞ tan δ, where ε∞ = 3.5. Δε and β values are taken from ref. 6. c From ref. 9. ε″ = ε∞ tan δ, where ε∞ = 4.0. | ||||||||
| Waterc | 136 | 1.0 | 187 | 26.4 (1 kHz) | 12.4 (10 kHz) | 10.8 | 16.0 (1 kHz) | 2 |
| Waterc | 136 | 0.75 | 187 | 26.4 (1 kHz) | 12.4 (10 kHz) | 9.4 | 17.0 (1 kHz) | 28 |
| Waterc | 136 | 0.60 | 187 | 26.4 (1 kHz) | 12.4 (10 kHz) | 7.7 | 18.7 (1 kHz) | 347 |
| Glycerola | 185 | 0.54 | 80 | 74 (1 kHz) | 54 (10 kHz) | 46 | 28 (1 kHz) | 143 |
| Propylene carbonatea | 155 | 0.60 | 97 | 55 (1 kHz) | 39 (10 kHz) | 34 | 21 (1 kHz) | 93 |
| N2H4·2H2Ob | 137.5 | 0.75 | 75 | 735 (10 Hz) | 123 (1 kHz) | 103 | 632 (10 Hz) | 7 |
On substituting the above-given Δε, β and ε″relaxation values in eqn. (5), we determine τ of water as 28 s at 136 ± 1 K. Also, if an unrealistic value of β = 1 is used, i.e., for a single relaxation time, the calculated τ is 2 s, and if β = 0.6, the lower most value of this limit, is used, the calculated τ is 347 s. The effect of experimental errors9 of ± 5 × 10−4 in tan δmeas (i.e., 2 × 10−3 in ε″meas) also needs to be determined. For the maximum difference between ε″meas(1 kHz) and ε″meas(10 kHz) due to these errors, i.e., ε″meas(1 kHz) = 28.4 × 10−3 and ε″meas(10 kHz) = 10.4 × 10−3, we obtain τ = 22 s. For the minimum difference, i.e., ε″meas (1 kHz) = 24.4 × 10−3 and ε″meas (10 kHz) = 14.4 × 10−3, we obtain τ = 48 s.
It should be noted that a contribution to dielectric loss from the J-G relaxation (refs. 21–33) also needs to be subtracted from the above-given value of 0.0172 for ε″relaxation (or equivalently tan δrelaxation). But, as already explained here, J-G relaxation makes a negligible contribution to ε″meas (or tan δmeas) of water at 1 kHz and 10 kHz frequencies at 136 K. If it were to be subtracted, the ε″relaxation would be less than 0.017 and hence τ calculated from eqn. (5) would be greater than the 22 s–48 s at 136 ± 1 K. It should also be noted that the calculated τ depends upon the combination of Δε, ε∞ and β values, the effect of the β being much larger than the effects of the other two.
We conclude that τ for water is in the range 22–48 s at 136 ± 1 K. This value may now be compared with the structural relaxation time estimated from the onset temperature of a Tg endotherm. After the required revision,35 structural relaxation time obtained from the onset temperature of a Tg endotherm measured by heating at 30 K min−1 rate1,2 is ca. 33 s at 136 K, which is within the range, 22–48 s, of the dielectric relaxation time at 136 ± 1 determined here. According to the Maxwell’s relation, this corresponds to a viscosity on the order of 1012 poise.
4. Extent of crystallization and comparative analyses
Growth of already existing nuclei in a solid, such as amorphous solid or glassy water, and nucleation–crystallization of their ultravisocus liquid produces a two phase mixture, with interfaces. Because of that, changes in the dielectric properties on their heating contain the effect of a homogeneous state evolving into a heterogeneous state and of redistribution of any impurities present to which dielectric properties are sensitive. This is quite different from the enthalpy release in calorimetry in which development of heterogeneity has no consequences. Despite this, one may consider that our findings have speculative implications for the extent of crystallization of ultraviscous water. We point out that experimental reasons prevent one from estimating the extent of crystallization, because, (i) neither the τ nor tan δrelaxation is accurate enough for calculating the temperature dependence of tan δbackground or the profile of the ε″meas peak from the data given in Table 1, (ii) the temperature dependence of tan δbackground needed to obtain the relaxation features is not known, and (iii) the extent of crystallization of ultraviscous water with increase in the temperature can not be compared against the extent of crystallization determined from the DSC method because crystallization is both time-, and temperature dependent, and the uncontrolled heating rate in the dielectric study9 was ca. 0.5 K min−1, which is 60 times slower than 30 K min−1 used in the DSC study.1,2 It is also to be noted that in the anneal and scan technique used frequently by us,1,2 ultraviscous liquid structurally relaxes over a period of several hours but does not crystallize, because the two are different phenomena, one involving arrangement to a disordered structure of lower enthalpy and entropy and the other nucleation and crystal growth by accumulation of molecules to produce an ordered structure, and their kinetics are greatly different.It should be pointed out that contrary to the occasional discussion, crystallization of ultraviscous water on heating at this rate does not occur explosively. Instead, it occurs over a temperature range of 30 K (Fig. 1, ref. 1) and 25 K (Fig. 2, ref. 2), and takes ca. 1 minute while heating. Moreover, the crystallized phase, which is cubic ice contained stacking faults, also has a tan δbackground and tan δrelaxation of its own that contributes to the tan δ of the mixture,9 and this contribution grows as more ultraviscous water crystallizes. An attempt at determining the extent of its crystallization without the information on the crystallized state would be scientifically meaningless. For the same reason, any attempt to determine τ at higher temperatures would not yield a value expected for ultraviscous water.
It seems also inappropriate to speculate on the extent of crystallization of water on heating to 150 K by using the dielectric loss data because, firstly, both tan δrelaxation and the calculated τ values are considerably uncertain, and secondly, nuclei-growth in ASW occurs at low temperatures and nucleation crystallization in the ultraviscous liquid at higher temperatures,9 as already stated here and earlier.9 Therefore, consequences of these two occurrences can not be included in a satisfactory manner. Attempt to deduce information on ultraviscous water by comparing its dielectric features against those of other substances, e.g. of N2H4·2H2O, is improper because their features are unique to them, and scaling of properties of one substance by using the properties of another has been shown to be misleading for water.3–5,7,8 Moreover, a search for causality is needed; comparisons and correlations are generally not the cause–effect approach used in a scientific inquiry.
5. Testing the new method for substances of known Tg
Finally, the method proposed and used here has been based on principles of dielectrics, and therefore seems reliable. Nevertheless, we also test the method’s validity by using the ε″ data for glasses that do not crystallize and whose Tg has been known. As an example, we use glycerol, propylene carbonate and N2H4·2H2O solution, which show an unusually small contribution to ε″relaxation from the J-G relaxation. (Data analysis on more glasses will be published elsewhere in a theoretical context.) These data are also provided in Table 1. Here tan δ of N2H4·2H2O solution was converted to ε″ by multiplying it by its ε∞ of 3.5. The calculated τ values are within 28–93 s for these glasses when their measured value for β and a realistic value of β = 0.75 for water is used. However, there is a considerable uncertainty in the reported tan δ values for N2H4·2H2O solution, which becomes evident from the unusually large separation of the plot for 10 Hz from the plot for 1 kHz in Fig. 4 of ref. 6. The 10 Hz plot lies much higher than the plot for 1 kHz frequency, thereby indicating that either there is a significant J-G relaxation contribution or there are measurements errors. This issue will be resolved in a future study. Nevertheless, it should be noted that extrapolated value of τ for the N2H4·2H2O solution at 137.5 K is 86 s,6 which is to be compared against the approximate value of τ of 7 s calculated here. Both values show that N2H4·2H2O solution is an ultraviscous liquid.The τ values would increase if a contribution from the J-G relaxation, already known for glycerol and propylene carbonate, was also subtracted from ε″ and/or the value of β was to be less than that used here. It is known that τ determined from the dielectric spectra at the calorimetric Tg varies with the purity of the sample, and since the samples used for dielectrics differ from those used for calorimetry, this also contributes to the inconsistency between the dielectric and calorimetric Tg. Also the calorimetric Tg does not correspond to an isoviscous state for different liquids even when the heating rates are the same.36 Thus the structural relaxation time at Tg are found to be in the 10–100 s range, and not exactly 100 s. In context of our study, the agreement of this range with the range of τ listed in Table 1 shows that the method proposed here can be used for ascertaining Tg of those glasses that rapidly crystallize on heating through their glass-softening range and whose Tg endotherm has been otherwise controversially interpreted. With the now available techniques of rapid and automated dielectric spectroscopy, our method of dielectric scanning and data analysis would be useful in studies of technologically important high enthalpy amorphs,5 and for determining the relaxation time of rapidly crystallizing liquids.
We conclude that even if the calculated dielectric relaxation time for water at 136 K were to be certain within an order of magnitude, our conclusion that ASW is already an ultraviscous liquid at 136 K would remain unaffected. This also means that the choice of β value between 0.6 and 1 has little effect on this conclusion. Ultraviscous water, and not its rigid glassy state, crystallizes rapidly to cubic ice at a rate that rapidly increases with temperature. No annealed glass has been found to rapidly crystallize at temperatures far below Tg.
Acknowledgements
I am grateful to G. Power and Prof. J. K. Vij of Trinity College, Dublin, for pointing out that strictly speaking the right hand side for ε″relaxation in eqn. (4) should be multiplied by sin βϕ, and the right hand side for τ0 in eqn. (4) be multiplied by (sin βϕ)1/β.References
- G. P. Johari, A. Hallbrucker and E. Mayer, Nature, 1987, 330, 552 CrossRef CAS.
- A. Hallbrucker, E. Mayer and G. P. Johari, J. Phys. Chem., 1989, 93, 4986 CrossRef CAS.
- G. P. Johari, J. Chem. Phys., 2002, 116, 8067 CrossRef CAS.
- G. P. Johari, J. Chem. Phys., 2003, 119, 2935 CrossRef CAS.
- G. P Johari, J. Phys. Chem. B, 2003, 107, 9063 CrossRef CAS.
- A. Minoguchi, R. Richert and C. A. Angell, Phys. Rev. Lett., 2004, 93, 215703 CrossRef; A. Minoguchi, R. Richert and C. A. Angell, J. Chem. Phys. B, 2004, 108, 19825 Search PubMed.
- G. P. Johari, J. Chem. Phys., 2005, 122, 36101 ; in its ref. 6: “118, 342” should read “119, 2935”, and in its ref. 21: “20 s” should read “200 s” and “0.2 s” should read “20 s”.
- G. P. Johari, J. Chem. Phys., 2002, 117, 2782 CrossRef CAS.
- G. P. Johari, A. Hallbrucker and E. Mayer, J. Chem. Phys., 1991, 95, 2955 CrossRef CAS.
- G. P. Johari and M. Goldstein, J. Chem. Phys., 1970, 53, 2372 CrossRef CAS . Instead of ε″tan δ was measured because it requires no knowledge of the cell constant, and is more accurately determined than ε″ since cracks that can form on cooling a glass and any air gap between the sample and the electrodes formed because of different expansion coefficients of the electrode spacers and the sample have a smaller effect on tan δ than on ε″.
- N. Hill, W. E. Vaughan, A. H. Price and M. Davies, Dielectric Properties and Molecular Behaviour, Van Nostrand, London, 1969 Search PubMed.
- D. W. Davidson and R. H. Cole, J. Chem. Phys., 1951, 19, 1484 CrossRef CAS . Another equation, known as the KWW equation is seen as equivalent to the Davidson–Cole equation, but P. Lunkenheimer, U. Schneider, R. Brand and A. Loidl, Contemp. Phys., 2000, 41, 15 Search PubMed , reported that the Davidson–Cole equation describes their spectra better than the KWW equation.
- E. M. Armheim and F. H. Muller, J. Am. Chem. Soc., 1968, 90, 3146 CrossRef.
- M. B. Weissman, Rev. Mod. Phys., 1988, 60, 537 CrossRef CAS.
- J. M. Haddad and M. Goldstein, J. Non-Cryst. Solids, 1978, 30, 1 CrossRef CAS.
- G. P. Johari, J. Chem. Phys., 1982, 77, 4619 CrossRef CAS.
- A. Sokolov, P. Kisliuk, A. V. N. Novikov and K. L. Ngai, Phys. Rev. B, 2001, 63, 172204 Search PubMed.
- K. L. Ngai, J. Habasaki, C. Leon and A. Rivera, Z. Phys. Chem., 2005, 219, 47 CrossRef CAS , and references therein.
- K. L. Ngai, J. Phys. Condens. Matter, 2003, 15, S1107 CrossRef CAS.
- K. L. Ngai, J. Chem. Phys., 1999, 110, 10576 CrossRef CAS.
- K. L. Ngai and C. L. Leon, Phys. Rev. B, 2002, 66, 64308 Search PubMed.
- K. L. Ngai, in Slow Dynamics in Complex Systems, ed. M. Tokuyama and I. Oppenheim, AIP Conf. Proc., 2004, 708, 515 Search PubMed.
- C. M. Roland, M. J. Schroeder, J. J. Fontanella and K. L. Ngai, Macromolecules, 2004, 37, 2630 CrossRef CAS.
- E. Muzeau, G. Johari and G. P. Perez, J. Macromol., 1991, 24, 4713 Search PubMed.
- E. Donth, Glass Transition, Relaxation Dynamics in Liquids and Disordered Materials, Springer-Verlag, Berlin, 2001 Search PubMed.
- A. Kudlik, S. Bankhoff, T. Blochowicz, C. Tschirwitz and E. Rossler, J. Mol. Struct., 1999, 479, 201 CrossRef.
- K. L. Ngai and M. Paluch, J. Chem. Phys., 2004, 120, 857 CrossRef CAS , and references therein.
- K. Schröter, R. Unger, S. Reissig, F. Garwe, S. Kahle, M. Beiner and E. Donth, Macromolecules, 1998, 31, 8966 CrossRef.
- U. Schneider, R. Brand, P. Lunkenheimer and A. Loidl, Phys. Rev. Lett., 2000, 84, 5560 CrossRef CAS.
- N. B. Olsen, T. Christensen and J. C. Dyre, Phys. Rev. E, 2000, 62, 4435 CrossRef CAS.
- K. L. Ngai, P. Lunkenheimer, C. Leon U. Schneider, R. Brand and A. Loidl, J. Chem. Phys., 2001, 115, 2001.
- G. Power, G. P. Johari and J. K. Vij, J. Chem. Phys., 2003, 119, 435 CrossRef CAS.
- G. Power and J. K. Vij, J. Chem. Phys., 2004, 120, 5455 CrossRef CAS.
- J. B. Hasted, Aqueous Dielectrics, Chapman and Hall, London, 1973 Search PubMed.
- In our earlier study (refs. 1 and 2 here), the structural relaxation time, τs, was estimated as ∼70 s at 136 K by analyzing the DSC scans obtained by heating ASW and HGW at 30 K min−1 rate according to a relation used by Angell and Torell, qτs = q′τ′s, where q and q′ are the heating rates and τs and τ′s are the structural relaxation times ( C. A. Angell and L. M. Torrell, J. Chem. Phys., 1983, 78, 937 Search PubMed ). For q = 10 K min−1, they gave, τs = 200 s at the onset temperature and τs = 20 s at the midpoint temperature. This relation ignores both the non-exponentiality of structural relaxation and the structure-dependence of τs. The τs value for q = 10 K min−1 has now been revised from 200 s to 100 s for the data analysis. Accordingly, τs of ASW and HGW should be revised from ∼70 s to ∼33 s at 136 K.
- W. Pascheto, M. G. Parthun, A. Hallbrucker and G. P. Johari, J. Non-Cryst. Solids, 1994, 171, 182 CrossRef CAS . It is shown that τ at the DSC endotherm’s Tg for the same q differs for different substances. The difference varies with the distribution of relaxation time, the activation energy and the non-linearity parameter that determines the increase in τs with decrease in the fictive temperature (see Fig. 5).
- P. Lunkenheimer, Dielectric Spectroscopy of Glassy Dynamics, Shaker-Verlag, Aachen, 1999 Search PubMed.
| This journal is © the Owner Societies 2005 |
