Probing the transition state with negative ion photodetachment: experiment and theory

Abstract

Experimental and theoretical results are presented on the spectroscopy of transition states and pre-reactive van der Waals wells using negative ion photodetachment. Several benchmark reactions are discussed, including the F + H₂, OH + H₂, and F + OH reactions, as well as the isomerization of cyclo-octatetraene. Photoelectron spectra of clustered transtion state precursor anions are presented, which examine the effects of solvation on anion structure and transition state dynamics. Finally, new experiments on the photodetachment of ClH₂⁻ are discussed in which the Cl·H₂ van der Waals well is probed.

---

Introduction

The concept of the transition state is one of the unifying themes in physical chemistry. The transition state represents a “dividing surface” between reactants and products on a reactive potential energy surface, and acts as a dynamical bottleneck to a chemical reaction. It serves as a construct to understand chemical reactivity under an enormously wide range of environments, ranging from the simplest gas phase reactions to enzyme-catalyzed processes in biology. Thus, the detailed characterization of the transition state has been a long-standing goal in chemical reaction dynamics.^1–4 Ideally, one wants to determine the energy of the transition state relative to separated reactants, the transition state geometry, and the frequencies of the 3N − 7 bound vibrational modes of the transition state that are perpendicular to the reaction coordinate. This goal has presented quite a challenge over the years because of the fleeting nature of the transition state, which generally does not correspond to even a local minimum on a reaction potential energy surface. One therefore cannot follow the usual methodology of spectroscopic characterization in which a sample is prepared and then studied.

One approach to this problem has been the development of increasingly sophisticated photodissociation and bimolecular scattering experiments in which reactants are prepared under very well-controlled conditions, and product attributes such as translational and internal energy distributions, angular distributions, and other vector correlations are measured in great detail.^5,6 In this case, one is dealing with asymptotic properties of the reaction, through measurement of the reaction attributes long after the products have separated and ceased to interact with one another. Nonetheless, these asymptotic properties generally reflect the transition state properties of the reactive potential energy surface. One can therefore attempt to reconstruct the transition state based on these measurements, often with the aid of electronic structure and scattering calculations. This process can be somewhat daunting, particularly in bimolecular scattering experiments where the reactant energy can be specified, but not the total angular momentum.

As a result, there is considerable impetus to develop spectroscopic probes of the transition state region itself. Kinetics and scattering experiments are of course sensitive to the attributes of the transition state region, but direct, spectroscopic probes of the transition state can, at the very least, complement scattering experiments, and often yield richer detail through the determination of the geometry, vibrational frequencies and lifetime of the transition state complex. While there have been attempts to probe the spectroscopy of transition state complexes formed in bimolecular collisions, nearly all successful transition state spectroscopy (TSS) experiments performed to date are “half-collision” experiments in which the transition state is accessed through photoexcitation of a stable transition state precursor, such as a closed shell molecule, a van der Waals complex, or a negative ion. These experiments can be divided into time-domain and frequency-domain studies. Since the transition state by its nature is short-lived, with passage through a transition state typically occurring on a time scale of 10–100 fs, experiments with ultrafast lasers would seem to be a natural way to probe reacting or dissociating systems, and this has indeed been the focus of “femtochemistry” experiments in the Zewail laboratory^7,8 and elsewhere. While most of these studies are pump–probe experiments with two laser pulses, success has recently been achieved using ultrafast electron diffraction⁹ as a probe, in which one can directly probe the geometries of the transient species produced by the pump pulse.

One of the more successful efforts in frequency-domain TSS has been the set of negative ion photodetachment experiments performed in our laboratory and by Lineberger and co-workers.^10–12 In these experiments, one photodetaches a stable negative ion similar in structure to a neutral transition state, and the resulting photoelectron spectrum can yield resolved vibrational structure characteristic of the transition state. In many cases, these experiments have revealed vibrational frequencies characteristic of nuclear motion perpendicular to the reaction coordinate. These frequencies are clearly of interest, since, for example, they could be used in the calculation of the transition state theory rate constant of a chemical reaction. More generally, the deviation of the transition state frequencies from those of isolated reactants or products is a direct measure of how chemical bonds evolve during the course of a reactive collision. The intensity distribution in the photoelectron spectra is also of interest, as it reflects the change in geometry between the anion and neutral.

While most studies of this type have been conventional photoelectron spectroscopy experiments, with a typical energy resolution of 50–100 cm⁻¹,¹³ considerably higher resolution is possible using anion zero electron kinetic energy (ZEKE) spectroscopy,¹⁴ and the recently developed slow electron velocity-map imaging (SEVI) method,¹⁵ results from which are described below.

A more elusive goal in TSS experiments has been the detection of dynamical resonances, loosely defined as levels of the transition state complex that are bound or quasi-bound along the reaction coordinate. Resonances have been predicted in reactive scattering calculations on model potential energy surfaces for many years,¹⁶ and are a very appealing target for TSS because they can be quite narrow and precisely located, thereby providing a particularly sensitive probe of the transition state. Thus far, however, the only TSS experiment that has definitively revealed the existence of resonances was the ZEKE spectrum of IHI⁻,¹⁷ which showed clear evidence for quasi-bound IHI levels and not just the broader vibrational structure characteristic of motion perpendicular to the reaction coordinate. The only other definitive observation of reactive resonances to date comes from scattering experiments on the F + H₂ and F + HD reactions by Liu and co-workers,^18–20 in which structure in the total reaction cross section and rapid changes in the differential cross section as a function of collision energy provided an unambiguous signature of FH₂ resonance states.

There are several promising new directions in the area of TSS. In the time-domain, the development of increasingly shorter laser pulses^21,22 and the recent implementation of time-dependent photoelectron spectroscopy^23,24 in several laboratories holds considerable promise for probing more rapid transition state dynamics in greater detail, as does further development of ultrafast electron²⁵ and X-ray light sources.^26–28 Negative ion photodetachment on mass-selected cluster anions has been used recently to probe the effects of solvation on transition state spectroscopy and dynamics,^29–31 thereby providing a key link between gas phase and condensed phase reaction dynamics. The gas phase infrared spectra of several bare and clustered transition state precursor anions have been measured for the first time,^32–34 yielding important information on the structure of these species that will enable better analysis of their photoelectron spectra. Finally, the recent observation of pre-reactive van der Waals states of the OH·H₂ and OH·CO complexes^35,36 points out the importance of studying a relatively neglected region of reactive potential energy surfaces, the shallow van der Waals (vdW) well between reactants. The importance of the reactant vdW well is exemplified in experimental and theoretical studies of the Cl + H₂ reaction,³⁷ which show that the interplay between the vdW well and the transition state can have a significant effect on transition state geometry as well as the overall reaction dynamics.

The main body of this review covers TSS using negative ion photodetachment. It represents an updated version of two recent reviews of this field,^38,39 and emphasizes recent theoretical results on the simulation of the experimental spectra. Several benchmark bimolecular reactions are discussed, followed by a description of TSS on isomerization reactions. Finally, recent work on TSS in cluster anions and experiments on reactant van der Waals wells are described.

TSS of benchmark chemical reactions

The promise of TSS using negative ion photodetachment is exemplified by our studies of transition states for the F + H₂, OH + H₂ and F + OH reactions by photoelectron spectroscopy of FH₂⁻, H₃O⁻ and OHF⁻, respectively. These are benchmark reactions that have been studied extensively by experiment and theory. The F + H₂ reaction, in particular, has defined the state-of-the-art in experimental reactive scattering studies, with increasingly sophisticated crossed molecular beams experiments yielding progressively more detail on the dependence of the integral and differential cross sections on collision energy, the partitioning of product translational, vibrational, and rotational energy, and the possible reactivity of spin–orbit excited F atoms.^{18,19,40–46} Although some features of the differential cross section, namely state-selected forward scattering of the HF(v = 3) product, were originally attributed to dynamical resonances,⁴⁰ these features could be largely reproduced by classical trajectory calculations^47,48 on potential energy surfaces with bent as opposed to linear transition states. We therefore hoped to address the issue of the FH₂ bend potential by photoelectron spectroscopy of FH₂⁻.

As shown in Fig. 1, this reaction is ideal from the TSS perspective, because electronic structure calculations indicate that the geometry of FH₂⁻ is similar to that of the FH₂ transition state;^49,50 in both, the distance of the F atom from the H₂ center-of-mass is relatively long, and the H–H bond distance is similar to that in diatomic H₂. These geometries reflect the fact that FH₂⁻ is essentially F⁻ weakly bound to H₂ (D₀ ≈ 0.20 eV), while the F + H₂ reaction has an early barrier. The calculations indicate FH₂⁻ is linear, so the existence or extent of bend progressions in the anion photoelectron spectrum would provide a direct probe of the bend potential at the neutral transition state.

Fig. 1 Photodetachment of FH₂⁻ probes the F + H₂ transition state region. The ground state vibrational wavefunction for FH₂⁻ (shaded region) is superimposed on a model collinear potential energy surface for F + H₂ reaction. The saddle point on the reactive surface is marked with an X (adapted from ref. 51).

The FH₂⁻ photoelectron spectrum^51,52 in Fig. 2 indeed shows progressions in the two vibrational modes perpendicular to the reaction coordinate: the H–H stretch and the F–H–H bend, which is more like an H₂ internal rotor. The bend progression is quite extended, indicating that the FH₂ transition state is bent rather than linear. This conclusion is supported by quantum mechanical simulations of the spectrum performed on a high level potential energy surface for the F + H₂ reaction.⁵² This system thus represents an example in which TSS resolved a key issue in a benchmark chemical reaction.

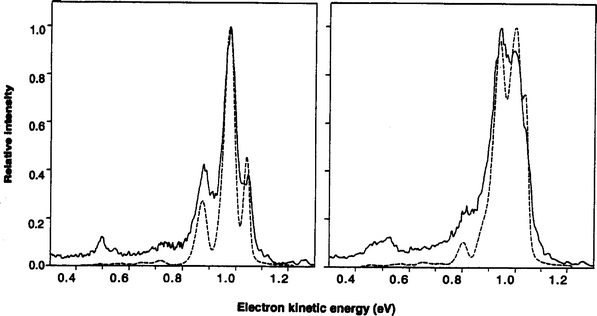Fig. 2 Solid lines are experimental photoelectron spectra of F⁻·para-H₂ (left) and F⁻·n-H₂ (right). Dashed lines are exact simulations using anion surface from ref. 49 and F + H₂ surface from ref. 50. The peaks around 1 eV are a progression in FH₂ internal rotor states, while the smaller peaks around 0.5 eV involve H₂ stretch excitation (adapted from ref. 52).

The FH₂⁻ photoelectron spectrum shows no clear evidence for resonances, i.e. states of the FH₂ complex that are bound along the reaction coordinate. The signature for resonances would be additional, low frequency vibrational progressions corresponding to either F⋯H₂ or HF⋯H vibrational motion, depending on whether the resonance wavefunction is localized on reactant or product region of the potential energy surface. Calculations by Manolopoulos⁵³ using the Stark–Werner⁵⁰ surface indicate that these progressions should be observable at higher resolution, but calculations of the reaction probability on a new potential energy surface constructed by Skodje and co-workers⁵⁴ show significantly reduced contributions from resonances on the product side. Planned higher resolution photodetachment experiments using our new photoelectron imaging instrument¹⁵ should shed further light on the issue of resonances in this reaction.

While the F + H₂ reaction is one of several three-atom benchmark reactions, along with H + H₂, O + H₂, and Cl + H₂, the OH + H₂→H₂O + H reaction is unique as a prototypical four atom reaction,⁵⁵ since the presence of three hydrogen atoms makes both electronic structure calculations of potential energy surfaces and the execution of scattering calculations on these surfaces tractable. As a consequence, high quality surfaces have been constructed and scattering calculations on these surfaces have been performed by several groups.^56–60 Scattering experiments by Casavecchia⁵⁶ and Davis⁶¹ have yielded product angular distributions and detailed vibrational energy distributions for the H₂O product. These experiments are complemented by studies of the OH·H₂ van der Waals complex by Lester and co-workers.^35,62

TSS of the OH + H₂ reaction via photoelectron spectroscopy of H₃O⁻ is complicated by the existence of two anion structures:^63–66 H⁻·H₂O, which has good Franck–Condon overlap with the neutral H₂O + H product valley, and OH⁻·H₂, which overlaps the neutral entrance valley and transition state. As shown in Fig. 3, the H⁻·H₂O structure is calculated to lie ≈0.125 eV lower in energy,⁶⁷ which might appear problematic from the perspective of TSS. Nonetheless, the anion photoelectron spectrum⁶⁸ was quite revealing.

Fig. 3 Bottom: Reaction coordinates for OH⁻ + H₂ and OH + H₂ reactions, showing calculated energetics of the H⁻(H₂O) and OH⁻(H₂) minima. Top: Contour plots for anion vibrational wavefunction in ground (bottom right) and second excited state (top left) (adapted from ref. 67).

The top spectrum in Fig. 4 shows the experimental photoelectron spectrum (grey line) of H₃O⁻, taken at a laser polarization angle θ = 0° (i.e. parallel to the direction of electron detection in our time-of-flight analyzer). The spectrum shows a resolved vibrational progression in which the peak spacing was slightly lower than the H₂O antisymmetric stretch frequency. This progression was assigned to transitions from the H⁻·H₂O anion structure to the H + H₂O exit valley, with the lowered frequency a signature of non-negligible interaction between the separating products in the Franck–Condon region. The H₃O⁻ photoelectron spectra show a strong angular dependence, with a broad feature appearing at high electron binding energy (eBE) at laser polarization angle θ = 90°. This feature becomes more intense when the ion source temperature is raised, suggesting it might be from the higher energy OH⁻·H₂ structure and therefore corresponds to photodetachment to the OH + H₂ transition state. The lower panel of Fig. 4 shows the θ = 90° spectrum minus the appropriately scaled θ = 0° spectrum to illustrate the feature at high eBE.

Fig. 4 Photoelectron spectra of H₃O⁻ at laser polarization angles θ = 0° (top) and 90° (bottom). Experimental and simulated spectra are shown as grey and black lines, respectively (adapted from ref. 67).

Simulations of the H₃O⁻ spectrum starting from both forms of the anion were carried out by de Beer et al.⁶⁸ in the original experimental paper and, subsequently, by several other research groups using improved potential energy surfaces and scattering methodology. Simulations from the H⁻·H₂O structure^68,69 on the best anion and neutral surfaces^70,71 available at the time of the experiment yielded an even lower frequency than that seen in Fig. 4A. This discrepancy indicates that the barrier on the model surface was too “late” along the reaction coordinate (i.e. the OH⋯H₂ distance is too small at the saddle point), resulting in an overly large effect on the peak spacings in the Franck–Condon region. In fact, the saddle points on more recent OH + H₂ surfaces occur at larger OH⋯H₂ distances (by 0.14 Å, on average^58,72), and simulations of the H⁻⋯H₂O photoelectron spectrum on these new surfaces^66,67 are in better agreement with experiment, with nearly perfect agreement achieved in recent work by Collins and co-workers,⁶⁷ as shown in Fig. 4A (black line). Hence, even though the H⁻·H₂O vibrational wavefunction has little or no overlap with the OH + H₂ saddle point, the nature of the vibrational structure in the photoelectron spectrum is quite sensitive to the location of the saddle point and therefore provides important information regarding the transition state of the reaction.

De Beer et al.⁶⁸ constructed a 2D potential energy surface for the H₃O⁻ anion and determined the 2D vibrational wavefunctions and energy levels supported by this surface. While the v = 0 wavefunction was localized in the H⁻·H₂O well, as expected, the v = 2 wavefunction showed significant amplitude in the OH⁻·H₂ well, and simulations of the photoelectron spectrum from the v = 2 wavefunction approximately reproduced the broad experimental feature. Hence, vibrational excitation of the anion results in considerably better overlap with the OH + H₂ entrance valley and transition state (see Fig. 3⁶⁷), a result supported in more sophisticated simulations of the photoelectron spectrum.^66,67,69,73 Again, the most recent work by Collins⁶⁷ (Fig. 4B, black line) shows excellent agreement with experiment.

Comparison of Figs. 4A and 4B shows that features in the H₃O⁻ PE spectrum have very different photoelectron angular distributions. This effect is generally associated with accessing multiple neutral electronic states upon photodetachment, as in the OHF⁻ example discussed below. In H₃O⁻, it can be understood in terms of the nature of the orbital from which detachment occurs; near threshold, H⁻ undergoes p-wave detachment, because an s-electron is being detached,^74,75 whereas OH⁻ undergoes s-wave detachment. The photoelectron angular distributions therefore reflect the dominance of the H⁻·H₂O structure in the v = 0 wavefunction and the dominance of the OH⁻·H₂ structure in the v = 2 wavefunction.

The reaction F + OH → HF + O(³P), which is exothermic by 34 kcal mol⁻¹, is a prototypical example of a reaction between two open-shell species. As a result, there are many more potential energy curves correlating to reactants and products than is the case for reactions involving a closed-shell species, thereby increasing the likelihood for non-adiabatic effects in the transition state region; effects of this type were inferred from measurements of the HF vibrational product distribution from the F + OH reaction.⁷⁶ One would expect triplet surfaces connecting the reactants to HF + O(³P) products, and singlet surfaces leading to the higher energy HF + O(¹D) channel; electronic structure calculations^76–79 have indeed shown this to be the case. Hence, the photoelectron spectrum of OHF⁻ can, in principle, probe transition state dynamics on multiple potential energy surfaces, a topic of considerable current interest in reaction dynamics.⁸⁰

Fig. 5 shows photoelectron spectra of OHF⁻ obtained at 213 nm, measured at two different laser polarization angles, θ = 0° and 90°.^81,82 The spectrum at θ = 90° shows a series of approximately equally spaced peaks. To analyze this spectrum, ab initio calculations were carried out that showed the OHF⁻ anion to be linear with a ²Π ground state, and 1D and 2D wavepacket simulations were performed projecting the anion ground state wavefunction onto a model neutral potential energy surface for the neutral ³Π state. The original simulations reproduced the positions and intensities of peaks A–E reasonably well, as did a more recent simulation on an improved triplet potential energy surface,⁷⁷ and showed that these peaks represented a progression in the H-atom stretching mode of the OHF transition state complex, analogous to results seen in the photoelectron spectra of symmetric and asymmetric bihalide anions.^83,84 However, peak F did not appear in either simulation, and it was suggested in the original work that this peak arises from a transition to a different neutral electronic state, possibly a singlet state leading to HF + O(¹D). This conjecture is supported by the photoelectron spectrum at θ = 0°,⁸² in which the intensity of peak F is clearly enhanced relative to the other features, showing that the photoelectron angular distribution of peak F is very different from that of the other peaks. Such a result is a signature of transitions to multiple electronic states in a photoelectron spectrum.⁸⁵

Fig. 5 Photoelectron spectra of OHF⁻ at 213 nm, taken at laser polarization angles θ = 0° (top) and θ = 90° (bottom).⁸²

Recent theoretical work by Gonzales-Sanchez et al.⁷⁹ has addressed the issue of multiple electronic transitions in the OHF⁻ photoelectron spectrum in considerable detail. They calculated collinear minimum energy paths for the two triplet surfaces (³Π and ³Σ⁻) leading to HF + O(³P) products, the three singlet surfaces (¹Δ, ¹Π and ¹Σ⁺) leading to HF + O(¹D) products, and several higher lying states as well. In addition, the photoelectron spectrum was simulated considering transitions to all these neutral states. Fig. 6 shows their simulations, obtained using 3D wavepacket propagation on the triplet states and 2D propagation on the singlet states. These results show that peak F appears only when transitions to singlet states are included, showing that it indeed results from transitions to overlapping singlet states in the OHF transition state region. Overall, while the F + OH reaction has received considerably less attention than the F + H₂ and OH + H₂ reactions, it appears to be an excellent model system for probing non-adiabatic effects in bimolecular collision dynamics.

Fig. 6 Simulated photoelectron spectrum of OHF⁻ using multiple 3D triplet surfaces and 2D singlet surfaces for F + HO reaction (bottom), and comparison with experimental spectrum (top) (adapted from ref. 79).

TSS of isomerization reactions

The above examples show how TSS can be applied to bimolecular reactions using anion photoelectron spectroscopy. Analogous experiments have be carried out by Lineberger and co-workers on unimolecular isomerization reactions.^12,86,87 In the work done so far, photodetachment of a stable anion accesses either an unstable neutral isomer or the transition state region for isomerization between two stable isomers.

For example, the C₂H₂ molecule can exist in two forms: HCCH (acetylene) and H₂CC (vinylidene). The vinylidene structure is higher in energy and is bound by only a small barrier of a 2–4 kcal mol⁻¹ with respect to isomerization to acetylene; as a result it is unstable with respect to isomerization to acetylene via a 1,2-hydrogen migration with a calculated lifetime of ≈1 ps.⁸⁸ However, the ground state of the C₂H₂ anion has the vinylidenic structure, H₂CC⁻. Photoelectron spectroscopy of H₂CC⁻ therefore cleanly accesses the neutral vinylidene structure, and indeed the photoelectron spectrum shows resolved but broadened vibrational peaks assigned to H₂CC on the basis of ab initio calculations.⁸⁷ Considerable effort has been expended on characterizing vinylidene through perturbations of the vibrational energy levels of acetylene,⁸⁹ but the photodetachment experiments remain the most definitive spectroscopic observations to date of the vinylidene isomer.

In a variation on this experiment, photodetachment of the cyclooctatetraene (COT) anion, C₈H₈⁻, was used to probe the transition state for neutral COT isomerization.¹² The photoelectron spectrum of COT⁻ is shown in Fig. 7A; the broader features at low electron binding energy are from transitions to the COT singlet ground state, whereas the narrow, higher energy peaks are from transitions to the lowest-lying triplet state of COT. The spectrum can be interpreted using the schematic potential energy curves for COT⁻ and COT shown in Fig. 7B. The singlet ground state of COT is a non-planar structure with D_2d symmetry, as shown in Fig. 7B. There are four degenerate D_2d structures in all, pairs of which can interconvert via a planar, D_4h transition state, in which alternating C–C bonds have the same bond length. In turn, the two D_4h transition states are separated by a small barrier that corresponds to a planar, D_8h transition state in which all C–C bonds are equivalent. The triplet excited state of COT has a single minimum corresponding to a highly symmetric D_8h structure. The negative ion has a planar D_4h ground state, but the extent of alternation is expected to be smaller than in the neutral D_4h planar transition states.

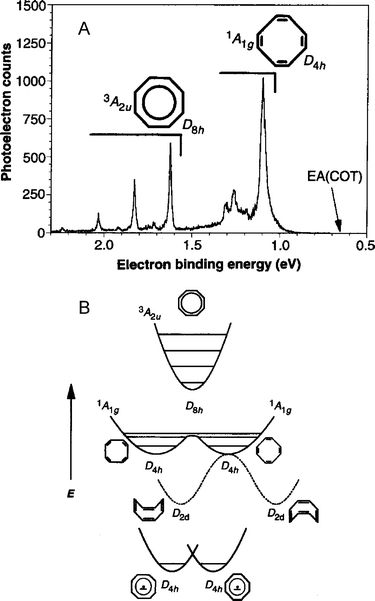Fig. 7 (A) Anion photoelectron spectrum of C₈H₈⁻. (B) Schematic anion and neutral potential energy surfaces for cyclooctatetraene (C₈H₈) isomerization (adapted from ref. 12).

Based on Franck–Condon (FC) considerations, the vibrational mode corresponding to C–C bond alternation should be the primary active mode in the triplet band of the anion photoelectron spectrum, and the frequency of the single progression in the triplet band, 1635 cm⁻¹, agrees with the frequency obtained from an ab initio calculation of the COT triplet state. The singlet band is more interesting. The anion clearly has poor FC overlap with the D_2d ground state, but should have good overlap with the planar transition states linking the ground state structures. In addition, one expects FC activity in the bond-alternation vibrational mode, just as in the triplet band. Consequently, in the singlet band, one observes a vibrational progression in the bond-alternation mode, but these peaks are broadened because each observed vibrational level is unbound with respect to out-of-plane bending to form the non-planar ground state structures. Hence, in analogy to the bimolecular transition state spectroscopy studies described in the previous section, this out-of-plane motion corresponds to the reaction coordinate, whereas the bond alternation vibration is the active, bound mode perpendicular to the reaction coordinate.

Transition state spectroscopy of clustered TS precursors

One of the more intriguing new directions for TSS via anion photoelectron spectroscopy is to investigate clustered transition state precursors. It is straightforward to generate mass-selected cluster anions of the type ABC⁻·(S_n), where ABC⁻ is a transition state precursor anion and S is a solvent atom or molecule. The photoelectron spectra of clusters of this type can probe the effects of solvation on the neutral transition state spectroscopy and dynamics,⁹⁰ thereby providing an important link between gas phase and condensed phase reaction dynamics.

We have recently initiated experiments using the bihalide transition state precursors BrHI⁻ and IHI⁻ clustered to one or more Ar atoms.^29,30 Photodetachment of the bare ions accesses the transition state region of the Br + HI and I + HI heavy + light–heavy reactions, and the photoelectron spectra of these anions^84,91 are dominated by progressions in the antisymmetric H-atom stretch. In addition, the higher resolution ZEKE spectrum of IHI⁻ showed lower frequency progressions in IHI hindered rotor states and symmetric stretch states;¹⁷ the latter represent a definitive observation of reaction resonances as defined above. In any case, the rich vibrational structure seen for both bihalide species provides a suitable template for determining the effects of solvation.

Our PE spectra of BrHI⁻·(Ar) and IHI⁻·(Ar), displayed in Fig. 8, showed that even a single weakly bound solvent species such as Ar induced significant changes in the photoelectron spectrum of the bare anion.³⁰ These changes are primarily due to cooling effects, since a cluster in which an Ar atom is clustered to a vibrationally excited bihalide anion will undergo predissociation before it passes through our mass spectrometer, leaving only those clusters in which the anion chromophore is vibrationally cold; similar effects have been seen in the PE spectrum of I₂⁻(Ar) and in the IR spectrum of clustered halide anions.^92,93 As a consequence, the vibrational features in the BrHI⁻·(Ar) PE spectrum are considerably narrower than in the BrHI⁻ spectrum,⁸⁴ enabling a more detailed comparison with theory. While the bare IHI⁻ spectrum shows a well-resolved progression in the relatively high frequency IHI antisymmetric stretch,⁹¹ the IHI⁻·(Ar) PE spectrum shows additional structure from progressions in low frequency hindered rotor states of the IHI complex.

Fig. 8 Effect of complexation of single Ar atom on photoelectron spectra of IHI⁻ (a) and BrHI⁻ (b) (adapted from ref. 30).

The PE spectra of IHI⁻·(Ar)_n (n = 1–15) clusters, shown in Fig. 9 exhibit several trends that reflect the effects of solvation on the anion and the neutral, and sorting these out is perhaps the most challenging aspect in the interpretation of the spectra.²⁹ We observe shifts with EA as a function of cluster size that are very similar to those seen for I₂⁻·(Ar)_n clusters,⁹² implying that the first six Ar atoms cluster around the waist of the IHI⁻, where they can interact with the partial negative charges on the two I atoms. Subsequent Ar atoms bind primarily to a single I atom. We also observe a change in the spacing of the IHI antisymmetric stretch frequency as a function of cluster size, an effect attributed to solvent-induced distortion of the IHI⁻ geometry. However, the most intriguing effect is that the low-frequency hindered rotor structure seen in the binary IHI⁻(Ar) cluster becomes more pronounced for the largest clusters we studied, an unusual result since clustering generally obscures vibrational structure in photoelectron spectra. This effect is attributed to caging of the neutral IHI complex by the surrounding Ar atoms, resulting in a longer lifetime and hence sharper structure than seen in the smaller clusters. It represents a remarkable demonstration of the effect of clustering on transition state dynamics, with clear analogies to the caging of photoexcited chromophore molecules such as I₂ and I₂⁻ in cryogenic matrices and clusters seen in several laboratories.^94,95

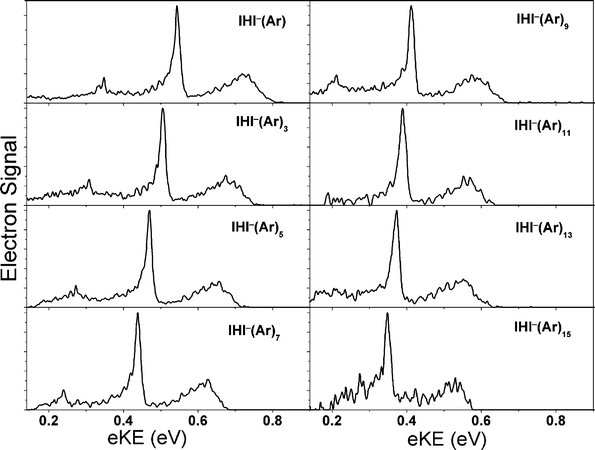Fig. 9 Photoelectron spectra of IHI⁻(Ar)_n, n ≤ 15 (adapted from ref. 29).

The Ar cluster experiments also provided evidence for an additional structural isomer of the form I⁻(Ar)_nHI,²⁹ suggesting that even a weakly interacting solvent species such as Ar can result in structural perturbations of the anion chromophore. This result has motivated studies of structural changes in transition state precursor anions induced by more strongly interacting solvent species. Specifically, we have measured photoelectron spectra of clustered bihalides XHX⁻·(M) (X = Br, I) and BrHI⁻·(M), where M = H₂O, HBr and HI.³¹

As shown in Fig. 10 for the case of bare and clustered IHI⁻, photoelectron spectra of the XHX⁻·(H₂O) ions show similar vibrational progressions as the spectra of the bare BrHBr⁻ and IHI⁻ anions, indicating that photodetachment of the bare and hydrated ions accesses similar XHX transition state geometries on the X + HX reaction potential energy surfaces. These results are consistent with electronic structure calculations that predict a double hydrogen-bonded XHX⁻·(H₂O) structure in which the symmetry of the strong XHX⁻ hydrogen bond is largely preserved. In contrast, photoelectron spectra of BrHBr⁻·(HBr)_1,2 and IHI⁻·(HI)_1,2 indicate that the addition of a single HBr or HI disrupts the symmetric XHX⁻ bond, resulting in structures of the form X⁻·(HX)_n, and altering the geometry of the Franck–Condon region accessed on the neutral potential energy surfaces. Similarly, photoelectron spectra of BrHI⁻·(HI) and BrHI⁻·(HBr) suggest anion structures of the form I⁻·(HBr)HI and I⁻·(HBr)₂, respectively.

Fig. 10 Photoelectron spectra of IHI⁻, IHI⁻(H₂O) and IHI⁻(HI)_1,2 taken at 213 nm (adapted from ref. 31).

Probing the van der Waals reactant well

Transition state spectroscopy is most generally defined as an experiment that yields spectroscopic information on the reaction complex, as opposed to separated products or reactants. The conventional wisdom in reaction dynamics is that a successful transition state spectroscopy experiment is one that probes the classical transition state, e.g. the barrier region for a direct reaction. However, for any direct reaction between neutral species, one expects shallow wells along the reaction coordinate on either side of the barrier due to the attractive van der Waals interaction between reactants or products. These wells have often been used to launch bimolecular reactions through either electronic excitation^96,97 or photodissociation^98,99 of one of the reactants constituting the complex. For example, photoexcitation of the metal atom in HgH₂ or NaFH complexes initiates an excited state chemical reaction,^97,100 and by probing the product yield as a function of excitation energy, one can essentially perform transition state spectroscopy of the excited state potential energy surface.

The possible role of vdW wells on ground state dynamics is an issue of considerable interest. Even though these wells occur at considerably larger internuclear distances than are characteristic of transition states, they can play an important role in the ground state reaction dynamics. For example, recent experiments and calculations on Cl + HD by Liu and co-workers³⁷ showed that the presence of a reactant vdW well was necessary to reproduce the experimental HCl : DCl product branching ratio. This effect arises because the vdW minimum is T-shaped, whereas the transition state geometry is linear,¹⁰¹ so the shallow vdW well results in a torque on the reactants en route to the transition state. In the F + H₂ reaction, the vdW well is also T-shaped,⁵⁰ and occurs at only a slightly larger F⋯H₂ distance than the transition state geometry. The barrier for F + H₂ is much lower than that for Cl + H₂, 1.9 kcal mol⁻¹vs. 7.6 kcal mol⁻¹,^101,102 so one can speculate that the bent nature of the transition state in F + H₂ arises in part from its proximity to the T-shaped well. Hence, experiments that probe the spectroscopy of ground state complexes between reactants may be quite important for gaining a global picture of the corresponding reaction.

The reactant vdW well has been probed in an elegant series of experiments by Lester and co-workers.^35,36 In these studies, open-shell, “pre-reactive” vdW complexes such as OH·H₂ and OH·CO are formed in a free jet expansion, and their infrared and Raman predissociation spectra are measured by action spectroscopy through detection of the OH radical. These complexes lie to the reactant side of small barriers for the OH + H₂ and OH + CO reactions. One question underlying these studies is whether vibrational excitation of the complexes can actually drive the chemical reaction; there is strong indirect evidence for this, although reaction products have yet to be observed experimentally. Regardless, these rotationally-resolved spectra provide a detailed probe of the van der Waals well and therefore provide new experimental insight into what now appears to be a very important region of the reactive potential energy surface.

The reactant vdW well can also be probed with negative ion photoelectron spectroscopy, so long as there is good overlap between the anion and neutral vdW well. This condition favors reactions with relatively “late” barriers; otherwise the reactants will be too far apart in the vdW well to be accessed by photodetachment. The slightly endothermic Cl + H₂ reaction is an ideal candidate for this experiment. Based on the rotationally resolved IR spectrum of ClH₂⁻ by Bieske,¹⁰³ calculations of the ClH₂⁻ potential energy surface and vibrational wavefunctions,^104,105 and electronic structure calculations of the Cl + H₂ surface,^101,106 photodetachment of ClH₂⁻ should have poor overlap with the transition state but excellent overlap with the van der Waals well in the Cl + H₂ reactant valley. The anion has a linear equilibrium geometry, while the vdW well is lowest for a T-shaped, C_2v structure. Hence, the ClH₂⁻ photoelectron spectrum should reveal progressions in the vdW low-frequency stretch and hindered rotor levels, providing a detailed characterization of the vdW well.

Photoelectron spectra of ClH₂⁻ and ClD₂⁻ are shown in Fig. 11.¹⁰⁷ Both spectra are dominated by two intense peaks A and B, separated by 0.11 eV, which is identical to the spin–orbit splitting in atomic chlorine of 0.109 eV. Peaks A and B are assigned to transitions to the Cl(²P_3/2)·H₂ and Cl(²P_1/2)·H₂ complexes, respectively. Apparently the Cl·H₂ interaction at the distances probed in the anion photoelectron spectrum is insufficient to perturb the spin–orbit splitting significantly, in contrast to the FH₂⁻ photoelectron spectrum where the strongly repulsive nature of the spin–orbit excited states closer to the transition state region is evident.⁵¹ This aspect of the ClH₂⁻ photoelectron spectrum is of interest in light of recent experimental and theoretical results^108,109 comparing the reaction cross sections for Cl*(²P_1/2) and Cl(²P_3/2) with H₂.

Fig. 11 Photoelectron spectra of ClH₂⁻ and ClD₂⁻ at a photodetachment wavelength of 299 nm (4.15 eV) (adapted from ref. 107).

The more interesting result in Fig. 11 is the peak widths, which are considerably broader than the experimental resolution (8–10 meV), and are about twice as broad in the ClD₂⁻ spectrum as in the ClH₂⁻ spectrum. These observations suggest the presence of unresolved, underlying structure, including progressions in the low-frequency van der Waals bend and stretch of the neutral complexes, and, in the case of peak A, overlapping contributions of transitions to two closely-spaced neutral electronic states (the ²Σ⁺ and ²Π_3/2 states in the collinear geometry¹¹⁰). In fact, recent theoretical work by Manolopoulos and Alexander¹¹¹ show all these effects to be present, and that by convoluting their simulated photoelectron spectra with our experimental resolution, the main features in Fig. 11 are recovered.

Nonetheless, from an experimental perspective, it certainly seems desirable to improve on the resolution of our photoelectron spectra. We have recently implemented a new experiment in our laboratory, slow photoelectron velocity-map imaging (SEVI) of negative ions, in which anions are photodetached with a tunable laser within several meV of a photodetachment threshold.¹⁵ The resulting slow photoelectrons are collected with a high resolution velocity-map imaging analyzer¹¹² and their kinetic energy (and angular) distributions are determined. This instrument has been shown to yield energy resolution of better than 1 meV, comparable to that of anion ZEKE spectroscopy,¹⁴ but is experimentally far more tractable. Fig. 12 shows the SEVI spectrum of peak A for ClD₂⁻; the spectrum¹⁵ reveals three partially resolved features attributed to a progression in hindered rotor levels of the ClD₂ complex. This new technique offers considerable additional capabilities in studying transition states and pre-reactive complexes via negative ion photodetachment.

Fig. 12 Slow photoelectron imaging (SEVI) spectrum of the Cl(²P_3/2)·D₂ feature (peak A) in Fig. 11, showing partially esolved structure assigned to D₂ hindered rotor motion. Bottom: SEVI spectrum of Cl⁻ for comparison and calibration (adapted from ref. 15).

Conclusions

Transition state spectroscopy has evolved into a useful tool in the arsenal of techniques available to probe chemical reaction dynamics in great detail. In this article, we have focused on TSS via negative ion photodetachment, a technique that has repeatedly been able to yield vibrational structure characteristic of the transition state, thereby providing a vital fingerprint of the potential energy surface in the vicinity of the transition state. Examples have been presented showing its application to benchmark bimolecular reactions, unimolecular isomerization reactions and reactions in size-selected clusters. Experiments of this type can also be used to probe reactant van der Waals wells. Interpretation of the experiments is facilitated by detailed theoretical simulations of the experiments using state-of-the-art scattering calculations on model potential energy surfaces.

Thus far, successful TSS experiments have been restricted to half-collision studies, in which the transition state is probed by photoexcitation of a stable species. The resulting restricted range of reactant geometries and total angular momentum is crucial to the resolution of vibrational structure in these experiments. However, techniques are currently under development in several laboratories to generate translationally cold atoms and molecules.¹¹³ Under such conditions, centrifugal barriers can limit reaction to collisions with very low (or zero) orbital angular momentum, thereby mitigating effects of angular momentum averaging in the total reaction cross section. Recent calculations^114,115 have predicted that total cross sections at collisions at energies well below the entrance barrier will be highly structured owing to enhanced tunneling and Feshbach resonance effects at these very low collision energies. Hence, it may soon be possible to study bimolecular reactive collisions at such low energies that TSS experiments will become feasible.

Acknowledgements

This work is supported by the Air Force Office of Scientific Research under Grant No. F49620-03-1-0085.

References

1. H.-J. Foth, J. C. Polanyi and H. H. Telle, J. Phys. Chem., 1982, 86, 5027.
2. P. R. Brooks, Chem. Rev., 1988, 88, 407.
3. D. M. Neumark, Annu. Rev. Phys. Chem., 1992, 43, 153.
4. J. C. Polanyi and A. H. Zewail, Acc. Chem. Res., 1995, 28, 119.
5. R. D. Levine and R. B. Bernstein, Molecular reaction dynamics and chemical reactivity, Oxford University Press, 1987.
6. C. B. Moore and I. W. M. Smith, J. Phys. Chem., 1996, 100, 12848.
7. A. H. Zewail, J. Phys. Chem., 1996, 100, 12701.
8. A. H. Zewail, J. Phys. Chem. A, 2000, 104, 5660.
9. H. Ihee, V. A. Lobastov, U. M. Gomez, B. M. Goodson, R. Srinivasan, C. Y. Ruan and A. H. Zewail, Science, 2001, 291, 458.
10. R. B. Metz, S. E. Bradforth and D. M. Neumark, Adv. Chem. Phys., 1992, 91, 1.
11. D. M. Neumark, Acc. Chem. Res., 1993, 26, 33.
12. P. G. Wenthold, D. A. Hrovat, W. T. Borden and W. C. Lineberger, Science, 1996, 272, 1456.
13. H. Hotop and W. C. Lineberger, J. Phys. Chem. Ref. Data., 1985, 14, 731.
14. T. N. Kitsopoulos, I. M. Waller, J. G. Loeser and D. M. Neumark, Chem. Phys. Lett., 1989, 159, 300.
15. A. Osterwalder, M. J. Nee, J. Zhou and D. M. Neumark, J. Chem. Phys., 2004, 121, 6317.
16. G. C. Schatz, J. Phys. Chem., 1996, 100, 12839.
17. I. M. Waller, T. N. Kitsopoulos and D. M. Neumark, J. Phys. Chem., 1990, 94, 2240.
18. R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S. H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2000, 112, 4536.
19. R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S. H. Lee, F. Dong and K. P. Liu, Phys. Rev. Lett., 2000, 85, 1206.
20. K. Liu, R. T. Skodje and D. E. Manolopoulos, PhysChemComm, 2002, 4, 1.
21. P. Corkum, Nature, 2000, 403, 845.
22. M. Drescher, M. Hentschel, R. Kienberger, M. Uiberacker, V. Yakovlev, A. Scrinizi, T. Westerwalbesloh, U. Kleineberg, U. Heinzmann and F. Krausz, Nature, 2002, 419, 803.
23. D. M. Neumark, Annu. Rev. Phys. Chem., 2001, 52, 255.
24. A. Stolow, A. E. Bragg and D. M. Neumark, Chem. Rev., 2004, 104, 1719.
25. B. J. Siwick, J. R. Dwyer, R. E. Jordan and R. J. D. Miller, Science, 2003, 302, 1382.
26. Z. H. Chang, A. Rundquist, H. W. Wang, M. M. Murnane and H. C. Kapteyn, Phys. Rev. Lett., 1997, 79, 2967.
27. M. Drescher, M. Hentschel, R. Kienberger, G. Tempea, C. Spielmann, G. A. Reider, P. B. Corkum and F. Krausz, Science, 2001, 291, 1923.
28. F. Benesch, T. W. Lee, Y. Jiang and C. G. Rose-Petruck, Optics Lett., 2004, 29, 1028.
29. Z. Liu, H. Gomez and D. M. Neumark, Faraday Discuss., 2001, 118, 221.
30. Z. Liu, H. Gomez and D. M. Neumark, Chem. Phys. Lett., 2000, 332, 65.
31. H. Gomez, G. Meloni, J. Madrid and D. M. Neumark, J. Chem. Phys., 2003, 119, 872.
32. N. L. Pivonka, C. Kaposta, M. Brummer, G. von Helden, G. Meijer, L. Woste, D. M. Neumark and K. R. Asmis, J. Chem. Phys., 2003, 118, 5275.
33. N. L. Pivonka, C. Kaposta, G. von Helden, G. Meijer, L. Woste, D. M. Neumark and K. R. Asmis, J. Chem. Phys., 2002, 117, 6493.
34. M. J. Nee, A. Osterwalder, D. M. Neumark, C. Kaposta, C. C. Uhalte, T. Xie, A. Kaledin, J. M. Bowman, S. Carter and K. R. Asmis, J. Chem. Phys., 2004, 121, 7259.
35. M. D. Wheeler, D. T. Anderson and M. I. Lester, Int. Rev. Phys. Chem., 2000, 19, 501.
36. M. I. Lester, B. V. Pond, M. D. Marshall, D. T. Anderson, L. B. Harding and A. F. Wagner, Faraday Discuss., 2001, 118, 373.
37. D. Skouteris, D. E. Manolopoulos, W. S. Bian, H. J. Werner, L. H. Lai and K. P. Liu, Science, 1999, 286, 1713.
38. D. M. Neumark, PhysChemComm, 2002, 5, 76.
39. D. M. Neumark, in Transition State Spectroscopy, ed. X. Yang and K. Liu, World Scientific, Singapore, 2004.
40. D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden and Y. T. Lee, J. Chem. Phys., 1985, 82, 3045.
41. D. M. Neumark, A. M. Wodtke, G. N. Robinson, C. C. Hayden, K. Shobatake, R. K. Sparks, T. P. Schafer and Y. T. Lee, J. Chem. Phys., 1985, 82, 3067.
42. M. Faubel, L. Rusin, S. Schlemmer, F. Sondermann, U. Tappe and J. P. Toennies, J. Chem. Phys., 1994, 101, 2106.
43. M. Baer, M. Faubel, B. Martinez-Haya, L. Rusin, U. Tappe and J. P. Toennies, J. Chem. Phys., 1999, 110, 10231.
44. W. B. Chapman, B. W. Blackmon, S. Nizkorodov and D. J. Nesbitt, J. Chem. Phys., 1998, 109, 9306.
45. F. Dong, S. H. Lee and K. Liu, J. Chem. Phys., 2000, 113, 3633.
46. G. Dharmasena, T. R. Phillips, K. N. Shokhirev, G. A. Parker and M. Keil, J. Chem. Phys., 1997, 106, 9950.
47. T. Takayanagi and S. Sato, Chem. Phys. Lett., 1988, 144, 191.
48. F. J. Aoiz, V. J. Herrero, M. M. Nogueira and V. S. Rabanos, Chem. Phys. Lett., 1993, 204, 359.
49. J. A. Nichols, R. A. Kendall, S. J. Cole and J. Simons, J. Phys. Chem., 1991, 95, 1074.
50. K. Stark and H. J. Werner, J. Chem. Phys., 1996, 104, 6515.
51. S. E. Bradforth, D. W. Arnold, D. M. Neumark and D. E. Manolopoulos, J. Chem. Phys., 1993, 99, 6345.
52. D. E. Manolopoulos, K. Stark, H. J. Werner, D. W. Arnold, S. E. Bradforth and D. M. Neumark, Science, 1993, 262, 1852.
53. C. L. Russell and D. E. Manolopoulos, Chem. Phys. Lett., 1996, 256, 465.
54. M. Hayes, M. Gustafsson, A. M. Mebel and R. T. Skodje, Chem. Phys., 2004, 308, 259.
55. I. W. M. Smith and F. F. Crim, Phys. Chem. Chem. Phys., 2002, 4, 3543.
56. M. Alagia, N. Balucani, P. Casavecchia, D. Stranges, G. G. Volpi, D. C. Clary, A. Kliesch and H. J. Werner, Chem. Phys., 1996, 207, 389.
57. D. C. Clary and G. Ochoa de Aspuru, J. Phys. Chem. A, 1998, 102, 9631.
58. G. Wu, G. C. Schatz, G. Lendvay, D. C. Fang and L. B. Harding, J. Chem. Phys., 2000, 113, 3150.
59. S. K. Pogrebnya, J. Palma, D. C. Clary and J. Echave, Phys. Chem. Chem. Phys., 2000, 2, 693.
60. M. J. Lakin, D. Troya, G. Lendvay, M. Gonzalez and G. C. Schatz, J. Chem. Phys., 2001, 115, 5160.
61. B. R. Strazisar, C. Lin and H. F. Davis, Science, 2000, 290, 958.
62. R. A. Loomis, R. L. Schwartz and M. I. Lester, J. Chem. Phys., 1996, 104, 6984.
63. G. Chalasinski, R. A. Kendall and J. Simons, J. Chem. Phys., 1987, 87, 2965.
64. S. S. Xantheas and T. H. Dunning, J. Phys. Chem., 1992, 96, 7505.
65. J. V. Ortiz, J. Chem. Phys., 1989, 91, 7024.
66. D. C. Clary, J. K. Gregory, M. J. T. Jordan and E. Kauppi, J. Chem. Soc., Faraday Trans., 1997, 93, 747.
67. D. H. Zhang, M. H. Yang, M. A. Collins and S. Y. Lee, Proc. Natl. Acad. Sci. USA, 2002, 99, 11579.
68. E. de Beer, E. H. Kim, D. M. Neumark, R. F. Gunion and W. C. Lineberger, J. Phys. Chem., 1995, 99, 13627.
69. W. H. Thompson, H. O. Karlsson and W. H. Miller, J. Chem. Phys., 1996, 105, 5387.
70. S. P. Walch and T. H. Dunning Jr, J. Chem. Phys., 1980, 72, 1303.
71. G. C. Schatz and H. Elgersma, Chem. Phys. Lett., 1980, 73, 21.
72. M. H. Yang, D. H. Zhang, M. A. Collins and S. Y. Lee, J. Chem. Phys., 2001, 115, 174.
73. M. Igarashi and H. Tachikawa, Int. J. Mass. Spectrom., 2000, 197, 243.
74. J. Cooper and R. N. Zare, J. Chem. Phys., 1968, 48, 942.
75. J. L. Hall and M. W. Siegel, J. Chem. Phys., 1968, 48, 943.
76. J. J. Sloan, D. G. Watson, J. M. Williamson and J. S. Wright, J. Chem. Phys., 1981, 75, 1190.
77. R. N. Dixon and H. Tachikawa, Mol. Phys., 1999, 97, 195.
78. S. Gomez-Carrasco, L. Gonzalez-Sanchez, A. Aguado, M. Paniagua, O. Roncero, M. L. Hernandez and J. M. Alvarino, Chem. Phys. Lett., 2004, 383, 25.
79. L. Gonzalez-Sanchez, S. Gomez-Carrasco, A. Aguado, M. Paniagua, M. L. Hernandez, J. M. Alvarino and O. Roncero, J. Chem. Phys., 2004, 121, 9865.
80. M. P. Deskevich, D. J. Nesbitt and H. J. Werner, J. Chem. Phys., 2004, 120, 7281.
81. S. E. Bradforth, D. W. Arnold, R. B. Metz, A. Weaver and D. M. Neumark, J. Phys. Chem., 1991, 95, 8066.
82. S. E. Bradforth, PhD Thesis, University of California, Berkeley, 1992.
83. R. B. Metz, A. Weaver, S. E. Bradforth, T. N. Kitsopoulos and D. M. Neumark, J. Phys. Chem., 1990, 94, 1377.
84. S. E. Bradforth, A. Weaver, D. W. Arnold, R. B. Metz and D. M. Neumark, J. Chem. Phys., 1990, 92, 7205.
85. C. Xu, G. R. Burton, T. R. Taylor and D. M. Neumark, J. Chem. Phys., 1998, 108, 7645.
86. S. M. Burnett, A. E. Stevens, C. S. Feigerle and W. C. Lineberger, Chem. Phys. Lett., 1983, 100, 124.
87. K. M. Ervin, J. Ho and W. C. Lineberger, J. Chem. Phys., 1989, 91, 5974.
88. T. Carrington, L. M. Hubbard, H. F. Schaefer and W. H. Miller, J. Chem. Phys., 1984, 80, 4347.
89. M. P. Jacobson and R. W. Field, J. Phys. Chem. A, 2000, 104, 3073.
90. H. B. Lavender and A. B. McCoy, J. Phys. Chem. A, 2000, 104, 644.
91. A. Weaver, R. B. Metz, S. E. Bradforth and D. M. Neumark, J. Phys. Chem., 1988, 92, 5558.
92. K. R. Asmis, T. R. Taylor, C. S. Xu and D. M. Neumark, J. Chem. Phys., 1998, 109, 4389.
93. C. G. Bailey, J. Kim, C. E. H. Dessent and M. A. Johnson, Chem. Phys. Lett., 1997, 269, 122.
94. R. Zadoyan, Z. Li, P. Ashjian, C. C. Martens and V. A. Apkarian, Chem. Phys. Lett., 1994, 218, 504.
95. V. Vorsa, P. J. Campagnola, S. Nandi, M. Larsson and W. C. Lineberger, J. Chem. Phys., 1996, 105, 2298.
96. B. Soep, S. Abbes, A. Keller and J. P. Visticot, J. Chem. Phys., 1992, 96, 440.
97. M. S. Topaler, D. G. Truhlar, X. Y. Chang, P. Piecuch and J. C. Polanyi, J. Chem. Phys., 1998, 108, 5378.
98. S. Buelow, G. Radhakrishnan, J. Catanzarite and C. Wittig, J. Chem. Phys., 1985, 83, 444.
99. N. F. Scherer, L. R. Khundkar, R. B. Bernstein and A. H. Zewail, J. Chem. Phys., 1987, 87, 1451.
100. W. H. Breckenridge, C. Jouvet and B. Soep, J. Chem. Phys., 1986, 84, 1443.
101. W. S. Bian and H. J. Werner, J. Chem. Phys., 2000, 112, 220.
102. M. H. Alexander, D. E. Manolopoulos and H. J. Werner, J. Chem. Phys., 2000, 113, 11084.
103. D. A. Wild, P. S. Weiser, E. J. Bieske and A. Zehnacker, J. Chem. Phys., 2001, 115, 824.
104. M. H. Alexander, J. Chem. Phys., 2003, 118, 9637.
105. A. A. Buchachenko, T. A. Grinev, J. Klos, E. J. Bieske, M. M. Szczesniak and G. Chalasinski, J. Chem. Phys., 2003, 119, 12931.
106. J. Klos, G. Chalasinski and M. M. Szczesniak, J. Chem. Phys., 2002, 117, 4709.
107. M. J. Ferguson, G. Meloni, H. Gomez and D. M. Neumark, J. Chem. Phys., 2002, 117, 8181.
108. F. Dong, S. H. Lee and K. Liu, J. Chem. Phys., 2001, 115, 1197.
109. M. H. Alexander, G. Capecchi and H. J. Werner, Science, 2002, 296, 715.
110. T. Lenzer, I. Yourshaw, M. R. Furlanetto, G. Reiser and D. M. Neumark, J. Chem. Phys., 1999, 110, 9578.
111. D. E. Manolopoulos and M. H. Alexander, Phys. Chem. Chem. Phys., 2004, 6, 4984.
112. A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477.
113. H. L. Bethlem, G. Berden and G. Meijer, Phys. Rev. Lett., 1999, 83, 1558.
114. N. Balakrishnan and A. Dalgarno, Chem. Phys. Lett., 2001, 341, 652.
115. E. Bodo, F. A. Gianturco and A. Dalgarno, J. Phys. B: At. Mol. Opt. Phys., 2002, 35, 2391.

---