Multivalency in supramolecular chemistry and nanofabrication
Alart
Mulder†
,
Jurriaan
Huskens
* and
David N.
Reinhoudt
*
Laboratory of Supramolecular Chemistry and Technology, MESA+ Institute for Nanotechnology, University of Twente, P. O. Box 217, 7500 AE, Enschede, The Netherlands. E-mail: j.huskens@utwente.nl; d.n.reinhoudt@utwente.nl; Fax: (+31)53-4894645
First published on 5th November 2004
Abstract
Multivalency is a powerful and versatile self-assembly pathway that confers unique thermodynamic and kinetic behavior onto supramolecular complexes. The diversity of the examples of supramolecular multivalent systems discussed in this perspective shows that the concept of multivalency is a general phenomenon, and that any supramolecular interaction can be employed in multivalent displays to attain the attractive aspects characteristic of multivalent interactions. After a general introduction reviewing the general aspects of multivalency, a number of different supramolecular multivalent complexes are discussed that highlight the different features of multivalent interactions. In contrast to the many biochemical multivalent interactions, supramolecular multivalent interactions are ideal to attain a quantitative and fundamental understanding of multivalency. Several examples in which multivalency has been utilized in supramolecular nanofabrication schemes are described in detail.
 Alart Mulder | Alart Mulder (1976) studied Chemical Technology at the University of Twente, the Netherlands. In 1999 he obtained his undergraduate degree with Professor David N. Reinhoudt and continued in the same group to study for his PhD. His doctoral studies involved the use of multivalency in nanotechnological applications and included work on β-cyclodextrin dimers with externally tunable binding properties and the use of β-cyclodextrin self-assembled monolayers as platforms for the creation of supramolecular patterns at surfaces. In 2004 he joined the group of Professor Robert Tampé at the Johann Wolfgang Goethe University, Frankfurt, as a post-doctoral co-worker, where he works on tunable multivalent biochemical tweezers for the labeling and immobilization of proteins and peptides. |
 Jurriaan Huskens | Jurriaan Huskens (1968) obtained his PhD with Professor Herman van Bekkum and Joop Peters from the Delft University of Technology, in 1994, in the field of homogeneous catalysis and coordination chemistry of lanthanide complexes. After postdoctoral stays with Professor Dean Sherry (University of Texas at Dallas) and Professor Manfred T. Reetz (Max-Planck-Institut für Kohlenforschung), he became an Assistant Professor in the group of Professor David N. Reinhoudt in 1998 at the University of Twente, where he has been an Associate Professor since 2003. Present research interests encompass: molecular recognition at interfaces, functionalized nanoparticles, nanofabrication, and single nanostructure manipulation. |
 David N. Reinhoudt | David N. Reinhoudt (1942) studied Chemical Technology at the Delft University of Technology and graduated in 1969 with Professor H. C. Beijerman. He was appointed as a part-time professor in 1975 at the University of Twente, and became full professor in 1978. His research is focused on supramolecular chemistry and technology with nanofabrication, molecular recognition, and non-covalent combinatorial synthesis as the major fields. He is the scientific director of the MESA+ Institute for Nanotechnology. Since 2002 he has been the chairman of the Board of NanoNed, the Dutch Network for Nanotechnology. He is the author of more than 750 scientific publications, patents, review articles, and books. He has been honored with the Izatt–Christensen award (1995), the Simon Stevin Mastership (1998) and Knight of the Order of the Dutch Lion (2002). |
1 Introduction
Within the field of supramolecular chemistry there is currently an increasing awareness of the potential of the multivalency concept:1 the simultaneous interaction between multiple functionalities on one entity and complementary functionalities on another. In fact, a quick scan through the recent publications in the different chemistry journals might leave the impression that multivalency is one of the foremost supramolecular themes in this era of nanotechnology. This is not surprising, as multivalency constitutes a self-assembly pathway that combines all the attractive characteristics of self-assembly, i.e. reversibility, self-sorting, and self-correction, with the possibility to achieve thermodynamic and/or kinetic assembly stability at nano- or even picomolar concentrations.Over the last decade multivalency has been a central topic in biochemistry since it became clear that it governs many biological interactions.1,2 In particular, protein–carbohydrate interactions are intensively investigated, as they play a pivotal role in for example the binding of the influenza virus to cell membranes3–6 and the recognition by carbohydrate-binding proteins (lectins)7–14 which are essential in membrane recognition events, for which Concanavalin A often serves as a model system.15–17 Within the field of biochemistry the multivalency concept has been successfully applied to the development of inhibitors with extremely low dissociation constants.18,19
For supramolecular chemists multivalency offers a means for the controllable, directional, and selective self-assembly of robust, functional nanostructures. Although the concept of multivalency has been used in supramolecular chemistry for many years, it is only in the last years that supramolecular multivalent interactions have been studied systematically.
The objective of this perspective is to give an overview of the current understanding of multivalency and its potential as a self-assembly tool in supramolecular chemistry and nanofabrication. For this reason, the focus will be on supramolecular multivalent interactions. Biochemical multivalent systems have been reviewed extensively elsewhere.1,2,20 After a general introduction reviewing the general aspects of multivalency, a number of different supramolecular multivalent complexes will be discussed that highlight the different features of multivalent interactions. It will be shown that, in contrast to the many biochemical multivalent interactions, supramolecular multivalent interactions are ideal to attain a quantitative and fundamental understanding of multivalency. The perspective will be concluded with several examples in which multivalency has been utilized in supramolecular nanofabrication schemes.
2 Multivalency
2.1 Definition and nomenclature
Multivalency describes the binding of two (or more) entities that involves the simultaneous interaction between multiple, complementary functionalities on these entities (see Fig. 1). In the case of supramolecular multivalency these entities can be any supramolecular display, ranging from a molecule to a self-assembled monolayer (SAM). In this perspective, the complementary interacting functionalities are referred to as host and guest, terms that are applicable to most supramolecular interactions. The interaction between a host and a guest leads to the formation of a complex. The valency of an entity is the number of separate connections of the same kind that it can form through host–guest interactions with entities bearing the complementary functionality. The valency of the complex is defined by the number of shared interactions between the two interacting entities. All interactions involving more than one host–guest interaction are considered multivalent.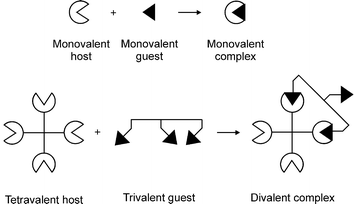 | ||
| Fig. 1 Terminology of valencies. | ||
There is a tendency to use the term multivalency for any interaction that involves entities displaying multiple functionalities, even though many of these concern the interaction of a multivalent entity with multiple monovalent species or the formation of high stoichiometry or even polymeric systems in which the interaction between each two species in such an assembly is monovalent.21 Here, we use the term multivalency exclusively for the self-assembly of well-defined complexes in which the separation of any entity or part from the complex requires the dissociation of at least two interactions.
2.2 Intra- versus intermolecular binding
There are many possible ways by which multivalent host and guest entities can interact with each other. Binding does not necessarily occur in a multivalent fashion, i.e. intramolecularly,22 an intermolecular interaction between two multivalent entities is also possible (Fig. 2). Whereas a multivalent interaction potentially gives rise to structures with defined geometries and binding motifs, intermolecular binding leads to the formation of large (insoluble) aggregates and polymeric structures. Binding does not necessarily have to follow a single pathway; combinations of intra- and intermolecular binding are also possible.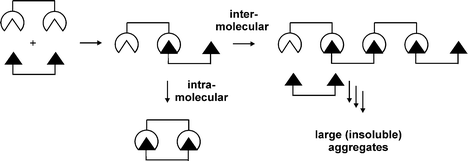 | ||
| Fig. 2 Multivalent vs. intermolecular binding. | ||
To specifically achieve multivalent binding, a certain degree of system design is required. The most important aspects that need to be considered in this respect are the architecture of the multivalent entities and the thermodynamics of the interactions.
The architecture, i.e. the size and shape, of the multivalent entities has a strong influence on the mode of binding.15c Self-assembled and hybrid monolayers, systems in which the host or guest functionalities are arranged in a two-dimensional plane with high directionality, are prone to multivalent binding. On the other hand, combinations of small, relatively rigid, three-dimensional entities such as particles and dendrimers are susceptible to intermolecular binding.23,24 This is also the reason why many of the studied multivalent biological hosts, which constitute rigid proteins with a low density of three-dimensionally arranged host sites, bind intermolecularly with multivalent molecules in solution. Concanavalin A, an extensively studied membrane protein, for example, has four potential binding sites in four opposite directions and is typically bound intermolecularly by multivalent guests.25–28 An exception are the pentavalent cholera toxins which are unique in the sense that they direct all five binding sites along a single axis. Additionally, specific toxins, such as the Shiga-like toxin, are unusually small, with intersite distances between host domains as small as 10 Å.29 Binding of multivalent guests to these toxins typically occurs in a multivalent, intramolecular fashion,18,30 and these systems have been the basis for a number of excellent models for the interpretation and prediction of multivalent interactions.31,32 Similarly, the large density of functionalities that is achieved by grouping them on supramolecular scaffolds typically leads to intramolecular binding between two complementary supramolecular entities.
In those cases where the architectures of the multivalent entities enable multivalent binding, the mode of binding is determined by thermodynamics, i.e. the relative free energies (ΔG°) of the two possible binding events. Both enthalpy (ΔH°) and entropy of binding (ΔS°) are important in this respect. The enthalpic and entropic contributions of the individual interactions to the multivalent binding have been described by Whitesides et al. in their review on multivalent interactions in biological systems.1 For multivalent interactions that are constituted of multiple, independent interactions of the same type, (ΔS°) is linearly related to the enthalpy of binding for a monovalent, intrinsic interaction and to the number of interactions involved, i.e. a divalent binding is expected to have an enthalpy of binding that is twice that of the corresponding monovalent interaction.
The traditional idea is that multivalency is mainly governed by entropy.1,12 In these approaches the binding enthalpy is typically assumed to be proportional to the number of interactions and the mode of binding is dependent on the entropy of binding. Intramolecular multivalent binding would be entropically favorable as the multivalent complex is assumed to involve the same rotational and translational entropy loss as its corresponding monovalent interaction.1 Therefore, it is reasoned that the mode of binding is determined by the loss of conformational entropy upon intramolecular binding. If the overall entropy balance is positive, the multivalent entities will bind intramolecularly, and if the conformational entropy penalty paid exceeds the gained translational and rotational entropy the multivalent interaction will be intermolecular. This philosophy implies that multivalent binding is associated with a favorable entropy term compared to the corresponding number of multiple monovalent interactions, an idealized phenomenon, which is in sharp contrast with the large negative entropy terms that are typically found for multivalent interactions. Several studies on intramolecular binding involving multivalent guests tethered by long flexible spacers, including some of the examples that will be discussed in the next section, indicate that entropic concerns should not be taken too seriously.33,34
2.3 Effective concentration
A term that provides a more understandable relation between the length and flexibility of the tether and the energy of binding is the effective concentration (Ceff). Effective concentration represents a probability of interaction between two reactive or complementary interlinked entities and symbolizes a “physically real” concentration of one of the reacting or interacting functionalities as experienced by its complementary counterpart. The concept of effective concentration originates from the field of polymer chemistry where it was introduced to account for intramolecular cyclization reactions in polymer synthesis.35 Similarly, effective concentration can be employed for the interpretation of (the entropic contribution to) multivalent interactions. The effective concentration concept for multivalent interactions is schematically depicted in Fig. 3. The first interaction of a multivalent guest with a multivalent host alters the guest site concentration as experienced by the neighboring free host site. If this so-called effective concentration is higher than the actual guest site concentration in solution, intramolecular (multivalent) binding is favored. If the guest site concentration in solution is higher than Ceff experienced by the host site the binding will most likely proceed in an intermolecular fashion.![Schematic representation of the concept of effective concentration, demonstrating the increased probability of interaction for intramolecular binding events. A free host site experiences an effective guest site concentration [B]eff in a solution with guest site concentration [B]sol. The dotted circle represents the probing volume that the pendent host site can probe to find available guest sites.](/image/article/2004/OB/b413971b/b413971b-f3.gif) | ||
| Fig. 3 Schematic representation of the concept of effective concentration, demonstrating the increased probability of interaction for intramolecular binding events. A free host site experiences an effective guest site concentration [B]eff in a solution with guest site concentration [B]sol. The dotted circle represents the probing volume that the pendent host site can probe to find available guest sites. | ||
For a multivalent interaction comprised of multiple independent interactions, the association constant for the n-valent interaction, Kn, can be directly related to the intrinsic association constant, Ki, and Ceff according to eqn. (1).32,36,37
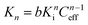 | (1) |
Here, b is a scaling factor incorporating statistical factors determining the numbers of possible association and dissociation pathways in the subsequent interaction steps. The concept of effective concentration gives rise to a concentration-dependent binding mode for multivalent interactions, favoring intramolecular binding at low concentrations and intermolecular binding at high concentrations. Indeed, this phenomenon has been observed for several biochemical5 and supramolecular multivalent systems.38,39
Effective concentration is conceptually similar to the more generally used effective molarity (EM).40 Whereas effective concentration is based on concentrations calculated or estimated from physical geometries of complexes, effective molarity denotes the ratio of intra- and intermolecular rate or association constants.40 In other words, effective concentration theoretically quantifies the advantage for an intra- over an intermolecular interaction, while effective molarity does that empirically. As shown by Page and Jencks, this advantage is mainly entropic and EM may amount up to 108 M, concentrations that are physically unachievable.41,42 The term effective molarity has been successfully applied to indicate the ease of cyclization reactions,43,44 feasibility of the self-assembly of defined multi-component systems,45,46 and has been used as a measure for affinity enhancement using multivalent interactions.47–49 For an intramolecular n-valent interaction with an association constant Kn, EM is given by eqn. (2).
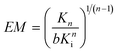 | (2) |
In contrast to the generally used effective molarity, effective concentration is used only scarcely. This is inherent to the difficulties associated with the correct determination of the latter. Recently, several approaches for the approximation of effective concentrations have been published. These are based on the determination of linker length by random-walk statistics, either used directly30,34 or in combination with probability functions,32,35,50 and the use of molecular modeling.51 Despite the problems associated with the exact determination of Ceff, it is predicted that the effective concentration depends on the inverse cube of the linker length, which is explained by the increase of the probing volume accessible by an uncomplexed guest (or host) site upon increase of the linker length.
In those cases where the multivalent interaction is comprised of multiple non-cooperative interactions, Ceff equals EM. As will be shown below in Section 3, this may well be the case for most multivalent supramolecular interactions as in many cases EM falls in a surprisingly narrow range, which are probable values for Ceff.
2.4 Multivalency and cooperativity
The assessment of cooperativity in multivalent interactions is notoriously difficult,1,52 and there are numerous examples in the literature where multivalent binding is incorrectly declared negatively or positively cooperative simply based on mono- and multivalent association constants.52 Before any conclusions can be drawn regarding cooperativity in multivalent interactions a thorough deconvolution of the effects of multivalency and cooperativity is required.Cooperativity has been rigorously defined for consecutive monovalent interactions at a multivalent platform.53,54 However, multivalent interactions are fundamentally different from monovalent interactions, and traditional methods used to experimentally verify extents of cooperativity for monovalent interactions, such as Hill and Scatchard plots or even a simple comparison of the free energies of binding, fail for multivalent systems, as was elegantly demonstrated by Ercolani.52 Ercolani clearly exemplified that cooperativity in multivalent interactions can only be assessed by considering the inter- and intramolecular processes separately and independently, i.e. cooperativity can only be assessed if the compared equilibrium constants have the same dimensions.52 By comparison of experimental and statistical association constants for intramolecular interactions, an indication of the extent of cooperativity can be attained. If the former exceeds the latter, there is positive cooperativity, whereas if the opposite occurs negative cooperativity is involved. Alternatively this can be translated in terms of effective concentration and effective molarity. Large deviations between the two parameters can be indicative of a negatively (EM < Ceff) or positively cooperative binding mode (EM > Ceff). As stated above, the difficulty lies in the estimation of Ceff. The proper assessment of cooperativity in multivalent systems requires the quantitative comparison of the multivalent and corresponding monovalent binding constants. Preferably these should be supported by enthalpy data.55
Cooperativity in multivalent systems is probably extremely scarce. One example of positive cooperativity in a multivalent system might be the self-assembly of a DNA double helix.56 However, the majority of (synthetic) multivalent systems reported in the literature can be analyzed using a statistical, non-cooperative binding mode, i.e. in terms of pure multivalency and effective concentration.30–32,34,48,57
2.5 Kinetics
The kinetics of multivalent interactions are fundamentally different from monovalent interactions.48 The association rate is, analogous to monovalent interactions, determined by the diffusion of the interacting species and the intrinsic association rate constant of a monovalent interaction. The overall dissociation rate, however, is determined by the dissociation rate of the monovalently bound species of the multivalent complex, i.e. the species in which two multivalent entities are bound by one interaction only. The rate constant of this dissociation process can be assumed equal to the intrinsic dissociation rate constant of the corresponding monovalent interaction. This means that the dissociation rate is solely dependent on the concentration of this monovalently bound species, which among others, is dependent on the effective concentration for the intramolecular multivalent interaction.36Ceff is in this case a quantitative measure for the ease of rebinding for partially dissociated complexes and constitutes the reason for the extremely low dissociation rates associated with multivalent interactions. Additionally, the concentration of the monovalently bound species of a multivalent complex is dependent on the concentration of competing (monovalent) functionalities, which are able to prevent rebinding of partially dissociated complexes. Low dissociation rates that can be increased by competition with (monovalent) functionalities are a hallmark of multivalent interactions, indicating that the dissociation of multivalent complexes proceeds via a stepwise dissociation scheme (Fig. 4).48 This means that with the use of multivalent interactions, complexes can be made that combine an (extremely) high affinity with the possibility of kinetic control and reversibility.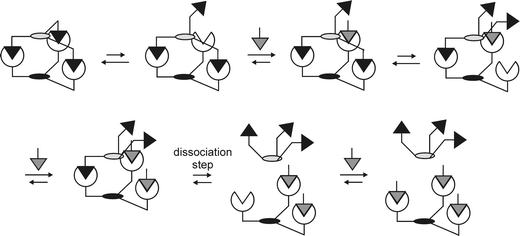 | ||
| Fig. 4 Stepwise dissociation of a multivalent complex by competition with a monovalent guest functionality. | ||
3 Supramolecular multivalent systems in solution
Several supramolecular multivalent motifs have been used to study the concept of multivalency systematically. These systems will be reviewed in this section, together with some examples of supramolecular systems that are of particular interest as they highlight one or more of the characteristic features of multivalent interactions. The different multivalent systems studied in solution have been categorized by interaction motif. A special section (Section 4) has been devoted to multivalent systems employing supramolecular interactions at surfaces to emphasize the differences between multivalent interactions in solution and at surfaces and to highlight current trends into nanofabrication.3.1 The vancomycin-D-alanine-D-alanine motif
A particularly well-studied example of multivalency is the interaction between multivalent vancomycin58 and multivalent D-alanine-D-alanine (DADA) or D-alanine-lactate (DALac), reported by Rao and Whitesides in a series of papers.19,48,59–61 Vancomycin is able to form five hydrogen bonds with DADA and four hydrogen bonds with DALac, which has an oxygen atom at a point where DADA has an amino group. The loss of this single hydrogen bonding possibility greatly decreases the affinity of vancomycin to DALac relative to that for DADA. However, by means of multivalency, this loss in affinity can be overcome. Fig. 5 depicts the different multivalent vancomycin hosts and multivalent peptide guests studied. The thermodynamic parameters obtained for these systems are summarized in Table 1.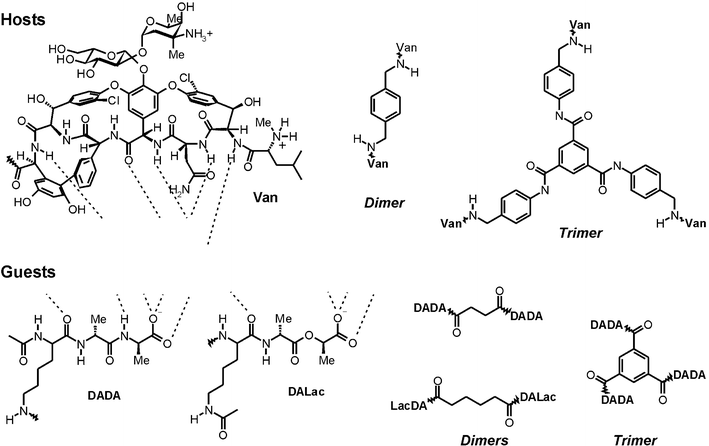 | ||
| Fig. 5 Multivalent host (vancomycin) and guest (DADA, and DALac) entities used by Rao and Whitesides.19,48,59–61 Hydrogen bonding patterns involved in the binding of the guests by vancomycin are illustrated by the dotted lines. | ||
| Host | Guest | K/M−1 | ΔG°/kcal mol−1 | ΔH°/kcal mol−1 | TΔS°/kcal mol−1 | Ref. |
|---|---|---|---|---|---|---|
| a All thermodynamic parameters were determined by isothermal calorimetry experiments, except the association constants labeled with an asterisk (*), which were determined using affinity capillary electrophoresis. b Values determined for the interaction of vancomycin with Nα,ε-diacetyl-L-Lys-D-Ala-D-Lac. c Values determined for the interaction of vancomycin with Nα,ε-diacetyl-L-Lys-D-Ala-D-Ala. d Values determined for the interaction of vancomycin with L-Lys-D-Ala-D-Ala with (part of) the linker group attached. | ||||||
| Mono | Mono-DALac | 5.6 × 102b | −3.8 | −3.7 | 0.1 | 61 |
| Mono | Mono-DADA | 6.3 × 105c | −7.9 | −12.0 | −4.1 | 48, 19 |
| 9.1 × 105d | −8.1 | −12.4 | −4.3 | 48, 19 | ||
| 2.1 × 105d* | −7.3 | — | — | 60 | ||
| Dimer | DALac-dimer | 2.3 × 104 | −6.0 | −6.5 | −0.5 | 61 |
| Dimer | DADA-dimer | 9.1 × 108* | −11.9 | — | — | 60 |
| Trimer | DADA-trimer | 2.5 × 1016 | −22 | −40 | −18 | 48, 19 |
The interaction of the vancomycin dimer with both dimeric DALac and DADA gave higher binding constants than the corresponding monovalent interactions; dimeric DALac is bound a factor of 40 more strongly,61 dimeric DADA a factor of 1440.60 These values correspond to effective molarities of 36 and 10 mM, respectively. This difference in effective molarity may be due to the different connectivity of the two dimeric guests. Whereas the DALac dimer is connected via the α-amino group of the Lysine, the DADA dimer is connected via the ε-amino group. The latter gives rise to a relatively more flexible structure, in spite of the use of the shorter succinimidyl tether for this dimer. Calorimetric studies with the divalent vancomycin–DAlac interaction gave an enthalpy of binding, −6.5 kcal mol−1, that was only slightly less than twice that found for the corresponding monovalent interaction, −3.7 kcal mol−1, indicating that the two binding sites can be considered independent.
The vancomycin trimer binds the DADA trimer with K = 2.5 × 1016 M−1, a factor of 40 billion more strongly than the corresponding monovalent interaction.48,19 The association constant for the formation of the trivalent complex was determined using competition experiments monitored with HPLC and is one of the largest quantified association constants in literature. Calorimetry was used to determine the enthalpy of binding for this trivalent system. The binding constant found for the trivalent interaction corresponds to an EM of 74 mM.62 The binding enthalpy, −40 kcal mol−1, was within experimental error three times that of the monovalent interaction, −12.0 kcal mol−1. Strongly negative entropy values partially compensated the gain in free energy of binding obtained by this enhanced enthalpy of binding.
Extremely slow dissociation was found for the trivalent vancomycin–DADA system, which showed no sign of decomplexation in HPLC for time spans over 45 min. In fact, a simple calculation shows that the half-life of the trivalent complex is over 200 days.63 With the use of competing monovalent DADA the dissociation could be sped up dramatically. In the presence of 86 mM monovalent DADA, 40% of the trivalent complex was dissociated with equilibration reached in less than 45 min. In principle, more complete and faster dissociation could have been achieved by using concentrations of competing monovalent DADA that are substantially higher than the effective molarity.
3.2 The zinc porphyrin-pyridyl motif
An interaction that has been comprehensively used in supramolecular multivalent systems is the coordination of pyridyl bases to zinc porphyrins. Several examples of multivalent systems employing this interaction are depicted in Fig. 6.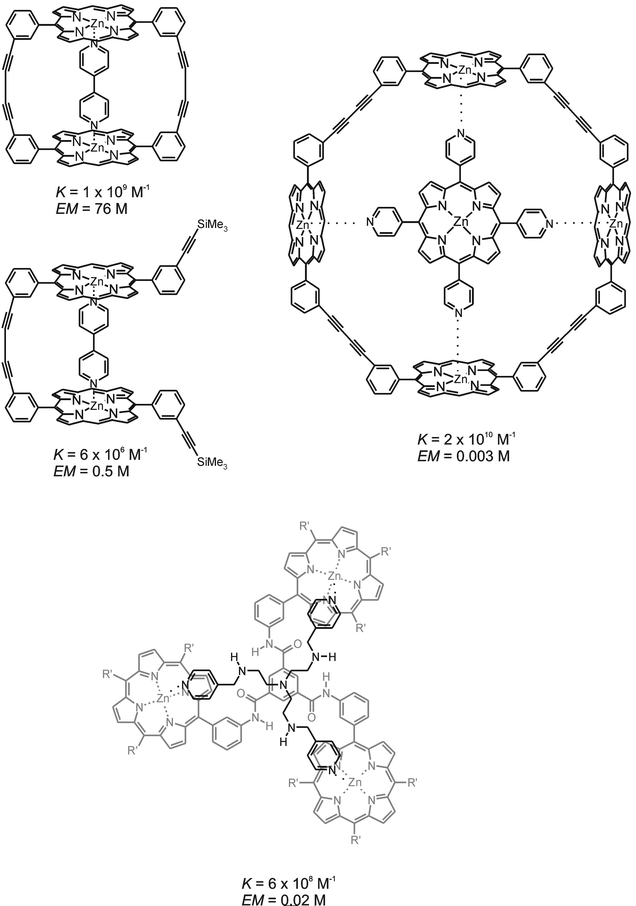 | ||
| Fig. 6 Examples of multivalent systems based on the coordination of multivalent pyridyl bases to multivalent Zn porphyrins; complexes with corresponding association constants and effective molarities (EM) obtained for the interaction of bipyridine with a cyclic (top left)47 and linear bis(Zn porphyrin) (center left)47, a tetrapyridyl porphyrin with cyclic tetra(Zn porphyrin) (top right)47, and a trivalent TREN-appended pyridine base with a tris(Zn porphyrin) (bottom).49 | ||
Anderson and Sanders' study on the interaction of a series of rigid cyclic and linear porphyrin dimers, trimers and tetramers with a series of rigid and flexible multivalent pyridyl bases has shown that proper design can give way to very efficient multivalent binding.47 The association between a cyclic zinc porphyrin dimer and 3,3′-bipyridine (see Fig. 6, top left) gave a binding enhancement of 3 × 105 compared to the corresponding monovalent interaction, implying an imposing effective molarity of 76 M. High effective molarities of this order were also obtained for a zinc porphyrin trimer and rigid bi- and tripyridyl guests. These high effective molarities can be attributed to the high complementarities between the rigid hosts and guests resulting in a nearly perfect fit. This demonstrates that, when designed properly, rigidity in multivalent systems may give access to high effective concentrations and therewith high association constants. For comparison, the interaction between a corresponding linear zinc-porphyrin dimer, also a highly rigid structure with only some rotational freedom around the central butadiyne bond, and 3,3′-bipyridine (Fig. 6, center left) gave an effective molarity of 0.5 M. Furthermore, the interaction between the cyclic zinc porphyrin and more flexible bipyridyls, in which the two pyridyl units were linked by an ethyl or propyl spacer, gave substantially lower effective molarities of 52 and 2 mM, respectively. However, such high degrees of rigidity employed in both host and guest require designs that have nano- or even picometer accuracy. This is clearly demonstrated by the interaction between a cyclic zinc porphyrin tetramer and a tetra-pyridyl porphyrin (Fig. 6, top right), for which an association constant of 2 × 1010 M−1 and an effective molarity of only 3 mM were determined.
Another interesting supramolecular multivalent interaction in which the pyridyl-zinc porphyrin coordination has been employed is that between a zinc porphyrin trimer and trivalent pyridyl bases reported by Hunter and Scrimin (Fig. 6, bottom).49 The pyridyl trimers consist of three pyridyl moieties linked via a tris(2-aminoethyl)amine unit (TREN), which offers a means for tuning the conformational flexibility of the pyridyl trimers by ligation of the four amines of TREN around a metal ion. Effective molarities obtained for the different multivalent interactions ranged from 3 to 24 mM. For the trivalent complex depicted in Fig. 6, coordination of zinc by the TREN moiety led to a factor of 6 decrease in effective molarity, implying that coordination of the pyridyl bases to the zinc porphyrins was hampered by the shortened and rigidified TREN tether upon metal complexation. This example clearly demonstrates the relation between effective concentration and the interaction strength of a multivalent complex and how this can be applied to achieve complexes with externally controllable stability constants. Also here careful design is required to result in effects. For a pyridyl trimer with a longer, more flexible, spacer between the pyridyl bases and the TREN moiety, the coordination of a Zn ion had virtually no effect.
3.3 Pseudorotaxanes
The groups of Stoddart and Gibson have been using pseudorotaxanes from crown ethers and charged ammonium-based cationic guests as interaction motifs for multivalent systems. Fig. 7 depicts some of the complexes studied.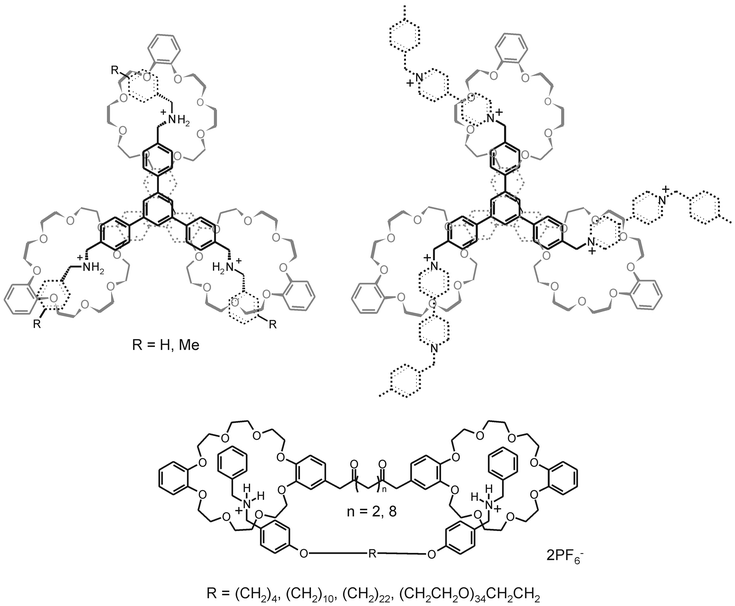 | ||
| Fig. 7 Examples of multivalent pseudorotaxane systems; trivalent complexes of a tris(crown ether) with a tris(dibenzylammonium) trication (top left)64,65 and a tris(bipyridiniumammonium) trication (top right).66 Divalent interactions of bis(dibenzylammonium) dications and bis(crown ethers), both with varying chain length (bottom).71 | ||
For the trivalent interaction between the triphenylene-based tris(crown ether) and the tris(dibenzylammonium) trication (Fig. 7, top left), an association constant of 106 M−1 in acetonitrile was determined. 64–66 This amounts to a binding enhancement of 104 compared to the corresponding monovalent interaction between a single cation and a single crown ether,64 which corresponds to an EM of 47 mM. The trivalent complex could be dissociated by deprotonation of the ammonium cations by addition of suitable bases or by addition of DMSO, which competes with the crown ether oxygens in hydrogen bonding of the ammonium cations. In the former case, complex dissociation was fully reversible, and complete re-association was readily achieved by the addition of acids. Monitoring of the complex dissociation upon addition of DMSO by NMR revealed a stepwise dissociation process in which the trivalent complex progressively dissociated through the divalently and monovalently bound states.64,65 The different states involved in the dissociation of this complex were in slow exchange on the NMR timescale and could be monitored simultaneously at increasing DMSO concentrations.
Indications for a stepwise association scheme for multivalent interactions were observed with the complex formation between the tris(crown ether) and a tris(bipyridinium) trication (Fig. 7, top right).66 The 1H NMR, recorded at 253 K, of a sample containing equimolar amounts of the two trivalent components initially revealed the presence of two species, the doubly and triply threaded complexes, which, over a time span of 235 h, converted nearly completely to the triply threaded complex.
Specifically for the study of multivalency in artificial systems, Stoddart et al. have synthesized a series of hexa- and heptavalent molecules in which crown ethers and dialkylammonium centers were appended to a benzene core67 and a β-cyclodextrin.68 It was shown that all these multivalent molecules bound complementary monovalent functionalities in a negatively cooperative fashion due to steric hindrance and electrostatic repulsion. For complementary divalent functionalities enhanced affinities of one to two orders of magnitude compared to the corresponding monovalent interactions were observed. However, the redundancy of these systems makes the interpretation in terms of multivalency intricate and therefore these multivalent interactions are less suited for a quantitative analysis.
The group of Gibson has carefully studied the divalent interaction between bis(crown ether)s and bis(dialkylammonium) cations (Fig. 7, bottom).38 Although their main interest lies in the development of pseudorotaxane polymers by means of intermolecular interactions between the two complementary counterparts, considerable attention has been devoted to (the competing) intramolecular, multivalent interactions. NMR spectra of equimolar amounts of two complementary divalent entities showed the presence of both inter- and intramolecularly bound species, the ratio of which was concentration-dependent. Association constants for both inter- and intramolecular interactions were determined. The effective molarities found for the intramolecular interactions varied from 1 to 0.05 mM and decreased with increasing tether length between the two interacting functionalities. This trend is in agreement with a theoretically predicted decreasing effective concentration with increasing tether length (see above). 1H NMR experiments with equimolar amounts of both divalent entities showed a transition between inter- and intramolecular complexes in the concentration ranges corresponding to the effective molarities. The relatively low effective molarities, which are amongst the lowest reported, suggest that the intramolecular binding is less efficient than intrinsic binding (thus negatively cooperative). This was corroborated by the enthalpies of binding for the intramolecular interaction, which decreased linearly with increasing tether length. The authors suggested that this is due to enthalpic penalties paid for the formation of large ring structures and by electrostatic repulsion. The latter, however, seems unlikely as Scatchard plots for titrations of monovalent to ditopic entities showed that the functionalities of all divalent entities behave as independent binding sites.69
3.4 Zippers, helices and ladders
Zippers, helices and ladders comprise a broad family of multivalent displays that consist of (self-)complementary, linear oligomers of functionalities. Several examples are depicted in Fig. 8. The functionalities are typically moieties with a self-complementary hydrogen-bonding motif, as in the oligo-2-aminopyridines,70 aromatic amide oligomers71 or oligotriazines,72 or ligands that are able to coordinate around a metal ion, as in the oligobipyridines73 and oligoporphyrins.74 With respect to multivalency, this class of molecules is of interest as many of these systems have been systematically elongated to enhance complex stability. Typically, strong enhancements in binding per added interaction are observed, characteristic for multivalent interactions. For several systems the ΔG° increased linearly with the number of shared interactions. Recently, Ercolani has shown that such systematic trends between ΔG° and the number of shared interactions are indicative of multivalent interactions comprised of multiple, independent binding interactions and that the vast majority of these systems can be analyzed in terms of pure multivalency, i.e. multiple consecutive independent intramolecular interactions.52 An exception are the aromatic amide oligomer zippers by Bisson et al. (Fig. 8, top) for which a positive curvature in a plot of ΔG° versus the valency of the complex was found.71 Together with the DNA double helix,56 this might be one of the few known positively cooperative multivalent interactions.![Examples of multivalent zippers, helices and ladders; duplexes of aromatic amide oligomers,71 oligo-2-aminopyridines,70 Zn-porphyrin oligomers connected by 1,4-diazabicyclo[2,2,2]octane,74 and bipyridine oligomers coordinated around metal ions.73](/image/article/2004/OB/b413971b/b413971b-f8.gif) | ||
| Fig. 8 Examples of multivalent zippers, helices and ladders; duplexes of aromatic amide oligomers,71 oligo-2-aminopyridines,70 Zn-porphyrin oligomers connected by 1,4-diazabicyclo[2,2,2]octane,74 and bipyridine oligomers coordinated around metal ions.73 | ||
3.5 Cyclodextrin host–guest complexes
Cyclodextrin dimers and multimers are probably one of the oldest and most thoroughly studied types of multivalent systems. The high affinity and selectivity for hydrophobic substrates displayed by cyclodextrin multimers compared to their native (monovalent) analogues exhibits another attractive characteristic of multivalent binding. The enhanced affinity of cyclodextrin multimers has often been ascribed to the chelate effect,75 a term that is often used in a qualitative sense. Recently, we have shown that the enhanced affinity of cyclodextrin dimers for multivalent guests can be well explained in a more quantitative sense, i.e. in terms of multivalency.37 The interaction between a cyclodextrin host dimer and a bis(adamantane) guest (Fig. 9) gave an association constant of 1 × 107 M−1, with a binding enhancement of 200 over the corresponding monovalent interaction. Calorimetry showed that the enthalpy of binding for the divalent interaction was twice that of the corresponding monovalent interaction, indicating an independent binding mode. The EM of 3 mM was in good agreement with the range of theoretically calculated effective concentrations.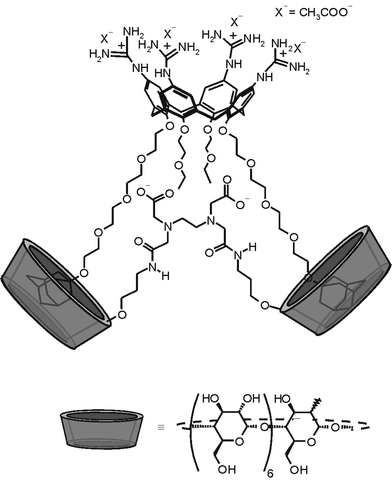 | ||
| Fig. 9 Example of a multivalent interaction between a β-cyclodextrin dimer and a bis(adamantyl) guest.37 | ||
It is very likely that many of the interactions of cyclodextrin multimers with hydrophobic guests can be similarly analyzed in terms of multivalency. Table 2 lists the EM values for a number of different combinations of cyclodextrin multimers and hydrophobic guests. It is evident that the majority of the EM values falls within a narrow range of 10 to 200 mM.
| Entry | Guest | Host | EM (M) | Ref. |
|---|---|---|---|---|
| a EM values were calculated using eqn. (2) from binding affinities determined for the dimer (K2) and the corresponding monovalent interaction (Ki). Only studies in which both the divalent and monovalent Ks were determined with a single technique have been used for the calculation of EM. The attachment point of the tether to the cyclodextrin cavity is given in parentheses. | ||||
| 1 |

|

|
0.2 | 75 |
| 2 |
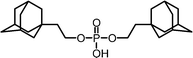
|

|
0.01 | 105 |
| 3 |

|
0.02 | 75 | |
| 4 |

|
0.002 | 75 | |
| 5 |

|
0.01 | 75 | |
| 6 |

|
1.0 | 106 | |
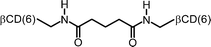
| 7 |

|
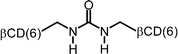
|
0.17 | 107 |
| 8 |

|
0.12 | 107 | |
| 9 |
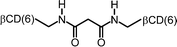
|
0.04 | 107 | |
| 10 |

|
0.06 | 107 | |
| 11 |

|
|
0.05 | 107 |
| 12 |

|
0.21 | 108 | |
| 13 |

|
0.10 | 108 | |
| 14 |
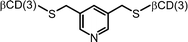
|
0.02 | 109 | |
| 15 |
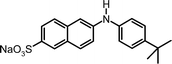
|
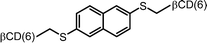
|
1.25 | 110 |
| 16 |

|

|
0.64 | 111 |
Secondary interactions between tether and guest molecule may lead to higher binding affinities and consequently give rise to relatively high EM values. A clear example is entry 6 of Table 2, in which ligation of the phosphate moiety of the guest molecule to the metal ion complexed at the tether resulted in an EM of 1.0 M. Similar effects have been observed for other metal-chelated cyclodextrin dimers and charged guest molecules,76 and for intramolecular chelation of the tether to metal-containing guest molecules.77 In most cases, however, the effective molarities are probable effective concentrations, indicating that guest molecules are generally bound in a non-cooperative, statistical fashion. An illustrative example is given by the work published by Petter and co-workers who studied the binding of toluidino-2-naphthalene sulfonate (TNS) by a range of β-cyclodextrin dimers tethered by spacers with variable length (Fig. 10).78 The authors determined a linear relation between the free energy of complexation (ΔG°) and the number of carbon atoms in the β-cyclodextrin dimer tether. However, no fundamental explanation for this ratio was given. Fig. 10 shows a plot of the complexation constant (K), taken from the publication of Petter et al., versus the inverse cubic tether length (based on a maximum chain extension, assuming an average bond length of 0.154 nm and an average bond angle of 109.5 °). The linear relation between binding affinity and inverse cubic tether length (see above) implies that this difference can be explained well in terms of effective concentration.
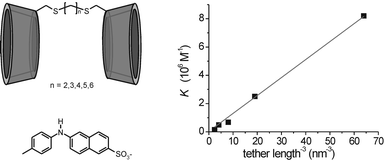 | ||
| Fig. 10 Plot of binding affinity versus inverse cubic tether length for complexation of TNS by β-cyclodextrin dimers with variable tether length. Host and guest structures are shown on the left. | ||
Trends of binding affinity for a guest molecule versus spacer length of a cyclodextrin dimer are a general phenomenon. For several cyclodextrin dimer systems linear relationships between binding affinity and inverse cubic tether length, similar to the plot in Fig. 10, can be determined.79,80
Also for cyclodextrin dimers, examples exist which show that rigidity in both host and guest can lead to very effective and tight binding. Illustrative are doubly linked cyclodextrin dimers synthesized by Breslow et al., which display extremely high affinities compared to their mono-linked analogues.81 However, again we emphasize that exact compatibility is required in such systems: mismatches for rigid systems may lead to extremely low effective concentrations and inefficient multivalent binding. We have taken advantage of this phenomenon in the development of β-cyclodextrin dimers with photoswitchable binding properties.82 β-Cyclodextrin dimers were tethered via a photoswitchable diarylethene that could be reversibly switched between a relative flexible and a more rigid state. The more rigid state of the flexible β-cyclodextrin dimer bound a rigid multivalent porphyrin guest a factor of 35 less efficiently than the open form of this dimer. This difference in binding affinity can be attributed mainly to a difference in effective concentration and allowed for the externally controlled, reversible release and uptake of the guest by the β-cyclodextrin dimer.
4 Supramolecular multivalent systems at surfaces
For mechanistic studies of multivalent interactions, monolayers on surfaces offer a number of advantages over the solution model systems discussed above. Metal substrates, such as gold, allow for example surface plasmon resonance spectroscopy, enabling the characterization of the kinetic behavior of multivalent interactions. Another point of interest is that the structure, density, and environment of the immobilized functionalities at monolayers are easily varied, enabling systematic studies concerning multivalency and effective concentration and the influence of competing functionalities on the dissociation rates of multivalent complexes. In this respect there are a few important examples from the field of biochemistry. Cremer and co-workers found that the affinity of labeled antibodies for hybrid layers with hapten functionalities decreased with decreasing hapten concentration, which illustrates the role of effective concentration at surfaces.83 Kahne et al. demonstrated that the specificity of a multivalent interaction can be dependent on the functionality density at surfaces.84 This might well be an operation mode for cells to bind specific proteins.There are only a few systematic studies on supramolecular multivalent interactions at surfaces. These are discussed hereafter.
4.1 Cyclodextrin host–guest complexes at interfaces
Ravoo and co-workers have studied the multivalent interaction between cyclodextrin vesicles and poly(isobutylmaleic acid) polymers modified with adamantyl or tert-butylphenyl groups.85 Binding studies showed that the interaction between vesicles and tert-butylphenyl-modified polymers with a 10% substitution degree was three orders of magnitude stronger than the interaction of the vesicles with tert-butylaniline. Interestingly, analogous polymers with a 42% substitution degree gave a less strong binding enhancement, only two orders of magnitude. Furthermore, adamantyl-modified polymers showed almost no increase in binding affinity compared to the corresponding monovalent interaction. The reduced affinities found for these more hydrophobic polymers were attributed to intramolecular association of the hydrophobic end groups, i.e. coiling of the polymers, resulting in a diminished probability and strength of interaction. Dynamic light scattering studies did not show aggregation of vesicles, indicating intramolecular multivalency.Our group has intensively studied multivalent interactions between β-cyclodextrin self-assembled monolayers (CD SAMs) and molecules suitably modified with multiple hydrophobic guest moieties. A study on the complexation of three different generations of adamantyl-terminated dendrimers (generation-2, -3, and -4 poly(propylene imine) dendrimers, having 8, 16, and 32 adamantyl end groups respectively) at CD SAMs showed that all dendrimers gave thermodynamically stable assemblies.86 None of the three assemblies at the CD SAMs showed appreciable desorption in pure water. The kinetics for the largest dendrimer, which has four interactions with the β-cyclodextrin SAM, could be tuned from extremely slow (in pure water) to relatively fast (in the presence of high concentrations of β-cyclodextrin in solution).
In an attempt to relate multivalent binding in solution to multivalent binding at surfaces we studied the interaction of the divalent bis(adamantyl) guest depicted in Fig. 9 with β-cyclodextrin SAMs. It was found that the divalent interaction at the SAM resulted in a binding constant (1 × 1010 M−1) that was three orders of magnitude higher than for the corresponding divalent interaction in solution with the EDTA dimer (Fig. 9; 1 × 107 M−1).37 This large difference in binding affinity was attributed to a difference in effective concentration.87 The probing volume for the uncomplexed guest at the surface is less than half that in solution and contains multiple cyclodextrin cavities, whereas there is only a single cavity available in solution in a larger probing volume (Fig. 11). Modeling of the effective concentration for the intramolecular interaction at the surface gave a Ceff of 0.2 M, substantially higher than the 3 mM determined for the divalent interaction in solution. Using this Ceff of 0.2 M at the β-CD SAMs, the divalent interaction could be completely interpreted in terms of two consecutive, independent binding events.
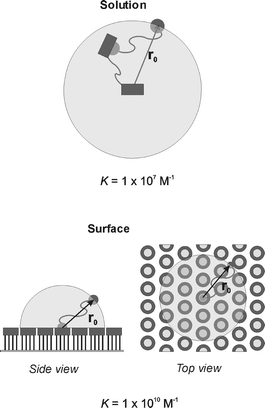 | ||
| Fig. 11 Schematic representation of the concept of effective concentration for the divalent interaction of a bis(adamantyl) guest to a CD dimer in solution (top) and to a CD SAM (bottom). | ||
Similarly, binding constants for the interactions of β-CD SAMs with the adamantyl-terminated dendrimers mentioned above and analogous ferrocene-terminated dendrimers88 was analyzed in terms of consecutive, independent interactions and a single, surface coverage-dependent effective concentration parameter.36 Based on these results we have developed a general model for describing the thermodynamics of multivalent interactions at surfaces.36 Theoretical simulations performed with this model gave insight in how the dissociation kinetics of multivalent interactions is influenced by the number of interactions involved and the presence of competing monovalent species in solution.
4.2 The vancomycin–D-alanine–D-alanine motif at SAMs
Whitesides and Rao have carefully studied the interaction of a vancomycin dimer (see Fig. 5) with SAMs presenting DALac or DADA functionalities.61,89 Also here, a relatively high effective concentration at the surface can explain the binding enhancements observed at the surface compared to solution. The dimer bound to a DALac SAM (χG = 0.50) with an association constant of 3 × 105 M−1,61 an order of magnitude higher than the corresponding divalent interaction in solution (2.4 × 104 M−1, see Table 1). The calculated effective molarity of 30 mM may appear rather low for an effective concentration experienced at a SAM, but this is probably a consequence of the rigidity of the vancomycin dimer.90 In a similar study with the vancomycin dimer at a DADA SAM, a lower guest concentration at the surface was used (χG = 0.05) and a binding constant of 2 × 109 M−1 was measured.89 In this case the association constant was comparable to the corresponding divalent interaction in solution (9 × 108 M−1; Table 1). For both interactions the dissociation of the complex could be accelerated by the addition of monovalent DALac or DADA.4.3 Multivalency in nanofabrication
The unique thermodynamic and kinetic characteristics of multivalent interactions make them ideal for application in supramolecular nanofabrication. So far, multivalent interactions have only scarcely been employed in nanofabrication, but the number of examples appearing in the literature is increasing rapidly.Multivalent interactions in solution have thus far mainly been used to achieve highly stable complexes (see section 3). Additionally, multivalency in solution has been extensively used as a powerful templating tool.91–93 A recent publication by Stoddart et al. suggests that multivalency in solution can also be employed in molecular machinery.94
The main application for multivalent supramolecular interactions at surfaces thus far has been the reversible immobilization of (bio)molecules at surfaces. A variety of interaction motifs has been used to achieve immobilization. Tampé and co-workers have employed metal chelation to histidine tags for the directional and specific immobilization of proteins at SAMs and lipid bilayers.95 Rotello et al. have immobilized multivalent diamidopyridine polymers at self-assembled thymine monolayers.96 Additionally, this same group has applied multivalent polymers to stabilize vesicles, which could be disrupted in the presence of monovalent functionalities.97 Several groups have taken advantage of the diverse possibilities to employ β-cyclodextrin monolayers for the sensing and reversible immobilization of (bio)molecules (see Fig. 12). Our group has employed mixed monolayers of a β-cyclodextrin mono-functionalized with a thiol chain and mercaptoundecanol for the detection of steroids at gold surfaces (Fig. 12A).98 Cao and co-workers immobilized adamantyl-modified cytochrome C at silver electrode surfaces coated with per-6-thiol-β-cyclodextrin (Fig. 12B).99 Matsui et al. employed azobenzene as a linking unit for the hydrophobic immobilization of peptide nanotubes at gold surfaces.100 UV light-induced trans–cis isomerization of azobenzenes led to the dissociation of the nanotubes (Fig. 12C). Another example in which the dissociation of multivalent complexes can be initiated by an external stimulus other than competitor concentration are the complexes of ferrocene-dendrimer and β-cyclodextrin SAMs (Fig. 12D).88,101 Oxidation of the ferrocene moieties weakens the interaction with the β-cyclodextrin SAMs and leads to the dissociation of the dendrimers.
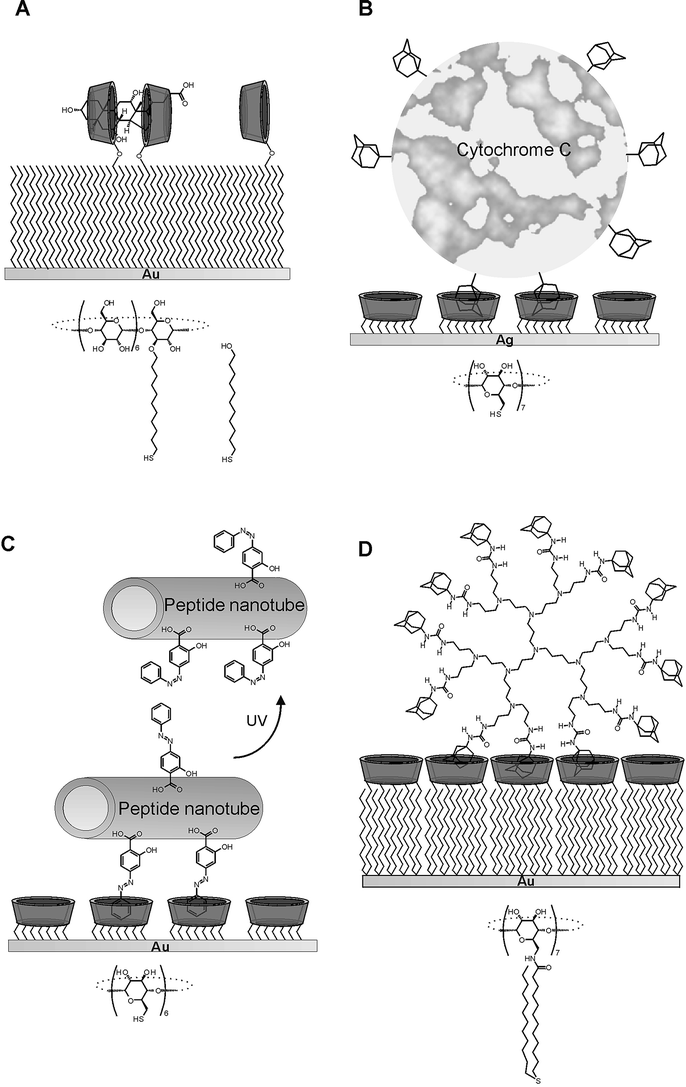 | ||
| Fig. 12 Multivalent interactions at cyclodextrin SAMs: divalent binding of steroids (A),98 immobilization of cytochrome C at silver electrodes (B),99 the positioning of peptide nanotubes (C),100 and multivalent binding of dendrimers (D).88,101 Actual adsorbate structures are shown under the schematic representations. | ||
Recently, we have shown that supramolecular multivalent interactions at surfaces can be combined with microcontact printing and dip-pen nanolithography to create supramolecular patterns at surfaces.101 We have created patterns of a variety of molecules modified with different hydrophobic groups at β-cyclodextrin surfaces on silicon oxide and gold.101,102 Some examples are shown in Fig. 13. The top three images in Fig. 13 show lateral force microscopy images of supramolecular patterns of a bis(adamantyl)-functionalized calix[4]arene (see Fig. 9) created by microcontact printing. In contrast to similar patterns created at reference layers, these patterns were stable to aqueous rinsing procedures (Fig. 13, top center). Substantial removal of the patterns was only achieved by exposure to concentrated, competing β-cyclodextrin solutions (Fig. 13, top right). Sub-100 nm supramolecular patterns at β-cyclodextrin SAMs were created using dip-pen nanolithography (Fig. 13, bottom left). In contrast to SAMs on gold, cyclodextrin monolayers on glass allow the use of fluorescence microscopy techniques for the detection of the specific and targeted adsorption of fluorescent guests.101–103 Analogously, microcontact printed lines of adamantyl-terminated PPI dendrimers at β-cyclodextrin SAMs were used for the selective encapsulation of anionic dyes (Fig. 13, right).101
![Supramolecular patterns at β-cyclodextrin surfaces based on multivalent interactions.101 Top row: microcontact printed lines of a bis(adamantyl)-functionalized calix[4]arene on β-cyclodextrin monolayers on gold, directly after printing (left), after rinsing with Millipore water (center), and after rinsing with 10 mM aqueous CD (right). Bottom left image: a sub-100 nm grid of a bis(adamantyl)-functionalized calix[4]arene on β-cyclodextrin monolayers on gold created by dip-pen nanolithography (line thickness 60 ± 20 nm). Bottom right images: microcontact printed lined of a fifth-generation adamantyl-functionalized PPI dendrimer (64 adamantyl moieties) at β-cyclodextrin monolayers on silicium oxide filled with Bengal rose (bottom center) and fluorescein (bottom right).](/image/article/2004/OB/b413971b/b413971b-f13.gif) | ||
| Fig. 13 Supramolecular patterns at β-cyclodextrin surfaces based on multivalent interactions.101 Top row: microcontact printed lines of a bis(adamantyl)-functionalized calix[4]arene on β-cyclodextrin monolayers on gold, directly after printing (left), after rinsing with Millipore water (center), and after rinsing with 10 mM aqueous CD (right). Bottom left image: a sub-100 nm grid of a bis(adamantyl)-functionalized calix[4]arene on β-cyclodextrin monolayers on gold created by dip-pen nanolithography (line thickness 60 ± 20 nm). Bottom right images: microcontact printed lined of a fifth-generation adamantyl-functionalized PPI dendrimer (64 adamantyl moieties) at β-cyclodextrin monolayers on silicium oxide filled with Bengal rose (bottom center) and fluorescein (bottom right). | ||
Yoon et al. have elegantly utilized the kinetic aspects of multivalent interactions for the organization of thymine-functionalized microcrystals on adenine monolayers on glass.104 Whereas the microcrystals gave random packing at the monolayer at 25 °C, highly organized close packing was achieved at 55 ° C.
5 Conclusions and perspectives
Multivalency is a powerful and versatile self-assembly pathway that confers unique thermodynamic and kinetic behavior onto supramolecular complexes. Assemblies can be made that are both thermodynamically and kinetically stable in isolation, but may show self-sorting and reorganization in the presence of other complementary (e.g. monovalent) functionalities. The diversity of the examples of supramolecular multivalent systems discussed in this perspective shows that the concept of multivalency is a general phenomenon, and that any supramolecular interaction can be employed in multivalent displays to attain the attractive aspects characteristic of multivalent interactions.Systematic studies have led to a fundamental understanding of multivalent interactions and have led to a growing awareness of the full potential of the multivalency concept as a self-assembly pathway. The development of various models for describing multivalent interactions have started to enable the controlled use of multivalency and the design of complexes with tailored thermodynamic and kinetic parameters. Within the limits of a chosen supramolecular assembly motif, it is possible to achieve virtually any desired complex stability with any given dissociation rate, simply by proper selection of the strength and number of interactions, the connectivity of the multiple functionalities, and eventually the use of (a specific concentration of) competing functionalities.
Although the many examples of multivalent supramolecular interactions in this perspective clearly demonstrate their potential usefulness in nanofabrication schemes, the field of supramolecular chemistry has just started to explore the possibilities of multivalency. Thus far application has mainly concentrated on the reversible immobilization of (bio)molecules at surfaces. However, multivalency has so much more to offer and this concept can be taken advantage of to a much larger extent. Supramolecular multivalency enables the assembly of kinetically and thermodynamically stable nanostructures at surfaces, and could be used to further sophisticate structures generated by layer-by-layer deposition techniques, or for the creation of organized 2- or 3-dimensional structures at surfaces by employing entities in which multiple multivalent interaction motifs are combined, and so on. With the use of supramolecular lithography all of this could in principle be achieved at a localized, molecular level. We foresee that the concept of multivalency will be one of the major themes in the field of supramolecular chemistry in the coming years and that it will have a large impact on the way supramolecular chemists approach nanotechnology.
Acknowledgements
We are grateful to the Council for Chemical Sciences of the Netherlands Organization for Scientific Research (CW-NWO) for financial support (A.M.: CW-programmasubsidie 700.98.305).References
- M. Mammen, S.-K. Choi and G. M. Whitesides, Angew. Chem., Int. Ed., 1998, 37, 2754–2794 CrossRef.
- A. Varki, Glycobiology, 1993, 3, 97–130 CrossRef CAS.
- M. N. Matrosovich, L. V. Mochalova, V. P. Marinina, N. E. Byramova and N. V. Bovin, FEBS Lett., 1990, 272, 209–212 CrossRef CAS.
- (a) A. Spaltenstein and G. M. Whitesides, J. Am. Chem. Soc., 1991, 113, 686–687 CrossRef CAS; (b) W. J. Lees, A. Spaltenstein, J. E. Kingery-Wood and G. M. Whitesides, J. Med. Chem., 1994, 37, 3419–3433 CrossRef CAS; (c) G. B. Sigal, M. Mammen, G. Dahmann and G. M. Whitesides, J. Am. Chem. Soc., 1996, 118, 3789–3800 CrossRef; (d) S.-K. Choi, M. Mammen and G. M. Whitesides, J. Am. Chem. Soc., 1997, 119, 4103–4111 CrossRef CAS.
- (a) G. D. Glick, P. L. Toogood, D. C. Wiley, J. J. Skehel and J. R. Knowles, J. Biol. Chem., 1991, 266, 23660–23669 CAS; (b) G. D. Glick and J. R. Knowles, J. Am. Chem. Soc., 1991, 113, 4701–4703 CrossRef CAS.
- S. Sabesan, J. Q. Duus, S. Neira, P. Domaille, S. Kelm, J. C. Paulson and K. Bock, J. Am. Chem. Soc., 1992, 114, 8363–8375 CrossRef CAS.
- R. T. Lee, P. Lin and Y. C. Lee, Biochemistry, 1984, 23, 4255–4261 CrossRef CAS.
- S. A. DeFrees, W. Kosch, W. Way, J. C. Paulson, S. Sabesan, R. L. Halcomb, D.-H. Huang, Y. Ichikawa and C.-H. Wong, J. Am. Chem. Soc., 1995, 117, 66–79 CrossRef CAS.
- R. Roy, Curr. Opin. Struct. Biol., 1996, 6, 692–702 CrossRef CAS.
- C. R. MacKenzie, T. Hirama, S. Deng, D. R. Bundle, S. A. Narang and N. M. Young, J. Biol. Chem., 1996, 271, 1527–1533 CrossRef CAS.
- (a) J. E. Gestwicki, L. E. Strong and L. L. Kiessling, Chem. Biol., 2000, 7, 583–591 CrossRef CAS; (b) L. L. Kiessling, J. E. Gestwicki and L. E. Strong, Curr. Opin. Chem. Biol., 2000, 4, 696–703 CrossRef CAS; (c) C. R. Bertozzi and L. L. Kiessling, Science, 2001, 291, 2357–2364 CrossRef CAS.
- J. J. Lundquist and E. J. Toone, Chem. Rev., 2002, 102, 555–578 CrossRef CAS.
- I. Vrasidas, S. André, P. Valentini, C. Böck, M. Lensch, H. Kaltner, R. M. J. Liskamp, H.-J. Gabius and R. J. Pieters, Org. Biomol. Chem., 2003, 1, 803–810 RSC.
- S. A. Kalovidouris, O. Blixt, A. Nelson, S. Vidal, W. B. Turnbull, J. C. Paulson and J. F. Stoddart, J. Org. Chem., 2003, 68, 8485–8493 CrossRef CAS.
- (a) M. Kanai, K. H. Mortell and L. L. Kiessling, J. Am. Chem. Soc., 1997, 119, 9931–9932 CrossRef CAS; (b) C. W. Cairo, J. E. Gestwicki, M. Kanai and L. L. Kiessling, J. Am. Chem. Soc., 2002, 124, 1615–1619 CrossRef; (c) J. E. Gestwicki, C. W. Cairo, L. E. Strong, K. A. Oetjen and L. L. Kiessling, J. Am. Chem. Soc., 2002, 124, 14922–14933 CrossRef CAS.
- T. K. Dam, R. Roy, S. K. Das, S. Oscarson and C. F. Brewer, J. Biol. Chem., 2000, 275, 14223–14230 CrossRef CAS.
- S. Akai, Y. Kajihara, Y. Nagashima, M. Kamei, J. Arai, M. Bito and K. Sato, J. Carbohydr. Chem., 2001, 20, 121–143 CrossRef CAS.
- P. I. Kitov, J. M. Sadowska, G. Mulvey, G. D. Armstrong, H. Ling, N. S. Pannu, R. J. Read and D. R. Bundle, Nature, 2000, 403, 669–672 CrossRef CAS.
- J. Rao, J. Lahiri, L. Isaacs, R. M. Weis and G. M. Whitesides, Science, 1998, 280, 708–711 CrossRef CAS.
- (a) R. Roy, Top. Curr. Chem., 1997, 187, 242–274; (b) H. Herzner, T. Reipen, M. Schultz and H. Kunz, Chem. Rev., 2000, 100, 4495–4537 CrossRef CAS; (c) L. L. Kiessling, L. E. Strong and J. E. Gestwicki, Annu. Rep. Med. Chem., 2000, 35, 321–330 Search PubMed; (d) N. Röckendorf and T. K. Lindhorst, Top. Curr. Chem., 2001, 217, 210–238; (e) B. T. Houseman and M. Mrksich, Top. Curr. Chem., 2002, 218, 1–44 CAS; (f) J. Rojo, J. C. Morales and S. Pendalés, Top. Curr. Chem., 2002, 218, 46–92; (g) K. T. Lindhorst, Top. Curr. Chem., 2002, 218, 201–235 CAS.
- J. J. Lundquist and T. E. Toone, Chem. Rev., 2002, 102, 555–578 CrossRef CAS.
- The term “intramolecular” is used here to indicate the formation of an interaction between two species between which such an interaction already existed; “intermolecular” indicates the formation of an interaction between two unlinked species.
- D. Page and R. Roy, Bioconjugate Chem., 1997, 8, 714–723 CrossRef CAS.
- (a) E. K. Woller and M. J. Cloninger, Org. Lett., 2002, 4, 7–10 CrossRef CAS; (b) E. K. Woller, E. D. Walter, J. R. Morgan, D. J. Singel and M. J. Cloninger, J. Am. Chem. Soc., 2003, 125, 8820–8826 CrossRef CAS.
- T. K. Dam, R. Roy, K. D. Sanjoy, S. Oscarson and C. F. Brewer, J. Biol. Chem., 2000, 275, 14223–14230 CrossRef CAS.
- (a) J. J. Lundquist, S. D. Debenham and E. J. Toone, J. Org. Chem., 2000, 65, 8245–8250 CrossRef CAS; (b) J. B. Corbell, J. J. Lundquist and E. J. Toone, Tetrahedron: Asymmetry, 2000, 11, 95–111 CrossRef CAS.
- J. E. Gestwicki, L. E. Strong, C. W. Cairo, F. J. Boehm and L. L. Kiessling, Chem. Biol., 2002, 9, 163–169 CrossRef CAS.
- S. D. Burke, Q. Zhao, M. C. Schuster and L. L. Kiessling, J. Am. Chem. Soc., 2000, 122, 4518–4519 CrossRef CAS.
- H. Ling, A. Boodhoo, B. Hazes, M. D. Cummings, G. D. Armstrong, J. L. Brunton and R. J. Read, Biochemistry, 1998, 37, 1777–1788 CrossRef CAS.
- (a) E. Fan, Z. Zhang, W. E. Minke, Z. Hou, C. L. M. J. Verlinde and W. G. J. Hol, J. Am. Chem. Soc., 2000, 122, 2663–2664 CrossRef CAS; (b) E. A. Merrit, Z. Zhang, J. C. Pickens, M. Ahn, W. G. J. Hol and E. J. Fan, J. Am. Chem. Soc., 2002, 124, 8818–8824 CrossRef CAS; (c) Z. Zhang, E. A. Merrit, M. Ahn, C. Roach, Z. Hou, C. L. M. J. Verlinde, W. G. Hol and E. J. Fan, J. Am. Chem. Soc., 2002, 124, 12991–12998 CrossRef CAS.
- P. I. Kitov and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 16271–16284 CrossRef CAS.
- J. M. Gargano, T. Ngo, J. Y. Kim, D. W. K. Acheson and W. J. Lees, J. Am. Chem. Soc., 2001, 123, 12909–12910 CrossRef CAS.
- F. Eblinger and H.-J. Schneider, Angew. Chem., Int. Ed., 1998, 37, 826–829 CrossRef CAS.
- Kramer and Karpen have employed divalent guests tethered by a 20 kD PEG polymer for multivalent complexation of a protein, see: R. H. Kramer and J. W. Karpen, Nature, 1998, 395, 710–713 Search PubMed.
- (a) W. Kuhn, Kolloidn Zh., 1934, 68, 2–15 Search PubMed; (b) H. Jacobsen and W. H. Stockmayer, Chem. Phys., 1950, 18, 1600–1606.
- J. Huskens, A. Mulder, T. Auletta, C. A. Nijhuis, M. J. W. Ludden and D. N. Reinhoudt, J. Am. Chem. Soc., 2004, 126, 6784–6797 CrossRef CAS.
- A. Mulder, T. Auletta, A. Sartori, S. Del Ciotto, A. Casnati, R. Ungaro, J. Huskens and D. N. Reinhoudt, J. Am. Chem. Soc., 2004, 126, 6627–6636 CrossRef CAS.
- (a) H. W. Gibson, N. Yamaguchi and J. W. Jones, J. Am. Chem. Soc., 2003, 125, 3522–3533 CrossRef CAS; (b) N. Yamaguchi and H. W. Gibson, Angew. Chem., Int. Ed., 1999, 38, 143–147 CrossRef CAS; (c) N. Yamaguchi and H. W. Gibson, Chem. Commun., 1999, 789–790 RSC.
- (a) R. P. Sijbesma, F. H. Beijer, L. Brunsveld, B. J. B. Folmer, J. H. K. K. Hirschberg, R. F. M. Lange, J. K. L. Lowe and E. W. Meijer, Science, 1997, 278, 1601–1604 CrossRef CAS; (b) S. Söntjens, R. P. Sijbesma, M. H. P. Van Genderen and E. W. Meijer, Macromolecules, 2001, 34, 3815–3818 CrossRef.
- L. Mandolini, Adv. Phys. Org. Chem., 1986, 22, 1–111 CAS.
- M. I. Page and W. P. Jencks, Proc. Nat. Acad. Sci. USA, 1971, 68, 1678–1683 CAS.
- As outlined by Galli and Mandolini, for independent intramolecular reactions/interactions (ΔHinter = ΔHintra) the effective molarity, which in this case is equal to the effective concentration, is mathematically related to the entropy according to: Ceff = e(ΔSintra − ΔSinter)/R. See: ref. 44.
- J. A. Kirby, Adv. Phys. Org. Chem., 1980, 17, 183–278 CAS.
- C. Galli and L. Mandolini, Eur. J. Org. Chem., 2000, 3117–3125 CrossRef CAS.
- (a) G. Ercolani, J. Phys. Chem. B, 2003, 107, 5052–5057 CrossRef CAS; (b) G. Ercolani, M. Ioele and D. Monti, New J. Chem., 2001, 25, 783–789 RSC; (c) G. Ercolani, J. Phys. Chem. B, 1998, 102, 5699–5703 CrossRef CAS; (d) G. Ercolani, J. Am. Chem. Soc., 1993, 115, 3901–3908 CrossRef CAS.
- G. A. Bielejewska, C. E. Marjo, L. J. Prins, P. Timmerman, F. de Jong and D. N. Reinhoudt, J. Am. Chem. Soc., 2001, 123, 7518–7533 CrossRef CAS.
- H. L. Anderson, S. Anderson and J. K. M. Sanders, J. Chem. Soc., Perkin Trans. 1, 1995, 2231–2245 RSC.
- J. Rao, J. Lahiri, R. M. Weis and G. M. Whitesides, J. Am. Chem. Soc., 2000, 122, 2698–2710 CrossRef CAS.
- F. Felluga, P. Tecilla, L. Hillier, C. A. Hunter, G. Licini and P. Scrimin, Chem. Commun., 2000, 1087–1088 RSC.
- M. A. Winnik, Chem. Rev., 1981, 81, 491–524 CrossRef CAS.
- P. I. Kitov, J. M. H. Shimizu, S. W. Homans and D. R. Bundle, J. Am. Chem. Soc., 2003, 125, 3284–3294 CrossRef CAS.
- G. Ercolani, J. Am. Chem. Soc., 2003, 125, 16097–16103 CrossRef CAS.
- B. Perlmutter-Hayman, Acc. Chem. Res., 1986, 19, 90–96 CrossRef.
- K. A. Conners, Binding Constants: The Measurement of Molecular Complex Stability, Wiley, New York, 1987, Chapter 2 Search PubMed.
- As noted in section 2.1, for multivalent interactions that are constituted of multiple, independent interactions of the same type ΔH°multi, is linearly related to the enthalpy of binding for a monovalent, intrinsic interaction and to the number of interactions involved. Deviations from this linearity are indicative of negative (ΔH°multi > nΔH°mono) or positive cooperativity (ΔH°multi < nΔH°mono). However, care should be taken in the analysis of the enthalpy data as secondary interactions between tethers may hamper correct interpretation, see ref. 1.
- D. Philip and J. F. Stoddart, Angew. Chem., Int. Ed. Engl., 1996, 35, 1154–1196 CrossRef and references cited therein.
- Also all the examples in Section 3 can be analyzed in terms of pure multivalency.
- Vancomycin is an important member of the group of glycopeptide antibiotics that are active against gram-positive bacteria. The interest in vancomycin dimers stems from the different activities of these dimers towards bacteria, some of which have grown resistant to monomeric vancomycin by replacement of the carboxy-terminal DADA sequences at their cell walls — one of the main anchoring points for vancomycin — with DALac.
- J. Rao, I. J. Colton and G. M. Whitesides, J. Am. Chem. Soc., 1997, 119, 9336–9340 CrossRef CAS.
- J. Rao and G. M. Whitesides, J. Am. Chem. Soc., 1997, 119, 10286–10290 CrossRef CAS.
- J. Rao, L. Yan, J. Lahiri, G. M. Whitesides, R. M. Weis and H. S. Warren, Chem. Biol., 1999, 6, 353–359 CrossRef CAS.
- It was assumed that the two intramolecular interactions are independent. Thus applying eqn. (2) with Kn = 2.5 ×1016 M−1, b = 6, and Ki = 1.1 × 106 M−1 gives EM = 74 mM.
- Based on the binding constant of 2.5 × 1016 M−1 and taking a diffusion limited association rate (kon = 1 × 109 M−1 s−1), Rao and Whitesides estimated a minimum dissociation rate, koff, of 4 × 10–8 s−1, which corresponds to a half-life of 1.7 × 107 s or 200 days.
- V. Balzani, M. Clemente-Léon, A. Credi, J. N. Lowe, J. D. Badjic, J. F. Stoddart and D. J. Williams, Chem. Eur. J., 2003, 9, 5348–5360 CrossRef CAS.
- M. C. T. Fyfe, J. N. Lowe, J. F. Stoddart and D. J. Williams, Org. Lett., 2000, 2, 1221–1224 CrossRef CAS.
- J. D. Badjic, S. J. Cantrill and J. F. Stoddart, J. Am. Chem. Soc., 2004, 126, 2288–2289 CrossRef CAS.
- J. N. Lowe, D. A. Fulton, S.-H. Chiu, A. M. Elizarov, S. J. Cantrill, S. J. Rowan and J. F. Stoddart, J. Org. Chem., 2004, 69, 4390–4402 CrossRef CAS.
- D. A. Fulton, S. J. Cantrill and J. F. Stoddart, J. Org. Chem., 2002, 67, 7968–7981 CrossRef CAS.
- Only the bis(dibenzylammonium) dication spaced by the poly(ethylene glycol) tether gave relatively low association constants compared to the intrinsic interaction. This was attributed to partial intramolecular complexation of the cations by the poly(ethylene glycol) tether.
- M.-K. Leung, A. B. Mandal, C.-C. Wang, G.-H. Lee, S.-M. Peng, H.-L. Cheng, G.-R. Her, I. Chao, H.-F. Lu, Y.-C. Sun, M.-Y. Shiao and P.-T. Chou, J. Am. Chem. Soc., 2002, 124, 4287–4297 CrossRef CAS.
- (a) A. P. Bisson, F. J. Carver, D. S. Eggleston, R. C. Haltiwanger, C. A. Hunter, D. L. Livingstone, J. F. McCabe, C. Rotger and A. E. Rowan, J. Am. Chem. Soc., 2000, 122, 8856–8868 CrossRef CAS; (b) A. P. Bisson, F. J. Carver, C. A. Hunter and J. P. Waltho, J. Am. Chem. Soc., 1994, 116, 10292–10293 CrossRef CAS; (c) A. P. Bisson and C. A. Hunter, Chem. Commun., 1996, 1723–1724 RSC.
- E. A. Archer, A. E. Sochia and M. J. Krische, Chem. Eur. J., 2001, 7, 2059–2065 CrossRef CAS.
- (a) A. Pfeil and J.-M. Lehn, J. Chem. Soc., Chem. Commun., 1992, 838–840 RSC; (b) T. M. Garret, U. Koert and J.-M. Lehn, J. Phys. Org. Chem., 1992, 5, 529–532 CAS.
- P. N. Taylor and H. L. Anderson, J. Am. Chem. Soc., 1999, 121, 11538–11545 CrossRef CAS.
- B. Zhang and R. Breslow, J. Am. Chem. Soc., 1993, 115, 9353–9354 CrossRef CAS.
- L. C. West, O. Wyness, B. L. May, P. Clements, S. F. Lincoln and C. J. Easton, Org. Biomol. Chem., 2003, 1, 887–894 RSC.
- T. Jiang and D. S. Lawrence, J. Am. Chem. Soc., 1995, 117, 1857–1858 CrossRef CAS.
- C. T. Sikorsky and R. G. Petter, Tetrahedron Lett., 1994, 35, 4275–4278 CrossRef CAS.
- H. Yamamura, S. Yamada, K. Kohno, N. Okuda, S. Araki, K. Kobayashi, R. Katakai, K. Kano and M. Kawai, J. Chem. Soc., Perkin Trans. 1, 1999, 2943–2948 RSC.
- (a) Y. Liu, B. Li, C.-C. You, T. Wada and Y. Inoue, J. Org. Chem., 2001, 66, 225–232 CrossRef CAS; (b) Y. Liu, Y. Chen, B. Li, T. Wada and Y. Inoue, Chem. Eur. J., 2001, 7, 2528–2535 CrossRef CAS; (c) Y. Liu, L. Li, H.-Y. Zhang and Y. Song, J. Org. Chem., 2003, 68, 527–536 CrossRef CAS.
- (a) R. Breslow, S. Halfon and B. Zhang, Tetrahedron, 1995, 51, 377–388 CrossRef CAS; (b) R. Breslow and S. Chung, J. Am. Chem. Soc., 1990, 112, 9659–9660 CrossRef CAS.
- (a) A. Mulder, A. Jukovic, L. N. Lucas, J. Van Esch, B. L. Feringa, J. Huskens and D. N. Reinhoudt, Chem. Commun., 2002, 2734–2735 RSC; (b) A. Mulder, A. Jukovic, F. W. B. van Leeuwen, H. Kooijman, A. E. Spek, J. Huskens and D. N. Reinhoudt, Chem. Eur. J., 2004, 10, 1114–1123 CrossRef CAS; (c) A. Mulder, A. Jukovic, J. Huskens and D. N. Reinhoudt, Org. Biomol. Chem., 2004, 2, 1748–1755 RSC.
- T. Yang, O. K. Baryshikova, H. Mao, M. A. Holden and P. S. Cremer, J. Am. Chem. Soc., 2003, 125, 4779–4784 CrossRef CAS.
- N. Horan, L. Yan, H. Isone, G. M. Whitesides and D. Kahne, Proc. Natl. Acad. Sci. USA, 1999, 96, 11782–11786 CrossRef CAS.
- B. J. Ravoo, J.-C. Jacquier and G. Wenz, Angew. Chem., Int. Ed., 2003, 42, 2066–2070 CrossRef CAS.
- J. Huskens, M. A. Deij and D. N. Reinhoudt, Angew. Chem., Int. Ed., 2002, 41, 4467–4471 CrossRef CAS.
- Williams et al. have shown that a high effective concentration of functionalities in lipid bilayers can give rise to complexes that cannot be achieved in solution. The systematic variation of the concentration of metal-chelating guests at lipid bilayer membrane surfaces revealed the presence of an extraordinary 4 : 1 receptor:copper(II) complex at high concentrations of guest functionalities in the bilayer. The formation of this complex was not observed in solution. See: E. L. Doyle, C. A. Hunter, H. C. Philips, S. J. Webb and N. H. Williams, J. Am. Chem. Soc., 2003, 125, 4593–4599 Search PubMed.
- C. A. Nijhuis, J. Huskens and D. N. Reinhoudt, J. Am. Chem. Soc., 2004, 126, 12266–12267 CrossRef CAS.
- J. Rao, L. Yan, B. Xu and G. M. Whitesides, J. Am. Chem. Soc., 1999, 121, 2629–2630 CrossRef CAS.
- Similarly, relatively low effective molarities have also been observed for the interaction of monoclonal antibodies with a SAM: see refs. 83 and 95.
- S. Anderson, H. L. Anderson and J. K. M. Sanders, J. Chem. Soc., Perkin Trans. 1, 2255–2267 Search PubMed.
- J. D. Badjic, V. Balzani, A. Credi, J. N. Lowe, S. Silvi and J. F. Stoddart, Chem. Eur. J., 2004, 10, 1926–1935 CrossRef CAS.
- J. D. Badjic, S. J. Cantrill, R. H. Grubbs, E. N. Guidry, R. Orenes and J. F. Stoddart, Angew. Chem., Int. Ed., 2004, 43, 3273–3278 CrossRef CAS.
- J. D. Badjic, V. Balzani, A. Credi, S. Silvi and J. F. Stoddart, Science, 2004, 303, 1845–1849 CrossRef CAS.
- (a) C. Dietrich, L. Schmitt and R. Tampé, Proc. Natl. Acad. Sci. U. S. A., 1995, 92, 9014–9018 CAS; (b) A. Thess, S. Hutschenreiter, M. Hofmann, R. Tampé, W. Baumeister and R. Guckenberger, J. Biol. Chem., 2002, 277, 36231–36328 CrossRef.
- A. Sanyal, T. B. Norston, O. Uzun and V. M. Rotello, Langmuir, 2004, 20, 5958–5964 CrossRef CAS.
- R. J. Thibault Jr., T. H. Galow, E. J. Turnberg, M. Gray, P. J. Hotchkiss and V. M. Rotello, J. Am. Chem. Soc., 2002, 124, 15249–15254 CrossRef.
- M. R. de Jong, J. Huskens and D. N. Reinhoudt, Chem. Eur. J., 2001, 7, 4164–4170 CrossRef CAS.
- A. Fragoso, J. Caballero, E. Almirall, R. Villalonga and R. Cao, Langmuir, 2002, 18, 5051–5054 CrossRef CAS.
- L. A. Banerjee, L. Yu and H. Matsui, J. Am. Chem. Soc., 2003, 125, 9542–9543 CrossRef CAS.
- T. Auletta, B. Dordi, A. Mulder, A. Sartori, S. Onclin, C. M. Bruinink, M. Péter, C. A. Nijhuis, H. Beijleveld, H. Schönherr, G. J. Vancso, A. Casnati, R. Ungaro, B. J. Ravoo, J. Huskens and D. N. Reinhoudt, Angew. Chem., Int. Ed., 2004, 43, 369–373 CrossRef CAS.
- S. Onclin, A. Mulder, J. Huskens, B. J. Ravoo and D. N. Reinhoudt, Langmuir, 2004, 20, 5460–5466 CrossRef CAS.
- A. Mulder, S. Onclin, M. Péter, J. P. Hoogenboom, H. Beijleveld, J. ter Maat, M. F. García-Parajó, B. J. Ravoo, J. Huskens, N. F. van Hulst and D. N. Reinhoudt, Small, 2005, 1 Search PubMed , in press.
- J. S. Park, G. S. Lee, Y.-J. Lee, Y. S. Park and K. B. Yoon, J. Am. Chem. Soc., 2002, 124, 13366–13367 CrossRef CAS.
- R. Breslow and B. Zhang, J. Am. Chem. Soc., 1996, 118, 8495–8496 CrossRef CAS.
- B. Zhang and R. Breslow, J. Am. Chem. Soc., 1997, 119, 1676–1681 CrossRef CAS.
- C. A. Haskard, C. J. Easton, B. L. May and S. F. Lincoln, J. Phys. Chem. B, 1996, 100, 14457–14461 Search PubMed.
- A. Harada, M. Furue and S.-I. Nozakura, Polymer J., 1980, 12, 29–33 Search PubMed.
- T. Jiang, D. K. Sukumaran, S.-D. Soni and D. S. Lawrence, J. Org. Chem., 1994, 59, 5149–5155 CrossRef CAS.
- W. B. Edwards, D. E. Reichert, D. A. d'Avignon and M. J. Welch, Chem. Commun., 2001, 1312–1313 RSC.
- R. R. French, P. Holzer, M. G. Leuenberger and W.-D. Woggon, Angew. Chem., Int. Ed., 2000, 39, 1267–1269 CrossRef CAS.
Footnote |
| † Present address: Johann Wolfgang Goethe-Universität, Frankfurt am Main, Institute for Biochemistry, Biocenter, Marie Curie Straße 9, D-60439 Frankfurt, Germany. |
| This journal is © The Royal Society of Chemistry 2004 |
