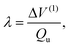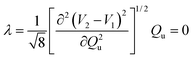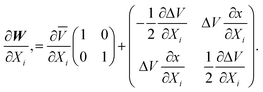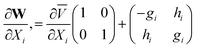General Discussion

Professor Balint-Kurti opened the discussion of Professor Truhlar’s paper: I commend Professor Truhlar on his excellent overview of nonadiabatic effects in chemical reactions. I would like to comment in particular on the diabatic curves and potential energy coupling terms produced by the fourfold way method he has developed. As Professor Truhlar has shown in his talk and in his published work, the coupling potentials produced by the fourfold way in the diabatic representation peak near an avoided crossing and decrease to small values away from the crossing, or avoided crossing, geometry. This behaviour is in keeping with previous expectations for these terms, but does not agree with the behaviour produced by many (or perhaps all) other ab initio methods. From a conceptual and a computational point of view this is clearly a very desirable behaviour. One reason for this is that it leads to the convergence of the adiabatic and diabatic potentials in regions far removed from the crossing, or avoided crossing, point.

Professor Truhlar has also presented interesting results for the Li + HF → LiF + H reaction. There is a barrier in the ground state of this reaction which he has attributed in his talk, and in his publications, as being due to an avoided crossing between the Li(2s) + HF and the Li(2p) + HF configurations. I would like to draw attention to our calculations on this system¹, published in Faraday Discussion 62 in 1977. These represented the first ab initio calculations of this potential energy surface and have proved correct in every qualitative aspect. In this paper we discuss the origin of the barrier to reaction and attribute it to an ionic–covalent avoided crossing arising from the interaction of Li + HF and the Li⁺ + HF⁻ valence bond structures. I believe that this interpretation of the physical origin of the barrier is more meaningful than that presented by Professor Truhlar. It is naturally difficult to discuss the role of valence bond structures when calculations are performed within a molecular orbital framework.

1 G. G. Balint-Kurti and R. N. Yardley, Faraday Discuss. Chem. Soc., 1977, 62, 77.

Professor Truhlar replied: Thank you for the compliment on my lecture. The behavior of the diabatic coupling depends on the system. For example, for LiH, ozone, and (H₂)₂, the diabatic coupling changes monotonically in the vicinity of avoided crossings.¹ The same behavior is observed for some nuclear motion paths for LiFH, but not always.^1,2 However, when it does not violate the physics of the transition under study, we prefer to define the diabats to equal the adiabats in asymptotic regions where scattering boundary conditions are to be applied. Then the diabatic coupling does tend to zero in asymptotic regions; this is indeed convenient, as noted by Professor Balint-Kurti.

I fully agree with Professor Balint-Kurti's interpretation of the avoided crossing in the Li + FH reaction as an ionic–covalent interaction; however, his comments about our work indicate a misunderstanding. In our scheme one of the diabatic states transforms quasiadiabatically from one dominant configuration state function at large Li–HF distances to another at small Li–HF distances. The labels for the diabatic states in the reactant region are valid only for large Li–HF distances. In fact, in our first paper¹ on diabatization of this system, we said that “the diabatic states of LiFH cannot be identified globally with a particular valence bond character that is found in asymptotic regions… In the product region, they are characterized by an ionic–covalent interaction…” This aspect makes the LiFH case a particularly challenging test case for a method that attempts to provide a direct diabatization. This success of our method in describing this system illustrates (i) the power of Ruedenberg and Achity's formulation³ of diabatic states by which they associate more than one electronic configuration or prototype with each diabatic state and (ii) our extension¹ of the concept of dominant CSF groups such that it is not necessary for all members of a dominant configuration state function group to always be simultaneously dominant or not. Our extension allowed us to treat a system where the diabatic prototypes change with the arrangement.¹ More specifically, the LiFH case shows that our method has the flexibility to obtain the required smooth changing in the character of the diabatic molecular orbitals.¹

Our method thus combines the advantages of the self-consistent-field method for variationally optimizing the changing chemical character of the occupied orbitals with the dynamical convenience of a diabatic representation, and it is robust enough to handle a situation that would require more diabatic states than adiabatic states if one did not introduce the concept of dominant configuration state function groups.

A similar situation is presented even by the less polar NaH₂ system, as we pointed out in 1982.⁴ When described in terms of an eight-configuration diabatic basis, this system exhibits Na(3s) and Na(3p) character in the Na + H₂ arrangement, with negligible ionic character in either state. But in the three-body interaction region and in the product region there is very significant incorporation of ionic character (summing to significantly more than 90%) into the two lowest adiabatic states.⁴ In this work^4,5 we also criticized previous work that had assumed that the diabatic coupling is peaked at a point on the crossing seam of the diabats.

The covalent-to-ionic transition in MXH systems was also a critical design element in our analytic diabatic coupled potential energy surfaces for NaFH^6,7 and LiFH.⁸

1 H Nakamura and D. G. Truhlar, J. Chem. Phys., 2001, 115, 10 353.

2 H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2002, 117, 5576.

3 K. Ruedenberg and G. J. Achity, J. Chem. Phys., 1993, 99, 3799.

4 D. G. Truhlar, J. W. Duff, N. C. Blais, J. C. Tully, and B. C. Garrett, J. Chem. Phys., 1982, 77, 764.

5 N. C. Blais, D. G. Truhlar, and B. C. Garrett, J. Chem. Phys., 1983, 78, 2956.

6 M. S. Topaler, D. G. Truhlar, X. Y. Chang, P. Piecuch, and J. C. Polanyi, J. Chem. Phys., 1998, 108, 5349.

7 M. D. Hack and D. G. Truhlar, J. Chem. Phys., 1999, 110, 4315.

8 A. W. Jasper, M. D. Hack, D. G. Truhlar, and P. Piecuch, J. Chem. Phys., 2002, 116, 8353.

Professor Martinez commented: The time-uncertainty hopping method for dealing with “frustrated hops” has some similarities to the steepest descent procedure we have used with multiple spawning.¹ Usually, we spawn a new basis function with the same position as its parent and adjust the momentum along the nonadiabatic coupling vector. If it is impossible to match the classical energy of the spawned and parent basis functions through this momentum adjustment, the spawned basis function is moved along a steepest descent path until it reaches the desired classical energy (see illustration below.) Thus, the spawned basis function is displaced in position from its parent. I think the physical intuition behind the steepest descent spawning and time-uncertainty hopping methods is similar. However, I wonder about the details in the time-uncertainty case. In spawning, the precise details may be less important since the spawned basis function begins with no population and only acquires population if it has non-zero Hamiltonian matrix elements connecting it to the parent function. How do you know how closely one must follow the uncertainty product? Since the time–energy uncertainty principle is an inequality, there might be some ambiguity here.

1 M. Ben-Nun and T. J. Martinez, J. Chem. Phys., 1998, 108, 7244.

Professor Truhlar replied: The nonlocal hops in the fewest-switches-with-time-uncertainty (FSTU) method simulate transitions that occur in the exponentially decreasing tails of wave packets, and I agree that the steepest-descent procedure described by Professor Martinez has some similarities. The time interval over which we allow nonlocal hops has a width of h/ΔE, where ΔE is the gap at the self-consistent hopping time, and although this seems reasonable, there is certainly some arbitrariness in it. In the original paper¹ we said: “The present formulation of the FSTU method is simple and straightforward, but it is not unique. For example the uncertainty relation…is strictly an inequality…” We also discussed other aspects of nonuniqueness.

There is a corresponding arbitrariness in the width of the wave packets that one uses in the multiple spawning method or in any unconverged Gaussian wave packet method, and there is a similar arbitrariness in the positioning and characteristics of spawned basis functions. For example, should one move the basis function along a steepest descents pass or along the actual trajectory path? In principle, one can converge the multiple spawning method with respect to the basis set, but to carry out converged quantum dynamics, one would typically need far more coupled basis functions than have typically been employed, so that the method has the same kinds of uncertainties as the FSTU method. In our joint paper² we agreed that spawning “creates basis functions that will be potentially populated at a later time through the coupled equations. However the final energy distributions…will be determined in part by where the basis functions are created and in particular by how their momentum is selected.” This can only be avoided by having a convergent series of basis functions, for example, enough Gaussians to represent motion in all possible directions and Gaussians both advanced in time and retarded in time as compared to the parent basis function.

A key aspect of the FSTU method is that it is well defined and the performance can be and has been tested by comparing the results to accurate quantum mechanical dynamics for a variety of cases.^1,3–5 In contrast the steepest descent method is not always employed,² and no systematic tests of a standard version of the steepest-descent method have been reported. All that being said, it appears to be a useful idea, and the multiple spawning method continues to offer useful insights.

1 A. W. Jasper, S. N. Stechmann, and D. G. Truhlar, J. Chem. Phys., 2002, 116, 5425; A. W. Jasper, S. N. Stechmann, and D. G. Truhlar, J. Chem. Phys., 2002, 117, 10 247, erratum.

2 M. D. Hack, A. M. Wensmann, D. G. Truhlar, M. Ben-Nun, and T. J. Martinez, J. Chem. Phys., 2001, 115, 1172.

3 A. W. Jasper and D. G. Truhlar, Chem. Phys. Lett., 2003, 369, 60.

4 S. Nangia, A. W. Jasper, T. F. Miller III, and D. G. Truhlar, J. Chem. Phys., 2004, 120, 3586.

5 C. Zhu, A. W. Jasper, and D. G. Truhlar, J. Chem. Phys., 2004, 120, 5543.

Dr Gidopoulos commented: Denote by ϕ_jR, ϕ_kR electronic adiabatic states that depend parametrically on the nuclear coordinate R. How sensitive are the matrix elements 〈ϕ_jR|∇ϕ_kR〉 and 〈ϕ_jR|∇²ϕ_kR〉 to electronic correlation effects? Would an independent-particle wavefunction for ϕ_jR, ϕ_kR be meaningful to calculate these matrix elements?

Professor Truhlar responded: The nonadiabatic coupling matrix elements can be very sensitive to electronic correlation, and in some cases one will obtain not just quantitatively wrong results from independent-particle wave functions, but qualitatively wrong results. An example is provided by the ionic–covalent curve crossing in the LiF molecule. The nonadiabatic coupling matrix elements are large near an internuclear distance of 5.6 Å when dynamical correlation is not included, but they are large near an internuclear distance of 6.6 Å when it is.¹

1 H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2002, 117, 5576.

Professor Greene said: Your talk had one comment saying that it is possible to “rigorously prove” that no diabatic representation exists for which the derivative couplings all vanish. This is puzzling to me because a simple basis set that is independent of nuclear positions would clearly have no such couplings. Would you clarify the sense in which such a “rigorous proof” exists, in light of the counterexample?

Professor Truhlar replied: This case was discussed in our original paper.¹ A more technical statement of the nonexistence theorem is: The transformation from an adiabatic electronic basis to a strictly diabatic electronic basis in which the nuclear momentum coupling terms vanish does not exist except in the trivial case of a complete (infinite) set of basis functions, in which case the electronic states become fixed electronic functions independent of the nuclear coordinates. The only significant exception is the case of diatomic electronic states of a given symmetry. In other words, a fixed basis, also called² the Longuet-Higgins representation, is considered to be a trivial solution to the problem of a finding a strictly diabatic basis. In general, when a range of nuclear geometries is considered, a fixed basis provides a poor approximation if the dimension of the space is small,^1,3,4 and such a basis will never permit the truncation to a subspace of small dimension over any sizable range of nuclear coordinates.⁵ However, a strict diabatic basis can be useful for certain discussions of vibronic interactions.²

1 C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1982, 77, 6090.

2 C. J. Ballhausen and A. E. Hansen, Annu. Rev. Phys. Chem., 1972, 23, 15.

3 H. Gabriel and K. Taulbjerg, Phys. Rev. A, 1974, 10, 741.

4 T. Pacher, L. S. Cederbaum, and H. Köppel, J. Chem. Phys., 1988, 89, 7367.

5 T. Pacher, L. S. Cederbaum, and H. Köppel, Adv. Chem. Phys., 1993, 84, 293.

Professor Brown addressed Professor Truhlar: In the grand finale of your talk, you presented results comparing the mean deviation from quantum mechanical results of a variety of methods. This was a mean with regard to 12 test cases. While seeing the mean deviation is useful, and, of course, one would like a method that provides results independent of the adiabatic/diabatic basis used, could you comment on if any methods were particularly poor or good for specific test cases?

Professor Truhlar replied: The decay of mixing methods appear to be more accurate than trajectory surface hopping methods and the semiclassical Ehrenfest method not just on the average but for all three kinds of systems examined: (i) moderately coupled systems where the diabats cross but there are no accessible conical intersections, (ii) weakly coupled systems where the diabats do not cross, and (iii) strongly coupled systems with conical intersections. Only cases (i) and (ii) were included in the introductory lecture, but unpublished work in our group¹ has addressed cases of type (iii).

1 A. W. Jasper, S. Nangia, C. Zhu, A. Anderson, and D. G. Truhlar, unpublished.

Professor Yarkony asked: In your four-fold way approach to diabatization the size of the active space is driven by the orbital requirements of the diabatic representation. This can lead to active spaces that are larger than might be required by a carefully chose MCSCF procedure. Can this limitation be avoided or is it too rare to be of consequence?

Professor Truhlar responded: In the fourfold way, as employed so far,^1–3 we have used a complete active space (CAS) as the reference for the treatment of dynamical correlation by CAS multi-reference second-order perturbation theory⁴ (CAS-MRMP2) or CAS multi-configuration quasi-degenerate perturbation theory⁵ (CAS-MC-QDPT). Adiabatic states can often be described with a smaller reference space, called a restricted active space (RAS), but in carrying out the transformation to diabatic molecular orbitals we took advantage of the invariance of a CAS wave function to a transformation of the active orbitals. Although the CAS-MRMP2⁴ and CAS-MC-QDPT⁵ methods are efficient, a full-valence active space becomes large as the molecule gets bigger, and it is impractical to include more than about 14 orbitals in a CAS reference. To avoid this problem one can use a smaller number of active orbitals or extend the method to make use of general multi-reference quasi-degenerate perturbation theory,⁶ which has no restrictions on the form of the reference space. Nakano et al. have shown that one can obtain very similar results to the CAS-reference method with much smaller reference spaces.⁶ Furthermore, even though MC-QDPT has performed very well for us, there will be advantages to switch to multi-reference averaged quadratic coupled clusters^7–10 (MR-AQCC) with linear response theory^10,11 (MR-AQCC-LRT) for greater stability and the availability of analytic gradients. The response formulation casts the problem in terms of the diagonalization of a state-independent effective Hamiltonian, which should provide consistent states near a conical intersection or locally avoided crossing. The analytic gradient algorithm has the advantage, for our purposes, that it does not require that the MCSCF reference function be defined in terms of variationally optimized orbitals,¹² although it does require the gradient of the transformation. The response formulation also provides explicit wave functions¹¹ as required for application of the configurational uniformity criterion in the last step of calculating the diabatic potential energy matrix. In addition, MCSCF state averaging^13,14 can be included in the gradient algorithm.¹⁵

Even for ground-state energies, it is known that a full-valence CAS reference space leads to a large number of ineffective configurations,^16,17 but the transformation to diabatic orbitals may be useful for concentrating the substitutions that lead to fast convergence of energy gaps into a classifiable and practically identifiable subset of substitution space. In this regard I note, in answer to your question, that analytic gradients can be obtained with the MR-AQCC-LRT method even when the reference space is smaller than the complete active space used to obtain diabatic orbitals.^12,18 In summary, the prospects are good for avoiding the limitation to complete active spaces.

1 H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2001, 115, 10 353.

2 H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2002, 117, 5576.

3 H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2003, 118, 6816.

4 K. Hirao, Chem. Phys. Lett., 1992, 190, 374.

5 H. Nakano, J. Chem. Phys., 1993, 99, 7893.

6 H. Nakano, R. Uchiyama and K. Hirao, J. Comput. Chem., 2002, 23, 1166.

7 P. G. Szalay and R. J. Bartlett, Chem. Phys. Lett., 1993, 214, 481.

8 P. G. Szalay and R. J. Bartlett, Chem. Phys. Lett., 1993, 103, 3600.

9 P. G. Szalay, T. Müller and H. Lischka, Phys. Chem. Chem. Phys., 2000, 2, 2069.

10 T. Müller, M. Dallos, H. Lischka, Z. Dubrovay and P. G. Szalay, Theor. Chem. Acc., 2001, 105, 227.

11 H. Lischka, R. Shepard, R. M. Pitzer, I. Shavitt, M. Dallos, T. Müller, P. G. Szalay, M. Seth, G. S. Kedziora, S. Yabutshita and Z. Zhang, Phys. Chem. Chem. Phys., 2001, 3, 664.

12 R. Shepard, H. Lischka, P. G. Szalay, T. Kovar and M. Enrzerhof, J. Chem. Phys., 1991, 93, 2085.

13 H. J. Werner and W. Meyer, J. Chem. Phys., 1981, 74, 5794.

14 R. N. Diffenderfer and D. R. Yarkony, J. Chem. Phys., 1982, 86, 5098.

15 H. Lischka, M. Dallos, and R. Shepard, Mol. Phys., 2002, 100, 1647.

16 J. Ivanic and K. Ruedenberg, Theor. Chem. Acc., 2001, 106, 339.

17 J. Ivanic and K. Ruedenberg, Theor. Chem. Acc., 2002, 107, 220.

18 R. Shepard, in Modern Electronic Structure, ed. D. R. Yarkony, World Scientific, Singapore, 1995, part 1, pp. 345–458.

Professor Köppel commented: You pointed out the difference between your diabatic potentials and coupling elements and those obtained earlier (by Woywod and Domcke). Did you compute also dynamical quantities like cross-sections or similar with these data, in order to reveal an influence of the different diabatization schemes on observable quantities?

Professor Truhlar said: We did not compare cross sections or other dynamical observables calculated with different diabatization schemes.

Professor Collins asked: In your “fourfold way” to diabatisation, over how large a region of configuration space must one consider the character of the electronic states?

Professor Truhlar replied: In the fourfold way one must define the group lists of the dominant configuration state functions at one or a few selected potential reference geometries, where adiabatic states are almost equal to diabatic states. If the potential reference geometries belong to two or more arrangements, one must identify a one-to-one correspondence between the diabatic MOs in the two arrangements by considering their changes along a path connecting the arrangements. This can typically be accomplished with large steps because one seeks only the correspondence, not a quantitative relationship.

Professor Arteca commented: During his presentation, Professor Truhlar highlighted a diabatization scheme with the following characteristics: (a) the size of the system is maintained during the transformation (e.g. three adiabatic states into three quasi-diabatic states), and (b) the non-adiabatic coupling terms (NACTs) are sufficiently small within a region M of interest in nuclear configuration space. I would like to point out that such a scheme can be taken a step further and design a useful physical picture where the basis set of quasi-diabatic states are coupled through the environment. To this end, we consider the quantum state |Ψ(q,R)〉, with electron coordinates of q, associated with a nuclear configuration R ∈ M. If {Ψ_i} are quasi-diabatic basis functions with the proper symmetries, they will be coupled with an external electric field vector A, even if one neglects all NACTs. Since the Ψ_i-functions are diabatic, their couplings in the field, V_ij = 〈Ψ_i|V_field|Ψ_j〉, V_field ≈ −eA·p/mc (with p the electronic linear momentum operator) will be constant over M, up to a first approximation, for a given A. The resulting quantum state |Ψ〉 at R can be represented by:

Ψ(q,R) = ∑_ic_i(R)ψ_i(q)

where the amplitudes |C_i|² on reactants and products can be modulated by the intensity and symmetry of A, as defined in a fixed laboratory frame. The field A can be thought of as translating the effects of a solvent or enzymatic active site over the minimalistic quantum model of interest. We show in our poster (see also ref. 1) that the environment can modify the effective energy barrier along a given reaction path and create product-like quantum states at configurations not far (geometrically) from the diabatic potential energy minimum of the reactant. The emerging physical picture is quantum mechanical, and appealing in the sense that the reaction phenomenology (e.g. nonintuitive “violations” to the Hammond postulate of reaction paths) is due to couplings among diabatic states caused by the environment, rather than by NACTs in nuclear configuration space.

1 G. A. Arteca and O. Tapia, J. Math. Chem., 2004, 35, 1–19

Professor Sundström opened the discussion of the paper by Dr Fuß: What is the reaction coordinate for the very fast ∼40 fs process taking the system from the FC region on the L_a state to the CT state? You indicated that it might be of similar nature of the coherent vibrational oscillations. But the time-scale of the formation process is much faster, so are there other contributions to the process?

Dr Fuß replied: In fact in PYRBN, the relaxation time from the Franck–Condon point to the CI (τ₁ + τ₂ = 45 fs) is substantially shorter than the time from the CI to the L_b well. The latter ≈ 262 fs, one quarter of the vibrational period or one half the observed period of the signal oscillation. The initial, very fast, acceleration must lead along a steep part of the potential, causing a rapid lowering of the electronic energy. (The ionization probability is sensitive to the ionization energy and hence to the electronic energy.) This coordinate may involve bond-length changes in the acceptor moiety (benzene ring and cyano group), induced by the partial electron transfer in the L_a state. This displacement will be restored on the lower (L_b) surface. (An oscillation of this kind was not observed; it would be below the experimental time resolution.)

Another source of the vibration, which may in particular apply to the amino-group inversion, is mentioned in the text and was suggested in ref. 1: On crossing from the 2A surface to the 1B surface at the CI, the wave packet must receive a momentum in a direction of symmetry species b, for example the inversion, even if neither L_a nor L_b nor the CI are displaced in this direction. In this case, the initial relaxation direction has in fact no component along the vibrational coordinate. In both cases we conclude that the direction of the reaction path is different before and after the CI, although components of the direction vectors have components in common, such as probably the twist.

1 S. A. Trushin, T. Yatsuhashi, W. Fuß, and W. E. Schmid, Chem. Phys. Lett., 2003, 376, 282.

Dr Blanchet asked: (1) Did you do a Fourier analysis of the oscillating signal of fragments at 1310 nm probe, as well as the parent signal at 810 nm? Indeed it seems on Fig. 1 of the paper that the periods of these oscillations are quite different from the ones observed on the parent signal at 1310 nm (analysed in Fig. 2 of the paper). Does it mean that the multiphoton ionization is sensitive to different modes in the L_b potential surfaces? Could you comment about this sensivity and the power dependency of the different signals?

(2) The anisotropy of the fragment signal, which plays an important role in revealing the charge transfer state, should not depend strongly on the probe wavelength. Did you also observe this anisotropy at other probe wavelengths than 810 nm?

(3) Since the anisotropy of the fragments plays a crucial rule in your experiment, could you comment on the different nature of the fragments of the two species? Indeed PBN, which is the most highly bound species, dissociates during the photoionisation to a larger fragment than PYRBN. I would expect the contrary, namely larger fragments for the lesser bound system, apart from if the dissociation in PYRBN leads to a richer mass spectrum than PBN, mainly due to a partial explosion of the molecule. If so, could you comment on the sensitivity of the probe process relative to vibrational wavepacket in L_b?

(4) Since the cross-correlation time of your experiment is around 80 fs and as the probe pulse is very intense at 10¹³ W cm⁻², which might couple the ground and the first excited states¹, induce non-adiabatic excitation², deform the molecular structure³ or cause a Coulomb explosion,⁴do you think that the potential surfaces during this first 80 fs are not coupled to each other? In such a case, how can your interpretation of decay times τ₁ and τ₂ being of the order of the cross-correlation time, remain valid ?

1 K. B. Møller and N. E. Henriksen, Chem. Phys. Lett., 2004, 385, 134–139.

2 A. N. Markevitch, D. A. Romanov, S. M. Smith, H. B. Schlegel, M. Yu. Ivanov and R. J. Levis, Phys. Rev. A, 2004, 69, 013401.

3 M. Comstock, V. Senekerimyan and M. Dantus, J. Phys. Chem. A, 2003, 107, 8271–8281.

4 H. Hirada, M. Tanaka, M. Murakami, S. Shimizu, T. Yatsuhashi, N. Nakashima, S. Sakabe, Y. Izawa, S. Tojo and T. Majima, J. Phys. Chem. A, 2003, 107, 6580–6586.

Dr Fuß replied: (1) The oscillation maxima of the fragment signal (Fig. 1b) and the parent signal (Fig. 2), both measured at 1.3 μm, coincide. (Note the different time scales in Figs. 1 and 2 of the paper.) The same is true for 2.1 μm. Hence the frequency and phase did not depend on the wavelength or the signal (parent or fragment ion). The relative amplitude of the modulation was larger at longer wavelength (λ_pr), perhaps because with smaller photon energies the ionization probability is more sensitive to the ionization energy that depends on the vibrational coordinate. Indeed, at 810 nm the amplitude of the modulation is too small to identify any oscillation with certainty. The signal-to-noise ratio was better for the parent signals than for the fragment ions, because the former were 10 times more intense. At even shorter probe wavelength, 614 nm, we found an oscillation with period 260 fs which we interpret as an overtone. We studied the wavelength effect on the oscillations in more detail in the similar molecule piperidinobenzonitrile (PIPBN), where the modulation is much more pronounced. The frequencies do not depend on λ_pr, and between 2100 and 700 nm also the phase is constant, whereas there is a phase jump at 680 nm and 400 nm by π, probably caused by an intermediate resonance¹. The modulation depths did not depend on the probe intensity; we did, however, not try to reach any saturation limit.

(2) We ascribe the anisotropy of the fragment signal to a resonance in the (parent) ion, causing photochemical dissociation to the fragment ion. (The parent signal is isotropic, see Fig. 4 of the paper.) As explained in Fig. 6 of the paper, for PYRBN⁺ the resonance would be at 1.9 eV (=energy difference between the two b₁ orbitals) in the Franck–Condon region, out of reach for the probe (≤1.53 eV). This energy difference drops on suitable displacement. Only if this decrease is sufficient, a resonance can also be reached with the longest λ_pr. In PYRBN and PBN we did not investigate the anisotropy at λ_pr ≠ 810 nm. In PIPBN we found very similar results for λ_pr = 810 nm, whereas at 2100, 680 and 400 nm also the parent ion showed a positive anisotropy (unpublished), consistent with resonances in the neutral molecule at these three wavelengths (two mentioned above); for these wavelengths we cannot know whether there is also a resonance in the ion.

(3) Besides the parent ion, we investigated in PYRBN and PBN the fragment ions of largest abundance, which was around 10% in each case at small delay time. (For longer delays, the abundance variation is reflected by the ratios of σ values in Table 1. This variation is small with λ_pr = 810 nm.) It seems plausible that PYRBN⁺ will easily eliminate an H atom from a CH₂ group, so that a partial double bond to N can be formed in the resulting fragment ion. This channel does not exist in PBN. It is less obvious why PBN can easily eliminate a fragment of mass 28. But the fragmentation pattern in the electron-impact spectrum is very similar.

(4) A single time constant below the width (80 fs) of the instrumental function ( i.e. the cross correlation of the pump pulse with the third power of the probe pulse) can be derived from the data, if the signal-to-noise ratio is good enough and if the instrumental function is well known. (Our τ₁ = 5 (±5) fs is at the limit of this possibility. We measure the instrumental function simultaneously with the other signals.) This is not in conflict with the idea of resolution. By contrast, two such constants cannot be resolved from one signal. However, two constants may be extracted, if there are two different signals. Ideally, there would be only one signal (e.g. the parent) from the first observation window and a second signal (the fragment) from the subsequent window. In practice, it is sufficient to have linearly independent signals. In fact, one time constant (τ₂) would be sufficient to simulate the early-time behavior of a single signal, and τ₁ is only needed to reproduce the difference of the two signals in the rising wing until the region of the maximum (see the difference in Fig. 1, center).

A different problem, which must be taken seriously, is the high probe intensity which might perturb the excitation process during the pump–probe overlapping time. In this context, we have only to consider processes requiring the presence of both fields simultaneously. We can ignore, for example, excitation (called “nonadiabatic” by Dr Blanchet) and ionization by the probe alone, because we subtract the probe-alone signals (measured at negative delay times) from the data; these terms were always ≪1% of the signal maxima. We can also ignore processes happening after ionization (hence also after the pump process) such as dissociation of the ions or Coulomb explosion. Nonvertical excitation (called “coupling of ground and first excited states” by Dr Blanchet) predicted for excitation by a weak UV and a strong resonant IR pulse will not apply for our cases, because the probe wavelengths are far out of resonance with any vibration, including overtones and combination vibrations. The most important perturbation of excitation will be the level shifts probably caused by the high-intensity probe field. (We prefer this picture over that using molecular deformation that is mentioned by Dr Blanchet.) But instead of considering theoretical predictions, experimental tests such as the following seem to us more compelling (see also ref. 2):

We always vary the probe intensity by a factor of at least three. Whereas the signals change thereby by a factor of 10 to >100 (the change is not the same for the different observation windows, because the order of ionization is different), the time constants are the same in the cases investigated so far. This probably means that level shifts (or differences thereof) are small compared to the spectral widths. Indeed and not surprisingly, the molecules with very short initial time constants have very broad spectra. The initial lifetime even seems to vary systematically: The better resolved the vibrational structure, the longer is the lifetime (compare e.g. the case of cyclohexadiene and two dialkyl derivatives of it, reported in ref. 3).

In the case of τ₂ of PYRBN and PBN (and in many other cases), we can (and did) evaluate the time constants also outside the pump–probe overlapping time, so that the pump process is not perturbed. This method^2,3 profits from the fact that the laser pulses decay like Gaussians, hence faster than the exponential signals. The range in question is between about 120 and 240 fs (Fig. 1b and c and 3 of the paper), corresponding to 3τ₂ to 6τ₂. (For visualization, it helps to subtract the more slowly varying long-time signal and to plot the result logarithmically,^2,3 although this is not required for the numerical simulation.) With the parent signals, the signal-to-noise ratio is still good enough to evaluate τ₂ in this time range, and it is the same as that found at smaller delay.

The time constants of the similar molecule dimethylaminobenzonitrile were initially measured with twice as long pulses than later with our present laser system. The time constants (including τ₁ and τ₂, which are similar to those of PYRBN and PBN) were identical in both experiments, as mentioned in ref. 4.

So in the cases investigated so far, the pump process was apparently not noticeably perturbed by the intense probe during the overlapping time. Future theories of molecules in strong laser fields should try to comply with this result. In this context it is worth mentioning that in some cases we had to add a term proportional to the instrumental function to simulate all the signals (a recent case was cis-stilbene⁵); it would correspond to an even smaller time constant (τ ≈ 0). We ascribed it to a process, where one probe and one pump photon excites—via a virtual intermediate state—a higher real state which is then also ionized by additional probe photons. This process exists only during the pump–probe overlapping time, and its apparent τ does not reflect any flow of population. We do not want to exclude that τ₁ can be assigned to such a process (see the error limit!), although it seems to us more likely that it reflects relaxation out of the Franck–Condon region.

1 T. Yatsuhashi, S. A. Trushin, W. Fuß, W. Rettig, W. E. Schmid, and S. Zilberg, Chem. Phys., 2004, 296, 1.

2 S. A. Trushin, W. Fuß, K. K. Pushpa, and W. E. Schmid, SPIE Proc., 2002, 4749, 313.

3 M. Garavelli, C. S. Page, P. Celani, M. Olivucci, W. E. Schmid, S. A. Trushin, and W. Fuß, J. Phys. Chem. A, 2001, 105, 4458.

4 S. A. Trushin, T. Yatsuhashi, W. Fuß, and W. E. Schmid, Chem. Phys. Lett., 2003, 376, 282.

5 W. Fuß, C. Kosmidis, W. E. Schmid, and S. A. Trushin, Chem. Phys. Lett., 2004, 385, 423.

Professor Child asked: You have discussed that ‘people thought that L_a relaxes directly to L_b’. Now you say there must be a conical intersection. Are there any systems that are known to relax so rapidly without a conical intersection?

Dr Fuß replied: We do not know any sub-picosecond diabatic process that would not pass through a conical intersection. By the Landau–Zener formula, applicable to avoided crossings, one can estimate that this time range is only reached, if the two surfaces come closer than 0.1 eV.¹ Because the surfaces are farther apart in the Franck–Condon region, this mechanism also requires an intermediate displacement.

1 W. Fuß, S. Lochbrunner, A. M. Müller, T. Schikarski, W. E. Schmid, and S. A. Trushin, Chem. Phys., 1998, 232, 161.

Professor Köppel commented: The τ₃ equilibration motion between the CT and the L_b states is assumed to follow a low-energy path around the conical intersection. Thus it should be adiabatic, but display the geometric phase effect, upon interference of the two parts of the wave packet encircling the lower cone on both sides. It would be of interest to observe this effect experimentally, e.g. by interferometric techniques.

Dr Fuß responded: It may be difficult to disentangle such phenomena from our data, because a given ion signal contains contributions not only from one observation window, but from all, although with different weight (see the sigma values in the table). Moreover, only the wave packet arriving to L_b directly from the conical intersection (CI) has conserved some coherence, whereas that (or: the two partial wave packets) going from the CT state around the lower CI cone within τ₃ seem to have lost their coherence, so that interference effects are not expected. A better chance might be provided by spectroscopy of the L_b state in a cold supersonic beam: It was repeatedly reported that the initially well resolved vibrational structure becomes congested above an excess energy of about 1000 cm⁻¹ (see e.g. PBN¹). Above a threshold energy not much higher, the vibrational wavefunction should be able to surround the lower CI cone, and the spectrum might show signatures of this phenomenon. The analysis can perhaps be done in a similar way as in Jahn–Teller systems.

1 L. Belau, Y. Haas, and W. Rettig, Chem. Phys. Lett., 2002, 364, 157.

Dr Burghardt asked: In view of the gas-phase mechanism you described for PYRBN/PBN, involving a transient population of the charge transfer state, what is the picture you propose for the corresponding process in solution phase (polar vs. non-polar solvents)? Beyond the aspect of solvent stabilization of the charge transfer state, a previous analysis for DMABN by Kim and Hynes¹ has shown that dynamical, nonequilibrium solvation effects can be of major importance for a solution phase TICT (twisted intramolecular charge transfer) type process.

1 H. J. Kim and J. T. Hynes, J. Photochem. Photobiol. A, 1997, 105, 337.

Dr Fuß replied: Compared to the gas phase, adding a solvent will (1) statically stabilize the L_a and CT states a little more than the L_b state (solvent arrangement as in S₀), (2) introduce additional time dependence, reflecting solvent reorientation in response to the dipole moment that changes on L_a → CT relaxation, for example, and (3) slow down an amino-group twist by friction (viscosity). Effect (1) will not much change the slopes, and friction in not too viscous media will not much affect the processes driven by the steepest slopes. Therefore we can expect that from L_a the molecule relaxes within not much more than τ₁ + τ₂ (perhaps within 100 fs) to a CT state that is not yet in equilibrium with the solvent; in hexane and acetonitrile it would have similar spectral properties. In hexane, it would then be depleted towards the L_b state in a time that will be >τ₃ (perhaps a few ps), because solvent reorientation can take place during this slower process along this relatively flat path, which also gives more chance to friction. In acetonitrile, however, the population will stay in the CT state, which will be energetically lowered within few hundred femtoseconds. The CT population will then be further increased within a few picoseconds by relaxation from the L_b state, which was populated (simultaneously with CT) by branching at the conical intersection. Just these processes have been observed in dimethylaminobenzonitrile in an experiment¹ that for the first time had sufficient time resolution. They were interpreted as above in ref. 2.

Another common effect of solvents is that they can, within a few picoseconds, cool down any excess vibrational energy released during relaxation. Activated processes, observed in the gas phase, can thus be suppressed in solution. We interpret in this sense (as previously²) a process occurring within several 100 ps as intersystem crossing to a higher triplet state (S₁ → T_n); in solution, one can only observe S₁ → T₁, which is much slower.

1 W. M. Kwok, C. Ma, D. Phillips, P. Matousek, A. W. Parker, and M. Towrie, J. Phys. Chem. A, 2000, 104, 4188.

2 W. Fuß, K. K. Pushpa, W. Rettig, W. E. Schmid, and S. A. Trushin, Photochem. Photobiol. Sci., 2002, 1, 255.

Professor Kohler asked: Can you detect the temporary population of the charge transfer (CT) state by time-resolved emission? Also, the CT state and the ¹L_a state are argued to be different stationary points on the same surface. Yet, there is significant change in nuclear geometry upon forming the CT state. In light of this change, will the radiative transition probability of the CT state be decreased compared to that of the ¹L_a state?

Dr Fuß replied: We did not try to detect fluorescence of the CT state. In our scheme it is expected to have a quantum yield a little below 10⁻⁴, the ratio of τ₃ over the radiative lifetime. To discriminate it against L_b fluorescence (expected quantum yield ≈ 0.1 under our conditions), it will be best to separate the emissions spectrally and resolve them in time. Such an experiment has been done with dimethylaminobenzonitrile in hexane, where the relative energies should be similar as in the gas phase, and a temporary emission was assigned to the CT state.¹ The oscillator strengths f carried by the L_a and CT states are indeed quite different: Assuming the twist as reaction coordinate, they were calculated² to f(L_a) = 1 and f(CT) = 0.06, in reasonable agreement with experimental observations. Instead of the geometry, one can invoke for interpretation also a different electronic parentage for the two states (as done in the main text): Along the twist coordinate, the L_a surface would rise and a higher-lying surface with more CT character (being π-antibonding between the amino group and benzene, in contrast to the L_a state) would go down; in the plane of the reaction coordinate they have an avoided crossing (Fig. 3 in ref. 3), resulting in two stationary points with different parentage and properties on the lower surface.

1 W. M. Kwok, C. Ma, D. Phillips, P. Matousek, A. W. Parker, and M. Towrie, J. Phys. Chem. A, 2000, 104, 4188.

2 R. Cammi, B. Mennucci, and J. Tomasi, J. Phys. Chem. A, 2000, 104, 5631.

3 W. Fuß, K. K. Pushpa, W. Rettig, W. E. Schmid, and S. A. Trushin, Photochem. Photobiol. Sci., 2002, 1, 255.

Professor Sundström asked: Did you excite the L_b state directly and can you then see the L_b ⇌ CT equilibration? That should tell something about the L_b–CT barrier.

Dr Fuß responded: We only excited the L_a state. A reaction L_b → CT would be endothermic in the gas phase and would require sufficient excess energy. The L_b state of a number of molecules has been studied spectroscopically in a cold supersonic beam (see the recent work on PBN¹). Spectral congestion beginning at an excess energy ≥1000 cm⁻¹ was suggested to indicate approaching the barrier to the L_b → CT reaction. It can also be interpreted as an approach to the (lower cone of the) conical intersection, which is, however, closely related to this barrier.

1 L. Belau, Y. Haas, and W. Rettig, Chem. Phys. Lett., 2002, 364, 157.

Professor Buma said: Did you expect that studying these molecules as van der Waals complexes with polar solvent molecules will shed more light on your decay dynamics? After all, the energy of the CT state will be significantly affected. Do you have any indication how much the CT state is above the ‘L_B state?

Dr Fuß answered: In van der Waals complexes, the L_a and CT states are probably more lowered than the L_b state. But the initial slopes are not expected to change much, so that τ₁ and τ₂ would be similar. τ₃ would probably lengthened, if the CT state is lowered enough that the CT → L_b relaxation becomes endothermic. But energetic considerations are not sufficient: Some intramolecular dynamics seems to be hindered in the cold cluster, and the hindrance can only be overcome with excess energy¹.

1 H. Saigusa, E. Iwase, and M. Nishimura, J. Phys. Chem. A, 2003, 107, 3759.

Professor Martinez asked: You have said that there are no dark states in photoionization. But surely they are not all equally bright? To what extent are your experiments affected by the variation of photoionization cross-sections, which could depend on molecular geometry and the electronic character of the state being ionized, for example?

Dr Fuß replied: We imagine that with nonresonant (long-wavelength) ionization, the ionization probability is mainly a matter of the ionization energy, i.e., the vertical difference of electronic energies of the neutral molecule in the given state and the parent ion. This difference increases (and the ionization cross section will decrease) on downward relaxation. But it also increases with displacement (e.g., toward the CT state, or during vibration), because vertical ionization will lead to a higher part of the ionic potential; i.e., geometry affects the ionization potential and cross-section via the Franck–Condon principle. Ionization at 810 nm from the ground state is typically four orders of magnitude less efficient than from the state excited at 270 nm (requiring for ionization three photons fewer than S₀). In relaxation among excited states with their small energy differences (≤0.6 eV for PYRBN and ≤0.3 eV for PBN), the variations are much smaller (less than a factor of 4 at 810 nm, see Table 1 in the text). But longer probe wavelengths (1.3 and 2.1 μm) improve the discrimination between the different states. It is remarkable that even a small-amplitude vibration can modulate the ionization probability.

In order to derive time constants and vibrational frequencies, it is in principle not necessary to know whether more parameters than only the ionization energy affect the ion yields. It was, however, pointed out by the Stolow group (including Dr Stolow’s paper at this meeting) that ionization by one or very few photons (shorter probe wavelengths than we used) from a two-electron excited state does not lead to the ionic ground state; the ionization cross section will therefore certainly be smaller than for a one-electron excited state.

Dr Soep made a general comment: Experimental work aimed at probing the passage at conical intersection should use diagnostics capable of characterising the shift in electronic configurations that describe the intersection. Along the descent from the initial state to the relaxed state the system experiences a continuous change in configuration as the system evolves. This should be probed with a tool directly sensitive to the traversed electronic states. Photoelectron spectroscopy represents this ideal tool for the investigation of electronic relaxation as shown by Hayden², Stolow¹ and others for the study of ultrafast electronic relaxation. Electron imaging³ provides in addition a great sensitivity which is essential for the use of the lowest laser powers. We wish to report here the potential of this technique combined with the use of femtosecond lasers, to investigate the passage from a valence initial configuration to a zwitterionic one in a substituted ethylene, namely tetrakis (dimethyl amino) ethylene (TDMAE). This relaxation pathway is known to represent the key mechanism leading to the internal conversion of excited ethylenes to the ground state. The present molecule, TDMAE, has a low ionisation potential, hence a well characterised zwitterionic state. The molecule is excited at 266 nm by a femtosecond laser at the red edge of the valence band, and is ionised with an 800 nm photon. Both lasers have 100 fs FWMH cross correlation width. In the figure, which represents the radially integrated image as a function of pump/probe laser delay, one observes on the low energy side, close to 0 eV, a decay of ∼200 fs. This is due to the direct ionisation of the valence “state” by one 800 nm photon. In turn next to it in energy, the zwitterionic configuration at ∼0.6 eV, grows in with an 800 fs time constant, as probed by two 800 nm photons. The missing step in the decay mechanism is then well brought into evidence by the observation at ∼1.2 eV of a band that grows in at a 200 fs rate and decays at a 800 fs rate. This band likely arises from a Rydberg “state” that links the valence and zwitterionic “states”. This shows the need of a powerful tool for the detailed description of a well known decay mechanism.

Fig. 1 Electron imaging of the time evolution of TDMAE excited at 266 nm and probed at 800 nm. The electron signal is radially integrated and displayed as a function of the pump/probe delay in fs.

1 V. Blanchet, M. Z. Zgierski, T. Seideman, and A. Stolow, Nature, 1999, 401, 52.

2 C. C. Hayden and D. W. Chandler, J. Phys. Chem., 1995, 99, 7897.

3 A. T. J. B. Eppink and D. H. Parker, Rev. Sci. Instrum., 1997, 68, 3477.

Professor Tully opened the discussion of Professor Köppel’s paper: The transformation to a diabatic representation is a valid procedure to remove singularities in the nonadiabatic coupling. However, to then neglect the remaining, non-removed, couplings may introduce errors. It would be valuable to carry out systematic, full quantum calculations to evaluate the importance of the non-removed couplings, as well as the importance of second derivative couplings which are also usually discarded.

Professor Köppel replied: For specific cases (nonadiabatic photodissociation of ozone¹ and quadratic Jahn–Teller effect²) we have performed companion calculations with full neglect and partial inclusion of the non-singular derivative couplings. The results agree very well.^1,2 Therefore, also the other non-removed couplings, which are all non-singular, are expected to play only a minor role for the dynamics of these systems. A similar remark holds for the second-order derivative couplings, where again the singular part is included in our treatment. Rigorous general conclusions can apparently not be drawn from numerical calculations on specific systems.

1 H. Köppel, J. Gronki and S. Mahapatra, J. Chem. Phys., 2001, 115, 2377

2 A. Thiel and H. Köppel, J. Chem. Phys., 1999, 110, 9371

Professor Truhlar addressed Professor Tully: The goal of diabatic transformation is to make the nonadiabatic coupling (nuclear momentum and kinetic energy coupling) small or negligible for the problem under consideration. In discussing diabatic transformations that remove a part of the nonadiabatic coupling, I believe it is important to distinguish various categories of nonadiabatic coupling: the singular term all along the seam of a conical intersection, the singular term at one point on the seam, the rest of the removable part of the coupling, and the nonremovable part. All diabatic transformations do not remove all of the removable coupling. Our transformation¹ removes the singular term in the nonadiabatic coupling everywhere, and it removes a portion of the rest of the removable coupling. We showed that, even in non-Born–Oppenheimer systems, non-singular contributions to the removable nonadiabatic coupling and the nonremovable part of the coupling are the same order of magnitude as each other as the Born–Oppenheimer breakdown terms in cases where the Born–Oppenheimer approximation is a good approximation.¹ Although one should be careful of formal analysis, and although small terms are sometimes important, this gives a general argument that the unremoved part of the coupling in our treatment is often small for nonadiabatic systems.

My question for Professor Köppel is concerned with this point. For the general multidimensional case, when the conical intersection does not correspond to a high-symmetry subspace, your transformation removes the infinite nonadiabatic coupling only at one point on the conical intersection seam.The questions are: (1) Is there a way to generalize this to remove all the infinite coupling? (2) Are there any dynamics calculations that indicate that such a diabatic representation is useful even when it does not remove all the infinite coupling?

1 H. Nakamura and D. G. Truhlar, J. Chem. Phys., 2003, 118, 6829

2 B. K. Kendrick, C. A. Mead, and D. G. Truhlar, Chem. Phys., 2002, 277, 31

Professor Köppel replied: (1) The current proposal for the general multidimensional case, when the conical intersection does not correspond to a high-symmetry subspace, amounts to a simplified treatment which is not claimed to be of the same accuracy as for the symmetry-allowed case (where all infinite couplings are removed). It is hoped to be useful for larger systems where the ab initio determination of all derivative couplings is not feasible computationally. When all singular couplings are known, the present construction scheme can be generalized to remove them entirely (work in progress).

The calculations asked for in question (2) are not known to me at present, although indirect evidence suggests that a diabatic representation may be useful even if it does not remove all the infinite coupling (e.g. the effect of infinite couplings may be only minor, as is the case for low-energy motion near the minimum of the seam of NO₂(X ²A₁–A ²B₂)—see, for example, ref. 1.

1 S. Mahapatra, H. Köppel, L. S. Cederbaum, P. Stampfuß and W. Wenzel, Chem. Phys., 2000, 259, 211.

Dr Woywod commented: The interstate coupling parameters λ are a critical component of Professor Köppel's approach for the construction of regularized diabatic states. The λ need to be determined accurately by electronic structure calculations for the method to work properly. I would like to address aspects of the numerical evaluation of λ, in particular the case of symmetry-allowed conical intersections. The paper provides formulas for deriving λ from the adiabatic potential energy surfaces V₁ and V₂ alone, without requiring information on the wave functions themselves.

Eqn. (25) of the paper states that, at a conical intersection, where Q_u denotes a displacement along a coupling coordinate and ΔV₍₁₎ is the part of ΔV = (V₁ − V₂)/2 that depends linearly on Q_u. Since ΔV → ΔV⁽¹⁾ at the intersection, λ can in general be obtained precisely by performing electronic structure calculations of V₁ and V₂ at small displacements Q_u and replacing ΔV⁽¹⁾ by ΔV in eqn. (25). However, the fact that eqn. (25) is obtained in the framework of the linear vibronic coupling (LVC) model, which is manifest in that only the first order part of ΔV contributes to eqn. (25), can lead to errors in λ since higher order terms ΔV^(k) with k ≥ 2 are neglected. It is characteristic for symmetry-allowed conical intersections that the electronic states are transforming as different irreducible representations as a function of the tuning coordinate Q_g with Q_u = 0. The LVC assumption that both diabatic oscillators have identical coupling mode frequencies built into eqn. (25) does therefore not generally hold. Of importance in this context are the so-called diagonal quadratic coupling coeffcients γ⁽ⁿ⁾ that define the curvature (ω₀ + γ⁽ⁿ⁾)/2 of the diabatic oscillators in the Q_u direction in the harmonic approximation (ω₀ denotes the frequency of the coupling mode in the electronic ground state).

In many cases, Δγ = γ⁽¹⁾ − γ⁽²⁾ will differ significantly from zero. The analysis of eqn. (25) provided by ref. 1 shows that the error in λ depends quadratically on Δγ and Q_u.

This indicates that determining λ numerically via eqn. (25) will usually be quite accurate since very small displacements Q_u are sufficient. The influence of additional errors arising from nonconsideration of bilinear and higher order terms in the formulation of eqn. (25) has not been investigated in ref. 1.

The paper in addition presents eqn. (30) for estimating λ at geometries that belong to the high-symmetry subspace but do not include the eigenvalue crossing, that is, the electronic energies differ by ΔE if Q_u = 0:

This equation also results from the LVC ansatz and implies Δγ = 0. In practice, eqn. (30) can be utilized in two ways: If accurate expressions are available for V₁ and V₂ then λ can be calculated analytically, otherwise V₁ and V₂ need to be determined by electronic structure methods for small displacements along Q_u followed by an approximate evaluation of eqn. (30) via finite differences. For both applications of eqn. (30), ref. 1 examines deviations of λ from the true value that are induced by Δγ ≠ 0. If V₁ and V₂ can be directly differentiated any error arising from discretization along Q_u will be avoided from the outset, but the linear dependence of the error on both ΔE and Δγ must be taken into account. Analysis of the finite difference version of Eq. (30) reveals the presence of a Q_u-dependent and a Q_u-independent component of the error in λ. The discretization error component increases quadratically with Δγ and Q_u. The Q_u-independent error term, in contrast, is a linear function of Δγ and ΔE.

Consideration of only one but important possible source of error, Δγ ≠ 0, thus leads to the conclusion that no pronounced inaccuracies will arise in the finite difference evaluation of λ at a conical intersection via application of eqn. (25) since Q_u can be kept very small and the limit Δγ and ΔE can be approached. The situation is quite different in the case of eqn. (30), where large values of Δγ and ΔE can impose serious deviations, even if analytical expressions are given for V₁ and V₂. If eqn. (30) needs to be evaluated numerically an additional error term scaling with Q²_u appears that may not be completely negligible because larger displacements along Q_u will be required for determining the second derivative as compared to the evaluation of the first derivative according to eqn. (25).

1 C. Woywod, unpublished work.

Professor Köppel replied: The determination of λ in the LVC approach may indeed suffer from possible ambiguities due to different curvatures of the potential energy surfaces along the coupling mode. However, as already stated by Dr Woywod, this problem does not occur at the crossing itself where the energy gap ΔE vanishes and the nonadiabatic couplings become infinite. Only the latter couplings are explicitly considered in the concept of regularized diabatic states, and they are thus not affected by the ambiguity in question. Away from the seam, different choices of λ amount to a different treatment of the non-singular couplings only. As stated in response to Professor Tully's question this has been found to have only very minor influence on the dynamics (for the case of the Chappuis band of ozone, cf. Fig. 3 of ref. 1). It should also be kept in mind that different choices of λ amount to different adiabatic-to-diabatic mixing angles only, while the adiabatic potential energy surfaces remain strictly identical within the concept of regularized diabatic states.

1 H. Köppel, J. Gronki and S. Mahapatra, J. Chem. Phys., 2001, 115 2377

Mr Evenhuis commented: The computational cost of non-adiabatic coupling matrix elements is now of the same order of a single point energy calculation. The non-adiabatic coupling matrix elements can be used in the expansion of the diabatic potential matrix. The diabatic potential matrix can be written as

As pointed out, this matrix is analytic and can therefore be expanded as a Taylor series. The first order Taylor series expansion coefficents for W can be written as
The diabatic representation is undetermined up to a rotation. For clarity we set α to 0,
In terms of the g and h vectors this is simply
which agrees with results from eqns. (24)–(27). This can be easily extended to second order
All of these quantities can be obtained from finite differences of ab initio calculations of the energy gradients and the derivative coupling or of the g and h vectors.

The second order expansion of W describes the curvature in the seam of conical intersections. Local Taylor series expansions from several points can be used to describe more complex seams of conical intersections. However the change in the adiabatic–diabatic transformation (ADT) angle between the points must be known so that the local expansions are consistent.

Professor Köppel replied: This comment seems to agree with my work, at least as far as the first-order couplings and a general conical intersection are concerned. While in Section 2.2 of the paper a simplified treatment is proposed, relying only on the derivative couplings at the minimum of the seam, this may be generalized when all couplings are known (as also mentioned in the reply to Professor Truhlar). On the other hand, for the symmetry-allowed case the further simplification presented in Section 2.3 of my paper seems very attractive, especially for larger systems. There, the computation of all derivative couplings is still cumbersome, in particular when required on a multidimensional grid. This holds the more for the second-order derivative couplings, where, again, the singular terms are correctly treated in the symmetry-allowed case. The cost-effectiveness of their ab initio determination (i.e. the additional accuracy gained in relation to the additional computational cost) seems quite unclear at present.

Professor Tapia commented: An exact basis function does not depend parametrically on nuclear configuration space (Q). A separability is imposed via quantum numbers first: the electronic (j) and subsidiary nuclear quantum numbers (k(j) ≡ jk); then Φ_j(q,Q) → ψ_j(q)χ_jk(Q). In a semiclassical approximation, the nuclear charges are represented by a positive charge background (PCB) in real 3D-space (ξ). The model electronic Hamiltonian H_e(q,ξ) being self adjoint can be diagonalised; a complete set of eigenfunctions defines a set of intrinsic diabatic (ID) basis functions {ψ_j(q)}. The ID potential is E_j(ξ) =〈ψ_j|H_e(q,ξ)|ψ_j〉_q. Some ID basis functions are confining and some other correlate with asymptotic states. The latter states are anti-bonding (and produce repulsive ID potential energy functions). These states are absent in the standard approach. The minimum energy geometry of the lowest confining state can be used to construct an ID basis set or a subset. The number of nodes, local symmetries and parity of the ID basis functions are conserved; only the ordering of {E_j(ξ)} depends upon ξ.

Professor Köppel replied: The model Hamiltonian H_e(q,ξ) in question should contain information about the nuclear configurations Q. If the ID basis functions are strictly independent of Q and/or ξ, this may derive from some continuous charge-background assumption as is possibly implied also by the phrasing (semiclassical approximation, charge background) of Professor Tapia. In this case, it would not be clear how actual molecular structures and properties can be reliably described by this approach. Further information would be needed on this point.

Professor Yarkony addressed Professors Tapia and Köppel: The question is: when is a diabatization exact? Professor Greene pointed out that any set of geometry independent basis states is diabatic. On the other hand this basis must be much larger than the adiabatic basis to obtain equivalent results. Therein lies the rub since a transformation to diabatic states can only be exact when there is no truncation.

The general proof is in ref. 1. The two state problem is representative. The rotation angle θ must satisfy

∇θ(R) = f^kl(R) = 〈ϕ_k(r;R)|∇_Rϕ_l(r;R)〉_r

where r denotes the electronic coordinates, R denotes the N^int internal nuclear coordinates X₁,…,X_N^int and ∇_R = (∂/∂X₁,∂/∂X₂,…,∂/∂X_N^int). Then, taking curl of θ(R)
The last sum will vanish for all R provided the range on m is k,l, that is the transformation is square.

1 C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1982, 77, 6090.

Professor Köppel responded: I agree with the comment of Professor Yarkony. As an additional supporting argument consider the (infinite) potential energy matrix generated by geometry-independent electronic basis states. This matrix in general has no particular block structure beyond standard point group symmetry. The quasi-diabatic potential energy matrix, one is usually seeking for, should act in a small electronic function space, and matrix elements with other electronic wave-functions should vanish. Thus it consists of much smaller blocks than in the former case, and the two sets of electronic wave-functions are usually different. The limitation to small electronic function spaces is crucial in practical applications. For more details see, for example, ref. 1.

1 T. Pacher, L.S. Cederbaum and H. Köppel, Adv. Chem. Phys., 1993, 84, 293.

Dr Zhu addressed Professor Köppel: You have shown a couple of tested cases in which the exact and the approximate diabatic basis could give the same results for the spectra. If we think of problems from the point of view of trajectory surface hopping, most trajectories (say 95%) do not intersect with the conic seams. So, I guess that the tested cases you showed are not sensitive to the approximation you have made. For example, if you could find the case in which most trajectories intersect with conic seams, it will be a definitive test for your approximate diabatic basis.

Professor Köppel replied: The present applications and test cases are all based on a quantal treatment of the nuclear motion. Thus they go, of course, even beyond an ‘infinite set of trajectories’, including those that intersect the conical seam. Given the quantal solution there is apparently no need to specifically focus on trajectories intersecting the seam.–More generally, since the present approach treats the singular couplings exactly, nuclear motion focussing on the seam should be treated with increasing accuracy since it is more and more governed by the singular couplings.

Professor Balint-Kurti and Dr Baloitcha made a general comment: Professor Köppel has presented a very interesting method for finding diabatic potentials in the vicinity of a general conical intersection. We would like to present some of our calculations on such a conical intersection between two of the excited electronic states of ozone. Fig. 2 shows a cut through the lowest five adiabatic ¹A′ potential energy curves of ozone with one of the O–O distances fixed at R₁ = 2.4 a₀ and the O–O–O angle fixed at 117°. The cut shows clearly that there are many crossings or closely avoided crossings.

Fig. 2 Cut through the lowest five adiabatic¹A′ potential energy curves of ozone with one of the O–O distances fixed at R₁ = 2.4 a₀ and the O–O–O angle fixed at 117°.

In the next figure (Fig. 3) we have reassigned the points on the curves to correspond to diabatic surfaces.

Fig. 3 Cut through the lowest¹A′ diabatic potential energy curves of ozone with one of the O–O distances fixed at R₁ = 2.4 a₀ and the O–O–O angle fixed at 117°.

We have examined, in detail the region of the crossing circled in the above diagram. Our purpose was to show that there was in fact a conical intersection close to this point in configuration space.

Fig. 4 shows the energy difference between the two energy levels as a function of the bending angle with the two O–O distances fixed at R₁ = 2.4 and R₂ = 2.869 a₀ respectively. The smallest difference we have succeeded in finding between the two electronic state energies is 5.5 × 10⁻⁶E_h. The shape of the energy difference curve in the figure is pleasingly similar to the cone-like shape expected close to a conical intersection.

Fig. 4 Energy difference between the first two excited¹A′ energy levels of ozone as a function of the bending angle with the two O–O distances fixed at R₁ = 2.4 and R₂ = 2.869 a₀ respectively.

Fig. 5 shows a contour plot of the same energy difference in the vicinity of the conical intersection with one of the O–O distances held fixed at 2.4 a₀. The main feature of the contour plot is the parallel nature of most of the lines. The oval contours in the centre of the plot may be a plotting artefact arising from the fact that the plot is based on only a small number of data points. The main conclusion to be drawn from the plot is that the locus of the conical intersection runs approximately down the centre of the diagram parallel to the majority of the contour lines.

Fig. 5 Contour plot of the energy difference between the first two excited ¹A′ energy levels of ozone with one of the O–O distances fixed at R₁ = 2.4 a₀.

The calculations on which the above energies are based are multireference configuration interaction (MRCI) calculations performed using the MOLPRO¹ code, using a specially augmented valence triple zeta basis set. The calculations used 153 primitive atomic orbitals and 349.9 million uncontracted configurations. Important aspects of the calculations were that they did not utilise any correction for size consistency and they used a specially augmented configuration reference space for the MRCI calculations. It was found that these special measures were essential to obtain reliable results close to the conical intersection. In the region of space examined the principal molecular orbital configurations of the two states participating in the conical intersection are …(8a′)²(9a′)(10a′)(1a″)²(2a″)²(3a″)² and …(a′)²(9a′)²(10a′)²(1a″)²(2a″)(3a″). The conical intersection discovered here will play a very important role in the photodissociation dynamics associated with the Hartley bands of ozone. It is also likely that other closely avoided crossings shown in Figs. 2 and 3 are associated with conical intersections.

1 MOLPRO is a package of ab initio programs written by H.J. Werner and P.J. Knowles, with contributions from J. Almlöf, R.D. Amos, A. Berning, D.L. Cooper, M.J.O. Deegan, A.J. Dobbyn, F. Eckert, S.T. Elbert, C. Hampel, R. Lindh, A.W. Lloyd, W. Meyer, A. Nicklass, K. Peterson, R. Pitzer, A.J. Stone, P.R. Taylor, M.E. Mura, P. Pulay, M. Schütz, H. Stoll, and T. Thorsteinsson.

Professor Yarkony addressed Professor Balint-Kurti: The accuracy of the location of a point of conical intersection of states k,l can be determined by using series of circles of whose radius approaches zero. For each circle the conceptually simplest test is to check the geometric phase effect that is if the wave function changes sign around the loop a conical intersection is enclosed. However, determining the overlap of wave functions involving sets of molecular orbitals that are nonorthogonal is computationally challenging. Instead we prefer¹ to check that

1 D. R. Yarkony, J. Phys. Chem. A, 1997, 101, 4263.

Professor Ashfold made a general comment: Köppel presents new results concerning non-adiabatic interactions between the S₂ and S₁ states of C₂H₂, but I would not wish this audience to be under the misconception that nuclear dynamics following excitation to the S₁ potential energy surface (PES) is a ‘closed book’. We would be very keen to see further detailed investigations of the possible non-adiabatic couplings involving the S₁ state of C₂H₂, at energies just above the first dissociation threshold for forming H + C₂H(X) products. We have applied the technique of H (Rydberg) atom photofragment translational spectroscopy (PTS) to C₂H₂ photolysis at wavelengths in the range 205 ≤ λ_phot ≤ 220 nm, (i.e. within the Ã ← X̃ absorption system, at energies close above this fragmentation threshold).^1–3 The H atom time-of-flight (TOF) spectra so obtained and, as Figs. 6 and 7 illustrate, the photofragment total kinetic energy release (TKER) spectra derived from the TOF spectra, show resolved structure – which can be attributed to formation of different rovibrational states of the C₂H(X) product. Analysis of such TKER spectra shows that, at any given λ_phot, the C₂H(X) products are formed in all bending (v₂) vibrational states allowed by energy conservation and that, within these states, there is a clear preference for populating levels in which the axial projection of this vibrational angular momentum is maximised (l = v₂). As Fig. 6 illustrates, the recoil velocity distributions of the H + C₂H(X) products show a marked angular anisotropy – particularly in the case of those channels that lead to formation of C₂H products in low rotational quantum states. Guided by the calculations of Cui and Morokuma⁴ we rationalised these observations by invoking two non-adiabatic pathways from the initially populated S₁ state to the H + C₂H(X) products. One involved sequential coupling from S₁via the manifold of triplet states (T₃, T₂ and then T₁) en route to dissociation. The observed propensity for forming C₂H products with l ∼ v₂ matched theoretical predictions that torsional motions play an important role in promoting the successive non-adiabatic interactions. The specific population of low rotational states with high recoil anisotropy we attributed to a second process, involving direct non-adiabatic coupling between S₁ and T₁, and subsequent fragmentation from a structure in which the breaking bond formed part of a near linear CCH moiety. The S₁ ← S₀ absorption spectrum of C₂H₂ at these energies shows predissociated rovibronic structure, much of which has been interpreted. Given the product state resolution that is also achievable experimentally, the S₁ state of C₂H₂ could still be a very attractive model system for exploring further details of the effects of non-adiabatic coupling in molecular photofragmentation processes.

Fig. 6 TKER spectra of the H + C₂H(X) products arising in the photolysis of jet-cooled C₂H₂ molecules at (a) 211.75 nm and (b) 211.51 nm with, in both cases, the electric (ε_phot) vector of the photolysis radiation aligned parallel to the detection axis. The combs superposed above the two TKER spectra label the individual rotational (N) levels associated with the ground (v₂ = 0) and first excited (v₂ = 1) vibrational levels of the C₂H(X) product.

Fig. 7 TKER spectra of the H + C₂H(X) products arising in the photolysis of jet-cooled C₂H₂ molecules at 205.54 nm, with ε_phot aligned (a) parallel and (b) perpendicular to the TOF axis. In preparing this figure the two spectra have been normalised to the same maximum peak height but, for the same incident light intensity, the 2190 cm⁻¹ peak in (a) is actually ∼2.5 times stronger than in (b).

Child posed the question as to whether there are any well-studied polyatomic molecular photofragmentations that involve one or more radiationless transitions that do not proceed via a conical (or seam of) intersection. Experience suggests that, upon sufficiently careful inspection, few if any such systems will exist, though the detailed fragmentation mechanism for CH₄(S₁) molecules continues to intrigue. Liu and co-workers^5,6 and our group⁷ have investigated H atom loss processes from CH₄ following excitation at 121.6 nm and concluded that the fragmentation involves radiationless transfer to both the T₁ and S₀ states, on timescales that are sufficiently rapid that the H atom recoil velocity distribution shows (kinetic energy dependent) spatial anisotropy. The details of the relevant S₁ [long arrow, wavy then straight] T₁ and S₁ [long arrow, wavy then straight] S₀ coupling mechanisms remain unclear, however.

1 D. H. Mordaunt and M. N. R. Ashfold, J. Chem. Phys. 1994, 101, 2630.

2 S. H. S. Wilson, C. L. Reed, D. H. Mordaunt, M. N. R. Ashfold and M. Kawasaki, Bull. Chem. Soc. Japan 1996, 69, 71.

3 D. H. Mordaunt, M. N. R. Ashfold, R. N. Dixon, P. Loeffler, L. Schnieder and K. H. Welge, J. Chem. Phys. 1998, 108, 519.

4 Q. Cui and K. Morokuma, Chem. Phys. Lett. 1997, 272, 319.

5 J.-H. Wang and K. Liu, J. Chem. Phys. 1998, 109, 7105.

6 J.-H. Wang, K. Liu, Z. Min, H. Su, R. Bersohn, J. Preses and J. Z. Larese, J. Chem. Phys. 2000, 113, 4146.

7 P. A. Cook, M. N. R. Ashfold, Y.-J. Jee, K.-H. Jung, S. Harich and X. Yang, Phys. Chem. Chem. Phys. 2001, 3, 1848.

Professor Köppel asked: (a) The nonadiabatic photodissociation of acetylene may also proceed through a S₀–S₂ conical intersection and needs thus not involve the triplet states.¹ Do you have evidence for or against this process? May I draw attention to our own results in this Discussion on the S₁–S₂ intersection in acetylene and to new results of Baer et al. in this Discussion on the S₀–S₂ intersection.

(b) In an earlier theoretical treatment² we have predicted strong excitation of the C–C stretching mode in the S₀–S₁ absorption. Do you find similar evidence from your experimental data?

1 Q. Cui, K. Morokuma and J. F. Stanton, Chem. Phys. Lett., 1996, 263, 46.

2 K. Malsch, G. Hohlreicher, R. Schork and H. Köppel, Phys. Chem. Chem. Phys., 2001, 3, 5393.

Professor Ashfold replied: Non-adiabatic coupling via a conical intersection linking the S₀ and S₂ potential energy surfaces (PESs), as predicted by Cui et al.,¹ was considered as another possible route to the H + C₂H(X) products observed in our PTS studies of the near threshold dissociation of C₂H₂. However, the calculated energy of the S₀/S₂ intersection (∼6.1 eV) is considerably higher than that of the highest barrier (∼5.65 eV)² in the minimum energy path involving triplet PESs. If these predicted energies are accurate, S₀–S₂ coupling is unlikely to provide a significant contribution to the overall dissociation yield close to threshold.

The H atom PTS experiment provides information about propensities for forming different quantum states of the fragmentation products. Experimental insights into the S₁ ← S₀ transition of C₂H₂ comes from absorption³ and resonance enhanced multiphoton ionization⁴ spectroscopy studies, both of which show the spectrum to be dominated by long progressions in the trans-bending vibration, ν^′₃, supplemented by progressions involving ν^′₃ in combination with ν^′₂ (the C–C stretching vibration).

1 Q. Cui, K. Morokuma and J. F. Stanton, Chem. Phys. Lett. 1996, 263, 46.

2 Q. Cui and K. Morokuma, Chem. Phys. Lett. 1997, 272, 319.

3 J. C. Van Craen, M. Herman, R. Colin and J. K. G. Watson, J. Mol. Spectrosc. 1986, 119, 137, and references therein.

4 A. J. Orr-Ewing, R. A. Morgan, S. H. S. Wilson, C. L. Reed and M. N. R. Ashfold, J. Chem. Soc. Faraday Trans. 1995, 91, 3327.

Professor Yarkony addressed Professor Ashfold: The question was raised whether examples of radiationless decay that do not involve conical intersections are known. The sudden quenching of the fluorescence from the B state of vinoxy (CH₂COH) was shown in ref. 1 to be just such an example.

1 S. Matsika and D. R. Yarkony, J. Chem. Phys., 2002, 117, 7198.

Ms Miller addressed Professor Yarkony: Our new experimental results¹ on the photodissociation of chloroacetaldehyde (CH₂ClCHO) have some interesting consequences regarding the internal conversion of the vinoxy radical. Photodissociation of chloroacetaldehyde at 193 nm produces vinoxy radicals directly in the ground (X(²A″)) state, from which those radicals with sufficient internal energy go on to form CH₃ + CO exclusively, with no detectable branching to H + ketene (CH₂CO). In contrast, when Osborn, et al.² photoexcited vinoxy radicals to the B(²A″) state, they found H + ketene to be the dominant dissociation channel by a factor of approximately 4∶1. Clearly, their assumption that the B state vinoxy radicals dissociate via internal conversion to the ground electronic state is not correct. By considering Matsika and Yarkony's calculations³, which suggest that the B state vinoxy radical undergoes internal conversion to the A(²A′) state via an avoided crossing, one can arrive at a better understanding of the Osborn et al. results. In the dominant electronic configuration of the A state vinoxy radical, the unpaired electron is in an in-plane orbital localized on the O atom. From this state it is electronically facile to break the in-plane C–H bond to form ketene + H. Therefore, if the B state vinoxy radical underwent internal conversion to the A state, rather than to the ground state, this would explain Osborn et al.'s observation of H + ketene as the dominant dissociation channel. In our experimental work, we found that branching to H + ketene was dramatically suppressed in the dissociation of ground state vinoxy radicals, for the following reason: in the dominant electronic configuration of the ground state vinoxy radical, the unpaired electron is in an a″ orbital localized on the terminal C atom, so the electronically diabatic C–H bond fission product in planar geometry is triplet ketene, which is not energetically allowed. We believe that electronically nonadiabatic recrossing of the C–H fission transition state contributes to the supression of the H + ketene dissociation channel of the ground state vinoxy radical

1 J. L. Miller, L. R. McCunn, M.J. Krisch, L.J. Butler and J. Shu, J. Chem. Phys., in press.

2 D.L. Osborn, H. Choi, D.H Mordaunt, R.T. Bise, D.M. Neumark and C.M. Rohlfing, 1997, J. Chem. Phys., 106, 3049.

3 S. Matsika and D. R. Yarkony, J. Chem. Phys., 2002, 117, 7198.

Professor Baer opened the discussion of Dr Liu’s paper: In his presentation Dr Liu suggested that his experimental enhanced rates for the reaction F(²P_1/2) + HD → HF(v = 3) + D are caused by a van-der-Waals potential well formed by the products, (HF(v = 3), D). In other words, the enhanced reaction is due to van-der-Waals potential wells in the exit channel.

We claim that a series of quantum mechanical (QM) calculations indicate that it is not the van-der-Waals potential well(s) in the exit channel that is (or are) responsible for this enhancement but a combination of a narrow barrier and a van-der-Waals potential well located in front of it, in the entrance channel.

A few years ago Rosenman et al.¹ established the fact that the Stark–Werner potential energy surface² which governs the reactions F(v = 0) + X₂ → XF(v′) + X; X = H,D possesses an adiabatic potential barrier (APB) which is high enough (∼0.88 kcal mol⁻¹) that, in principle, it can prevent the reaction at low enough energies (i.e.E < 20 meV). However the full 3D QM treatment¹ of these processes did not support this expectation and, in fact, showed that the reaction threshold is practically at E ∼ 0. Analysis indicates that the reason for this unusually low threshold is likely to be due to a rare situation where the APB is narrow enough to enable tunneling, for the hydrogen and to a lesser extent the deuterium, and that this process is enhanced by a van-der-Waals potential well situated (in the reagents channel) just in front of the barrier. Thus according to this explanation the van-der-Waals potential forms Feshbach-type resonances³ which keep the three interacting atoms (F,X,X) long enough together so that the tunneling process is enhanced by many orders of magnitudes.

This proposition was probed in subsequent publications^4,5 and was found to be valid. Recent QM calculations carried out for the F(v = 0) + HD → F(v′)H(D) + D(H) reactions yield further support for the existence of the combination of the van-der-Waals potential well (in the entrance channel) and the enhanced tunneling process.^6,7 In this respect I would like also to mention the detailed study of Balakrishnan and Dalgarno who formed a model that revealed these features in a simple and elegant way.⁸

1 E. Rosenman, S. Hochman-Kowal, A. Persky and M. Baer, Chem. Phys. Lett., 1996, 257, 421.

2 K. Stark and H-J. Werner, J. Chem. Phys., 1996, 104, 6515.

3 M. Baer, in The Theory of Chemical Reaction Dynamics, ed. M. Baer, CRC Press, Boca-Raton, FL, 1985, vol. I, p. 136.

4 E. Rosenman, A. Persky and M. Baer, Chem. Phys. Lett., 1996, 258, 639.

5 T. Takayanagi and Y. Kurasaki, Chem. Phys. Lett., 1998, 286, 35.

6 M. Baer, Chem. Phys. Lett., 1999, 312, 203.

7 D.H. Zhang, S-Y. Lee and M. Baer, J. Chem. Phys., 2000, 112, 9802.

8 N. Balakrishnan and A. Dalgarno, J. Phys. Chem., 2003, 107, 7101.

Dr Liu replied: The proposed interpretation for the non-adiabatic reaction of F*(²P_1/2) + HD → HF(v = 3) + D invokes a resonant tunneling mechanism from the presence of a Feshbach (or reactive) resonance, which has nothing to do the van der Waals potential well formed by the products. The resonance state here has previously been identified and its nature been elucidated,¹ approximately as three quanta excitation in the F–H bond and zeros in the bend and the H–D bond in the transition state region, which is not those in the van der Waals region of either the entrance or the exit channels.

1. R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2000, 112, 4536.

Professor Balint-Kurti asked: In your paper you conclude that for F + HD → HF(v = 3) + D the ground spin orbit state (F(²P_3/2)) is the more reactive. In the paper of Alexander et al. it is stated that for Cl + H₂ you found that the excited spin–orbit state of Cl was the more reactive. Is there any inconsistency in these two conclusions?

Dr Liu responded: The electronically-adiabatic correlation rule is a powerful route to predict the spin–orbit reactivity. But, it is a propensity rule, not a selection rule. Thus, our conclusion that for F(²P) + HD → HF(v = 3) + D the reactivity of the spin–orbit excited state (F(²P_1/2)) is finite but smaller than the ground spin orbit state (F(²P_3/2)) is entirely consistent with the conventional adiabatic correlation rule, and in accordance with the theoretical calculations.^2,3 On the other hand, our findings of an opposite propensity in spin–orbit reactivities for Cl(²P) + H₂ → HCl + H is totally unexpected and violating the adiabatic correlation rule, which have been amply discussed in our original papers.^4,5 Here, I merely wish to re-mention that the abnormal reactivities of Cl(²P) + H₂ is not unprecedented. In an isoelectronic ion-molecule reaction of Ar⁺(²P) + H₂(D₂) → ArH⁺(ArD⁺) + H(D), the excited Ar⁺(²P_1/2) ion was found to be more reactive than the ground Ar⁺(²P_3/2) ion.⁶ Yet, no such propensity was observed for the analogous reaction with Kr⁺(²P).⁷ To make situation more perplexing, in a recent study of Cl(²P) + CH₄(CD₄) → HCl(DCl) + CH₃(CD₃) the reactivity of the spin–orbit excited Cl(²P_1/2) state was found to be negligibly small.⁸ Clearly, we don't fully understand the spin–orbit reactivity in general, which nonetheless makes the study of non-adiabatic transition more exciting. Because the non-adiabatic transitions may involve various electrostatic, spin–orbit, and Coriolis couplings, detailed theoretical investigations and analysis are absolutely essential to our further understanding.

1 R. T. Skodje, D. Skouteris, D. E. Manolopoulos, S.-H. Lee, F. Dong and K. Liu, J. Chem. Phys., 2000, 112, 4536.

2 M. H. Alexander, D. E. Manolopoulos and H.-J. Werner, J. Chem. Phys., 2000, 113, 11 084.

3 Y. Zhang, T.-X. Xie, K.-L. Han and J. Z. H. Zhang, J. Chem. Phys., 2003, 119, 12 921.

4 S.-H. Lee and K. Liu, J. Chem. Phys., 1999, 111, 6253.

5 F. Dong, S.-H. Lee and K. Liu, J. Chem. Phys., 2001, 115, 1197.

6 K. Tanaka, J. Durup, T. Kato and I. Koyano, J. Chem. Phys., 1980, 73, 586; 1981, 74, 5561.

7 K. M. Ervin and P. B. Armentrout, J. Chem. Phys., 1986, 85, 6380.

8 J. Zhou, J. J. Lin, B. Zhang and K. Liu, J. Phys. Chem. A., 2004, in press, R. Bersohn memorial issue.

Professor Truhlar said: Your discussion argues that at a downward surface hop, there is a large increase in kinetic energy but an increase in nuclear angular momentum of at most ℏ. Thus one has high kinetic energy and low nuclear angular momentum. However, in practice the energy is released gradually, not at a single F–H₂ distance. Any portion of the energy that is released before reaching the maximum of the centrifugal barrier can enable higher partial waves to surmount this barrier, raising the angular momentum. Can you comment on the relative locations along the reaction path of the centrifugal barrier and location of electronic energy release?

Dr Liu replied: Professor Truhlar raised a very important question. I believe that in the present reaction the centrifugal barrier is located earlier than the location of electronic energy release. This is an early barrier reaction and there is a dynamically significant van der Waals potential well in the entrance channel. Although it is certainly true that the electronic energy release will not be at a single F–H₂ distance, numerous recent theoretical studies all suggested that the dominant non-adiabatic couplings occur within the entrance van der Waals well region.^1–4 At low collision energies (near the threshold region), the centrifugual barrier associated with the van der Waals well in the entrance channel could prevent the large impact parameter collisions from penetrating into the non-adiabatic transition region.

1 M. H. Alexander, D. E. Manolopolous and H.-J. Werner, J. Chem. Phys., 2000, 113, 11 084.

2 V. Aquilanti, S. Cavalli, F. Pirani, A. Volpi and D. Cappelletti, J. Phys. Chem. A, 2001, 105, 2401.

3 W. B. Zeimen, J. Klos, G. C. Groenenboom and A. van der Avoid, J. Chem. Phys., 2003, 118, 7340.

4 Y. Zhang, T.-X. Xie, K.-L. Han and J. Z. H. Zhang, J. Chem. Phys., 2004, 120, 6000.

Dr Soep commented: You have shown a nice correspondence between the hindered rotor states in FH₂⁻ and the scattering amplitude. There must be a threshold effect to allow such a correspondence.

Dr Liu replied: Yes, there will be threshold effects. In addition to the opening of the quantized transition states¹ at the reaction barrier (not to be confused with the Feshbach resonance state in this reaction, which is topologically located behind the barrier and is quasi-bound along the reaction coordinate), there will be a centrifugal shift associated with the large angular momentum incoming wavepacket. In a full collision experiment, the best way to detect such a correspondence might be to focus on the state-resolved differential cross sections in the forward direction, as illustrated in Fig. 4 of our paper. Other nice examples of this phenomenon include the recent studies of H + D₂ → HD + D (ref. 2) and H + HD → D + H₂ (ref. 3) reactions.

1. D. C. Chatfield, R. S. Friedman, D. W. Schwenke and D. G. Truhlar, J. Phys. Chem., 1992, 96, 2414.

2. S. C. Althorpe, F. Fernandez-Alonso, B. D. Bean, J. D. Ayers, A. E. Pomerantz, R. N. Zare and E. Wrede, Nature, 2002, 416, 67.

3. S. A. Harich, D. Dai, C. C. Wang, X. Yang, S. D. Chao and R. T. Skodje, Nature, 2002, 419, 281.

Professor Child said: I understand that the D products from F* + HD and F + HD are distinguished by time of flight, on the basis that the total energy for the F* reaction is higher than that for F. If the two reactions go through the same transition state resonance, why is there not a similar shift in the energy dependence of the two angular distributions?

Dr Liu responded: This is exactly the crux of this paper. Based on the conventional transition state theory and energetic arguments, one would have anticipated a similar shift in energy dependence to the energy splitting of the two spin–orbit states, F(²P_3/2) and F(²P_1/2). The proposed mechanism invokes resonant tunneling for which both energy and angular momentum must be conserved. Because of a range of impact parameters in a full collision experiment, there will be a (rotational) progression of resonance states (associated with any given reactive (vibrational) resonance state) with the energy levels approximately characterized by E_r(J) = E_r(J = 0) + BJ(J + 1). Note the one-to-one correspondence between the resonance energy E_r(J) and the resonance angular momentum J. At low collision energies, it is the mismatch between the energy and angular momentum of the incoming, “hopped” wave packets and those of the shifted resonance states making the two spin orbit reagents to exhibit different energy dependences.

Professor Connor remarked: (a) You have observed forward–backward angular scattering in the spin–orbit selected states of the F(²P) + HD → FH(v′ = 3) + D reaction. You also remark on the forward angle scattering that occurs in the related F + H₂ → FH(v′ = 3) + H reaction. (b)

I have recently examined¹ theoretically the forward angle scattering in the F + H₂ → HF(v′ = 3) + H reaction and shown that it is an example of a glory. The analysis was carried out for the state-to-state transition, F + H₂(v_i = 0, j_i = 0, m_i = 0) → FH(v_f = 3, j_f = 3, m_f = 0) + H, at a total energy of 0.3872 eV, where v_i, j_i, m_i and v_f, j_f, m_f are initial and final vibrational, rotational and helicity quantum numbers respectively. A uniform semiclassical analysis was carried out, which expresses the scattering amplitude in terms of Bessel functions of order zero and unity, together with nearside(N) and farside(F) cross sections and phases. The input to the theory consists of accurate quantum scattering matrix elements. It has the important attribute that it provides physical insight by bringing out semiclassical and NF aspects of the scattering. Fig. 8 compares the forward angle scattering from the partial wave series (PWS) with that from the uniform semiclassical approximation (USA) for reactive scattering angles, θ_R in the range 0° to 40°. Two additional approximations, the integral transitional approximation (ITA) and the classical semiclassical approximation (CSA) are also shown; they are derived and discussed in ref. 2. The good agreement between the PWS and USA can be seen. Note that for θ_R ≳ 40°, the mechanism of the reaction changes.¹ The forward angle scattering of the H + D₂(v_i = 0, j_i = 0, m_i = 0) → HD(v_f = 3, j_f = 0, m_f = 0) + D reaction at a total energy of 2.00 eV is another example of a glory.¹

Fig. 8 Solid curve: PWS angular distribution. Long dashed curve: USA angular distribution. Short dashed curve: ITA angular distribution, Very long dashed curve: CSA angular distribution.

Does Dr Liu think that the forward and backward angle scattering in the F(²P) + HD → FH(v′ = 3) + D reaction measured in his experiments are examples of forward and backward glories?

(b) You also discuss the range of angular momenta that contribute to the forward angle scattering. I have recently made this notion more precise by introducing the concept of a local angular momentum-local impact parameter (LAM-LIP) for a Legendre partial wave series.²Fig. 9(a) shows the results of a LAM-LIP analysis for the F + H₂(v_i = 0, j_i = 0, m_i = 0) → FH(v_f = 3, j_f = 3, m_f = 0) + H reaction, at a total energy of 0.3872 eV. Also shown are the results of a NF decomposition of the LAM(θ_R). It can be seen that at forward angles, the scattering is F dominated with values in the range 15.6 to 17.8. The corresponding N, F and full differential cross sections are shown in Fig. 9(b). More discussion of the results in Fig. 9 can be found in ref. 2.

Fig. 9 (a) Full curve: LAM(θ_R). Dashed curve: LAM(θ_R) for N scattering. Dotted curve LAM(θ_R) for F scattering. (b) Full curve: PWS angular distribution. Dashed curve: N angular distribution. Dotted curve: F angular distribution. R = 0 means that no resummation of the PWS has been performed.

I hope that a LAM-LIP analysis will also be helpful in understanding the experimental results presented by Dr Liu.

1 J. N. L. Connor, Phys. Chem. Chem. Phys., 2004, 6, 377.

2 J. N. L. Connor and R. Anni, Phys. Chem. Chem. Phys., 2004, 6, 3364.

Dr Liu responded: Professor Connor mentioned some important theoretical contributions to understanding reactive angular distributions. If I understand it correctly, a glory arises from the slowing down of the wave packets (or trajectories) near the top of a barrier and is usually associated with the vibrationally adiabatic thresholds of the quantized transition states (see the above reply to Dr Soep's question). It can be viewed as a direct scattering component (rather than a resonant scattering) and can have a classical analogy, such as an orbiting collision. On the other hand, a Feshbach (or reactive) resonance is a purely quantum mechanical phenomenon. Both a glory and a resonance mechanism can yield forward and/or backward peaking angular distributions, but their underlying physics are somewhat different. The time-delay for a glory originates from the slowing down of the radial motion, whereas for a resonance it is from the trapping of the quasi-bound state. For the present F(²P_3/2,1/2) + HD → HF(v′ = 3) + D reaction, both mechanisms likely contribute to the observed forward and backward scatterings, as presented in our arguments.

I am delighted to hear that in his analysis, Professor Connor also found the dominant contributions of large angular momenta to the forward scattering, which is in accordance with our interpretations.

Professor Yarkony opened the discussion of Professor Alexander’s paper:† My question concerns possible omissions that might lead to the discrepancy between theory and experiment. The nonrelativisitic wavefunctions are diabatized and spin–orbit interaction (effectively) evaluated in that basis. Thus the basis is not truly diabatic with respect to the spin–orbit interaction. What might be the effect of neglecting this effect in the region where the spin–orbit interaction and nonrelativistic state splittings are comparable?

Professor Alexander communicated in response:‡ This is an interesting question. In the spin–orbit-free treatment, diabatization requires only a 2π rotation of the two states of A′ symmetry. In the entrance channel, the spin–orbit coupling exhibits only a very slight dependence on geometry, because the Cl ²P_1/2 and ²P_3/2 states are little perturbed by the approach of the H₂ molecule. At closer distances, as discussed in our paper, as the energy difference between the ²Σ⁺ and ²Π states increases dramatically, there is a strong remixing of the atomic ²P_1/2 and ²P_3/2 states. In principle it should also be possible to diabatize the states only after the addition of the spin–orbit coupling.

Dr Liu said: (1) Several years ago, Connor, Schatz and coworkers did a model calculation on Cl + HCl → ClH + Cl reaction, treating the spin–orbit coupling interaction as a continuous variable.¹ What they found was that the spin–orbit reactivity can be adiabatic, statistical or “inverted” depending on the relative magnitude of the spin–orbit coupling interactions and the difference potential between the Σ and Π surfaces. This study seems to suggest the key to understand the spin–orbit reactivity lies on how B and |V_Σ − V_Π| vary as the reaction proceeds.

(2) Professor Han's group at Dalian Institute of Chemical Physics recently recalculated the three PESs for the Cl(²P) + H₂ reaction. All aspects are nearly identical to the Werner's results, except the off-diagonal spin–orbit coupling interaction, B, which starts to decrease much earlier in the entrance channel than in Werner's calculations. As a result, they obtained comparable Cl* versus Cl reactivity. Can you comment on this?

1 G. C. Schatz, P. McCabe and J. N. L. Connor, Faraday Discuss., 1998, 110, 139.

Professor Connor responded: Alexander et al. have shown for the Cl(²P) + H₂ → ClH + H reaction that electronic non-adiabaticity is governed, almost exclusively, by the spin–orbit coupling. In addition they report that ignoring the coordinate dependence of the spin–orbit coupling and using the asymptotic value for the Cl(²P) atom is an excellent approximation. We have a question and two comments that arise from our own studies of the influence of spin–orbit effects on chemical reactions.^1–6

(a) We have been investigating the origins of electronic non-adiabaticity in the Cl(²P) + HCl → ClH + Cl(²P) reaction. In particular, we have varied⁵ the spin–orbit coupling parameter λ from −150% to +150% of its true value for Cl(²P). For λ close to the true Cl(²P) value, we found that the ²P_3/2 state dominates the reactivity, whereas for λ close to −1 times the true Cl(²P) value, we found that the ²P_1/2 state is the dominant one. For values of λ in between these two limits, the fine-structure-resolved cumulative reaction probabilities exhibit oscillations, with statistical behaviour for λ = 0. An example is shown in Fig. 10 for a total energy of 0.5 eV and a total angular momentum quantum number of J = ½.

Fig. 10 Fine-structure-resolved cumulative reaction probabilities and the total cumulative reaction probability versus scaling parameter s, where s = +1 corresponds to the true spin–orbit coupling parameter for Cl(²P).

Can Professor Alexander vary the sign and magnitude of the spin–orbit coupling parameter in his calculations to see if he obtains results analogous to those in Fig. 10?

(b) We have also investigated⁵ the neglect of the diabatic coupling in our scattering calculations [when ? has its true value for Cl(²P).] For the Cl(²P) + HCl reaction, we found significant differences when the diabatic coupling matrix element (called V₁₂ in ref. 5) was set equal to zero. In particular Stueckelberg-like oscillations in the energy dependence of the cumulative reaction probabilities disappeared when V₁₂ = 0, although higher energy resonances remained. These effects are displayed in Figs. 2a and 6 of ref. 5.

(c) In our most recent work,⁶ we have examined the influence of the long range van der Waals wells on the scattering dynamics of the Cl(²P) + HCl reaction. We did this by scaling the interaction of the Cl quadrupole with the HCl multipoles. This procedure results in van der Waals wells that are either shallower or deeper than the unscaled reference case. We found that the total cumulative reaction probability for J = ½ is only weakly perturbed by changes in the van der Waals well depths, indicating that total reactivity is primarily sensitive to the short-range region of the potential surfaces. However when the van der Waals depths were increased, the cumulative reaction probabilities for the spin–orbit non-adiabatic transitions for j = ½ → j′ = ½ and j = 3/2 → j′ = 1/2 were enhanced, whereas the cumulative reaction probability for j = 3/2 → j′ = 3/2 was suppressed. These results can be understood in terms of the enhancement of non-adiabatic coupling between the j = 3/2 and j = ½ spin states by the long range electrostatic coupling. Here j and j′ are the initial and final total electronic angular momentum quantum numbers respectively.

1 G. C. Schatz, J. Phys. Chem. A, 1995, 99, 7522.

2 C. S. Maierle, G. C. Schatz, M. S. Gordon, P. McCabe and J. N. L. Connor, J. Chem. Soc. Faraday Trans., 1997, 93, 709.

3 G. C. Schatz, P. McCabe and J. N. L. Connor, Faraday Discuss., 1998, 110, 139.

4 T. W. J. Whiteley, A. J. Dobbyn, J. N. L. Connor and G. C. Schatz, Phys. Chem. Chem. Phys., 1999, 1 957.

5 G. C. Schatz, M. Hankel, T. W. J. Whiteley and J. N. L. Connor, J. Phys. Chem. A, 2003, 107, 7278.

6 M. Hankel, J. N. L. Connor and G. C. Schatz, J. Chem. Phys., 2004, DOI: 10.1016/jchemphys.2004.03.02b.

Professor Alexander communicated to Dr Liu and Professor Connor: (1) Professor Liu is indeed correct in his observation that, as pointed out by eqn. (16) and the ensuing discussion in our paper, it is the interplay between the off-diagonal coupling between the reactive ²Σ_1/2 and repulsive ²Π_1/2 states and the splitting between these states which governs the degree of non-adiabaticity in the reaction. Professor Liu mentions the work of Connor and co-workers, mentioned also by the contribution here by Professor Connor. This work is quite thought provoking. In reality, however, the spin–orbit coupling will vary only if the electronic configuration (and the underlying orbitals) themselves change. This will forcibly change the interaction potentials at the same time. Consequently, it may be a bit artificial to vary the spin–orbit coupling while keeping the potential surfaces unchanged.

(2) Although we have seen Professor Han's manuscript, few details of the ab initio calculations were described. Consequently, it is difficult to assess why his results differ from the earlier calculations of Capecchi and Werner.¹ Since our calculations on the CW PES predicted a much smaller reactivity than seen experimentally, and since the degree of nonadiabaticity is proportional to the off-diagonal spin–orbit coupling, it is difficult to understand how a decrease in the B matrix element can lead to an increase in the relative Cl* reactivity. Also, in the version of Han's manuscript we have seen, the B spin–orbit constant goes to zero in the product (HF + H) region, whereas in the calculation of Capecchi and Werner¹ it takes on the proper constant value appropriate to the spin–orbit coupling between the X ¹Σ⁺ and a ³Π₀ states of the HF molecule.

1 G. Capecchi and H.-J. Werner, to be published.

Dr Liu asked: (1) The photodetachment spectra may be more sensitive to the location and the shape of vdw wells. But, it is not clear how sensitive it is to the off-diagonal spin–orbit coupling interaction (B) which you have shown in your paper is responsible to the Cl* + H₂ reactivity. Can you comment on this?)

(2) What's the comparison between the BW surface and the ground state surface of the CW surfaces in the vdw region? We know that BW surface is quite accurate to account for the crossed beam scattering experiment on the isotope branding of Cl + HD.¹

1 D. Skouteris, D. E. Manolopoulos, W. Bian, H.-J. Werner, L.-H. Lai, and K. Liu, Science, 1999, 286, 1713.

Professor Alexander communicated in reply: The photodetachment spectra will be sensitive only to the region of configuration space where the van der Waals bend-stretch wavefunction of the Cl⁻H₂ anion is large. As can be seen in Fig. 4 of our earlier paper,¹ these wavefunctions are localized primarily in the region 5 ≤ R ≤ 7 a₀. Fig. 4 of our contribution to this Discussion shows that over this range, the B spin–orbit constant differs by less than 1% from its asymptotic value. Consequently, the photodetachment spectra can surely be simulated to a very high degree of accuracy under the assumption that the spin–orbit constant remains equal to its asymptotic value (B_∞). In any case, in our simulations we include the full coordinate dependence of the spin–orbit constant, as contained in the Capecchi–Werner PESs.²

Turning to Dr Liu's second question, we show in the following figures contour plots of the Bian–Werner³ and lowest of the three fully-adiabatic⁴ Capecchi–Werner ClH₂ PESs² in the region of the van der Waals well. This fully-adiabatic PES is defined by taking the lowest root of the sum of eqn. (11) and eqn. (15) of our contribution to this Discussion. As can be seen, the van der Waals well is significantly reduced by inclusion of the the spin–orbit coupling. We have already commented on a similar effect in the FH₂ system.⁶ Under high enough resolution, photodetachment studies should, in principle, be able to resolve this difference.

Dr Liu has mentioned the earlier paper by Skouteris et al.,⁶ in which the theoretical simulations of his experimental excitation functions for the Cl + HD reaction were found to be sensitive to a correct description of the van der Waals region of the PES. We observe in Figs. 11 and 12 that the fully-adiabatic CW and BW PES show a qualitatively similar description of the effect of the van der Waals well on the repulsive wall of the PES. In both cases the PESs predict less repulsion for perpendicular approach. It was this topological feature which Skouteris et al.,⁶ found to be responsible for a correct prediction of the relative magnitudes of the excitation functions for the Cl + HD ⇌ ClH + D as compared to Cl + HF ⇌ ClD + H reactions.

Fig. 11 Contour plot (in cm^–1) of the Bian–Werner ClH₂ PES (ref. 4). The H–H distance is held to its equilibrium value of r = 1.4 a₀. The abscissa and ordinate are the Jacobi coordinates R and γ. The zero of energy is Cl + H₂(r = 1.4) at infinite separation (R = ∞).

Fig. 12 Contour plot (in cm^–1) of the lowest fully-adiabatic (refs. 2 and 4) Capecchi–Werner ClH₂ PES, The H–H distance is held to its equilibrium value of r = 1.4 a₀. The abscissa and ordinate are the Jacobi coordinates R and γ. The zero of energy is Cl(²P_3/2) + H₂(r = 1.4) at infinite separation (R = ∞).

1 M. H. Alexander, J. Chem. Phys., 2003, 118, 9637.

2 G. Capecchi and H.-J. Werner, to be published, potential available at http://www.theochem.uni-stuttgart.de/

3 W. Bian and H.-J. Werner, J. Chem. Phys., 2000, 112, 220.

4 M. H. Alexander, G. Capecchi, and H.-J. Werner, Science, 2002, 296, 715.

5 M. H. Alexander, D. E. Manolopoulos, and H. J. Werner, J. Chem. Phys., 2000, 113, 11 084.

6 D. Skouteris, D. E. Manolopoulos, W. Bian, H.-J. Werner, L.-H. Lai, and K. Liu, Science, 1999, 286, 1713.

Professor Jaquet communicated: The PES, presented in Fig. 2 of the paper, has a small van der Waals minimum of lower than −0.2 kcal mol⁻¹ ≈ 70 cm⁻¹. To my knowledge, diagonal adiabatic corrections have not been taken into account. From the work of H₃⁺ we know that these contributions can change along R (near the minimum in r) by about more than 20 cm⁻¹. Is, in the case of ClH₂, the contribution of the diagonal adiabatic correction (coming mostly from two hydrogen atoms) of minor importance for the investigation of scattering?

Professors Alexander and Werner‡ communicated in response: It is correct that diagonal adiabatic corrections have not been included. In ongoing work,¹ we are assessing the importance of these, and other previously neglected terms, on the controlling features of the FH₂ PES. Similar work is certainly warranted for the ClH₂ system.

1 H.-J. Werner, M. Kallay, and J. Gauss, work in progress.

Mr Rackham commented:§ Nearly twenty years ago, Butler, Wiesenfeld and co-workers used laser induced fluoresence detection to probe the OH products of the O(¹D) + H₂ reaction over a wide range of product rotational levels.¹ They found that, for a given rotational state, the two spin–orbit manifolds of the open-shell OH product were roughly equally populated, whilst the relative populations of the two Λ-doublet levels consistently favoured the so-called ²Π(A′) state. This propensity is made remarkable by the fact that the Λ-doublet splitting is <1 cm⁻¹, whilst the spin–orbit splitting is ≈139 cm⁻¹ Most recent studies of non-adiabatic effects in A + BC reactions, using exact quantum mechanics, have focused on halogen + H₂ abstraction reactions.³ However, it is considerably more difficult to carry out quantum treatments of insertion reactions that proceed over deep potential energy wells, such as O(¹D) + H₂. Indeed, it is only within the last few years that a quantum study of this reaction on a single potential energy surface (PES) been published.⁴

More recently, Rackham, Manolopoulos and co-workers have developed a simple statistical model which can reproduce exact single-PES differential and integral cross-sections for a variety of insertion reactions, including O(¹D) + H₂, at a fraction of the computational cost.⁵ In this model, the reactant and product arrangements are treated rigorously within coupled-channel capture theory to give probabilities for the capture of reactants or products into the intermediate complex. When combined with the statistical assumption of a long-lived complex, these probabilities can be used to calculate reaction cross-sections.⁵

In contrast to halogen + H₂ reactions, the products of insertion reactions are typically open-shell molecules. In the case of O(¹D) + H₂ → OH(X ²Π) + H, four potential energy surfaces correlate asymptotically with the products, of which only one corresponds to the deep H₂O (¹A′) well. Non-adiabatic effects occur as the products separate and the potential well meets the other three states. This is illustrated in Fig. 13. Since these couplings become important only in the asymptotic region, where the magnitude of the splitting between the repulsive and attractive surfaces becomes comparable to the strength of the coupling, it is reasonable to assume that the statistical model could be extended to include the electronic degrees of freedom and thereby be used to predict the relative branching among the energetically accessible OH(X ²Π) product states.

Fig. 13 Schematic illustration of the reaction path for the O(¹D) + H₂ → OH(X ²Π) + H reaction, showing all four electronic states that correlate with the products.

Here we present some results of the first adaptation of the statistical model to include non-adiabatic effects in the product arrangement of O(¹D) + H₂ → OH(X ²Π) + H. The Hamiltonian in this arrangement includes non-adiabatic and spin–orbit coupling between ro-vibrational-electronic states, including those of ^1,3A′ and ^1,3A″ symmetry that correlate with OH(X ²Π) + H. Fig. 14 shows integral reactive cross-sections for the formation of OH(X ²Π) in the v′ = 0,1 vibrational manifolds. The upper two panels reveal a strong propensity toward population of the Π(A′)Λ-doublet levels. By contrast, the remaining panels reveal that the two spin–orbit manifolds are equally populated. Both results are in qualitative agreement with the experiments of Butler, Wiesenfeld and their co-workers.¹

Fig. 14 Computed integral cross-sections for the O(¹D) + H₂(v = 0,j = 0) → OH(X ²Π,v′,j′) + H reaction at a collision energy of 25 meV. Upper two panels: scattering into Π(A′) vs. Π(A″) Λ-doublet levels. Lower two panels: scattering into F₁vs.F₂ spin–orbit manifolds.

To the best of our knowledge, this is the first time that an electronically non-adiabatic effect has been studied theoretically in the product region of an insertion reaction. What makes this observation remarkable is the fact that a “statistical” model has predicted a distinctly non-statistical effect! This is because our model only treats the intermediate complex statistically whilst the dynamics in the reactant and product arrangements are accounted for correctly. As a result, non-statistical effects can be seen in the integral cross-sections. Full details and further applications will be presented in future publications.

1 J. E. Butler, G. M. Jursich, I. A. Watson and J. R. Wiesenfeld, J. Chem. Phys., 1986, 84, 5365.

2 M. H. Alexander, P. Andresen, R. Bacis, R. Bersohn, F. J. Comes, P. J. Dagdigian, R. N. Dixon, R. W. Field, G. W. Flynn, K.-H. Gericke, E. R. Grant, B. J. Howard, J. R. Huber, D. S. King, J. L. Kinsey, K. Kleinermanns, K. Kuchitsu, A. C. Luntz, A. J. MacCaffery, B. Pouilly, H. Reisler, S. Rosenwaks, E. Rothe, M. Shapiro, J. P. Simons, R. Vasudev, J. R. Wiesenfeld, C. Wittig and R. N. Zare, J. Chem. Phys., 1988, 89, 1749.

3 M. H. Alexander, D. E. Manolopoulos and H. J. Werner, J. Chem. Phys., 2000, 113, 11 084; M. H. Alexander, G. Capecchi and H.-J. Werner, Science, 2002, 296, 715.

4 P. Honvault and J.-M. Launay, J. Chem. Phys., 2001, 114, 1057.

5 E. J. Rackham, F. Huarte-Larranga and D. E. Manolopoulos, Chem. Phys. Lett., 2001, 343, 356; E. J. Rackham, T. Gonzalez-Lezana and D. E. Manolopoulos, J. Chem. Phys., 2003, 119, 12 895.

6 M. H. Alexander, E. J. Rackham and D. E. Manolopoulos, J. Chem. Phys., 2004, 121, in press.

Professor Alexander then communicated: As we have discussed earlier at this Discussion, nonadiabatic transitions in the reaction of Cl(²P) with H₂ are most likely to occur when the Cl–H₂ distance approaches ∼6 a₀, where the spin–orbit coupling between the ²Σ_1/2 and ²Π_1/2 states is comparable in magnitude to the energetic splitting between the states.

Recent experimental¹ and theoretical^2,3 investigations reveal that the ground state of the closed-shell Cl–H₂ anion occurs for linear geometry with a centre-of-mass separation of ∼5.7 a₀. Consequently, the photodetachment experiments of Ferguson et al.⁴ as well as more recent velocity map imaging experiments from the Neumark group⁵ will probe the ClH2 complex precisely in the region most important for nonadiabatic transitions. As a result, the details of the photodetachment spectra of Cl–H₂ and its isotopomers may provide additional information on the importance of nonadiabaticity in the reaction of Cl with H₂.

Fig. 15 illustrates the lower adiabatic bender potentials⁶ of the Cl–pH₂ complex. These potentials arise from approach of H₂ along the ²Σ_1/2, ²Π_3/2 and ²Π_1/2 potentials illustrated in Fig. 1 of our paper. In a time-dependent formulation of the photodetachment,⁷ photofragmentation of the Cl⁻pH₂ anion will project the ground-state wavefunction of the Cl⁻pH₂ complex onto these various adiabatic-bender states of ClpH₂, either into the bound (or quasi-bound) states or onto the repulsive walls of the adiabatic-bender potentials shown in Fig. 1. The resulting spectrum will reflect both the intensities of the initial Franck–Condon projection as well as the non-adiabatic couplings between the various adiabatic-bender potentials, as the ClH₂ wavepacket evolves.

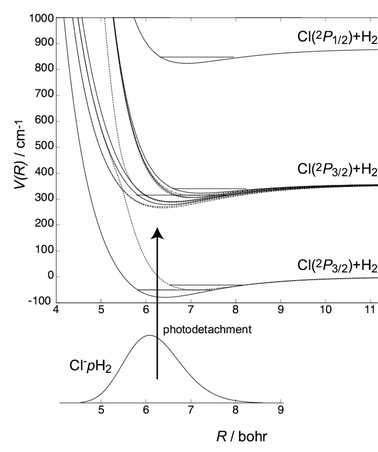Fig. 15 Adiabatic bender potentials (ref. 6) for the Cl–pH₂ complex. The solid, dashed, and short–long-dash curves correspond, respectively, to states with projection quantum numbers of p = 1/2, 3/2, and 5/2, respectively. The positions of some of the lower bend–stretch levels of the complex are shown by the horizontal line. Also superimposed on the figure is the lowest vibrational wavefunction of the Cl–pH₂ complex.

We have carried out an essentially exact, time-dependent simulation of the photodetachment of several isotopomers of Cl⁻H₂, in which all non-adiabatic couplings are described exactly.⁸ The vibration–rotation wavefunctions for the van der Waals motion of the Cl⁻H₂ complex were taken from ref. 3 and the necessary ClH₂ potential energy surfaces and couplings, from the ab initio calculations of Capecchi and Werner.⁹Fig. 16 displays the predicted photofragmentation spectra for Cl⁻nH₂ at a resolution of 1 meV along with an assignment of the various features in the spectra.

Fig. 16 Schematic diagram of the photodetachment of the Cl–H2 anion. The zero of energy is the lowest vibration-rotation state of the anion complexes of either para- or ortho-H₂. Optical excitation followed by release of an electron, produces bound (or quasi-bound) complexes of pH₂ or or oH₂ with Cl in either its ground or excited spin–orbit state. The spectrum shown on the left is our theoretical simulation at a resolution of 1 meV. The strong, narrow peaks correspond to the bound and quasi-bound (Feshbach resonance) levels of the ClH₂ complex.

In addition, simulations were also carried out under an adiabatic approximation, in which photodetachment flux is propagated on each of the three electronically adiabatic PESs (²Σ_1/2,²Π_1/2 and ²Π_3/2) separately. Non-adiabatic coupling effects the positions of the van der Waals quasi-bound and bound states, particularly in the region of the Cl–H₂ asymptote. This results in small, but noticeable, differences in the simulated photofragmentation spectra, which should be detectable in photofragmentation experiments at high resolution (∼1 meV).

Simulations at a resolution of 10 meV agree extremely well with the published results of Neumark and co-workers.⁵ Full details of these simulations will be published shortly.

1 D. A. Wild, R. L. Wilson, P. S. Weiser and E. J. Bieske, J. Chem. Phys., 2000, 113, 10 154; D. A. Wild, P. S. Weiser, E. J. Bieske and A. Zehnacker, J. Chem. Phys., 2001, 115, 824.

2 M. H. Alexander, J. Chem. Phys. 2003, 118, 9637.

3 A. A. Buchachenko, T. A. Grinev, J. Klos, E. J. Bieske, M. M. Szczesniak and G. Chalasinski, J. Chem. Phys. 2003, 119, 12 931.

4 M. J. Ferguson, G. Meloni, H. Gomez and D. M. Neumark, J. Chem. Phys. 2002, 117, 8181.

5 D. Neumark, personal communication, 2004.

6 M. H. Alexander and M. Yang, J. Chem. Phys., 1995, 103, 7956.

7 C. L. Russell and D. E. Manolopoulos, Chem. Phys. Lett., 1996, 256, 465.

8 M. H. Alexander, D. E. Manolopoulos and H. J. Werner, J. Chem. Phys., 2000, 113, 11 084.

9 M. H. Alexander, G. Capecchi and H.-J. Werner, Science, 2002, 296, 715.

Professor Buma asked: Your calculation is based on the Condon approximation. To what extent do you think that your results will change when the geometry dependence of the transition moment is taken into account and issues like rotational excitation?

Professor Alexander communicated in response:¶ Since the bound-free electronic transition is localized on the Cl atom, the variation with the position of the H₂ molecule will probably not be significant. Determination of the geometry dependence of the transition moment would require a full electronic structure calculation of the photodetached (continuum) ClH₂ + e⁻ wavefunction as a function of both geometry and, more importantly, as a function of excitation energy. This has not yet been done, but, eventually, may become warranted with the advent of increased resolution in the experimental photodetachment spectra.

Professor Child said: I should like to comment that the branching ratio between Cl and Cl* from the resonances described by Manolopoulos and Alexander would give a direct measure of the strength of spin–orbit coupling in the entrance valley.

Professor Alexander communicated in reply:¶ Professor Child's comment is indeed correct. Since, as we show in the paper, it is the strength of the spin–orbit coupling which is responsible for the nonadiabaticity in the Cl + H₂ reaction, the experimental investigation of the photodetachment spectra of the ClH₂ anion by Neumark and co-workers,¹ and our concurrent theoretical interpretation, will provide additional information of the effect of the spin–orbit coupling, complementary to the reactive scattering studies.²

1 M. J. Ferguson, G. Meloni, H. Gomez and D. M. Neumark, J. Chem. Phys., 2002, 117, 8181.

2 S.-H. Lee and K. Liu, J. Chem. Phys., 1999, 111, 6253; F. Dong, S.-H. Lee and K. Liu, J. Chem. Phys., 2001, 115, 1197.

Dr Althorpe made a general comment: The papers by Lee et al. and Alexander et al. demonstrate that there is still a lot that simple bimolecular reactions can tell us about non-adiabatic reaction dynamics, especially when detailed experimental measurements are backed up by rigorous theoretical calculations. We would like to mention a different, but related example—namely the use of the H-exchange reaction to study the effect of the Berry or geometric phase (GP) on bimolecular reaction dynamics.

It has long been known¹ that the H-exchange reaction has a conical intersection at equilateral triangle geometries. Reaction paths which encircle these geometries (by passing over all three of the linear transition states) are thus expected to pick up GP effects. However, recent theoretical predictions of GP effects in this reaction have been controversial: A series of calculations by Kuppermann and co-workers² predict narrow resonances that occur only when the GP is correctly taken into account. Experiments have so far uncovered no evidence for such resonances, and yield results in excellent agreement with theoretical calculations that ignore the GP³. A more recent study by Kendrick⁴ predicts the opposite effect, which is that, although GP effects appear in the state-to-state opacity functions, they cancel exactly when the partial waves are summed to give the cross sections.

To test out these two sets of predictions, we have performed the first time-dependent quantum reactive scattering calculations to include the GP, using the vector potential approach of Mead and Truhlar⁵. Our results reproduce the predictions of Kendrick⁶. For example, Fig. 17 shows a selection of state-to-state opacity functions, computed for the H + H₂ reaction, both with and without inclusion of the GP. Fig. 18 shows a selection of state-to-state integral cross sections. The marked differences between the GP and NGP state-to-state opacity functions, such as illustrated in Fig. 19, have evidently cancelled out exactly in the integral cross sections (within the limits of numerical convergence). This reproduces the effect first predicted by Kendrick⁴, that there are no experimentally observable consequences of the GP in the state-to-state integral cross sections for this reaction. Given that our time-dependent calculations used a completely different method⁶ from the time-independent calculations of Kendrick⁴, the agreement between our results and those of Kendrick suggests very strongly that these predictions are correct.

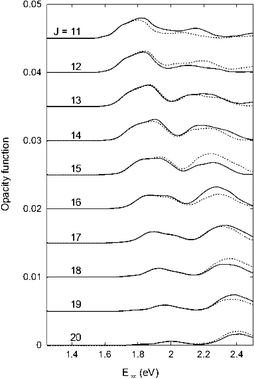Fig. 17 State-to-state opacity functions, computed for the (v = 1, j = 0 → v′ = 2, j′ = 5, Ω′ = 0) transition of the H + H₂ reaction, obtained with the GP (solid lines) and without the GP (dashed lines).

Fig. 18 State-to-state integral cross sections for the H + H₂ reaction, computed (a) for (v = 1, j = 0 → v′ = 0, j′ = 0) and (v = 1, j = 0 → v′ = 2, j′ = 5) over a range of total energies, and (b) for the v′ = 0 and v′ = 2 vibrational manifolds, at E_total = 2.3 eV.

We note that at higher energies the agreement between the GP and NGP results is not perfect in the state-to-state differential cross sections (DCS). Fig. 19 shows that, at 1.8 eV, the agreement between the results obtained with and without the GP is very close, although there are small differences which appear as ‘wiggles’. Similar wiggles were reported by Kendrick⁴ in some DCS, and were attributed to numerical convergence errors. We have tested extensively the numerical convergence of the calculations, and are confident that the wiggles are real. At 2.3 eV, the disagreement between the GP and NGP results is pronounced, with a shift in phase of the rapid oscillations that appear in the DCS as a function of the scattering angle θ.

Fig. 19 State-to-state differential cross sections computed for the H + H₂ reaction, for (v = 1, j = 0 → v′ = 2, j′ = 5), at E_total = 1.8 eV and 2.3 eV.

At present we can give no explanation for the total cancellation of the GP effects in the integral cross sections, and the near-cancellation in the DCS. Nor can we suggest whether this is a general effect, or whether it is specific to the H-exchange reaction. Recent work⁷ has shown that the majority of the wave packet does not encircle the conical intersection in H + H₂. Clearly a small amount of the packet must encircle the intersection (otherwise there would be no GP effects at all, even in the opacity functions). Finally, we do not think that the cancellation is a symmetry effect (as has been suggested⁴). Inspection of Fig. 17 (and similar plots produced for the other cross sections) shows that differences between the GP and NGP functions do not alternate exactly with J. It is only when all the partial waves are summed that the differences between the GP and NGP results cancel in the integral cross sections.

1 G. Herzberg and H. C. Longuet-Higgins, Discuss. Faraday Soc., 1963, 35, 77.

2 See: A. Kuppermann and Y. S. M. Wu, Chem. Phys. Lett., 2001, 349, 537, and references therein.

3 F. Fernández-Alonso and R. N. Zare, Annu. Rev. Phys. Chem., 2002, 53, 67.

4 B. K. Kendrick, J. Phys. Chem. A, 2003, 107, 6739.

5 C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284.

6 S. C. Althorpe, F. Fernández-Alonso, B. D. Bean, J. D. Ayers, A. E. Pomerantz, R. N. Zare and E. Wrede, Nature, 2002, 416, 67; S. C. Althorpe, J. Chem. Phys., 2002, 117, 4623.

7 J. C. Juanes-Marcos and S. C. Althorpe, Chem. Phys. Lett., 2003, 381, 743.

Dr Woywod said: Dr Althorpe has been addressing the question of the presence of geometric phase (GP) effects on the H + H₂ reaction. I would like to examine if the frequently used terminology of “GP effects” on molecular spectra and chemical reactions is appropriate because it suggests that the GP could be a “real” property of a molecule and might even be observable by experiment. I believe that the concepts “physical system” on one side and “model treatment of the physical system” on the other should be clearly separated in this case. In my opinion, the GP discussed in the context of molecular dynamics is a mathematical object that is only of practical relevance for the solution of the Schrödinger equation for nuclear motion but not a mechanism, like electrostatic repulsion, that could in reality influence the behaviour of a molecule. The reason is that the existence of the GP is due to the complete decoupling of nuclear and electronic motion in the Born–Oppenheimer approximation which induces a change of sign of the adiabatic electronic wave functions along a trajectory that is restricted to a single electronic potential energy surface and encloses a conical intersection. The fact that a change of sign has to be imposed on the wave functions describing nuclear motion around an electronic degeneracy in order to compensate for the sign reversal of the adiabatic electronic states and ensure the isotropy of the full vibronic wave function, as has been demonstrated for the Na₃ system in ref. 1, is therefore purely a consequence of the artificial splitting into a vibrational and an electronic subsystem. By constructing a diabatic representation for the two intersecting electronic states and propagating the nuclear wave packet on the coupled potential energy surfaces, exactly the same vibronic spectrum could be obtained as with the adiabatic single surface approach of ref. 1, but no inclusion of the GP in the dynamical calculations would be necessary. With respect to the issue if the GP has to be included in simulations of a chemical reaction on a single adiabatic potential energy surface that features a conical intersection I would say in principle yes. The interpretation that the GP has an effect on the reaction would be incorrect, however, because the GP is required exclusively from the technical point of view. In order to test this I suggest to compare the result of a diabatic two surface calculation with that of the adiabatic single surface approach, not taking the GP into account. In some cases, the reaction dynamics predicted by the two methods should differ and then only the solution provided by the diabatic picture will be valid.

1 H. v. Busch, V. Dev, H.-A. Eckel, S. Kasahara, J. Wang, W. Demtröder, P. Sebald and W. Meyer, Phys. Rev. Lett., 1998, 81, 4584.

Dr Althorpe replied: I think the term ‘GP effects’ is useful. It refers to the effects brought about by the extra non-Born–Oppenheimer terms¹ that appear in the nuclear Hamiltonian, when the GP phase is included in the electronic wave function. As Dr Woywod says, GP effects cannot be turned on and off in the physical system: they will necessarily be present if the dynamics encircles a conical intersection. Hence it is necessary to do calculations to find out what the GP effects are, and to predict how (or whether) they show up in the experimental observables.

1 C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284.

Professor Truhlar commented: It has been commented that the geometric phase comes about due to the separation of the wave function into an electronic part and a nuclear part and that for that reason it should perhaps be regarded as somewhat artificial. However it is important to point out that geometric phase effects can be very important even when the separation of electronic and nuclear motion is a very good approximation so that the electronic and nuclear wave functions are well defined. Thus, for example, the effects of geometric phase can be observed even for systems with negligible probability amplitude at the conical intersection itself.¹ An example of systems where the geometric phase effect should be observable in principle is in the spectroscopy of X₃ trimers where one can observe half-odd-integer quantization in the pseudorotational motion that carries the system from one isosceles triangle to another,^2–15 although there may be complications.^16–21

1 C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284

2 C. A. Mead, Chem. Phys., 1980, 49, 23

3 T. C. Thompson, D. G. Truhlar and C. A. Mead, J. Chem. Phys., 1985, 82, 2392

4 T. C. Thompson, G. Izmirlian, Jr., S. J. Lemon, D. G. Truhlar and C. A. Mead, J. Chem. Phys., 1985, 82, 5597

5 D. G. Truhlar, T. C. Thompson and C. A. Mead, Chem. Phys. Lett., 1986, 127, 287

6 G. Delacretaz, E. R. Grant, R. L. Whetten, L. Wöste and J. W. Zwanziger, Phys. Rev. Lett., 1986, 56, 2598

7 E. E. Wedum, E. R. Grant, P. Y. Cheng, K. F. Wiley and D. A. Ducan, J. Chem. Phys., 1994, 100, 6312

8 E. Sjoqvist and O. Goscinski, Chem. Phys., 1994, 197, 17

9 H. Koizumi and S. Sugano, J. Chem. Phys., 1994, 101, 4903

10 B. Kendrick, Int. J. Quantum Chem., 1997, 64, 581

11 B. Kendrick, Phys. Rev. Lett., 1997, 79, 2431

12 R. G. Sadygov and D. R. Yarkony, J. Chem. Phys., 1999, 110, 3639

13 J. Schön and H. Köppel, J. Phys. Chem. A, 1999, 103, 8579

14 A. J. C. Varandas, H. G. Yu, and Z. R. Xu, Mol. Phys., 1999, 96, 1193

15 A. J. Varandas and Z. R. Xu, Int. J. Quantum Chem., 1999, 75, 89

16 H. Koizumi and S. Sugano, J. Chem. Phys., 1995, 102, 4472

17 H. Koizumi and S. Sugano, Surf. Rev. Lett., 1996, 3, 317

18 D. R. Yarkony, J. Chem. Phys., 1999, 111, 4906

19 I. B. Bersuker, Chem. Rev., 2001, 101, 1067

20 J. R. Lombardi and B. Davis, Chem. Rev., 2002, 102, 2431

21 B. E. Applegate, T. A. Barckholtz and T. A. Miller, Chem. Soc. Rev., 2003, 32, 38

Professor Köppel addressed Professor Baer: We have performed wavepacket calculations for the cumulative reaction probability of the hydrogen exchange reaction. The coupled DMBE potential energy surfaces have been used and the flux operator formalism of Miller and others been suitably generalized. The initial energy was chosen to cover a broad range of translational energies from the onset of the reaction to the three-body dissociation limit. Only very minor effects of the nonadiabatic couplings on the reaction probability could be identified, although the energies covered are well above the minimum energy of intersection. The time-dependent population of the upper adiabatic surface always remains below 1%.¹ We expect this result to be related to the collinear transition state of this reaction, though a precise explanation is still missing.

1 S. Mahapatra et al., J. Phys. Chem. A, 2001, 105, 2321.

Dr Gidopoulos asked: In principle, how can the geometric phase due to the molecular Aharonov–Bohm effect lead to measurable effects? Let me explain my point: Denote by Φ(R) an electronic adiabatic state that depends parametrically on the nuclear coordinate R. When Φ(R) is not degenerate for any R with another electronic state then, Φ(R) can be chosen real and continuous with respect to R. Therefore the vector-potential-like quantity i〈Φ(R)|∇Φ(R)〉 vanishes and there is no geometric phase. In the case of degenerate electronic levels, one may argue that infinitesimally close to the degenerate system lies another system where the degeneracy is just avoided. So, the slightest perturbation in the system that lifts the degeneracy would cancel the geometric phase effect.

Does this imply that at least in cases where degeneracy is not dictated by symmetry there can be no measurable effects due to the geometric phase?

Professor Child replied: The question as to the value of geometric phase in systems involving a slightly avoided conical intersection arises in situations such as the ²E state of Na₃,¹ where the vibronically coupled electronic components are split by spin–orbit coupling. As first discussed by Stone,² the coupling matrix may be expressed, in a complex electronic representation, as

where (r,φ) are the polar variables for the degenerate, Jahn–Teller active vibration and 2Δ is the spin–orbit splitting. Δ and k in principle are functions of all N nuclear coordinates. The eigensurfaces
therefore reduce to the normal double cone in any N − 3 dimensional space where both Δ and kr vanish. However Δ may remain finite over physically relevant geometries (as for example in the case of the spectroscopy of Na₃) in which case W_± define an avoided double cone, split by 2Δ.

To obtain the geometric phase in such situations, it is sufficient to note that the matrix V has the mathematical structure of the spin-1/2 system in a magnetic field, discussed in Berry's famous paper.³ The result for a cycle of φ at fixed Δ is found to be equal to the solid angle swept out by the motion in the space (x,y,z) = (kr cos φ,kr sin φ,Δ); namely

γ = −[1 − cos θ(r,Δ)π

where

tan θ(r,Δ) = kr/Δ

Consequently the geometric phase γ varies with the size of the circle; it vanishes as r → 0 and reverts to the normal value, γ = ±π, as r → ∞.

Further details are discussed in a recent historical review.⁴

1 H. van Bosch, V. Dev, H. A. Eckel, J. Wang, W. Demtroder, P. Sebald and W. Meyer, Phys. Rev. Lett., 1999, 82, 3560.

2 A. J. Stone. Proc. R. Soc. London, Ser. A, 351, 141 (1976)

3 M. V. Berry, Proc. R. Soc.London, Ser. A, 392, 45 (1984)

4 M. S. Child, Adv. Chem. Phys., 2002, 124, 1.

Professor Tapia said: I would like to make a comment concerning separability following Professor Truhlar’s remark. We have to distinguish electronuclear wave functions corresponding to a given quantum state, Φ(q,Q), from the basis set functions used to represent them, say {ψ_j(q,Q)}. The latter are identified by quantum numbers (basis states), the former have no quantum numbers; the quantum states are linear superpositions in the given basis. Φ(q,Q) is not separable. However, the basis functions can be made separable. From the molecular spectra it is evident that the basis quantum number can be split into two: j → jk(j), where j is the electronic quantum number and k(j) = jk are nuclear quantum number(s). The electrons (leptons) and nuclei (hadrons) belong to different families. The basis functions can be constructed as simple products, i.e.

ψ_j(q,Q) → ψ_jk(q,Q) → ϕ_j(q)χ_jk(Q)

The BO scheme is given by:

ψ_j(q,Q) → ψ_jk(q,Q) → Ψ_j(q;Q)χ_jk(Q)

Both approaches require of specific algorithms to determine the electronic basis functions by changing the configurational nuclear space into a space formed by sets of positive charge (PC) in real space. The generalized electronic diabatic (GED) scheme can be found in ref. 1. The BO approach is defined by infinitely many Coulomb Hamiltonians, one for each PC-arrangement; the GED can be defined with only one Hamiltonian. Separability is granted via algorithms incorporating part of the system in real space.

1 G. A. Arteca and O. Tapia, J. Math. Chem., 2004, 35, 1–19.

Professor Truhlar made a general comment: The question was put forth as to how there can be a difference between the transport of a wave function around a point of very small near degeneracy (10^−x with x very large) and around an actual degenerate point (i.e. a conical intersection). This is an interesting conceptual question that gets to the very heart of the theory of the geometric phase. The key issue is that degeneracies are singularities in the net of curvature lines, and the geometric phase in molecular physics is a consequence of the global topological properties of the potential energy surfaces whose consequences cannot be gauge transformed away; the differential geometries of the potential energy surfaces of systems with and without a degeneracy have fundamentally different curvature properties, and the geometric phase is a topological indicator of the presence of a degeneracy.^1–4

1 A. J. Stone, Proc. R. Soc. London, Ser. A, 1976, 351, 141

2 C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1979, 70, 2284; C. A. Mead and D. G. Truhlar, J. Chem. Phys., 1983, 78, 6344

3 M. V. Berry, in Geometric Phases in Physics, ed. A. Shapere and F. Wilczek, World Scientific, Singapore, 1989, pp. 7–28

4 H. Kuratsuji and S. Iida, Prog. Theor. Phys., 1985, 74, 439.

Professor Child opened the discussion of Professor Stancil’s paper: Could you explain why charge transfer to the O²⁺ (2p3s) states are the most important?

Professor Stancil replied: The charge transfer process for multiply-charged systems usually occurs at the locations of avoided-crossings between electronic states. The probability for a transition depends sensitively on the internuclear distance of the avoided-crossing R_x and is optimal for intermediate values between ∼5 and ∼12 a₀. Avoided-crossings associated with the 2p3s states occur in this range. For the 2p3p states R_x > 17 a₀, while for the ground state of O²⁺, the avoided crossing for the 2p² state is likely less than 5 a₀. Therefore to simplify the calculations, only the presumed dominant transitions, those to the 2p3s states, were included.

Professor Greene remarked: You have performed these calculations using the infinite-order sudden approximation (IOSA), which traditionally ignores closed-channel physics in the entrance and exit vibrational channel manifold. Have you considered the possible role of closed-channel effects, which could produce Feshbach resonances at low energies? In some systems we have been looking at, the controlling pathway goes through such closed vibrational channels as intermediate states. Examples of this idea applied in other contexts can be found in the literature, e.g. refs. 1 and 2. The applicability of these ideas to extend the power of the IOSA has hardly been studied, but may be a promising direction.

1 U. Fano and A. R. P. Rau, Atomic Collisions and Spectra, Academic Press, Orlando, FL, 1986.

2 J. P. Burke, Jr, C. H. Greene and J. L. Bohn, Phys. Rev. Lett., 1998, 81, 3355.

Professor Stancil replied: For the electronic states considered in the current collision system, O³⁺ + H₂(v = 0) → O²⁺(2p3s) + H₂⁺(v′), there are no closed channels for the product states except for some portion of the vibrational continuum of H₂⁺. Closed channels would be present in the entrance channel if excited vibrational states of H₂ were included, but we neglected those since the available experiments are presumed to contain only ground vibrational levels of H₂. In future calculations we plan to include the vibrational excited states of H₂ and it would be very interesting to look for Feshbach resonances. For H₂(v = 1), the resonance would occur near 0.29 eV u⁻¹, while for T₂(v = 1) it would appear at 0.12 eV u⁻¹. However, these collision energies are close to the presumed lower limit of ∼0.1 eV u⁻¹ for applicability of the IOSA method. One could of course consider higher vibrational states or higher levels of theory such as the coupled-states or close-coupling methods. Finally, there is a history of searching for resonances in charge transfer experiments with little success primarily as a consequence of considerable energy uncertainty for low collision energies.

Dr Hernandez asked: (a) In your IOSA calculations, at low energies, do you find that the cross-section has a strong θ-dependence, in other words, that capture takes place in a localised region of space?

(b) I would expect a large contribution from θ = 90° which corresponds with the geometry of the van der Waals minimum. We have observed this type of behaviour in IOSA calculations of vibrational relaxation for the O₂ + O₂ system¹, and given a qualitative explanation for this behaviour. I wonder if the same applies in your calculations and perhaps is a general feature of the method.

1 R. Hernandez, R. Toumi and D. C. Clary, J. Chem. Phys., 1995, 102, 9544.

Professor Stancil answered: We do find an orientation-dependence in our IOSA calculations with the larger contributions usually coming from the more perpendicular arrangement, but the dependence is not strong. This behaviour is typical of multiply-charged collision systems in which the transitions are driven by long-range non-adiabatic couplings. The capture is localized, at the location of the avoided-crossings, and it is this location, which is sensitive to the H–H stretching coordinate, which dictates the interaction behaviour more so than the orientation. The van der Waals minimum occurs at a shorter distance and therefore plays less of a role. However, for singly-charged systems, which is not the topic of the current paper, orientation dependence is pronounced.¹

1 M. Kimura, J.-P. Gu, G. Hirsch, R. J. Buenker, and P. C. Stancil, Phys. Rev. A, 2000, 61, 032708.

Dr Harvey said: As a comment on the previous question, the optimum geometry of the analogous He²⁺⋯H₂ ion–molecule complex is indeed T-shaped (θ = 90°).

---

Footnotes

† Professor Alexander’s paper was presented by Dr David Manolopoulos, Physical and Theoretical Chemistry Laboratory, University of Oxford, South Parks Road, Oxford, UK OX1 3QZ.

‡ Also Professor Hans-Joachim Werner, Institute for Theoretical Chemistry, University of Stuttgart, Pfaffenwaldring 55, D70569 Stuttgart, Germany.

§ Also Professor Alexander and Dr David Manolopoulos.

¶ Also Dr David Manolopoulos.

---