Systematic empirical analysis of calcium–oxygen coordination environment by calcium K-edge XANES
F. E.
Sowrey
*a,
L. J.
Skipper
a,
D. M.
Pickup
a,
K. O.
Drake
b,
Z.
Lin
b,
M. E.
Smith
b and
R. J.
Newport
a
aSchool of Physical Sciences, University of Kent, Canterbury, UK CT2 7NR. E-mail: fes@kent.ac.uk
bDepartment of Physics, University of Warwick, Coventry, UK CV4 7AL
First published on 27th November 2003
Abstract
The X-ray absorption near edge structure (XANES) at the calcium K-edge is rich in information, but complex and difficult to interpret fully. We present here a systematic study of a range of calcium/oxygen containing compounds and minerals and show that the XANES may be used to obtain qualitative information on the calcium coordination environment.
Introduction
The structural chemistry of calcium is of widespread importance to understanding materials as diverse as cements, dental materials and high temperature ceramic superconductors. Compounds of calcium are also of significant biological interest, fulfilling a wide range of roles in living organisms: from bone, teeth and shell formation to calcium binding proteins such as Troponin and Parvalbumin.Many of these biological systems involve materials, which are either non- or “poorly” crystalline and are therefore well suited to structural investigations using X-ray absorption spectroscopy. Whilst the use of extended X-ray absorption fine structure (EXAFS) at the calcium K-edge is well documented in the literature for a wide range of fields,1a–f there are relatively few studies of the X-ray absorption near edge structure (XANES).
The XANES part of the X-ray absorption spectrum is usually defined as the region extending from just below the absorption edge to 30–50 eV past the edge. Near edge features arise from a number of physical processes including core electronic transitions and multiple scattering of the excited photoelectron, the XANES are therefore highly dependent on the local environment of the absorbing atom. Whereas EXAFS gives first-order pair correlations, XANES gives information on higher order correlations, making full interpretation of complex coordination environments very difficult. Of the studies which have been carried out, most are qualitative with little discussion of the nature of the calcium coordination environment and based upon the study of a very limited number of compounds of similar nature (such as comparisons of garnets and other minerals2–4). The most detailed studies have been carried out on the calcium binding site in Troponin C and Parvalbumin5 where a shift in the absorption edge position of ∼1 eV was reported, this was qualitatively attributed to changes in coordination environment. Some preliminary XANES studies at the Ca L-edge have also been reported.6,7
We report the XANES of a wide range of ‘model’ (i.e. well characterised, crystalline) calcium compounds and minerals, and we correlate these spectra to the known calcium/oxygen coordination environment in order to generate a means by which calcium K-edge XANES spectra from novel compounds of unknown structure might be more fully interpreted to elucidate the calcium environment. The K-edge for absorption in atomic calcium is at an energy of 4038 eV.
Experimental
Samples of calcium carbonate (99%+), hydroxide (99.995%), oxide (99.995%), tungstate, molybdate (99%+), titanate (99%+), zirconate, silicate (99%+), hydrogen phosphate (99%), dihydrogen phosphate (technical grade 85%) and acetate monohydrate (99%) were purchased from Sigma-Aldrich. Hydrated calcium nitrate (99%+) and calcium fluoride (99%+) were purchased from Fisher; all samples were used as received. X-Ray powder diffraction was used to confirm that the calcium carbonate supplied was 100% calcite with no aragonite.Wollastonite (CaSiO3, Union Carbide Vanadium Mine, Arkansas, USA), Okenite (Ca10Si18O46(H2O)18, Bombay, India), Gyrolite (NaCa16(Al Si23O60)(OH)8(H2O)14, Poona, India), Xonotlite (Ca6(Si6O17)(OH)2, Taimyr, Russia and Foshagite (Ca4(Si3O9)(OH)2, Crestmore Quarry, Riverside County, California) were obtained from Richard Tayler Minerals.8
Pseudowollastonite (CaSiO3) was synthesised from calcium silicate following the method of Yamanaka.9 Grossite (Ca(Al4O7)) and CaAl12O19 were synthesised using the method of MacKenzie et al.10
Data collection
EXAFS and XANES measurements were performed on station 7.1 at the SRS, Daresbury Laboratory, UK and on station E4 at the HASYLAB, Hamburg, Germany.Samples were ground to a fine powder and diluted in polyethylene; these were pressed into pellets and run in transmission mode using ion chambers before and after the sample to measure incident and transmitted X-ray intensity.
Spectra were collected at the Ca K-edge at 4038 eV. The SRS ring energy is 2 GeV and the current is up to 200 mA. The X-ray energy incident on the sample was defined using a Si(111) reflection from a double crystal which allowed the beam to be sagitally focussed. In order to improve the energy resolution only the central segment of the focussing crystal was used, giving an overall energy resolution of 1 eV at the Ca edge. The monochromator crystals were offset to provide a harmonic rejection of 80%. The edge region was scanned in monochromator angle steps of 1 mdeg, and the associated incident X-ray energy was calibrated using a Ti foil placed downstream of the post-sample transmission detector, and before a third ion chamber. At Hasylab the energy of the ring is 4.45 GeV, with a beam current of 120 mA. The X-ray beam was monochromated by two independently driven Si(111) crystals. The instrument was evacuated to ∼10−5 Pa in order to reduce X-ray losses due to attenuation in the air. An overall energy resolution of 0.8 eV at the Ca edge was achieved. The edge region was scanned in 0.1 eV steps, and the energy was calibrated using CaF2 as a calibrant placed between the transmission and a third ion chamber.
Data reduction
For general information about the XANES technique we refer the reader to Koningsberger and Prins.11 Data reduction was performed using EXCALIB and EXBACK.12 SRS data were summed and converted from monochromator angle to the equivalent energy scale using EXCALIB; Hasylab data was output directly as energy data. All spectra were isolated from the background absorption profile using EXBACK to fit polynomials to the pre- and post-edge regions, with the edge step being normalised to 1. The edge position was determined by fitting the near-edge region using a Boltzmann sigmoidal function of the form | (1) |
Results and discussion
Determination of coordination environment
The following analysis is necessarily based primarily on those compounds which afford relatively simple, well-defined coordination environments; however, with certain exceptions, this methodology can be extended to give estimates of the coordination environment of more complex systems.The coordination chemistry of calcium and oxygen is complex, with many compounds showing large variations in Ca–O distances and containing several different Ca environments. To some extent, any discussion of coordination number is limited by assumptions made about the nature of the Ca–O bond: ionic radii, oxidation state, etc. It is necessary to define a limit outside of which atoms are not considered to interact to any significant extent, the exact radial distance at which this cut-off is made will have an effect on the defined coordination sphere.
Bond valence theory can be used to make predictions about the dependence of bond length on coordination number.16,17 We have analysed the structures available in the ISCD database18 to a radius of 4 Å around Ca, a plot of bond length vs. coordination number compares favourably with the values obtained using bond valence predictions up to and including nine-coordinate geometries (see Fig. 1). Compounds with a twelve-coordinate Ca environment have considerably longer average Ca–O distances than is predicted by bond valence theory. On the basis of this study, although there is no clear cut-off for first shell coordination, we suggest that a value of 2.9 Å represents an acceptable compromise for twelve-coordinate Ca–O, this being 0.3 Å longer than that predicted by bond-valence calculations and encompasses all the structures found in the database. Thus, the coordination numbers taken from the database and used herein include all first shell Ca–O bonds of less than 2.9 Å, where a single bond distance is quoted for a compound this distance is an average of all the bond distances less than 2.9 Å.
 | ||
| Fig. 1 Correlation between bond length and coordination number as predicted by bond valence theory (diamonds/line) and for compounds found in the ISCD database18 (squares). | ||
Calcium oxide and hydroxide have single, well-defined six-coordinate calcium environments of six oxygen atoms coordinated at distances of 2.40 and 2.37 Å respectively. Calcium carbonate and Okenite are also relatively well defined. Calcite has a single Ca environment consisting of a six-coordinate Ca–O shell at 2.36 Å and a second Ca–O shell of six oxygens at 3.46 Å. Okenite has four distinct calcium environments, all show a six-coordinate Ca–O shell at an average distance of 2.37 Å and a variable second Ca–O shell ranging from five oxygens at an average distance of 3.74 Å to three oxygens at an average distance of 3.36 Å.
Calcium tungstate and molybdate have well defined eight-coordinate Ca–O environments. CaMoO4 has an eight-coordinate first Ca–O shell at 2.46 Å and a second shell of four oxygens at 3.77 Å, while CaWO4 has a first shell at 2.45 Å and a second shell of four oxygens at 3.79 Å.
The synthetic calcium aluminate, CaAl12O19, has a well defined twelve-coordinate calcium environment at 2.75 Å.
The XANES spectra for these model compounds are shown in Fig. 2. Several features are immediately evident. There are several peaks in the pre-edge region. XANES studies on titanium show a clear relationship between the position and intensity of the pre-edge features and coordination number,19 in this case however no clear correlation has been observed. A small feature at approximately −3.2 eV (4035 eV) is present in all compounds measured and can be assigned to a 1s–3d transition as observed in CaF2,20 this peak is however not singular and in several complexes there are clear indications that the feature is composed of at least two overlapping peaks, again no clear correlation between the presence of this second feature and coordination environment can be seen. The complexity of the subsequent pre-edge features is most likely related to the local symmetry of the calcium environment, interpretation of these features is very difficult without a full molecular orbital treatment (the authors are not aware of any such treatments in the literature except specialised treatments such as the study of calcium doped lanthanum cuprates21). The six-coordinate compounds all show an intense feature at approximately 2.0 eV (0 eV in the case of CaO), which is not present, or is of low intensity, for the higher coordination compounds.
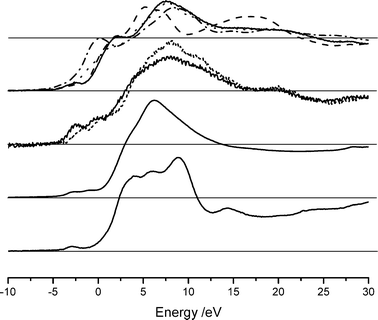 | ||
| Fig. 2 XANES spectra of compounds with well defined coordination shells. From top: six-coordinate, Okenite (solid), calcium carbonate (dashed), calcium hydroxide (dotted) and calcium oxide (dash–dot), eight-coordinate calcium molybdate (solid) and calcium tungstate (dotted), nine-coordinate calcium nitrate, twelve-coordinate CaAl12O19. All spectra have been normalised to an absorbance edge jump of 1, indicated by the grey horizontal lines. | ||
As has been noted already, the spectra shown in Fig. 2 have been normalised such that the height of the absorbance edge step is 1. However, the immediate post edge region encompassing the remaining XANES features rises above this absorbance value and the shape of this region is evidently strongly correlated with coordination. In compounds with higher Ca–O coordination environments there are several sharp features which fall back below unity at about 11 eV: the corresponding features are much broader for compounds with six-coordinate Ca–O environments, with the energy at which these fall below unity being between 22 and 27 eV. The intermediate coordination environments fall between these two extremes, with the post-edge absorbance falling below unity at about 13 eV for nine-coordinate and at about 15 eV for eight-coordinate compounds.
The XANES spectra from the remaining compounds, with more complex coordination environments, are shown in Fig. 3.
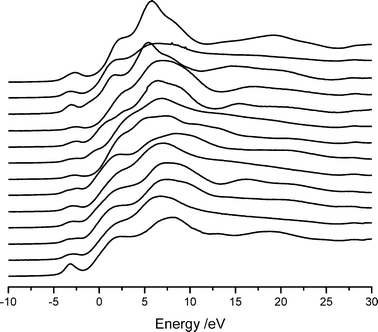 | ||
| Fig. 3 XANES spectra of compounds with complex Ca–O coordination shells. From top, and with the coordination number shown in parentheses: calcium titanate (12), hydroxyapatite (8.4), calcium zirconate (8), calcium dihydrogen phosphate hydrate (8), Pseudowollastonite (8), calcium acetate (7.5), calcium hydrogen phosphate (7.5), Wollastonite (6.67), CaSiO3 (6.67), Xonotlite (6.5), Gyrolite (6.3), Foshagite (6.25) and Grossite (5). | ||
The correlation between edge position and coordination number for compounds up to nine-coordinate is shown in Fig. 4. The six-coordinate environments have edge positions clustered around 0 eV (±0.3 eV), eight-coordinate environments are clustered about 0.9 eV (±0.2 eV) and the single example of a nine-coordinate environment lies almost 1 eV higher than this at 1.8 eV. It should be noted that the determination of edge position varies between the data collected at the SRS and that collected at Hasylab. Statistical fitting errors will be affected by instrument resolution, which as noted previously is 20% better for measurements recorded at Hasylab than at the SRS. However, given that the differences between the Hasylab and SRS data are comparable to the overall scatter in the data and that there is no clearly discernable systematic variation, these differences do not have a significant effect on our conclusions. There are several compounds which do not fit into this correlation, hydroxyapatite, calcium zirconate, calcium molybdate and calcium tungstate. The coordination environment of hydroxyapatite is known to be poorly defined (see ref. 22, and references therein), there are two distinct calcium environments, Ca1 is best described as 6 (2.43 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 (2.79 Å) coordination environment while Ca2 is best described as either 4 (2.36 Å)
3 (2.79 Å) coordination environment while Ca2 is best described as either 4 (2.36 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.51 Å)
2 (2.51 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (2.71 Å) or 5 (2.35 Å)
1 (2.71 Å) or 5 (2.35 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.51 Å)
2 (2.51 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (2.71 Å); Ca1 and Ca2 are present in a 2∶3 ratio. The single coordination number of 8.4 used here is an oversimplification, if a cut-off for the Ca–O first shell is taken as 2.6 Å instead of the more relaxed limit of 2.9 Å this would give an average coordination number of 6, which would bring the associated data point in Fig. 4 within the scatter seen for the other compounds. A similar situation applies with calcium zirconate,23 calcium zirconate is best described as 4 (2.38 Å)
1 (2.71 Å); Ca1 and Ca2 are present in a 2∶3 ratio. The single coordination number of 8.4 used here is an oversimplification, if a cut-off for the Ca–O first shell is taken as 2.6 Å instead of the more relaxed limit of 2.9 Å this would give an average coordination number of 6, which would bring the associated data point in Fig. 4 within the scatter seen for the other compounds. A similar situation applies with calcium zirconate,23 calcium zirconate is best described as 4 (2.38 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.68 Å)
2 (2.68 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) +
+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.84 Å) again this means that depending on where the first shell cut off is chosen the compound can be described as either four-, six- or eight-coordinate, again if a six-coordinate Ca–O environment is postulated the associated data point moves to lie within the scatter seen for the other compounds. Calcium tungstate and molybdate represent different problems in that, although these compounds have a relatively simple coordination environment and therefore a coordination number that is easy to define, the sample is highly absorbing to the soft X-rays necessarily used here. Thus the intrinsic quality of the XANES data is reduced, which introduces larger uncertainties in the fitting process used to determine the edge position.
2 (2.84 Å) again this means that depending on where the first shell cut off is chosen the compound can be described as either four-, six- or eight-coordinate, again if a six-coordinate Ca–O environment is postulated the associated data point moves to lie within the scatter seen for the other compounds. Calcium tungstate and molybdate represent different problems in that, although these compounds have a relatively simple coordination environment and therefore a coordination number that is easy to define, the sample is highly absorbing to the soft X-rays necessarily used here. Thus the intrinsic quality of the XANES data is reduced, which introduces larger uncertainties in the fitting process used to determine the edge position.
 | ||
| Fig. 4 Correlation between XANES edge position and coordination number. Data collected at the SRS are shown as filled squares, data collected at Hasylab are shown as filled circles. Open data points are data for calcium zirconate, hydroxyapatite calcium tungstate and calcium molybdate and were excluded from the fit for reasons discussed in the text. | ||
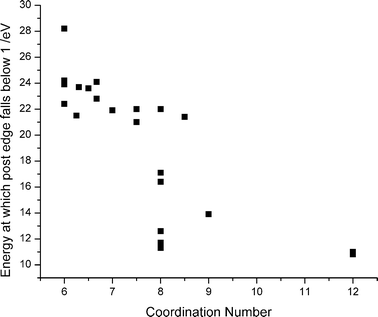 | ||
| Fig. 5 Correlation between coordination number and point at which the envelope of the immediate post edge spectral feature falls below unity. | ||
Line shape
The edge position is not diagnostic for materials with coordination numbers above nine. For instance, the edge position for CaAl12O19 occurs at 1.4 eV whilst that for calcium titanate is at 0.7 eV. However, the overall shape of the post-edge spectral envelope is evidently indicative of high coordination. It may be seen in Fig. 3 that the post edge spectral features samples having Ca in lower coordination environments continues out to ∼22 eV beyond the edge before dropping below the normalised post-edge level of unity. As the coordination number increases, this envelope falls below unity by ∼16 eV to the high energy side of the edge for eight-coordinate compounds, and at ∼11 eV beyond the edge for twelve-coordinate compounds. In other words, the immediate post-edge features become narrower as the Ca–O first shell coordination number increases. The correlation between coordination number and post-edge for all the compounds measured is shown in Fig. 5.Prediction of coordination number from edge position
If compounds with 9-fold oxygen coordination or higher are identified on the basis of post-edge spectral shape as detailed above, it is then possible to plot a linear correlation between coordination number and edge position for all lower coordination numbers. A fit to the model compounds data thereby allows a coordination number to be predicted for any sample once the K-edge position has been measured. In the case of the model compounds studied here, the coordination numbers generated in this way (i.e. from the fitted straight line) compare well with the X-ray crystallography measured literature values, the scatter of the values for model compounds has a standard deviation of 0.4. Therefore we can expect to predict coordination numbers with an accuracy of ±0.5 atom. Table 1 summarises the coordination numbers, average bond lengths, edge positions and energies beyond which the post edge peak falls beneath unity (Epost edge).| Compound | Coord. numbera (n) | Av. bond length/Å | Edge position relative to 4038 eV (SRS)/eV | Edge position relative to 4038 eV (Hasylab)/eV | E post edge/eV |
|---|---|---|---|---|---|
a Coordination number calculated from data in the ISCD database including all first shell Ca–O bonds of less than 2.9 Å.18
b Calcium zirconate is best described as 4 (2.38 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.68 Å) 2 (2.68 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.84 Å).
c Grossite is best described as a 5 (2.372 Å) 2 (2.84 Å).
c Grossite is best described as a 5 (2.372 Å)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (2.872 Å) coordination shell.
d N.c. = Not collected.
e Pseudowollastonite has a very diffuse Ca–O environment, bond lengths lie in the range 2.28–2.72 Å. 2 (2.872 Å) coordination shell.
d N.c. = Not collected.
e Pseudowollastonite has a very diffuse Ca–O environment, bond lengths lie in the range 2.28–2.72 Å.
|
|||||
| CaCO3, calcite | 6 | 2.36 | −0.005 | −0.27 | 22.4 |
| Wollastonite | 6.67 | 2.439 | −0.37 | −0.25 | 24.1 |
| Xonotlite | 6.5 | 2.402 | 0.066 | −0.215 | 23.6 |
| Gyrolite | 6.3 | 2.432 | −0.22 | −0.05 | 23.7 |
| CaZrO3b | 8 (4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
2.885 | 0.036 | −0.015 | 22.0 |
| Okenite | 6 | 2.37 | −0.078 | −0.01 | 24.2 |
| Foshagite | 6.25 | 2.442 | 0.398 | 0.02 | 21.5 |
| Grossitec | 7 (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) + +![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) 2) |
2.515 | 0.039 | 0.03 | 21.9 |
| Hydroxyapatite | 8.4 | 2.499 | N.c.d | 0.18 | 21.4 |
| CaSiO3 | 6.67 | 2.439 | 0.285 | 0.24 | 22.8 |
| Ca(OH)2 | 6 | 2.37 | 0.189 | 0.28 | 23.9 |
| CaHPO4 | 7.5 | 2.468 | 1.026 | 0.73 | 22.0 |
| CaTiO3 | 12 | 2.712 | 0.741 | 0.745 | 10.8 |
| Pseudowollastonitee | 8 | 2.531 | 0.803 | 0.79 | 11.7 |
| Calcium acetate | 7.5 | 2.453 | 1.327 | 0.91 | 21 |
| CaMoO4 | 8 | 2.46 | 1.957 | 1.02 | 16.4 |
| CaH2PO4(H2O) | 8 | 2.48 | 1.29 | 0.73 | 12.6 |
| CaAl12O19 | 12 | 2.747 | 1.352 | 1.47 | 11.0 |
| CaWO4 | 8 | 2.45 | 1.28 | 1.65 | 17.1 |
| Ca(NO3)2·4H2O | 9 | 2.53 | N.c.d | 1.81 | 13.9 |
| CaO | 6 | 2.402 | −0.155 | N.c.d | 28.2 |
Conclusions
It is possible to use XANES at the Ca K-edge to determine average oxygen coordination numbers of up to nine atoms. Compounds with a higher coordination number have a distinctive shape in the post edge region and can be identified on this basis. In compounds with average coordination numbers up to and including nine, the edge position is diagnostic for coordination number via a shift of 0.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ±
±![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.1 eV per atom. When the measured edge position is used in conjunction with a qualitative analysis of the post-edge absorption spectrum shape it is now possible, on the basis of the “fingerprint library” presented herein, to comment with a high degree of confidence on the Ca–O coordination environment in more complex (e.g. amorphous) materials.
0.1 eV per atom. When the measured edge position is used in conjunction with a qualitative analysis of the post-edge absorption spectrum shape it is now possible, on the basis of the “fingerprint library” presented herein, to comment with a high degree of confidence on the Ca–O coordination environment in more complex (e.g. amorphous) materials.
Acknowledgements
We wish to acknowledge the use of the EPSRC's Chemical Database Service at Daresbury, the EPSRC for funding the work at Kent and Warwick on calcium silicate materials (GR/R59492 and GR/R59298), CCLRC (SRS staff, facilities and computing), Hasylab and UKC (funding for L. J. S.).References
- (a) J. E. Harries, D. W. L. Hukins and S. S. Hasnain, Calcif. Tissue Int., 1988, 43, 250–253 CAS; (b) L. S. Nelson, C. Holt and D. W. L. Hukins, Physica B, 1989, 158, 103–104 CrossRef CAS; (c) A. Mottana, T. Murrata, Z. Wu, A. Marcelli and E. Paris, J. Electron Spectrosc. Relat. Phenom., 1996, 79, 76–82 CrossRef; (d) T. Taniguchi, M. Okuno and T. Matsumoto, J. Non-Cryst. Solids, 1997, 211, 56–63 CrossRef CAS; (e) N. Richard, N. Lequeux and P. Boch, J. Phys. III, 1995, 5, 1849–1864 Search PubMed; (f) A. Becker, U. Bismayer, M. Epple, H. Fabritius, B. Hasse, J. M. Shi and A. Ziegler, Dalton Trans., 2003, 4, 551–555 RSC.
- E. Paris, Z. Wu, A. Mottana and A. Marcelli, Eur. J. Mineral., 1995, 7, 1065–1070 CAS.
- J. Chaboy and S. Quartieri, Phys. Rev., 1995, 52, 6349–6357 Search PubMed.
- S. Quartieri, J. Chaboy, M. Merli, R. Oberti and L. Ungaretti, Phys. Chem. Miner., 1995, 22, 159–169 CAS.
- A. Bianconi, A. Giovannelli and L. Castellani, J. Mol. Biol., 1983, 165, 125–138 CAS.
- F. M. F. deGroot, J. C. Fuggle, B. T. Thole and G. A. Swatzky, Phys. Rev. B, 1990, 41, 928–937 CrossRef.
- S. J. Naftel, T. K. Sham, Y. M. Yiu and B. W. Yates, J. Synchrotron Radiat., 2001, 8, 255–257 CrossRef CAS.
- Richard Tayler Minerals, (richard.tayler@minerals.freeserve.co.uk) Cobham, Surrey.
- T. Yamanaka and H. Mori, Acta Crystallogr., Sect. B, 1981, 37, 1010–1017 CrossRef.
- K. J. D. MacKenzie, M. Schmücker, M. E. Smith, I. J. F. Poplett and T. Kemmitt, Thermochim. Acta, 2000, 1–2, 181–188 CrossRef.
- X-Ray Absorption, Principles, Applications, Techniques of EXAFS, SEXAFS and XANES, ed, D. C. Koningsberger and R. Prins, Wiley, New York, 1987 Search PubMed.
- N. Binsted, J. W. Campbell, S. J. Gurman and P. C. Stephenson, EXAFS Analysis Programs, Daresbury Laboratory, Warrington, 1991 Search PubMed.
- L. Galoisy, G. Calas and M. A. Arrio, Chem. Geol., 2001, 174, 307–319 CrossRef CAS.
- G. Calas and J. Petiau, Solid State Commun., 1983, 48, 625–629 CrossRef CAS.
- G. Waychunas, Am. Mineral., 1987, 72, 89–101 CAS.
- A. C. Hannon and J. M. Parker, J. Non-Cryst. Solids, 2000, 274, 102–109 CrossRef CAS.
- N. E. Brese and M. O'Keeffe, Acta Crystallogr., Sect. B, 1991, 47, 192–197 CrossRef.
- The United Kingdom Chemical Database Service: D. A. Fletcher, R. F. McMeeking and D. Parkin, J. Chem. Inf. Comput. Sci., 1996, 36, 746–749 Search PubMed.
- G. Mountjoy, D. M. Pickup, G. W. Wallidge, R. Anderson, J. M. Cole, R. J. Newport and M. E. Smith, Chem. Mater., 1999, 11, 1253–1258 CrossRef CAS.
- J. H. Barkyoumb and A. N. Mansour, Phys. Rev. B, 1992, 46, 8768–8776 CrossRef CAS.
- J. Okasinski, J. B. Cohen, J. Hwang, T. O. Mason, Z. Ding, O. Warschkow and D. E. Ellis, J. Am. Ceram. Soc., 1999, 82, 2451–2459 CAS.
- J. E. Harries, D. W. L. Hukins and S. S. Hasnain, J. Phys. Chem. C: Solid State Phys., 1986, 19, 6859–6872 Search PubMed.
- H. J. A. Koopmanns, G. M. H. van de Velde and P. J. Gellings, Acta Crystallogr., Sect. C, 1983, 39, 1323–1325 CrossRef.
| This journal is © the Owner Societies 2004 |
