Density functional study of Pd nanoparticles with subsurface impurities of light element atoms

Abstract

Atomic H, C, N and O at the surface and in the subsurface region of Pd nanoparticles were studied theoretically using an all-electron scalar relativistic density functional approach. We modelled nanosize metal clusters by the three-dimensional crystallites Pd₇₉ and Pd₁₁₆ chosen as octahedral fragments of bulk Pd; these clusters expose (111) and (001) facets. Adsorbed atoms were located at the three-fold hollow sites in the centre of (111) facets. Migration of the atoms from the surface of the cluster Pd₇₉ to the octahedral subsurface (oss) site below was considered. Migration of C from the surface hollow site to the oss position was found to be almost isoenergetic; migration of H is somewhat endothermic (by 0.5 eV). For N and O, a lager endothermicity was calculated. Both H and C species exhibit moderate activation barriers for the diffusion to the oss site. C and O atoms in the tetrahedral subsurface (tss) position of the cluster Pd₁₁₆ were also studied. For both species, this location is energetically disfavoured, although the endothermic effect of O atom migration to the tss position is ∼0.5 eV smaller than to the oss site. Subsurface C impurities were calculated to reduce the adsorption energy of CO molecules at Pd clusters.

---

1 Introduction

Impurity atoms can significantly modify chemical properties of metal surfaces. For instance, Pd particles on an oxide support (e.g., SiO₂) exhibit low activity and only modest selectivity in the synthesis of methanol from syngas, whereas addition of a suitable promoter (impurity) results in an active and very selective catalyst for methanol synthesis.^1,2

One can distinguish between impurities bound externally to the surface from those incorporated into the outermost layers of the substrate, i.e.subsurface impurities. The latter in turn can be divided into substitutional and interstitial impurities.³ In Pd samples, interstitial impurities can be formed by atoms of light elements, occupying octahedral and tetrahedral subsurface (oss and tss, respectively) holes between Pd atoms of the face centred cubic (fcc) lattice. In particular, hydrogen is known to dissolve in Pd bulk and to form an ordered hydride phase PdH_0.5 at higher concentrations.⁴ At low temperature (T < 130 K) hydrogen is first chemisorbed at the surface up to a monolayer coverage; then a small fraction of further dosed hydrogen penetrates the surface.⁵ Recently, occupation of interstitial oss sites of Pd by C and O species at low concentrations was proposed on the basis of scanning tunnelling microscopy (STM) study.³ Oxygen impurities are of great interest for oxidation catalysis. The ability of atomic oxygen to form rather stable subsurface species on Pd and the role of such subsurface impurities in surface oxidation reactions have been extensively discussed.^6–9

Nevertheless, lack of knowledge on the stability and local structure of subsurface O species may still lead to controversial interpretations of experimental data. For instance, recently a significant intake of oxygen by alumina-supported Pd particles (Pd/Al₂O₃/NiAl(110) system) was found at low temperature (250–300 K) and initially attributed to penetration of oxygen into the subsurface space of the supported Pd clusters, up to PdO_0.5 stoichiometry.¹⁰ Surprisingly, the overall morphology of the Pd particles was not affected by this significant oxygen uptake.¹⁰ Later on, the formation of a PdO-like phase was ruled out and the anomalous oxygen intake was rationalised by oxidation of the NiAl substrate beneath the alumina film.¹¹

We recently investigated Pd nanoclusters, ranging from Pd₅₅ to Pd₁₄₆, by means of all-electron relativistic density functional (DF) calculations.^12,13 We considered the interaction of CO molecules with three-fold hollow sites in the centre of (111) facets of such clusters and we analysed how adsorption parameters varied with cluster size.¹² We also examined how observables calculated for that adsorption position of CO on cluster facets relate to observables for CO on the corresponding sites at the single-crystal surface Pd(111). We demonstrated that cluster models of about 80 and more Pd atoms describe various adsorption properties of the Pd(111) surface (including the adsorption energy) in quantitative fashion.¹²

In the present work, we applied the same computational approach and the same type of cluster models to study subsurface interstitial impurities of light elements in Pd nanoparticles. Surface and subsurface atomic O and C species were of primary interest for us. However, we also considered N and H atoms because these impurities are also expected to appear under experimental conditions of some reactions over Pd catalysts. Furthermore, for subsurface H, the most extensive experimental information has been accumulated which can be used for benchmarking the computational approach. The cluster method employed allows one to clarify the phenomenon of adatom diffusion into the subsurface region (including a description of transition states), accounting in full for the structural relaxation of the Pd substrate.

In this DF study, we explored surface and subsurface monatomic H, C, N and O species at/in octahedral Pd clusters that represent three-dimensional crystallites of fcc structure and expose (111) and (001) facets. The adsorbed atoms were located at the three-fold hollow sites in the centre of (111) facets, a single adatom per facet. Migration of the adatoms from fcc surface hollow sites to interstitial oss hole sites was studied for the cluster Pd₇₉. The relative stability of surface and subsurface species as well as the activation barrier for migration from the surface into the subsurface position were calculated. For C and O species, the relative stability of complexes at surface hexagonal closed packed (hcp) hollow sites and tss sites were compared, using the cluster Pd₁₁₆. Finally, we addressed the issue of CO adsorption at surface sites above subsurface impurities.

2 Computational details and models

All-electron calculations were performed using the linear combination of Gaussian-type orbitals fitting-functions DF (LCGTO-FF-DF) method¹⁴ as implemented in the parallel code ParaGauss.^15,16 We used the scalar relativistic variant of the LCGTO-FF-DF method which employs a second-order Douglas–Kroll transformation of the Dirac-Kohn–Sham equation.^17,18 Self-consistent solutions of the Kohn–Sham equations were obtained within the local density approximation (LDA; VWN parameterisation¹⁹). Energies were evaluated for generalised-gradient approximation (GGA, Becke-Perdew, BP,^20,21) of the exchange-correlation functional, using the electron density of the self-consistent LDA calculations. This economic computational strategy was found very accurate for geometric parameters, binding energies and vibrational frequencies.²² Our benchmark self-consistent BP calculations of adsorption complexes on Pd nanoclusters confirmed this; CO adsorption energies were reproduced better than to 1%.

As previously,^12,13 we employed an orbital basis set²³ for Pd which was extended to (18s,13p,9d) and contracted to [7s,6p,4d] using relativistic VWN atomic eigenvectors.²⁴ C, N and O atoms were described by orbital basis sets of the quality (14s,9p,4d)²⁵ using the original general contraction [6s,5p,2d];²⁵ the corresponding basis for H was (8s,4p) → [4s,3p].²⁵ To evaluate the classical Coulomb contribution to the electron-electron interaction, the electron density was represented with the help of an auxiliary basis set,¹⁴ constructed as explained earlier.^12,13 For Pd, the auxiliary basis set was of the size (17s,6r²,5p,5d); for C, N and O atoms–(14s,9r²,5p,5d); for H atom–(8s,4r²,5p).

Because spin-polarised test calculations revealed a closed-shell electronic structure of the clusters, we discuss in the following only results of spin-restricted calculations. Atomic reference energies were always calculated in spin-polarized fashion. To ensure convergence of the electron density during iterations, a technique of fractional occupation numbers with a level broadening of 0.1 eV was applied throughout.¹⁴ Unless explicitly stated otherwise, we carried out full geometry optimisations (subject only to O_h symmetry restrictions) of the models under study at the LDA (VWN) level. Finally, the GGA (BP) energy was evaluated at the LDA optimised geometry (combined BP//VWN approach). In line with our previous studies,^12,13 the LDA geometry optimisation strategy was chosen because GGA functionals considerably overestimated Pd–Pd distances²⁶ compared to the experimental bulk value 2.75 Å.²⁷ Periodic slab calculations with BP functional yield 2.86 Å for the nearest interatomic distance of Pd bulk.²⁸ On the other hand, with the VWN functional, Pd–Pd distances from cluster calculations of growing size extrapolated to bulk limits of 2.73–2.76 Å,^12,26 in close agreement with experiment.

The cuboctahedral substrate models Pd₇₉ and Pd₁₁₆ with (111) and (001) facets (Fig. 1) were obtained by truncating the octahedral clusters Pd₈₅ and Pd₁₄₆, respectively, to yield eight hexagonal (111) facets. These symmetric (three-dimensional) clusters contain a significantly larger fraction of Pd atoms with high coordination numbers compared to “planar” (“two-dimensional”) cluster models, commonly used in chemisorption studies.^29,30 Boundary metal atoms of such conventional cluster models are a source of inaccuracy in calculations of chemisorption complexes. On the other hand, boundary atoms of three-dimensional cluster models of this study (Fig. 1) are described much more realistically.¹²

Fig. 1 Model nanoparticles of O_h symmetry: Pd₇₉ and Pd₁₁₆. One of the eight symmetrical adsorption positions in the centre of an (111) facet is marked by an arrow.

Activation barriers of surface-to-subsurface diffusion were determined by scanning the potential energy profile along the line which connects the local minima of the surface and subsurface impurity atoms with the centre of the Pd clusters (Fig. 2). For each sampling point, the radial distance of the impurity atom was fixed while all other geometry variables of the Pd cluster were optimised while preserving the O_h symmetry of the system.

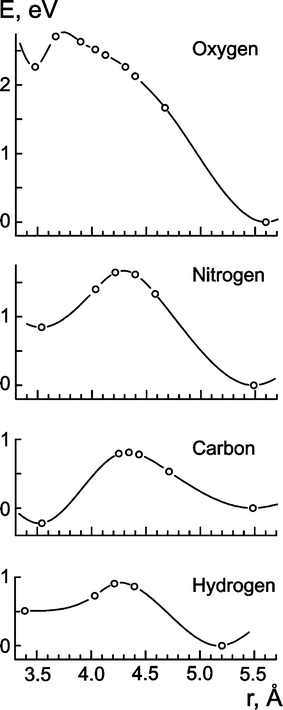Fig. 2 Potential energy profiles along the normal of (111) facets of the cluster Pd₇₉. Local minima correspond to impurity atom adsorbed at fcc three-fold hollow sites (right-hand) and in octahedral subsurface holes (left-hand).

In calculations of CO adsorption, we kept all Pd atoms at their positions calculated without the adsorbate, i.e. we neglected the cluster relaxation induced by adsorbed CO. To approach the equilibrium geometry of adsorption complexes with CO molecules oriented to fit the symmetry group O_h, we consecutively varied Pd–C and C–O distances until deviations were below 0.005 Å, using BP energies. We corrected the CO adsorption energy for the basis set superposition error (BSSE) via the counterpoise technique.³¹ The C–O vibration was approximated by the C–O internal mode with the CO centre of mass kept fixed; to determine harmonic vibrational frequencies, polynomials of degree 4 were fitted to five total energy values near the minimum of the potential curve.

3 Results and discussion

3.1 Impurities occupying subsurface sites

The fcc lattice of palladium offers two types of interstitial subsurface sites – oss and tss: holes formed by regular octahedra or tetrahedra of Pd atoms, respectively. In the ideal Pd lattice with Pd–Pd distance of 2.751 Å, the distance between hole centres and the neighbouring Pd nuclei is 1.945 Å (oss) and 1.685 Å (tss). Subtracting the covalent radius of Pd atoms, 1.28 Å,³² one assigns radii of 0.665 and 0.405 Å to the oss and tss holes, respectively. Comparison of these values with covalent radii of light element atoms (O: 0.66 Å, N: 0.70 Å, C: 0.77 Å, H: 0.30 Å; according to Pauling)³² implies that oss sites are more suitable for occupation by light elements, only for hydrogen the covalent radius is small enough to occupy tss sites. The surface positions above oss and tss holes are three-fold fcc and hcp hollow sites, respectively. Three-fold sites are known to be energetically most favourable at the surface for the adsorption of such light atoms as H, N and O.³³ Hence, subsurface interstitial impurities can be directly formed by diffusion from the surface three-fold hollows to the subsurface holes.

Let us consider first impurity atoms occupying the oss interstitial positions just beneath the (111) facets of the clusters. Table 1 summarises the calculated energies for O, N, C and H atoms at the surface fcc three-fold site and in the oss hole including the activation barrier for diffusion between these sites. An important observation is that VWN and BP//VWN energies (see Section 2) for subsurface species are not much different. However, because of the well-known tendency of LDA to overestimate binding energies, we discuss here only BP//VWN desorption energies. Note that, even at the BP level, desorption energies deviate by 0.5–0.8 eV from the experimental results: 3.77, 5.64 and 2.69 eV for O, N and H, respectively.³³ This discrepancy is partly due to the inability of a Kohn–Sham approach to accurately reproduce energies of open-shell atomic states.³⁴ One can repair this drawback and improve the agreement with experiment by calculating adsorption energies with respect to gas phase molecules;³⁵ for instance, the desorption energy of oxygen with respect to O₂ is calculated at 1.36 eV, which compares much better with the experimental value of 1.16 eV.³³

Table 1 Migration energy, ΔE_sub, of an impurity atom X (X = H, C, N, O) from a surface fcc site to a subsurface oss site and activation barrier, ΔE^≠_sub, of the migration calculated for the clusters Pd₇₉X₈ at the VWN level with respect to the surface adsorption state, where eight atoms X occupy the central fcc positions at the cluster facets. Values in parentheses are for calculations at the BP//VWN level (see text). The reference for the desorption energy, ΔE_des, of atom X is the sum of the total energies of the bare cluster Pd₇₉ and of a free atom in the gas phase

	H		C		N		O
ΔEsub/eV	0.51	(0.52)	−0.22	(−0.14)	0.85	(0.86)	2.26	(1.97)
ΔE^≠sub/eV	0.91	(0.62)	0.81	(0.62)	1.64	(1.36)	2.71	(2.29)
ΔEdes/eV		(3.22)		(6.88)		(4.87)		(4.34)

---

The strongest bonds with Pd(111) facets are formed by C atoms, followed by N and O, whereas H atoms exhibit the weakest bonds. This trend is in agreement with the experimental desorption energies of the atoms N, O and H, just mentioned.³³ There is an interesting correlation between the binding energies and the Mulliken negative charges on the adsorbed atoms: −1.16 e (C), −0.84 e (N), −0.61 e (O), −0.22 e (H) (Fig. 3). Of the atomic species under investigation, only C atoms are slightly more stable in the subsurface region than at the surface. However, the energy gain of 0.1–0.2 eV is close to the accuracy limit of the methods and models used in the present study; surface and oss states should probably be classified as almost isoenergetic. H atoms exhibit a moderate energy preference, 0.5 eV, for the surface state. For N and O, the surface states are significantly more stable, by 0.9 and ∼2 eV, respectively. Moreover, occupation of the oss site by oxygen is endothermic with respect to O₂ molecules in the gas phase. Although the GGA BP correction yielded a large deviation from the VWN result, ∼0.3 eV, for subsurface O, this energy change constitutes less than 15% of the energy difference between the surface and subsurface states and the qualitative picture is unequivocal. Note, that our result for O impurities is close to that of slab model calculations, where the adsorption at the three-fold surface site was reported by 2.2 eV more stable than in the oss position.³⁶ The GGA PBE (Perdew, Burke and Ernzerhof)³⁷ approach was applied in the latter work to a four-layer slab with a PBE-optimised geometry resulting in a Pd–Pd nearest-neighbour distance of 2.81 Å. Calculated activation barriers for migration of atoms adsorbed at the surface fcc sites to the oss holes (Table 1) follow the same trend as the energies of this process in agreement with the Polyani–Semenov principle:³⁸ the lowest barrier is calculated for C, followed by H, N and O.

Some information rationalising the different stability of subsurface species formed by different elements can be obtained from an analysis of the geometric structure. In the optimised bare cluster Pd₇₉, the oss site below the central fcc position at the (111) facet exhibits the shape of an almost regular octahedron formed by six Pd atoms with the interatomic distances of 2.70 Å. The distance from the centre of the oss hole to the neighbouring Pd nuclei is 1.91 Å. Impurities or adsorbed atoms entail an expansion of the cluster. In the case of H atoms, this expansion is essentially negligible; the strongest changes occur for subsurface O species. Not unexpectedly, the local expansion is most pronounced, i.e. the structure of the moieties in direct contact with the light atom is affected most. In particular, adsorption at the surface elongates the distances between Pd atoms forming the three-fold hollow site by about 0.05 Å with respect to the distance 2.70 Å in the bare cluster Pd₇₉ (0.02 Å in the case of adsorbed H; Table 2). As can be judged from the changes in the distance from the cluster centre to the outermost corner Pd atoms (Table 2), the cluster as a whole also enlarges upon interactions with the light atom impurities compared to the value of 5.94 Å computed for the bare cluster. For adsorption at the surface, this distance is only slightly longer, by at most 0.03 Å in the case of C adsorbates. More significant changes in both the overall cluster size and the local structural parameters were found for subsurface impurities. As in the case of surface adsorption, location of C and N species in oss holes results in very similar local structural characteristics and their average distance to the neighbouring Pd centres is about 1.99 Å. A slightly stronger cluster expansion can be noticed in the case of N. The most distorted structure corresponds to a cluster with O atoms occupying oss positions: the average Pd–O distance is 2.03 Å and the cluster expands overall by ∼0.1 Å. Therefore, it is not surprising that O species are found to be the least stable among the subsurface impurities considered here.

Table 2 Selected structural characteristics (in Å) calculated with VWN functional for the clusters Pd₇₉X₈ (X = H, C, N, O) with light atoms X at surface three-fold hollow adsorption sites, in subsurface (oss) positions, and in the transition state structure of the diffusion from the surface to the subsurface sites

	H	C	N	O
Surface
r(Pd–X)	1.738	1.871	1.872	1.941
r(Pd–Pd)^a	2.718	2.748	2.751	2.744
R cluster ^b	5.935	5.972	5.967	5.954

---

Subsurface
r 1(Pd–X)^c top layer	1.911	1.938	1.945	2.068
r 2(Pd–X)^d sublayer	1.959	2.048	2.045	2.008
r(Pd–Pd)	2.707	2.815	2.826	2.921
R cluster	5.949	6.023	6.033	6.035

---

Transition state
a r(Pd–Pd) is the distance between the three Pd atoms forming a surface three-fold hollow site. b R cluster is the distance between the cluster origin and Pd atoms most remote from it. c Surface Pd atom. d Subsurface Pd atom.
r(Pd–X)	1.632	1.788	1.820	1.857
r(Pd–Pd)	2.757	3.081	3.092	3.217
Rcluster	5.963	6.147	6.147	6.175

---

For the second row elements, the energy change of migration to the subsurface site (and the activation barrier) shows a clear trend, C < N < O, concomitant with the size of the perturbation of the cluster geometry. Note the significant increase of the Pd–X distance from 1.87 Å for Pd–C to 1.94 Å for Pd–O (Table 2). The increasing distortions of the cluster structure when going from C to O impurities become even more noticeable for the transition states of the surface-subsurface migration (Table 2). In the unperturbed bare cluster, the distance from the centre of the three-fold hollow Pd₃ triangle (with an edge of 2.70 Å) to its apex is 1.56 Å. Therefore, in the transition state, the triangle edges elongate to 3.08, 3.09 and 3.22 Å to enable penetration of C, N and O atoms, respectively, into the oss hole. Such significant local distortions of the Pd cluster frame are partially compensated by a relaxation of other Pd atoms; hence, the overall cluster size in the transition state increases by at most 0.23 Å in the case of oxygen. The Pd–X distances for adsorbates exhibit a trend opposite to the tabulated covalent radii of Pauling: C > N > O. Thus, to rationalise trends in the stability of the subsurface aggregates with respect to the corresponding adsorbed species, one has to consider not only the bond length Pd–X, but also the binding energy and the transfer of electronic charge from the metal surface to the adsorbate (Fig. 3). Interaction with palladium is most favoured for atomic carbon which exhibits the strongest bond with the surface and the largest charge transfer from the surface; it is followed by N and O.

Fig. 3 Comparison of calculated characteristics of different atoms, X = H, C, N, O, adsorbed at the surface of the cluster Pd₇₉: energy of migration, ΔE_sub (eV), from a surface fcc position to an oss site; energy of adsorption, ΔE_des (eV), at an fcc site from the gas phase (negative value displayed); Mulliken charge q of a species X adsorbed at an fcc site (e); Pd–X distance, r(Pd–X) (Å), for species X adsorbed at an fcc site.

The hydrogen atom represents a special case: it is small, its single 1s electron cannot form multiple bonds and it interacts with a Pd surface notably weaker than C, N and O adsorbates (Table 1, Fig. 3). According to our results, a subsurface H species exhibits (despite its smaller size) a lower stability relative to the surface adsorption state than a C impurity. Hydrogen adsorption at Pd surfaces as well as hydrogen solution in Pd bulk was extensively studied experimentally.^4,5 A number of studies deals with H solution in Pd nanocrystalline particles as well.^39–41 It is long established that hydrogen can easily dissolve into palladium bulk through the close-packed Pd(111) surface.^42,43 However, in the low concentration limit, the enthalpy of hydrogen solution in Pd bulk, –0.10 eV per atom,⁴ is less than the enthalpy of adsorption at Pd(111) surface, −0.46 eV per atom.⁴² An ordered hydride phase PdH_0.5 emerges at higher concentrations where all oss sites are occupied by H atoms. The enthalpy of formation for the hydride phase is −0.40 eV per atom,⁴i.e. almost equal to the enthalpy of adsorption. Our calculated energy difference of 0.52 eV per H atom between surface adsorption and occupation of the oss site (Table 1) agrees with the experimental enthalpy difference at low H concentrations, 0.36 eV. (Note that in this work only a symmetric mode was considered for the motion of Pd atoms.) There is no experimental data available on the activation energy of the surface-subsurface migration of hydrogen. However, the diffusion coefficient D for hydrogen in Pd bulk at low concentrations can be well expressed as D = D₀exp(−E_a/kT) with E_a = 0.13 eV in the low temperature range (130–220 K) and E_a = 0.23 eV at T > 230 K.⁴ We can compare these energies with calculated activation barrier for the diffusion from the oss site to the surface fcc site, although one should keep in mind that these two processes are not identical. The calculated values for the diffusion barrier range from 0.40 eV (VWN optimised) to 0.10 eV (BP//VWN), Table 1.

The potential energy profile for the migration of hydrogen adsorbed at a Pd(111) surface into the subsurface region was also studied by means of DF-GGA (BP) approaches.^44,45 For a rigid three-layer slab model at the experimental lattice constant 3.89 Å and H coverages θ = 1/3 and 1, the adsorption at the fcc site was found to be 0.56 eV more favourable than occupation of the oss site;⁴⁴ or 0.43 eV with the optimal BP value of lattice constant 3.95 Å at θ = 1. The latter value changed to 0.31 eV when a partial relaxation was taken into account which allowed displacements of the top layer Pd atoms along the surface normal. Thus, despite significant methodological differences with the present cluster model study, the periodic slab model approach yields the relative energy for hydrogen occupation of the fcc and oss positions sufficiently close to the present value of ∼0.5 eV (Table 1), favouring the surface fcc site. The activation barrier for the diffusion of H atoms from the fcc site to the oss site calculated for the rigid experimental bulk-terminated Pd lattice was 0.79 eV for θ = 1/3 or 0.85 eV for θ = 1. In-plane relaxation of the three Pd atoms forming the fcc site in the top layer decreased the energy of the transition state by 0.29 eV at θ = 1/3,⁴⁴ hence the barrier height can be estimated as 0.5 eV. Unfortunately, no consistent relaxation of fcc and oss sites was performed in that study; therefore, the above values should be considered as rather rough estimates. Nevertheless, our fcc-oss diffusion barrier of 0.62 eV (Table 1), which yields a barrier of 0.1 eV for the reverse oss-fcc diffusion, is consistent with the results of Løvvik and Olsen.⁴⁴ This comparison to periodic slab model calculations implies that results of the present cluster model approach can be applied not only to the (111) facets of Pd nanoparticles, but also to the single-crystal Pd(111) surface, provided that adsorption species is far enough from cluster edges and other surface irregularities.^12,13

An important issue related to the latter statement is a comparison of (111) facets of Pd nanoparticles and the single crystal (111) surface with regard to H adsorption and absorption on or beneath the surface. For a simple albeit rather crude estimate, one can employ a Pd nanocluster taken at the bulk-terminated experimental geometry as a model of a single-crystal Pd(111) surface. For this model, we studied the interaction of an H atom at the fcc surface site, the oss subsurface site and the corresponding transition state, using the same cluster Pd₇₉ (Fig. 1), but keeping all its Pd–Pd bond lengths fixed at the experimental value of 2.75 Å. The adsorption energy per H atom at the fcc site of this model, 3.14 eV, is slightly lower than the value of 3.22 eV for the fully relaxed model (Table 1). For the subsurface oss species, one also finds a destabilization: 2.57 eV compared to 2.70 eV (Table 1). As expected, the rigid Pd₇₉ model gave a higher activation energy for the fcc-oss diffusion, 0.86 eV compared to 0.62 eV for the relaxed system; the barriers of reverse diffusion are very small, 0.29 (fixed structure) and 0.10 eV, respectively. These data of a low concentration model do not provide evidence for the notably enhanced accessibility of subsurface H atoms absorbed in the (111) facets of Pd nanoclusters compared to the Pd(111) single crystal samples; however, these effects seem to be subtle. Recently, in an experimental study, it was deduced that subsurface hydrogen is able to participate more easily in hydrogenation reactions at the surface of Pd nanoclusters than on single-crystal Pd.⁴⁶ This easy accessibility of subsurface hydrogen on the nanoparticles agrees with the present calculated results. On the other hand, our nanocluster models are not suited for modeling hydrogen diffusion from Pd bulk.

Oxygen diffusion to Pd subsurface layers or in the bulk was reported by many authors.^3–8 However, there is still no general consensus on the nature of subsurface O species. While some authors suggest the formation of a PdO phase,⁷ others argue that they do not find any specific features, characteristic of oxide formation.⁸ Recently, using a STM technique, Rose et al.³ discriminated two types of impurities occupying interstitial oss sites beneath a clean Pd(111) surface under ultra high vacuum (UHV) conditions. Attempts to identify conclusively these impurity species failed. However, based on indirect evidence, atomic C and O were suggested to be the most likely candidates.³ The activation energies of impurity diffusion in the subsurface region parallel to the surface were estimated (with a large uncertainty in the pre-exponential factor) at 0.7–0.9 eV. (Diffusion experiments at T ∼ 1223–1378 K and an inelastic relaxation study at T ∼ 430–460 K estimated the diffusion barrier of C atoms in Pd bulk at 1.2 eV.⁴⁷) Because the diffusion barrier of H in the Pd bulk is only 0.2 eV,⁴ it was proposed that H atoms move too fast to be detected by STM at the experimental temperatures.³ These experiments are compatible with the present studies of isolated atomic impurities. Our results support the tentative assignment of one of the observed interstitial impurities as C species. However, we find it very unlikely that O atoms would stay in oss sites in case of a clean Pd(111) surface, i.e. in the absence of adsorbates. Even if a certain concentration of subsurface O atoms was somehow created (e.g. at high O₂ pressure), subsurface oxygen impurities would rapidly leave the oss sites and move to the surface after all adsorbates were removed from the surface. Indeed, the calculated BP//VWN activation barrier of O diffusion from the oss site to the surface is only 0.3 eV (Table 1). Note that according to experimental results, boron is another element, besides hydrogen and carbon, that exhibits a substantial interstitial solubility in Pd bulk.⁴⁸

The calculated stability of subsurface C species and the relatively low activation barrier for diffusion from the surface to the bulk is in line with the formation of a phase PdC in supported Pd catalysts, as repeatedly reported.^49–52 It appears that the source of carbon in all these studies was an organic precursor used to prepare the catalyst or chemicals used during the investigation.⁵³ On the other hand, no carbide phase was found due to migration of C from the powder carbon support in the supported Pd catalyst.⁵³ Thus, C–C bonds in the support are strong enough to prevent carbon diffusion into Pd bulk. Actually, the experimental adhesion energy of graphite, 7.37 eV per atom,²⁷ is higher than the calculated interaction energy of C atoms with fcc sites on a Pd(111) surface, 6.88 eV (Table 1). It is also known that the presence of carbon in the Pd lattice may suppress the hydrogen adsorption capacity and the formation of a hydride phase.⁵³ This agrees with our finding that C atoms bind significantly more strongly to the Pd(111) surface than H atoms.

Subsurface O species in different interstitial positions of various metals recently became the subject of a number of theoretical studies.^54–59 In particular, incorporation of oxygen into the basal plane of Al^54,55 and the late 4d metals Ru,⁵⁶ Rh⁵⁷ and Ag⁵⁸ was investigated by means of periodic slab model DF approaches. In all these studies, subsurface O moieties were found to be less stable compared to their adsorbed congeners, in full agreement with our results. Only above a certain critical surface O coverage (depending on the metal), the occupation of subsurface sites becomes more favourable than the continued filling of surface sites.⁵⁹

It was also found that in most cases the combination of surface fcc O adsorbates and subsurface O impurities occupying tetrahedral holes (tss) directly below the surface hcp positions is favourable.⁵⁹ Therefore, next we shall discuss the location of atomic O and C impurities in the tss positions of the cluster Pd₁₁₆ (Fig. 1).

As for the oss positions, we consider a single atomic adsorbate per (111) cluster facet, with the impurity atoms located either at three-fold hcp hollow positions in the centres of the (111) facets or in tss holes directly under the surface hcp site. For both C and O moieties, the tss position is strongly unstable compared to the respective adsorption complex, 0.84 eV for C and 1.89 eV for O at the VWN (BP) level (Table 3); the corresponding values at the BP level are 1.21 eV for C and 1.48 eV for O. (GGA periodic slab model calculations showed that occupation of tetrahedral cavities at low subsurface O content and zero surface coverage is about 1.8 eV less stable than adsorption.⁵⁹) Remarkably, the destabilisation of oxygen in the tss hole at the BP level is 0.4 eV smaller than in the oss hole (2.3 eV, see above). This indicates that O atoms prefer a lower Pd coordination, such as occurs in a tetrahedral environment. Indeed, in crystalline PdO, each O atom is bound to four nearest-neighbour Pd atoms, with Pd–O distances of 2.024 Å.⁶⁰ The coordination sphere has the shape of a strongly distorted tetrahedron, where Pd atoms are divided into two pairs with a Pd–Pd distance of 3.043 Å within the pair, and of 3.428 Å between atoms of different pairs. Thus, incorporation of O atoms into tss holes may comprise an initial step for the formation of a surface oxide. (Periodic slab model calculations showed that this process becomes energetically favoured at higher surface oxygen coverage.⁵⁹) Of course, more rigorous consideration of the energetics of oxygen in tss sites would require to reduce the symmetry of the site, which in the present work is characterised by a C₃ axis; in this way, the site would become more similar with the oxygen environment in PdO. In contrast to atomic O, C atoms clearly prefer to occupy oss sites of Pd(111) facets.

Table 3 Selected structural characteristics (in Å) and energies (in eV) of surface and subsurface (tss) atomic C and O species calculated for the clusters Pd₁₁₆O₈ and Pd₁₁₆C₈ at the VWN level; BP//VWN results are given in parentheses.^a

	C	O
Surface
ΔEdes	(7.01)	(4.33)
r(Pd–X)	1.858	1.955

---

Subsurface
a See Tables 1 and 2 for an explanation of the notation. b Surface Pd atoms. c Subsurface Pd atoms
ΔEsub	0.84 (1.21)	1.89 (1.48)
r(Pd–X)^b	1.730	1.889
r(Pd–X) ^c	1.827	1.994

---

3.2 CO Adsorption at the sites above subsurface impurities

It is interesting to inspect the influence of subsurface impurities on the adsorption properties of a Pd(111) surface. For such an analysis, we chose adsorbed CO molecules because they are often used as a probe; also, CO is an important reagent in a number of catalytic transformations. Adsorption of CO at the Pd(111) surface containing subsurface C impurities was studied using the cluster Pd₇₉C₈. Eight CO molecules were adsorbed at the three-fold hollow sites just above the oss holes occupied by atoms C. Elsewhere we had studied in detail the adsorption of CO on impurity-free high-symmetry Pd nanoclusters.^12,13

Calculated results for CO adsorption on the clusters Pd₇₉ and Pd₇₉C₈ are given in Table 4. As shown above, incorporation of impurity C atoms into the subsurface region leads to substantial structural changes. Therefore, in order to separate the structural and electronic effects on adsorption properties of the fcc surface Pd(111) site, we compare the results obtained for the geometry of Pd₇₉ and Pd₇₉C₈ clusters optimised at the VWN level with those calculated at fixed structure of these cluster with the Pd–Pd distance of 2.75 Å as observed for Pd bulk. Here, we neglect the further rather small geometry changes that occur due to the surface relaxation induced by adsorbed CO.¹³ All adsorption parameters for CO (Table 4) were calculated with the BP approach because the GGA corrections are essential for an adequate description of adsorption energies.

Table 4 Characteristics of adsorption complexes of eight CO molecules on fcc three-fold hollow sites of (111) facets of the clusters Pd₇₉ and Pd₇₉C₈, calculated at the BP level: r(Pd–C), r(C–O)–interatomic distances (in Å), ω(C–O)–harmonic C–O stretching frequency (in cm⁻¹), E_des is the desorption energy per CO molecule (in eV, corrected for the basis set superposition error). A: the nearest-neighbour Pd–Pd distances are kept frozen at the experimental bulk-terminated value 2.75 Å, B: structure of the substrate cluster fully optimised at the VWN level under O_h symmetry constraints

Substrate cluster	Pd79		Pd79C8
	A	B	A	B
r(Pd–C)	2.038	2.047	2.177	2.208
r(C–O)	1.192	1.190	1.174	1.173
ω(C–O)	1739	1755	1822	1831
ΔEdes	1.82	1.62	0.94	0.84

---

As one can see from Table 4, subsurface C species significantly weaken the CO binding at the surface: 0.9 eV compared to 1.8 eV for CO on pure Pd₇₉ when the Pd bulk cluster geometry is used. Evidently, the influence of structural differences is small, 0.1–0.2 eV, and changes in adsorption properties are caused mainly by electronic effects. The nature of the latter effects can be rationalised as follows. The general mechanism of CO bonding at metal surfaces is described by electron back-donation from the metal to the antibonding 2π* orbital of CO (more important) and donation from the bonding 5σ orbital of CO to the metal (less important).⁶¹ With a more detailed experimental and theoretical analysis, one can discriminate three-orbital interactions in the σ as well as the π channel.⁶²

In total, our results indicate adsorbed CO to be slightly negatively charged. As already mentioned, impurity C atoms withdraw electron density from a Pd particle, i.e. oxidise it locally. Therefore, CO adsorbates form a weaker bond with such a partially oxidised site of the Pd(111) surface. Interestingly, the interstitial impurities, detected by STM experiments on Pd(111) single-crystal samples in concentrations below 2% but not conclusively identified,³ interact more strongly with a CO adsorbate than impurity-free sites of a Pd surface: CO molecules diffuse quickly from clean places at a Pd(111) surface and bind to impurities. If the tentative assignment of one of the two interstitial impurity species to atomic carbon³ is correct, the observed effect on CO (co)adsorbates would imply a dramatic reduction of the electrostatic destabilisation compared to that found in our calculations for a concentration of ∼10% subsurface C impurities in the rather small Pd₇₉ species. However, the electron density of the macroscopic Pd samples investigated experimentally³ is expected to screen the negative charge of electron-rich subsurface C species (present in low concentration) more efficiently than the electron density of nanoparticles of ∼80 Pd atoms. Thus, coadsorbed CO molecules over massive Pd samples should be destabilised notably less. However, no mechanism of stronger CO adsorption on Pd surfaces with subsurface C impurities³ is consistent with our computational results: our calculations indicated that the Pd–CO interaction is weakened also when subsurface C species occupy interstitial positions further away from the CO adsorbate than that just beneath it.

The C–O vibrational frequency of CO molecules adsorbed above subsurface C impurities in Pd nanoclusters is notably increased, by ∼80 cm⁻¹, compared to the adsorption complexes on the three-fold hollow sites of a clean Pd(111) surface. The frequency values of CO species adsorbed above impurities are only 30–50 cm⁻¹ below the values that we calculated earlier for CO adsorbates at bridge sites of (111) facets and edges of impurity-free Pd clusters.¹³ The fact that the bridge sites are characterised by similar frequencies but significantly stronger CO binding compared to the sites above subsurface C reflects the different nature of the two kinds of observables: vibrational frequencies are mainly determined by the local structure of the adsorption site whereas the bonding is a more global property.

The last remark concerns the opportunity to identify surface and subsurface carbon impurities on Pd(111) facets by means of X-ray photoelectron spectroscopy. According to our calculations, C 1s core level shifts of atomic carbon species (approximated by differences of Kohn–Sham C 1s eigenvalues) on or in Pd samples with respect to the values of adsorbed CO are predicted to be ∼1.5 and ∼0.9–1.0 eV (to lower binding energies), respectively. These shifts are large enough to be detected experimentally.⁶³

4 Conclusions

We have carried out a DF computational study of adsorption of H, C, N and O monatomic species at the surface and in the subsurface region of Pd nanoparticles; we used the three-dimensional nano-crystallites Pd₇₉ and Pd₁₁₆ exhibiting (111) facets. The results of this study showed that: (i) subsurface C species occupying octahedral holes below the surface three-fold fcc sites are almost isoenergetic with adsorption complexes at fcc surface sites; (ii) for H, the subsurface species is slightly less stable than the corresponding surface species; (iii) occupation of subsurface octahedral holes by N and O atoms involves a significant destabilisation. These results correspond to isolated adsorbates on clean and regular Pd(111) facets. Atomic H and C species exhibit moderate activation barriers for the diffusion from surface fcc sites to oss sites. The ability of hydrogen to dissolve in Pd bulk without changing its morphology is well-known; our results show that carbon can behave similarly. Based on the calculated significant instability of oss O moieties and a very small barrier, ∼0.4 eV, for O migration from these subsurface sites to the surface, we concluded that the occupation of octahedral subsurface holes by O species in the absence of surface adsorbates is hardly possible. Location of C and O impurities in tss positions of the cluster Pd₁₁₆ was also considered. For both species, this subsurface position is energetically disfavoured, although migration of O atoms to tss sites is ∼0.5 eV less endothermic than migration to oss sites. Occupation of subsurface tetrahedral sites by oxygen atoms represents a conceivable first step to the formation of a surface oxide phase. The presence of subsurface C species in oss holes significantly decreases the energy of CO adsorption on (111) facets of Pd nanoclusters.

Acknowledgements

This paper is dedicated to Prof. G. M. Zhidomirov in the occasion of his 70th birthday; as senior colleague and co-author, he generously shared his understanding of catalysis. The authors are grateful to C. Inntam and K.-H. Lim for assistance with test calculations. K. M. N. thanks Prof. H.-J. Freund for his support and the opportunity to complete this work. This work was supported by the Deutsche Forschungsgemeinschaft and the Fonds der Chemischen Industrie.

References

1. A. F. Gusovius, T. C. Watling and R. Prins, Appl. Catal. A, 1999, 188, 187.
2. A. Gotti and R. Prins, J. Catal., 1998, 175, 302.
3. M. K. Rose, A. Borg, T. Mitsui, D. F. Ogletree and M. Salmeron, J. Chem. Phys., 2001, 115, 10 927.
4. The Metal-Hydrogen System, ed. Y. Fukai, Springer Series in Materials Science, Vol. 21, Springer, Berlin, 1993.
5. M. Wilde, M. Matsumoto, K. Fukutani and T. Aruga, Surf. Sci., 2001, 482–485, 346.
6. V. A. Bodzie, P. Kleban and D. J. Dwyer, Surf. Sci., 1996, 347, 319.
7. E. H. Voogt, A. J. M. Mens, O. L. J. Gijzeman and J. W. Geus, Surf. Sci., 1997, 373, 210.
8. F. P. Leisenberger, G. Koller, M. Sock, S. Surnev, M. G. Ramsey, F. P. Netzer, B. Klötzer and K. Hayek, Surf. Sci., 2000, 445, 380.
9. B. Klötzer, K. Hayek, C. Konvicka, E. Lundgren and P. Varga, Surf. Sci., 2001, 482–485, 237.
10. I. Meusel, J. Hoffmann, J. Hartmann, M. Heemeier, M. Bäumer, J. Libuda and H.-J. Freund, Catal. Lett., 2001, 71, 5.
11. Sh. Shaikhutdinov, M. Heemeier, J. Hoffmann, I. Meusel, B. Richter, M. Bäumer, H. Kuhlenbeck, J. Libuda, H.-J. Freund, R. Oldman, S. D. Jackson, C. Konvicka, M. Schmid and P. Varga, Surf. Sci., 2002, 501, 270.
12. I. V. Yudanov, R. Sahnoun, K. M. Neyman and N. Rösch, J. Chem. Phys., 2002, 117, 9887.
13. I. V. Yudanov, R. Sahnoun, K. M. Neyman, N. Rösch, J. Hoffmann, S. Schauermann, V. Johánek, H. Unterhalt, G. Rupprechter, J. Libuda and H.-J. Freund, J. Phys. Chem. B, 2003, 107, 255.
14. B. I. Dunlap and N. Rösch, Adv. Quantum Chem., 1990, 21, 317.
15. T. Belling, T. Grauschopf, S. Krüger, M. Mayer, F. Nörtemann, M. Staufer, C. Zenger and N. Rösch, in High Performance Scientific and Engineering Computing, Lecture Notes in Computational Science and Engineering, ed. H.-J. Bungartz, F. Durst and C. Zenger, Springer, Heidelberg, 1999, vol. 8, p. 439.
16. T. Belling, T. Grauschopf, S. Krüger, F. Nörtemann, M. Staufer, M. Mayer, V. A. Nasluzov, U. Birkenheuer, A. Hu, A. V. Matveev, A. M. Shor, M. S. K. Fuchs-Rohr, K. M. Neyman, D. I. Ganyushin, T. Kerdcharoen, A. Woiterski and N. Rösch, ParaGauss, Version 2.2, Technische Universität München, 2001.
17. O. D. Häberlen and N. Rösch, Chem. Phys. Lett., 1992, 199, 491.
18. N. Rösch, S. Krüger, M. Mayer and V. A. Nasluzov, in Recent Developments and Applications of Modern Density Functional Theory, ed. J. M. Seminario, Elsevier, Amsterdam, 1996, p 497.
19. S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200.
20. A. D. Becke, Phys. Rev. A, 1988, 38, 3098.
21. J. P. Perdew, Phys. Rev. B, 1986, 33, 8622; J. P. Perdew, Phys. Rev. B, 1986, 34, 7406.
22. L. Fan and T. Ziegler, J. Chem. Phys., 1991, 94, 6057.
23. S. Huzinaga, J. Chem. Phys., 1977, 66, 4245.
24. In refs. 12 and 13 a p-exponent added to the original orbital basis set of Pd was erroneously given as 0.0214 instead of 0.2143 as used in the calculations.
25. P.-O. Widmark, P.-A. Malmqvist and B. O. Roos, Theor. Chim. Acta, 1990, 77, 291.
26. S. Krüger, S. Vent, F Nörtemann, M. Staufer and N. Rösch, J. Chem. Phys., 2001, 115, 2082.
27. CRC Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Raton, FL, 77th edn., 1996.
28. J.-F. Paul and P. Sautet, Phys. Rev. B, 1996, 53, 8015.
29. Cluster Models for Surface and Bulk Phenomena, ed. G. Pacchioni, P. S. Bagus and F. Parmigiani, NATO ASI Series B, Vol. 283, Plenum, New York, 1992.
30. J. L. Whitten and H. Yang, Surf. Sci. Rep., 1996, 24, 59.
31. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
32. Periodensystem der Elemente, VCH Verlag, Weinheim, 1995.
33. G. Ertl, in The Nature of the Chemical Bond, ed. T. N. Rhodin and G. Ertl, North Holland, Amsterdam, 1979, p. 315.
34. A. Matveev, M. Staufer, M. Mayer and N. Rösch, Int. J. Quantum Chem., 1999, 75, 863.
35. P. Gisdakis, S. Antonczak and N. Rösch, Organometallics, 1999, 18, 5044.
36. K. Honkala and K. Laasonen, J. Chem. Phys., 2001, 115, 2297.
37. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
38. N. N. Semjonow, Einige Probleme der chemischen Kinetik und Reaktionsfähigkeit, Akademie-Verlag, Berlin, 1961.
39. T. Mütschele and R. Kirchheim, Scr. Metall., 1987, 21, 101.
40. H. Natter, B. Wettmann, B. Heisel and R. Hempelmann, J. Alloys. Compd., 1997, 253, 84.
41. C. Nützenadel, A. Züttel, D. Chartouni, G. Schmid and L. Schlapbach, Eur. Phys. J. D, 2000, 8, 245.
42. H. Conrad, G. Ertl and E. E. Latta, Surf. Sci., 1974, 41, 435.
43. T. Engel and H. Kuipers, Surf. Sci., 1979, 90, 162.
44. O. M. Løvvik and R. A. Olsen, Phys. Rev. B, 1998, 58, 10 890.
45. K. Nobuhara, H. Kasai, H. Nakanishi and A. Okiji, J. Appl. Phys., 2002, 92, 5704.
46. A. Doyle, Sh. K. Shaikhutdinov, D. Jackson and H.-J. Freund, Angew. Chem., Int. Ed. Engl., 2003, 42, 5240; A. Doyle, Sh. K. Shaikhutdinov, D. Jackson and H.-J. Freund, Angew. Chem., 2003, 115, 5398.
47. H. Yokoyama, H. Numakura and M. Koiwa, Acta Mater., 1998, 46, 2823.
48. M. Beck, M. Ellner and E. J. Mittemeijer, Acta Mater., 2001, 49, 985.
49. S. Nakamura and T. Yasui, J. Catal., 1970, 17, 366.
50. S. B. Ziemecki, J. A. Jones, D. G. Swatzfager and R. L. Harlow, J. Am. Chem. Soc., 1985, 107, 4547.
51. S. A. H. Zaidi, J. Catal., 1981, 68, 255.
52. N. Krishnankutty and M. A. Vannice, J. Catal., 1995, 155, 312.
53. N. K. Nag, J. Phys. Chem. B, 2001, 105, 5945.
54. A. Kiejna and B. I. Lundqvist, Surf. Sci., 2002, 504, 1.
55. A. Kiejna and B. I. Lundqvist, Phys. Rev. B, 2001, 63, 85 405.
56. K. Reuter, C. Stampfl, M. V. Ganduglia-Pirovano and M. Scheffler, Chem. Phys. Lett., 2002, 352, 311.
57. M. V. Ganduglia-Pirovano, K. Reuter and M. Scheffler, Phys. Rev. B, 2002, 65, 245 426.
58. W.-X. Li, C. Stampfl and M. Scheffler, Phys. Rev. B, 2002, 65, 75 407.
59. M. Todorova, W.-X. Li, M. V. Ganduglia-Pirovano, C. Stampfl, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2002, 89, 96 103.
60. R. W. G. Wyckoff, Crystal Structures, Wiley, New York, 2nd edn., 1963, vol. 1.
61. G. Blyholder, J. Phys. Chem., 1964, 68, 2772.
62. A. Föhlisch, M. Nyberg, P. Bennich, L. Triguero, J. Hasselström, O. Karis, L. G. M. Pettersson and A. Nilsson, J. Chem. Phys., 2000, 112, 1946.
63. V. V. Kaichev, I. P. Prosvirin, V. I. Bukhtiyarov, H. Unterhalt, G. Rupprechter and H.-J. Freund, J. Phys. Chem. B, 2003, 107, 3522.

---

Footnote

† Present address: Catalan Institute for Research and Advanced Studies (ICREA) associated to the Departament de Química Física, Universitat de Barcelona, C/ Marti i Franques 1, 08028 Barcelona, Spain. E-mail: konstantin.neyman@icrea.es

---