Analysis of the ortho effect: acidity of 2-substituted benzoic acids

Abstract

The classical term ortho effect was quantitatively analyzed and decomposed into its real or supposed components, using the acidity of eleven 2-substituted benzoic acids as a sample. The substituent effects were evaluated by calculations at the B3LYP/6-311+G(d,p) level by means of isodesmic reactions, separately for the acid molecules and for their anions. An intramolecular hydrogen bond, affecting the acidity moderately, was found only in the case of 2-methoxy- and 2-dimethylaminobenzoic acids. For the other acids, the often-employed interpretation invoking a hydrogen bond is wrong: the pertinent form was not revealed by calculations or by infrared spectroscopy. Another widespread explanation relying on the steric inhibition of resonance of the COOH group is also not correct in most cases: only some acid molecules are nonplanar (with substituents tert-Bu, CH₂Cl, CF₃, NO₂, Cl) and the steric inhibition exists also in the anions, thus partly cancelling this effect.

The main part of the ortho effect consists of polar effects (inductive and resonance) transmitted through the ring and of purely steric effects. Their tentative separation was based on comparison with the 4-substituted isomers. Polar effects are most important for the acidity and are not very different in the ortho and para positions (rough estimate 0.8∶1). Steric effects are strong but mostly of similar magnitude in the acid as in the anion; hence they are of restricted importance for the acidity. They may be better described as van der Waals interactions rather than as short-range field effects. The whole analysis leads to the conclusion that the acidity of ortho-substituted benzoic acids cannot be interpreted by a simple universal theory.

---

Benzene ortho derivatives have received less attention compared to their meta and para isomers. While in the latter the dependence of the reactivity and properties on structure is simple and can be approximated by the Hammett equation, effects of ortho substituents are much more complex.^1,2 Mostly they have been assumed to arise from two contributions: one similar as in the meta and para isomers, called inductive effect and resonance,^1,3 the other commonly called steric. The latter was further divided into several tentative components,^2,4,5 which were not always exactly identified: primary steric effect, steric inhibition to resonance (SIR), short-range field effect, hydrogen bonds (HB), steric inhibition to solvation and others. In numerous treatments of this subject, certain of these effects were more or less stressed and sometimes they were expressed quantitatively by an empirical equation with limited success.⁴ Note that some of these effects are only simplified models, sometimes poorly defined: for instance, one can hardly distinguish a short-range field effect from a primary steric effect. As an extreme opinion, reactivities of ortho derivatives were explained without referring to any steric effects at all,³ either by a blend of inductive and resonance effects^3a,b or most simply, by correlation with the reactivities of para derivatives.^3c However, the bulkiest substituents (tert-butyl) were not included^4a and sometimes also the smallest substituent, hydrogen, had to be eliminated. In contrast to these concepts, other theories are immediately related to observable quantities, viz. steric inhibition of resonance (SIR) and hydrogen bonds (HB). SIR assumes a nonplanar, minimum energy conformation and this assumption can be tested.⁶ HB can involve either a hydrogen atom of the substituent^2,7,8 or of the functional group;^2,7,9 both cases can be submitted to test. A fecent chemometrical study stressed HB as the most important factor;⁷ in other empirical correlations, compounds with HB were excluded from the beginning.^3b Another special case is represented by the substituents COX, which allow an intramolecular cyclization.¹⁰ It is note that most of the named terms were defined and experimentally proven using 2-substituted benzoic acids as the model. One of the reasons may be that their meta and para isomers were thoroughly investigated as the standard model for the Hammett equation.

In our opinion, the outlined treatment of the ortho effect has a major deficiency, which is that it has been experimentally supported mainly by dissociation constants or rate constants in water or in aqueous solvents. Thus, in 2-substituted benzoic acids, the substituent effect is defined by the Gibbs energy of the isodesmic reaction [eqn. (1)]:.

2-XC₆H₄COOH + C₆H₅COO⁻ ⇄ 2-XC₆H₄COO⁻ + C₆H₅COOH (1)

More recently, some acidobasic equilibria were also investigated in the gas phase,¹¹ such as the equilibrium in eqn. (1).^11a The results can be better related to the structures of isolated molecules than the results obtained in solution but a marked solvent effect was observed with only few substituents (e.g., OH).^11a However, there is still another shortcoming, which is that the substituent effect is given only by the difference between the effect in the acid molecule and in the anion (or in the base and in the cation). It may happen that the two effects are rather similar and that their difference is thus small and difficult to interpret.^6,12 One previous attempt to treat separately the ortho-substituted benzoic acids and their anions¹³ remained restricted to the electrostatic treatment and neglected any steric effects. We have attempted to resolve this general problem using the principle of isodesmic reactions¹⁴ and have applied it to inductive¹⁵ and resonance¹⁶ effects, to their combination,¹⁷ as well as to steric^6,18 effects and polarizability.¹⁹ In the case of 2-substituted benzoic acids, the isodesmic reactions have the form of eqns (2) and (3), defining the substituent effects in the acid molecule and in the anion, respectively:

C₆H₅COOH + C₆H₅X ⇌ 2-XC₆H₄COOH + C₆H₆ (2)

C₆H₅COO⁻ + C₆H₅X ⇌ 2-XC₆H₄COO⁻ + C₆H₆ (3)

All reactions in eqns. (1)–(3) are not only isodesmic but also homodesmotic.²⁰ When we applied them to study the substituent effects of nonpolar groups: methyl,⁶ isopropyl,^18a and tert-butyl,^18b,c we found that purely steric effects are similar in the acid and in its anion. The main effect on the acidity is operating in the anion and is most properly described as the polarization of the alkyl group.^6c Steric inhibition of resonance cannot be present in the case of small alkyls, such as 2-methylbenzoic acid, since its molecule is planar.⁶ In the case of stronger steric effects (2-tert-butyl substituent), SIR is evident but is of comparable magnitude in the acid as in the anion; hence it has only a weak effect on the acidity.^18c

In this paper, we have applied the isodesmic reactions [eqn. (1)–(3)] to acids 1–11 (listed in Table 1) that contain selected polar substituents not having any acidic hydrogen atoms: F, Cl, CH₂Cl, CF₃, N(CH₃)₂, OCH₃, CN and NO₂. Of these, the substituents CH₃,^6c and C(CH₃)₃^18c were already investigated but at different levels of theory. The reaction enthalpies of eqn. (2) and (3), Δ₂H and Δ₃H, would also be in principle obtainable from the enthalpies of formation of all species involved but the few available values for substituted benzoic acids²¹ are not sufficiently accurate.²² Hence we calculated the reaction energies within the framework of the density functional theory²³ (DFT) at the B3LYP/6-311+G(d,p) level. The choice of this theoretical model was essential for comparison with the previous results on similarly substituted 4-substituted benzoic acids.^17b

Table 1 Calculated and experimental energies of the isodesmic reactions (kJ mol⁻¹)

Substituent	Conformations^a	Δ2E^b	Δ2H° ^c	Δ3E^b	Δ1E^b	Δ1G° ^d	Δ1G° expt^e
a Given are conformations with an assumed population of more than 5%; for a more detailed description see Table S2 (Electronic supplementary information). b Energies of isodesmic reactions, eqn. (1)–(3) were calculated from the DFT energies of 1–11 (Table S2) and of the mono-substituted benzenes.^16b c Calculated according to eqn. (2) from the experimental enthalpies of formation (298 K) in refs 21 and 24. d Calculated including only the entropy arising from the presence of conformers. e Experimental relative gas-phase acidities from ref. 11a f These values differ slightly from those given previously in refs 6a,b and 18b as result of a different choice of ΔfH°(g) for benzoic acid. g Ref. 6a,b h In ref. 18b there is a misprint giving the erroneous value of −16.5 kJ mol^−1.
H	1b	0	0	0	0	0	0
CH3	2b, 2c	9.08	7.4 ^f	11.64	2.56	1.21	−2.5 ^g
C(CH3)3	3e, 3f	39.56	26.3 ^f	24.06	−15.50	−15.82	−15.5^h
CH2Cl	4e, 4f	16.50		−12.40	−28.90	−30.10
CF3	5f, 5e	35.77		6.04	−29.72	−30.33
CN	6c, 6b	24.66		−14.72	−39.38	−39.83
N(CH3)2	7g, 7a	10.31		28.58	18.27	16.61
NO2	8f, 8e	40.43		−1.04	−41.47	−42.61	−39.33
OCH3	9a	12.25	12.3 ^f	18.15	5.90	4.35	−2.09
F	10c, 10b	19.48		10.64	−8.84	−9.78	−9.62
Cl	11e, 11f	28.72	−1.2	10.23	−18.49	−18.82	−15.90

---

Restriction to the named substituents will eliminate HB between the substituent and oxygen atoms in the anion but not the possible HB in the acid molecule. Our first goal was to reveal these hydrogen bonds, both by calculations and from the parallel investigation by IR spectroscopy. Of our compounds, HB was already proven in 2-methoxybenzoic acid (9) in the gas phase^9a and in solution,^9b as well as in 2-dimethylaminobenzoic acid (7).^9c In the case of substituents X = F, Cl, NO₂ or even CH₃, conformation a (see Scheme 1) was sometimes assumed^9d,11a but an actual HB was not found.^9a,25

The second goal of our calculations was to determine the actual conformation of the COOH group. Knowing this conformation we were able to check the occurrence of SIR,² which has been assumed either to be a common contribution to the ortho effect^5,11a or to operate at least with some bulky substituents.³ SIR would not be possible in the coplanar conformations a, b and c but would require non-coplanar conformations as in d, e or f (see Scheme 1). After eliminating or subtracting HB and SIR, we wanted to calculate and interpret the remaining effects with the final intention—perhaps not perfectly realizable—of factorizing the ortho effect into simpler components, some of them possibly operating only with certain substituents.

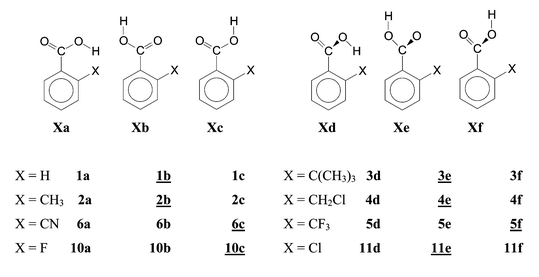Scheme 1 Conformers and numbering of compounds in this work. Conformers of minimum energy are underlined.

Experimental

IR spectroscopy

IR absorption spectra were recorded on a Nicolet Impact 400 FTIR spectrometer in tetrachloromethane solution at a concentration of 0.003 mol l⁻¹ with d = 1 cm. The bands of the dimer could not be completely eliminated by dilution. With the resolution used (2 cm⁻¹), our program did not allow an interval of wavenumber readings finer than 0.64 cm⁻¹. Therefore, we used a graphical procedure and obtained the apparent maxima of the ν(C=O) bands as the point of intersection of the band axis with the spectral curve. With sufficient enlargement, the accuracy of reading was better than 0.1 cm⁻¹. Separation of the ν(C=O) bands was carried out choosing a 100% Lorentzian shape for the bands; the bands of the monomer and dimer were treated together. The spectral data are collected in Table S1 (ESI).

Calculations

Energies of the 2-substituted benzoic acids 1–11 (Table 1) and of their anions were calculated by the DFT method²³ at the B3LYP/6-311+G(d,p) level with the Gaussian 94 program.²⁶ Planarity or any symmetry was never anticipated. Geometry optimization was carried out with redundant internal coordinates. All reasonable conformations were taken into consideration and calculations were started from the pertinent near structures. For instance, conformations 2a–2f were considered for 2; when necessary the conformations of the substituent, for instance in 5a–5f and 7a–7h, were also taken into account. All structures were checked by vibrational analysis and behaved as energy minima.

The calculated energies E(DFT) are listed in Table S2 (ESI) together with the most important geometrical parameters. The population of the conformers was estimated for 298 K with the assumption that ΔG°(298) ≅ ΔE(DFT). The relative acidities Δ₁E° and the energies Δ₂E° and Δ₃E° defined by eqn. (2) and (3) were then calculated as effective values for the given mixture of conformers (Table 1).

The frozen conformations of some 4-substituted benzoic acids with a fixed dihedral angle ϕ were calculated in such a way that all remaining geometry parameters were optimized with internal coordinates. The results are given in Table S3 (ESI).

Results and discussion

Conformations and their population

The presence of the pertinent conformers is an experimental fact representing a necessary but not sufficient condition for attempted interpretation of the acidity, say by HB^7,11a in the conformers a, or by SIR² in the conformers d, e and f. For this reason, we have to deal with this aspect in some detail. The relative abundance of the other conformers is less important in this respect. All conformations investigated and found as energy minima are listed in Table S2, the predominant conformations are also given in Table 1.

Conformations a with a possible HB were revealed as prevailing only for 7 and 9 (Scheme 2, 7ag, 9a). For 9 we calculated that 94% of 9a was present; the possibly present conformers 9c and 9b were not detected in the IR spectrum. In the case of 7, we have obtained two energy minima for the two possible HB forms, separated by a barrier: the zwitterion 7g and the uncharged structure 7a. They are populated equally (51∶49) and we have not distinguished them in the IR spectra. A previous IR study^9c claimed three carbonyl bands were obtained by deconvolution and assigned them tentatively to 7a, 7c and 7g, the last being the least populated in nonpolar solvents. With the other acids, the H-bonded forms are only negligibly represented. A relatively larger value was predicted for 10a (3%) but could not be proven spectroscopically. With 8, the H-bonded form 8a with a short O⋯H distance would be sterically possible but its energy is high due to distorted planarity. Our IR spectra as well as previous studies^9a,25 did not reveal this form. In 2-cyanobenzoic acid (6), the H-bonded form 6a was not detected either in the present work or in a previous IR study.²⁷

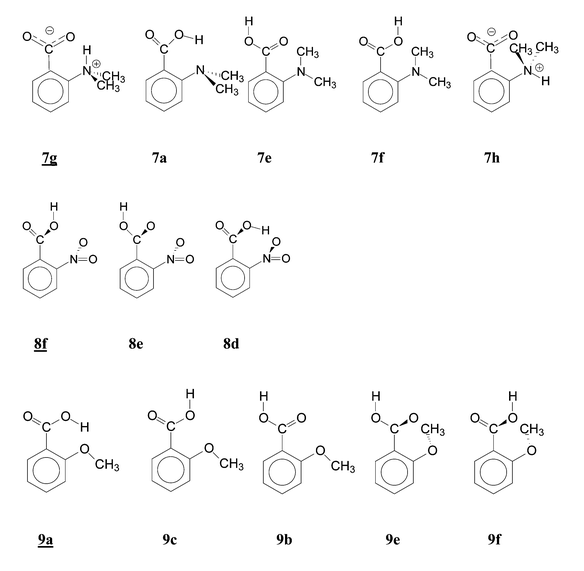Scheme 2 Calculated conformations of some 2-substituted benzoic acids in the sequence of increasing energy.

Our results are at variance with some previous claims and hypotheses. The presence of the conformer 11a in the gas phase was claimed^9a on the basis of shifts in the carbonyl frequency ν(C=O) but in a fundamental IR study²⁵ of 11 the conformation 11a was not found. Explanation of the gas-phase acidity of 8, 10 and 11 in terms of H-bonds^11a must be rejected. A weak H-bond of opposite direction in 2-methylbenzoic acid (2) should involve a hydrogen atom of the methyl group in 2b. This idea was rebutted already in the classical literature,^2a but recently it was taken into consideration again when discussing the carbonyl frequency.^9a Even a weak H-bond would be at variance with the conformation of the methyl group in 2b: the carbonyl oxygen is situated between two methyl hydrogens. A detailed study of solution reactivity^4g assumed no HB in 5, 6, 10 and 11, estimated correctly the conformation 8f but did not reveal the HB in 9a.

The remaining conformations may be classified into two groups. In the case of smaller substituents (CH₃, F, CN) the carboxyl group is coplanar with the benzene ring, in other cases it is more or less twisted, up to 54° in 3f. Planar conformation of 2 was discussed together with further methyl derivatives⁶ and supported by electron diffraction of methyl 2-methylbenzoate.²⁸ Most remarkably, the conformation of the anions is not always the same as that of the acids. In the anions of 2 and 10 the carboxylate group is twisted (by 31° and 59°, respectively) while in the anion of 4 it is coplanar.

A feature of secondary importance is the relative population of the conformers b (sp conformation around the C–C bond) and c (ap) or of e (sc) and f (ac) since their energies are rather similar. Our populations calculated with the approximation ΔG ≅ ΔE agreed well with those from IR spectra (Table S1) with the exception of 8e,f, for which a misassignment is possible (Table S2, footnote b). There is also good agreement with the conformation of some corresponding methyl esters.^29,30 For 11 one strongly twisted conformation was anticipated without convincing reasons.³¹ In 4 the substituent CH₂Cl prefers a perpendicular conformation, the same as in chloromethylbenzene.¹⁶

Some general features can be observed, viz. that similar conformations are preferred as those found in 3-substituted benzoic acids^17b, whose functional groups are more separated. Alkyl groups are preferably located near to the carbonyl oxygen (2b and 3e), groups bearing lone electron pairs lie near to the OH group (5f, 6c, 8f, 10c). The substituent Cl in 11e is an exception.

Strength of the hydrogen bond

The existence of a HB is of primarily importance for our investigation since it can be proved or disproved the most surely of all factors influencing acidity. Even when the molecule possesses a favorable conformation, HB can be of variable strength, which can be estimated from further spectroscopic and energetic quantities. We have listed them in Table 2 for the acids in which a HB comes into consideration. The table reveals striking differences between two groups of compounds: 7 and 9 contain a rather strong HB, in the other compounds a HB does not exist and an explanation of their acidity in this way^7,9a,11a is incorrect. An energy decrease due to HB, as given in Table 2, column 4, must overcome the energy increase due to the unfavorable conformation around the C–O bond. This is seen from the two conformers of benzoic acid, 1b and 1a (Table 2, at the bottom). With most acids, the stabilizing energy of the HB itself does not overcome the conformational energy and the HB rotamers are populated only very slightly. The HB is further weakened when the molecule is not planar (ϕ < 180°).

Table 2 Some properties of the hydrogen bond in 2-substituted benzoic acids

	Substituent	ϕ/deg	ΔE(HB)^a/kJ mol^−1	H⋯X ^b/Å	Calcd Δν(O–H)/cm^−1	Expt Δν(O–H)/cm^−1
a Calculated energy difference between the HB form and a related conformer differing only in the conformation on the C–O bond (for instance 9a and 9c). b Calculated distance to the nearest atom of the ortho substituent. c Not observed.
7a	N(CH3)2	180	−16.8	1.75	731	∼900
9a	OCH3	180	−8.1	1.75	133	165
10a	F	180	+7.6	1.84	4	—^c
11d	Cl	172	+10.4	2.10	75	—^c
8d	NO2	146	+13.7	1.71	230	—^c
4d	CH2Cl	138	+15.5	2.34	72	—^c
5d	CF3	136	+16.0	2.00	28	—^c
6a	CN	177	+17.1	2.25	45	—^c
1a	H	0	+28.5	—

---

The standard measure of HB strength is the difference of the O–H wavelengths, free and bonded. Our calculated and experimental values (Table 2, last two columns) agree only moderately well since even the other calculated frequencies do not match very well the experimental values (Table S1). Nevertheless, the difference between bonded and non-bonded acids is striking, even for this quantity. A particular case is the nitro derivative with a rather strong HB in the nonplanar form 8d and with a short H⋯O distance of 1.71 Å. However, at equilibrium the HB rotamer is populated only to 0.3%. Hence it cannot influence the acidity and can be viewed as not existing.

Comparison with the experimental energies

The reaction energies Δ₂E and Δ₃E of the isodesmic reactions in eqns (2) and (3), respectively (Table 1, columns 3 and 5) were calculated for the assumed conformer mixtures, although the presence of higher-energy conformers introduces only a small correction. (This correction is negligible when the energies of the conformers differ either very little or very much; at most it can attain^16b 0.63 kJ mol⁻¹.) The relative acidities Δ₁E (Table 1, column 6) were obtained as Δ₃E − Δ₂E. Comparison with experiments is possible on two levels. First, one can calculate Δ₂H° of eqn. (2) (given in Table 1, column 4) from the experimental gas-phase enthalpies of formation,^21,24 Δ_fH°(g), of the individual compounds. The bad agreement with Δ₂E is due mainly to experimental errors in Δ_fH°(g).^16b,22

Comparison of Δ₁E with the gas-phase acidities,^11a Δ_acidG°(g) (given in Table 1, column 8), is more significant. We have abandoned the transformation of Δ₁E into Δ₁G°(T) by means of statistical thermodynamics due to previous experience.¹⁹ Instead, we restricted the corrections only to the symmetrical entropy. In the case of meta- or para-substituted benzoic acids, the symmetry correction in δΔG° is practically equal to −RTln 2: for para derivatives this is due to the external symmetry number of the anion, for meta ones it is due to the presence of two rotamers in an approximately 1∶1 ratio.^17b In the case of ortho benzoic acids, the correction differs since the population of rotamers is not 1∶1 (Table S2, last column). The corrected δΔG° are given in Table 1, column 7, but the corrections are minute. The best comparison is a graph showing all isomers (Fig. 1). We conclude that the acidities of all isomers of benzoic acids are calculated with a similar precision; the entropy corrections are immaterial.

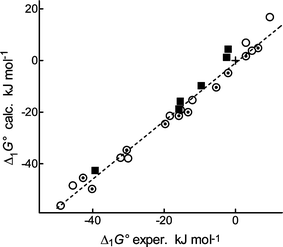Fig. 1 Comparison of DFT calculated and experimental acidities of substituted benzoic acids: ○ para derivatives, ⊙ meta derivatives, + hydrogen^17b, ■ ortho derivatives, this work. Correction for symmetrical entropy has been included; the regression line is related to the meta and para derivatives.

Substituent effects

The substituent effects in the acid molecule, Δ₂E, and in the anion, Δ₃E, reveal two main features: Δ₂E and Δ₃E are of comparable magnitude and are not proportional to each other (Fig. 2). In this respect, 2-substituted benzoic acids differ from all model systems investigated insofar: their meta and para isomers,¹⁷ 4-substituted bicyclo[2.2.2]octane-1-carboxylic acids,¹⁵ alkyl-substituted pyridines,¹⁹ polymethylbenzoic acids^6b and alkyl-substituted benzonitriles.¹² In all these compounds, substituent effects in the ion were decisive for the acidity or basicity; effects in the neutral molecule were roughly proportional but several times smaller. An explanation may be offered that steric effects are important both in the anion and in the acid molecules, polar effects mainly in the anions (see the positions of the points for tert-Bu and NO₂ in Fig. 2). We attempted to separate the polar effects transmitted through the benzene ring using the classic approach,^4a that is comparison with the para derivatives. Fig. 3 reveals proportionality of the acidities for the majority of substituents, particularly for the strongly polar ones; the points for tert-Bu and CH₂Cl deviate in the sense that ortho acids are stronger. The effect of HB is not very important. An explanation may be suggested that polar effects are almost equal in the two positions and that an ortho effect is observed only for bulky polarizable substituents, which can be understood as stabilization of the anion by polarization. Moderate steric effects—van der Waals interactions—are not evident; they must be of similar magnitude in the anion and in the acid molecule and are of little importance for the acidity. This explanation was already suggested for the alkyl groups^6c and is acceptable as an approximation for many polar substituents. It is in agreement with Charton's description^3b based on the reactivity in solution and operating only with inductive and resonance effects. It also agrees with the criticism^4a that certain substituents, which were absent in Charton's correlations,^3a,b would break their validity.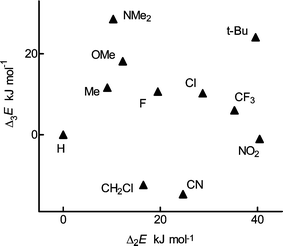

Fig. 2 Plot of the calculated substituent effect in the molecules of 2-substituted benzoic acids, Δ₂E, vs the effect in their anions, Δ₃E.

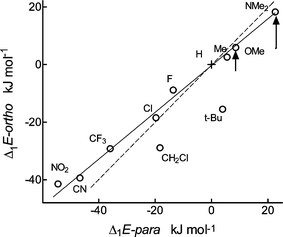Fig. 3 Comparison of calculated acidities Δ₁E of ortho- and para-substituted benzoic acids; the full line has a slope of 0.81, the broken line has unity slope. The length of the arrows shows the effect of intramolecular H-bonds.

This separation of polar and steric effects is based on the assumption that polar effects in the ortho position are equal to those in the para position. However, they have also been claimed to be somewhat stronger^7a,32 or weaker.^3a,33 In any case, the approximate equality is acceptable for weakly polar alkyl groups^6,12,18 but need not be acceptable for the strongly polar groups dealt with here. From Fig. 3 we estimate that the ortho polar effect is 0.81 weaker than that in the para position and used this factor in further calculations. It agrees well with the value of 0.75 derived from solution reactivities.^3c Note, however, that our final conclusions are not sensitive to this exact value. For the time being, we regard this value only as a preliminary estimate, which must be confirmed on further compounds. Attempts at its interpretation, for instance in terms of the π-inductive effect, would be premature.

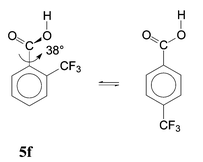
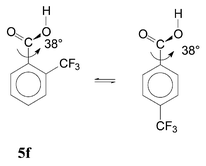
An attempted semi-quantitative separation of the ortho substituent effects is presented in Table 3. Effects of HB (column 4) were calculated as the energy difference between the real conformer mixture and a supposed mixture in which the HB conformer would be lacking. The polar effect (PE) was obtained from the substituent effects in the para isomers^17b by multiplying by 0.81; this was done both for the acid molecules and for the anions (column 5). The rest of the substituent effect can be attributed to SIR and other steric effects (SE). We attempted their separation by the approximate approach developed previously,^6c referring to structures with fixed geometry. Eqn. (4) is equilibrium of two real structures and its reaction energy, Δ₄E, involves SIR. Eqn. (5) is a fictive equilibrium between the real minimum-energy structure 5f and an artificial structure of the para isomer with the same fixed dihedral angle ϕ; Δ₅E cannot involve any SIR.

By subtracting Δ₄E from Δ₅E, respecting the factor 0.81, we calculated SIR and SE as given in Table 3, columns 6 and 7, respectively. SIR and SE of the anions were calculated in the same way. (Energies of the distorted structures of 4-substituted benzoic acids are listed in Table S3.)

Table 3 Separation of substituent effects on the acidity of 2-substituted benzoic acids (kJ mol⁻¹)

	Substituent	Form	H-bond	Polar effect (PE)^a	SIR^b	Steric effect (SE)^b	Total^c	Acidity	ΔEel
								Δ1E
a Taken as the substituent effect in isomeric 4-substituted benzoic acids, ref. 17b, multiplied by 0.81. b Calculated according to the principle of eqn. (4). c Repeated from Table 1; the values are identical with ΔE2 and ΔE3 for the acid and the anion, respectively. d Relates to the zwitterionic form.
2	CH3	Acid	0	−2.0	0	11.1	9.1		0
		Anion	0	2.5	3.8	5.3	11.6	2.5	0
3	C(CH3)3	Acid	0	−2.1	11.4	30.3	39.6		0
		Anion	0	1.0	12.2	10.9	24.1	−15.5	0
4	CH2Cl	Acid	0	1.5	1.7	13.3	16.5
		Anion	0	−13.3	0	0.9	−12.4	−28.9
5	CF3	Acid	0	4.9	6.7	24.2	35.8		2.1
		Anion	0	−24.3	8.9	21.5	6.1	−29.7	−17.5
6	CN	Acid	0	5.3	0	19.4	24.7		4.9
		Anion	0	−32.5	0	17.8	−14.7	−39.4	−52.2
7	N(CH3)2	Acid^d	−12.7	−10.2	0	33.2	10.3
		Anion	0	8.1	−3.2	23.7	28.6	18.3
8	NO2	Acid	0	7.0	7.5	25.9	40.4
		Anion	0	−37.2	1.3	34.8	−1.1	−41.5
9	OCH3	Acid	−8.0	−5.0	0	25.2	12.2
		Anion	0	2.0	1.7	14.4	18.1	5.9
10	F	Acid	0.2	0.0	0	19.3	19.5		0.4
		Anion	0	−11.0	11.8	9.9	10.7	−8.8	−7.7
11	Cl	Acid	0	1.1	2.0	25.6	28.7		2.9
		Anion	0	−14.9	13.6	11.5	10.2	−18.5	−12.5

---

Data in Table 3 are given to tenths of kJ mol⁻¹ with respect to the accuracy of calculations but the underlying approximations may contain errors of unknown magnitude, certainly of several kJ mol⁻¹. While the values of HB are reasonably reliable, the values of SE in particular may be uncertain since they are obtained as the remainder after subtracting the other components. With this provision, one can say that Table 3 confirms semi-quantitatively the predictions. Note that SE is always positive and greater for the acid than for the anion, although one could guess that the groups COOH and COO⁻ should be isosteric. Nevertheless, the difference is not great and partial compensation of acid vs. anion is of importance for many substituents. Compensation takes place also in the values of SIR, which are of importance only for some substituents and mostly greater in the anion than in the acid. This possibility was often neglected in discussions. The slight importance of HB was stated above. Polar effects transmitted through the benzene ring are decisive in the case of strongly polar substituents, in accord with the previous analyses of solution reactivities.^3,4g When polar substituents prevail in the given sample, direct correlations with the para derivatives^3c or with polar constants σ^3a,b are possible.

The values of SE can be best denoted as a proximity effect since they can be described either as vdW interactions or as short-range polar effects; even a description in terms of polarizability is possible. A decision on the basis of observable facts may be difficult but in our opinion the problem is of secondary importance and may be merely in the nomenclature. We prefer the description as vdW because the effect is stronger in the acids than in the anions and also with respect to the electrostatic calculations described in the next section. On the other hand, we have not found any correlation of SE and steric constants⁵υ. We also analyzed the substituent effects on the geometrical parameters of 1–11, in particular on the angle ϕ, C1–C2 bond length and C(O)–C1–C2 angle (Table S2) in comparison to the standard geometrical parameters in mono-substituted benzenes.³⁴ All these parameters reveal a steric effect but they are not simply related to υ or to each other. A correlation was found only for the total steric effect (SE + SIR) with two parameters: the angle C(O)–C1–C2 and cos ϕ (R = 0.956, N = 9). It can be interpreted in the following manner: twisting of the COOH group and widening of the C(O)–C1–C2 angle act together to relieve the steric strain. In general, steric strain is relieved differently in different molecules: when one parameter is more deformed, the others are less so.

Electrostatic calculations

In terms of electrostatic theory,³⁵ the inductive effect is expressed by eqn. (6) as the Coulombic interaction of the anionic charge and a dipolar substituent. In the uncharged molecules, this effect is either neglected or calculated by eqn. (7) as the interaction of two dipoles.

ΔE_el = eN_Aμcos θ/r²(4πε_oε_ef) (6)

ΔE_el = −N_Aμ₁μ₂(2cosθ₁cosθ₂ − sinθ₁sinθ₂)/r³(4πε_oε_ef) (7)

In eqn. (6)r is the distance between the substituent and the charge, μ is the point dipole of the substituent and θ is the angle of the vectors r and μ. (This equation was sometimes given erroneously^35c,f without the factor N_A but the results of the calculations were correct.) The effective relative permittivity ε_ef in the gas phase is usually taken as equal to unity.^35a In eqn. (7) there are two dipoles, μ₁ and μ₂, and two corresponding angles, θ₁ and θ₂. The equations were applied with some success in the case of the pure inductive effect³⁶ or even to benzene derivatives,¹³ but even with the most favorable conditions there remains a considerable systematic error.³⁶ The main problem is the arbitrary choice of parameters, viz. the exact position of the point dipole and of the charge.^15b,36 Thus, one could obtain electrostatic calculations on the same compounds that were appraised to be in agreement^35f or in disagreement^15b with experiments.

When this theory is applied to acids 1–11, some of its inherent approximations are possible exceeded, for instance the assumption that the length of the dipole μ is small compared to r. On the other hand, these acids offer an opportunity to examine the effect of large values of θ. (In previous examples, θ was mostly near to zero.) We attempted a test on only the acids with one prevailing conformation and with an unambiguous position of the dipole. The calculated values of ΔE_el are given in Table 3, last column. There are no doubts that they cannot express the total substituent effects but the contribution of resonance can be neglected,¹³ at least in the case of strongly polar substituents. If our SE represented some kind of short-range polar effects, they should be included in ΔE_el and a similarity of ΔE_el and Δ₂E (or Δ₃E) would result. On the other hand, if SE were purely vdW effects, they could have nothing in common with ΔE_el and a similarity of ΔE_el and PE would be expected. The latter case seems to be in better agreement with the observations. In our opinion, this is a supporting argument of limited value that our SE are to be viewed merely as vdW interactions.

The electrostatic theory is in any case a rough approximation valid only for simple and strongly polar substituents.^15b,35a,f It was used here as a possible simple tool for distinguishing polar and purely steric interactions. We do not deal here with its function in defending the transmission “through space” against the transmission “through bonds”.³⁵ In our opinion,^35a the problem is ill-formulated.

Conclusions

Our analysis of the ortho substituent effect may be somewhat overly sophisticated, certainly its accuracy is limited and all results are not equally dependable. Therefore, we have arranged our conclusions according to decreasing reliability and accuracy. In our opinion, at least the first two cannot be doubted as far as the qualitative sense is concerned.

1. An intramolecular H-bond is absent in most 2-substituted benzoic acids, although it has been anticipated in the literature. In the compounds where it is present, it affects the acidity only moderately and the effect can be calculated with some reliability.

2. SIR is also operative in only some acids and is sometimes largely canceled in the acid molecule and in the anion. Its calculation is somewhat less reliable since it depends on the model. However, it is evident that SIR has been overestimated in the literature.

3. Inductive and resonance effects transmitted through the benzene ring are very important. They are roughly proportional to those in the para isomers but slightly weaker; our provisional estimate of their ratio is 0.81. However, it is certain that these effects can be decisive when strongly polar substituents are present in a given series. In this case they can be the cause of the reported correlations with the para derivatives or with the σ constants.

4. Purely steric effects have been evaluated as what remains after subtracting all preceding terms, and are thus endowed with an unknown error. Nevertheless, they are probably of importance only for bulky substituents; otherwise they can cancel considerably in the acid molecule and in the anion. In our opinion, they are better described as pure vdW interactions rather than as short-range polar effects as it is often done in the literature.

In conclusion, the so-called ortho effect is a complex phenomenon: the term is of unclear significance and should be not further proliferated. In any case, the acidities of carboxylic acids are not a good example for its analysis; more progress is expected from simpler models.

Acknowledgements

This work was carried out within the framework of the research project Z4 055 905 of the Academy of Sciences of the Czech Republic and supported by the Ministry of Education of the Czech Republic (Project LN00A032, Center for Complex Molecular Systems and Biomolecules).

References

1. O. Exner, Correlation Analysis of Chemical Data, Plenum Press, New York, 1988, p. 135–137.
2. (a) H. C. Brown, D. H. McDaniel and O. Häfliger, in Determination of Organic Structures by Physical Methods, eds. E. A. Braude and F. C. Nachod, Academic Press, New York, l955, pp. 567–662; (b) G. S. Hammond, in Steric Effects in Organic Chemistry, ed. M. S. Newman, Wiley, New York, 1956, pp. 425–470.
3. (a) M. Charton, Can. J. Chem., 1960, 38, 2493–2499; (b) M. Charton, Prog. Phys. Org. Chem., 1971, 8, 235–317; (c) K. Bowden and G. E. Manser, Can. J. Chem., 1968, 46, 2941–2944.
4. (a) J. Shorter, in Advances in Linear Free Energy Relationships, eds. N. B. Norman and J. Shorter, Plenum Press, London, 1972, pp. 71–118; (b) R. W. Taft, in Steric Effects in Organic Chemistry, ed. M. S. Newman, Wiley, New York, 1956, pp. 556–675; (c) T. Fujita and T. Nishioka, Prog. Phys. Org. Chem., 1976, 12, 49–89; (d) U. Berg, R. Gallo, G. Klatte and J. Metzger, J. Chem. Soc., Perkin Trans. 2, 1980, 1350–1355; (e) A. C. Farthing and B. Nam, in Steric Effects in Conjugated Systems, ed. G. W. Gray, Butterworths, London, 1958, pp. 131–140; (f) M. T. Tribble and J. G. Traynham, J. Am. Chem. Soc., 1969, 91, 379–388; (g) M. H. Aslam, A. G. Burden, N. B. Chapman, J. Shorter and M. Charton, J. Chem. Soc., Perkin Trans. 2, 1981, 500–508.
5. M. Charton, in Similarity Models in Organic Chemistry, Biochemistry and Related Fields, eds. R. I. Zalewski, T. M. Krygowski and J. Shorter, Elsevier, Amsterdam, 1991, p. 629–687.
6. (a) M. Decouzon, P. Ertl, O. Exner, J.-F. Gal and P.-C. Maria, J. Am. Chem. Soc., 1993, 115, 12 071–12 078; (b) M. Decouzon, J.-F. Gal, P.-C. Maria, S. Bőhm, P. Jiménez, M. V. Roux and O. Exner, New J. Chem., 1997, 21, 561–573; (c) S. Böhm and O. Exner, Chem.-Eur. J., 2000, 6, 3391–3398.
7. (a) O. Pytela and O. Prusek, Collect. Czech. Chem. Commun., 1999, 64, 1617–1628; (b) O. Pytela and J. Kulhánek, Collect. Czech. Chem. Commun., 2002, 67, 596–608.
8. A. Y. Kaminskii, V. M. Ivanova, S. S. Gitis, E. G. Kaminskaya and L. I. Khabarova, Reakts. Sposobn. Org. Soedin., 1971, 8, 343–362.
9. (a) Y. Y. Kharitonov and I. I. Oleinik, Dokl. Akad. Nauk SSSR, 1987, 294, 151–154; (b) O. Exner, P. Fiedler, M. Buděšínský and J. Kulhánek, J. Org. Chem., 1999, 64, 3513–3518; (c) C. I. Jose, A. A. Belhekar and M. S. Agashe, Spectrochim. Acta, Part A, 1988, 44, 899–901; (d) Y. Y. Kharitonov and I. I. Oleinik, Dokl. Akad. Nauk SSSR, 1990, 313, 907–914.
10. K. Bowden and G. R. Taylor, J. Chem. Soc. B, 1971, 1390–1394.
11. (a) T. B. McMahon and P. Kebarle, J. Am. Chem. Soc., 1977, 99, 2222–2230; (b) R. T. McIver, Jr. and J. H. Silvers, J. Am. Chem. Soc., 1973, 95, 8462–8464; (c) S. Böhm, M. Decouzon, O. Exner, J.-F. Gal and P.-C. Maria, J. Org. Chem., 1994, 59, 8127–8131.
12. O. Exner, S. Böhm, M. Decouzon, J.-F. Gal and P.-C. Maria, J. Chem. Soc., Perkin Trans. 2, 2002, 168–172.
13. C. S. Yoder and C. H. Yoder, J. Am. Chem. Soc., 1980, 102, 1245–1247.
14. (a) A. Pross, L. Radom and R. W. Taft, J. Org. Chem., 1980, 45, 818–826; (b) O. Exner, Org. React. (Tartu), 1995, 29, 1–6.
15. (a) O. Exner and P. Nauš, J. Phys. Org. Chem., 2000, 13, 693–698; (b) O. Exner and S. Böhm, Chem.-Eur. J., 2002, 8, 5147–5152.
16. (a) O. Exner and S. Böhm, J. Chem. Soc., Perkin Trans. 2, 2000, 1994–1999; (b) O. Exner and S. Böhm, Collect. Czech. Chem. Commun., 2001, 66, 1623–1637.
17. (a) K. B. Wiberg, J. Org. Chem., 2002, 67, 4787–4794; (b) O. Exner and S. Böhm, J. Org. Chem., 2002, 67, 6320–6327.
18. (a) P. Fiedler, J. Kulhánek, M. Decouzon, J.-F. Gal, P.-C. Maria and O. Exner, Collect. Czech. Chem. Commun., 1999, 64, 1433–1447; (b) J. Kulhánek, M. Decouzon, J.-F. Gal, P.-C. Maria, P. Fiedler, P. Jiménez, M.-V. Roux and O. Exner, Eur. J. Org. Chem., 1999, 1589–1594; (c) S. Böhm and O. Exner, New J. Chem., 1997, 21, 561–573.
19. J. Roithová and O. Exner, J. Phys. Org. Chem., 2001, 14, 752–758.
20. P. George, M. Trachtman, C. W. Bock and A. M. Brett, J. Chem. Soc., Perkin Trans. 2, 1976, 1222–1227.
21. G. Pilcher, in The Chemistry of Functional Groups. Supplement B: The Chemistry of Acid Derivatives, ed. S. Patai, Wiley, New York, 1992, vol. 2, pp. 51–94.
22. For instance, there is a serious disagreement with the recent values for 2-chloro- and 2-bromobenzoic acids: R. Sabbah and A. R. Aguilar, Struct. Chem., 1996, 7, 383–390.
23. (a) A. D. Becke, Phys. Rev. A: At., Mol., Opt. Phys., 1988, 38, 3098–3100; (b) C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter, 1988, 37, 785–789; (c) B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Lett., 1989, 157, 200–206; (d) A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
24. (a) E. S. Domalski and E. D. Hearing, J. Phys. Chem. Ref. Data, 1993, 22, 805–1159; (b) M. Bureš, R. Holub, J. Leitner and P. Voňka, Thermochemické veličiny organických sloučenin (Thermochemical Quantities of Organic Compounds), Institute of Chemical Technology, Prague, 1987; (c) J. O. Fenwick, D. Harrop and A. J. Head, J. Chem. Thermodyn., 1975, 7, 943–954.
25. J. H. S. Green, Spectrochim. Acta, Part A, 1977, 33, 575–581.
26. M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. Keith, G. A. Petersson, J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe, C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. J. P. Stewart, M. Head-Gordon, C. Gonzales and J. A. Pople, Gaussian 94, Revision C.3, Gaussian Inc., Pittsburgh, PA, 1995.
27. R. F. C. Brown, K. J. Coulston and F. W. Eastwood, Aust. J. Chem., 1994, 47, 47–60.
28. D. Hnyk, K. B. Borisenko, S. Samdal and O. Exner, Eur. J. Org. Chem., 2000, 2063–2069.
29. The population of the two conformers of the methyl esters of 6, 10 and 11 was estimated from both the IR spectra and dipole moments: (a) O. Exner and Z. Friedl, Collect. Czech. Chem. Commun., 1977, 42, 3030–3039; (b) O. Exner, Z. Friedl and P. Fiedler, Collect. Czech. Chem. Commun., 1983, 48, 3086–3096.
30. The dipole moment of 11 in dioxan is not compatible with the moment of 4-chlorobenzoic acid and does not allow the determination of the conformer ratio: A. Srivastava, S. Singh and V. Kumar, J. Indian Chem. Soc., 1988, 65, 729–731.
31. W. Brandt and W. Gründler, Z. Phys. Chem (Leipzig), 1983, 264, 1121–1129.
32. O. Pytela and J. Liška, Collect. Czech. Chem. Commun., 1994, 59, 2005–2021.
33. H. W. Thompson and G. Steel, Trans. Faraday Soc., 1956, 52, 1451–1457.
34. O. Exner and S. Böhm, Acta Crystallogr., Sect. B, 2002, 58, 877–883.
35. (a) O. Exner, J. Phys. Org. Chem., 1999, 12, 265–274; (b) M. Charton, J. Phys. Org. Chem., 1999, 12, 275–282; (c) K. Bowden and E. J. Grubbs, Chem. Soc. Rev., 1996, 25, 171–177; (d) O. Exner and Z. Friedl, Prog. Phys. Org. Chem., 1993, 19, 259–294; (e) M. A. P. Segurado, J. C. R. Reis and J. D. G. de Oliveira, J. Chem. Soc., Perkin Trans. 2, 2002, 323–328; (f) K. B. Wiberg, J. Org. Chem., 2002, 67, 1613–1617.
36. O. Exner and S. Böhm, Chem. Eur. J., 2003, 9, 4718–4723.

---

Footnote

† Electronic supplementary information (ESI) available: Table S1 giving the DFT calculated energies of 2-substituted benzoic acids 1–11 in all conformations, population of conformers, important bond lengths and bond angles; Table S2 giving the DFT energies of twisted structures of some 4-substituted benzoic acids with a fixed dihedral angle and Table S3 giving the IR spectral data of those 2-substituted benzoic acids in which a H-bond may be present. See http://www.rsc.org/suppdata/nj/b3/b305986c/

---