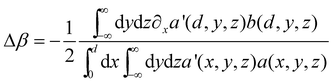Theoretical studies of the electronic properties of confined aromatic molecules in support of electronic confinement effect

Abstract

Theoretical studies of the electronic properties of three confined aromatic molecules—benzene, naphthalene and anthracene—have been presented in support of the electronic confinement effect. The confined space of the cavities has been modeled using a mica sheet with the molecule–surface distance in the range of 1.5–4.0 Å. Evidence of the confinement has been revealed by semiempirical calculations, which are theoretically interpreted by means of the Hückel molecular orbital theory. It has been found that the HOMO has been predicted to be more sensitive to the confinement than the LUMO and the overall effect is a reduction on the band gap of the frontier molecular orbitals when the molecule–surface distance is less than ca. 2.5 Å. The variations of the frontier orbital energies and band gaps are correlated with the increase of both Coulomb integral, α, and resonance integral, β. The order of magnitude of the energy increment of Δα and Δβ values is evaluated from data of the above semiempirical calculations. It is also found that the confinement effect is associated with the conjugated system of the aromatic molecules. The theoretical evaluations here prove that confining organic molecules in the cavities is sufficient to alter their electronic properties as a consequence of changes in the molecular orbital energies and band gaps.

---

Introduction

The study of size effect on the electronic properties of semiconductor nanocrystallites has long been a subject under intense investigation in the field of physical chemistry and materials chemistry.^1–5 It is of fundamental interest to understand how these properties vary as the crystallite size grows from the molecule to the bulk material. Calculations of this energy level based on the effective-mass approximation have been proposed.⁶ The study of electronic properties of organic molecules in nanoscale confined spaces adds a new dimension to chemical physics, as verified by highly efficient nanovessel reactors and quantum-confined materials.⁷ Because of their intriguing structural and chemical features, semicrystalline periodic nanoporous silicas of the M41S family are considered as one of the most attractive host materials.^8,9 Their intrinsic zeolite-like pore architecture with tunable pore sizes and narrow pore size distributions provides a unique platform for studying the encapsulation of highly reactive organic molecules. Encapsulation of these molecules in the nanoporous channels host may produce significant changes on the electronic properties of the guest species, which result in the variations of optical band gaps and excited-state lifetimes of the organic molecules in these complex systems in experimental studies by various groups.^10–13 Additionally, there have been previous nice theoretical studies on similar clusters, which give useful comparisons.¹⁴

We believe that the electronic confinement theory is responsible for the variation of electronic properties of the guest species.¹⁰ In this theory, the confinement produces an increase in energy of all the orbitals of guest molecules in confined spaces, but the increase is different for the HOMO (highest occupied molecular orbital) and LUMO (lowest unoccupied molecular orbital): the HOMO has been predicted to be more sensitive than the LUMO, and the predicted effect is a reduction of the band gap of the frontier molecular orbitals. Therefore, the changes of electronic structures can be explained as produced by electronic confinement in which the electron density of the guest is constrained to mainly localize within the cavity as a result of the strong short-range repulsion with the electrons of the channel walls. It is generally accepted that the sizes of the channels and cavities are crucial for understanding the different electronic properties involved under incorporation of guest molecules into the host. So, it is rather important to study exclusively the influence of the confinement effect at various host environments in order to achieve a better understanding of the host–guest interactions in these complex systems. In a previous communication, we have presented experimental studies in support of the electronic confinement effect;¹⁰ we report in this contribution the theoretical evaluations of three confined aromatic molecules and find that the confinement is truly responsible for remarkable changes, such as the increase in energies of molecular orbitals and the decrease of band gaps.

Computational methodology

Three typical aromatic molecules—benzene, naphthalene and anthracene—have been considered for calculation in this work. The geometric parameters of these three compounds have been optimized. In order to mimic the confinement induced by the inorganic channels of the host, a simple but effective way is to place the aromatic molecules parallel to a sufficiently large mica sheet at a fixed distance. Fig. 1a shows the geometry of the mica sheet, a layered silicate formed by an infinite array of edge-sharing SiO₄ tetrahedra. In this work, the aromatic molecules are located in the central area of the mica sheet. While additional adjustments of this model can be introduced by using larger mica sheet, similar conclusions are expected by simply increasing the number of atoms far away from the center. It is noteworthy that the atomic coordinates of these three aromatic molecules are all equal to zero in the z direction, indicating their planar structures. Thus, the distance between the guest molecule and the surface atoms of the host mica sheet can be easily and precisely adjusted by altering the atomic coordinates of the aromatic molecules in the z direction (see Fig. 1b). The overall atom number in our model systems in this work is fairly large, being 115, 121 and 127 atoms, respectively. To provide a quantum chemical prediction of the confinement effect at a reasonable computational cost, we have performed semiempirical calculations of all these model systems at the PM3 level using the Gaussian 98 suite of programs.¹⁵ All calculations have been performed on a Legend 586 computer.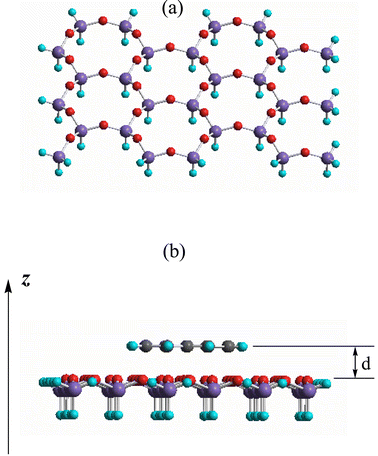

Fig. 1 Molecular structure diagrams of the mica sheet (a) and the aromatic molecule–mica sheet complex system (b). The colours for the atoms are: H = green, C = black, O = red, Si = purple.

Results and discussion

Semiempirical calculations

As we have mentioned, the electronic confinement on the electronic energy states of the guest organic molecules should be connected with the distance between the aromatic molecules and the surface atoms of the mica sheet. As seen from Fig. 1a, the mica sheet shows a two-dimensional planar structure. So, the molecule–surface distance can be precisely adjusted by simply altering the z coordinates. The confinement effect is due to the stronger short-range overlap repulsion between electrons rather than long ranged dispersion forces and the weak electron interactions involved in the confinement effect account for forces of the van der Waals type. Thus, the computational results obtained at long distances should have no meaning. On the other hand, as the molecule approaches close to the surface, the strict symmetry-based separation of σ (in plane) and π (out-of-plane) orbital is lost so that hybridization can occur; in extreme cases this may result in non-planarity of the rings themselves, which is irrespective of and disadvantageous to our explanation of the confinement effect. Therefore, the distance between the aromatic molecules and the mica sheet should be selected in a limited range. Through progressive increase (0.1 Å) of the molecule–surface distance from 1.5 to 4.0 Å, we have determined the influence of the mica sheet on these aromatic molecules by examining the distortions on their HOMO-1, HOMO and LUMO orbitals.

Plots of the energies of the HOMO-1, HOMO and LUMO of confined benzene, naphthalene and anthracene are provided in Figs. 2a, 2b and 2c, respectively. It is clear that the variation of the energy levels of HOMO-1 and HOMO orbitals exhibit similar trends. In agreement with the electronic confinement theory, remarkable increase in their energy levels has been observed as revealed by the theoretical calculations. This suggests essentially the same confinement effect on the occupied molecular orbitals. It is also noteworthy that the HOMO orbitals of large conjugated aromatic molecules are more sensitive to the confinement than those of small conjugated ones, which is evidenced by different onsets of the increase of HOMO orbital energies. However, the energy changes of unoccupied molecular orbitals seem less influenced when compared to those of occupied ones. In the case of the benzene molecule, noticeable variation of LUMO orbital energies is not even observed. In the order of increasing conjugated π system of the aromatic compounds, the confinement effect on LUMO orbitals becomes apparent, which means that increasing conjugation (larger aromatics) shows greater destabilizing effects on the LUMOs. These results indicate that the confinement effect is associated with not only the molecule–surface distance, but also the conjugation of the guest molecules.

Fig. 2 Plots of the energies of the HOMO-1 (□), HOMO (○) and LUMO (△) of confined benzene (a), naphthalene (b) and anthracene (c), respectively. 1 Hartree = 27.2 eV.

Plots of the band gap energies of confined benzene, naphthalene and anthracene are shown in Fig. 3. The band gaps decrease in the order: benzene > naphthalene > anthracene, which is connected with their conjugated structures. No variation of the band gap energies is actually detected until the molecule–surface distance decreases to ca. 2.5 Å for these three complex systems. Considering that the energy increase of HOMO orbitals is more significant than those of LUMO ones, the band gaps decrease markedly. This indicates that the electronic confinement is truly exceptional when the aromatic molecules approach rather close to the mica sheet, which is also in agreement with experiments.^7,10 It is expected from the figure that for molecule–surface distances smaller than ca. 2.5 Å, the band gaps of the aromatic molecules are reduced by 14, 30 and 11% for benzene, naphthalene and anthracene, respectively.

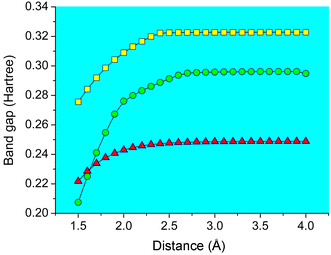Fig. 3 Plots of the band gap energies of confined benzene (□), naphthalene (○) and anthracene (△), respectively. 1 Hartree = 27.2 eV.

Theoretical interpretations

To gain a better understanding of the variations of electronic states that concern the changes in the optical band gap, it is necessary to present here a theoretical interpretation of the above computational results. Starting from the closed-shell single-determinant approximation which treats each electron as moving independently in a mean electrostatic field of other electrons and the nuclei, HMO (Hückel molecular orbital) theory is a method that allows one to obtain a chemical characterization of conjugated π systems without need to involve quantum chemical calculations.¹⁶ Its goal is to give an adequate description of π molecular orbitals (their energy and atomic orbital composition) by only two empirical parameters, namely, the Coulomb integral, α, and the resonance integral, β. For these aromatic compounds, the frontier molecular orbital energies given by the HMO theory are E_HOMO = α + nβ and E_LUMO = α − nβ, where E_HOMO and E_LUMO are the frontier orbital energies given as a function of α and β parameters. For benzene (C₆H₆), naphthalene (C₁₀H₈), and anthracene (C₁₄H₁₀), n values are 1.000, 0.618, and 0.445, respectively.

A confined model system can be built by locating the conjugated molecules parallel to a surface which, for simplicity, may be simulated by an infinite plane located at a certain distance. The electrons in this model do not result in a serious loss of generality, since the essential features of the confined electrons of a conjugated molecule near a surface are present here. The symmetry of the system does not change with respect to the unconfined molecule, and this implies that the energies of frontier MOs will conserve the same form as for the unconfined system: E_HOMO′ = α′ + nβ′ and E_LUMO′ = α′ − nβ′, where α′ and β′ are the Coulombic and resonance integrals for the confined system, respectively, and n retains the same values as above. In this case, the atomic orbitals can still have as the normal 2p_z orbitals a node at the molecular plane but they are adapted to the confinement, which makes them vanish beyond the limit of the plane. This comes from the condition that the probability of finding an electron belonging to the molecule outside the plane should be null. That is, the density of the confined 2p_z orbitals (i.e., the probability for finding the electrons) drop to nearly zero suddenly when reaching the infinite plane as a consequence of the short-range repulsion with the delocalized electronic clouds. This implies that a contraction of the molecular orbitals of the guest molecules will occur, with the consequent changes in its energy levels. Hence, the energy changes of these aromatic compounds may be expressed as ΔE_HOMO = Δα + Δβ and ΔE_LUMO = Δα − Δβ, where Δα and Δβ are (in atomic units) (see supporting information)†

In this expression, a(x,y,z) and b(x,y,z) are the 2p_z atomic orbitals on the neighboring carbon atoms a and b, respectively, while a′(x,y,z) and b′(x,y,z) are the equivalent confined atomic orbitals. Although we do not know the actual expression of the atomic orbitals in the confined system, we can state that Δα and Δβ are always positive quantities. Since a(x,y,z) and b(x,y,z) are always positive at z = d, then a′(x,y,z) decreases when approaching the surface, which means that its derivative in such a direction should be negative. Therefore, we obtain α′ = α + Δα > α and nβ′ = nβ + Δβ > nβ for the Coulomb and resonance integrals of the confined system. Since α and β are both negative quantities, the above equations indicate that α and β become less negative when confining the molecule. Fig. 4 shows the qualitative correlation energy diagram of the confined aromatic molecule.

Fig. 4 Qualitative description of the frontier orbital energy diagram of the confined aromatic molecule.

Implications on catalysis

As shown in the above figure, the band gap between HOMO and LUMO orbitals decreases dramatically when the molecule–surface distance is less than ca. 2.5 Å. Therefore, the HOMO orbital becomes weaker than when unconfined. A small band gap indicates that a quasi-degeneracy of the electronic states should occur at the ground state.¹⁰ A single configuration model of the many-particle wave function cannot be assumed, and one expects that the actual wave function can be properly represented by a multireferential function which accounts for a partially biradical character of the bond.¹⁷ Thus, the smaller the band gap, the greater the likelihood of having some unpaired electron density on each carbon atom. So, the molecule would become intrinsically more reactive when confined in the cavities. This means that reactions involving a loss of the π character of the molecule would be favored. Consequently, addition reactions of alkenes or polyenes, including those acting in a concerted way, such as the Diels–Alder type, should occur more easily when performed inside the molecular sieves. Several experimental results on the catalytic reactivity match this analysis.^18,19

The increase in frontier orbital energies is consistent with the increase of both α and β values. To determine quantitatively the order of magnitude of the confinement effect, Δα and Δβ values are evaluated from the above semiempirical calculation data. The results are shown in Fig. 5, in which Δα and Δβ are depicted versus different molecule–surface distances. In this figure, Δα and Δβ are all positive quantities, which indicate that our present HMO model is conceptually right and can well interpret the semiempirical calculations. It can be observed that the electronic confinement becomes significant when the aromatic molecules approach the mica sheet. Also, molecules with large conjugated π systems are more sensitive to the confinement, which are as indicated by the different onsets of the energy increment of Δα.

Fig. 5 Variation of the Coulomb integral Δα (△) and resonance integral Δβ (▽) depicted versus different molecule–surface distances of confined benzene (a), naphthalene (b) and anthracene (c), respectively. 1 Hartree = 27.2 eV.

Conclusions

In summary, we have presented here a theoretical study of the electronic properties of three confined aromatic molecules—benzene, naphthalene and anthracene—in support of the electronic confinement effect. Evidence of the confinement has been revealed by semiempirical calculations and then theoretically interpreted by the HMO model. It has been found that the HOMO has been predicted to be more sensitive to the confinement than the LUMO and the overall effect is a reduction on the band gap of the frontier molecular orbitals when the molecule–surface distance is less than ca. 2.5 Å. The variations of the frontier orbital energies and band gaps are correlated with the increase of both Coulomb integral, α, and resonance integral, β. It is also noteworthy that the confinement effect is associated with the conjugated system of the aromatic molecules. Taken all together, the theoretical evaluations in this contribution have clearly proved that confining organic molecules in cavities is sufficient to alter their electronic properties as a consequence of the increase in the molecular orbital energies and decrease of the band gaps.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Nos. 90101028, 50173011) and the TRAPOYT of MOE, China. One of the authors (L.Z.Z.) truly appreciates one of the referees for his patience during evaluation, and for profound comments.

References

1. A Special Report on Frontiers in Materials Science Science (Washington, D. C.), 1997, 277, 1213..
2. Nanoscale Materials Special Issue Acc. Chem. Res. 1999, 32, 387.
3. C. Burda, A. C. S. Samia, D. J. Hathcock, H. J. Huang and S. Yang, J. Am. Chem. Soc., 2002, 124, 12400.
4. C. Burda, S. Link, M. B. Mohamed and M. El-Sayed, J. Chem. Phys., 2002, 116, 3828.
5. C. Burda, S. Link, M. Mohamed and M. El-Sayed, J. Phys. Chem. B, 2001, 105, 12286.
6. L. E. Brus, J. Chem. Phys., 1983, 79, 5566; L. E. Brus, J. Chem. Phys., 1984, 80, 4403.
7. A Special Issue on Organic–Inorganic Nanocomposite Materials Chem. Mater. 2001, 13, 3059.
8. C. T. Kresge, M. E. Leonowicz, W. J. Roth, J. C. Vartuli and J. S. Beck, Nature (London), 1992, 359, 710.
9. P. J. Langley and J. Hulliger, Chem. Soc. Rev., 1999, 28, 279.
10. L. Z. Zhang, P. Cheng and D.-Z. Liao, J. Chem. Phys., 2002, 117, 5959.
11. B.-H. Wang, H.-A. Xi, J. Yin, X.-F. Qian and Z.-K. Zhu, Synth. Met., 2003, 139, 187.
12. H.-G. Xi, Y.-B. Zhang, Z.-K. Li, X.-F. Qian, J. Yin and Z.-K. Zhu, J. Mater. Sci. Lett., 2002, 21, 1817.
13. Y.-F. Yao, M.-S. Zhang, J.-X. Shi, M.-L. Gong, H.-J. Zhang and Y.-S. Yang, Mater. Lett., 2001, 48, 44.
14. G. Sastre, P. M. Viruela and A. Corma, Chem. Phys. Lett., 1997, 264, 565.
15. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, Jr., R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, R. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98 (Revision A.9), Gaussian, Inc., Pittsburgh, PA, 1998.
16. J. K. Burdett, Prog. Solid State Chem., 1984, 15, 173.
17. M. A. Fox and F. A. Matsen, J. Chem. Educ., 1985, 62, 367; M. A. Fox and F. A. Matsen, J. Chem. Educ., 1985, 62, 477; M. A. Fox and F. A. Matsen, J. Chem. Educ., 1985, 62, 551.
18. Y. V. S. Narayana Murty and C. N. Pillai, Synth. Commun., 1991, 21, 783.
19. R. M. Dessau, J. Chem. Soc., Chem. Commun., 1986, 1167.

---

Footnote

† Electronic Supplementary Information (ESI) available: A general solution for the confined system. See http://www.rsc.org/suppdata/qu/b3/b307440d/

---