DOI:
10.1039/B304717B
(Paper)
PhysChemComm, 2003,
6, 42-46
Algebraic description of n-alkane molecules: first overtone of CH stretching modes
Received
30th April 2003
, Accepted 21st May 2003
First published on 4656th June 2003
Abstract
The one-dimensional algebraic model is applied to analyze infrared spectra of n-alkane molecules. We consider CH stretching vibrations in both fundamental (v
= 1) and first overtone (v
= 2) energy regions. We show that a relatively small set of well-defined parameters leads to a very good agreement with observed data. Both CH2 and CH3 vibrations are accounted for. In particular, we suggest that first overtone infrared spectra can be fairly well described without adding complex anharmonic (Fermi) interactions. Their inclusion is required however to obtain a closer agreement with the available experimental spectra.
1 Introduction
Since the pioneering work by Snyder1–3 and Schachtschneider,3 vibrational spectroscopy of molecular chains of finite length such as n-alkanes, CH3–(CH2)n−2–CH3, has provided a challenging sequence of case studies from several viewpoints. A particularly interesting issue of concern is to establish a reliable assignment of observed CH vibrational modes in both infrared and Raman spectra. Moreover, the specific role of anharmonic (Fermi) resonances, involving overtone and combination CH bending modes, is still to be convincingly settled. Such couplings have been described with sensible accuracy in the Raman spectra of solid and liquid samples of n-alkanes and of several polymers in the region of fundamental CH stretches (3000 cm−1).4–7 It has been also shown that similar mechanisms could be considered to explain some minor features in the infrared spectrum of this same energy region.8,9 More recently, the infrared spectra of the first CH stretching overtone region of n-butane, n-pentane, n-heptane and polyethylene (in both solid and liquid states) have been measured and reported.10 In the present work, we adopt a one-dimensional algebraic (vibron) model to obtain, in terms of a unique set of parameters, energies and infrared intensities of both fundamental and first overtone modes of CH stretches of n-alkanes (arbitrary n). The algebraic parameters are optimized to reproduce fundamental infrared spectra in the gas phase. The algebraic Hamiltonian leads to a very good agreement for v
= 2 CH stretching modes as well. In particular, we show that anharmonic resonances are not of dramatic relevance to obtain such an agreement, which is instead based on a careful calibration of the electric dipole algebraic representation. A further refinement of the computed spectra is however achieved by adding quite a typical 1 ∶ 2 anharmonic resonant term involving CH bending modes. Raman intensities will be addressed in a forthcoming paper.
The use of an algebraic (vibron) model has some advantages over more traditional approaches, the most appealing one being related to the intrinsically anharmonic nature of the Morse basis which is the building block of this model. Such an aspect becomes important as soon as one addresses vibrational overtone/combination manifolds of levels, which is in fact a point of concern in the present work. Moreover, there are still controversial results concerning reliable values of ab initio dipole surfaces of carbon based molecular chains such as n-paraffins. Our approach, even if quite simple in these respects, can nonetheless give a fair contribution to such a discussion since it provides a straightforward way to compute local bond dipole operators, as already discussed elsewhere and shown in the following.
2 Algebraic model
The application of the one-dimensional vibron model to molecular chains has been introduced in ref. 11 and extended to practical situations (n-paraffins or n-alkanes) in ref. 12. Here, we limit ourselves to recall the most important features of the algebraic technique, i.e. we start from the replacement of molecular interatomic bond coordinates with boson creating/annihilating operators. Such operators generate anharmonic sequences of vibrational levels associated with Morse or Poeschl–Teller potential functions (for stretching or bending modes, respectively). These same operators are also put in close correspondence with unitary algebraic structures which are then combined to provide the so called spectrum generating algebra of the physical system. More specifically, it can be shown that vibrational modes of a single anharmonic oscillator are labelled in terms of the irreducible representations of the algebraic ket |U(2)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⊃
⊃![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O(2)〉.13 The corresponding energies are obtained in terms of the expectation values of the invariant (Casimir) operator of the subgroup O(2), i.e. in terms of the Hamiltonian operatorwhose eigenvalues are given by
O(2)〉.13 The corresponding energies are obtained in terms of the expectation values of the invariant (Casimir) operator of the subgroup O(2), i.e. in terms of the Hamiltonian operatorwhose eigenvalues are given by| | | E(ν)
=
e0
+
αν(N
−
ν), ν
= 0, 1, … , | (2) |
where N is the label of the irreducible representation of U(2) and here also plays the role of the anharmonicity parameter and number of total bound vibrational states. The operator h0 in eqn. (1) and its eigenvalues e0 in eqn. (2) are used to displace the zero-energy value. One recognizes in eqn. (2) the eigenvalues of a one-dimensional Morse or Poeschl–Teller potential whose strength is regulated by the parameter α.
Interbond couplings are then introduced in terms of operators associated with products of U(2) and O(2) algebras corresponding to different, interacting bonds. One thus obtains, among other terms, the non-diagonal Majorana operator which, besides conserving the total vibrational (polyad) quantum number, has matrix elements in a local (bond) vibrational basis given by
| | 〈νh
+ 1,νk
− 1|![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) hk|νh,νk〉
=
[νk(νh
+ 1)(N
−
νh)(N
−
νh
+ 1)]1/2/N hk|νh,νk〉
=
[νk(νh
+ 1)(N
−
νh)(N
−
νh
+ 1)]1/2/N | (3) |
The Majorana operator is used to describe local mode interactions in pairs. Following a well-established route, these ingredients are applied to the molecular chain (
n-alkane) as schematically shown in
Fig. 1. The total Hamiltonian operator, as discussed elsewhere,
12 is composed by three leading terms,
i.e. contributions devoted to describe CH
2, CH
3 motions and their interactions, respectively. CH
2 modes, for example, are described by the operator
| |  | (4) |
in which we introduce Casimir operators
Ci to generate 2(
n
− 2)-fold degenerate sets of levels representing the local, uncoupled CH stretching vibrations (a similar expression, with different numerical parameters, is written for other degrees of freedom, such as CH bends). The operators
Mhk describe intrasite (
λ) and intersite, first-neighbour direct (
fd) and cross (
fc) interactions involving bonds h and k. Similar expressions can be written for CH
3 and CH
2/CH
3 Hamiltonian operators. In
ref. 12 it is explained how the parameters of such operators have been optimized to reproduce observed CH stretches and bends in the fundamental energy regions (∼3000 cm
−1 for CH stretching modes and ∼1500 cm
−1 for out-of-plane bends). Within the framework of this model, it is also possible to compute infrared intensities in terms of a simple bond–dipole model. As widely discussed elsewhere,
14,15 the infrared intensity of the fundamental transition
vk
← 0 corresponding to the excitation of the bond k, is based on the formula for the matrix element of the local dipole operator given by
| | 〈νk|![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) k|0〉
≅
tke−βνk, k|0〉
≅
tke−βνk, | (5) |
in which
tk is the strength of the local transition and
β is a slope parameter used to calibrate overtone
vs. fundamental transition intensities. The total dipole operator is usually written in terms of sums of Cartesian components of local bond dipoles, in such a way that both
tk and
β parameters can be optimized against observed values.
 |
| | Fig. 1 Schematic representation of labelling of algebraic coupling terms in n-alkane molecules. | |
3 Fundamental CH stretching vibrations of gaseous n-alkane molecules
The energy region of the fundamental CH stretches of the gaseous n-alkanes has been an object of experimental studies as reported in ref. 16. The algebraic model has been used to fit the complete sequence of both CH2 and CH3 stretches for molecules with n
= 4 (butane) up to n
= 11 (undecane). The complete set of algebraic parameters is reported in Table 1, while in Fig. 2 we show the direct comparison between observed and computed infrared spectra of n-butane, n-pentane and n-heptane. We stress that in this work the computation has been extended to include both CH2 and CH3 terminal sites. We notice an overall good agreement in terms of both energy positions and infrared intensities.
 |
| | Fig. 2 Comparison between computed (continuous line) and observed (crosses, ref. 16) infrared intensities of n-alkane molecules (n
= 4, 5, 7) in the fundamental CH stretching region. Stick spectra are also shown as vertical segments (continuous: CH2 modes, dashed: CH3 modes). Continuous curves are computed by constructing Lorentzian shapes, FWHM = 20 cm−1. The normalization adopted takes the maximum experimental and computed values as equal quantities. | |
Table 1 Parameters of the algebraic Hamiltonian operator used to compute CH stretches (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v
1 and v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in n-alkanesa
2) in n-alkanesa
| Term |
Parameter value |
|
All values in cm−1 except N, which is dimensionless. The meaning of algebraic parameters is schematically summarized in Fig. 1. Parameters aCH3, λβγ, λα, ft, fbd, fbc refer to CH3 end-effects terms (see ref. 12 for their meaning; their values in the present work are slightly different since they have been optimized to reproduce the spectra of gaseous samples rather than solid or liquid state n-alkanes).
|
|
N
|
43 |
|
a
|
2970.00 |
|
λ
|
−25.00 |
|
f
d
|
5.00 |
|
f
c
|
0.10 |
|
a
CH3
|
3009.00 |
|
λ
βγ
|
−27.00 |
|
λ
α
|
−30.00 |
|
f
t
|
0.03 |
|
f
bd
|
0.07 |
|
f
bc
|
0.08 |
It is claimed that in both solid and liquid alkanes, the infrared spectrum is to some extent influenced by the action of anharmonic 1 ∶ 2 resonances between fundamental CH stretches and overtone/combination of out-of-plane CH bends.8,9 At the present level of resolution, there is no evident need to include such resonances to achieve a satisfying description of the most relevant features of the observed spectra. As discussed in ref. 12, the (quite weak) anharmonic couplings at issue are almost completely masked in these spectra due to the overlap of resonant modes with strong, antisymmetric CH2 bands. In the gas phase, we still realize that the leading infrared features are the CH2 symmetric/antisymmetric peaks split by ∼60 cm−1, the symmetric contribution being located at lower energy that the antisymmetric one, while CH3 modes give rise to less and less important peaks with increasing n. So, we find that the full set of spectral characteristics in the infrared regime of n-alkane molecules is fairly accounted for within the one-dimensional algebraic model. As shown in Table 1, we limit the Hamiltonian operator to the inclusion of first-neighbour interactions in the molecular chain, since at this level of experimental resolution one is not allowed to calibrate second-neighbour effects (such terms have instead been included in the calculation reported in ref. 12 devoted to higher resolution spectra of solid or liquid state samples).
4 CH stretching overtones
In this section we describe the extension of the algebraic Hamiltonian operator to the first CH stretching overtone region. To our knowledge, there exists only one paper devoted to this problem.10 In that work, the infrared spectra of liquid and solid samples of three n-alkane molecules (n
= 4, 5, 7) are measured and analyzed in terms of a simple force-field method which includes Fermi resonances but does not account for terminal CH3 groups. The agreement between computed and observed spectra is far from being a satisfying one and several arbitrary assumptions are introduced in the model, mainly concerning how combination bands and their intensities affect this energy region.
In the present work we show that the Hamiltonian operator optimized for describing the v
= 1 CH stretching region is still applicable to reproduce in a quantitative way the v
= 2 region at least in case of liquid samples. The extension to the overtone region is relatively straightforward since the algebraic formulation contains the vibrational anharmonicity from the beginning (its value is determined and fixed in terms of the vibron number, N
= 43 for CH stretches13,14). Moreover, we show that with the inclusion of a relatively weak anharmonic coupling with combination/overtone of CH bends, the agreement becomes even more persuasive. As discussed in ref. 12 for bending modes, the Hamiltonian operator of n-alkanes in the v
= 2 space of CH stretching vibrations leads also to (n
− 2)(2n
− 3) CH2 modes whose dispersion laws, induced by intersite couplings, can be written in close analytical form within the algebraic framework. Here, we also include CH3 stretches which, in the v
= 2 space, lead to 21 further vibrations and to 12(n
− 2) mixed CH2/CH3 modes. The origin of such polyads of levels is understood in terms of local excitations whose quantum numbers are (…20…) and (…11…), respectively. In the n-butane molecule, for example, CH3 overtone/combination bands are classified according to local modes with quantum numbers (200;vavbvcvd;000), (020;vavbvcvd;000), … , (000;vavbvcvd;002), a total of six, and (110;vavbvcvd;000), (101;vavbvcvd;000), … , (000;vavbvcvd;011), a total of fifteen, in which (vavbvcvd) are local labels for vibrations of the two CH2 units. One thus discovers that in the n-heptane molecule, for example, the v
= 2 CH stretching space is populated by 136 states, of which 21 are CH3 pure vibrations, 55 are CH2 modes and 60 CH2/CH3 combinations. Such modes are distributed in energy according to a pattern in which CH stretches span an interval of about 300 cm−1 in which CH2 and CH3 modes are all present even if with increasing n the latter are less and less important than the former.
We have computed energies and infrared intensities of CH stretches in this region preserving the v
= 1 Hamiltonian. Yet, we find that infrared intensities, to reproduce the observed data with reasonable accuracy, cannot rely only on the simple dipole operator adopted in the fundamental region.12 In our opinion, experimental data show quite clearly that both (20) and (11)-type vibrations give a comparable, non-negligible contribution to the infrared spectra. According to settled procedures of algebraic electric dipole definition,14,15
(10) and (20)-type excitations differ in their infrared activity (vs. the ground state) because the associated electric dipole expectation values are given by exp(−β) and exp(−2β), respectively (β is the slope parameter of eqn. (5)). However, within this same framework, (11)-type excitations have zero infrared activity. Here we suggest that it is necessary to modify the dipole operator in order to account for active transitions involving the “collective”
(11)-type excitation of CH2 sites. In a similar way, we propose that (11)-type excitations involving the terminal CH3 sites also lead to non-zero contributions to the infrared spectrum. More specifically, (11) excitations induce a dipole variation along the axis perpendicular to the “heavy” molecular axis (parallel to the CC skeletal axis) and belonging to the plane which contains the CC chain itself. We are thus left with an extended algebraic operator which depends on two new, arbitrary parameters, κ and ξ, related to (11) excitations for CH2 and CH3 sites. The final form of the electric dipole operator can then be written as
| | 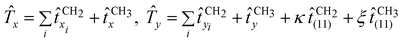 | (6) |
where the sums extend to the Cartesian components of CH
2 dipoles and
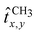
refer to end-effect dipole operators, see again
ref. 12. With a calibration of the parameters
κ and
ξ
(made through a direct, manual adjustment looking at the experimental results), we obtain that the computed spectra of
n-alkanes in the
v
= 2 region are in fair agreement with observed data for liquid samples of such molecular chains. Yet, we find that some minor features are not reproduced convincingly well. Following the general ideas discussed in
ref. 12 related to the construction of an algebraic version of 1 ∶ 2 anharmonic interactions, we have introduced in the present computation CH bending overtones (CH
B) according to the coupling tier
| | | CHS
(v
= 2)
∼ CHS
(v
= 1)
+ CHB
(v
= 2). | (7) |
The details of such a computation will be presented in a longer paper. Here, we limit ourselves to observe that, for example, in
n-heptane the computation involves about 1500 vibrational states in addition to the 105 CH stretching overtones. The Hamiltonian operator used to compute bending overtones is based on the algebraic parameters listed in
Table 2. The anharmonic interaction added to the Hamiltonian operator of the studied
n-alkanes (
n
= 4, 5, 7) has a fixed strength of 14 cm
−1. It is based on a direct mechanism of energy exchange between adjacent stretching and bending excitations within a given CH
2 site as already suggested in
ref. 12. More specifically, we introduce the anharmonic, resonant interaction
à la Fermi given by
| | 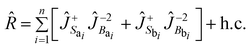 | (8) |
where we make use of pseudospin operators
Ĵk(±) which create/destroy one anharmonic vibrational quantum in the local mode
k15
(subscripts
S,
B refer to stretches and bends, respectively). The strength of the operator
R has been adjusted by hand once again through direct comparison with
experimental data.
Table 2 Parameters of the algebraic Hamiltonian operator used to compute CH bends (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in n-alkanes for including anharmonic 1 ∶ 2 resonant terms in the stretching Hamiltonian operatora
2) in n-alkanes for including anharmonic 1 ∶ 2 resonant terms in the stretching Hamiltonian operatora
| Term |
Parameter value |
|
In this operator, second-neighbour terms (sd, sc) are included as required by the different nature of bending modes in comparison to stretching ones. All values in cm−1 except N, which is dimensionless.
|
|
N
|
180 |
|
a
|
1120.00 |
|
λ
|
350.00 |
|
f
d
|
−20.00 |
|
f
c
|
15.00 |
|
s
d
|
5.00 |
|
s
c
|
−10.00 |
|
a
CH3
|
1450.00 |
|
λ
βγ
|
30.00 |
|
λ
α
|
300.00 |
|
f
t
|
0.01 |
|
f
bd
|
0.01 |
|
f
bc
|
0.01 |
The final results of our computations are shown in Fig. 3, in which one observes a secondary, non-negligible peak located at about 5850 cm−1 associated with resonating stretch/bend modes. The leading peaks are correctly located in terms of both energy positions and infrared intensity ratios. In particular, we discover that the most intense infrared transition (∼5830 cm−1) is an (11)-type CH2 vibration, while at lower energy (∼5650 cm−1) one finds (20)-type CH2 modes. CH3 modes give contributions at ∼5700 and ∼5900 cm−1 with dominant (20) and (11) characters, respectively. A less intense, broader maximum at 5500 cm−1 appearing in the experimental spectra is not reproduced in our model. It could be related to intramolecular couplings affecting the liquid state dynamics. Yet, more complex anharmonic interactions other than the 1 ∶ 2 coupling considered here could at least partly explain such smaller peaks. We defer such an analysis to a forthcoming publication devoted to IVR mechanisms in these kinds of molecules. The values of the new (11) excitation terms of the dipole operator introduced in this work are κ
= 0.42 (CH2 modes) and ξ
= 1.00 (CH3 modes) in arbitrary units such that the maximum computed peak height is equal to the observed one.
 |
| | Fig. 3 Comparison between computed (continuous line) and observed (crosses, ref. 10) infrared intensities of n-alkane molecules (n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) = =![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 5, 7) in the first overtone CH stretching region. Stick spectra are also shown as vertical segments (continuous: CH2 modes, dashed: CH3 modes). Continuous curves are computed by constructing Lorentzian shapes, FWHM = 30 cm−1. The normalization adopted takes the maximum experimental and computed values as equal quantities. 4, 5, 7) in the first overtone CH stretching region. Stick spectra are also shown as vertical segments (continuous: CH2 modes, dashed: CH3 modes). Continuous curves are computed by constructing Lorentzian shapes, FWHM = 30 cm−1. The normalization adopted takes the maximum experimental and computed values as equal quantities. | |
5 Conclusion
In this paper we have applied the one-dimensional algebraic model to n-alkane molecules. The Hamiltonian operator for CH stretches has been used to compute their energies and infrared transition intensities. The computation has been done for both fundamental (v
= 1) and first overtone (v
= 2) regions. The algebraic parameters have been adapted to reproduce the fundamental CH modes of gaseous n-alkanes (n
= 4, …, 11). Without further adaptation of parameters, the same Hamiltonian has been used to compute the first overtone region. We have compared such calculations with the only available experimental data for liquid n-alkanes (n
= 4, 5, 7). By introducing an extended form of the algebraic dipole operator including a new, specific contribution for collective (11) modes in a given CH2/CH3 unit, we find that the most important features of the infrared spectra are for the first time well reproduced. We also find that it is possible to further improve the overall agreement between computed and observed data, as well as to better describe some smaller features, by adding a 1 ∶ 2 anharmonic coupling involving overtone/combination modes of CH bending/stretching modes.
We think that these results, besides providing a solid and complete realization of the algebraic model to a non-trivial class of molecules of practical and current interest, also give a new, direct, essential description of an intriguing process involving a complex vibrational dynamics. The Hamiltonian and dipole operators presented and discussed in this work will be extended to obtain detailed information on the general behaviour of longer chains (eventually polymers) including sites other than methylene groups. We also hope that this work will stimulate new research on infrared spectroscopy of gaseous n-alkanes in their first and higher CH stretching overtone regions.
Acknowledgements
We thank F. Iachello for useful discussions during the development of this work.
References
- R. G. Snyder, J. Mol. Spectrosc., 1960, 4, 411 CrossRef CAS.
- R. G. Snyder, J. Mol. Spectrosc., 1961, 7, 116 CrossRef CAS.
- J. H. Schachtschneider and R. G. Snyder, Spectrochim. Acta, 1963, 19, 117 CrossRef CAS.
- R. G. Snyder and J. R. Scherer, J. Chem. Phys., 1979, 71, 3221 CrossRef CAS.
- R. G. Snyder, H. L. Strauss and C. A. Elliger, J. Phys. Chem., 1982, 86, 5145 CrossRef CAS.
- L. Ricard, S. Abbate and G. Zerbi, J. Phys. Chem., 1985, 89, 4793 CrossRef CAS.
-
G. Zerbi and M. Del Zoppo, in Modern Polymer Spectroscopy, ed. G. Zerbi, Wiley-VCH, Weinheim, 1999 Search PubMed.
- R. G. Snyder, S. L. Hsu and S. Krimm, Spectrochim. Acta, 1978, 34A, 395 CrossRef.
- S. Abbate, G. Zerbi and S. L. Wunder, J. Phys. Chem., 1982, 86, 3140 CrossRef CAS.
- L. Ricard-Lespade, G. Longhi and S. Abbate, Chem. Phys., 1990, 142, 245 CrossRef CAS.
- F. Iachello and P. Truini, Ann. Phys. (NY), 1999, 276, 120 Search PubMed.
- T. Marinković and S. Oss, PhysChemComm, 2002, 5, 66 RSC.
- F. Iachello and S. Oss, Phys. Rev. Lett., 1991, 66, 2976 CrossRef CAS.
-
F. Iachello and R. D. Levine, Algebraic Theory of Molecules, Oxford University Press, Oxford, 1994 Search PubMed.
- S. Oss, Adv. Chem. Phys., 1996, XCIII, 455.
-
NIST Standard Reference Data Program, Collection (C), © US Secretary of Commerce on behalf of the USA, CAS Registry no. 106-97-8, 109-66-0, 142-82-5, 2001 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2003 |
Click here to see how this site uses Cookies. View our privacy policy here. ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ⊃
⊃![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O(2)〉.13 The corresponding energies are obtained in terms of the expectation values of the invariant (Casimir) operator of the subgroup O(2), i.e. in terms of the Hamiltonian operator
O(2)〉.13 The corresponding energies are obtained in terms of the expectation values of the invariant (Casimir) operator of the subgroup O(2), i.e. in terms of the Hamiltonian operator![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) hk|νh,νk〉
=
[νk(νh
+ 1)(N
−
νh)(N
−
νh
+ 1)]1/2/N
hk|νh,νk〉
=
[νk(νh
+ 1)(N
−
νh)(N
−
νh
+ 1)]1/2/N
![[T with combining circumflex]](https://www.rsc.org/images/entities/i_char_0054_0302.gif) k|0〉
≅
tke−βνk,
k|0〉
≅
tke−βνk,

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and v
1 and v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in n-alkanesa
2) in n-alkanesa
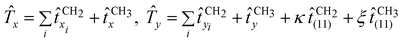
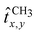 refer to end-effect dipole operators, see again ref. 12. With a calibration of the parameters κ and ξ
(made through a direct, manual adjustment looking at the experimental results), we obtain that the computed spectra of n-alkanes in the v
= 2 region are in fair agreement with observed data for liquid samples of such molecular chains. Yet, we find that some minor features are not reproduced convincingly well. Following the general ideas discussed in ref. 12 related to the construction of an algebraic version of 1 ∶ 2 anharmonic interactions, we have introduced in the present computation CH bending overtones (CHB) according to the coupling tier
refer to end-effect dipole operators, see again ref. 12. With a calibration of the parameters κ and ξ
(made through a direct, manual adjustment looking at the experimental results), we obtain that the computed spectra of n-alkanes in the v
= 2 region are in fair agreement with observed data for liquid samples of such molecular chains. Yet, we find that some minor features are not reproduced convincingly well. Following the general ideas discussed in ref. 12 related to the construction of an algebraic version of 1 ∶ 2 anharmonic interactions, we have introduced in the present computation CH bending overtones (CHB) according to the coupling tier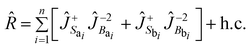
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in n-alkanes for including anharmonic 1 ∶ 2 resonant terms in the stretching Hamiltonian operatora
2) in n-alkanes for including anharmonic 1 ∶ 2 resonant terms in the stretching Hamiltonian operatora

![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) =
=![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 5, 7) in the first overtone CH stretching region. Stick spectra are also shown as vertical segments (continuous: CH2 modes, dashed: CH3 modes). Continuous curves are computed by constructing Lorentzian shapes, FWHM = 30 cm−1. The normalization adopted takes the maximum experimental and computed values as equal quantities.
4, 5, 7) in the first overtone CH stretching region. Stick spectra are also shown as vertical segments (continuous: CH2 modes, dashed: CH3 modes). Continuous curves are computed by constructing Lorentzian shapes, FWHM = 30 cm−1. The normalization adopted takes the maximum experimental and computed values as equal quantities.