Quantum dynamical characterization of unimolecular resonances
Hong
Zhang
and
Sean C.
Smith
*
Centre for Computational Molecular Science, Chemistry Building 68, The University of Queensland, Qld 4072, Brisbane, Australia. E-mail: s.smith@uq.edu.au
First published on 20928th February 2003
Abstract
We give a selective review of quantum mechanical methods for calculating and characterizing resonances in small molecular systems, with an emphasis on recent progress in Chebyshev and Lanczos iterative methods. Two archetypal molecular systems are discussed: isolated resonances in HCO, which exhibit regular mode and state specificity, and overlapping resonances in strongly bound HO2, which exhibit irregular and chaotic behavior. Future directions in this field are also discussed.
1 Introduction
Resonances are temporarily trapped meta-stable states—the analogue of bound vibrational states in the continuum part of the molecular spectrum. Resonances can be formed by bound-free excitations or by collisions between reactants, hence they are manifested in both unimolecular reactions and bimolecular complex-forming reactions. Unless stabilized by collisional relaxation or spontaneous infrared emission, they will decay into products on a finite time scale that is characterized by their lifetime. In essence, resonances are quantum mechanical phenomenon because they occur at discrete energies (resonance positions), but unlike bound states they have a finite width (resonance width).Though the phenomenon of resonances has long been recognized and qualitatively understood, the quantitative determination of resonances started to appear only during past two decades. Such quantitative studies are presently limited mostly to triatomic systems. Conceptually, there are two basic approaches to determining resonance energies and widths via computation. The first approach formulates the resonance problem in terms of an eigenvalue/eigenvector calculation, and has many affinities to bound-state calculations. In this approach, the resonance positions and widths are determined as the real and imaginary parts of complex eigenvalues associated with the Hamiltonian under dissipative boundary conditions. The dissipative boundary conditions can be imposed in a number of ways, principal among them being the use of a complex absorbing potential (CAP), e.g.ref. 1, a complex scaled Hamiltonian, e.g.ref. 2, or an incrementally damped matrix recursion, e.g.ref. 3. The second approach is a scattering one which relies on the calculation of the scattering S matrix.4–6 Resonance states are associated with the complex poles of the S matrix and thus all S matrix related quantities such as the lifetime matrix or scattering probabilities will reflect the resonance structures in their energy-dependent profiles. Analysis of such profiles can enable the determination of resonance energies as well as widths.
A third quantity which is characteristic of a resonance is the product state distributions arising from its decay. The energy of a resonance is essentially determined by the potential energy surface (PES) in the inner region, while its width depends on the coupling between the inner region and the exit channel. The product state distributions reflect scattering from the resonance into product states through the transition state region of the PES, and thus contain additional clues about the intra- and inter-molecular dynamics of the system. To specify product state distributions arising from resonance decay, the resonance eigenfunctions of the dissipative Hamiltonian must be calculated and analyzed for their amplitudes in different product channels. For the case of a bimolecular complex-forming reaction, the scattering waves associated with specific incoming reactant channels must be computed and analyzed in the asymptotic region to extract information about product state distributions. These product state distributions may comprise of contributions from one or more (overlapping) resonances which are accessed at the given scattering energy, together with possible direct scattering components. In order to fully characterize the reaction dynamics, it is necessary to consider resonance energies, widths and product state distributions for as many resonances as possible.
In recent years, quantum calculations based on iterative methods have become increasingly common. These methods have better scaling properties than direct methods because they do not require explicit storage of the Hamiltonian matrix, rather only the multiplication of the Hamiltonian onto a vector. When combined with a sparse representation of the Hamiltonian such as a discrete variable representation (DVR),7 both memory and CPU time can be reduced dramatically. In this perspective we will focus on an overview of the application of such iterative methods, highlighting in particular two of the most promising approaches: Chebyshev methods, e.g.ref. 8–12, and Lanczos methods, e.g.ref. 13–19. Other quantum methods2,5,6,20 based on direct matrix diagonalisation techniques have also continued to develop. Due to limited space, we shall only summarise such approaches briefly. We choose two molecular systems which are dynamically quite different for illustration of the type of information that can be obtained from such detailed computations: the HCO molecule, e.g.ref. 4, 21–23, and the HO2 molecule, e.g.ref. 3, 6, 15–18 and 24. Not all related references have been listed here, see ref. 25 and 26 for more references for HCO. The HCO molecule represents essentially a regular system, whereas HO2 represents essentially a chaotic system. Most resonances for HCO are isolated and can be assigned normal mode or local mode labels. In contrast, most resonances in HO2 are overlapping and defy spectroscopic assignment. Although the quantum fluctuations appear for both systems, the underlying mechanisms are quite different.
Advances in this topic have been in large part due to interplay between experiments and theories. In recent years tremendous progress has been made in detecting resonances in the fully state resolved level for both unimolecular dissociation and bimolecular reactions. Excellent reviews of the experimental studies in this field have appeared, e.g.ref. 27–29, and we limit ourselves here to quantum theoretical investigations. Additionally, we refer the curious reader to several excellent related theoretical reviews on this topic, e.g.ref. 26, 30 and 31. This review is arranged as follows: in Section 2 we describe advances in quantum iterative methods. The two case studies are discussed in Section 3, emphasizing the underlying resonance mechanisms that govern the observables. A summary with outlook to possible future developments is provided in Section 4.
2 Theoretical methods
In the context of the iterative methods which we review in this perspective, it is appropriate identify two general approaches which have been found useful for obtaining stable representations of the Hamiltonian [or equivalently the causal Green operator G+(E)] under scattering boundary conditions (see, e.g.ref. 1 and 32). The first involves the incorporation into the Hamiltonian of a (negative imaginary) complex absorbing potential (CAP). The resulting augmented Hamiltonian operator can then be stably represented in terms of a real basis (e.g., a discrete variable grid representation), yielding a complex-symmetric matrix. This approach has many affinities to earlier complex scaling methods. The second general approach involves representation of the real Hamiltonian in terms of a complex basis which satisfies the outgoing-wave scattering boundary conditions, which again leads to a complex-symmetric matrix representation. The two classes of iterative techniques which we review below are, respectively, illustrations of these two general approaches to incorporation of the scattering boundary conditions. The most important contribution of the developments in iterative matrix scattering methods is the ability to implement the essential physics within the context of an efficient low-storage algorithm with scaling properties superior to conventional direct matrix methods.The “direct” approach to computing quantum resonances involves solving the homogeneous time-independent Schrödinger equation
| (E − H′)ψE = 0. | (1) |
If the process of interest is a bimolecular complex-forming reaction, then one can solve the wavepacket-Lippmann–Schwinger equation9 and obtain resonance information by characterizing the poles of the S matrix,
 | (2) |
2.1 Lanczos subspace method
We begin with the complex-symmetric Lanczos methods which involve the CAP-augmented Hamiltonian. The Lanczos diagonalisation method34,35 has a long history of use for the calculation of eigenvalues in physics, chemistry, engineering and indeed almost every applied field one can imagine. It is a powerful iterative method for computing eigenvalues and eigenvectors of large matrices (real symmetric, Hermitian or complex symmetric). From a seed vector it generates using a three-term matrix-vector recursion a sequence of states which yield a tridiagonal representation of the original matrix. Its attractive scaling properties stem from the fact that typically just three recursion vectors need be kept in core memory at any one time, and the resulting tridiagonal matrix can be easily diagonalized to yield a spectrum which will contain both converged, unconverged and some spurious or ghost eigenvalues. The tridiagonal representation of the original matrix can also be utilized to iteratively solve linear systems, leading to Lanczos-based iterative linear system solvers such as MINRES36 or QMR37 which can be applied to the solution of eqn. (2). Conventionally, if physically-relevant information such as scattering amplitudes or product state distributions need to be obtained from analysis of the eigenvectors (or linear system solutions), then these need to be computed explicitly in the original DVR representation so that the analysis can be carried out. Recently, however, several advances have been made in application of the Lanczos iteration methods which obviate the need to compute explicit solutions in the primary representation, thus greatly enhancing the flexibility and applicability of the Lanczos approach. These developments include Lanczos-based filter diagonalisation, e.g.ref. 15, 17, for the calculation of real or complex eigenvalues; implicit product state distribution analysis of resonance eigenfunctions;18,38 and quasi-minimum residual (QMR) solution of the subspace time-independent (TI) wavepacket-Lippmann–Schwinger eqn. (2) to obtain reactive scattering probabilities for arbitrary scattering energies.19,39 We summarize these new theoretical developments below.(i) Choose a normalised, randomly generated initial vector v1 ≠ 0 and set β1, v0 = 0. Then use the 3-term Lanczos algorithm for complex-symmetric matrices
| βk+1vk+1 = H′vk − αkvk − βkvk−1 | (3) |
(ii) For all j = 1, 2, … , jmax, generate filtered states ϕ(Ej) by solving the homogeneous linear system
 | (4) |
(a) Choose ϕM, the Mth element of ϕ(Ej), to be arbitrary (but non-zero; usually set ϕM = 1), and calculate
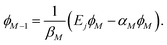 | (5) |
(b) For k = M − 1, M − 2, …, 2, update scalar ϕk−1:
| βkϕk−1 = Ejϕk − αkϕk − βk+1ϕk+1. | (6) |
(iii) Construct the overlap matrix with elements Sjj′ = (ϕ(Ej)|ϕ(Ej′)) and subspace Hamiltonian matrix with elements Wjj′ = (ϕ(Ej)|TM|ϕ(Ej′)). Note that Wjj′ can be calculated using a three-term summation:
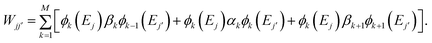 | (7) |
(iv) Solve the generalised complex-symmetric eigenvalue problem WB = SBε to obtain the complex energies, {ε}.
(v) Span the energy domain by repeating (ii)–(iv) window by window.
To check the convergence of the eigenvalues as well as the quality of the eigenpairs generated by the above iterative methods, one can typically compute the error norm about the eigenenergy E,
 | (8) |
One starts with the observation that the wave functions can be transformed between the primary representation and the tri-diagonal Lanczos representation through:
| ζ(ER) = VTψER | (9) |
 | (10) |
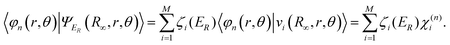 | (11) |
 | (12) |
| (E − TM)|ϕ(E)〉 = e1 . | (13) |
 | (14) |
![[t with combining tilde]](https://www.rsc.org/images/entities/i_char_0074_0303.gif) M+1
=
QM+1e1 need to be stored. The subspace scattering wavefunction is obtained via:
M+1
=
QM+1e1 need to be stored. The subspace scattering wavefunction is obtained via: | (15) |
Since the Lanczos subspace is independent of a constant energy shift, E, we are able to solve the linear system in eqn. (13) and obtain the desired subspace scattering wave functions for arbitrary E from a single Lanczos recursion.41 Once again, in a manner similar to that outlined for product state distribution analysis in the previous section, all the overlap integrals necessary for subsequent scattering amplitude analysis can be easily accumulated as the Lanczos recursion progresses. This implies that the scattering wave solutions to eqn. (2) need not be computed explicitly but rather just their subspace analogues from eqn. (13).
2.2 Real Chebyshev recursion methods
The Chebyshev iteration method was first introduced into the reaction dynamics calculations by Tal-Ezer and Kosloff8 to expand the evolution operator exp(−iĤt/ħ). Subsequently, Kouri and co-workers9 derived a new time-independent (TI) wavepacket-Lippmann–Schwinger equation and presented Chebyshev expansion expressions for both the Green operator and the Dirac delta function. Mandelshtam and Taylor3 introduced a real damping scheme into the Chebyshev recursion, which made the real algorithms possible for dissipative systems. The real Chebychev propagation method can be viewed in an alternative way as a modification of the time-dependent Schrödinger equation. In this respect, two related (discrete/continuous time) forms of the modified equations have been proposed by Chen and Guo42 and more generally by Gray and Balint-Kurti.12 Real Chebyshev recursion methods have grown rapidly in recent years, and have been successfully applied to different fields such as bound or resonance states calculations, e.g.ref. 10, reactive scattering, e.g.ref. 43, and surface scattering, e.g.ref. 44.The basic Chebyshev iteration is also a three-term recursion:
 | (16) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) )/ΔH with
)/ΔH with ![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) = 0.5(Hmax
+
Hmin), and ΔH
= 0.5(Hmax
−
Hmin). Φ(0) is an initial wavepacket, and e−
= 0.5(Hmax
+
Hmin), and ΔH
= 0.5(Hmax
−
Hmin). Φ(0) is an initial wavepacket, and e−![[r with combining circumflex]](https://www.rsc.org/images/entities/i_char_0072_0302.gif) is a damping operator. As will become apparent below, relevant information such as resonance energies, widths, product state distributions or other scattering probabilities can be extracted from either autocorrelation functions cn
=
(ξŷ0,ξŷn) or correlation functions
is a damping operator. As will become apparent below, relevant information such as resonance energies, widths, product state distributions or other scattering probabilities can be extracted from either autocorrelation functions cn
=
(ξŷ0,ξŷn) or correlation functions  , which can be accumulated during the Chebyshev recursion.
, which can be accumulated during the Chebyshev recursion.
 | (17) |
![[H with combining macron]](https://www.rsc.org/images/entities/i_char_0048_0304.gif) )/ΔH. Time-dependent and time-independent derivations about ψ(E) do exist, but the final expressions of ψ(E) are the same48
(see the following part for more details). Like the time-independent Lanczos subspace method, we can arrive at a similar expression for product state distributions in terms of overlapping integrals after obtaining the resonance wave functions.18 Thus, analogous to the Lanczos algorithm described above, a single sequence of Chebyshev iterations allows us to calculate both energies and product state distributions for different resonances. The difference between the Chebyshev and Lanczos methods is that the coefficient in ψ(E) is analytical in the former case, thus there is no need to solve a linear system as we do for the Lanczos method.
)/ΔH. Time-dependent and time-independent derivations about ψ(E) do exist, but the final expressions of ψ(E) are the same48
(see the following part for more details). Like the time-independent Lanczos subspace method, we can arrive at a similar expression for product state distributions in terms of overlapping integrals after obtaining the resonance wave functions.18 Thus, analogous to the Lanczos algorithm described above, a single sequence of Chebyshev iterations allows us to calculate both energies and product state distributions for different resonances. The difference between the Chebyshev and Lanczos methods is that the coefficient in ψ(E) is analytical in the former case, thus there is no need to solve a linear system as we do for the Lanczos method.
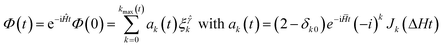 . Here Jk is the Bessel function. The energy-domain wave function can be obtained by a partial Fourier-transformation of the TD wave function Φ(t), which is indeed eqn. (17). In a novel time-dependent framework,12 a modified time-dependent Schrödinger equation is utilised to propagate the real part of the wavepacket
. Here Jk is the Bessel function. The energy-domain wave function can be obtained by a partial Fourier-transformation of the TD wave function Φ(t), which is indeed eqn. (17). In a novel time-dependent framework,12 a modified time-dependent Schrödinger equation is utilised to propagate the real part of the wavepacket | (18) |
 , the real part of the wavepacket Re(Φ′(t))
= Re(Φ′(kτ))
=
ξŷk can be propagated as a damped Chebyshev iteration. Thus, by performing Fourier transformation of the real part of Φ′(t) and changing the variable from the angle domain to the energy domain, one can again obtain the same energy-dependent wave function as in eqn. (17). In the time-independent framework, one can use Chebyshev polynomials to expand the Green operator
, the real part of the wavepacket Re(Φ′(t))
= Re(Φ′(kτ))
=
ξŷk can be propagated as a damped Chebyshev iteration. Thus, by performing Fourier transformation of the real part of Φ′(t) and changing the variable from the angle domain to the energy domain, one can again obtain the same energy-dependent wave function as in eqn. (17). In the time-independent framework, one can use Chebyshev polynomials to expand the Green operator  , where the expansion coefficient is
, where the expansion coefficient is  . Since energy domain wave function is related to the Green operator via
. Since energy domain wave function is related to the Green operator via , once again we are leading to eqn. (17).
, once again we are leading to eqn. (17).
Over the past few years, the applications of real Chebyshev methods into reactive scattering have grown rapidly. For example, Neuhauser et al. combine their FD scheme with damped real Chebyshev algorithm, and extend the real Chebyshev method into molecule-surface scattering.44 Gray et al. derived the S matrix formulation from real wavepacket propagation12 and applied the approach to more challenging systems such as H2 + O(1D), (see e.g.ref. 49). Smith et al.18,48 have recently compared different real Chebyshev versions and the Lanczos method for resonance calculations and scattering calculations. One of their conclusions is that the Chebyshev method can converge the broad outline of the scattering probabilities quickly, whereas the resolution of the individual resonances takes much longer. This indicates that real Chebyshev method is suitable for the large-scale nonzero total angular momentum calculations in reactive scattering for complex forming reactions, in which the fine structures of resonances are not so important to obtain experimental observables. Such J > 0 calculations have been reported recently for half state-resolved probabilities using exact real wavepacket methods, e.g.ref. 43, which require the repeated calculations for many J values. One can predict that exact J > 0 calculations including those at a fully state-resolved level using the real Chebyshev method will grow rapidly in the near future, though they are still very challenging with today's computational resources.
2.3 Related quantum methods
There are several other quantum mechanical methods which have been utilized to deal with resonances. While space does not permit us to discuss them in any detail, we mention in particular the modified version of the log-derivative Kohn's variational principle,6 and the truncation/recoupling method,20 which have been very effectively used for resonance calculations in recent years.3 Case studies
Case 1 HCO—a regular system
HCO is a relatively weakly bound molecule (dissociation energy 0.834 eV and dissociation threshold approximately 0.133 eV), with a low density of resonance states and weak intramolecular coupling. In this case the discrete level structure is important in the dissociation dynamics. There have been many experimental and theoretical studies on HCO, e.g.ref. 4, 21–23, and several review articles related to this molecule have appeared.26,29 The potential energy surfaces most studies used for this system are RLBH PES50 and WKS PES.21 The PES has a shallow well and a small barrier separates the inner region from the exit channel. Various quantum methods have been used for this molecule and the results may be summarized as follows:(i) Most of the resonances for HCO are isolated, and can be unambiguously assigned to three normal mode quantum numbers (ν1, ν2, ν3). Here v1, v2, and v3 represent the H–C stretch mode, the C–O stretch mode, and the bending mode, respectively. Only in some cases does strong coupling between two energetically close-lying zero-order states disturb this clear picture. The assignments can be done by analyzing the nodal structures of the resonance wave functions and several examples are given in Fig. 1 for illustration.51 The non-vanishing tails of the wave functions toward large values of the dissociation coordinate R are only visible in (e) and (f). The assignment is clear in (a)–(c) and (e). The wave function in (d) seems to follow a particular periodic classical orbit and the state in (f) seems to be unassignable.
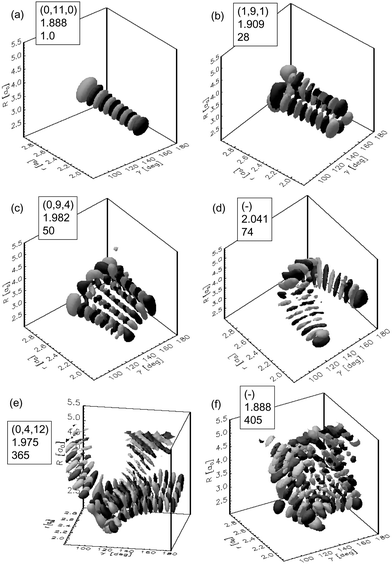 | ||
| Fig. 1 Typical resonance wave functions for HCO. The boxes show the assignments, the resonance positions in eV, and the linewidths in cm−1. Reproduced with permission of the American Institute of Physics from ref. 51. | ||
(ii) The resonance widths (rates) show particularly the striking dependence on the normal mode quantum numbers (ν1, ν2, ν3), i.e., the widths follow the pattern ΓCH > Γbend > ΓCO. Fig. 2 shows resonance widths for three progressions as a function of the CO stretching quantum number ν2.22 Resonances with pure excitation in the CO stretching mode (0, ν2, 0) have the smallest widths (the longest lifetime). This is due to the inefficient energy transfer from r to R, such that the system needs a long time before enough energy is accumulated in the dissociation coordinate to permit dissociation. The bending mode is more strongly coupled to R and addition of one or two quanta of the bending motion can significantly increase the widths. Excitation in R allows a rather rapid bond rupture, and therefore the resonances (ν1, 0, 0) have the largest widths (the shortest lifetimes). There is quite satisfactory agreement between the quantum results22 and the experimental ones.23
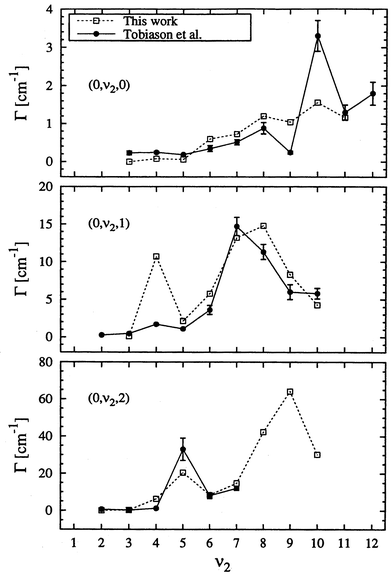 | ||
| Fig. 2 Resonance widths as a function of CO stretching quantum number for three progressions. Open squares are calculated results,22 while the full dots are measured ones.23 Reproduced with permission of the American Institute of Physics from ref. 22. | ||
(iii) The nascent product state distributions of CO also exhibit remarkable mode and state specificity. The CO rotational state distributions are non statistical and highly structured and depend sensitively on the modes excited and on the number of quanta in each mode. Each of the progressions yields distinct distributions. Fig. 3 shows several examples of the final state distributions of CO following the decay of some (0, ν2, 0) resonances.21 These distributions all look rather similar, having a bimodal shape, which reflects the similar shape of the corresponding (0, ν2, 0) resonance wave functions. In addition, the mode specificity is also shown in the nascent CO vibrational state distributions. For example, the vibrational state distributions from (0, ν2, 0) resonances are consistently inverted.21
 | ||
| Fig. 3 Final state distributions of CO following the decay of (0, ν2, 0) resonances with ν2 = 4–8. The vibrational state of CO is the state with the largest probability. Reproduced with permission of the American Institute of Physics from ref. 21. | ||
In summary, the unimolecular reaction of HCO is a clear, illustrative example of mode- and state-specific decomposition. HCO exhibits the isolated resonances that can be assigned normal or local mode labels. Thus the dissociation of HCO is essentially regular. For this system, experimental and theoretical results are in general agreement. This is one example of the great success of quantum mechanical calculations carried out on accurate PES, even at a state resolved level.
Case 2 HO2—an irregular system
Reactions in which a strongly-bound intermediate exists often support a large number of resonance states, and in this case the reaction dynamics can be completely controlled by resonance formation. Quantum dynamical modeling of such reactions is very challenging since large basis sets are needed to be able to represent the degree of vibrational excitation involved. One option available is to make recourse to theories such as Ramsperger–Rice–Kassel–Marcus (RRKM) theory, e.g.ref. 52, or phase space theory (PST), e.g.ref. 53, which invoke certain statistical approximations (rapid ergodic mixing, no recrossing of the transition state, etc.). Deep-well triatomic molecules such as HO2 provide a good opportunity to compare the statistical theories with fully quantum simulations. Here we choose HO2 as an example and present some computational results pertaining to its dissociation rates and product state distributions.The HO2 PES (e.g., DMBE IV54) has a considerably deeper potential well (De = 2.37 eV) than HCO and exhibits no pronounced potential barrier (i.e., no saddle point) during bond rupture. For this system, a meaningful assignment of the resonance states is impossible, and in fact the bound states close to the threshold are already irregular.55Fig. 4 depicts the resonance energies and rates calculated from both Lanczos and Chebyshev methods.18 Note that the rates are widths divided by ħ, and therefore are true unimolecular decay rates only for narrow isolated resonances. From Fig. 4 we see that resonance energies acquired via the two methods are in fairly sound agreement (i.e., 3 or 4 digits of relative accuracy). The resonance rates predicted by both methods agree within 20% of one another. This is because the absorbing boundary conditions are different for the two different methods, and the resonance widths are highly sensitive on the details of absorbing potential or damping function. Strictly speaking, a stabilisation procedure56 must be employed to determine more accurate resonance widths. Of course, such stabilisation calculations are still very challenging for large molecules. Analysis of the resonance widths shows that only at very low energies are these resonances are isolated. With increasing energy the resonances begin to overlap. The quantum rates (widths) show a large fluctuation, with the general tendency that the rates increase with energy. Just above threshold, the rates vary over three orders of magnitude, and then the extent of fluctuation decreases with increasing energy. This fluctuating behaviour has been predicted by other quantum calculations on the HO2 system, e.g.ref. 3, 6.
 | ||
| Fig. 4 Plot of the logarithmic resonance rates, log10(k), versus resonance energy in the energy range 0.09 to 0.47 eV. Circles represent the results from Lanczos subspace filter diagonalisation method and squares denote the results from Chebyshev low storage filter diagonalisation method. The unit of decay rate is s−1. Reproduced with permission of the American Institute of Physics from ref. 18. | ||
Fig. 5(a–d) shows the O2 rotational distributions for the ground vibrational state at different resonance energies.18 Firstly, the number of occupied rotational channels increases steadily with energy, which is simply the result of energy conservation. Secondly, the distributions show a very complicated oscillatory behaviour, with the number of oscillations generally increasing with energy. Thirdly, the fluctuations in the distributions seem to be random and unpredictable from resonance to resonance. The rotational state distributions of the fragments reflect the angular dependence of wavefunction at the translational state and the anisotropy of the PES in the exit channel. The rotational state distributions for the HO2 dissociation are complicated mainly due to the translational–rotational coupling being weak but not negligible. The distributions cannot, therefore, be explained by a simple model such as the Franck–Condon mapping picture or the rotational reflection principle.57 The vibrational distributions also fluctuate from resonance to resonance,18 as can be expected from the rotational state distributions. The general trend is that the ratio increases with energy, approaching unity for the highest resonance energies. For all but several resonances, no population inversion was achieved.
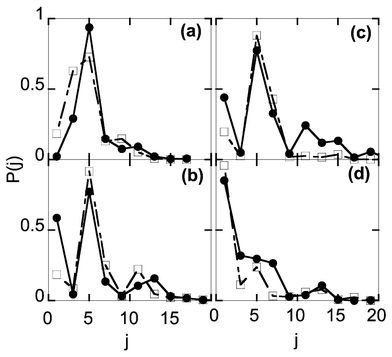 | ||
| Fig. 5 The O2 (ν = 0) rotational distributions, at E = (a) 0.154; (b) 0.252; (c) 0.264; and (d) 0.362 eV. Symbols are the same as Fig. 4. All distributions are normalised. Reproduced with permission of the American Institute of Physics from ref. 18. | ||
Whether or not the statistical theories correctly predict the average rates is a question at the heart of unimolecular dissociation. For this system, the decay rates, on average, can be well described by the statistical RRKM theories6 (recently, we compared quantum rates with PST for H2S dissociation and found reasonable agreement38). However, the fluctuations in the rates and product state distributions cannot be produced by the statistical theories. Those fluctuations are purely quantum effects due to the interference of the overlapping resonances. Experimentally, the fluctuations have been observed for NO2 system in individual NO product distributions as well as in the product vibrational distributions.58 Unfortunately, so far there are still no experimental data available for HO2 system. Thus direct comparisons with experiment for the HO2 dissociation are still not possible at this time.
Finally, we emphasize the differences of the fluctuation mechanisms in HCO and HO2 systems. For HO2, most resonances are overlapping ones and when resonances overlap, interferences will dominate. Thus, the wild fluctuations in the rates and in the product state distributions are a manifestation of prominent quantum interference effects between overlapping resonances. This is manifestly different from the mechanism of HCO fluctuations, for which mode-specificity is responsible. Fluctuations in HCO basically reflect systematically the different types of wave functions of resonance states with different normal or local mode labels. Due to the strong mode specificity, RRKM or PST (which assume rapid ergodic mixing after initial excitation) is seemingly inappropriate for a molecule such as HCO.59
Recently, the real Chebyshev recursion and the complex-symmetric Lanczos recursion have been applied to very challenging scattering calculations for complex-forming reactions. As we are primarily concerned with the unimolecular resonances in this review, we give just one example of state-to-state reaction probabilities for the complex forming reaction H + O2 → HO + O, which also show the signature of the complex resonance structure of the intermediate HO2. Fig. 6 depicts the state-to-state reactive probabilities associated with the ground O2 reactant state (ν0 = 0, j0 = 1) and ground OH product state (ν = 0, j = 0).19 Here the resonance energies are well above the unimolecular resonances discussed above. It is apparent that the reaction probabilities are dominated by resonances, most of them being overlapping ones. Analysis of some resonance widths indicates the lifetime of the resonances is of the order of picoseconds. These resonances are clear manifestations of the complex forming and decaying process, and differ from unimolecular resonances only by the way the energized complex is prepared. For more details, the reader is referred to ref. 19.
 | ||
| Fig. 6 The calculated state-to-state reactive probabilities for H + O2 (ν0 = 0, j0 = 1) → O + OH (ν = 0, j = 0) reaction from Lanczos subspace TI wavepacket method. Reproduced with permission of the American Institute of Physics from ref. 19. | ||
4 Concluding remarks
In recent years, resonances in unimolecular and bimolecular reactions have received much attention and tremendous progress has been made in our understanding of resonance-mediated processes at a quantum state-to-state level. Quantum iterative methods such as the Lanczos or Chebyshev recursions have become powerful tools in calculating and characterizing resonances at a detailed level. Such progress is due in part to the increasingly close interplay between experimental and theoretical investigations. So far the most well studied systems are molecules having low threshold energies and weak internal coupling. Resonances in such systems show striking mode and state specificity, which can only be understood by the detailed knowledge of the full PES and the dynamical behavior which governs the unimolecular dissociation in the exit channel. Quantum dynamical methods have proven a triumph in this respect, and statistical theories based on assumptions of rapid ergodic coupling between modes fail.For complex-forming reactions with a deep well, the overlapping resonances interfere and the resulting fluctuations dominate in rates and in the product state distributions. Statistical theories can predict average rates reasonably well, but have had limited success in capturing the detail of product state distributions. The agreement between theory and experiment has not reached the same level as for weakly bound systems: exact quantum methods are very time-consuming (especially when stabilizing the resonance widths) and the fine details of resonance structure prove quite sensitive to the parameters of the computation (basis set, iterative recursion, method of imposing absorbing boundary conditions, etc.). In light of this, one can make the observation that it will be very difficult to reproduce experimental data at the state-to-state level for such reactions. Going further, one could provocatively query the value of pursuing the theory at all, given that the numerics are clearly so very difficult. In reality, we are not so pessimistic! The fact that one can perform the quantum calculations and observe internally consistent properties and trends (even though the absolute accuracy may still be uncertain) is already an important advance. Even if theory and experiment are not gelling together quantitatively, there are many important issues which can be explored with both approaches.
For the future, there are a number of areas that require further investigation. The role of total angular momenta J > 0 is a major target, especially for bimolecular reactions. The role of IVR in the exit channel in determining the disposal of excess energy into the products is another active area of investigation. For the HCO system several exact or approximate J > 0 calculations60,61 have been performed and are used to rationalize discrepancies or agreement between experimental and theoretical results. For HO2, QCT calculations62 have inferred that rotational effects will play a significant role. However, while some initial-state-resolved J > 0 scattering calculations have been performed (e.g.ref. 43), no exact J > 0 resonance calculations have been available until very recently.63 In addition, iterative matrix methods have yet to be extended to deal with differential cross sections, a necessary step if the full richness of data from crossed beam experiments is to be modeled. Clearly, it will be important to develop more efficient computational algorithms if questions such as these are to be addressed for such challenging molecular systems.
Using unimolecular resonances to control chemical reactions is another intriguing direction for future investigation. By using intense coherent femtosecond pulses it is possible to excite resonances coherently. For most molecules the laser wave-length needed to reach the unimolecular dissociation limit is in the near-visible range, so it is more practical and economical to manipulate these resonances than to control the dynamics electronically excited states via UV radiation. The use of van der Waals resonances as precursors to a chemical reaction has been proposed several years ago,64 and we believe there is much to be done in this area.
Acknowledgements
We are grateful to the Australian Research Council for supporting this work (Discovery Project No. DP0211019). We thank Dr. Anthony Rasmussen and Dr. Hua-Gen Yu for helpful discussions.References
- D. Neuhauser and M. Baer, J. Chem. Phys., 1989, 90, 4351 CrossRef.
- N. Moiseyev, Phys. Rep., 1998, 302, 211 CrossRef.
- V. A. Mandelshtam, T. P. Grozdanov and H. S. Taylor, J. Chem. Phys., 1995, 103, 10074 CrossRef CAS.
- K. T. Lee and J. M. Bowman, J. Chem. Phys., 1986, 85, 6225 CrossRef CAS.
- H. W. Jang and J. C. Light, J. Chem. Phys., 1995, 102, 3262 CrossRef CAS.
- A. J. Dobbyn, M. Stumpf, H.-M. Keller and R. Schinke, J. Chem. Phys., 1996, 104, 8357 CrossRef CAS.
- J. C. Light, I. P. Hamilton and J. V. Lill, J. Chem. Phys., 1985, 82, 1400 CrossRef CAS.
- H. Tal-Ezer and R. Kosloff, J. Chem. Phys., 1984, 81, 3967 CrossRef CAS.
- D. J. Kouri, M. Arnold and D. K. Hoffman, Chem. Phys. Lett., 1993, 203, 166 CrossRef CAS.
- V. A. Mandelshtam and H. S. Taylor, J. Chem. Phys., 1997, 107, 6756 CrossRef CAS.
- R. Chen and H. Guo, J. Chem. Phys., 1999, 111, 464 CrossRef CAS.
- S. K. Gray and G. G. Balint-Kurti, J. Chem. Phys., 1998, 108, 950 CrossRef CAS.
- H. G. Yu and S. C. Smith, Chem. Phys. Lett., 1998, 283, 69 CrossRef CAS.
- H. G. Yu and S. C. Smith, Ber. Bunsen-Ges. Phys. Chem., 1997, 101, 400 CAS.
- H. G. Yu and S. C. Smith, J. Chem. Phys., 1997, 107, 9985 CrossRef CAS.
- S. C. Smith, H. G. Yu, C. Leforestier and J. C. Rayez, Phys. Chem. Chem. Phys., 1999, 1, 1311 RSC.
- H. Zhang and S. C. Smith, Phys. Chem. Chem. Phys., 2001, 3, 2282 RSC.
- H. Zhang and S. C. Smith, J. Chem. Phys., 2001, 115, 5751 CrossRef CAS.
- H. Zhang and S. C. Smith, J. Chem. Phys., 2002, 116, 2354 CrossRef CAS.
- S. Skokov, J. X. Qi, J. M. Bowman, C. Y. Yang, S. K. Gray, K. A. Peterson and V. A. Mandelshtam, J. Chem. Phys., 1998, 109, 10273 CrossRef CAS.
- H. J. Werner, C. Bauer, P. Rosmus, H. M. Keller, M. Stumpf and R. Schinke, J. Chem. Phys., 1995, 102, 3593 CrossRef CAS.
- H.-M. Keller, H. Floethmann, A. J. Dobbyn, R. Schinke, H.-J. Werner, C. Bauer and P. Rosmus, J. Chem. Phys., 1996, 105, 4983 CrossRef CAS.
- J. D. Tobiason, J. R. Dunlop and E. A. Rohlfing, J. Chem. Phys., 1995, 103, 1448 CrossRef CAS.
- B. Kendrick and R. T. Pack, Chem. Phys. Lett., 1995, 235, 291 CrossRef CAS.
- J. M. Bowman, J. Phys. Chem. A, 1998, 102, 3006 CrossRef CAS.
- R. Schinke, C. Beck, S. Y. Grebenshchikov and H. M. Keller, Ber. Bunsen-Ges. Phys. Chem., 1998, 102, 593 CAS.
- G. C. Schatz, Science, 2000, 288, 1599–1600 CrossRef CAS.
- K. Liu, Annu. Rev. Phys. Chem., 2001, 52, 139 CrossRef CAS.
- S. A. Reid and H. Reisler, Annu. Rev. Phys. Chem., 1996, 47, 495 CrossRef CAS.
- R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Blackwell Scientific Publishers, Oxford, 1990 Search PubMed.
- T. Baer and W. L. Hase, Unimolecular Reaction Dynamics: Theory and Experiments, Oxford University Press, New York, 1996 Search PubMed.
- W. H. Miller and B. M. D. D. Jansen op de Haar, J. Chem. Phys., 1987, 86, 6213 CrossRef CAS.
- M. R. Wall and D. Neuhauser, J. Chem. Phys., 1995, 102, 8011 CrossRef CAS.
- C. Lanczos, J. Res. Natl. Bur. Stand., 1950, 45, 255 Search PubMed.
- J. K. Cullum and R. A. Willoughby, Lanczos Algorithms for Large Symmetric Eigenvalue Computations, Birkhauser, Boston, 1985 Search PubMed.
- C. C. Paige and M. A. Saunders, SIAM J. Numer. Anal., 1975, 12, 617 Search PubMed.
- R. W. Freund, SIAM J. Sci. Stat. Comput., 1992, 13, 425 Search PubMed.
- H. Zhang and S. C. Smith, J. Phys. Chem. A, 2002, 106, 6129 CrossRef CAS.
- H. Zhang and S. C. Smith, J. Phys. Chem. A, 2002, 106, 6137 CrossRef CAS.
- A. J. Rasmussen, S. J. Jeffrey and S. C. Smith, Chem. Phys. Lett., 2001, 336, 149 CrossRef CAS.
- R. W. Freund, in Numerical Linear Algebra, ed. L. Reichel, A. Ruttan and R. S. Varga, De Gruyter, Berlin, 1993, pp. 101 Search PubMed.
- R. Chen and H. Guo, J. Chem. Phys., 1996, 105, 3569 CrossRef CAS.
- E. M. Goldfield and A. J. H. M. Meijer, J. Chem. Phys., 2000, 113, 11055 CrossRef CAS.
- D. A. McCormack, G.-J. Kroes and D. Neuhauser, J. Chem. Phys., 1998, 109, 5177 CrossRef CAS.
- J. W. Pang, T. Dieckmann, J. Feigon and D. Neuhauser, J. Chem. Phys., 1998, 108, 8360–8368 CrossRef CAS.
- H. Zhang and S. C. Smith, Chem. Phys. Lett., 2001, 347, 211 CrossRef CAS.
- D. Xie, R. Chen and H. Guo, J. Chem. Phys., 2000, 112, 5263 CrossRef CAS.
- H. Zhang and S. C. Smith, J. Chem. Phys., 2002, 117, 5174 CrossRef CAS.
- M. Hankel, G. G. Balint-Kurti and S. K. Gray, J. Phys. Chem. A, 2001, 105, 2330 CrossRef CAS.
- H. Romanowski, K.-T. Lee, J. M. Bowman and L. B. Harding, J. Chem. Phys., 1986, 84, 4888 CrossRef CAS.
- H.-M. Keller and R. Schinke, J. Chem. Phys., 1999, 110, 9887 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1952, 20, 359 CrossRef CAS.
- P. Pechukas and J. C. Light, J. Chem. Phys., 1965, 42, 3285 CrossRef CAS.
- M. R. Pastrana, L. A. M. Quintales, J. Brandao and A. J. C. Varandas, J. Phys. Chem., 1990, 94, 8073 CrossRef CAS.
- A. J. Dobbyn, M. Stumpf, H.-M. Keller and R. Schinke, J. Chem. Phys., 1995, 103, 9947 CrossRef CAS.
- A. U. Hazi and H. S. Taylor, Phys. Rev. A, 1970, 1, 1109 CrossRef.
- R. Schinke, Photodissociation Dynamics, Cambridge University Press, Cambridge, UK, 1993 Search PubMed.
- S. A. Reid and H. Reisler, J. Phys. Chem., 1996, 100, 474 CrossRef CAS.
- M. Stumpf, A. J. Dobbyn, D. H. Mordaunt, H.-M. Keller, H. Fluethmann and R. Schinke, Faraday Discuss., 1995, 102, 193 RSC.
- C.-Y. Yang and S. K. Gray, J. Chem. Phys., 1997, 107, 7773 CrossRef CAS.
- J. Qi and J. M. Bowman, J. Chem. Phys., 1996, 105, 9884 CrossRef CAS.
- J. M. C. Marques and A. J. C. Varandas, J. Phys. Chem. A, 1997, 101, 5168 CrossRef CAS.
- H. Zhang and S. C. Smith, J. Chem. Phys. 2003, submitted Search PubMed.
- G. Radhakrishnan, S. Buelow and C. Wittig, J. Chem. Phys., 1986, 84, 727–738 CrossRef.
| This journal is © The Royal Society of Chemistry 2003 |
