Intermittent dynamics and hyper-aging in dense colloidal gels

Abstract

We investigate the slow dynamics of strongly aggregated particle gels by diffusing wave spectroscopy (DWS) using a charge coupled device (CCD) camera as a multispeckle detector. The evolution of the slow dynamics after the gel-point is followed using two different techniques, the multispeckle method and a novel correlation scheme, time resolved correlation (TRC), which allows us to obtain time resolved information on the dynamics of the gel. We find that the intensity autocorrelation function measured by multispeckle DWS exhibits an ultraslow relaxation, whose characteristic time strongly depends on the age of the gel. An analysis of the TRC data reveals that the slow dynamics is intermittent. We propose that the intermittency is due to rare disruptions or formations of bonds affecting the elastic backbone of the network, which lead to sudden long range rearrangements of the particle position and thus to a sudden change of the speckle pattern.

---

Introduction

Slow dynamics and aging phenomena are characteristics shared by many disordered, metastable solids. As a system is quenched into a jammed state¹ the constituent of the system becomes kinetically trapped, precluding further exploration of phase space. Because of the non-equilibrium nature of this state, however, most systems tend to evolve after the quench, where this evolution sensitively depends on the quench depth and on the history of the sample. Although there has been considerable theoretical effort devoted to understanding the essential physics of aging in spin and structural glasses,^2–5 as well as in soft glassy materials,^6,7 the rather general phenomena of slow dynamics in jammed systems is still poorly understood. Experiments exploring the detailed dynamics of the constituent of a system are sparse;^8–12 however, they are essential to gain insight in the origin of slow relaxation processes.

Experimental

Colloidal gels are obtained by salt-induced aggregation of polystyrene (PS) particles of radius a = 85 nm, suspended in a buoyancy-matching mixture of H₂O and D₂O at a volume fraction ϕ = 0.045. In order to obtain homogeneous destabilization the ions are produced in situvia an enzymatic reaction.¹³ We set the final ionic strength to 310 mM, which is 3 times higher than the critical ionic strength required to fully screen the surface charge of the PS-particles. The critical ionic strength is reached after ∼200 s and the gel-point after ∼400 s, indicating a gradual change of the aggregation conditions from reaction limited to diffusion limited cluster aggregation.

The dynamics of particle gels are probed by diffusion wave spectroscopy (DWS).¹⁴ The measurements are performed in transmission with a setup similar to that described by Viasnoff et al.:¹⁵ a combination of the two-cell technique^16,17 and the multispeckle method¹⁸ is used to measure the intensity correlation function g₂(τ) for time delays spanning 13 decades, 10⁻⁸ < τ < 10⁵ s.

Results and discussion

The typical time evolution of the correlation function of an aging gel is shown in Fig. 1. With the onset of gelation,¹⁶ which we define as the sample age t_w = 0, the appearance of a second decay in the intensity correlation function is observed. This decay quickly develops as the sample ages and can be approximated by an exponential decay, as denoted by the solid lines in Fig. 1. The corresponding relaxation time, τ_exp, is shown in the inset of Fig 1 as a function of the sample age, t_w. For t_w < 5 × 10⁵ s the dependence of the final relaxation is well described by a power law of τ_exp ∼ t_w^μ, where we find μ = 1.37 ± 0.02. Similar aging behavior has been observed for other jammed materials, although the exponent is usually μ ≤ 1.^19–21 The aging exponent being larger than one indicates that the relaxation time would eventually exceed the sample age and thus, become undetectable. Instead we find that the final relaxation time eventually decreases again, which seems to indicate the complete collapse of the gel.

Fig. 1 Intensity autocorrelation functions as measured by DWS for a PS-gel at ϕ = 0.045. From bottom to top t_w = 500, 2000, 5300, 21300 s. The data obtained by the two-cell technique and by the multispeckle scheme are denoted as solid and open symbols, respectively. The solid lines correspond to exponential fits of the data at large lag times. The inset shows the age dependence of the corresponding relaxation time, where the different symbols correspond to different runs, albeit reflecting the good reproducibility of this experiment.

To gain insight in this intriguing aging behavior we develop a new scheme, which we term time resolved correlation (TRC).²² We use the CCD camera to take pictures of the speckle field scattered by the sample at regular time intervals. The degree of correlation, c_I(t_w,τ), between two images spaced by a lag time τ is then calculated as a function of t_w, where we define t_w as the sample age at which the first image was taken. The degree of correlation is calculated according to:

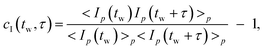where I_p(t_w) is the intensity measured at age t_w for the pth CCD pixel and <...>_p denotes the average over pixels. Note that in the traditional correlation scheme, g₂(τ) − 1 has a form similar to that of c_I(t_w,τ), except that the intensity fluctuations are measured for a single speckle (p = 1) and the pixel averaging is replaced by an extensive time average.

The age dependence of c_I(t_w,τ) is shown in Fig. 2 for different lag times. As a general trend, c_I(t_w,τ) grows with t_w at all lag-times before it catastrophically decreases at t_w ≥ 5 × 10⁵ s. The way the data is plotted may at first appear unusual, since we normally plot the degree of correlation as a function of lag time instead of t_w. Indeed, the lag time dependence of c_I(t_w,τ) at a given t_w can be obtained from a vertical cut through the data, which in principle enables us to generate a two point correlation function g₂(τ,t_w) − 1. Corresponding to the increase of the relaxation time shown in Fig. 1, we find in Fig. 2 that c_I(t_w,τ) becomes larger than zero for increasingly large delays as the sample ages. The increase of c_I(t_w,τ) at the smallest delay τ = 10 s corresponds to the growth of the intermediate plateau values of g₂(τ) − 1 in Fig 1 and reflects an increase of the rigidity of the gel.²³ The large drops observed at t_w ∼ 1.5 × 10⁵ s and t_w ≥ 5 × 10⁵ s thus correspond to the decrease of the relaxation time, which can be seen for large t_w in the inset of Fig 1.

Fig. 2 Evolution of the degree of correlation c_I(t_w,τ), measured by TRC, for different lag times. From top to bottom τ = 10¹, 10², 10³, 2 × 10³, 4 × 10³, 10⁴, 2 × 10⁴, 4 × 10⁴, 10⁵, 2 × 10⁵ s.

The TRC data, however, gives access to a more detailed view of the dynamics of a system. Remarkably, it reveals that the aging-process is not smooth and continuous, but rather results from a series of discrete rearrangement events as can be seen in magnified sections of the c_I(t_w,τ)-traces. An example of such a section is shown in the inset of Fig. 3(b). Contrary to the case of Brownian particles, which is shown in the inset of Fig. 3(a), the noise of c_I(t_w,τ) is not symmetric for the gel. We observe remarkable drops of the degree of correlation, which indicate that, from time to time, the particles undergo larger-than-usual movements; whenever such an anomalous motion occurs in the time lag between two images, the degree of correlation, c_I(t_w,τ), exhibits a sudden drop. This behavior is clearly reflected in the probability density function (PDF) of c_I(t_w,τ) shown in Fig. 3(b), which is markedly skewed towards smaller values of c_I(t_w,τ). By contrast, we expect and find a Gaussian PDF of c_I(t_w,τ), as shown in Fig. 3(a), in the case of smooth continuous motion of Brownian particles.

Fig. 3 Probability density function (PDF) of c_I(t_w,τ) for (a) Brownian particles at τ = 0.02 s and (b) the gel at τ = 1.6 s and 4.6 × 10³ < t_w < 1.5 × 10⁴ s. As denoted by the skewed distribution of c_I(t_w,τ), the dynamics of the gel is intermittent. The lag time dependence of the intensity correlation and that of the skewness are shown in (c) for the brownian particles and in (d) for the gel. While the skewness fluctuates around zero for the brownian particles, the skewness for the gel develops from strongly negative values towards zero as the lag time approaches the relaxation time, which is denoted as a dashed line.

To quantify the asymmetry of the PDF compared to a Gaussian PDF, we calculate the skewness s = m₃/m₂^3/2, where m_i is the ith moment of c_I(t_w,τ) with respect to its mean. We analyze the development of s as a function of τ and plot the result for both the Brownian particles and the particle-gel in Fig. 3(c) and (d), respectively. While the value of s fluctuates around zero for the Brownian particles, it is a strong function of the lag time for the particle-gel. At short lag we find s to be negative with only little dependence on τ, it then increases and reaches a value of zero as the lag time equals the relaxation time, which is denoted as a dashed line in Fig. 3(d).

We account for this behavior by considering the scenario of rare and sudden events determining the long time dynamics of our system. The events are spaced in time by T_e. For lag times below T_e the events are clearly resolved in c_I(t_w,τ) and the PDF is skewed. However, when τ exceeds the event spacing, the fluctuations in c_I(t_w,τ) average out and the PDF becomes Gaussian, s = 0.

The events leading to a considerable change in the speckle pattern can be interpreted as the occasional formation and rupture of bonds, affecting the elastic backbone of the network. Because of the long-range connectivity of the backbone they lead to a rearrangement of the particle positions in a large volume and thus to a significant drop of the degree of correlation.

The agreement between the lag time at which the PDF becomes Gaussian and the final relaxation time of g₂(τ) − 1 persists for different ages, as shown in Fig. 4. This strongly suggests that the rare and sudden events are the origin of the slow dynamics of colloidal particle gels.

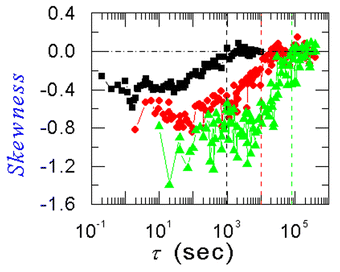Fig. 4 Skewness as a function of τ for 4.6 × 10³ < t_w < 1.5 × 10⁴ s (black squares), 3.7 × 10⁴ < t_w < 4.0 × 10⁵ s (red circles), 1.82 × 10⁵ < t_w < 6.9 × 10⁵ s (green triangles). The vertical dashed lines indicate the characteristic time τ_exp of the final relaxation of g₂(τ) − 1. Note the agreement between the crossover to Gaussian behavior and the characteristic time persists for different ages.

In conclusion, we have developed a new scheme, time resolved correlation, which enables us to explore in a detailed way the dynamics of a system. The application of this method to particle gels revealed that the slow aging dynamics of these systems is intermittent. We explain this behavior assuming the occasional formation or rupture of bonds within the gel, causing a rearrangement of the particle positions. When the formation or rupture of bonds affect the elastic backbone of the network, the rearrangements are larger than average, leading to sudden drops in the degree of correlation.

Ongoing experiments on other jammed systems reveal similar intermittent dynamics,²² thus suggesting that intermittency is a general feature of aging systems.

Acknowledgements

Financial support from the Swiss National Science Foundation (Grant 20-65019.01) and the CNRS, Région Languedoc-Rousillon is gratefully acknowledged.

References

1. A. J. Liu and S. R. Nagel, Nature, 1998, 396, 21.
2. J.-P. Bouchaud, L. Cugliandolo, J. Kurchan and M. Mezard, Physica A, 1996, 226, 243.
3. J.-P. Bouchaud, L. F. Cugliandolo, J. Kurchan and M. Mezard, in Spin Glasses and Random Fields, ed. A. P. Young, World Scientific, Singapore, 1998.
4. G. Parisi, Phys. Rev. Lett., 1997, 79, 3660.
5. J.-L. Barrat and W. Kob, Europhys. Lett., 1999, 46, 637.
6. P. Sollich, F. Lequeux, P. Hebraud and M. E. Cates, Phys. Rev. Lett., 1997, 78, 2020.
7. P. Sollich, Phys. Rev. E, 1998, 58, 738.
8. W. K. Kegel and A. van Blaaderen, Science, 2000, 287, 290.
9. E. R. Weeks, J. C. Crocker, A. C. Levitt, A. Schofield and D. A. Weitz, Science, 2000, 287, 627.
10. E. V. Russell and N. E. Israeloff, Nature, 2000, 408, 695.
11. C. T. Thurau and M. D. Ediger, J. Polym. Sci., Part B: Polym. Phys., 2002, 40, 2463.
12. L. Buisson, L. Bellon and S. Ciliberto, Cond-mat, 2002, 0210490 (http://arxiv.org/archive/cond-mat).
13. L. J. Gauckler, T. Graule and F. Baader, Mater. Chem. Phys., 1999, 1, 2509.
14. D. A. Weitz and D. J. Pine, in Dynamic Light Scattering, ed. W. Brown, Clarendon Press, Oxford, 1993.
15. V. Viasnoff, F. Lequeux and D. J. Pine, Rev. Sci. Instrum., 2002, 73, 2336.
16. S. Romer, F. Scheffold and P. Schurtenberger, Phys. Rev. Lett., 2000, 85, 4980.
17. F. Scheffold, S. E. Skipetrov, S. Romer and P. Schurtenberger, Phys. Rev. E, 2001, 63, 61404.
18. L. Cipelletti and D. A. Weitz, Rev. Sci. Instrum., 1999, 70, 3214.
19. A. Knaebel, M. Bellour, J.-P. Munch, V. Viasnoff, F. Lequeux and J. L. Harden, Europhys. Lett., 2000, 52, 73.
20. L. Cipelletti, S. Manley, R. C. Ball and D. A. Weitz, Phys. Rev. Lett., 2000, 84, 2275.
21. L. Ramos and L. Cipelletti, Phys. Rev. Lett., 2001, 87, 245503.
22. L. Cipelletti, H. Bissig, V. Trappe, P. Ballesta and S. Mazoyer, J. Phys.: Condens. Matter, 2003, 15, S257.
23. A. H. Krall and D. A. Weitz, Phys. Rev. Lett., 1998, 80, 778.

---

Footnote

† This paper was originally presented as a poster at the Faraday Discussion 123 meeting.

---