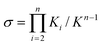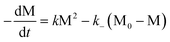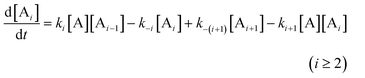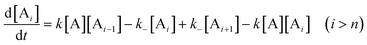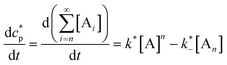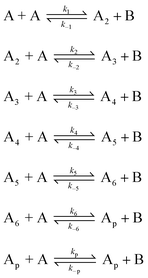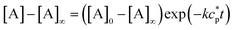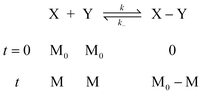DOI:
10.1039/B308788C
(Perspective)
Org. Biomol. Chem., 2003,
1, 3471-3491
Nucleation–elongation: a mechanism for cooperative supramolecular polymerization
Received
28th July 2003
, Accepted 3rd September 2003
First published on 29th September 2003
Abstract
The kinetic and thermodynamic characteristics of polymerizations following a cooperative, nucleation–elongation mechanism are discussed in comparison to those of non-cooperative, isodesmic polymerizations. Nucleation–elongation polymerization is a relatively unexplored avenue of synthetic polymer chemistry and offers some unique and interesting thermodynamic and kinetic attributes not found in the more classical mechanisms of polymer chemistry.
| Dahui Zhao was born in China in 1974. She graduated from Beijing University in 1997 with a Bachelor of Science degree in Chemistry. In 1999, she joined Professor Moore's research group at the University of Illinois at Urbana-Champaign for her PhD studies. Currently, her research is focused on folding-driven polymerization of imine-containing m-phenylene ethynylene oligomers. |
 Dahui Zhao (left) and Jeffrey S. Moore (right). | Jeffrey Moore was born outside of Joliet, IL in 1962. After receiving his B.S. in chemistry from the University of Illinois (1984), he completed his Ph.D. in Materials Science and Engineering, also at the University of Illinois, with Samuel Stupp (1989). He then went to Caltech as a NSF postdoctoral fellow to study with Robert Grubbs. In 1990 he joined the chemistry faculty at the University of Michigan in Ann Arbor, but returned to the University of Illinois in 1993 where he is currently the William H. and Janet G. Lycan Professor of Chemistry and Materials Science and Engineering. His research focuses on molecular self-assembly and self-organization, structure-controlled macromolecules and foldamers, stimuli-responsive materials, and self-healing polymers.Dahui Zhao (left) and Jeffrey S. Moore (right). |
1 Introduction
Classical polymer chemistry gives three basic mechanisms of chain growth (step, addition and living).1,2 Are there any others? Biology teaches us that there is at least one more mechanism that is especially relevant to supramolecular assemblies and covalent polymers that are supramolecularly structured (i.e., folded). This mechanism is known as nucleation–elongation chain growth.
A number of globular proteins have long been known to form filamentary “polymers” both in vivo and in vitro.3 These protein “polymers” are quasi-one dimensional supramolecular assemblies (Fig. 1). The “repeating units” consist of globular protein molecules, bonded not with covalent linkages but non-covalent interactions. The polymerization process is thus reversible and proceeds to thermodynamic equilibrium—a state determined by environmental conditions such as temperature, pH and the concentrations of various ions or small molecules. At equilibrium, both polymerization and de-polymerization are taking place at the same rate; therefore, the structures of these polymers are dynamic and constantly fluctuating. Under appropriate conditions, these polymerizations are spontaneous, indicating that the polymeric structures are thermodynamically stable. A widely cited example is the tobacco mosaic virus which can be reconstructed from dispersed protein molecules in the presence of nucleic acids at neutral pH.4 Even in the absence of the nucleic acid template, the tubular assembly of proteins forms spontaneously, only in this case the length distribution of the resulting polymers is not uniform. Similar reconstitution behavior was also observed with flagellin molecules.5 Although in biological systems these polymerizations are regulated by proteins and/or small molecules,6 most protein polymerizations can take place without the aid of these regulatory species.
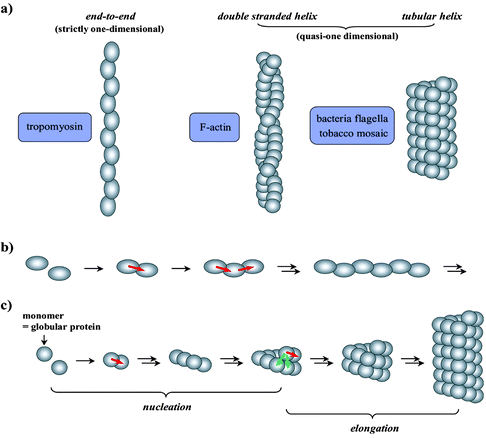 |
| | Fig. 1 a) Representative models of helical and tubular protein polymers in comparison to a linear structure; b) illustrative schematic of the simple elongation of a linear polymer, and c) nucleation and elongation stages of polymerization into a tubular structure (the arrows represent the interactions among the repeating units; the interactions denoted by green arrows are absent from the assembly of the first turn of the tubule and from the linear polymer formation). These secondary interactions (green arrows) are the molecular origins of cooperative assembly. | |
Representative structures adopted by these protein polymers are illustrated in Fig. 1a. Among these supramolecular assemblies, a group of proteins distinguish themselves by constructing helical or tubular structures (i.e., quasi-one dimensional), in contrast to those that are formed by simply joining the subunits end-to-end in a linear fashion (i.e., strictly one dimensional). In addition to the structural difference, the polymerization behaviors of these two types of polymers are distinct. Strictly one dimensional polymers are assembled by a non-cooperative, isodesmic polymerization mechanism (Fig. 1b).7–9 In contrast, the helical and tubular structures are realized by a cooperative nucleation–growth process (Fig. 1c).10–14 Specifically, the initial oligomerization of protein monomers is slow and energetically disfavored (nucleation) relative to the subsequent rapid chain propagation into long filaments (elongation). Due to the unique disposition of repeating units within the helix or tubular structure, each protein molecule is simultaneously in contact with multiple neighboring units. Hence, the addition of a monomer to a preexisting helix end is favored by multiple associations with other monomers from the same and neighboring turns of the helix. Consequently, the helical chain growth is an energetically favorable, cooperative process. However, neighbor–turn interactions are absent from the first turn of the helix (Fig. 1c). The entropic cost of assembling the first turn is thus not compensated by an offsetting enthalpic gain; the result is an energetically disfavored initiation event.
Such nucleation–elongation behavior was first discovered in protein polymerization decades ago, and it has attracted attention ever since. As a result, substantial information has been acquired from biological systems, especially actins polymers,6,15,16 regarding both the thermodynamic and kinetic characteristics that this nucleation–elongation mechanism entails. In great contrast, examples of synthetic polymers known to exhibit such a nucleation process during polymerization are limited. From the discussion below we will see that in order to possess such a cooperative chain growth, some fundamental criteria must be met by the polymerization system. Most important is the requirement that the repeating units be capable of engaging in multiple interactions with other units in the same chain. Apparently, such a requirement cannot easily be fulfilled solely by covalent bonds. Most conventional synthetic polymers rely exclusively on covalent bonds to join adjacent repeating units and typically lack any kind of well-defined, higher-order structure that results from interactions between non-adjacent units. Nevertheless, with the ever-increasing understanding and rapid development in the area of supramolecular chemistry, designing and synthesizing chain molecules manifesting intramolecular non-covalent interactions has produced helical conformations in a variety of structures.17–26 Thus, synthetic polymerizations exhibiting a nucleated chain growth process can now be envisioned. Therefore, relevant theoretical analyses specifically directed toward nucleation–elongation behaviors in synthetic polymers are necessary.
To this end, the current perspective will be devoted to nucleation–elongation phenomena in the regime of synthetic polymer chemistry, starting with a survey of non-biological systems that show a nucleation process during polymerization. In order to elucidate the design rules for nucleation–elongation chain growth, general structural characteristics of the known cooperative systems will be summarized. Then, quantitative analyses of the thermodynamic and kinetic properties of the nucleation–elongation polymerization will be made in comparison to those of the conventional non-cooperative, step-growth polymerizations, with the aid of polymerization models representing these two different mechanisms. Since the goal of the current perspective is focused on synthetic systems, the discussion will concentrate on the most primitive models; more complex models such as those involving regulatory mechanisms,27,28 which are common in biological polymerizations, are beyond the scope of the present perspective. As most previously proposed models are intended for biological polymers, necessary modifications that make them more applicable to synthetic systems will also be developed. Lastly, the perspective of future applications of synthetic, supramolecular polymers resulting from nucleation–elongation will be briefly discussed, and a folding-driven approach to globular, soluble heterosequenced copolymers (“masterpiece sequences”29) will be proposed.
2 Synthetic examples of nucleation–elongation polymerization
Distinct nucleation behavior has long been recognized and investigated in protein polymerizations, and substantial information has accumulated over several decades.3 In great contrast, synthetic polymerizations having similar nucleation–elongation mechanisms are rare. The known examples of synthetic systems that exhibit nucleation behavior in their polymerization reactions are reviewed below.
The first example of a synthetic macromolecule that seemingly exhibited a nucleation process in its polymerization came in the early 1960s. Kern and Jaacks studied the kinetics of the polymerization of 1,3,5-trioxane (i.e., the cyclic trimer of formaldehyde) in which they observed an unusually long induction period.30 This polymerization is a cation-mediated, ring-opening chain reaction, which can be initiated by Lewis acids such as boron trifluoride. The mechanism of this polymerization reaction was believed to be the one shown in Scheme 1. Boron trifluoride (BF3) first reacts with a trioxane molecule to form a stable adduct, which then undergoes a slow ring-opening transformation to give a carbonium ion, stabilized by resonance. This zwitterion then undergoes successive ring-openings with trioxane to generate polyoxymethylenes.
However, this simple mechanism could not account for the long induction period observed in the polymerization of trioxane in dichloromethane. Kern and Jaacks then proposed that, in the polymerization starting with the cyclic trioxanes, the initially formed oxymethylene oligomers depolymerize to generate formaldehyde (Scheme 2). When the formaldehyde concentration is low, the rate of formaldehyde production is faster than that of chain extension through trioxane addition followed by ring-opening. In other words, formaldehyde keeps accumulating in solution until its concentration reaches a limit whereby the dissociation of formaldehyde from oligomers is balanced by its addition to the chain end. Further reactions between the zwitterion and trioxane afford the polymer products, while the concentration of formaldehyde in solution remains constant. This mechanism explained the long induction period that preceded the acceleration of the polymerization rate.
This proposition was supported by an experiment in which the concentrations of formaldehyde within the polymerization system were analytically determined at various time intervals.30 It was found that the formaldehyde concentration kept increasing during the initiation of the reaction; it reached a maximum and remained constant thereafter. Further evidence was provided by polymerizations of trioxane in the presence of added free formaldehyde. The length of the induction period was observed to be progressively reduced, or even eliminated, when an increasing amount of monomeric formaldehyde was added to the trioxane solution in the presence of the acid catalyst.
Strictly speaking, if the induction period observed in the polymerization of trioxane solely results from dissociations of formaldehyde, the mechanism cannot be classified as a nucleation–elongation process, but one having a divergent, competitive pathway. However, further experimental evidence revealed a steady increase in the number of growing cationic species as the reaction proceeded, which suggested that the initial ring-opening of the BF3–trioxane adduct was slower than further chain growth into polymers. This qualified the reaction as a nucleation–elongation polymerization.
This nucleation–elongation behavior became even more pronounced when the polymerization of trioxane took place in a poor solvent for polyoxymethylenes, resulting in crystallization of the polymers. Following Kern and Jaacks' work, Leese and Baumber studied the kinetics of heterogeneous trioxane polymerization in ethylene dichloride using chemical and adiabatic calorimetric methods.31 Their investigation elucidated that the polymerization of trioxane, again catalyzed by BF3 etherate, experienced a slow induction period, which included the initial ring-opening of trioxane–BF3 complexes, the degradation of the resultant linear molecules into formaldehyde to the point of saturation, followed by growth of the soluble, low molecular weight oligomers. As chain elongation continued, a solubility limit was reached. Thereafter, concomitant polymerization and crystallization resulted in an exothermic reaction that proceeded at a greatly accelerated rate.
The observation of simultaneous polymer chain propagation and crystal growth led researchers to speculate about the morphology of the resultant crystalline polymer structures.32 If the chain propagation proceeded via direct additions of monomer onto the crystal surface instead of via successive precipitations of chain molecules grown from dispersed nuclei upon reaching the solubility limit, the reactive chain ends must have remained on the surface of the growing crystals during the entire course of polymerization, and the resultant polymers should have chains arranged in a relatively extended conformation along the direction in which the crystal grows. This speculation was confirmed by the structural studies on the polyoxymethylene crystals conducted by Kawai et al.32 Apparently, under these circumstances, the heterogeneous polymerization of 1,3,5-trioxane is a nucleation–elongation process, in which the acceleration in polymerization rate arose from coupling of the crystalline lattice energy to the chain propagation.
2.2 Polymerization of N-carboxy α-amino acid anhydride (NCA)
Another example of nucleation–elongation behavior was found in the polymerizations of amino acid anhydrides.33 The polymer products of NCAs, i.e., synthetic polypeptides, were anticipated to adopt certain ordered secondary structures (such as α-helix and β-sheet structures) in solution or the solid state, and this should induce some unique polymerization properties and morphological characteristics.
In the polymerization of L-alanine NCA in acetonitrile with n-butylamine as the initiator (Scheme 3), the monomer solution was found to become turbid soon after n-butylamine was added.34 As the polymerization proceeded further, fibrous, ribbon-like crystals precipitated, although these fibers continued to grow thicker with time. Based on X-ray diffraction, IR spectroscopy and electron micrograph analyses on the structures of products obtained at different stages of polymerization, Ōya and coworkers proposed a nucleation–growth mechanism for this polymerization reaction (Fig. 2). In acetonitrile, which is a good solvent for the NCA monomers but a poor solvent for the polypeptide, the growing chain molecules became insoluble once the degree of polymerization reached a critical length of ca. 3 repeating units (the system became turbid at this point). It was proposed that the precipitated oligopeptides existed in a β-sheet structure with chains arranged antiparallel to each other, nearly perpendicular to the fiber axis of the crystals. At this stage, the molecules were mainly stabilized by intermolecular H-bonds. With the reactive chain termini positioned on the surface of the fibers instead of occluded inside the crystal lattice, these molecules were capable of further propagation. Once the dangling chains achieved a sufficient length, they started to adopt the α-helical conformation, driven by the favorable intramolecular H-bond interactions. Thereafter, monomeric NCAs were continuously appended onto the reactive chain end on the surface of the crystalline, and the helices and crystal lattice thus progressively extended. This process corresponded to the thickening stage of the fibrous crystals. X-Ray diffraction studies supported this mechanism by illustrating that, at the early stage of the polymerization when the chains are short, the diffraction pattern of the product was characteristic of a β-sheet structure. As the chain grew longer, the reflections gradually became dominated by a peak characteristic of α-helix crystals.34 IR spectroscopy further confirmed the presence of these structures and their transition at different stages of the polymerization. Independently, the critical chain length for helix formation in solution was determined by optical rotatory dispersion measurements to be between 7–10 repeat units. This agreed well with the observation that, during the polymerization, the α-helix structures were not stabilized until a chain length of ca. 13 was attained, which included the ca. 3 repeat units participating in the β-sheet domain.35 Additionally, the thickness of the ribbon-like crystals obtained from electron micrographs was also in good agreement with the sum of twice the helix length and the width of the extended β-structure calculated from the average degree of polymerization at the corresponding reaction conversion.36
Solvent and the peptide backbone structure were also found to play important roles in determining the occurrence of the nucleation and growth in NCA polymerizations. Acetonitrile represented a suitable solvent for striking an optimal balance between solvating the short oligomers but not long polymers, thus preventing continuous β-structure formation. Moreover, the solvent should be non-disruptive to H-bonding and facilitate helix formation for longer peptide chains.35L-Leucine,37L-methionine38 and L-proline39 NCAs were other amino acids that were found to give rise to helical chain crystals in acetonitrile, while β-alanine, glycine40 and L-valine37 were among a series of NCAs proven incapable of adopting helical conformation during polymerization. To summarize the polymerization of NCAs, the growth of the crystalline lattice is coupled to the chain propagation in the polymerization. It should be mentioned, however, that this polymerization is not reversible.
2.3 Folding-driven reversible polymerization of oligo(m-phenylene ethynylene) imines
In the above two examples of polymerizations exhibiting a nucleation process, the nucleation event must at least have partially coincided with the formation of crystal nuclei from the low oligomers that were soluble in solution. The supramolecular energy in these polymerizations was mostly derived from polymer crystallization.41 More recently, the design and performance of a solution-phase, nucleation–elongation polymerization of synthetic molecules was accomplished by Moore and coworkers with a metathesis polymerization of m-phenylene ethynylene (mPE) imine oligomers (Scheme 4).42,43 This reaction resembles protein polymerizations in that the driving energy for the polymerization is derived from the formation of higher-order structure in the polymers, and that the nucleation effect is believed to arise as a consequence of the helical conformation of the products. The polymerization proceeded in solution without crystallization or precipitation, which greatly helps delineating the effects of folding on the polymerization mechanism, such as whether the folding energy is sufficient to drive the polymerization equilibrium toward high polymers and whether the end-group effect of a helix structure does entail a type of nucleation behavior.
The design of this nucleation–elongation polymerization was based on previous studies on the mPE oligomers. These oligomers were demonstrated to adopt an ordered, helical conformation in polar solvents such as acetonitrile, presumably driven by the solvophobically favored aromatic stacking interactions among the backbone units.44 Folding stability of these mPE oligomers was found to be governed by a critical chain length.45 An oligomer containing ten mPE units exhibited only marginal folding stability (partially folded) in acetonitrile while oligomers of smaller size did not exhibit a stable, folded conformation. On the other hand, as the chain length increased, higher folding stability ensued. As chloroform was known to be a denaturing solvent that unfolds the oligomers and favors a random conformational state, it was possible to quantitatively determine the folding energy by following the helix-to-coil transition as the solvent composition was gradually changed from pure acetonitrile to pure chloroform.44 By examining the folding energy change with chain length, the critical size of the mPE oligomers was found to be approximately eight to ten mPE units, beyond which the folding energy increased nearly linearly with chain length. A folding energy of ca. 0.7–0.8 kcal mol−1 per mPE unit beyond the critical size was estimated for oligomers in pure acetonitrile at room temperature.45
Based on these results, it was envisioned that this folding energy might be harnessed to drive a reversible polymerization to generate high polymers (Fig. 3). To help overcome nucleation and to avoid macrocyclic traps, short oligomeric segments (i.e., “starter sequences”) were polymerized rather than monomer. For example, using the pair of starter sequences 1 and 2, each containing four mPE units, the immediate product (5) from a single coupling reaction will have eight mPE units, and thus is incapable of folding. Adding another starter sequence segment to this oligomer will produce a molecule of twelve mPE units, 6, which should be able to fold under appropriate conditions (e.g., in acetonitrile). Further extending the molecules will result in polymers having greater folding stabilities. Therefore, a nucleation–elongation polymerization should occur with the nucleus size being ca. 2 or 3. Evidently, varying the chain length of the starter sequences will alter the nucleus size and the step-wise equilibrium constant. For instance, using a pair of starter sequences each comprising two mPE units will increase the nucleus size to over 4 and reduce the free energy change accompanying each monomer (i.e., starter sequence) addition by one half. On the other hand, the employment of longer starter sequences (e.g., exceeding the nucleus size) will result in elimination of the nucleation process, although the step-wise driving force for polymerization will become larger.
 |
| | Fig. 3 Schematic diagram of folding-driven polymerization of oligo(m-phenylene ethynylene) imines having a nucleation–elongation mechanism. | |
In order to be most suitable for a nucleation–elongation process, the choice of the covalent ligation is critical. A large free-energy gain from covalent bond formation will overwhelm the folding energy, causing the polymerization to be favored at each step. Polymerizations based on metathesis reactions avoided this problem. For a metathesis (i.e., exchange) reaction, the sum of the covalent bond energy of the reactants is nearly equal to that of the products. Thus, a minimal bond energy change will occur with each covalent coupling during the polymerization. Consequently, the energy gained from folding, i.e., the supramolecular interactions within the chain, will solely be responsible for driving the polymerization equilibrium. The occurrence of high polymers, should they be observed, can thus be attributed to supramolecular organization of the folded chain. The equilibrium distribution of the chain length will thus be controlled by the relative stabilities of the folded and unfolded chains. Another design consideration for selecting this metathesis reaction is that it is a reversible process (dynamic covalent bond).46 The reversibility ensures that the polymerization proceeds to thermodynamic equilibrium rather than being dictated by the kinetics of the coupling reaction. Additionally, a reversible coupling reaction would allow erroneous sequences to be corrected in a heterosequence polymerization.
Based on the above analyses, starter sequences 1 and 2 were prepared and their polymerization was studied. Indeed, it was demonstrated that high polymers were obtained from the metathesis polymerization only under conditions that favored folding. Only low molecular weight oligomers resulted under non-folding conditions, such as in chloroform. This result supported the folding-driven nature of the polymerization. Particularly, in polymerizations under conditions that promoted folding, monomers 1 and 2 were invariably found to be present in significant amounts, coexisting with high molecular weight products at equilibrium. This observation is consistent with what is predicted by polymerization models following a nucleation–elongation mechanism (vide infra).
3 General features of nucleation–elongation polymerization
3.1 Clarification of terms
The protein subunits of protein polymers associate with each other through non-covalent interactions; thus, the protein polymers are unambiguously supramolecular polymers or assemblies. For most synthetic polymers including those with folded supramolecular structures, the repeating units are linked through covalent bonds. Therefore, these molecules cannot be classified as supramolecular polymers.47 However, if we consider the polymerization mechanism, the issue is not the presence or absence of continuous covalent connectivity in the final product, but rather what interactions provide the dominant driving force for high polymer formation. Therefore, it is suggested that a polymerization be considered as a supramolecular polymerization if non-covalent interactions contribute significantly to the driving force for polymer growth.
3.2 Minimum requirements for a nucleation–elongation polymerization
Structural analyses (such as X-ray diffraction, electron micrograph, etc.) on protein polymers have unambiguously elucidated regular structures and many are of helical symmetry. All the protein monomers, which are complex, globular structures with irregular shapes,48,49 are generally arranged in equivalent, or approximately equivalent, positions relative to their neighboring molecules. Each monomeric unit simultaneously interacts with multiple neighboring protein molecules. Mathematical analysis has shown that continued application of a general identity operation to an asymmetric element must result in a helical structure (straight linear and cyclic structures are considered special limiting cases of helices).3,48 In other words, a linear polymer derived from asymmetric repeating units all of which have the same relative positions must be helical.
In a covalently linked polymer where each unit is divalent, adjacent units can be defined as the segments joined directly through covalent bonds. Thus, non-adjacent interactions refer to the connections between two segments that are not directly linked through covalent bonds but interact with each other through space (e.g., units belonging to adjacent turns within a helix). However, the differentiation between adjacent and non-adjacent units would be hard to make for polymers that are constructed exclusively from non-covalent interactions (e.g., as in protein polymers). Nevertheless, if helical or tubular protein assemblies are imagined as structures resulting from winding a single or multiple strands of linear protein polymers, analogies can be drawn between synthetic and biological systems.
For a helical or tubular structure (Fig. 1) having more than one unit per turn, a nucleation–elongation polymerization arises from the process of forming the first turn. The free energy change for each repeating unit assembling to form the first turn of a helix is different from that of adding a monomer to an existing helical chain end. In forming the first turn, there is no neighboring turn and thus fewer subunit interactions are possible. If the nearest-neighbor interactions contribute significantly to helix stability, then nucleation behavior arises. Another way of thinking about this is breaking a helix into two fragments (each containing more than one complete turn) would be energetically more demanding than the dissociation of a single molecule from the chain end, as fragmentation involves disrupting multiple monomer–monomer interactions. In contrast, breaking a chain that is strictly one dimensional (e.g., tropomyosin, Fig. 1a) is no more energetically demanding than monomer dissociation.
Based on the above analyses, the minimum criterion for nucleation–elongation polymerization would be the presence of modular building blocks capable of multi-site interactions resulting in a helical assembly. The interactions must be highly specific and selective in order to circumvent random aggregation of the building blocks. The distribution of these interactive sites on the surface of the monomer has to be highly regulated, as it determines the geometric characteristic of the resulting structures. The strength of these interactions is another critical factor: the interactions between the monomers from neighboring turns must be strong enough, compared to intra-turn or adjacent-unit interactions. When inter-turn interactions are strong, elongation is favored relative to nucleation, thus facilitating high polymer formation. For synthetic molecules multiple, non-adjacent interactions can be realized by supramolecular interactions within the polymer chain. This requires that the chain adopt a compact conformation (as the distance between non-adjacent units is short).
4 Mathematical models
In order to quantitatively describe, analyze and predict the thermodynamics and kinetics of nucleation–elongation polymerizations, mechanistic-based models have been proposed.3Eqn. (1) is a general set of relationships, in which polymerization is described as successive monomer addition to i-mer fragments. If i represents the degree of polymerization, the rate constants of the forward and backward reactions for adding or cleaving a monomer unit are designated as ki and k−i, from which the equilibrium constant Ki can be derived (brackets represent molar concentration). Based on these parameters and other relevant information, such as total monomer concentrations, thermodynamic and kinetic properties of a polymerization reaction can be calculated or estimated.| | 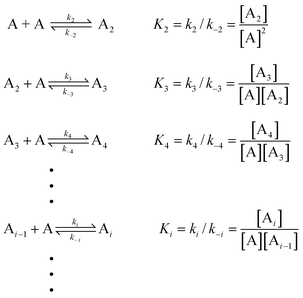 | (1) |
Although eqn. (1) is adequate for most protein polymerizations, an additional factor has to be considered when such a model is applied to systems producing a small-molecule byproduct along with the polymers. Such would be the case for synthetic polymers involving a condensation byproduct. In such a case, relationships given by eqn. (2) must be used (i.e., an extra term B denoted for the byproduct is incorporated in each step). In a closed system, wherein none of the products is removed from the equilibration during the reaction, B will keep accumulating until equilibrium is reached. In the polymerization reaction shown in Scheme 4, for instance, B represents the small-molecule byproduct 4.
| |  | (2) |
It is should be noted that the units of the equilibrium constants (Ki) and the rate constants for the reverse reactions (k−i) are different in the above two cases. For eqn. (1) the association constants have units of (conc.)−1, while for eqn. (2) the association constants are unitless. This difference will have practical consequences for polymerization behavior. For instance, in the former case, the equilibrium and kinetic properties should be dependent on concentration. In the latter, only the approach to equilibrium depends on concentration while the equilibrium state itself is independent of concentration. Details of these analyses will be discussed in the following sections.
4.1 Isodesmic model
The isodesmic model is the simplest model of polymerization or aggregation and it is generally suited to strictly one dimensional polymers. In this model, it is assumed that any monomer addition to another monomer or a polymer occurs with identical free energy changes. Thus, the equilibrium constants for all steps in eqns. (1) and (2) are the same (K2
=
K3
=
…
=
Ki
…). Accordingly, there should be no energy difference between adding a monomer to a polymer or to another monomer (Fig. 4a). In other words, no nucleation occurs in this type of polymerization. The reaction is non-cooperative. Few protein polymerizations actually follow such a mechanism; one example is tropomyosin.7,8 Nevertheless, this model is adequate for simulating most synthetic polymerizations including non-cooperative supramolecular polymerization, because synthetic polymers are generally linear and incapable of non-adjacent interactions or secondary, or higher-order, supramolecular structure formation. The reactivity of the functional groups in synthetic polymers responsible for covalent couplings has long been proven to remain constant, irrelevant of the lengths of the chains to which they are attached.1,2 This model has also been used to describe the self-association of small molecules, biological and synthetic, which tend to aggregate into strictly one dimensional columnar structures, under the conditions where only two nearest-neighbor interactions are significant.9
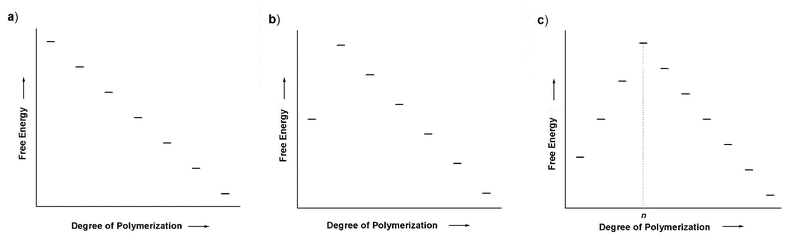 |
| | Fig. 4 Qualitative plots of free energy as a function of degree of polymerization for different models of polymerization: isodesmic (a) and nucleation–elongation with a nucleus size of two (b) and n
(c). | |
4.2 Single-step nucleation
A simple modification to the isodesmic model is to allow the equilibrium constant of the first step (i.e., dimerization) in eqns. (1) and (2) to differ from the others (K2
≠
K3
=
K4
=
…
=
Ki
…). If K2 is larger than the equilibrium constants of the remaining steps, the system experiences tight dimerization followed by isodesmic elongation. On the contrary, if K2 is smaller than Ki
(i > 2), nucleation–elongation occurs, with a nucleus size of two. Accordingly, for a disfavored dimerization (nucleation) followed by favorable chain growth, a plot of product free energy vs. the degree of polymerization is shown in Fig. 4b.
4.3 Multiple-step nucleation
If the monomer addition becomes unfavorable for more than one step, i.e., association constants K2 through Kn are all smaller than Kn
+ 1 and so on, a multi-step nucleation mechanism occurs. Accordingly, oligomerizations up to the n-mer are considered nucleation steps (the nucleus size, n) and elongation ensues from this point on (Fig. 4c). Alternatively, the nucleus size may be defined as the smallest oligomers of which the elongation is faster than dissociation (kn
+ 1 > k−n).
4.4 Others
In addition to the models mentioned above, a number of other models have been used to describe polymerizations or aggregations. For example, if the equilibrium constants taper off during the elongation steps, e.g., due to increasingly less favorable entropy change as the chain grows longer, an attenuated (or non-equal)
K model can be developed.9,50 Alternatively, various models with additional steps to explain the regulatory mechanisms in protein polymerizations (such as the roles of ATP and cations involved in actin polymerization) have also been proposed.27,28,51 These models will not be the focus of the current perspective, since they involve more complicated mechanisms. Here we are trying to capture the most fundamental and distinguishing features of polymerizations that exhibit cooperativity from those that are non-cooperative. In the following sections, thermodynamic and kinetic properties of polymerizations will be analyzed in detail using the simple nucleation–elongation as the cooperative model and this will be compared to the non-cooperative, isodesmic polymerization.
5 Thermodynamics
5.1 General formula
Since thermodynamics is only concerned with the equilibrium state of a polymerization rather than the kinetically most favorable pathway to each product of different size, the choices of certain expressions in the polymerization mechanism over others will not alter the results of thermodynamic calculations, as long as correlations between all possible species are correctly expressed in terms of equilibrium constants Ki. Therefore, successive equilibrium equations between monomers and i-mers as expressed in eqns. (1) and (2) should be suitable for analyzing the equilibrium properties of a polymerization, such as the molecular size distribution and its average value.
According to eqn. (1), the molar concentration of molecules with different degrees of polymerization at equilibrium can be written as follows:
| |  | (3) |
| |  | (4) |
| | 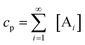 | (5) |
where
ct is the initial total concentration of monomer, and
cp is the total concentration of all products, including monomers, oligomers and
polymers at different degrees of
polymerization.
In the case of eqn. (2), the corresponding expressions are slightly different:
| | 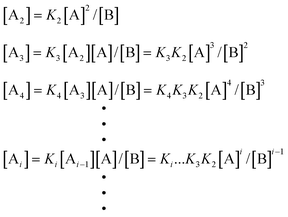 | (6) |
| | 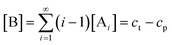 | (7) |
where the expressions for total concentrations,
ct and
cp, remain the same as eqns.
(4) and
(5).
5.2 Isodesmic model (non-cooperative polymerization)
In the isodesmic model without byproduct formation, the equilibrium constants for all monomer additions are identical (K2
=
K3
=
…
=
Ki
…
=
K). Therefore, eqns. (3)–(5) simplify to:| |  | (9) |
| | 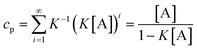 | (10) |
If ct is known, eqn. (9) can be rearranged into:| | 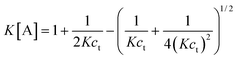 | (11) |
Based on this equation, as ct approaches infinity, the monomer concentration [A] tends to, but never equals, K−1. Accordingly, the condition for justifying eqn. (9), K[A] < 1, is satisfied. From the above results, one can calculate the number- and weight-average degrees of polymerization 〈dp〉n and 〈dp〉w, respectively, as well as the polydispersity index (PDI) at equilibrium:| | 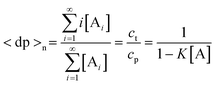 | (12) |
| |  | (13) |
| | 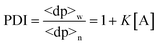 | (14) |
As [A] approaches K−1
(i.e., ct
→ infinity), the polydispersity index approaches 2.0. Combining eqn. (11) with eqns. (12)–(14), respectively, one can obtain the product of the equilibrium constant and monomer concentration (K[A]), the relative concentration of monomer ([A]/ct), and average degrees of polymerization at equilibrium (〈dp〉n and 〈dp〉w) as functions of Kct
(Fig. 5). Based on these results, gradual transitions of these values with increasing Kct are expected from an isodesmic polymerization.
![Plots of K[A]
(I, —), [A]/ct
(I, ), 〈dp〉n
(II, —), and 〈dp〉w
(II, ) as functions of Kct under the conditions of an isodesmic polymerization without byproduct.](/image/article/2003/OB/b308788c/b308788c-f5.gif) |
| | Fig. 5 Plots of K[A]
(I, —), [A]/ct
(I, ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ), 〈dp〉n
(II, —), and 〈dp〉w
(II, ), 〈dp〉n
(II, —), and 〈dp〉w
(II, ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) as functions of Kct under the conditions of an isodesmic polymerization without byproduct. ) as functions of Kct under the conditions of an isodesmic polymerization without byproduct. | |
The size distribution at equilibrium can also be derived. This can either be expressed as the mole fraction (Xi) or weight fraction (Wi) of molecules with a degree of polymerization of i:
| |  | (15) |
| |  | (16) |
From
eqn. (15), it can be seen that monomer is always the most abundant species in number within the system, regardless of the values of the equilibrium constant and the total concentration.
Correspondingly, for isodesmic polymerizations in which there is a byproduct formed, the corresponding concentrations of monomer A, byproduct B and the total concentrations at equilibrium can be obtained from eqns. (4)–(7):
| | | [Ai]
=
K−1[B](K[A]/[B])i | (17) |
| |  | (18) |
| | 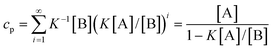 | (19) |
| |  | (20) |
Combining
(18) and
(20), one can solve [A] and [B] as functions of
ct:
| |  | (21) |
| | 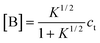 | (22) |
Accordingly, the number- and weight-distributions of degree of polymerization and their average values at equilibrium can be derived:
| |  | (23) |
| |  | (24) |
| |  | (25) |
| |  | (26) |
| |  | (27) |
It is clear that when a byproduct is generated during
polymerization, the average degrees of
polymerization and size distributions [
eqns. (23)–(27)] at equilibrium become independent of the total concentration of monomer and solely depend on the equilibrium constant
K. This is in great contrast to the systems without the byproduct B, wherein all these values are related to both
K and
ct. The results shown above can be derived independently by statistical considerations.
1,2
5.3 Nucleation–elongation (cooperative) polymerization
As demonstrated above, if a polymerization follows the isodesmic addition mechanism, its molecular weight distribution, as well as other properties, can be predicted by analytical solutions. However, from early investigations of protein polymers, it was noted that polymerization behavior deviated from these predictions. It was found that the polymerization only took place above a critical total concentration and that protein polymers always coexisted in equilibrium with a significant amount of monomer that remained in solution.10 Once the polymer (e.g. F-actin) is formed, its molecular weight is rather large, even at a total concentration near the critical value. Further increasing the total concentration beyond this critical value only increases the polymer concentration, while the monomer concentration remains constant at this critical value.3,10,52,53 These observations are inconsistent with the predictions of the isodesmic model, in which the average degree of polymerization for equilibrium should gradually but consistently increase with increasing total concentration at a given association equilibrium constant. Additionally, the relative weight percentage of the monomer within the equilibrated isodesmic polymerization system should be minimal and depend on the total concentration (Fig. 5, I). In contrast, protein polymerizations behave cooperatively, like gas–liquid condensation or small molecule crystallization in regard to the existence of a critical concentration. The discrepancies between the observed behaviors of protein polymerizations and the predictions of the isodesmic model suggested a different polymerization mechanism must be operating. Based on experimental evidence from systematic kinetic and equilibrium studies on a variety of protein polymerizations, a nucleation–elongation mechanism was proposed.54 Such a cooperative mechanism was considered reasonable because the nucleation process can be imagined to result from the helical and tubular structures exhibited by these polymers (vide infra). Moreover, the thermodynamic and kinetic characteristics predicted by the proposed model explained the observed polymerization behaviors. The following sections will be devoted to thermodynamic results obtained from this nucleation–elongation polymerization model.3,54,55
5.3.1 Polymerization with a single nucleation step.
The simplest version of nucleation–elongation polymerization model has only one step of nucleation followed by isodesmic elongation steps. In other words, only the dimerization step in eqn. (1) is energetically disfavored relative to the following steps (i.e., K2 < K3
=
…
=
Ki
=
…
=
K).50 The nucleus size, n, is 2. According to the equilibrium conditions, eqn. (3) can be modified:| | 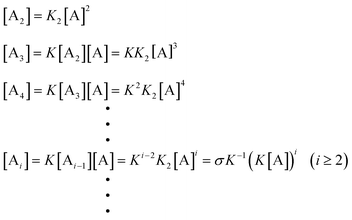 | (28) |
where
Accordingly,| |  | (29) |
The nucleation factor, σ, turns out to be a very important parameter. By rearranging eqn. (29), [A]/ct and K[A] can be solved and plotted as functions of Kct
(Fig. 6). From these plots, it can be seen that, in a highly cooperative system (i.e., when elongation is far more favored than nucleation, and σ
≪ 1), when ct < K−1, almost all the molecules exist in the monomeric form (i.e., [A]
≈
ct, Fig. 6, I). As ct increases, the concentration of monomer rises, but only to a limit. Once ct exceeds K−1, the monomer concentration rises no further but remains constant at the value of K−1
(Fig. 6, II). All the rest of the molecules (ct
−
[A]) are transformed into polymers. Therefore, K−1 is defined as the critical concentration, cc, below which almost no polymerization occurs. Another point that is worth noting is that when Kct is around unity, given the same value of K, the equilibrium monomer concentration in a nucleation–elongation polymerization is substantially higher than that found in an isodesmic system. This explains the experimental results in which a significant amount of protein monomer was observed to coexist with high polymers at equilibrium. Naturally, when σ approaches unity, the polymerization tends to behave like a polymerization without a nucleation process (cf. Fig. 5). The disappearance of the sharp transitions of K[A] and [A]/ct around the region of Kct
= 1.0 as σ
→ 1 indicates the loss of the critical monomer concentration cc.
![Plots of [A]/ct
(I) and K[A]
(II) as functions of Kct from cooperative nucleation–elongation polymerizations (without byproduct) with σ values as indicated.](/image/article/2003/OB/b308788c/b308788c-f6.gif) |
| | Fig. 6 Plots of [A]/ct
(I) and K[A]
(II) as functions of Kct from cooperative nucleation–elongation polymerizations (without byproduct) with σ values as indicated. | |
The number- and weight-average degrees of polymerization can be derived as in eqns. (30) and (31).
| |  | (30) |
| | 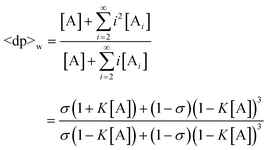 | (31) |
Combined with
eqn. (29), plots of 〈dp〉
n and 〈dp〉
w as functions of
Kct can be obtained (
Fig. 7). Consistently, these results reconfirmed the existence of a critical concentration. When
σ
≪ 1, high molecular weight species are nearly non-existent below the critical concentration
K−1. Both number- and weight-average degrees of
polymerization abruptly increase once
ct exceeds
K−1. Most remarkably, the plots in
Fig. 7 show that 〈dp〉
n and 〈dp〉
w increase with decreasing
σ value when
Kct > 1. Thus a higher average degree of
polymerization can be achieved by a nucleated polymerization than an isodesmic reaction at a given total monomer concentration. The magnitude of this molecular weight enhancement is determined by the cooperativity of the system,
i.e., the value of
σ. The less favorable the nucleation step, the higher average molecular weight is attained at equilibrium. Additionally, the abrupt increase of 〈dp〉
w around
Kct
= 1.0 illustrates that high
polymers are produced even if the total concentration is near the critical concentration. This prediction is consistent with the experimental results.
10 The fact that almost all the experimental observations about the
protein polymerization can be qualitatively explained by this model suggests that the nucleation–elongation mechanism is plausible, although more quantitative analyses are necessary to determine the accurate
nucleus size and the kinetic constants for the nucleation and elongation processes.
 |
| | Fig. 7 Plots of 〈dp〉n
(I) and 〈dp〉w
(II) as functions of Kct from cooperative nucleation–elongation polymerizations (without byproduct) with σ values as indicated. | |
As mentioned earlier, due to the lack of real experimental systems, few investigations have been carried out on cooperative nucleation–elongation polymerizations in which a small-molecule byproduct is generated. Intuitively, a nucleation process should also bring about similar properties as seen for the above non-byproduct reactions. As it turns out, the situation is a little different when a small-molecule byproduct forms along with the polymers. Again, for K2 < K3
=
…
=
Ki
=
…
=
K, the following relations can be derived from eqns. (6) and (7):
| | 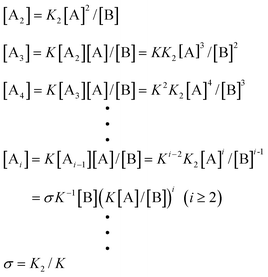 | (32) |
| | 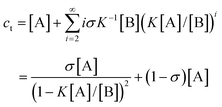 | (33) |
| |  | (34) |
| |  | (35) |
From eqns.
(33) and
(35), one can get:
| |  | (36) |
| |  | (37) |
| | 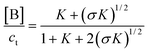 | (38) |
Therefore,
| | 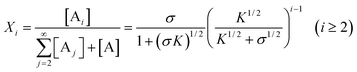 | (39) |
| | 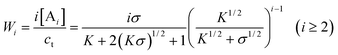 | (40) |
| |  | (41) |
| |  | (42) |
It is clear that the relative concentrations of A ([A]/ct) and B ([B]/ct) at equilibrium are independent of the total concentration ct and only determined by the values of σ and K. In other words, the absolute concentrations linearly increase with ct at constant σ and K. Accordingly, the equilibrium mole and weight fractions of i-mers (i.e., size distributions) are solely determined by the constants σ and K, irrespective of the total monomer concentration. Another important finding about byproduct-generating systems is that, if [A]/ct, 〈dp〉n or 〈dp〉w is plotted against logK, the sharp transitions that occurred with the above non-byproduct system do not exist in the current case (Figs. 8 and 9). The relative concentrations and average degrees of polymerization experience more gradual changes as the equilibrium constants (K and K2) are varied at constant σ. In fact, as σ approaches zero, [A]/ct becomes less sensitive to the σ value (Fig. 8, II). In other words, when K2≪
K, the relative concentration of monomer at equilibrium is largely dependent only on K being insensitive to K2. This is in great contrast to the average molecular weight, which is influenced by both K and σ, and substantially increases with decreasing σ value (Fig. 9). Interestingly, when 〈dp〉n is plotted against K2 at constant K
(Fig. 10), sigmoidal curves arise, showing that 〈dp〉n rapidly increases with diminishing K2. This transition always takes place within a certain range of K2
(i.e., ca. K2
= 0.1–10). Outside this range, 〈dp〉n becomes less sensitive to K2, tending to be linearly proportional to K on the smaller K2 side and tending to very small values on the larger K2 side. From the standpoint of molecular design, the important conclusion is that as long as K2 is significantly small (e.g., smaller than 0.01), large 〈dp〉n can be attained even from only moderate K values, which is in great contrast to isodesmic systems.
![Plots of [A]/ct
(I) and its derivative (II) as a function of K from nucleation–elongation polymerizations that produce a small-molecule byproduct with σ values as indicated. Curves a and b represent functions resulting from tight dimerization and isodesmic mechanisms, respectively. Curves c through g represent nucleation–elongation with a one-step nucleation event.](/image/article/2003/OB/b308788c/b308788c-f8.gif) |
| | Fig. 8 Plots of [A]/ct
(I) and its derivative (II) as a function of K from nucleation–elongation polymerizations that produce a small-molecule byproduct with σ values as indicated. Curves a and b represent functions resulting from tight dimerization and isodesmic mechanisms, respectively. Curves c through g represent nucleation–elongation with a one-step nucleation event. | |
 |
| | Fig. 9 Plots of 〈dp〉n
(I) and 〈dp〉w
(II) as a function of K from nucleation–elongation polymerizations that produce a small-molecule byproduct with σ values as indicated. Curves a and b represent functions resulting from tight dimerization and isodesmic mechanisms, respectively. Curves c through g represent nucleation–elongation with a one-step nucleation event. | |
 |
| | Fig. 10 Plots of 〈dp〉n/KversusK2 from nucleation–elongation polymerizations that produce a small-molecule byproduct. The K values are as indicated (curves c–e overlap). | |
5.3.2 Multiple nucleation steps.
Obviously, the nucleation process can be more complex than simple dimer formation. Without going through the details of derivation, results from multi-nucleation step polymerizations will be summarized here. The total concentration ct has a very similar expression to eqn. (29):| |  | (43) |
| | 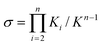 | (44) |
where n is the nucleus size.3,54,55 Due to the similarity in these mathematical expressions, one should expect analogous behaviors from multi-nucleation step polymerizations as compared to single nucleation step reactions: a critical total monomer concentration cc
=
K−1 arises from a very small value of σ. If ct < cc, the dominant species within a polymerization system is monomer and polymers are essentially non-existent; when ct > cc, high polymer forms and the monomer concentration remains nearly constant at all different total concentrations. Additionally, the following equation is obtained:| |  | (45) |
which indicates that, even at a total concentration close to critical concentration cc, a small value of σ gives rise to a large 〈dp〉.3,54
Furthermore, the breadth of the size distribution at equilibrium has been examined.3,55 The mean square deviation of the degree of polymerization from the average value is defined by:
| 〈δi2〉
=
〈(i
−
〈i〉)2〉
=
〈i2〉
−
〈i〉2 |
where
Since the concentration of
i-mer is given as a function of the size
i in a form of (
K[A])
i, or exp(-α
i), for large values of 〈
i〉, one can find:
In other words, the size distribution of the
polymers at equilibrium should be a broad exponential distribution. The polydispersity index (〈dp〉
w/〈dp〉
n) tends to 2.0 at large 〈
i〉 values.
56 This equilibrium state is reached
via a unique and interesting route in nucleation–elongation polymerizations, as will be discussed in more detail below.
Qualitatively summarizing the size distribution of a nucleation–elongation polymerization, since the nucleation factor, σ, is generally a very small value (i.e., K2
≪
K), all species smaller than the nucleus are unstable. Additionally, as the nucleus size is usually small (3 or 4 for F-actin)15,51,57–59 compared to the average size of the polymers, the overall population (concentration) of these short oligomers is negligible, except for the monomer. Since the equilibrium constant for the nucleation step(s) is minuscule, of all the oligomers that are below the size of the nucleus, the monomer is by far the most abundant species. The size distribution among high polymers for a nucleation polymerization should not be particularly different from that of an isodesmic polymerization, since the relative thermodynamic stabilities of high polymers are similar for the two systems. Nonetheless, the average degree of polymerization from a nucleated polymerization should be higher than that from an isodesmic reaction with a similar elongation constant, presumably due to the destabilization of the low oligomers. A broad exponential distribution among high polymers in the presence of a relatively large amount of monomers is expected from a highly cooperative nucleation–elongation polymerization.
6 Kinetics
The discussion that follows focuses on the approach to equilibrium and the rate by which this process is achieved. The kinetic features and mechanistic based models of polymerizations resulting from a cooperative nucleation event will be presented. The discussion will again start with the non-cooperative isodesmic model, and comparison will then be made to the nucleation–elongation polymerization.
6.1 Isodesmic chain growth (non-cooperative polymerization)
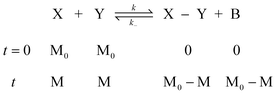
Under the assumption of chain-length independent reactivity of polymerizable groups60 in an isodesmic polymerization, the product size distribution should strictly follow statistical predictions both at equilibrium and at any point prior to that. Thus, the kinetic profile of an isodesmic polymerization can be conveniently obtained. If X and Y represent the two complementary polymerizable groups of all i-mers within a polymerization system, in the case of no small-molecule byproduct, one has:
where k and k− are the kinetic rate constants for the forward and reverse coupling reactions, M0 is the initial and total concentration of the polymerizable group, and M as the remaining concentration of the polymerizable group at reaction time, t. Thus, starting with stoichiometric ratio of X and Y, based on the rate equation law:| | 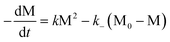 | (46) |
Let the reaction conversion p be defined as:Solving the differential equation (46) gives:61| |  | (48) |
where K
(=
k1/k2) is the equilibrium constant of the coupling reaction. Based on eqns. (47) and (48), one can further determine p, 〈dp〉n, and 〈dp〉w as functions of time (Fig. 11).62
 |
| | Fig. 11 Plots of M/M0
(I), reaction conversion p
(II), 〈dp〉n
(III), and 〈dp〉w
(IV) as a function of reaction time t in an isodesmic polymerization without a small-molecule byproduct, under various initial concentrations and rate constants. | |
Similarly, for an isodesmic polymerization system in which a byproduct is formed, solving the analogous kinetic differential equation gives the corresponding variants as a function of time:
| |  | (49) |
| |  | (50) |
Plots of M (the total concentration of all molecules but the byproduct), reaction conversion
p, and average degrees of
polymerization, 〈dp〉
n and 〈dp〉
w,
vs. time
t are shown in
Fig. 12. In this case, although the rate at which the polymerization approaches equilibrium varies with the initial total monomer concentration as well as with rate constants
k and
k−, the final equilibrium state is only determined by the equilibrium constant
K
(independent of M
0). If the byproduct is continuously removed out of the equilibrium (open system) so that its concentration remains low and constant during
polymerization, the reaction will then behave like one without the byproduct formation, since the concentration of the byproduct can be incorporated into the rate constant
k− as a constant.
 |
| | Fig. 12 Plots of M/M0
(I), reaction conversion p
(II), 〈dp〉n
(III), and 〈dp〉w
(IV) as a function of reaction time t in an isodesmic polymerization in which a small-molecule byproduct is produced, under various initial concentrations and rate constants. | |
Another distinct feature of isodesmic polymerizations is that the initial rate of polymerization linearly increases with time and is linearly proportional to the total concentration M0 and the forward rate constant k
(regardless of whether or not a byproduct is formed). This is evident from Figs. 11 and 12, and can be proven by examining the rate equations. At the initial stage of the polymerization (t
→ 0), the reverse reaction is negligible due to the low concentration of X–Y (M ≈ M0 and k−(M0
− M)
→ 0), eqns. (46) and (49) reduce into:
Thus,
As to be demonstrated later, the linear relationships presented in these equations distinguish the isodesmic polymerizations from the nucleation–elongation polymerizations.
6.2 Nucleated chain growth (cooperative polymerization)
Equal reactivity of the polymerizable groups allows the kinetics of the isodesmic polymerization to be analyzed with a simple statistical method. However, when the reactivity of the polymerizable group becomes dependent on the size of the molecule, multiple equations and rate constants are needed to represent the different reaction rates of chains of various lengths, and thus the analysis becomes considerably more complicated.
Specifically, for a polymerization that has a nucleation event, the end group of molecules of sizes smaller than the nucleus is less reactive than those i-mers larger than the nucleus. Qualitatively, as the polymerization proceeds, the average size of molecules within the system gradually increases; thus, the average reactivity will change over time, and the polymerization should exhibit a kinetic profile distinct from an isodesmic polymerization.
For a system with size-dependent reactivity, the rate equations of i-mers should be individually expressed with associated rate constants [cf. eqns. (1)]:
| | 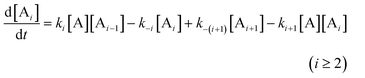 | (51) |
where the rate constants
k±i and
k±(i
+ 1) may, or may not, be equal to each other. The terms in
eqn. (51) account for the emergence of
i-mer
via monomer addition to the (
i
− 1)-mer and depolymerization of (
i
+ 1)-mer, and the loss of
i-mer through depolymerization and polymerization into molecules one repeating unit shorter and longer, respectively (the validity of the choice of these specific pathways to represent the kinetic mechanism will be discussed later).
As rigorous algebraic solutions to the entire set of interrelated differential equations appear to be impractical, approximations and/or simplifications are usually made when deriving kinetic models. If the rate constants of chain elongation are assumed independent of the degree of polymerization i, when i is larger than the nucleus size n
(i.e., kn
+ 1
=
kn
+ 2
=
kn
+ 3
…
=
ki
…
=
k and k−(n
+ 1)
=
k−(n
+ 2)
=
k−(n
+ 3)
…
=
k−i
…
=
k− and i > n), the rate equations of polymers larger than nuclei can be generalized as:
| | 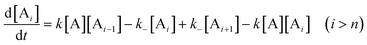 | (52) |
In the kinetic model initially developed by Oosawa and Kasai, the nucleation is assumed to be a pre-equilibrium association of n monomer units, followed by a slow, rate limiting transformation of the resultant n-mer into the nucleus.3,54 Accordingly, the following equation was employed to describe the rate of nuclei formation:
| |  | (53) |
where
k* and
k−* represent the rate constants for the formation and dissociation of nuclei. The sum of
eqns. (53) and
(52) for all
i >
n gives:
| | 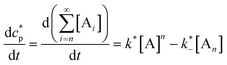 | (54) |
| |  | (55) |
where
cp* is the total concentration of all
polymers equal to or larger than
nucleus size,
n, and
ct* is the concentration of monomers incorporated into these
polymers. In
eqn. (55),
ct* is assumed equal to (
ct
−
[A]), implying the concentrations of any species smaller than the
nucleus are negligible (except for monomer). Chain fragmentation (
polymers breaking into two fragments) and reannealling (association of
polymers) are not taken into consideration at this point.
Furthermore, with the assumption that dissociations of polymers and nuclei are negligible (i.e., k− and k−* equal zero), eqn. (55) was combined with eqn. (54) and further reduced into:
| |  | (56) |
Integration of
eqn. (56) gives:
| |  | (57) |
where again,
ct is the initial concentration of monomers.
3,54 Since
ct* is equal to (
ct
−
[A]), the total concentration of monomer units incorporated in the
polymers as a function of time can be obtained (
Fig. 13). In these plots, a noticeable period of induction can be seen, consistent with experimental observations on
protein polymerizations.
27,51,57,58,63
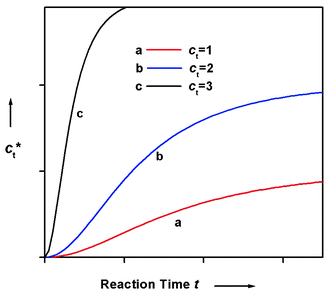 |
| | Fig. 13 Qualitative plot of ct*
vs. reaction time t based on the Oosawa–Kasai model.3 The concentration was of arbitrary unit. | |
Based on eqns. (56) and (57), the initial polymerization rate is approximately proportional to the (n
+ 1)-power of the total monomer concentration ct, and the time to reach the half-way point of the polymerization, t1/2
(defined as the time needed for half of the total monomers to be transformed into polymers, ct*
=
ct/2), should be inversely proportional to ctn/2. Therefore, the nucleus size can be obtained by measuring the full time kinetic profile of a polymerization, provided the model's assumptions are valid.
Independently, Wegner and Engel simplified the kinetic differential equations using steady-state approximations:58,63
where
Kinetic simulations were achieved by numerical integration of the above two differential equations. Although nucleation was again assumed as a fast pre-equilibrium process, no assumption about irreversibility of the polymerization was made in this model. Refinements to these models included processes such as fragmentation and reannealling.
Later, Frieden and Goddette used a series of descriptive mechanistic equations [eqns. (58)] to simulate the polymerization kinetics through computer-programmed numerical integrations.64,65
| |  | (58) |
One of the distinguishing features of this model is that the mechanistic scheme is composed of a set of circular reaction equations; that is, the association of a monomer with A
p generates the same molecule A
p. The quantity A
p represents all
polymers larger than a particular value [
e.g., larger than 6 units for
eqn. (58)]. Thereby, the total number of differential equations was limited to allow the computation to be accomplished within a practical period of time. In order to prevent the concentration of A
6 from fluctuating with the accumulation of A
p,
k−6 was always set to zero, which was proven not to substantially alter the time course simulations of the polymerization. Expressions that represented successive monomer association with species up to the hexamer were shown to be sufficient to simulate actin
polymerization. Further increasing the number of equations to incorporate distinct rate constants for larger molecules did not significantly change the results. The percentage of monomers incorporated into
polymers was designated by
| (ct
−
[A]
− 2[A2]
− 3[A3]
− 4[A4]
− 5[A5])/ct |
where
ct is the total monomer concentration. This percentage value was used to represent the extent of polymerization. The availability of software packages such as KINSIM
65 makes it practical for various mechanistic schemes to be evaluated without experience in solving complete differential equations.
The value of this model is that it can be very informative regarding the evaluation of kinetic constants for the initial oligomerization steps of the polymerization. Important insight into the nucleation steps and the steps immediately following has been gained. These steps turn out to be especially influential over the time course of polymerization.64 However, as a consequence of the uniform expression for all the long, polymeric species, the size distribution information was necessarily lost. Moreover, the mechanistic scheme can be easily modified to accommodate additional steps and different processes. For example, the following equation could be incorporated to describe a conformational change undertaken by the monomer prior to participation in the polymerization:
Alternatively, a step reflecting the monomer bound to a
ligand, followed by a conformational change is represented as:
The Frieden–Goddette mechanistic scheme may be modified to accommodate byproduct generation in polymerizations, by simply adding an extra term to each equation within the model:
| | 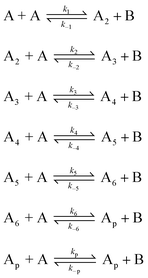 | (59) |
Representative results are shown in
Fig. 14. The kinetic constants employed in the plot of
Fig. 14 are for illustrative purposes only. Nonetheless, the explicit values of these rate constants should not alter the overall trend of the time course of
polymerization, since different numbers can all be reduced to the same value by varying the time scale. It is the relative ratio of these kinetic constants that determine the final equilibrium state and the overall shape of the kinetic profiles.
 |
| | Fig. 14 Simulated time courses of a nucleation–elongation polymerization generating a small-molecule byproduct at two different concentrations (a, ct
= 0.1; b, ct
= 0.05). For both curves, k1–k6 and kp
= 1.0, k−1and k−2
= 0.25, k−3–k−5 and k−p=10−4, and k−6
= 0. Concentrations and rates constants are of arbitrary units. | |
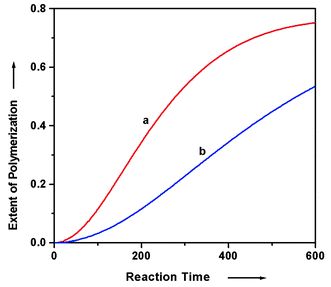
It is worth noting that kinetic simulations from these models invariably reveal a period of induction at the initial stage of the nucleation–elongation polymerizations. Specifically, the velocity of polymerization is slow in the beginning, but it then accelerates before slowing down again due to monomer consumption. This induction period may well be explained by the nucleation–elongation mechanism of the polymerization. At the initial phase of the polymerization, the dominant species within the system are monomers and oligomers below the nucleus size. Once a small amount of oligomers larger than nuclei have formed, rapid growth to high polymer consumes the monomers, which accounts for the acceleration period of the polymerization. As discussed earlier, this is in contrast to isodesmic polymerization systems, wherein the polymerization rate remains nearly constant at the initial stage of the polymerization before it tapers off. A noticeable induction period thus provides experimental evidence of a cooperative mechanism.
Finally, one should consider whether these specific sets of reaction equations [eqns. (58) and (59)] can be justified to simulate the polymerization kinetics. Do these selected equations represent the most favorable (probable) pathways that lead to the final products? Alternatively, do the reversible associations/dissociations of oligomers actually contribute to the polymerization course? Based on the concentrations at the end of the simulated time course, the monomer was indeed the dominant species in the case of polymerizations that do not generate a byproduct. Successive monomer addition to the oligomers and high polymers thus seems to be a reasonable choice as the major kinetic pathway. However, in the case of polymerization with byproduct formation, this may or may not be justifiable depending on the equilibrium constants provided to the simulation. Therefore, in the examples shown in Fig. 14, the simulation was limited to the low reaction conversion stage when monomer concentration was still significant to ensure the mechanism shown in eqns. (59) remains valid.
It is commonly known that the addition of small crystals or liquid drops into supersaturated solution or gas accelerates the rate of crystallization or gas–liquid condensation, respectively. Similarly, “seeding” effects have also been observed in actin and flagellin polymerizations. When a small amount of F-actin fragments was added to a G-actin solution, in which the salt concentration was too low to induce spontaneous polymerization, these fragments were observed to grow instantaneously.66 This acceleration effect of adding pre-existent nuclei was even more evident in the polymerization of flagellin.11 At neutral pH and low salt concentrations, flagellin monomers did not polymerize until a small amount of flagella fragments were added. Furthermore, it was proven that the filament length increases in direct proportion to the amount of monomers present, suggesting that the total number of flagella upon completion of polymerization was equal to the number of flagella fragments initially added. Consequently, the polymerization only took place by appending flagellin monomers to the pre-existing nuclei. These observations can reasonably be explained by the nucleation–elongation mechanism of the polymerization.
Seeded polymerizations are most effective under conditions in which the rate of nucleus formation is exceptionally slow but elongation is extremely favored and fast (e.g., k*
→ 0 and k
≫
k−). If pre-formed polymers capable of fast elongation are added to a monomer solution under such conditions, the association of monomers to these “seed” molecules will dominate the polymerization and the consumption of the monomers. Therefore, eqn. (55) reduces to:
where
cp* is a constant value determined by the concentration of “seeds”
(nuclei) added. Integration of the above equation gives:
| | 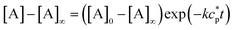 | (60) |
where
corresponds to the monomer concentration coexisting with
polymers at polymerization equilibrium, and [A]
0 is the initial monomer concentration. Thus, the reaction behaves like a “living” polymerization.
2
It should be noted that the addition of preformed nuclei that are indistinguishable from spontaneously formed ones has no influence over the final equilibrium state but only alters the time course of the polymerization. This notion was supported by the experimental evidence in that the concentration of the monomer coexisting with polymers was independent of the amount of added “seeds”.52,67
As discussed earlier, the equilibrium size distribution of a nucleation–elongation polymerization should be a broad, exponential one. However, under the conditions that spontaneous nucleation is inhibited (or extremely slow), the polymerization is dominated by the addition of monomer to the nuclei added into the system. Since it is reasonable to assume that the all the nuclei have equal capability to associate with monomers and grow, the growth rate of all nuclei are nearly equal and thus the size distribution of a “seeded” polymerization is expected to be narrow. A rational explanation to this discrepancy has to be that the equilibrium size distribution is established via two steps: (1) the monomer concentration tends to the equilibrium value quickly by reacting with the nuclei while the size distribution remains narrow; (2) as the polymerization proceeds, the concentration of monomer decreases, and thus depolymerization is no longer negligible; gradually, the size distribution broadens and tends to the final exponential state. This supposition was proven by Oosawa et al. by analyzing the kinetics of size distribution during a nucleation–elongation polymerization.3,55
7 Perspectives
The characteristics of the nucleation–elongation polymerization mechanism have been discussed. This polymerization mechanism is based on the reversible joining of monomer units by either covalent or non-covalent linkages; however, we argue that whatever the nature of the “primary backbone”, non-covalent interactions must be present to provide the dominant driving force for polymer formation. Nucleation–elongation polymerization is a cooperative process. The roots of this cooperative behavior are in the supramolecular structure of the final polymeric product. Specifically, if the polymeric product is strictly a one dimensional chain, cooperative behavior is probably impossible. In such a case, there can be no nucleation event that triggers subsequent polymer growth. In contrast, if the final polymeric product has a structure in which the repeat units are stabilized by interactions with multiple neighboring monomers, cooperative behavior is expected. From a thermodynamic standpoint, cooperative behavior manifests itself as an all-or-none transition between monomer and polymer. We have shown here that this transition may or may not involve a critical monomer concentration. When a critical concentration is involved (i.e., polymerizations producing no byproduct), polymerization ensues only when monomer concentration is greater than this critical value; otherwise, no polymerization occurs. For polymerizations having no critical monomer concentration (i.e., byproduct-generating polymerization), the transition between monomer and polymer is only a function of the equilibrium constants that govern the formation of the nucleus. Concerning the time course of polymerization, cooperative behavior manifests itself by an induction period, with rates of polymer formation that depend on the details of the pathway leading to the nucleus. Seeded growth can overcome this induction period.
The mechanism of nucleation–elongation is widely employed in biology as a means to assemble in dynamic fashion the beams and girders that support the cell's shape, motility, and organization of subcellular components. In great contrast, the mechanism has rarely been seen in synthetic polymer chemistry. Most of the known synthetic polymers that exhibit features of nucleation–elongation growth are tied to crystallization phenomena. We recently disclosed a soluble helical polymer in which an intrachain supramolecular structure drives a metathesis polymerization reaction.42,43 Many aspects of this polymerization remain to be investigated, but if further studies uphold the postulated nucleation–elongation behavior of this polymerization, it will be—to the best of our knowledge—the first soluble synthetic polymer produced by such a mechanism.
The void in synthetic examples of nucleation–elongation polymerization probably exists for several reasons. For one thing, the polymeric products must involve a fairly sophisticated internal supramolecular structure. Progress in achieving synthetic polymers with the necessary compact “folded” structure has been made only recently.17–26 Another reason for this void may simply be the lack of a perceived need. What does one do with a dynamic polymer that exhibits all-or-none polymerization behavior? What special properties might such a system have that are not achievable with current technology? The best answers to these questions may only come after examples of such behavior are widely known and readily available. Nonetheless, the ability to reversibly assemble and disassemble polymeric molecules according to environmental conditions would seem to offer special behavior and properties not common to today's synthetic macromolecules. For example, by analogy to cellular biology, it is possible to imagine that such dynamic polymeric systems could play important roles in the creation of nanoscale machines. Other applications that come to mind are self-healing materials68 in which a fluid monomer, in the absence of a nucleus, is capable of existing as a metastable solution. This fluid state would be useful for transporting monomer to the site of damage. If damage exposes a seed that nucleates the start of the polymerization reaction, a means to automatically repair the material's damage is conceived. Another application of such a reaction is stimuli-responsive fluids. Here a change in environmental conditions (e.g., a change in temperature) could bring about a reversible transition in a monomer to polymer equilibrium that manifests itself as an abrupt change in the fluid's viscoelastic properties (e.g., smart fluids).
Finally, we suggest that nucleation–elongation polymerizations may provide a natural route to prepare synthetic mimics of protein-like globular, soluble macromolecules. The preparation of non-biological macromolecules that are folded with tertiary structure remains an impossible task for the synthetic polymer chemist. The problem is challenging for many reasons, but mostly because complex polymeric sequences are involved. Homopolymers are simply incapable of adopting uniquely folded structures.69 Both the rational design and synthesis of high molecular weight heterosequences having well-defined tertiary structure is not possible today. How might we achieve such structures with a cooperative nucleation–elongation polymerization process?
The folding of proteins into globular structures is believed to be driven predominantly by the solvophobic interaction.70 This is supported by the fact that most globular proteins have a hydrophobic “core” and a largely hydrophilic “shell”.71 The former stabilizes the overall compact shape while the latter maintains solubility. Such a balance between globularity and solubility requires very precise compositional heterogeneity distribution of the constituent amino acids.72–74 Both theoretical and experimental studies have suggested that only a fraction of all possible sequences give rise to such globular, soluble structures.75–80
Fig. 15 illustrates a hypothetical approach to selectively synthesize soluble, globular macromolecules based on a reversible polymerization. A pair of amphiphilic comonomers (black and white spheres representing solvophilic and solvophobic units, respectively) is to be joined into polymers through reversible covalent bonds; thus, all sequences generated within the systems are inter-convertible with one another. The formation of the covalent bonds between the monomers is intentionally chosen to cause minimal free energy change; consequently, the relative population of each sequence will predominantly be determined by its kinetic and/or thermodynamic stability, which in turn is related to the details of internal supramolecular structure. By carefully choosing equilibration conditions to favor solvophobic interactions, the overall equilibrium may be shifted to selectively generate the compactly folded structures. This approach bypasses the design and separation of specific sequences, focusing on the desired globular molecules to be spontaneously produced.
 |
| | Fig. 15 Schematic model of a reversible polymerization of an amphiphilic pair of monomers (white sphere—solvophobic, black sphere—solvophilic). The free energy gained from the association of the solvophobic units will shift the polymerization equilibrium to selectively produce the sequences that favor globular conformation for a given set of conditions. | |
Sequences of predominantly solvophilic residues [via pathway (a)] will be soluble and not collapsed due to the relatively few solvophobic associations. Such chains are unlikely to be favored since insufficient stabilizing energy would be gained from solvophobic interactions; their population will remain small. At the other extreme, molecules with solvophobic-rich sequences will tend to aggregate and become insoluble, precipitating from solution [pathway (b)]. One may anticipate this pathway to dominate the polymerization, as solvophobic monomers will prefer to associate and hence favorably react with one another. Deep traps such as pathway (b) in which precipitation drains away all the solvophobic units must be avoided if this approach is to produce globular, soluble macromolecules. We suggest that such aggregation and precipitation may be circumvented by designing suitable “starter sequences” in which a given number of monomer units are irreversibly linked together. By excluding segments entirely composed of solvophobic residues from the starter sequence library, the maximum consecutive solvophobic repeat units within the polymer chain will be limited to a certain number. This approach will enable the monomer composition (solvophobic vs. solvophilic) of all chains to fall within a specified window, set by the range of compositions in the starter sequence library. Even for polymer chains possessing a suitable overall composition of solvophobic and solvophilic residues, a large fraction of the possible sequences will still not be optimally stabilized (i.e., fold poorly) due to the unfavorable distribution of the solvophobic/solvophilic units [pathway (c)]. Consequently, this set of sequences is not likely to be formed to any significant degree. Only a subset of all sequences will have the optimal distribution of monomers able to adopt a compact conformation having a minimum free energy [pathway (d)].
Since the stability of a given sequence is determined by the number of non-adjacent, intramolecular solvophobic interactions, the proposed polymerization should naturally be a cooperative process. As the occurrence of non-adjacent interactions requires a minimum chain length, which is related to the intrinsic flexibility of the chain, favorable interactions within subcritical chains must be minimal, or non-existent. A nucleation event should thus emerge. As the chain grows longer, non-adjacent interactions become possible and progressively stabilize those sequences allowing maximum solvophobic interactions. Correspondingly, rate acceleration in polymerization should ensue.
It is therefore reasonable to envision that a reversible, nucleation–elongation polymerization as described above would spontaneously produce a smaller subset of the entire sequence library in a cooperative fashion. The result should be structures that are kinetically or thermodynamically most favored, some of which may be uniquely folded into soluble, globular structures under suitable conditions.
Nucleation–elongation polymerization is a relatively unexplored avenue of synthetic polymer chemistry. This mechanism of macromolecular chain growth offers some unique and interesting thermodynamic and kinetic attributes not found in the more classical mechanisms of polymer chemistry. The practical benefits of this type of polymerization await further discoveries and more readily available examples. With greater sophistication and deeper insights in the field of supramolecular polymerizations, the exploitation of cooperative chain growth as dynamic and responsive materials is likely to emerge.
8 Appendix
Definition of terms/variables:
| A | Polymerization monomer |
| [A] | Concentration of species A |
| Ai | Polymer of A at a degree of polymerization of i |
|
c
t
| Total concentration of monomer/repeating unit |
|
c
p
| Total concentration of polymer molecules |
| 〈dp〉n | Number-average degree of polymerization |
| 〈dp〉w | Weight-average degree of polymerization |
|
i
| Degree of polymerization |
|
K
| Equilibrium constant |
|
k
| Rate constant of an association reaction |
|
k
−
| Rate constant of a dissociation reaction |
| PDI | Polydispersity index |
|
σ
| Nucleation factor |
|
t
| Reaction time |
|
X
i
| Mole fraction of i-mer |
|
W
i
| Weight fraction of i-mer |
9 Acknowledgements
This material is based upon work supported by the National Science Foundation under NSEC Grant No. 0117792 and the U.S. Department of Energy, Division of Materials Sciences, under Award No. DEFG02-91ER45439, through the Frederick Seitz Materials Research Laboratory at the University of Illinois at Urbana-Champaign.
10 References and notes
-
P. J. Flory, Principles of Polymer Chemistry, Cornell University Press, Ithaca, 1953 Search PubMed.
-
G. Odian, Principles of Polymerization, John Wiley & Sons, New York, 1991 Search PubMed.
-
F. Oosawa and S. Asakura, Thermodynamics of the Polymerization of Protein, Academic Press Inc., New York, 1975 Search PubMed.
- H. Fraenkel-Conrat and R. C. Williams, Proc. Natl. Acad. Sci. U.S.A., 1955, 41, 690 CAS.
- D. Abram and H. Koffler, J. Mol. Biol., 1964, 9, 168 CAS.
- M.-F. Carlier, J. Biol. Chem., 1991, 266, 1 CAS.
- T. Ooi, K. Mihashi and H. Kobayashi, Arch. Biochem. Biophys., 1962, 98, 1 CAS.
- A. D. Sousa and C. S. Farah, J. Biol. Chem., 2002, 277, 2081 CrossRef CAS.
- R. B. Martin, Chem. Rev., 1996, 96, 3043 CrossRef CAS.
- F. Oosawa, S. Asakura, K. Hotta, N. Imai and T. Ooi, J. Polym. Sci., 1959, 37, 323 Search PubMed.
- S. Asakura, G. Eguchi and T. Iino, J. Mol. Biol., 1964, 10, 42 CAS.
- S. Asakura, J. Mol. Biol., 1968, 35, 237 CAS.
- T. M. Schuster, R. B. Scheele and L. H. Khairallah, J. Mol. Biol., 1979, 127, 461 CAS.
- S. J. Shire, J. J. Steckert and T. M. Schuster, J. Mol. Biol., 1979, 127, 487 CAS.
- A. Wegner, Nature, 1982, 296, 266 CAS.
- E. D. Korn, M.-F. Carlier and D. Pantaloni, Science, 1987, 238, 638 CAS.
- D. Seebach and J. L. Matthews, Chem. Commun., 1997, 2015 RSC.
- S. H. Gellman, Acc. Chem. Res., 1998, 31, 173 CrossRef CAS.
- K. Kirshenbaum, R. N. Zuckermann and K. A. Dill, Curr. Opin. Struct. Biol., 1999, 9, 530 CrossRef CAS.
- A. E. Barron, Curr. Opin. Chem. Biol., 1999, 3, 681 CrossRef CAS.
- K. D. Stigers, M. J. Soth and J. S. Nowick, Curr. Opin. Chem. Biol., 1999, 3, 714 CrossRef CAS.
- E. A. Archer, H. G. Gong and M. J. Krische, Tetrahedron, 2001, 57, 1139 CrossRef CAS.
- B. Gong, Chem. Eur. J., 2001, 7, 4336 CrossRef CAS.
- M. S. Cubberley and B. L. Iverson, Curr. Opin. Chem. Biol., 2001, 5, 650 CrossRef CAS.
- D. J. Hill, M. J. Mio, R. B. Prince, T. S. Hughes and J. S. Moore, Chem. Rev., 2001, 101, 3893 CrossRef CAS.
- C. Schmuck, Angew. Chem., Int. Ed., 2003, 42, 2448 CrossRef CAS.
- R. Fesce, F. Benfenati, P. Greengard and F. Valtorta, J. Biol. Chem., 1992, 267, 11289 CAS.
- A. Wegner, J. Mol. Biol., 1976, 108, 139 CAS.
- J. S. Moore and N. W. Zimmerman, Org. Lett., 2000, 2, 915 CrossRef CAS.
- W. Kern and V. Jaacks, J. Polym. Sci., 1960, 48, 399 Search PubMed.
- L. Leese and M. W. Baumber, Polymer, 1965, 6, 269 CrossRef CAS.
- M. Iguchi, H. Kanetsuan and T. Kawai, Makromol. Chem., 1969, 128, 63 CrossRef CAS.
- Y. Iwakura, K. Uno and M. Oya, J. Polym. Sci.: Part A-1, 1967, 5, 2867 Search PubMed.
- T. Komoto, T. Akaishi, M. Oya and T. Kawai, Makromol. Chem., 1972, 154, 151 CrossRef CAS.
- A. Fujie, T. Komoto, M. Oya and T. Kawai, Makromol. Chem., 1973, 169, 301 CrossRef CAS.
- T. Komoto and T. Kawai, Makromol. Chem., 1973, 172, 221 CrossRef CAS.
- T. Komoto, K. Y. Kim, M. Oya and T. Kawai, Makromol. Chem., 1974, 175, 283 CrossRef CAS.
- T. Komoto, M. Oya and T. Kawai, Makromol. Chem., 1974, 175, 301 CrossRef CAS.
- K. Y. Kim, T. Komoto and T. Kawai, Makromol. Chem., 1979, 180, 465 CrossRef CAS.
- T. Komoto, K. Y. Kim, Y. Minoshima, M. Oya and T. Kawai, Makromol. Chem., 1973, 168, 261 CrossRef CAS.
- Crystallization of the polymers has also been reported to induce reactions within polymer chains. See:
(a) R. W. Lenz, E. Martin and A. N. Schuler, J. Polym. Sci., 1973, 11, 2265 Search PubMed;
(b) R. W. Lenz, K. Ohata and J. Funt, J. Polym. Sci.: Polym. Chem., 1973, 11, 2273 CrossRef CAS;
(c) R. W. Lenz and S. Go, J. Polym. Sci.: Polym. Chem., 1973, 11, 2927 CrossRef CAS;
(d) R. W. Lenz and S. Go, J. Polym. Sci.: Polym. Chem., 1974, 12, 1971;
(e) R. W. Lenz and A. N. Schuler, J. Polym. Sci.: Polym. Symp., 1978, 63, 1343–1363 Search PubMed;
(f) K. Kimura, S. Kohama and Y. Yamshita, Macromolecules, 2002, 35, 7545 CrossRef CAS;
(g) K. Kimura, S. Kohama and Y. Yamshita, Macromolecules, 2003, 36, 5043 CrossRef CAS.
- D. Zhao and J. S. Moore, J. Am. Chem. Soc., 2002, 124, 9996 CrossRef CAS.
- D. Zhao and J. S. Moore, Macromolecules, 2003, 36, 2712 CrossRef CAS.
- J. C. Nelson, J. G. Saven, J. S. Moore and P. G. Wolynes, Science, 1997, 277, 1793 CrossRef CAS.
- R. B. Prince, J. G. Saven, P. G. Wolynes and J. S. Moore, J. Am. Chem. Soc., 1999, 121, 3114 CrossRef CAS.
- S. J. Rowan, S. J. Cantrill, G. R. L. Cousins, J. K. M. Sanders and J. F. Stoddar, Angew. Chem., Int. Ed., 2002, 41, 898 CrossRef.
- Recently, there has been considerable interest in synthetic polymers that are also strictly supramolecular, but these structures probably polymerize by a non-cooperative mechanism. See: L. Brunsveld, B. J. B. Folmer, E. W. Meijer and R. P. Sijbesma, Chem. Rev., 2001, 101, 4071 Search PubMed.
- L. Pauling, Discuss. Faraday Soc., 1953, 13, 170 RSC.
- D. S. Goodsell and A. J. Olson, Trends Biochem. Sci., 1993, 18, 65 CrossRef CAS.
- D. Winklmair, Arch. Biochem. Biophys., 1971, 147, 509 CAS.
- C. Frieden, Proc. Natl. Acad. Sci. U.S.A., 1983, 80, 6513 CAS.
- B. R. Gerber, S. Asakura and F. Oosawa, J. Mol. Biol., 1973, 74, 467 CAS.
- F. Gaskin, C. R. Cantor and M. L. Shelanski, J. Mol. Biol., 1974, 89, 737 CAS.
- F. Oosawa and M. Kasai, J. Mol. Biol., 1962, 4, 10 CAS.
- F. Oosawa, J. Theor. Biol., 1970, 27, 69 CAS.
- More recently, a slightly different approach has been employed to derive the thermodynamic length distribution of polymer products from nucleation–elongation
polymerizations and an approximate expression for average polymer size at equilibrium was established. See: L. Edelstein-Keshet and G. B. Ermentrout, Bull. Math. Biol., 1998, 60, 449 Search PubMed.
- L. S. Tobacman and E. D. Korn, J. Biol. Chem., 1983, 258, 3207 CAS.
- A. Wegner and P. Savko, Biochemistry, 1982, 21, 1909 CrossRef CAS.
- J. A. Cooper, E. L. Buhle, S. B. Walker, T. Y. Tsong and T. D. Pollard, Biochemistry, 1983, 22, 2193 CrossRef CAS.
- By polymerizable group we refer to the associating segments of a supramolecular polymer or the segments that form covalent linkages of a covalent polymer.
-
J. H. Espenson, Chemical kinetics and reaction mechanisms, McGraw-Hill, Inc., New York, 1981 Search PubMed.
- For isodesmic systems, the relationships between the reaction conversion and average degrees of polymerization can be conveniently obtained using statistical methods (refs. 1 and 2): 〈dp〉n
= 1/(1 −
p), 〈dp〉w
=
(1 +
p)/(1 −
p).
- A. Wegner and J. Engel, Biophys. Chem., 1975, 3, 215 CrossRef CAS.
- C. Frieden and D. W. Goddette, Biochemistry, 1983, 22, 5836 CrossRef CAS.
- B. A. Barshop, R. F. Wrenn and C. Frieden, Anal. Biochem., 1983, 130, 134 CrossRef CAS.
- M. Kasai, S. Asakura and F. Oosawa, Biochim. Biophys. Acta, 1962, 57, 22 CrossRef CAS.
- Y. Nakaoka and M. Kasai, J. Mol. Biol., 1969, 44, 319 CAS.
- S. R. White, N. R. Sottos, P. H. Geubelle, J. S. Moore, M. R. Kessler, S. R. Sriram, E. N. Brown and S. Viswanathan, Nature, 2001, 409, 794 CrossRef CAS.
- P. G. Wolynes, Nat. Struct. Biol., 1997, 4, 871 CAS.
- G. D. Rose and R. Wolfenden, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 381 CrossRef CAS.
- J. C. Kendrew, Science, 1963, 139, 1259 CAS.
- K. A. Dill, Biochemistry, 1985, 24, 1501 CrossRef CAS.
- R. E. Gates and H. F. Fisher, Proc. Natl. Acad. Sci. U.S.A., 1971, 68, 2928 CAS.
- S. H. White, Annu. Rev. Biophys. Biomol. Struct., 1994, 23, 407 CrossRef CAS.
- A. Yamauchi, T. Yomo, F. Tanaka, I. D. Prijambada, S. Ohhashi, K. Yamamoto, Y. Shima, K. Ogasahara, K. Yutani, M. Kataoka and I. Urabe, FEBS Lett., 1998, 421, 147 CrossRef CAS.
- I. D. Prijambada, T. Yomo, F. Tanaka, T. Kawama, K. Yamamoto, A. Hasegawa, Y. Shima, S. Negoro and I. Urabe, FEBS Lett., 1996, 382, 21 CrossRef CAS.
- C. J. Camacho and D. Thirumalai, Phys. Rev. Lett., 1993, 71, 2505 CrossRef CAS.
- K. F. Lau and K. A. Dill, Macromolecules, 1989, 22, 3986 CrossRef CAS.
- S. P. Rao, D. E. Carlstrom and W. G. Miller, Biochemistry, 1974, 13, 943 CrossRef CAS.
- H. F. Fisher, Proc. Natl. Acad. Sci. U.S.A., 1964, 51, 1285 CAS.
|
| This journal is © The Royal Society of Chemistry 2003 |
Click here to see how this site uses Cookies. View our privacy policy here. 

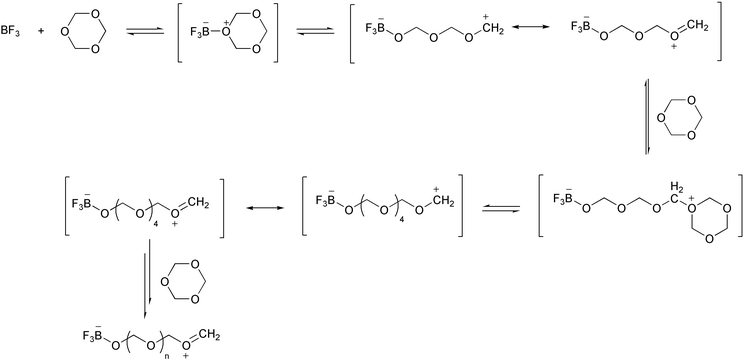
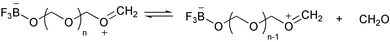


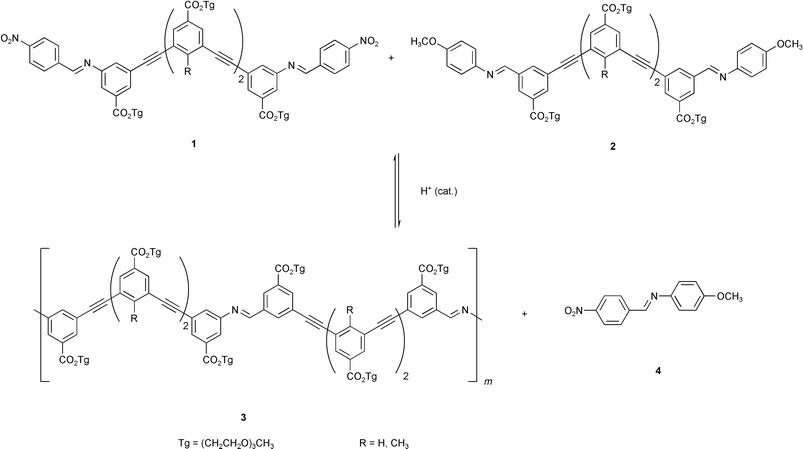






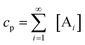
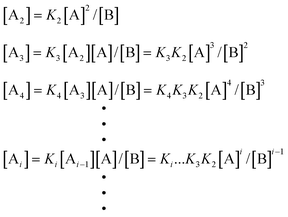
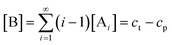

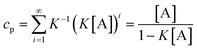
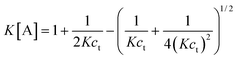
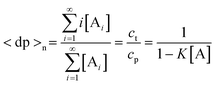

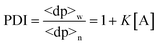
![Plots of K[A]
(I, —), [A]/ct
(I, ), 〈dp〉n
(II, —), and 〈dp〉w
(II, ) as functions of Kct under the conditions of an isodesmic polymerization without byproduct.](/image/article/2003/OB/b308788c/b308788c-f5.gif)
![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ), 〈dp〉n
(II, —), and 〈dp〉w
(II,
), 〈dp〉n
(II, —), and 〈dp〉w
(II, ![[dash dash, graph caption]](https://www.rsc.org/images/entities/char_e091.gif) ) as functions of Kct under the conditions of an isodesmic polymerization without byproduct.
) as functions of Kct under the conditions of an isodesmic polymerization without byproduct.


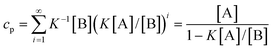


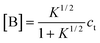





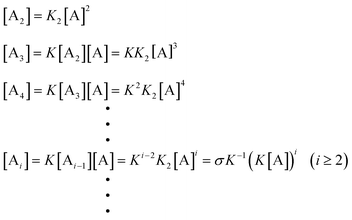

![Plots of [A]/ct
(I) and K[A]
(II) as functions of Kct from cooperative nucleation–elongation polymerizations (without byproduct) with σ values as indicated.](/image/article/2003/OB/b308788c/b308788c-f6.gif)

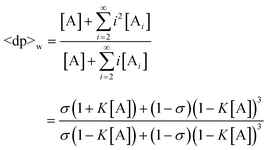

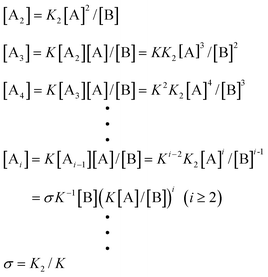
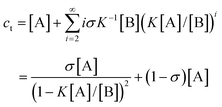




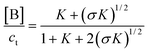
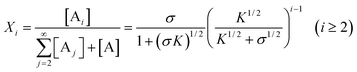
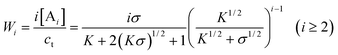


![Plots of [A]/ct
(I) and its derivative (II) as a function of K from nucleation–elongation polymerizations that produce a small-molecule byproduct with σ values as indicated. Curves a and b represent functions resulting from tight dimerization and isodesmic mechanisms, respectively. Curves c through g represent nucleation–elongation with a one-step nucleation event.](/image/article/2003/OB/b308788c/b308788c-f8.gif)