Experimental and theoretical study of α-acetoxylation of ketones by (diacetoxy)iodobenzene

Abstract

Herein, we investigated the α-acetoxylation of ketones through various experiments. These include screening of reaction conditions, analysis of reactivity and selectivity over diverse ketones, kinetic study of the reaction of monoacetoxylation and diacetoxylation, density functional theory calculations for estimating the energy and structure, and analysis of natural bond orbitals. Based on the reaction products of the study, the pseudo first-order model is determined as the best model for the reaction, and the identification of the reaction intermediates indicates that iodonium is an essential intermediate in the reaction. Additionally, kinetic studies and theoretical calculations reveal that the reaction may utilize a different mechanism depending on the ketone structure; in this case, however, we focused on the α-acetoxylation of 4-tert-butylcyclohexanone. Based on these findings, we propose a reaction mechanism and the corresponding behavior description for iodine(III) in α-acetoxylation reactions.

---

Introduction

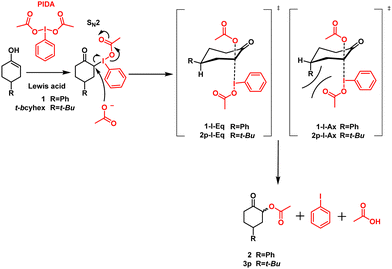
Hypervalent iodine(III) compounds function as effective reagents for synthesizing various compounds, such as α-hydroxy carbonyl,^1–3 α-tosylate carbonyl,^4,5 and α-acetoxy carbonyl,^3,6–9 as well as in alcohol oxidations,^10–12 rearrangements,^13,14 and other reactions.^15–18 Several organic chemists have studied these reactions; nevertheless, the α-acetoxylation of ketones using diacetoxyiodobenzene (PIDA) is a reaction with many protocols and mechanistic studies.^3,6–9 Although the mechanism of these reactions has been approximated by many authors,^6,9,19 the mechanism behind the α-acetoxylation of ketones with PIDA needs to be discussed further.

Moriarty and Maruoka proposed that the first step in the α-acetoxylation of ketones with PIDA is the nucleophilic attack of the enol double bond (i.e., 1) on the electrophilic iodine of PIDA, forming α-iodine (III) (1-I) as the intermediate.^9,19 After this step, the addition of acetoxy is mediated by bimolecular (S_N2) nucleophilic substitution, forming α-acetoxy carbonyl (2), iodobenzene, and acetic acid (Scheme 1).⁹

Scheme 1 α-acetoxylation mechanism proposed in previous work.

However, to determine a better approach mechanism for this type of α-acetoxylation, the nature of PIDA must be considered. To activate PIDA, Lewis or Brønsted–Lowry acids,⁶ such as boron trifluoride^9,20 and transition metals,^21,22 are required. Legault et al. studied the reactivity and formation of iodonium from iodine (III) compounds.²³ As evident from their findings, acids promote the ionization of iodine (III) compounds by heterolytically breaking the weak I–O bond and generating the intermediate iodonium. This newly generated iodonium has a sufficient lifetime to be detected and studied in equilibrium using nuclear magnetic resonance (NMR) spectroscopy. The lifetime and formation of iodonium also depend on the acid strength, polarity of the solvent, and I–O bond strength.²³ Accordingly, based on the characteristics of iodine (III) compounds, iodonium serves as a chemical intermediate in reactions.

Because the chemoselectivity, diastereoselectivity, and regioselectivity depend on the acetoxy attack involved in the reaction, it also comprises a crucial step in the reaction mechanism discussed above. Marouka studied the diastereoselectivity of α-acetoxylation on anancomeric cyclohexanones. The α-acetoxylation proceeds with a good yield and high selectivity, affording the most stable product (acetoxy in the equatorial position). In accordance with their results, the nucleophilic attack of acetoxy must occur on the antibonding orbital, which is available when the intermediate iodine(III) is in the axial position. Herein, 1-I-Eq is the thermodynamically and kinetically preferable intermediate and yields the equatorial acetoxy product, whereas 1-I-Ax must reorganize its configuration to produce the axial acetoxy product (Scheme 1).⁹ In this way, a part of diastereoselectivity is explained; nevertheless, herein, our research team has uncovered data that suggest an alternative mechanism.

Exploring the reaction condition

A simple model was designed to study the reaction conditions and mechanisms using acetophenone as the reactant and acetic acid for activation. We began investigating the reaction in solvents with different polarity and protic properties and determined that acetonitrile and ethanol provide the optimum conversion (Table 1, entries 1–4). Subsequently, we investigated the required number of acetic acid equivalents. No conversion was observed if the reaction lacked acetic acid equivalents; nevertheless, the reaction exhibited an excellent conversion with 10 acetic acid equivalents (Table 1, entries 5, 7–10). The formation and stabilization of the intermediates, enol from acetophenone and iodonium from PIDA, confirmed that the reaction was dependent on the polar solvent and acetic acid.

Table 1 Screening of the solvent and acid effect in the reaction

Entry	Solvent	Solvent (mL)	Eq. AcOH	Conversion^a (%)
a The percent conversion was determined from the crude reaction product by ^1H NMR spectroscopy.
1	Toluene	5	35	16
2	CH2Cl2	5	35	5
3	MeCN	5	35	18
4	EtOH	5	35	26
5	MeCN	3	35	37
6	EtOH	3	35	25
7	MeCN	3	—	0
8	MeCN	3	1	19
9	MeCN	3	5	27
10	MeCN	3	10	40

---

The effect of the PIDA equivalents in the reaction was investigated (Table 2, entries 1–5), demonstrating that 1.5 PIDA equivalents were sufficient for the highest percentage conversion. In accordance with the reaction mechanism, α-acetoxylation requires just one PIDA equivalent to oxidize the α position of the ketone; nevertheless, practically, the reaction requires an excess of PIDA equivalents owing to the high-temperature PIDA decomposition.²⁴ Following the effect of temperature on the reaction, the reaction was screened at different temperatures (Table 2, entries 3 and 6–9). The optimal temperature range for a moderate conversion was 70–80 °C. When the reaction temperature was between 0 °C and 25 °C, no conversion to 3a was observed. In contrast, if the temperature of α-acetoxylation was 90 °C, the conversion decreased owing to the thermal decomposition of PIDA.²⁴ Following the temperature study, we investigated the time required to complete the reaction (Table 2, entries 8–10). The reaction was monitored for three days and determined via a preliminary kinetic study of the logarithmic behavior of the reaction. The α-acetoxylation reached the asymptote in two days. Using the information obtained from the screening, we identified some characteristics of the reaction intermediate. Correspondingly, the high temperature and extended duration of the reaction could be attributed to the formation of a high-energy iodonium intermediate. In light of this, we used a stronger and interchangeable acid to analyze the reaction in detail.

Table 2 Screening of the PIDA amount, temperature, and reaction time

Entry	Temperature (°C)	Time (days)	Eq. PIDA	Conversion^a (%)
a The percent conversion was determined from the crude reaction product by ^1H NMR spectroscopy.
1	80	1	0.5	27
2	80	1	1	29
3	80	1	1.5	40
4	80	1	2.5	40
5	80	1	5	45
6	0	1	1.5	0
7	25	1	1.5	0
8	70	1	1.5	37
9	90	1	1.5	14
10	80	2	1.5	59
11	80	3	1.5	67

---

Cross-over acid experiment

We selected p-TsOH as the acid because it is stronger than acetic acid and can replace the acetoxy group of PIDA with a tosyl group. As shown in Table 3, different amounts of acetic acid and p-TsOH were added to the reaction to produce two products, 3a and 4a. If the nucleophilic attack of enol is faster than the exchange, the yield of 3a may be greater than that of 4a; conversely, if the exchange is faster, 4a may be the main product of the reaction. In all the experiments with one equivalent of p-TsOH, 4a was the primary product with a conversion of >96%. In addition, the reaction was completed within one day; however, when just 0.5 equivalents of p-TsOH were added, the conversions of 4a and 3a were 49% and 8%, respectively. This experiment demonstrates two aspects of the mechanism. The first aspect concerns the formation of iodonium and the exchange of acetyls, which are faster and more favorable than enol nucleophilic attack (Scheme 2). The second aspect discusses the strength of the acid by comparing the reaction with p-TsOH and acetic acid. According to Legault,²³ the formation of the iodonium intermediate occurs faster as the strength of the acid increases. This corroborates well with the increase of the α-oxidation reaction rate that depends on the strength of the acid.

Table 3 Screening of the exchange between acetoxy and tosyloxy in the reaction

Entry	Eq. p-TsOH	Eq. AcOH	Conversion^a3a (%)	Conversion 4a^a (%)
a The percent conversion was determined from the crude reaction mixture by ^1H NMR spectroscopy. All reactions were carried out using acetophenone 2a (1.5 mmol).
1	5	10	Trace	97
2	10	5	Trace	96
3	1	1	Trace	97
4	0.5	10	8	49

---

Scheme 2 Proposed reaction mechanism of the α-tosyloxylation via acid exchange.

Exploring the role of ketones in the reaction

Subsequently, the effect of α-acetoxylation (with PIDA) on different ketones was investigated. A single product, 3b, was obtained; based on the selectivity of the reaction, the unique enol at position 3 of 2b was favored. Therefore, the reaction proceeds via enol. The dependence of the enol intermediate in the α-acetoxylation was demonstrated using a nonenolizable ketone (2-adamantanone). Because there was no conversion to 1-acetoxy adamantan-2-one in this reaction, the product is confirmed to be dependent on enol formation.

The α-acetoxylation in the less substituted position is preferred in aliphatic ketones such as 2,5-hexanedione, 2-pentanone, and 4-methyl-2-pentanone, where main products 3d-1, 3e-1, and 3f, are formed (Scheme 3). Despite thermodynamic conditions that favor the most substituted enol, the steric demand of the iodo(III) intermediate is sufficient to produce the acetoxy in the less substituted position of the ketone. For acetone and cyclic ketones such as cyclopentanone, cyclohexanone, and cycloheptanone, the conversion to the corresponding α-acetoxy ketone was 50%, 75%, 91%, and 77%, respectively (Scheme 3). Using the ketones 4-methyl-3-penten-2-one, 2-indanone, and 2,3-cyclopentenopyridine, acetoxylation proceeds as expected, affording 72%, 60%, and 70% conversions to the corresponding α-acetoxy ketone, respectively (Scheme 3 and Table S1, ESI†).

Scheme 3 Products of α-acetoxylation in several types of ketones (benzylic, aliphatic, and cyclic ketones).

The selectivity of acetoxylation on different anancomeric ketones, such as 3-methylcyclohexanone, 2-methylcyclohexanone, and 4-tert-butylcyclohexanone, was also investigated herein. 3-Methylcyclohexanone had a conversion of 93%, favoring acetoxylation at position 5 and the trans configuration, yielding trans-3n-5 as the main product. In addition, trans-3n-5, cis-3n-5, and trans-3n-2, in the ratio of 2.3 : 1.2 : 1, respectively, were obtained as the diastereomer products. Using 2-methylcyclohexanone, α-acetoxylation proceeded with a conversion of 73%, preferring the trans configuration of the acetoxy at position 5; the acetoxy at position 3 was not observed. The two diastereomer products were trans-3o-5 and cis-3o-5 in the ratio of 1.63 : 1. 4-tert-Butylcyclohexanone underwent a 90% conversion, and only two diastereomers were produced, trans-3p and cis-3p in the ratio of 7.3 : 1 (Scheme 4). These ketones typically produce the most stable diastereomers.

Scheme 4 Products of α-acetoxylation in different substituted cyclohexanones.

The isomers and number of the products for 3-methylcyclohexanone and 2-methylcyclohexanone were consistent with Marouka's mechanism; however, this mechanism does not account for the number of the diastereomer products for 4-tert-butylcyclohexanone (t-bcyhex). As previously reported, trans-3p and cis-3p diastereomers were produced in the ratio of 7.3 : 1. According to Marouka's mechanism, the enol might attack to form a C–I bond and obtain 2p-Ax and 2p-Eq as intermediaries. Subsequently, the intermediates must change the conformation to place the antibonding molecular orbital near the nucleophilic acetoxy group. Thus, 2p-Ax and 2p-Eq are transformed into 2p-I-Ax and 2p-I-Eq intermediates. 2p-I-Ax is the intermediate requiring the least amount of energy. Therefore, α-acetoxy ketone cis-3p is the most favorable product. Because the tert-butyl group and iodine(III) are in an axial position and produce steric strain, 2p-I-Eq is the intermediate requiring high energy (Scheme 1). Considering the A value of tert-butyl in cyclohexanone, the single conformation change from equatorial to axial tert-butyl has an approach ratio of 10 000 : 1.²⁵ Motivated to uncover a mechanism to explain the products of α-acetoxylation, we conducted kinetic tests and theoretical calculations on the reaction with t-bcyhex.

Experimental study of tert-butyl-cyclohexanone

The α-acetoxylation of t-bcyhex was performed under the same reaction conditions as mentioned above, and ¹H NMR studies were conducted for six days. We compared the information on the reactants consumed using the equation of the different reaction orders (ESI†).^26,27 The order reaction that fits the pseudo first–order reaction is shown in Fig. 1. On the graph depicting the natural logarithm (Ln) of the concentration of the reactants vs. time (Fig. 1), the R² value approached 1. The slope was used to calculate the rate constant of the reagents (k_obs). A straight line with a positive slope was shown on the graph of reaction rates (d[P]/dt) vs. concentration of consumed reagents to confirm the reaction sequence. This observation relates the important reaction step with a unimolecular process.²⁷ In agreement with the reaction mechanism, two steps are necessary: the nucleophilic attack by enol at PIDA and α-acetoxylation associated with the reduction of iodine(III) to iodine(I). Therefore, we propose that the unimolecular behavior of the process is related to the iodonium intermediate formation of the iodine(III) compounds before the nucleophilic attack in the reaction.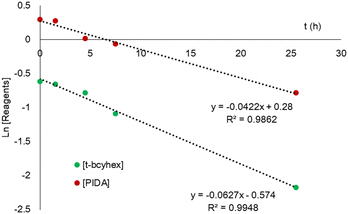

Fig. 1 Graph of natural logarithm (Ln) vs. time showing the reagent concentrations during mono α-acetoxylation.

The unimolecular behavior of the iodonium-catalyzed reaction is supported by the presence of iodonium peaks in the ¹H and ¹³C NMR spectra of the kinetic screening. The phenyl iodonium peaks correspond to the ortho, para, and meta phenyl proton resonances at 7.8, 7.5, and 7.3 ppm, respectively (Fig. 2 and ESI†). The iodonium peak of the ortho proton is located between the ortho peaks of PIDA and iodobenzene and coincides with the phenyl protons peaks of the iodonium compounds studied by Legault.²³ The peaks of iodonium support two aspects of the mechanistic reaction: (i) the iodonium intermediate is sufficiently stable to participate in the reaction, and (ii) the equilibrium between PIDA and iodonium is relatively fast, with a timescale in the microseconds.

Fig. 2 ¹H NMR spectrum recorded at 500 MHz in CDCl₃. PIDA shown in blue, iodobenzene in purple and iodonium intermediary in red.

The behavior of the two main products of the α-acetoxylation of t-bcyhex, the trans-3p and cis-3p, follows a pseudo first–order reaction over 35 h, as shown in the plot of Ln{[t-bcyhex]₀/([t-bcyhex]₀[P])} vs. time (where P refers to the total product, as shown in Fig. 3). The pattern of product formation can be predicted using pseudo first-order equations (ESI†) and the k_obs (k_obs = 0.0475). The value of the rate constant on the products (0.0522) is close to k_obs, contributing to the concordance of the values in the model.

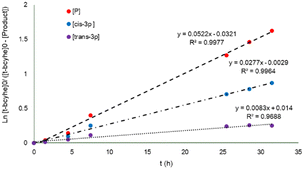Fig. 3 Graph of Ln{[t-bcyhex]₀/([t-bcyhex]₀[P])} vs. time depicting the reaction products in the mono α-acetilation. [P] = [cis-3p] + [trans-3p].

The concentration of trans-3p decreased after 35 h of the reaction, whereas the concentration of cis-3p underwent a minor decrease during the reaction (Fig. 4). The concentration drop was due to the formation of diacetoxylation products, trans-4p and cis-4p. The products trans-4p and cis-4p were observed after 28 h of the reaction with a ratio of 7 : 3. The selectivity for trans-4p was unexpected, considering the intermediaries and the A value of the substitutes. Motivated to explore the reaction further, we studied the kinetic formation of diacetoxylketones using a 7 : 3 mixture of cis-3p and trans-3p as a reagent under identical α-acetoxylation conditions. We calculated the k of the second acetoxylation of trans-3p and cis-3p by plotting the Ln of reagent concentration against time (Fig. S5, ESI†). The k_trans-3p of trans-3p has a greater value (k_trans-3p = 0.0117) than the k_cis-3p of cis-3p (k_cis-3p = 0.0058). We confirmed the reaction order by plotting d[P]/dt vs. the concentration of the consumed reagents. The plot shows a straight line with a positive slope (Fig. S5, ESI†), elucidating the behavior of the second acetoxylation as a pseudo first–order reaction, similar to the first α-acetoxylation of t-bcyhex but with a low value of the reaction rate.

Fig. 4 Graph of the mono and di α-acetoxylation products of t-bychex.

Similar to the previous acetoxylation, we used k_trans-3p and k_cis-3p to predict the products and validate this model of the reaction. The number of trans-4p depends on k_trans-3p and k_cis-3p, with the k_trans-3p value used to calculate the trans-3p to trans-4p conversion and a fraction of the k_cis-3p value (0.73) used to estimate the cis-3p to trans-4p conversion. The number of cis-4p was estimated using the other fraction of k_cis-3p (0.26) to determine the number of cis-3p that transformed to cis-4p. The estimated number of trans-4p to the experimental data yielded an error of 22% and a comparable growth trend. While comparing the estimated number of cis-4p with the experimental data, the error was 76% and the plot of the growth tendency of cis-4p was different. According to this model (isolated model), cis-3p and trans-3p are not related by tautomerism, i.e., trans-3p is transformed directly into trans-4p and cis-3p is transformed directly into trans-4p and cis-4p (Scheme 5).

Scheme 5 Top: The isolated model of di α-acetoxylation. Bottom: The connected model of di α-acetoxylation.

We probed a second model (connected model) considering the possible α-acetoxy epimerization of trans-3p to cis-3p.²⁸k_trans-3p is the observable rate constant of epimerization of trans-3p to cis-3p (k₁) and the second α-acetoxylation of trans-3p (k₂). k_cis-3p is a part of the observable constant of k₃ and is associated with k₁ as the concentration of cis-3p increases and decreases with k₁. The concentration of trans-4p depends on k₂ and on a fraction of k₁ and k₃, whereas the concentration of cis-4p depends on the remaining fraction of k₁ and k₃ (Scheme 4, bottom). The value of k_trans-3p (0.0117) is divided into constants k₁ and k₂. In this reaction, k₂ > k₁ because acetoxylation occurs more rapidly than epimerization. The estimated values for k₁ and k₂ are 0.00028 and 0.0112, respectively. The value of k₃, which is 0.00255, is incorporated into the value k₁; this value is divided into 0.00153 for the rate constant of trans-4p and 0.00102 for the rate constant of cis-4p. Using this model and rate constant values, the estimated increase in trans-4p and cis-4p concentration was compared to the experimental data. The estimated error for trans-4p and cis-4p is lower than for the isolated model, with values of 26% and 23%, respectively. However, the estimated growth trend is similar to the experimental trend. Thus, the high degree of error in the estimation of the number is owing to the omission of the second reactions of trans-3p, cis-3p, trans-4p, and cis-4p (α,β-unsaturated ketones and acetyl enolates).

Comparing the isolated model, the connected model, and the experimental data, we determined the rate constant of each product. The experimental rate constants of trans-4p (k_trans-4p-ex) and cis-4p (k_cis-4p-ex) are 0.0006 and 0.0017, respectively. The estimated rate constants of the isolated model for trans-4p (k_trans-4p-iso) and cis-4p (k_cis-4p-iso) are 0.00078 and 0.0022, respectively. In the connected model, the rate constants for trans-4p (k_trans-4p-con) and cis-4p (k_cis-4p-con) are 0.0128 and 0.0010, respectively. The estimated constants in the two models of cis-4p have comparable values; however, k_cis-4p-iso is closer to the experimental rate constant with an error of 30%. In contrast, the estimated rate constants of trans-4p were important for finding a model to explain the behavior of the reaction; in the isolated model, the k_trans-4p-iso has a 30% error and a positive value, whereas the k_trans-4p-con has a high error (2033%); therefore, the isolated model is the most appropriate to describe the reaction mechanism.

We plotted the logarithm of the experimental and estimated concentrations of the products vs. the time required to rectify the correct model selection. The isolated model calculates the production trend for cis-4p, whereas the trans-4p production trend has a negative slope. The connected model is anticipated to generate a substantial amount of cis-4p and trans-4p. Consequently, we choose the isolated model to represent the reaction mechanism.

The connected model, the first and second α-acetoxylation, and the synthesis of trans-3p and cis-3p using an intermediate before adding acetoxyl indicate a crucial aspect of the reaction mechanism. To improve our reaction mechanism approach, we used density functional theory (DFT) calculations.

Theoretical approach to the reaction mechanism

To support the mechanistic approach of α-acetoxylation via PIDA, we performed DFT calculations^9,17,23 using the Gaussian 09 program.²⁹ All the geometries were optimized using the functional ωB97X-D³⁰ with the basis set Def2TZVP³¹ for C, H, and O atoms and LANL2DZ for iodine atoms, with effective core potential and adding polarization (P) and diffuse (D) functions.^32,33 Adding P and D functions to the LANL2DZ basis set affords geometries that are more similar to those obtained via experimental methods, as described previously by Cerioni et al.³⁴ The energy calculation and natural bond orbital (NBO)^35,36 analysis were conducted using the basis set AUG-cc-pVTZ for C, H, and O atoms and AUG-cc-pVDZ-PP for I with effective core potential as described by Peterson.³⁷ The basis sets were obtained from the Basis Set Exchange data base.³⁸ The solvation effect was estimated using continuum solvation model SMD.³⁹ The calculated theoretical geometries of iodine derivatives were compared with the crystallographic data of Nemykin and Novák.^40,41

The optimized structure of PIDA exhibits a characteristic “T” shape with two acetoxy groups in synclinal conformation (Fig. S6, ESI†). The acetoxy in the vertical plane (with oxygens labeled as 1O and 2O) has a shorter distance than the acetoxy in the horizontal plane (with the oxygens labeled as 3O and 4O). The distance between 3O and I is 212 pm, making this the I–O bond with the shortest distance. In other words, the distance between 1O and I is 213 pm. Meanwhile, the distance between 2O and I is 288 pm less than that between 4O and I (312 pm). According to the study by Cerioni,³⁴ these distances and locations of the 1O and 2O are associated with the exchanging and ionization nature of PIDA. Angles of 88° for 3O–I–1C and 81° for 1O–I–1C are characteristic of iodine(III) compounds. As a result of these features, the NBO analysis shows the interaction between the lone pair (LP) orbital situated in 2O and the antibonding lone pair orbital (LP*) of the I, and the σ* of the I–1C (Fig. S6, ESI†); these remote interactions have the stabilization energy of 22.2 kJ mol⁻¹ and 12.0 kJ mol⁻¹ respectively. The occupancy of I LP* (0.652) and σ*_I–1C (0.0780) points at the significant remote interaction of 2O with I. The value of the stabilization energy of the interaction and the occupancy of orbitals provide information about the antibonding orbitals that participate in the acetoxy interchange at PIDA.

We estimated the contribution of acid in the reaction. In this case, when the proton of acetic acid interacts with 2O (Fig. S7, ESI†), the calculated structure shows a 5 pm increase in the 1O–I bond (218 pm) and an 8 pm decrease in the 3O–I bond (204 pm). In the second part, the angle of 3O–I–1C changes to 90°, indicating its proximity to iodonium compounds.³⁸ The NBO analysis of the acid interaction on PIDA hints that the stabilization energy between 2O LP with I LP* and I–1C σ* decreases to 11.42 kJ mol⁻¹ and 5.9 kJ mol⁻¹, respectively. Consequently, when acid interacts with PIDA, the stabilization energy of 1O LP with I LP* in PIDA energy decreases by 104.2 kJ mol⁻¹ (ΔE = E_PIDA − E_PIDA+CH3CO2H = 709–604.8 kJ mol⁻¹), and the stabilization energy of 3O LP with I LP* increases by 110.1 kJ mol⁻¹ (ΔE = E_PIDA − E_PIDA+CH3CO2H = 691.5–801.65 kJ mol⁻¹). These changes in the structure and the stabilization energy imply that the 3O–I bond becomes covalent, while the 1O–I bond is more polarized. The requirement of acid, the increase in reaction rate correlated with the strength of the acid, and estimated changes in the structure of the activated PIDA by acid confirm the necessity of the iodonium intermediate in the reaction.

Similarly, we evaluated the estimated structure of the 2p-Ax and 2p-Eq intermediates. The 2p-Ax intermediate (Fig. 5) has the same distance between 1C and I as PIDA (209 pm); however, the lengths of the 2C–I and 1O–I bonds differ from the lengths of the O–I bonds on PIDA, which are 224 pm and 232 pm, respectively. The long distance of the 1O–I bond indicates the ionic character of the intermediates, which suggests the presence of an ion pair between acetoxy and iodine. The distance between 2O and I is 295 pm, sufficient for the lone pair electrons of the carbonyl oxygen to interact with the antibonding orbital on iodine, stabilizing the intermediate ion pair. The intermediate 2p-Eq iodine structure differs from the 2p-Ax structure (Fig. 5). The bond length of 1C–I is identical to that of 2p-Ax (209 pm), although 2C–I and 1O–I have shorter bond lengths of 220 pm and 229 pm, respectively.

Fig. 5 Optimized structure by theoretical calculation: top, 2p-Ax; middle, 2p-Eq-Ax; bottom, 2p-OI.

Consequently, the acetoxy group in the intermediate 2p-Eq is less ionic than the acetoxy group in 2p-Ax. The other important difference is the relatively long distance between 2O and I (442 pm), which indicates that the oxygen 2O does not interact with iodine; hence, the exchange cannot occur with this acetoxy group. In contrast, the distance between 3O and I is shorter than that of 2O at 295 pm, sufficient to stabilize lone pair electrons in the antibonding orbital of iodine. This increases the probability of the exchange between the 2C–I and 2O–I bonds, forming 2p-OI as another intermediate (Fig. 5). In the case of 2p-Ax, the formation of intermediate 2p-Eq is preceded only by 2p-OI; consequently, the oxygen 3O does not have the necessary distance and location for the exchange.

To gain a deeper understanding of the reaction mechanism, we analyzed the NBO of the intermediates in the reaction. In the 2p-Ax intermediate, the antibonding orbital that receives the nucleophilic attack is σ*_2C–I (Fig. 6). This orbital is available to interact with the nucleophilic oxygen of the acetoxy group or acetic acid, consistent with the mechanism proposed by Maruoka.⁹ In contrast, the antibonding orbital in 2p-Eq could not interact with the nucleophilic oxygen of the intermolecular acetoxy group that is unavailable, making nucleophilic attack impossible in this intermediate. In contrast, the conformation change was proposed to have σ*_2C–I in a free position (2p-Eq-Ax); nevertheless, 2p-Eq-Ax is an intermediate with high energy cost for the tert-butyl, and the exchange of 2p-Eq for 2p-OI could be more favorable. In this part of the reaction, the orbitals play an important role; the LP orbital localized on carbonyl oxygen 3O overlaps with σ*_1C–I. This overlap has an occupancy of 1.88 in 3O LP and 0.0745 in σ*_1C–I, and it |has a stabilization energy of 13.2 kJ mol⁻¹. This parameter enhances the probability of 3O and I interaction, allowing the exchange to 2p-OI. The orbitals of 2p-Ax are not in the same position; the 3O orbital is far from the σ*_1C–I (Fig. 7). Therefore, the interaction required for the exchange is not achievable in the 2p-Ax intermediate. These characteristics of 2p-Ax and 2p-Eq imply the coexistence of two reaction pathways: (a) the direct acetoxy nucleophilic attack to the antibonding σ orbital in 2p-Ax, and (b) the intermolecular acetoxy attack to the antibonding π orbital in 2p-OI.

Fig. 6 (a) Orbital σ*_2CI–I of 2p-Ax. (b) Orbital σ*_2C–I of 2p-Eq.

Fig. 7 (a) Interaction of the orbitals 2OLP with σ*_I–1C of 2p-Eq. (b) Interactions of the orbitals 3OLP with σ*_I–1C of 2p-Ax.

The molecular orbitals of the 2p-OI intermediate are distinct from those of the 2p-Eq and 2p-Ax intermediates. ILP* and σ*_1C–I are comparable to PIDA, the stabilization energy of interaction O2–LP to ILP* and σ*_1C–I are 18.33 kJ mol⁻¹ and 10.92 kJ mol⁻¹, respectively (Fig. 8). This intermediary allows the interaction between the enol π orbital with the π* orbital of the iodine, and the energy of stabilization of the π–π* interaction is 795 J mol⁻¹. The stabilization energy of the enol π orbital with ILP* is 3.77 kJ mol⁻¹ (Fig. 8).

Fig. 8 Interaction of the orbitals 2OLP to I LP*of 2p-OI. (b) Interaction of the orbitals 2O LP to σ*_I–1C of 2p-OI. (c) Interaction of the orbitals on the enol π to aryl π* of 2p-OI. (d) Interactions of the orbitals on the enol π to I LP* of 2p-OI. (e) Enol π* orbitals.

The free energy of the intermediaries could be estimated from the frequencies’ calculation, supporting the NBO analysis and kinetic study. The 2P-Ax is 30.5 kJ mol⁻¹ more stable than 2P-Eq. The hyperconjugation of σ_2C–I with the π* orbital of the carbonyl group stabilized 2P-Ax by 64.14 kJ mol⁻¹, while in the case of 2P-Eq, this hyperconjugation is not localized; for this intermediary, the hyperconjugation with σ_αH–I is available with the stabilization energy of 35.69 kJ mol⁻¹. The energy estimation of 2P-Eq and 2P-Ax coincides with the selectivity of the reaction, giving cis-3p as the main product.

We propose the reaction mechanism of α-acetoxylation based on our kinetic screening and theoretical calculations. The initial steps of the reaction involve the chemical equilibrium between keto–enol of t-bcyhex ketone and PIDA and iodonium. The enol of the t-bcyhex forms the C–I bond through a nucleophilic attack on the iodine of iodonium. This nucleophilic attack on iodonium is the slowest step in the reaction owing to the reversible nature of the reactants and the energy required to generate 2p-Ax and 2p-Eq intermediates. The energy of the intermediates favors the formation of intermediate 2p-Ax over 2p-Eq. The 2p-Ax and 2p-Eq intermediates differ in their orbital availability and chemical structure-based reactivity, dividing the reaction mechanism into two pathways. (i) The primary pathway in which the nucleophilic attack by intermolecular acetoxy/acetic acid on the antibonding orbital (LUMO+1) of the 2p-Ax intermediate, forming the C–O bond and reducing the iodine(III) intermediate to iodine(I). The products of this final step are cis-3p, iodobenzene, and acetic acid. (ii) The secondary pathway occurs when 2p-Eq exhibits an equilibrium over 2p-OI. This equilibrium is more favorable owing to the spatial arrangement of iodine and carbonyl oxygen in 2p-Eq than the conformation change of the tert-butyl and iodine. In the secondary pathway, the nucleophilic attack of acetoxy/acetic acid is on the enol double bond of the 2p-OI intermediate, which polarizes the electronic charge to carbonyl and breaks the C–I bond, reducing the iodine(III) intermediary to iodine(I). The acetoxy/acetic acid performs a nucleophilic attack on both the faces of the enol. When the nucleophilic attack is on the tert-butyl side (topside), the α-acetoxyl product is cis-3p. In contrast, when the attack is on the face opposite to the tert-butyl side (bottom side), the α-acetoxyl product is trans-3p. The selectivity of the reaction mechanism indicates a strong preference for cis-3p over trans-3p, which is consistent with our kinetic screening result (Scheme 6).

Scheme 6 The proposed mono α-acetoxylation reaction mechanism.

The function of the equatorial exchange is evident in the reaction mechanism of the second α-acetoxylation (Scheme 7). The second α-acetoxylation of cis-3p begins with enol formation for its nucleophilic attack on iodonium. After the nucleophilic attack, the C–I bond is formed in the axial or equatorial position, assigned as 5p-Ax-Eq and 5p-Eq-Eq intermediates, respectively. In the 5p-Ax-Eq intermediate, the nucleophilic attack by acetoxy/acetic acid on the antibonding orbitals forms di-α-acetoxy cis-4p. In the 5p-Eq-Eq intermediate, the configuration shift from equatorial to axial position is impossible because of the high steric hindrance of all the substitutes in the axial position. Thus, the exchange between the C–I and O–I is more feasible, producing the 5p-OI-Eq intermediate. The nucleophilic attack of the acetoxy/acetic acid on 5p-OI-Eq can be on the topside and bottomside. If the attack is on the topside, the product is di-α-acetoxy cis-4p; otherwise, the product is di-α-acetoxy trans-4p. Consequently, the principal products of cis-3p are cis-4p and trans-4p. The second α-acetoxylation of trans-3p cannot occur in the axial position owing to the steric hindrance of the acetoxyl group; consequently, the nucleophilic attack of enol on iodonium forms only the equatorial intermediate, 5p-Eq-Ax. This intermediate has reactivity similar to 5p-Eq-Eq; the configuration change of the substitutes is not possible for steric hindrance, therefore the exchange of C–I to O–I is the most probable pathway of the reaction, forming the intermediate, 5p-OI-Ax. For this intermediate, the nucleophilic attack by acetoxy/acetic acid occurs predominantly on the topside, forming di-α-acetoxy trans-4p. The bottom side of 5p-OI-Ax is shielded by the axial acetoxy group; thus, we observed the trace of the cis axial di-α-acetoxy in ¹H NMR experiments. In accordance with this mechanism, the majority of trans-3p is converted to trans-4p, while cis-3p is converted to cis-4p and trans-4p. Based on our experimental findings, trans-4p (0.034 M) was more abundant than trans-3p (0.027 M), indicating that cis-3p is converted to trans-4pvia the 5p-OI-Eq pathway.

Scheme 7 The proposed di α-acetoxylation reaction mechanism.

Conclusions

We demonstrated and validated the importance and role of the iodonium intermediate in the α-acetoxylation reaction mechanism. The experimental study of the reaction conditions revealed the acid dependency on iodonium formation for the reaction to proceed as well as the enhancement of the reaction based on the polarity of the medium. In this case, acetonitrile favors the formation of iodonium over less polar solvents. In addition, the iodonium intermediate in the kinetic reaction of t-bcyhex was identified and assigned via¹H NMR, confirming its relative stability and presence in the reaction mechanism. The conversion of acetic acid to p-TsOH demonstrated the rapid rate (ms range) of iodonium formation and the interchange of acetoxy to tosyloxy. Regarding the α-acetoxylation reaction mechanism, we better understood the reactivity of iodine(III) in the intermediates. In addition, the study of the reaction mechanism on different types of ketones supported the necessity of the enol intermediate and the selectivity of the reaction mechanism, with the preference of acetoxylation occurring in the position with the least steric hindrance and the most stable enol. The reaction mechanism in anancomeric cyclohexanones as t-bcyhex was determined via the kinetic screening of mono-α-acetoxylation and di-α-acetoxylation, to which we assigned a pseudo first–order reaction owing to the formation of an iodonium intermediate. Accordingly, the products of the kinetic reaction, estimated theoretical chemical structure, and molecular orbitals supported the steps of the reaction mechanism and the intermediates; in this case, how the structure and chemistry of the intermediates drive the reaction when the reaction prefers the direct pathway (direct nucleophilic attack on antibonding Sigma orbitals) or the interchange pathway (nucleophilic attack on the enol–iodine complex intermediate). Thus, we present a comprehensive study of the reactivity of iodine(III) in α-acetoxylation reactions.

Author contributions

Osvaldo J. Quintana-Romero carried out the conceptualization, formal analysis, experimental and theoretical methodology and writing – original draft. Alejandro Hernández-Tanguma contributed with the computational part and review. Jorge Camacho-Ruiz contributed with validation. Armando Ariza-Castolo carried out the conceptualization, funding acquisition, project administration, resource management, supervision, data curation, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. H.-T. expresses his gratitude to Conacyt for providing their scholarships. We appreciate the support of the Xiuhcoatl supercomputer service at Cinvestav.

References

1. R. M. Moriarty and K.-C. Hou, Tetrahedron Lett., 1984, 25, 691–694.
2. R. M. Moriarty and H. Hu, Tetrahedron Lett., 1981, 22, 2747–2750.
3. C. Chen, X. Feng, G. Zhang, Q. Zhao and G. Huang, Synthesis, 2008, 3205–3208.
4. O. Prakash, N. Saini, M. P. Tanwar and R. M. Moriarty, Contemp. Org. Synth., 1995, 2, 121–131.
5. M. S. Yusubov and T. Wirth, Org. Lett., 2005, 7, 519–521.
6. M. Ochiai, Y. Takeuchi, T. Katayama, T. Sueda and K. Miyamoto, J. Am. Chem. Soc., 2005, 127, 12244–12245.
7. G. Deng and J. Luo, Tetrahedron, 2013, 69, 5937–5944.
8. M. Chen, W. Zhang, Z. H. Ren, W. Y. Gao, Y. Y. Wang and Z. H. Guan, Sci. China: Chem., 2017, 60, 761–768.
9. J. Tan, W. Zhu, W. Xu, Y. Jing, Z. Ke, Y. Liu and K. Maruoka, Front. Chem., 2020, 8, 467.
10. M. Uyanik and K. Ishihara, Chem. Commun., 2009, 2086–2099.
11. A. M. P. Salvo, V. Campisciano, H. A. Beejapur, F. Giacalone and M. Gruttadauria, Synlett, 2015, 1179–1184.
12. N. N. Karade, G. B. Tiwari and D. B. Huple, Synlett, 2005, 2039–2042.
13. Hypervalent Iodine Chemistry/Reagents, ed. T. Wirth, Springer, Switzerland, 2016.
14. R. H. C. N. Freitas, Aust. J. Chem., 2017, 70, 338.
15. H. Gottam and T. K. Vinod, J. Org. Chem., 2011, 76, 974–977.
16. J. Tao, C. D. Estrada and G. K. Murphy, Chem. Commun., 2017, 53, 9004–9007.
17. E. G. Bakalbassis, S. Spyroudis and E. Tsiotra, J. Org. Chem., 2006, 71, 7060–7062.
18. A. Asouti and L. P. Hadjiarapoglou, Tetrahedron Lett., 1998, 39, 9073–9076.
19. R. M. Moriarty, H. Hu and S. C. Gupta, Tetrahedron Lett., 1981, 22, 1283–1286.
20. J. Sheng, X. Li, M. Tang, B. Gao and G. Huang, Synthesis, 2007, 1165–1168.
21. W. B. Liu, C. Chen, Q. Zhang and Z. B. Zhu, Beilstein J. Org. Chem., 2012, 8, 344–348.
22. T. Chen, H. Ren, M. Zhang and A. Q. Zhang, J. Chem. Res., 2016, 40, 413–416.
23. A. Labattut, P. L. Tremblay, O. Moutounet and C. Y. Legault, J. Org. Chem., 2017, 82, 11891–11896.
24. J. E. Leffer and L. J. Story, J. Am. Chem. Soc., 1967, 89, 2333–2338.
25. S. Winstein and N. J. Holness, J. Am. Chem. Soc., 1955, 77, 5562–5578.
26. E. V. Anslyn and D. A. Dougherty, Modern physical organic chemistry, University Science Books, USA, 2006.
27. K. J. Laidler and S. Glasstone, J. Chem. Educ., 1948, 25, 383–387.
28. C. C. Su, C. K. Lin, C. C. Wu and M. H. Lien, J. Phys. Chem. A, 1999, 103, 3289–3293.
29. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
30. J. Da Chai and M. Head-Gordon, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
31. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
32. W. R. Wadt and P. J. Hay, J. Chem. Phys., 1985, 82, 284–298.
33. C. E. Check, T. O. Faust, J. M. Bailey, B. J. Wright, T. M. Gilbert and L. S. Sunderlin, J. Phys. Chem. A, 2001, 105, 8111–8116.
34. F. Mocci, G. Uccheddu, A. Frangia and G. Cerioni, J. Org. Chem., 2007, 72, 4163–4168.
35. E. Reed, R. B. Weinstock and F. Weinhold, J. Chem. Phys., 1985, 83, 735–746.
36. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88(6), 899–926.
37. K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, J. Chem. Phys., 2003, 119, 11113–11123.
38. B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820.
39. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
40. V. N. Nemykin, A. Y. Koposov, B. C. Netzel, M. S. Yusubov and V. V. Zhdankin, Inorg. Chem., 2009, 48, 4908–4917.
41. B. L. Tóth, F. Béke, O. Egyed, A. Bényei, A. Stirling and Z. Novák, ACS Omega, 2019, 4, 9188–9197.

---

Footnote

† Electronic supplementary information (ESI) available: Experimental procedures, characterization, kinetic determination and computational details; additional figures and schemes. See DOI: https://doi.org/10.1039/d3nj01563g

---