Magnetic properties of silver lanthanide molybdates AgLnMo₂O₈ (Ln = lanthanide)

Abstract

The magnetic properties of scheelite related compounds AgLnMo₂O₈ (Ln = lanthanide) are reported. Magnetic susceptibility measurements show that the compounds are paramagnetic down to 2 K with AgSmMo₂O₈ and AgEuMo₂O₈ showing Van Vleck paramagnetism. A ¹⁵¹Eu Mössbauer spectrum for AgEuMo₂O₈ indicates that the Eu ion is in the trivalent state and that an axial electric field gradient exists in this compound. Both magnetic susceptibility and electron paramagnetic resonance (EPR) measurements show that the Gd³⁺ ion is in the ⁸S_7/2 state.

---

Introduction

There are a considerable number of scheelite (CaWO₄) related molybdates. The compositions of these compounds are represented as AMoO₄ or A′A″Mo₂O₈, where A = alkaline earth ion, Pb²⁺ or Hg²⁺; A′ = alkali metal ion or Ag⁺; A″ = lanthanide ion or Bi³⁺. We are interested in the latter composition-type of compounds containing lanthanide elements, ALnMo₂O₈ (Ln = lanthanide ion). The preparation, crystal structures, and some physical properties of lanthanide molybdates containing silver, AgLnMo₂O₈, have been reported by several researchers.^1–5 These compounds crystallize in the scheelite related structure as shown in Fig. 1. Rath and Müller-Buschbaum elucidated that the crystal structures of AgSmMo₂O₈ and AgYbMo₂O₈ had tetragonal symmetry with space group I4̄ (no. 82), by the X-ray diffraction method for their single crystals. The crystal structures are closely related to the scheelite type, with Ag⁺ and Ln³⁺ ions in statistical distribution.³ Shi et al. reported that the temperature dependence of the magnetic susceptibilities for AgLnMo₂O₈ (Ln = Ce–Nd, Sm, Gd and Tb) reveals Curie–Weiss law behavior with three anomalies occurring at 100, 160 and 230 K, which are observed in all samples investigated in the temperature range studied (77 ≤ T ≤ 300 K).^4,5

Fig. 1 Crystal structure of AgLnMo₂O₈.

In this study, we prepared a series of lanthanide molybdates with silver, AgLnMo₂O₈ (Ln = lanthanide) and determined their crystal structures by X-ray diffraction measurements. Magnetic susceptibilities were measured in the temperature range 2–300 K to investigate whether magnetic anomalies are observed and to elucidate the magnetic behavior at lower temperatures. In addition, electron paramagnetic resonance (EPR) and Mössbauer spectrum measurements have been performed.

Experimental

Sample preparation

As starting materials, Ag metal powder, rare earth oxides Ln₂O₃ (Ln = Y, La, Nd, Sm, Eu, Gd, Dy, Ho, Er, Tm, Yb, and Lu), CeO₂, Pr₆O₁₁, Tb₄O₇, and molybdenum(VI) oxide MoO₃ (all with purity >99.9%) were used. Before use, the rare earth oxides were heated in air at 1173 K to remove any moisture and oxidized to the stoichiometric compositions, i.e., Ln₂O_3.00, CeO_2.00, Pr₆O_11.00 and Tb₄O_7.00. They were weighed in the appropriate metal ratios (Ag∶Ln∶Mo = 1∶1∶2), and intimately mixed in an agate mortar. The mixtures were pressed into pellets and then heated in air at 1073 K for 12 h. After cooling to room temperature, the pellets were crushed into a powder, re-ground, re-pressed into pellets, and heated again at 1073 K for 12 h to complete the reaction.

Analysis

X-Ray powder diffraction measurements were performed with Cu-Kα radiation on a Rigaku MultiFlex diffractometer equipped with a curved graphite monochromator. Intensity data were collected by step scanning in the range 10–120° at intervals of 0.02°. The structure and lattice parameters were refined with a Rietveld program RIETAN 2000.⁶

Magnetic measurements

Magnetic susceptibility measurements were performed with a SQUID magnetometer (Quantum Design MPMS model). The temperature dependence of the magnetic susceptibilities was investigated under both zero-field-cooled condition (ZFC) and field-cooled condition (FC). The former was measured on heating the sample to 300 K after zero-field cooling to 2 K. The applied magnetic field was 1000 G. The latter was measured on cooling the sample from 300 to 2 K at 1000 G.

¹⁵¹Eu Mössbauer spectrum measurements

¹⁵¹Eu Mössbauer spectra were measured with a VT-6000 spectrometer (Laboratory Equipment Co., Japan) at room temperature. The absorber material AgEuMo₂O₈ was mixed with fine graphite powder and ground in an agate mortar. The average thickness of AgEuMo₂O₈ was 10 mg Eu cm⁻². The ¹⁵¹Sm₂O₃ source emitting 21.6 keV γ-rays was maintained at room temperature. The spectrometer was operated in the velocity range ±10 mm s⁻¹. The velocity scale was calibrated with the six-line magnetic hyperfine spectrum of α-Fe using a ⁵⁷Co source. Zero velocity was taken as the absorption of ¹⁵¹Eu in crystalline EuF₃.

Electron paramagnetic resonance measurements

The EPR spectra at X band (9.096 GHz) were measured using a JEOL RE–2X spectrometer. The magnetic field was swept from 100 to 8000 G, which was monitored with a proton NMR gaussmeter, and the microwave frequency was measured with a frequency counter. Before the samples were measured, a blank tube was recorded to eliminate the possibility of interference by the background resonance of the cavity and/or the sample tube.

Results and discussion

1. Crystal structures

The results of the X-ray diffraction measurements show that the desired tetragonal scheelite-type compounds AgLnMo₂O₈ (Ln = Y, La–Nd and Sm–Lu) with space group I4̄ could be prepared as single-phase materials. Fig. 2 shows the X-ray diffraction pattern for AgGdMo₂O₈, as an example. We have performed Rietveld analysis for the XRD data. Table 1 lists the lattice parameters for AgLnMo₂O₈. The lattice parameters for AgLnMo₂O₈ are in excellent agreement with those reported by other workers.^2–5 It has been found that the silver and lanthanide atoms randomly occupy the 2b and 2d sites. The (1/2Ag + 1/2Ln)1, (1/2Ag + 1/2Ln)2, Mo1, Mo2, O1 and O2 ions occupy the 2d(1/2,0,1/4), 2b(1/2,1/2,0), 2a(0,0,0), 2c(0,1/2,1/4), 8g(x,y,z), and 8g(x,y,z) sites, respectively. The crystallographic positional parameters for AgLnMo₂O₈ after refinement are listed in Table 1.

Fig. 2 Observed and calculated X-ray powder diffraction patterns for AgGdMo₂O₈. The observed data are indicated by crosses and the calculated pattern is the solid line. The short vertical lines below the patterns mark the positions of all possible Bragg reflections. The bottom continuous line is the difference between the observed and the calculated intensity.

Table 1 Lattice parameters and crystallographic positional parameters for AgLnMo₂O₈ ^a

	Y	La	Ce	Pr	Nd	Sm	Eu	Gd	Tb	Dy	Ho	Er	Tm	Yb	Lu
a Note: (1/2Ag + 1/2Ln)1, (1/2Ag + 1/2Ln)2, Mo1, and Mo2 occupy 2d(1/2,0,1/4), 2b(1/2,1/2,0), 2a(0,0,0) and 2c(0,1/2,1/4) sites, respectively.
a/nm	0.52139(2)	0.53568(2)	0.53348(2)	0.53192(3)	0.53021(1)	0.52753(1)	0.52629(2)	0.52522(1)	0.52385(1)	0.52260(1)	0.52153(1)	0.52046(1)	0.51952(2)	0.51853(2)	0.51744(2)
c/nm	1.14403(5)	1.17527(4)	1.16885(4)	1.16529(8)	1.16186(3)	1.15593(2)	1.15391(4)	1.15175(3)	1.14824(2)	1.14593(3)	1.14362(3)	1.14179(3)	1.13940(3)	1.13754(4)	1.13699(6)
V/nm^3	0.31100(2)	0.33724(2)	0.33266(2)	0.32970(4)	0.32662(1)	0.32168(1)	0.31961(2)	0.31772(1)	0.31509(1)	0.31297(1)	0.31105(1)	0.30928(1)	0.30752(2)	0.30585(2)	0.30442(2)
O(1) x	0.249(7)	0.257(2)	0.283(2)	0.254(3)	0.215(3)	0.260(3)	0.259(2)	0.254(2)	0.248(3)	0.210(3)	0.219(3)	0.249(2)	0.211(3)	0.222(4)	0.232(2)
O(1) y	0.151(7)	0.122(4)	0.086(3)	0.150(1)	0.177(4)	0.144(5)	0.135(5)	0.141(4)	0.142(5)	0.154(6)	0.127(3)	0.158(3)	0.113(3)	0.125(4)	0.127(6)
O(1) z	0.084(3)	0.082(2)	0.064(1)	0.077(1)	0.090(1)	0.082(2)	0.082(2)	0.083(1)	0.081(2)	0.087(1)	0.075(1)	0.087(1)	0.076(1)	0.080(1)	0.084(2)
O(2) x	0.241(7)	0.207(3)	0.224(3)	0.223(1)	0.245(3)	0.218(3)	0.206(3)	0.198(3)	0.211(3)	0.247(2)	0.245(3)	0.216(2)	0.253(3)	0.249(4)	0.247(4)
O(2) y	0.652(9)	0.656(5)	0.666(3)	0.649(1)	0.616(4)	0.629(5)	0.663(6)	0.648(6)	0.656(7)	0.646(4)	0.658(2)	0.631(3)	0.667(3)	0.664(4)	0.658(5)
O(2) z	0.163(5)	0.170(2)	0.169(1)	0.161(1)	0.177(1)	0.169(3)	0.165(2)	0.164(2)	0.165(2)	0.170(1)	0.162(1)	0.172(1)	0.162(1)	0.161(1)	0.162(1)

---

2. Magnetic susceptibilities

The results of the magnetic susceptibility measurements for AgLnMo₂O₈ except for the diamagnetic Y, La and Lu compounds show that they are paramagnetic down to 2 K. No magnetic anomaly is detected for any AgLnMo₂O₈ in our investigation. The temperature dependences of the reciprocal magnetic susceptibilities for AgLnMo₂O₈ compounds are shown in Figs. 3 and 4. No difference between the ZFC magnetic susceptibilities and the FC magnetic susceptibilities is observed. The electronic configurations of Ag⁺ and Mo⁶⁺ are [Kr]4d¹⁰ and [Kr]4d⁰ ([Kr]: krypton core), respectively, i.e., these ions are diamagnetic. Therefore, the only paramagnetic ion in AgLnMo₂O₈ is Ln³⁺. The susceptibilities, χ_M, for AgLnMo₂O₈ generally obey the Curie–Weiss law except for AgSmMo₂O₈ and AgEuMo₂O₈. Deviation from the Curie–Weiss law is, however, clearly seen in the susceptibilities for the Ce, Pr, Nd and Yb compounds. The reciprocal susceptibilities χ⁻¹ of these compounds at low temperatures decrease rapidly with decreasing temperature except for the Pr compound. This deviation may originate from crystal field effects. The temperature dependence of the magnetic susceptibilities for the Sm and Eu compounds is characteristic of Van Vleck paramagnets, which will be discussed later. Table 2 shows the effective magnetic moments of these compounds, μ_exptl, and calculated moments for the free Ln³⁺ ions, μ_calc. The effective magnetic moments obtained experimentally (μ_exptl) are in good agreement with the calculated values (μ_calc). In the following, we will discuss the magnetic behavior of the Ln³⁺ ions in each of these compounds.

Fig. 3 Temperature dependence of reciprocal magnetic susceptibilities for AgLnMo₂O₈ (Ln = Ce, Pr, Nd, Sm and Eu).

Fig. 4 Temperature dependence of reciprocal magnetic susceptibilities for AgLnMo₂O₈ (Ln = Gd, Tb, Dy, Ho, Er, Tm and Yb).

Table 2 Experimental magnetic moments of Ln³⁺ (μ_exptl) and calculated magnetic moments (μ_calc) for AgLnMo₂O₈

Ln^3+	μ exptl/μB	μ calc/μB
Ce^3+	2.56	2.54
Pr^3+	3.58	3.58
Nd^3+	3.78	3.62
Gd^3+	7.92	7.94
Tb^3+	9.71	9.72
Dy^3+	10.54	10.63
Ho^3+	10.62	10.60
Er^3+	9.53	9.59
Tm^3+	7.62	7.57
Yb^3+	4.70	4.54

---

3. Magnetic properties of AgSmMo₂O₈

Fig. 5 shows the temperature dependence of the magnetic susceptibilities of the Sm³⁺ ion in AgSmMo₂O₈. This shows a large variation at lower temperatures and small variation at higher temperatures. This behavior can be explained using Van Vleck theory.⁷ The ground state of the Sm³⁺ ion is ⁶H_5/2. At low temperatures, only the magnetic ⁶H_5/2 ground multiplet is populated. However, since the energy difference between the ground state and the first excited state ⁶H_7/2 is not so large compared to the thermal energy k_BT (k_B is the Boltzmann constant), we cannot neglect the mixing effect in the calculation of the magnetic susceptibilities at higher temperatures. According to the Van Vleck theory, the molar magnetic susceptibility of the Sm³⁺ ion is given by eqn. (1):where N_A and μ_B are the Avogadro number and the Bohr magneton, respectively. The parameter y = λ/k_BT is 1/55 and corresponds to the ratio of the overall multiplet width (the spin–orbit coupling constant, λ) and the thermal energy (k_BT). Although the fitting of eqn. (1) to the experimental data (solid line in Fig. 5) is not good at lower temperatures, the spin–orbit coupling constant λ is found to be λ = 306 cm⁻¹. Then, the energy difference between the ground state ⁶H_5/2 and the first excited state ⁶H_7/2 is determined to be 1071 cm⁻¹, which is near to the theoretical value.⁷

Fig. 5 Temperature dependence of the magnetic susceptibility of the Sm³⁺ ion in AgSmMo₂O₈; fitting with eqn. (1) is shown (solid line).

4. Magnetic susceptibilities of AgEuMo₂O₈

Fig. 6 shows the magnetic susceptibility of the Eu³⁺ ion in AgEuMo₂O₈ as a function of temperature. Except at very low temperatures, the shape of this susceptibility vs. temperature curve is characteristic of Van Vleck paramagnetism, with a constant susceptibility for the lower temperature range and a decreasing susceptibility with increasing temperature for T ≥ 100 K. At very low temperatures (T ≤ 10 K), the magnetic susceptibilities increase suddenly with decreasing temperature. This behavior may be attributable to paramagnetic Mo⁵⁺ ions formed to a small extent due to the oxygen deficiency.

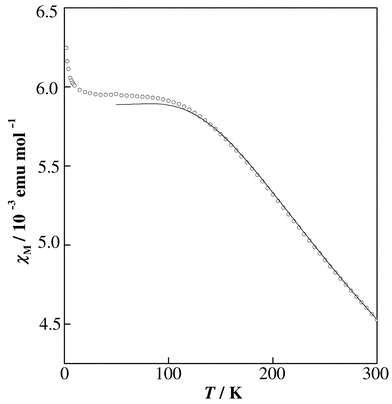Fig. 6 Temperature dependence of the magnetic susceptibility of the Eu³⁺ ion in AgEuMo₂O₈; fitting with eqn. (2) is shown (solid line).

The ground state ⁷F₀ of Eu³⁺ is nonmagnetic and the excited state ⁷F₁ is close enough to it to give an energy difference comparable to k_BT at room temperature. Therefore, the magnetic susceptibility becomes independent of temperature at lower temperatures. The molar magnetic susceptibility of the Eu³⁺ ion is expressed by eqn. (2):⁷

where x = λ/k_BT is 1/21 corresponding to the ratio of the overall multiplet width to k_BT. The magnetic susceptibilities calculated by using eqn. (2) are fitted to the measured susceptibilities in the range 50–300 K, as shown in Fig. 6 with a solid line. The spin–orbit coupling constant λ of Eu³⁺, which is the energy-level difference between the ground state ⁷F₀ and the first excited state ⁷F₁, is determined to be 354 cm⁻¹ for AgEuMo₂O₈. This value is close to the values reported in other complex oxides, for example, 339 cm⁻¹ (Ba₂EuNbO₆)⁸ and 364 cm⁻¹ (Ba₂EuIrO₆).⁹

5. ¹⁵¹Eu Mössbauer spectrum of AgEuMo₂O₈

The ¹⁵¹Eu Mössbauer spectrum of AgEuMo₂O₈ measured at room temperature is shown in Fig. 7. The Eu ions in AgEuMo₂O₈ are located in two crystallographically nonequivalent sites, 2b and 2d. Both of them occupy fourfold symmetry sites (4̄ symmetry), therefore, the electric field gradient (EFG) tensor at this site is axially symmetric (asymmetry parameter, η = 0). The hyperfine quadrupole interaction for this axial EFG can be written as shown in eqn. (3):where I is the nuclear spin, Q is the quadrupole moment, and eq = V_zz is the principal EFG. The eight allowed transitions due to a quadrupole interaction were taken into account. Fig. 8 shows eight possible transitions due to a quadrupole interaction. The observed spectrum in Fig. 7 was fitted with the sum of these Lorenzian lines. The fit assumes eight transition lines with equal linewidths. The positions of these lines are specified by the isomer shift δ and the quadrupole coupling constant e²qQ₀. The intensity ratios of the eight lines are determined by the Clebsh–Gordan coefficients. The ratio of the excited and ground state quadrupole moments Q_e/Q₀ is taken to be 1.34.¹⁰ Since there are two nonequivalent Eu sites the Mössbauer spectrum should consist of 16 lines. We thus attempted to fit the spectrum with 16 transition lines. However, these lines were not completely resolved, indicating that the environments of the two Eu sites are quite similar. The line width used to fit the AgEuMo₂O₈ spectrum and that for the reference EuF₃ spectrum were 2.14(9) and 2.72(7) mm s⁻¹, respectively. The average isomer shift δ for AgEuMo₂O₈ is 0.388(9) mm s⁻¹, which confirms that the Eu ions are in the trivalent state. The average quadrupole coupling constant e²qQ₀ is −3.07(49) mm s⁻¹ and negative in this compound.

Fig. 7 ¹⁵¹Eu Mössbauer spectra of AgEuMo₂O₈. The solid line is a computed fit with eight Lorentzians.

Fig. 8 Eight transitions due to a quadrupole interaction of ¹⁵¹Eu.

6. Magnetic properties of AgGdMo₂O₈

The temperature dependence of the reciprocal magnetic susceptibilities of the Gd³⁺ ion in AgGdMo₂O₈ is shown in Fig. 9. The reciprocal susceptibilities χ⁻¹ are almost linear with temperature in the measured temperature range of 2–300 K. The effective magnetic moment of the Gd³⁺ ion is determined to be 7.92 μ_B, which is close to the theoretical value of 7.94 μ_B for the free Gd³⁺ ion. The result indicates the eight-fold ground state ⁸S_7/2 is not split by the crystal field.

Fig. 9 Temperature dependence of the magnetic susceptibility of Gd³⁺ ion in AgGdMo₂O₈; Curie–Weiss law fitting is shown by the solid line.

Fig. 10 shows the X-band EPR spectrum for AgGdMo₂O₈ measured at room temperature. A single broad spectrum centered at a magnetic field of 3336 G was observed. The effective magnetic moment of the Gd³⁺ ion is calculated to be 8.02 μ_B from the EPR data (g = 2.02). The effective magnetic moments of the Gd³⁺ ion determined from the magnetic susceptibility and the EPR measurements are in good agreement with the calculated magnetic moment (7.94 μ_B), which indicates that the ground state of the Gd³⁺ ion in AgGdMo₂O₈ is a pure ⁸S_7/2 state.

Fig. 10 EPR spectrum of Gd³⁺ in AgGdMo₂O₈ at room temperature.

In summary, the magnetic properties of AgLnMo₂O₈ (Ln = lanthanide element) have been investigated. Magnetic susceptibility measurements show that they are paramagnetic down to 2 K. ¹⁵¹Eu Mössbauer and EPR spectra measurements indicate that lanthanide ion is in the trivalent state for AgLnMo₂O₈.

References

1. A. W. Sleight, K. Aykan and D. B. Rogers, J. Solid State Chem., 1975, 13, 231–236.
2. A. P. Perepelitsa, M. V. Artemenko and V. N. Ishchenko, Russ. J. Inorg. Chem., 1983, 28, 1123–1124.
3. M. Rath and Hk. Müller-Buschbaum, J. Alloys Compd., 1993, 198, 193–196.
4. F. Shi, J. Meng and Y. Ren, Mater. Res. Bull., 1995, 30, 1401–1405.
5. F. Shi, J. Meng and Y. Ren, J. Alloys Compd., 1996, 233, 56–60.
6. F. Izumi and T. Ikeda, Mater. Sci. Forum, 2000, 198, 321–324.
7. J. H. Van Vleck, Theory of Electric and Magnetic Susceptibilities, Clarendon, Oxford, 1932.
8. K. Henmi, Y. Hinatsu and N. M. Masaki, J. Solid State Chem., 1999, 148, 353–360.
9. M. Wakeshima, D. Harada, Y. Hinatsu and N. Masaki, J. Solid State Chem., 1999, 147, 618–623.
10. C. L. Chein, S. DeBenedetti and F. de S. Barros, Phys. Rev. B, 1974, 10, 3913–3922.

---