Uncertainty calculation on the determination of calcium absorption in nutritional experiments with enriched stable isotopes and detection by double focusing sector field ICP-MS with a shielded torch
Stefan
Stürup
Dartmouth College, Department of Earth Sciences, 6105 Sherman Fairchild Hall, Hanover, NH 03755-3571, USA. E-mail: stefan.sturup@dartmouth.edu
First published on 28th November 2001
Abstract
A new method for the measurement of calcium isotope ratios and total calcium, using a double focusing sector field inductively coupled plasma mass spectrometry (ICP-MS) instrument equipped with a shielded torch, is presented. The method was applied for the measurement of the 44Ca/43Ca, 42Ca/43Ca and 44Ca/42Ca ratios and total calcium by isotope dilution in urine samples from two different nutritional experiments set up to determine the calcium absorption from various foods. The isotope ratios were measured with a precision of 0.25%, 0.23% and 0.05% RSD for 44Ca/43Ca, 42Ca/43Ca and 44Ca/42Ca, respectively. The precision of the 44Ca/42Ca ratio is only limited by counting statistics, whereas the precision is limited by uncertainty from the needed background and interference corrections when the minor 43Ca isotope is used for analysis. Uncertainty calculations on the determination of calcium absorption in the nutritional experiments are presented. These calculations show that, for a double stable isotope procedure (administration of enriched stable 44Ca and 42Ca), the overall uncertainty is controlled by the precision of the ICP-MS measurement of the isotope ratios (44Ca/43Ca, 42Ca/43Ca), whereas, for a mixed radioisotope–stable isotope procedure (administration of enriched stable 44Ca and the 47Ca radioisotope), the overall uncertainty is mainly controlled by the uncertainty in the measurement of total calcium by isotope dilution ICP-MS. From these results, it was concluded that, when optimizing the performance of nutritional experiments, the emphasis should be placed on different parameters depending on the exact analysis involved. The results also show that uncertainty calculations are very useful in pinpointing the critical parameters of an experiment.
Introduction
Calcium is essential to humans, and a daily intake of 800 mg is recommended for adults in order to maintain calcium homeostasis.1 Calcium serves many different purposes in the body. Most prominent is the incorporation of calcium in skeleton and teeth, where more than 99% of the body calcium is deposited. Other important metabolic functions of calcium include the regulation of hormonal secretion and action, regulation of growth by cell division, regulation of body fluids and of several membrane effects, i.e. calcium pump action, contraction of muscles and conduction of nerve impulses.2 Calcium homeostasis is tightly regulated; in deficiency, the calcium balance turns negative, and calcium is resorbed from the bones. One of several factors affecting calcium homeostasis is the calcium intake via food and beverages.Nutritional experiments investigating different factors influencing calcium absorption are useful tools in understanding calcium metabolism. Most of these nutritional experiments use single or dual isotope labelling, requiring the administration of either enriched stable calcium isotopes or calcium radioisotopes, followed by isotope analysis of various human samples. Traditionally, nutritional experiments with calcium were carried out using radioisotopes (45Ca and 47Ca).3–5 However, when mass spectrometric techniques became more commonly used, thermal ionization mass spectrometry (TIMS) became the preferred analytical technique for the determination of stable calcium isotopes (42Ca, 44Ca, 46Ca and 48Ca) because of its excellent measurement precision.6–8 Furthermore, the use of enriched stable isotopes has the advantage that they are non-toxic, as opposed to radioisotopes. Over the last 5–10 years, during which several new developments in inductively coupled plasma mass spectrometry (ICP-MS) instrumentation have been introduced to the market (sector field MS, cold plasma, reaction cells and multicollector instruments), several papers on the measurement of calcium isotopes using different ICP-MS techniques have been published.9–12 The use of ICP-MS techniques has certain advantages over the TIMS technique. First, ICP-MS instruments are found in many laboratories throughout the world, as they are less specialized instruments and are often purchased to cover a wide range of applications. Secondly, they are often less expensive and easier to operate than TIMS instruments. In addition, the sample preparation required is often less extensive and time-consuming.
The precision of the isotope ratio measurement is a critical and important factor in evaluating which analytical technique should be used, as the precision (and the amount of isotope administered) makes up a large fraction of the total uncertainty in the final calcium absorption determination.13 In general, a measurement precision better than 1% is required for an analytical technique to be useful for nutritional studies with stable isotopes,14 but often a significantly better precision is desired. Several papers have reported on the analytical techniques fulfilling this requirement. Price et al.,7 in a dual isotope study, were able to measure the 40Ca/42Ca and 43Ca/42Ca ratios in urine and blood with a precision better than 0.1% RSD using sector field multicollector TIMS. Likewise, Turnlund et al.8 were able to measure the 46Ca/48Ca ratio with a precision better than 0.1% RSD in urine and faecal samples applying similar TIMS instrumentation. Besides producing very precise data, the TIMS technique also has the advantage of having the most abundant calcium isotope (40Ca) available for analysis. The 40Ca isotope suffers severe interference by 40Ar in most ICP-MS techniques. Thus, in applying ICP-MS for the measurement of calcium isotopes, normally only the minor isotopes are available for analysis; however, these isotopes also suffer from interference, and interferences from polyatomic ions and doubly charged ions need to be overcome in order to obtain reliable results. Using a sector field ICP-MS instrument equipped with a single detector, Stürup et al.9 were able to resolve these interferences by applying a mass resolution of 4000. The 44Ca/43Ca and 42Ca/43Ca ratios could then be measured with a precision of 0.3–0.4% RSD in urine samples. Patterson et al.,10 on the other hand, used a quadrupole ICP-MS instrument in the cool plasma mode to greatly minimize interferences, and were able to measure the 44Ca/43Ca and 42Ca/43Ca ratios with a precision of 0.25% RSD in human samples, such as serum, urine, faeces and breast milk. By applying hexapole collision cell ICP-MS, the 40Ar+ interference on 40Ca+ can be eliminated, making the analysis of the major calcium isotope possible. This approach was used by Boulyga and Becker,12 who were able to measure the 40Ca/44Ca, 42Ca/44Ca and 43Ca/44Ca ratios with precisions of 0.26%, 0.40% and 0.82% RSD, respectively. A precision of 0.01% RSD was obtained by Halicz et al.11 using a multiple collector ICP-MS instrument for the measurement of 44Ca/42Ca and 43Ca/42Ca in carbonates. These papers demonstrate the potential of various ICP-MS techniques for the measurement of calcium isotope ratios, and show that the measurement precision is higher than but comparable to that of TIMS. Recently, microwave induced plasma (MIP) time-of-flight mass spectrometry has been used for the measurement of calcium isotope ratios. This is a promising technique by which the 40Ca isotope can also be measured, although the precision (1–2% RSD) is poorer than when applying TIMS or ICP-MS techniques.15
This paper presents a new sector field ICP-MS method for the measurement of calcium isotope ratios and total calcium, using isotope dilution in human urine and applying a sector field ICP-MS instrument equipped with a shielded torch. Furthermore, uncertainty calculations on the measurement of calcium absorption from two different nutritional experiments are presented, together with guidelines on how to optimize nutritional experiments for the best possible precision using uncertainty budgets. The method was applied to urine samples from two different nutritional studies, one using 44Ca as the intravenous tracer and 47Ca as the oral tracer, and one using 44Ca as the oral tracer and 42Ca as the intravenous tracer. The results from these experiments will be reported in detail elsewhere.
Experimental
Instrumentation
All measurements were performed on an Element 1 sector field inductively coupled plasma mass spectrometer (Finnigan MAT GmbH, Bremen, Germany), equipped with a shielded torch, in operation at the Dartmouth Trace Metal Analysis Core Facility, Dartmouth College, NH, USA. Throughout this study, the medium mass resolution setting was applied, which produced a mass resolution of approximately 4000. All measurements were made with a standard sample introduction system that comprised a peristaltic pump (Perimax 12, Spetec, Erding, Germany), a concentric nebulizer (AR35-1-F04, Glass Expansion, Hawthorn, Australia) and a Scott-type spray chamber maintained at 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C. The instrument settings and the method parameters are summarized in Table 1.
°C. The instrument settings and the method parameters are summarized in Table 1.
| RF power | 1450 W |
| Plasma gas flow | 14.0 L min−1 |
| Auxiliary gas flow | 1.04 L min−1 |
| Nebulizer gas flow | 1.075 L min−1 |
| Sample uptake rate | 0.35 mL min−1 |
| Sample/skimmer cones | Nickel |
| Scan type | Electric |
| Magnet settle time | 1 ms |
| Magnet mass | 41.959 u |
| Mass ranges | 42Ca+: 41.948–41.969 |
| 43Ca+: 42.947–42.969 | |
| 43.5Sr2+: 43.443–43.464 | |
| 44Ca+: 43.944–43.966 | |
| Sensitivity (1 mg L−1 Ca) |
44Ca+: 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps 000 cps |
| Dwell time | 1 ms |
| Sweeps | 1200 |
| Samples per peak | 30 |
| Integration window | 60% |
| Segment duration | 50 ms |
| Measurement time | 4 min |
Standard solutions and reagents
All samples and standards were prepared by dilution with 0.45 M nitric acid. The nitric acid was prepared from 65% baseline nitric acid (Seastar Chemicals, Sidney, BC, Canada), diluted with ultrapure water (>18.2 MΩ cm) produced by a Purelab Plus water purifier (US Filter, MA, USA). Calcium standard solutions were prepared from a 1000 mg L−1 Ca standard (VHG LABS, Manchester, NH, USA) by dilution with 0.45 M nitric acid. A 1 mg L−1 standard solution was used for instrument optimization. For the isotope dilution measurements, samples were spiked with a 44Ca-enriched (97% 44Ca) Ca standard solution; the enriched 44Ca (as 44CaCO3) was obtained from Chemgas, Boulogne, France. Two reference urine samples (Lyphocheck®, 62081 and 62082, BIO-RAD Laboratories, ECS Division, Anaheim, CA, USA) were used to evaluate the accuracy of the total measurement of calcium by isotope dilution ICP-MS.Samples and sample preparation
The nutritional experiments were set up and performed at the Research Department of Human Nutrition, The Royal Veterinary and Agricultural University, Copenhagen, Denmark, where all the urine samples were also collected. The collected urine samples (49 mL) were acidified with 1 mL of 65% nitric acid and kept frozen (−18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) until analysis. The sample preparation step was very simple. The acidified human urine was diluted 40 times with 0.45 M nitric acid and thereafter aspirated directly into the ICP-MS instrument.
°C) until analysis. The sample preparation step was very simple. The acidified human urine was diluted 40 times with 0.45 M nitric acid and thereafter aspirated directly into the ICP-MS instrument.
Optimization, measurements and calculations
Before a measurement sequence was started, the instrument was carefully mass calibrated and optimized using a 1 mg L−1 Ca standard solution. Normally, a signal of approximately 600![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cps on 44Ca+ was achieved for this solution. The shielded torch narrows the ion energy spread in the plasma from approximately 20 eV to less than 5 eV and, as a result, the ion transmission (and thereby the sensitivity) is significantly increased.16 The above sensitivity is 8–10 times higher than the sensitivity obtained using a sector field ICP-MS instrument without a shielded torch.9 This increased sensitivity improves the precision of isotope ratio measurements as the counting statistics are significantly improved by the increased number of ions counted.
000 cps on 44Ca+ was achieved for this solution. The shielded torch narrows the ion energy spread in the plasma from approximately 20 eV to less than 5 eV and, as a result, the ion transmission (and thereby the sensitivity) is significantly increased.16 The above sensitivity is 8–10 times higher than the sensitivity obtained using a sector field ICP-MS instrument without a shielded torch.9 This increased sensitivity improves the precision of isotope ratio measurements as the counting statistics are significantly improved by the increased number of ions counted.
At the beginning of every measurement sequence, two blanks and four calcium standards (1, 2, 3 and 5 mg L−1) were measured in order to determine the background level, the detector dead time and the mass discrimination according to the methods outlined in the literature.17–21 Any possible drift in mass discrimination was monitored by the analysis of a 1 mg L−1 Ca standard for every six samples. Typical values for the detector dead time and mass discrimination were ∼3 ns and 1% u−1. These values are low compared with values from the literature, where a detector dead time in the 10–25 ns range is normally found,17–19,22 together with mass discrimination factors of 2–6% for the low mass range.9,13,21,23 The 3 ns dead time of the electron multiplier used in this study was found to be constant over time (several days) and over the whole mass range (from magnesium to lead). It was therefore believed to be the true dead time of that particular multiplier. In a study by Held and Taylor,19 it was shown that, during the lifetime of a multiplier, the dead time increases, reaches a maximum and then rapidly drops towards the end of its lifetime. The multiplier used in this work might very well be close to the end of its lifetime, as it is approximately 2 years old. This may explain the unusually low observed dead time. The reason for the low mass discrimination is the use of the shielded torch. The shielded torch narrows the ion energy spread of the ion beam, whereby space charge effects in the instrument interface are reduced. Space charge effects are one of several processes making up the observed mass discrimination, and therefore the mass discrimination is lower than in sector field ICP-MS instruments operated without a shielded torch.13 This is in good agreement with the findings of Prohaska et al.,24 who found a mass discrimination factor of 0.7% amu−1 for the measurement of sulfur isotope ratios using a sector field ICP-MS instrument equipped with a shielded torch.
All sample solutions were analysed three times in order to improve the precision of the final result, as the standard deviation of the mean is found by division of the standard deviation by the square root of the number of replicates (Ssem = S/√n). Between samples, a 2 min wash with 0.45 M nitric acid was applied. No memory effects were observed for calcium concentrations below 10 mg L−1. For the samples in which both 44Ca/43Ca and 42Ca/43Ca ratios were measured, the parameters given in Table 1 were used. For samples from single stable isotope tracer experiments and samples for the measurement of total calcium by isotope dilution experiments, only the 44Ca/42Ca ratio was determined, and therefore the 43Ca mass was omitted in order to optimize the measurement cycle. A 60% peak integration window was applied, which was found to produce more precise isotope ratio data than when the whole peak was integrated. During acquisition, a 150% scan window was used to make the method robust to mass drift during long (several hours) measurement sequences. For the analysis of short sequences (less than 1 h), the scan window can be reduced to 60%, which also reduces the measurement time down to less than 2 min. All integrated data were exported into a spreadsheet program, where all calculations, including background correction, detector dead time correction, mass discrimination correction and isotope dilution calculations, were performed.
For isotope dilution, 5 µL of enriched 44Ca solution (diluted to approximately 17 mg L−1) was added to the 40 times diluted urine sample (3.9 mL 0.45 M nitric acid and 0.1 mL urine). This spiking produced a 44Ca/42Ca ratio of 4–6 in the mixed sample–spike solution. All dilutions and spiking were performed by weight. From the isotope dilution data, the total calcium concentration was calculated using the following equation:25,26
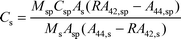 | (1) |
Calculation of calcium absorption
The calcium isotope ratios and total calcium concentrations measured were used, together with other data, to calculate the fractional calcium absorption from a test meal. In order to estimate and evaluate the overall uncertainty in the calcium absorption, it is important not only to look at the uncertainty in the isotope ratio measurement, but to use the combined uncertainty of all the different terms in the equations used for the calculation of the absorption. The uncertainty budgets were estimated using the guidelines based on error propagation outlined by EURACHEM/CITAC.27 The equations used for the calculation of calcium absorption are given below for the two different nutritional experiments applied. In this paper, only the uncertainty aspects will be discussed; the actual calcium absorption results will be published elsewhere. | (2) |
 | (3) |
Results and discussion
Spectral interferences
When analysing urine using sector field ICP-MS, all the calcium isotopes are overlapped by polyatomic ions and/or doubly charged ions at low resolution. In Table 2, the natural abundance of the calcium isotopes, the most commonly encountered interferences and the mass resolution needed to resolve these from the analyte peaks are presented. The 42Ca, 43Ca and 44Ca isotopes were chosen for analysis as they can be measured reliably using a mass resolution of 4000 and a correction for overlap by Sr2+.9 The most severe interference experienced by these selected isotopes is for 42Ca+, which is overlapped by 40ArH2+ and 40Ar2H+. The signal of these interferences corresponds to a signal of approximately 1.8 mg L−1 calcium, but can be easily separated from the calcium signal using medium mass resolution. The 44Ca isotope only experiences interference from minor polyatomic ions, which are easily separated from the calcium signal at medium mass resolution.| Isotope | Natural abundance (%) | Interference | Resolutiona |
|---|---|---|---|
| a The resolution, calculated as m/Δm, needed to separate the interfering species from the analyte signal. | |||
| 40Ca+ | 96.941 | 40Ar+ | 192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 497 497 |
| 42Ca+ | 0.647 | 40Ar2H+ | 2350 |
| 40Ar1H2+ | 2165 | ||
| 84Sr2+ | 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 992 |
||
| 43Ca+ | 0.135 | 86Sr2+ | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 391 391 |
| 44Ca+ | 2.086 | 12C16O2+ | 1281 |
| 28Si16O+ | 2688 | ||
| 88Sr2+ | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 447 447 |
||
| 46Ca+ | 0.004 | 46Ti+ | 43![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 503 503 |
| 14N16O2+ | 1173 | ||
| 48Ca+ | 0.187 | 48Ti+ | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 457 457 |
| 36Ar12C+ | 3195 | ||
| 32S16O+ | 3318 | ||
All three selected calcium isotopes experience interference from doubly charged strontium ions; this interference cannot be eliminated using even a high mass resolution, and therefore a mathematical correction is applied using the 87Sr2+ signal on m/z = 43.5. The formation rate of Sr2+ was found to be 1%, which is significantly lower than the 6.5% reported earlier for similar measurements in a different sector field ICP-MS instrument.9 This difference is probably due to differences in instrumental design. Although the formation rate is relatively low, the interference is still significant, as urine contains a high level of strontium: approximately 0.2 mg L−1.30 On average, the signal from doubly charged strontium constitutes 0.2–0.3% of the recorded 44Ca signal and 0.3–0.6% of the 43Ca signal in the analysed urine samples. As such, the correction is important in order to achieve accurate results for the isotope ratios. The contribution of doubly charged strontium to the 42Ca signal is negligible, as the 84Sr isotope has a low natural abundance of only 0.56%.
Precision of the isotope ratio measurements
The precision of the isotope ratio measurements by ICP-MS is limited by counting statistics (Poisson statistics). However, other sources of error, such as plasma flicker noise, noise from the peristaltic pump and changes in the nebulization, ionization and extraction processes, also contribute to the overall measurement precision. The choice of a short dwell time (1 ms) and many sweeps (1200) was made in order to eliminate the majority of noise from the above noise components, as suggested by other research groups.22,31,32 The high number of sweeps is beneficial, as the averaging of the sweeps in each measurement is an effective means of noise reduction. If the noise reduction is successful, the ratio between the measured and the theoretical precision should approach unity. In Table 3, the precision obtained for 10 replicate analyses of the calcium isotope ratios in a 1 mg L−1 solution is given; all data were corrected for overlap by doubly charged strontium, background, detector dead time and mass bias before the precision was calculated. The theoretical precision is calculated from Poisson statistics as %RSD = 100√(1/N1 + 1/N2), where N1 and N2 are the number of ions observed for isotopes 1 and 2, respectively. The ratio between the theoretical and the measured precision is close to unity for the 44Ca+/42Ca+ ratio; it can hence be concluded that the precision is only limited by counting statistics. For the 42Ca+/43Ca+ and 44Ca+/43Ca+ ratios, the calculated precision ratios are in the 1.5–2.0 range, indicating that sources other than counting statistics are adding to the noise. The most likely sources are noise and/or inaccuracies from the doubly charged strontium correction and background correction, as the background and doubly charged strontium signals make up a relatively larger fraction of the small 43Ca+ signal (the natural abundance is 0.135%) than of the 42Ca+ and 44Ca+ signals. The precision of the 44Ca+/42Ca+ ratio is comparable to that obtained by TIMS,7,8 whereas the precision of the 42Ca+/43Ca+ and 44Ca+/43Ca+ ratios is almost identical to the precision of 0.25% RSD obtained by quadrupole ICP-MS utilizing the cool plasma mode.10 Although the precision obtained is still significantly higher than that obtained by multiple collector ICP-MS,11 it shows that single detector double focusing sector field ICP-MS is a valid technique for the measurement of calcium isotope ratios in nutritional experiments. The measurement precision also gives guidance on the relative changes in isotope ratio necessary to produce a ratio distinguishable from the natural value. While the detection limit for measuring a change in isotope ratio is three times the RSD, it is customary to design nutritional experiments to result in an average shift in isotope ratio of approximately 10 times the RSD (the quantification limit).14 For the method presented here, the detection limit shifts in isotope ratios are 0.69%, 0.75% and 0.15% for the 42Ca+/43Ca+, 44Ca+/43Ca+ and 44Ca+/42Ca+ ratios, respectively, while nutritional experiments should be set up to produce shifts of at least 2.3%, 2.5% and 0.5% for the three ratios, respectively.| Isotope ratio | RSDmeasured (%) | RSDtheoretical (%) | Ratio |
|---|---|---|---|
| 42Ca+/43Ca+ | 0.23 | 0.14 | 1.6 |
| 44Ca+/43Ca+ | 0.25 | 0.13 | 1.9 |
| 44Ca+/42Ca+ | 0.05 | 0.07 | 0.7 |
Total calcium by isotope dilution
Normally, ICP-MS is not the preferred technique for the measurement of total calcium in urine; more often, either inductively coupled plasma optical emission spectrometry (ICP-OES) or atomic absorption spectrometry (AAS) is used.29,33 Isotope dilution ICP-MS, on the other hand, shows better accuracy and precision than these methods, which is important in order to obtain accurate estimates for calcium absorption and to reduce the overall uncertainty. Therefore, isotope dilution ICP-MS was applied in this study. In order to evaluate the accuracy of the isotope dilution ICP-MS method, two urine quality-control samples (Lyphocheck®, 62081 and 62082), containing known amounts of calcium, were analysed in duplicate; furthermore, 10 replicate measurements of the calcium content in a urine sample were performed to obtain an estimate of the precision. The results are presented in Table 4. The results for the control samples are within the certified ranges and show that the accuracy of the total measurements is good. The precision of the measurements was found to be 3.0% RSD, which is similar to the 2–5% RSD normally obtained when applying AAS or ICP-OES.29,33 However, with isotope dilution ICP-MS measurements, a precision in the range 0.5–1% RSD is normally found;25,34 hopefully, in future analyses, the precision can be improved with more method development and experience. In addition, spiking with enriched 42Ca instead of 44Ca would be beneficial, as a 44Ca/42Ca ratio close to unity in the sample–spike solution can be obtained, which eliminates some of the uncertainties in the isotope ratio measurement, i.e. the uncertainty from the detector dead time correction. Although the isotope dilution experiment did not produce the expected improvement in precision, the accuracy is better than when AAS or ICP-OES is applied. This was demonstrated by the excellent correlation found between the calcium absorption estimated for the same subjects when applying two different methods, using both stable and radioisotope experiments or the radioisotope alone,35 a correlation that was not found when AAS was used for the total measurements.29Combined uncertainty of the estimation of calcium absorption
The goal of most nutritional experiments estimating calcium absorption from test meals is to measure changes in absorption as a function of different dietary factors. The uncertainty of the estimated absorption values is therefore important in order to be able to evaluate if an apparent change in absorption rate is significant. For the nutritional experiments discussed in this study, the absorption was calculated using either eqn. (2) or (3), which obviously have different uncertainties attached to them. Therefore, the combined uncertainty was calculated differently for the two experiments.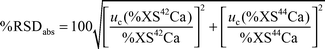 | (4a) |
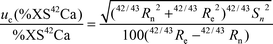 | (4b) |
 | (4c) |
Two factors control this uncertainty: the precision of the measurement of the isotope ratios and the percentage atom enrichment in the second day urine sample; the latter is controlled by the amount of stable isotope administered and absorbed. The amount of the administered dose absorbed is affected by the bioavailability, as well as by the total amount of calcium in the test meal, due to the reverse correlation between the relative absorption of the added enriched isotope and the total amount of calcium ingested with the test meal. Improving the precision of the measurement, increasing the isotope dose or decreasing the amount of natural calcium given in the test meal will therefore improve the uncertainty of the absorption rate. It is therefore very important that these factors are considered in the set-up of nutritional experiments.
For the double stable isotope nutritional experiment discussed in this paper, the eleven subjects were given 2.3 mg 42Ca intravenously and 19.5 mg 44Ca orally with a meal containing 225 mg calcium in total. These doses resulted in average atom enrichments of 4% and 5% for 42Ca and 44Ca, respectively (i.e. the average enriched ratios were 4.98 for 42Ca/43Ca and 16.22 for 44Ca/43Ca, where the natural values are 4.79 and 15.45).36 All samples were measured in triplicate with a measurement precision of 0.25% RSD. From this information, the combined uncertainty in the calcium absorption is estimated to be 6.7% RSD from the above equations. This figure is an average for the eleven subjects in the study. The combined uncertainty should be multiplied by a coverage factor to obtain the expanded uncertainty. If a coverage factor of two is chosen, the expanded uncertainty provides an interval containing approximately 95% of the distribution of values,27 resulting in an expanded uncertainty of 13.4% RSD. Therefore, for an observed change in calcium absorption (either positive or negative) to be significant, it should be at least 13.4%. This value is probably higher than expected, but it is a realistic value and should be kept in mind when evaluating the final data from nutritional experiments with the above outline.
The calcium absorption was calculated from eqn. (3). The uncertainties in the individual terms were calculated and are shown in Table 5 (for one subject), from which it is clear that the uncertainty is completely controlled by the first three terms in the table: the total calcium measurement and the measurement of 47Ca and 44Ca/42Ca. The uncertainty in the remaining three terms can be neglected. The combined uncertainty can hence be calculated using eqn. (5):
 | (5) |
 | (6) |
| Term | Y | u c(Y) | (uc(Y)/Y)2 | % of total error |
|---|---|---|---|---|
| a Y is the value of the different terms, uc(Y) is the combined standard uncertainty and (uc(Y)/Y)2 is the uncertainty expressed as the relative standard deviation. The terms are defined as follows: total calcium concentration (Catot), % of 47Ca dose in second day urine (%47Caurine), % atom enrichment of 44Ca (%XS44Ca), natural abundance (ACa44), urine volume (Vurine) and 44Ca dose administered (44Caiv). | ||||
| Catot | 79.39 | 2.38 | 9.00 × 10−4 | 93.0 |
| %47Caurine | 2.20 | 0.016 | 5.29 × 10−5 | 5.5 |
| %XS44Ca | 11.71 | 0.043 | 1.37 × 10−5 | 1.4 |
| A Ca44 | 2.086 | 0.002 | 9.19 × 10−7 | <0.1 |
| V urine | 2.8243 | 0.0018 | 3.98 × 10−7 | <0.1 |
| 44Caiv | 18.18 | 0.0023 | 1.60 × 10−8 | <0.1 |
Comparing the uncertainty budgets for the two different nutritional experiments, it is obvious that, although they produce the same result, the calcium absorption, the uncertainty of the results are different and controlled by different parameters; therefore, they should also be optimized differently. For the double stable isotope procedure, the key to precise and reliable results is the precision of the sector field ICP-MS measurements of the 44Ca/43Ca and 42Ca/43Ca isotope ratios, whereas, for the mixed double isotope procedure, it is the precision of the isotope dilution sector field ICP-MS measurement of total calcium that controls the uncertainty.
For the parameters given above, the mixed double isotope procedure has the lowest (best) uncertainty in the final calcium absorption results and should therefore be preferred. The disadvantage of this procedure is that it requires access to both sector field ICP-MS and β-ray detection.
The above calculations for the two different nutritional experiments are of a general nature and should be performed whenever nutritional experiments are carried out using stable isotopes or radioisotopes, in order to obtain an estimate of the overall expanded combined uncertainty of the results. This information is important and crucial when drawing conclusions from the final data set. The absolute value of the uncertainty varies with the chosen experimental parameters, such as the isotope dose, calcium content in the test meal, atom enrichment, measurement precision, etc.; therefore, the expanded uncertainty should be recalculated every time the experimental conditions are changed.
In addition, it may be advantageous to perform the uncertainty calculation for the nutritional experiment prior to the actual analysis using estimated values for the parameters, such as the measurement precision, atom enrichment, etc. (chosen from earlier experiments and experience). This will produce a rough estimate of the uncertainty of the future results and offer some guidance on whether or not the results will produce an uncertainty that allows the desired conclusions to be drawn. The uncertainty calculations presented above are also important in pinpointing the critical parameters in an experiment, i.e. those that should be optimized in order to obtain the best overall performance.
Acknowledgements
The author wishes to thank Susanne Højbjerg Bügel, Marianne Hansen, Christian Mølgaard, Anne Bjørn Brendstrup and Brittmarie Sandström (Research Department of Human Nutrition at the Royal Veterinary and Agricultural University, Copenhagen, Denmark) for many fruitful discussions, for performing the nutritional experiments and for providing the enriched stable isotopes needed for this study. In addition, the author wishes to thank Michael Jensen and Susanne Svalling (Department of Nuclear Medicine, University State Hospital, Copenhagen, Denmark ) who performed the 47Ca determinations and provided useful information on the technique for the uncertainty calculations.References
- Nordiske Näringsrekommendationer (1996), Nord 1996: 28, Nordiske Ministerrådet, Copenhagen, 1996 (in Swedish) Search PubMed.
- R. J. Kutsky, in Handbook of Vitamins, Minerals and Hormones, Van Nostrand Reinhold Company, New York, 2nd edn., 1981, pp. 17–29 Search PubMed.
- S. P. Nielsen, O. Bärenholdt and O. Munck, Scand. J. Clin. Lab. Invest., 1975, 35, 197 CAS.
- M. Griessen, A. Jung, B. Cochet, P. Bartholdi, J.-M. Gaspoz, F. Infante, A. Donath, E. Loizeau and B. Courvoisier, J. Lab. Clin. Med., 1985, 105, 641 CAS.
- J. A. DeGrazia, P. Ivanovich, H. Fellows and C. Rich, J. Lab. Clin. Med., 1965, 5, 822.
- A. L. Yergey, N. E. Vieira and D. G. Covell, Biomed. Environ. Mass Spectrom., 1987, 14, 603 CAS.
- R. I. Price, G. N. Kent, K. J. B. Rosman, D. H. Gutteridge, J. Reeve, J. P. Allen, B. G. A. Stuckey, M. Smith, G. Guelfi, C. J. Hickling and S. L. Blakeman, Biomed. Environ. Mass Spectrom., 1990, 19, 353 CAS.
- J. R. Turnlund, W. R. Keyes, K. C. Scott and R. A. Ehrenkranz, J. Anal. At. Spectrom., 1993, 8, 983 RSC.
- S. Stürup, M. Hansen and C. Mølgaard, J. Anal. At. Spectrom., 1997, 12, 919 RSC.
- K. Y. Patterson, C. Veillon, A. D. Hill, P. B. Moser-Veillon and T. C. O'Haver, J. Anal. At. Spectrom., 1999, 14, 1673 RSC.
- L. Halicz, A. Galy, N. S. Belshaw and R. K. O'Nions, J. Anal. At. Spectrom., 1999, 14, 1835 RSC.
- S. F. Boulyga and J. S. Becker, Fresenius' J. Anal. Chem., 2001, 370, 618 CrossRef CAS.
- S. Stürup, PhD Thesis, Risø National Laboratory, Roskilde, Denmark, 2000.
- H. M. Crews and F. A. Mellon, in Stable Isotopes in Human Nutrition—Inorganic Nutrient Metabolism, ed. B. Sandström and F. A. Mellon, Academic Press, London, 1996, pp. 57–58 Search PubMed.
- Y. Duan, Y. Su, Z. Jin, M. Koby and V. Majidi, J. Anal. At. Spectrom., 2001, 16, 756 RSC.
- J. S. Becker and H.-J. Dietze, J. Anal. At. Spectrom., 1999, 14, 1493 RSC.
- P. K. Appelblad and D. C. Baxter, J. Anal. At. Spectrom., 2000, 15, 557 RSC.
- S. M. Nelms, C. R. Quetel, T. Prohaska, J. Vogl and P. D. P. Taylor, J. Anal. At. Spectrom., 2001, 16, 333 RSC.
- A. Held and P. D. P. Taylor, J. Anal. At. Spectrom., 1999, 14, 1075 RSC.
- P. J. Turner, D. J. Mills, E. Schröder, G. Lapitajs, G. Jung, L. A. Iacone, D. A. Haydar and A. Montaser, in Inductively Coupled Plasma Mass Spectrometry, ed. A. Montaser, Wiley-VCH, New York, 1998, pp. 421–501 Search PubMed.
- G. P. I. Russ and J. M. Bazan, Spectrochim. Acta, Part B, 1987, 42, 49 CrossRef.
- F. Vanhaecke, L. Moens, R. Taylor and P. Taylor, Anal. Chem., 1996, 68, 567 CrossRef CAS.
- F. Vanhaecke, L. Moens, R. Dams, I. Papadakis and P. Taylor, Anal. Chem., 1997, 69, 268 CrossRef CAS.
- T. Prohaska, C. Latkoczy and G. Stingeder, J. Anal. At. Spectrom., 1999, 14, 1501 RSC.
- T. Catterick, B. Fairman and C. Harrington, J. Anal. At. Spectrom., 1998, 13, 1009 RSC.
- H. E. Taylor, R. A. Huff and A. Montaser, in Inductively Coupled Plasma Mass Spectrometry, ed. A. Montaser, Wiley-VCH, New York, 1998, pp. 681–807 Search PubMed.
- EURACHEM/CITAC Guide, Quantifying Uncertainty in Analytical Measurement, ed. S. L. R. Ellison, M. Rosslein and A. Williams, EURACHEM/CITAC, London, 2nd edn., 2000 Search PubMed.
- W. van Dokkum, S. J. Fairweather-Tait, R. Hurrel and B. Sandström, in Stable Isotopes in Human Nutrition—Inorganic Nutrient Metabolism, ed. B. Sandström and F. A. Mellon, Academic Press, London, 1996, pp. 23–42 Search PubMed.
- A. B. Brendstrup, MSc Thesis, The Royal Veterinary and Agricultural University, Copenhagen, Denmark, 2000.
- S. Caroli, A. Alimonti, F. Coni, F. Petrucci, O. Senofonte and N. Violante, Crit. Rev. Anal. Chem., 1994, 24, 363 Search PubMed.
- I. S. Begley and B. L. Sharp, J. Anal. At. Spectrom., 1994, 9, 171 RSC.
- N. Furuta, J. Anal. At. Spectrom., 1991, 6, 199 RSC.
- G. Morisi, M. Patriarca, F. Petrucci, L. Fornarelli and S. Caroli, Spectroscopy, 1990, 5, 31 Search PubMed.
- A. A. van Heuzen, T. Hoekstra and B. van Wingerden, J. Anal. At. Spectrom., 1989, 4, 483 RSC.
- A. B. Brendstrup, S. H. Bügel, M. Jensen, S. Stürup and B. Sandström, in preparation.
- M. Hansen, S. Stürup and B. Sandström, Book of abstracts, Exp. Biol., 1998 Search PubMed.
- M. Jensen, Department of Nuclear Medicine, University State Hospital, Copenhagen, Denmark, personal communication, 2000.
| This journal is © The Royal Society of Chemistry 2002 |
