Serendipitous assembly of polynuclear cage compounds

Abstract

The idea of synthesising polynuclear cage compounds without strictly designing the final product is an extremely productive means of producing new polymetallic cages. Some of the considerations behind this approach—termed “serendipitous assembly”—are briefly reviewed, and one project is discussed in some detail to illustrate how such a programme develops. The complexes discussed involve nickel and cobalt cages, ranging as large as cages containing twenty-four metal centres. The magnetic properties of the more interesting cages, including a {Ni₁₂} cyclic single molecule magnet, are discussed.

---

Richard Winpenny

Richard Winpenny has recently been appointed to the Chair of Inorganic Chemistry at the University of Manchester. He had previously been a Lecturer and then Reader at the University of Edinburgh. Prior to appointment at Edinburgh he was a post-doctoral researcher with Professor John Fackler Jr. at Texas A&M University. His university education was at Imperial College, London, carrying out his PhD under the supervision of Professor David Goodgame.

---

Introduction

Much has been made of the supramolecular approach to synthesis of complexes containing more than one metal centre. For example, Fujita's beautiful work on use of “molecular panelling” to create polynuclear compounds containing palladium fragments illustrates what can be achieved by designed synthesis.¹ Aesthetically this approach is very appealing, however, at present, it is unquestionably true that the polymetallic complexes with the most interesting physical properties have been made, at least initially, by accident. For example, the first “single molecule magnets” (SMMs), [Mn₁₂O₁₂(O₂CR)₁₆(H₂O)₄] (R = Me or Ph) were made by accident from a reaction involving permanganate and an Mn(III) triangle.² These SMMs have attracted enormous attention as they store magnetic information at a molecular level, and also display resonant quantum tunnelling of magnetisation,³ which is of interest to physicists studying the mechanism of quantum tunnelling. It is only a slight exaggeration to say that at present the “designed assembly” approach is strong on design, and weak on making molecules that have interest beyond the fact that their formation was predicted.

A further danger of the designed assembly approach is that it relies on a limited range of experience and on the imagination of the scientists involved. The comment from Siegel and co-workers in a recent issue of Angewandte Chemie,⁴ “the concept of an accessible and controllable molecular program, even within the limited arena of metal coordination structures, seems premature”, is entirely apposite. It is apposite for two reasons: as highlighted in the article, designed assembly can make incorrect predictions; secondly, and more importantly, it limits our horizons. If we only use ligands where we are confident of their behaviour, we will restrict ourselves to a limited number of products. The inevitable result if we only target predictable molecules, is that our synthetic work will become first predictable and then dull.

To illustrate this point: the {Mn₁₂} cages¹ mentioned above have a metal core involving an Mn₄O₄ heterocubane encapsulated within an Mn₈ wheel. Not only is it presently impossible to design a synthesis of such a molecule, it is not a conceivable synthetic target because the structure is complicated with low symmetry. It is not a structure we would choose to design. The interesting magnetic properties of {Mn₁₂} are dependent on structure, but could not have been predicted. Therefore the phenomena could only have been discovered by accident rather than design.

As a contrast to the designed assembly approach, we have been pursuing an approach that we term, somewhat tongue in cheek, “serendipitous assembly”. In this work the element of strict design is absent. In contrast to designed assembly, ligands are used that display several different coordination modes, combined with metal centres that can vary their coordination geometries. However, little progress would be made if serendipity were our only guide. Later experiments and synthetic tactics are informed by observations made in earlier studies. This article will attempt to show how one project in serendipitous assembly developed. The justification for writing such an account is partly to defend ourselves against accusations that we've been indulging in a successful scientific fishing trip, but mainly an attempt to convince supramolecular chemists that there is a rational alternative to designed assembly. There is still a need to explore the chemistry of ligands with coordinative flexibility.

Many of the approaches to serendipitous assembly rely on creating a mismatch between the number or type of coordination sites available on a single metal site, and the donor set supplied by the ligand. This can be illustrated with two examples. The influential work of Powell and Heath has used a range of polycarboxylates,⁵e.g. N(CH₂COOH)₂(CH₂CH₂OH), where the number or disposition of the donor atoms on the ligand makes it impossible for all donor atoms to bind to a single metal centre. The mismatch leads inevitably to bridging between metal sites, and the degree of bridging can be elegantly controlled through pH and metal ∶ ligand ratio. Most famously this has resulted in a series of {Fe₁₇} and {Fe₁₉} cages, and more recently Powell has extended this work to produce a {Cu₃₆} cage.⁶ Others are now adopting a similar approach, e.g. Murrie et al. have used citrate to produce {Ni₂₁} cages.⁷

The second example creates the opposite mismatch—removing ligands from complexes to create coordinative unsaturation. If the well-known basic chromium carboxylates, [Cr₃O(O₂CR)₆(H₂O)₃]X (X = NO₃⁻ or OH⁻), are heated to temperatures above 300 °C, the triangular cage will lose either the terminally bound water molecules or carboxylic acid, depending on the carboxylate present.^8–11 In either case this creates vacant coordination sites, and the remaining ligands rearrange to bridge between metals, creating larger structures. For example, if R = Ph [Cr₈O₄(O₂CPh)₁₆] forms in good yield,⁹ which is a dehydration of the original triangle. The structure contains a Cr₄O₄ heterocubane with the oxides each bridging to a further chromium centre; the oxide ligands change from μ₃-bridging in the triangle, to μ₄-bridging in the octanuclear cage. In this case it is possible to anticipate that the loss of a ligand will disrupt the structure, but it is not possible to predict the product that will result. This is a frequent observation in serendipitous assembly: you can predict there will be an effect, but cannot predict how that effect will be manifested.

As serendipitous assembly generates unpredictable results this influences the choice of ligands. Ligands that require considerable synthetic effort should be avoided, as it cannot be foreseen whether they will be useful. Secondly, as minor variations in the ligands may influence structure ideally a series of related ligands should be explored. Thirdly, as a range of solvents will need to be examined for crystallisation of the cage compound, it is useful if the ligand has solubility in as many solvents as possible. One depressingly frequent result is the formation of perfect, colourless crystals of ligand grown from intensely coloured solutions of complex.

In the following the binding mode of the ligands will be described using Harris notation.¹² Harris notation describes the binding mode as [X˙Y₁Y₂Y₃…Y_n], where X is the overall number of metals bound by the whole ligand, and each value of Y refers to the number of metal atoms attached to the different donor atoms. The ordering of Y is listed by the Cahn–Ingold–Prelog priority rules, hence O before N. Therefore for the pyridonate and carboxylate ligands discussed below there will be two values of Y, as there are two donor groups. The bonding modes of the pyridonates, and the Harris notation to describe these modes, are given in Scheme 1.

Scheme 1

Background

The observation, initially made by Benelli et al.,¹³ that the magnetic exchange between copper(II) and gadolinium(III) is ferromagnetic was made in 1985, and suggested a method of making molecular compounds with unusual magnetic properties. The original work, which has since been developed by a number of other groups,¹⁴ involved use of Schiff bases to bind to both metal centres, using N-donors to bind copper and O-donors to bind to the lanthanoid centre. In attempting to extend this work it seemed possible that use of simpler ligands might lead to larger cages. One of the simplest ligands that contains both an N- and O-donor is 2-pyridonate, therefore we began to explore the chemistry of this ligand and its derivatives.

When carrying out reactions involving copper acetate and pyridonate derivatives, octanuclear copper complexes formed with monotonous regularity.¹⁵ [Cu₈O₂(O₂CMe)₄(chp)₈] 1 (Fig. 1) (chp = 6-chloro-2-pyridonate) is remarkably easy to make. One route was from direct reaction of [Cu₂(O₂Me)₄(H₂O)₂] and [Cu₂(chp)₄], and this was intriguing as it is far from obvious why two stable dimeric species should react together to make an octanuclear cage. Similar cages could be made with other carboxylates and pyridonates. This led us to the hypothesis that it was the presence of a mixture, or blend, of bridging ligands that was leading to the larger cluster.

Fig. 1 The structure of [Cu₈O₂(O₂CMe)₄(chp)₈] 1 in the crystal. Colours: Cu, blue; O, red; N, dark blue; Cl, green. C-atoms shown as lines for clarity.

This leap of faith appeared to be confirmed by the existence in the literature of a report¹⁶ of the structure of [Co₁₂(OH)₆(O₂CMe)₆(mhp)₁₂] 2 (mhp = 6-methyl-2-pyridonate). This compound, synthesised by Garner and co-workers in the early 1980s, was one of the larger cage complexes known at the time. Surprisingly no further studies had been reported on the compound, nor had other derivatives been synthesised.

As the Garner group had been successful with cobalt(II), and we had managed to synthesise a copper(II) complex, the rational extension of the work was to look at the intermediate element, nickel.

Complexes with carboxylate and pyridonate ligands

Synthesis and structures

The reaction of nickel acetate with 6-chloro-2-hydroxypyridine at 130 °C produces a green paste. This paste can be extracted with THF and green crystals grow very quickly from the solution. The crystals contain a cyclic dodecanuclear cage [Ni₁₂(chp)₁₂(O₂CMe)₁₂(H₂O)₆(THF)₆] 3 (Fig. 2).¹⁷

The molecule crystallises about a 3 crystallographic axis, with two nickel sites in the asymmetric unit. Both nickel sites are octahedral, bound to six O-donors. The pyridonate ligands bind with the 2.20 mode, with the N-atom finding an H-bond to a bridging water molecule. The carboxylates belong to two classes; one lies within the wheel and adopts the 3.21 mode, while the second lies outside the cage and has the more conventional 2.11 mode. Although a conventional ball-and-stick representation (e.g.Fig. 2) suggests there is a cavity within the molecule, a space-filling representation would show that the internal carboxylates pack very tightly with the H-atoms of the methyl groups interdigitating.

Fig. 2 The structure of [Ni₁₂(chp)₁₂(O₂CMe)₁₂(H₂O)₆(THF)₆] 3 in the crystal. Colours: Ni, blue; O, red; N, dark blue; Cl, purple. C-atoms shown as lines for clarity.

The formation of 3 owes a great deal to serendipity, as each component of the reaction is vital to generate the final structure. For example, no other carboxylate would have the correct size to occupy the central cavity, while the 2.20 bonding mode adopted by the pyridonate is only found for chp; if mhp had been used the greater basicity of the ring nitrogen would disfavour this mode. Furthermore, THF is the only solvent that supports formation of the wheel; we have tried many other similar solvents without success. Therefore, we must admit our good fortune and not pretend it is the “result of a dynamic combinatorial library”. Exploitation of this good fortune is entirely rational. The simplest exploitation is to make the dodecanuclear cobalt wheel, which is isostructural to 3,¹⁸ and we can also replace 6-chloro-2-pyridonate with 6-bromo-2-pyridonate.¹⁸

Comparing 1, 2 and 3 it is immediately obvious that the metal–pyridonate–carboxylate system is extremely rich. The three cages feature different metals, and were crystallised from different solvents and feature a variety of pyridonates and carboxylates. It is therefore rational to vary the reaction conditions within this limited system—“parameter space” if you prefer—to see what other cages result. In passing it is worth noting that it is not presently possible to design the synthesis of a structure such as 3.

Restricting work to nickel, and varying the carboxylate, pyridonate and solvent rapidly generated a series of cages.¹⁹ The least interesting are a series of linear trinuclear cages, which result from reaction of 6-chloro-2-pyridonate and most nickel carboxylates when crystallised from MeOH or EtOH.^18,19 The cages have the general formula [Ni₃(chp)₄(O₂CR)₂(R′OH)₆], where R = Me, Ph, CH₂PH, CMe₃ and R′ = Me or Et. The central nickel atom is on a crystallographic inversion centre, and is bridged to each of the two symmetry equivalent outer nickel sites by a 2.11-carboxylate and two 2.20-chp ligands. The two terminal sites have their coordination spheres completed by three molecules of the respective alcohol. The linear arrangement of three nickel sites can be recognised as a fragment of 3, with the presence of the alcohol molecules restricting the growth of the cage.

If trichloroacetate is used as the carboxylate a different cage results. The tetranuclear cage, [Ni₄(OMe)₄(chp)₄(MeOH)₇] 4, also crystallises from MeOH (Fig. 3).¹⁹ The instability of trichloroacetate when heated in protic environments probably explains the change in reactivity, with the decomposition of the carboxylate to chloroform and CO₂ giving a cage other than the trinuclear fragments. 4 is held together by four 3.3-bridging methoxides. The pyridonate ligands adopt the 1.10 and the chelating 1.11 bonding modes. The exterior of the cluster is coated by seven methanol ligands, which block coordination sites on the cage in a similar manner to the binding of solvate molecules in the trinuclear cages. In both cases the use of a coordinating solvent restricts growth in nuclearity of the cages. A more rational synthesis of 4 is from nickel chloride reacted with Na(chp) and Na(OMe) in MeOH.

Fig. 3 The structure of [Ni₄(OMe)₄(chp)₄(MeOH)₇] 4 in the crystal. Colours as Fig. 2.

Use of less polar, aprotic solvents leads to a series of larger cages related in structure to 2. All are based on a centred pentacapped trigonal prism, with different parts of the structure missing. The parent structure is found for [Ni₁₂(OH)₆(mhp)₁₂(O₂CCH₂Cl)₆] 5 (Fig. 4), which has the identical array of metal sites to those in 2.²⁰ The central nickel site is bound to six μ₃-hydroxides that bridge to nine further metals forming the tricapped trigonal prism. The metal atoms at the vertices of the prism share one 3.3-OH with the central nickel, while the metal atoms capping the rectangular faces of the prism share two 3.3-hydroxides with the central site forming three M₂O₂ rings.

Fig. 4 The structure of [Ni₁₂(OH)₆(O₂CCH₂Cl)₆(mhp)₁₂] 5 in the crystal. Colours as Fig. 2.

The exterior of this central tricapped trigonal prism is bridged by six mhp and six carboxylates. Each pyridonate adopts the 3.31 bonding mode, binding to one of the nickel atoms at the vertices of the prism through the N-donor. The six μ₃-O-donors from the pyridonates occupy the six triangular faces around the “waist” of the tricapped trigonal prism, i.e. they centre the faces bounded by one-cap- and two-vertex-metal sites. The chloroacetates bridge in 2.11-fashion between cap- and vertex-sites, with each cap attached to two chloroacetate ligands. The result of these various bridges is to create a central [M₁₀(3.3-OH)₆(3.21-xhp)₆(2.11-O₂CR)₆]²⁺ fragment.

The metal sites are each six-coordinate, with the central metal bonded exclusively to 3.3-hydroxides. The capping sites are bonded to two 3.3-hydroxides, two μ₃-O-atoms from mhp, and two oxygens derived from carboxylates. The vertex-sites are bound to only five donors from within this central fragment: one 3.3-hydroxide, two μ₃-O-atoms from mhp, one oxygen from a carboxylate and one N-donor from an mhp ligand. The final coordination site for these vertex-metals is where the structural variation in these cages takes place. In 5 six μ-O-atoms from mhp ligands each occupy one of these sites, with these ligands part of two [Ni(mhp)₃]⁻ fragments which occupy both the upper and lower triangular faces of the trigonal prism. Thus the [Ni(mhp)₃]⁻ fragments could be regarded as trinucleating complex ligands. The nickel centres are then caps on the trigonal faces of the central trigonal prism.

With other pyridonates and carboxylates these final coordination sites are not always occupied by [Ni(mhp)₃]⁻ fragments.²⁰ If acetate is the carboxylate {Ni₁₁} cages result where one of these sites is occupied by an [Ni(mhp)₃]⁻ unit, while the other site is occupied either by three water molecules to give [Ni₁₁(OH)₆(mhp)₉(O₂CMe)₆(H₂O)₃]⁺6 or by a mixture of acetate and pyridonate to give [Ni₁₁(OH)₆(mhp)₉(O₂CMe)₇(Hmhp)₂] 7. 6 exists in the solid-state as a hydrogen-bonded dimer (Fig. 5); the counter-ion appears to be a single carbonate ion. With other carboxylates such as benzoate, diphenylacetate and isobutyrate cages can be crystallised where both caps on the trigonal faces are missing, resulting in a series of {Ni₁₀} cages. A representative structure, [Ni₁₀(OH)₆(chp)₆(O₂CCHPh₂)₆(Cl)₂(Hchp)(H₂O)₂(MeOH)] 8, is shown in Fig. 6.

Fig. 5 The structure of the H-bonded dimer of [Ni₁₁(OH)₆(mhp)₉(O₂CMe)₆(H₂O)₃]⁺6 in the crystal. Colours as Fig. 2.

Fig. 6 The structure of [Ni₁₀(OH)₆(chp)₆(O₂CCHPh₂)₆(Cl)₂(Hchp)(H₂O)₂(MeOH)] 8 in the crystal. Colours as Fig. 2, except Cl, green.

The existence of other derivatives of the central tricapped trigonal prism lead us to return to the cobalt chemistry, to see whether cages related to 2 could be made. This led to two {Co₁₀} cages containing the same metal core as 8, crystallised with benzoate or pivalate (trimethylacetate) as the carboxylate and mhp as the pyridonate.²⁰

The family of trigonal prisms could be extended still further if required—indeed the synthesis of the decanuclear cages is sufficiently straightforward that “new” reactions can be given to undergraduate project students with some expectation of success. It is possible to predict that many further related cages with different carboxylates and pyridonates could be made.

Two other structural types have been found from this reaction, which appeared to be exceptions to the rule. With cobalt, use of chp as the pyridonate produced three {Co₇} cages,²¹ for example [Co₇(OH)₂(O₂CPh)₄(chp)₈(MeCN)] 9 (Fig. 7), with either benzoate or pivalate as the co-ligand. The metal core is perhaps best described as a square-based pyramid capped on one triangular face and on an adjacent edge by two further cobalt centres. Two 3.3-hydroxides lie at the centre of the cage; the first bridges between the cobalt at the vertex of the pyramid and two Co atoms within the square base, while the second bridges between the remaining Co centres in the square base and the edge-capping cobalt. The four carboxylates in these cages all have a 2.11-binding mode, while the chp ligands show four distinct bridging modes 2.20, 2.21, 3.21 and 3.31.

Fig. 7 The structure of [Co₇(OH)₂(O₂CPh)₄(chp)₈(MeCN)] 9 in the crystal. Colours as Fig. 2, plus Co, green.

Use of pivalate as carboxylate leads to the final structural type. This has been found for both nickel and cobalt, and with mhp and chp as pyridonate.²⁰ A representative structure, [Ni₁₀(OH)₄(mhp)₁₀(O₂CCMe₃)₆(MeOH)₂] 10, is shown in Fig. 8. The core has much less symmetry than the trigonal prism, and is so irregular that both descriptions we have used for the structure involve considering it to be a fragment of a larger polyhedron. The metal core can be related to a tetraicoshedron, i.e. a hexagonal anti-prism capped on the hexagonal faces. A better description is given below. The carboxylates present all show the 2.11-binding mode while the pyridonates show four bridging modes: 1.11, 2.21, 3.31 and 3.21. This ability for the pyridonates to show variation in the binding mode is vital in stabilising the range of structures found.

Fig. 8 The structure of [Ni₁₀(OH)₄(mhp)₁₀(O₂CCMe₃)₆(MeOH)₂] 10 in the crystal. Colours as Fig. 2.

The blend of nickel or cobalt with carboxylates and pyridonates therefore appears to be generating a range of different structures. In some cases, for example cobalt with pivalate, three structures can be found for minor changes in reaction conditions. The similarity between the reagents used to produce these various cages suggested that they must be derived from a common parent. Use of molecular graphics shows that the metal cores in both the {Co₇} cages and the final group of decanuclear cages are related to the core of 2 and 5.²¹

This is illustrated in Fig. 9. Of the seven metal vertices of 9, six match well with those of the centred-pentacapped-trigonal prism in 5. Matches are found for the central metal site, three vertices of the prism and two caps on square faces. One of the cobalt sites in 9, which lies within the square-base of the pyramid, does not fit well with the vertices of 5. 5 and 10 fit together still better, with all ten vertices of 10 close to vertices in 5; the two vertices present in 5 but absent in 10 are an edge of the trigonal prism. Therefore 10 could be described as a centred-pentacapped-trigonal prism missing one edge, whereas cages such as 6–8 can be described as missing caps on the trigonal axis.

Fig. 9 (a) The fit of metal sites in 9 and 5; (b) the fit of metal sites in 10 and 5. Metal vertices of 5 shown as blue, other vertices as green.

This synthetic project has therefore produced around a score of cages that can be related to one common structural type.^20,21 It is not immediately obvious why a centred-pentacapped-trigonal prism should be favoured. Working on the assumption that the common polyhedron must be related to a mineral, we generated an extended lattice based on this polyhedron by making each cap the centre of a further prism (Fig. 10); this generates a lattice with alternating hexagonal and trigonal layers, with the vertices of the prism belonging to the trigonal layers and the caps/centres belonging to the hexagonal layers. What is striking is that all the metal sites, even those which do not fit well with the centred-pentacapped-trigonal prism, fit extremely well with metal sites from within this lattice (Fig. 11). Even better, the twelve metal sites of the wheel 3 also fit to the lattice (Fig. 11).

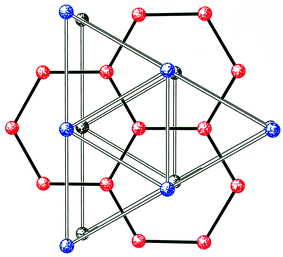Fig. 10 Three layers of the “parent” lattice based on an extended pentacapped centred trigonal prism. Bottom level, black; middle layer, red; top level, blue.

Fig. 11 The fit of the metal sites of (a) 3 and (b) 9 to the parent lattice. Lattice vertices, grey; vertices of 3 and 9, red.

The relationship between this lattice, derived from a centred-pentacapped-trigonal prism, and the M(OH)₂ structures is quite straightforward. Both nickel and cobalt hydroxide are layer structures, adopting the “cadmium iodide” structure with octahedral metal sites bridged by μ₃-hydroxides. Octahedral holes are found between the layers within the M(OH)₂ structures (Fig. 12); dropping every third metal from the layer into an octahedral hole generates a lattice with alternating hexagonal layers and trigonal layers (Fig. 13).

Fig. 12 A view of the structure of Ni(OH)₂, with an inter-layer octahedral hole illustrated by the presence of a green octahedron. Colours: Ni, blue; O, red.

Fig. 13 The lattice derived from dropping every third metal from the Ni(OH)₂ structure into the inter-layer octahedral hole. Colours: Ni sites in layer, blue; Ni sites in octahedral holes, green; O, red.

This suggests that the apparently random structures adopted by these cages are, in fact, related to the appropriate metal hydroxide. Previously structural correlations between cages and minerals have tended to be drawn where the relationship is obvious, e.g. a {Co₂₄} cage made in our group is clearly a fragment of cobalt hydroxide,²² while {Fe₁₇} and {Fe₁₉} cages appear to be fragments of goethite or lepidocrocite.⁵ In general, if a cage does not resemble a fragment of a mineral, then no attempt has been made to explain why a specific array has been formed. This is surprising. The observation that several cobalt and nickel structures can be related to a suitable mineral, in a less obvious way, suggests a possible method for explaining the seemingly irregular structures of many other polymetallic cages. If such relationships could be proven then it would be a first step to understanding the structures of polynuclear cages in general. For such a principle to become predictive many more steps are required including: a rational method for choosing a specific mineral; an explanation of any deviations observed from the ideal mineral; finally an understanding of why certain metal sites of the lattice are found in specific metal cages.

Magnetic properties

In 3 ferromagnetic exchange between the Ni(II) centres leads to an S = 12 ground state for the cage.¹⁷ Modelling the exchange interaction is difficult, and the original exchange interaction parameter reported was derived by a very simplistic treatment involving a single exchange interaction, J.¹⁷ The fit of data gave an estimate of J/k (where k is the Boltzmann constant) as 13.5 K for the Hamiltonian H = JS_iS_{i + 1}. A more sophisticated method based on quantum statistical mechanics has led to a smaller exchange interaction, with J/k = 8.5 K for the same Hamiltonian.²³ Very recent results²⁴ show that the cage shows slow relaxation of magnetisation at low temperature, i.e. that it is a single molecule magnet. Analysis of a.c. susceptibility data allows us to calculate that E_a/k (where E_a is the activation energy for reorientation of the magnetisation) is around 10 K, compared with typically 61 K in the {Mn₁₂} SMMs.

The centred-tricapped-trigonal prisms show more complicated magnetic behaviour because they have much more complicated structures.²⁰ Studies of the variable temperature magnetic susceptibility behaviour of the {Ni₁₂} cage 5, the {Ni₁₁} cage 6 and the {Ni₁₀} cage 8 show that the spin ground state for each cage is different. This is illustrated in Fig. 14 by a plot of χ_mT against T. In each case the magnetic behaviour down to around 10 K is typically “ferrimagnetic”, i.e. anti-ferromagnetic exchange stabilising non-diamagnetic ground states. The spin of these ground states clearly must vary between the three cages. For 2χ_mT goes through a maximum at 12 K, where the value is around 42 cm³ K mol⁻¹. Such a value, allowing for two additional S = 1 centres in the molecule, is consistent with an S = 8 ground state for the central centred-tricapped-trigonal prism. For 4 the maximum in χ_mT is much less dramatic, and the value of 11 cm³ K mol⁻¹ suggests an S = 4 ground state for the M₁₀ core. For 7, the maximum is almost unnoticeable, and this leads us to believe we have an S = 2 ground state.

Fig. 14 Plots of χ_mT against T for 5 (green), 6 (blue) and 8 (red).

As the structures are similar, differing only in the number of caps on the trigonal faces of the central prism, it seemed worthwhile to attempt to model the magnetism using the same mathematical model for each cage. Therefore the caps on the trigonal faces were included in the model as non-interacting S = 1 centres (two for 5, one for 6 and zero for 8), and the magnetic exchange interactions were assumed to be restricted to the central decanuclear cage. This assumption is rather extreme, but necessary to limit the number of parameters in the system.

The Hamiltonian used in modelling the data is given below, and is illustrated in Fig. 15.

H = −J₁S₁(S₂ + S_2a + S_2b + S₃ + S_3a + S_3b) − J₂S₁(S₅ + S_5a + S_5b) − J₃[S₅(S₃ + S_2b) + S_5a(S₂ + S_3a) + S_5b(S_2a + S_3b)]

Fig. 15 The coupling scheme used to model the magnetic data of 5, 6 and 8. The possible spin ground states are illustrated: (a) S  =  8; (b) S  =  2; (c) S  =  4. Relative orientation of spins shown as green arrows (“spin-up”) or purple arrows (“spin-down”).

S ₁ is the spin on the central nickel site, S₅, S_5a and S_5b are the spins on the nickel sites capping the rectangular faces and S₂, S_2a, S_2b, S₃, S_3a and S_3b are the spins on the nickel sites comprising the trigonal prism. The model therefore assumes at least D₃ symmetry for the cage, which is not crystallographically imposed for any of these cages. Any lower symmetry would require more exchange interactions.

The model can explain why S = 8, 4 and 2 are possible spin ground states for these cages. The model involves six triangles, each centred on a hydroxide unit and involving the central nickel site. The relative magnitudes and signs of the exchange interactions along the edge of the triangle decide the ground state. Thus, if J₁ is largest and anti-ferromagnetic it will align the spins on the vertices of the prism anti-parallel with the spin at the centre. If J₂ is more anti-ferromagnetic than J₃ it will align the spin at the caps anti-parallel with the spin at the centre, rather than anti-parallel with the spin on the prism vertices. The result is nine spins in one direction, opposed to the single spin at the centre and hence an S = 8 ground state (Fig. 15(a)). If J₃ were more anti-ferromagnetic than J₂, but both were less anti-ferromagnetic than J₁, then the spins at the cap would align parallel to the spin at the centre, giving six spins in one direction and four in the opposite direction, and an S = 2 ground state (Fig. 15(b)). Finally, if the values for J₁, J₂ and J₃ are chosen such that the spins at the centre and vertices align parallel, but anti-parallel to the spin at the caps, then an S = 4 state would result (Fig. 15(c)). The magnetic behaviour can then be fitted as shown in Fig. 14 with suitable values for J₁, J₂ and J₃.²⁰ The absolute values of these numbers are probably less important than the observation that the occurrence of triangular fragments within these cages leads to many possible spin ground states due to spin frustration.

Further variations

As the reaction system involving nickel or cobalt, a carboxylate and a pyridonate has been so productive, it seemed worthwhile to see whether further, more extreme variations would generate new structures.

Variation of the 3d-metal

The use of different 3d-metals has not generated many new compounds. Unfortunately for 3d-metals earlier than iron the pyridonate ligands do not bind well, and the chemistry found has been very similar to the carboxylate chemistry of these ligands. For iron(III) one very interesting molecule results from the reaction of [NEt₄]₂[Fe₂OCl₆] with Na(chp) and Na(O₂CPh).²⁵ [Fe₁₀Na₂O₆(OH)₄(O₂CPh)₁₀(chp)₆(H₂O)₂(Me₂CO)₂] 11 has an Fe₁₀O₁₀ core, which is perhaps best described as two Fe₆O₆ hexagonal prisms sharing a square face (Fig. 16). Alternatively the core of the structure can be envisaged as a close-packed array of O-centres, with iron atoms occupying octahedral holes in the lattice. The benzoate ligands bridged in a 2.11-fashion while the chp ligands adopt the 2.20-mode seen in 3. Two sodium centres are also found in the cage, bound to O-donors from carboxylates and pyridonates with their coordination environment completed by coordination of acetone. Other solvates can be prepared, with differing molecules bound to these positions.

Fig. 16 The structure of [Fe₁₀Na₂O₆(OH)₄(O₂CPh)₁₀(chp)₆(H₂O)₂(Me₂CO)₂] 11 in the crystal. Colours as Fig. 2 plus Fe, dark red; Na, yellow.

Magnetic studies of 11 reveal the predominant exchange interactions within the cage are anti-ferromagnetic, but result in a high spin ground state due to spin frustration.²⁵ The ground state appears to be around S = 11. Monte Carlo methods have been used²⁶ to calculate the magnitude of the exchange interactions, while low temperature a.c. susceptibility studies reveal that 11 is a single molecule magnet with an activation barrier of 5.3 K to reorientation of the magnetisation.²⁶11 therefore has the dubious distinction of being one of the fastest relaxing single molecule magnets.

Therefore it appears that this reaction system cannot be extended fruitfully to earlier transition metals. However it has been possible to produce heterometallic cages involving cobalt or nickel and copper.²⁷ The synthetic procedure is simple; in place of a single metal carboxylate precursor a mixture of two metal carboxylates are used. Thus mixing copper acetate, cobalt acetate and Hchp, and heating the mixture to above the melting point of Hchp, followed by extraction and crystallisation produces [Co₇Cu₂(OH)₂(chp)₁₀(O₂CMe)₆], which has a very irregular structure (Fig. 17), while the analogous reaction involving benzoates and Hmhp gives [Co₆Cu₂(OH)₄(mhp)₂(O₂CPh)₁₀(Hmhp)₄(H₂O)₂] which is equally irregular (Fig. 18).²⁷ The {Ni₆Cu₂} analogue of the latter cage has also been made, however the approach has not been investigated in depth.²⁷

Fig. 17 The structure of [Co₇Cu₂(OH)₂(chp)₁₀(O₂CMe)₆] in the crystal. Colours: Co, green; Cu, blue; O, red; N, dark blue; Cl, small green balls; C, lines.

Fig. 18 The structure of [Co₆Cu₂(OH)₄(mhp)₂(O₂CPh)₁₀(Hmhp)₄(H₂O)₂] in the crystal. Colours as Fig. 17.

Variation of the carboxylate

The reactions that produce centred-tricapped-trigonal prisms suggest some dependence on the steric requirements of the carboxylate. For example, the {M₁₀} cages missing caps on the trigonal faces all involve carboxylates that are disubstituted at the α-carbon, e.g. diphenylacetate, benzoate, while the {M₁₀} cages missing an edge of the pentacapped-trigonal-prism involve pivalate, which is trisubstituted at this carbon.²⁰ A rational extension was therefore to examine more sterically demanding carboxylates.

Use of triphenylacetate has produced several unexpected results.^28,29 The favoured product for smaller carboxylates, based on the tricapped-trigonal-prism is disfavoured, but can still be isolated in very low yields. However in addition new structures can be crystallised²⁸—all in low yield and after extended crystallisation periods. For example, [Co₁₀(OH)₆(mhp)₆(O₂CCPh₃)₆(Hmhp)₃(HCO₃)₃] can be crystallised in four months in ca. 4% yield.²⁹ This structure contains a centred-trigonal-prism of cobalt sites, but now capped on the edges of the square faces of the prism rather than at the centre. The conclusion has to be that by disfavouring the preferred reaction path we are opening up a whole range of new “secondary” products, i.e. the selectivity for tricapped-trigonal prisms has been removed, but not replaced by any selectivity for an alternative cage. It is as if on a potential energy surface we have closed off the global minimum, and are now finding the structures related to a host of local minima. From a purely synthetic viewpoint this is therefore a poor procedure, however to understand the structural chemistry of polymetallic cages such an approach is intriguing as it suggests how complex the reaction soup can be from which the single crystals of product grow.

Another possible route is to replace the monocarboxylates in the synthesis with dicarboxylates. This has led to two very large cages, [Co₁₃(OH)₂(phth)₂(chp)₂₀] 12 (Fig. 19)²¹ and [Ni₁₆Na₆(chp)₄(phth)₁₀(Hphth)₂(MeO)₁₀(OH)₂(MeOH)₂₀] 13 (Fig. 20),³⁰ where phth is the dianion of phthalic acid. 12 can be described as a dimer of the heptanuclear cobalt cages such as 9, and the vertices of this extremely irregular polyhedron can all be found within the parent lattice derived from the centred-pentacapped-trigonal prisms (see above).²⁰13 is more unusual, containing four Ni₄(OMe)₄ heterocubanes disposed around a central Na₆ octahedron.³⁰ Four pairs of phthalate ligands link the four heterocubanes to the central sodium cage. While we had found the heterocubane structure previously (see 4 above), it was not found with a carboxylate present; linear trinuclear cages were preferred. Therefore the formation of the 13 was unexpected. Both 12 and 13 illustrate that larger polymetallic arrays are accessible by using dicarboxylates in place of monocarboxylates. Christou had previously demonstrated the same principle could be applied in manganese chemistry to produce an octadecanuclear manganese cage.³¹

Fig. 19 The structure of [Co₁₃(OH)₂(phth)₂(chp)₂₀] 12 in the crystal. Colours as Fig. 2, plus Co, green.

Fig. 20 The structure of [Ni₁₆Na₆(chp)₄(phth)₁₀(Hphth)₂(MeO)₁₀(OH)₂(MeOH)₂₀] 13 in the crystal. Colours as Fig. 2, except Cl shown as green lines. Na, yellow.

Variation of the heterocycle

The pyridonates have proven so fecund that it seems rational to examine other N-heterocycles that contain a hydroxide group in the 2-position. There are many such heterocycles in the literature, and in the catalogues of chemical suppliers. Examining 3-methyl-3-pyrazolin-5-one (Hmpo) in this chemistry has generated one of the largest paramagnetic cages known, [Ni₂₄(OH)₈(mpo)₁₆(O₂CMe)₂₄(Hmpo)₁₆] 14 (Fig. 21).³² The structure consists of an octamer of chemically equivalent trinuclear building blocks {Ni₃(OH)(mpo)₂(O₂CMe)₃(Hmpo)₂}. A 2.11-carboxylate and two μ-oxygen atoms bridge each Ni⋯Ni contact, with the latter groups derived from mpo, acetate and hydroxide groups. Each nickel has an approximately octahedral geometry.

Fig. 21 The structure of [Ni₂₄(OH)₈(mpo)₁₆(O₂CMe)₂₄(Hmpo)₁₆] 14 in the crystal. Colours as Fig. 2, plus H, beige with H-bonds shown as dashed lines.

The Ni₂₄ structure is much less circular than other cyclic structures. The trinuclear fragments are so disposed that they point approximately at the centre of the neighbouring unit, rather than at the end, with a 51° angle between the lines described by one trinuclear unit and its neighbour. In addition to the metal–ligand bonding, the structure is stabilised by a large quantity of H-bonding, in general involving the proton on the second N-atom within the pyrazolinone ligands. As with 3 protons from methyl groups occupy the cavity of the metallocycle—in this case the methyl groups belong to the mpo ligands. We are optimistic that other pyrazolinone ligands will generate new structures from this chemistry.

Conclusions

The dichotomy between “designed” and “serendipitous” assembly can be exaggerated. Much interesting synthetic work is now arising where results, originally obtained by chance, are being exploited through design, or where careful design has not completely excluded the possibility of a fortunate accident. However, there is an unfortunate impression that those involved in designed assembly are unaware of what is going on elsewhere: for example, a recent review³³ is entitled “Strategies for Construction of Supramolecular Compounds Through Coordination Chemistry”, yet never describes a coordination compound containing more than four metals. The community is missing major opportunities if supramolecular chemists only ever reference and read papers by other supramolecular chemists.

In the area of molecular magnetism, SMMs were discovered by accident, however if devices that operate at ambient temperatures are to be made from these new compounds, then we must begin to consider design criteria for the next generation of SMMs. There are three parameters to consider. The first two parameters are related to the energy barrier for reorientation of the magnetisation. These are the spin of the ground state (S_gs), and the axial zero-field splitting parameter (D), which relates to the anisotropy of that spin. The energy barrier is then equal to DS_gs², and for room temperature SMMs DS_gs²/k (where k is the Boltzmann constant) must be greater than 300 K.

The final parameter is the magnetic exchange coupling, J. As single molecule magnetism is a ground state phenomenon, for it to be observed at room temperature then the ground state must be exclusively occupied at this temperature. This means that the magnetic exchange must be very strong. This consideration also influences whether maximising D or S_gs is the more promising route to maximising the energy barrier. The only method for increasing S_gs further is to increase the number of paramagnetic centres interacting. A problem is that as S_gs increases the number of different spin states also increases, e.g. if S_gs = 12, then all other spin values from 11 to 0 are allowed for excited states. A very large spin implies very many states, and makes the condition that the spin ground state must be energetically isolated difficult to fulfil. This suggests that the more feasible target is a molecule with moderate to large spin but very large anisotropy of that spin, rather than a molecule with a massive ground state spin and weak anisotropy, i.e.S_gs = 8–10, D/k = −3 K may be more promising than S_gs > 20, D/k = −0.5 K. Inclusion of metal ions with very high anisotropy must become a primary consideration in the design of new SMMs.

More generally, the potential of the bottom-up approach to the nanoscale is immense. Exploiting this potential will require the qualities of a traditional synthetic chemist, i.e. an ability to design and test new procedures, and a capacity to develop results obtained by serendipity to maximise your good fortune. It is irrational to restrict ourselves to “rational synthesis” so early in this game. Excluding serendipity from the available tools is both impossible and undesirable. When asked what was the most important quality for a successful general, Napoleon replied, “Luck”. Chemists are perhaps no different.

Acknowledgements

The above account is in the main based on the PhD work of three talented scientists: Craig Grant, Euan Brechin and Alasdair Graham. Drs Greg Solan and Angela Dearden made the Fe₁₀ and Ni₂₄ cages respectively. Annela Seddon—an undergraduate in Edinburgh—realised that all the Ni and Co structures were related to trigonal prisms. Simon Parsons and Steve Harris performed the crystal structure determinations. I am also grateful to Andrew Parkin for help in preparing the figures. Cristiano Benelli and Roberta Sessoli (Florence) and Carley Paulsen and Wolfgang Wernsdorfer and Vincent Villar (Grenoble) performed the magnetic measurements. Yves Journaux and Joan Cano (Paris-Orsay) performed the Monte Carlo simulation of the susceptibility of the {Fe₁₀} cage. Funds came from the EPSRC(UK), The Leverhulme Trust and The European Union TMR network on “Molecules as Nanomagnets”, HPRN-CT-1999-00012.

References

1. M. Fujita, K. Umemoto, M. Yoshizawa, N. Fujita, T. Kusukawa and K. Biradha, Chem. Commun., 2001, 509–518.
2. (a) R. Sessoli, H.-L. Tsai, A. R. Schake, S. Wang, J. B. Vincent, K. Folting, D. Gatteschi, G. Christou and D. N. Hendrickson, J. Am. Chem. Soc., 1993, 115, 1804–1816; (b) R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–142.
3. (a) J. R. Friedman, M. P. Sarachik, J. Tejada and R. Ziolo, Phys. Rev. Lett., 1996, 76, 3830–3832; (b) L. Thomas, F. Lionti, R. Ballou, D. Gatteschi, R. Sessoli and B. Barbara, Nature, 1996, 383, 145–146.
4. S. Toyota, C. R. Woods, M. Benaglia, R. Haldimann, K. Wärnmark, K. Hardcastle and J. S. Siegel, Angew. Chem., Int. Ed., 2001, 40, 751–754.
5. (a) A. K. Powell, S. L. Heath, D. Gatteschi, L. Pardi, R. Sessoli, G. Spina, F. Del Giallo and F. Pieralli, J. Am. Chem. Soc., 1995, 117, 2491–2502; (b) J. C. Goodwin, R. Sessoli, D. Gatteschi, W. Wernsdorfer, A. K. Powell and S. L. Heath, J. Chem. Soc., Dalton Trans., 2000, 1835–1840.
6. A. K. Powell, M. Murugesu and C. E. Anson, personal communication.
7. M. Murrie, H. Stoeckli-Evans and H. U. Güdel, Angew. Chem., Int. Ed., 2001, 40, 1957–1960.
8. A. S. Batsanov, G. A. Timco, Yu. T. Struchkov, N. V. Gérbéléu and K. M. Indrichan, Koord. Khim., 1991, 17, 662–669.
9. I. M. Atkinson, C. Benelli, M. Murrie, S. Parsons and R. E. P. Winpenny, Chem. Commun., 1999, 285–286.
10. F. E. Mabbs, E. J. L. McInnes, M. Murrie, S. Parsons, G. M. Smith, C. C. Wilson and R. E. P. Winpenny, Chem. Commun., 1999, 643–644.
11. S. Parsons, A. A. Smith and R. E. P. Winpenny, Chem. Commun., 2000, 579–580.
12. R. A. Coxall, S. G. Harris, D. K. Henderson, S. Parsons, P. A. Tasker and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 2000, 2349–2356.
13. A. Bencini, C. Benelli, A. Caneschi, R. L. Carlin, A. Dei and D. Gatteschi, J. Am. Chem. Soc., 1985, 107, 8128–8136.
14. R. E. P. Winpenny, Chem. Soc. Rev., 1998, 27, 447–452 and references therein..
15. A. J. Blake, C. M. Grant, C. I. Gregory, S. Parsons, J. M. Rawson, D. Reed and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 1995, 163–175.
16. W. Clegg, C. D. Garner and M. H. Al-Samman, Inorg. Chem., 1983, 22, 1534–1538.
17. A. J. Blake, C. M. Grant, S. Parsons, J. M. Rawson and R. E. P. Winpenny, J. Chem. Soc., Chem. Commun., 1994, 2363–2364.
18. E. K. Brechin, PhD thesis, The University of Edinburgh, 1996.
19. A. J. Blake, E. K. Brechin, A. Codron, R. O. Gould, C. M. Grant, S. Parsons, J. M. Rawson and R. E. P. Winpenny, J. Chem. Soc., Chem. Commun., 1995, 1983–1985.
20. C. Benelli, E. K. Brechin, S. J. Coles, A. Graham, S. G. Harris, S. Meier, A. Parkin, S. Parsons, A. M. Seddon and R. E. P. Winpenny, Chem. Eur. J., 2000, 6, 883–896.
21. E. K. Brechin, A. Graham, A. Parkin, S. Parsons, A. M. Seddon and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 2000, 3242–3252.
22. E. K. Brechin, S. G. Harris, A. Harrison, S. Parsons, A. G. Whittaker and R. E. P. Winpenny, Chem. Commun., 1997, 653–654.
23. G. Kamieniarz, R. Matysiak, A. C. D'Auria, F. Esposito and C. Benelli, Acta Phys. Pol. A, 2000, 98, 721–727.
24. C. Cadiou, C. M. Grant, C. Paulsen, V. Villar and R. E. P. Winpenny, Chem. Commun., 2001, 2666.
25. C. Benelli, S. Parsons, G. A. Solan and R. E. P. Winpenny, Angew. Chem., Int. Ed. Engl., 1996, 35, 1825–1828.
26. C. Benelli, J. Cano, Y. Journaux, R. Sessoli, G. A. Solan and R. E. P. Winpenny, Inorg. Chem., 2001, 40, 188–189.
27. E. K. Brechin, S. G. Harris, S. Parsons and R. E. P. Winpenny, J. Chem. Soc., Dalton Trans., 1997, 3403–3404.
28. A. Graham, PhD thesis, The University of Edinburgh, 2001.
29. A. Graham, S. Meier, S. Parsons and R. E. P. Winpenny, Chem. Commun., 2000, 811–812.
30. E. K. Brechin, R. O. Gould, S. G. Harris, S. Parsons and R. E. P. Winpenny, J. Am. Chem. Soc., 1996, 118, 11293–11294.
31. R. C. Squire, S. M. J. Aubin, K. Folting, W. E. Streib, D. N. Hendrickson and G. Christou, Angew. Chem., Int. Ed. Engl., 1995, 34, 887–889.
32. A. L. Dearden, S. Parsons and R. E. P. Winpenny, Angew. Chem., Int. Ed., 2001, 40, 151–154.
33. B. J. Holliday and C. A. Mirkin, Angew. Chem., Int. Ed., 2001, 40, 2022–2043.

---