⁹⁹Ru Mössbauer effect study of ruthenium nitrosyls

Abstract

The ⁹⁹Ru Mössbauer effect has been measured in a series of ruthenium nitrosyls at 4.2 K. The isomer shifts (IS ≈ −0.20 mm s⁻¹) for most of the compounds are nearly equal and consistent with a +2 charge for ruthenium. However, the IS for K₂[Ru(NO)Cl₅], which is still Ru(II), is much more negative (IS = −0.43 mm s⁻¹). This implies that the ligand field strength is much stronger in this compound than the other compounds. Two of the compounds are broadened single lines or have small quadrupole interactions, but the compounds [Ru(NO)Cl(py)₄](PF₆)₂, [Ru(NO)Br(py)₄](PF₆)₂ and [Ru(NO)(NH₃)₅]Cl₃ each display two distinct lines (ΔE_Q ≈ 0.40 mm s⁻¹), which shows the non-symmetric Ru environment in these compounds.

---

Introduction

Complexes of ruthenium(II) bearing nitrosyl groups (RuNO compounds) have long been known. Early studies on these compounds were driven by the synthetic accessibility of a large number of complexes of this type.¹ More recently, RuNO compounds have been investigated as possible sources of NO for medical applications² and as a possible information storage medium.³ The latter use stems from the formation of a metastable state (MS1) for many of these compounds upon irradiation with blue light. MS1 has been shown to be a linkage isomer formed by flipping the NO from the normal, N-bound state to a Ru–ON binding mode.⁴ In some cases the linkage isomer is stable at temperatures well above 250 K before reverting to the ground state.⁵ In some complexes, another metastable state (MS2) is observed at lower temperatures and has been shown to contain a side bound NO ligand.⁴

Although the Mössbauer effect was first observed for ruthenium-99 in 1963,⁶ Ru-99 Mössbauer spectroscopy is a relatively unexplored technique for characterizing and studying molecular complexes of ruthenium.⁷ Recently, a number of solid state structures, including high T_c superconductors, have been studied with this technique.⁸ One disadvantage of the technique for studying molecular complexes is the requirement of at least 100 mg cm⁻² of ruthenium to be present in the sample. This often necessitates the synthesis of several grams of a ruthenium complex. This is largely due to the low recoil free fraction of these compounds, which implies low Debye temperatures relative to metals.

In our ongoing search for RuNO compounds with a thermally stable MS1, we embarked on a ⁹⁹Ru Mössbauer study of several of the compounds to determine if any correlation exists between the Mössbauer isomer shift (IS) and the transition temperature (T_d) for the decay of MS1. The results of our studies are presented below.

Results and discussion

The compounds (1–5) chosen for study are shown in Scheme 1. Each is a diamagnetic, octahedrally coordinated Ru(II) complex with an approximate four-fold symmetry axis. The compounds each display a strong ν(N=O) IR stretching frequency near 1900 cm⁻¹, characteristic of linear coordination for the NO ligand. This geometry has also been supported by X-ray crystallographic work in several cases.^5a,b,9 Represented within the complexes are four different trans ligands (NH₃, Cl, OH, Br) and four different equatorial ligands (NH₃, Cl, NO₂, py).

Scheme 1

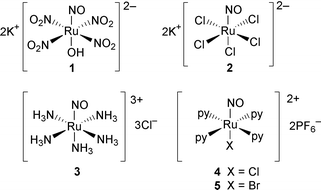
The 4.2 K Mössbauer spectrum for K₂[Ru(NO)(NO₂)₄(OH)] (1) consists of a sharp, single line (Fig. 1). It qualitatively represents the largest recoil free fraction. The data were fitted with a single Lorentzian line with a full width at half maximum (FWHM) of 0.23(0.01) mm s⁻¹ and an IS of −0.22(0.01) mm s⁻¹. This is an exceptionally narrow experimental linewidth, though it is still larger than the natural linewidth (0.15 mm s⁻¹). This is in part due to the γ-ray source, which produces somewhat broadened lines due to the hexagonal structure of ruthenium.

Fig. 1 The ⁹⁹Ru Mössbauer spectrum of compound 1 at 4.2 K.

⁹⁹Ru spectra often show two resonance lines due to quadrupole splitting (ΔE_Q) of the I = 3/2⁺ first excited state. With this in mind, the data for compound 1 were also fitted to two Lorentzians to determine the upper limit of this splitting for this compound. A quadrupole splitting of no larger than 0.07 mm s⁻¹ could be fit to the data while still maintaining an experimentally reasonable linewidth (FWHM > 0.20 mm s⁻¹).

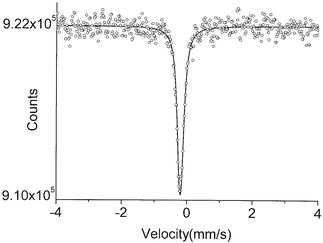
The data for K₂[Ru(NO)Cl₅] (2) appeared to display a small quadrupole splitting. Two Lorentzians (FWHM = 0.20(0.03) mm s⁻¹) of approximately equal intensity fit well to the data, giving an IS value of −0.43 mm s⁻¹ and a ΔE_Q of 0.11(0.03) mm s⁻¹ (Fig. 2). These values compare favorably with those of a previous study in which the very similar complex Rb₂[Ru(Cl)₅NO] was analyzed.¹⁰ In that study, an IS value of −0.37(0.03) mm s⁻¹ was reported. These same authors reported a broadened line (FWHM of 0.50 mm s⁻¹), which allowed them to calculate a quadrupole splitting of 0.24(0.13) mm s⁻¹. Another report places the quadrupole splitting value for this complex at 0.18 mm s⁻¹.^7c Our data seem to discount such a large splitting for this compound. It is possible that some of the discrepancy is due to lattice effects, but a more likely explanation lies in the nature of our γ-ray source, which can consistently produce lines with an FWHM ∼0.20 mm s⁻¹.

Fig. 2 The ⁹⁹Ru Mössbauer spectrum of compound 2 at 4.2 K.

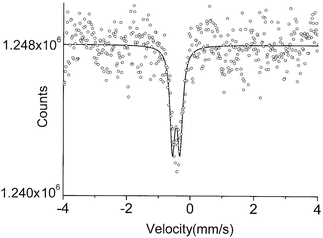
The spectrum of [Ru(NO)(NH₃)₅]Cl₃ (3) consists of two lines, FWHM = 0.25(0.01) mm s⁻¹, of unequal intensity and an IS of −0.20(0.03) mm s⁻¹ (Fig. 3). The split lines of spacing 0.41(0.03) mm s⁻¹ probably represent an EQ split spectrum, as previously noted by Greatrex et al.¹⁰ The previously reported values for this complex were IS = −0.20(0.03) mm s⁻¹ and FWHM = 0.79 mm s⁻¹. The observed broadening allowed these investigators to calculate a quadrupole splitting of 0.36(0.03) mm s⁻¹, a value in close agreement with that in this report. Earlier investigators reported a value of IS of −0.19 mm s⁻¹ and a ΔE_Q of 0.39(0.01) mm s⁻¹ for this same complex.^7c

Fig. 3 The ⁹⁹Ru Mössbauer spectrum of compound 3 at 4.2 K.

The [Ru(NO)Cl(py)₄](PF₆)₂ (4) and [Ru(NO)Br(py)₄](PF₆)₂ (5) spectra shown in Fig. 4 each show two lines of nearly equal intensity, FWHM = 0.22(0.01) mm s⁻¹, and the same IS or center shift of −0.20 mm s⁻¹. The split lines can either represent an electric quadrupole splitting (EQ) of 0.37(0.03) mm s⁻¹ or two inequivalent Ru sites within the materials. The former is a more likely explanation because of the molecular nature of the compounds. We view it as unlikely that two otherwise identical molecules occupying different sites within the crystal structure would have such markedly different IS values.

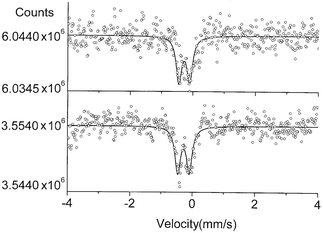Fig. 4 The ⁹⁹Ru Mössbauer spectra of compound 4 (top) and 5 (lower) at 4.2 K.

The results, along with the IR data, and decay temperatures for MS1 (T_d) are summarized in Table 1. The IS values are similar to those found in other RuNO complexes and are consistent with a +2 oxidation state for Ru. In a series of RuNO complexes, the IS was found to increase with ligand field strength.¹⁰ In this regard, the important considerations are the σ-donor and π-acceptor characteristics of the ligands. Both of these bonding interactions tend to increase the s-electron density at the Ru nucleus. Back-donation to the π* orbitals of the NO⁺ ligand is very strong and is expected to dominate the ligand field.¹¹ However, this contribution to the total ligand field is approximately the same for each of the complexes studied as can be seen by the relatively small variations in ν(NO). Thus the small variations seen in the IS values are a result of the contribution to the ligand field from the remaining ligands. No correlation exists between the IS and the decay temperatures for the MS1 states of these compounds.

Table 1 Isomer shift, quadrupole splitting, IR and decay temperature data for compounds 1–5

Compound	IS/mm s^−1	ΔEQ 3/2/mm s^−1	ν(NO)/cm^−1	T d (MS1)/°C
1	−0.22	<0.07(0.03)	1886	208
2	−0.43	0.11(0.03)	1902	216
3	−0.20	0.41(0.03)	1927, 1911	260
4	−0.20	0.37(0.03)	1911	256
5	−0.20	0.37(0.03)	1902	231

---

The ΔE_Q values show that the electronic environments around the Ru ion in the complexes are asymmetrical and produce an electric field gradient (efg) across the Ru nucleus coinciding with the four-fold symmetry axis. The efg results both from valence electrons and lattice effects, although it is probably reasonable to neglect the latter and focus on the distribution of electrons in the five 4d-orbitals of the metal atom.¹⁰ Assuming a positive sign for the efg for all of the compounds, larger values of ΔE_Q correspond to less electron density in the orbitals oriented towards the axial ligands (d_z², d_xz, and d_yz) relative to those oriented in the xy plane (d_{x² − y²} and d_xy). This suggests that the Ru–NO bonding interactions (σ and π) should weaken with increasing values of ΔE_Q. This suggestion is supported by the trend towards higher values of ν(NO) with increased quadrupole splitting. Previous studies have noted a general correlation between ν(NO) and the decay temperatures for the MS1 states.⁵ Inspection of the data shows a possible correlation between the quadrupole splitting and the decay temperature as well. In general, the larger the quadrupole splitting, the higher the decay temperature.

The relative magnitudes of the quadrupole splitting in this series of compounds can be explained using Bancroft's partial quadrupole splitting (PQS) treatment developed for ⁵⁷Fe complexes.¹² In this approach, the PQS values for each ligand are combined according to the geometry of the complex. For compounds of general formula trans-FeA₄B(NO), the quadrupole splitting can be calculated as 2PQSB + 2PQSNO − 4PQSA. For compounds of formula FeA₅(NO), the splitting becomes 2[PQSNO − PQSA]. Because the bonding in Ru(II) complexes is expected to be similar to that in the analogous low-spin Fe(II) complexes, the PQS values and corresponding quadrupole splitting in Ru(II) complexes should be nearly proportional to those in Fe(II) complexes. Using this approach, the quadrupole splittings have been calculated for the analogous Fe complexes (1′–5′) and are shown in Table 2.

Table 2 Calculated quadrupole splittings for the Fe complexes (1′–5′)

Compound	1′	2′	3′	4′	5′
a Calculated using the formulas provided in the text with the following PQS values in mm s^−1 (values from references 12 and 13): NO^+ (+0.02), NO2^− (−0.41), Cl^− (−0.30), Br^− (−0.28), NH3 (−0.52), and py (−0.48). b Value calculated using a PQS value for OH^− = −0.73 mm s^−1. See text.
ΔEQ 3/2/mm s^−1^a	+0.21^b	+0.64	+1.08	+1.40	+1.44

---

The method approximately reproduces the trend for ΔE_Q in the RuNO complexes. Unfortunately, due to the lack of discreet low-spin Fe(II)–OH complexes in the literature, a PQS value cannot be directly assigned for the OH⁻ ligand. We have therefore used our data to make an estimate of its value. Using 0.07 mm s⁻¹ for the quadrupole splitting in 1 and 3.0 for the ratio ΔE_Q(⁵⁷Fe)/ΔE_Q(⁹⁹Ru),¹⁴ a PQS value of −0.73 mm s⁻¹ can be calculated for the OH⁻ ligand. This value is reasonable, as PQS values for ligands with no π-accepting tendencies get progressively more negative as σ-donor ability increases. Thus PQS(OH⁻) should be more negative than PQS(NH₃) and PQS(H₂O), which are −0.52 mm s⁻¹ and −0.44 mm s⁻¹ respectively. The PQS value for H⁻, a powerful σ-donor, is −1.04 mm s⁻¹. A similar treatment of the ⁹⁹Ru Mössbauer data for the complex [Ru(NH₃)₄(NO)(OH)]Cl₂ (IS = −0.16 mm s⁻¹, ΔE_Q = 0.25 mm s⁻¹) returns a PQS value of −0.69 mm s⁻¹. As has been previously noted, it is possible since these are all charged species that a significant lattice effect resulting from nearby ions could contribute to the electric field gradient, resulting in substantial deviations from the expected values.

Experimental

The compounds were obtained as follows. Compound 1 was synthesized from RuCl₃ as described in the literature.¹⁵ Compound 2 was a commercial sample obtained from Aldrich. Compound 3 was synthesized by the action of NO gas on an aqueous solution of [Ru(NH₃)₆]Cl₃.¹⁶ Compounds 4 and 5 were synthesized in four steps by the published method¹⁷ starting from Ru(DMSO)₄Cl₂.¹⁸

The Mössbauer experiments were performed in a transmission geometry using a ⁹⁹Rh(Ru) source prepared by irradiating a mixed target of ¹⁰⁰Ru and ¹⁰¹Ru using 30 MeV protons in a cyclotron.¹⁹ The decay of ⁹⁹Rh produces the 3/2 Mössbauer state (lifetime = 20 ns) which emits a 90 keV gamma ray in the transition to the 5/2 ground state. Both the source and absorber were maintained in the cryostat at 4.2 K by helium exchange gas. In previous work with ruthenium samples, ruthenium masses from 57 mg cm⁻² to 290 mg cm⁻² produced a range of FWHM linewidths from 0.18 to 0.23 mm s⁻¹.⁸ The variation in linewidth with absorber thickness for ⁹⁹Ru is much lower than that of ⁵⁷Fe due to the differences in maximum resonant cross section and the recoil free fraction.²⁰ Absorber samples with the amount of Ru in parentheses are: K₂[Ru(NO)(NO₂)₄(OH)] (1, 240 mg cm⁻²), K₂[Ru(NO)Cl₅] (2, 160 mg cm⁻²), [Ru(NO)(NH₃)₅]Cl₃ (3, 76 mg cm⁻²), [Ru(NO)Cl(py)₄)](PF₆)₂ (4, 145 mg cm⁻²), and [Ru(NO)Br(py)₄](PF₆)₂ (5, 135 mg cm⁻²). The sample size of complexes 4 and 5 was limited by the size of the absorber holder. In the other samples, the absorber amounts were limited by the amount of material produced or purchased.

The samples were placed in aluminium containers and placed below the source inside the cryostat. The 3 mm thick NaI detector was placed below the Mylar windows outside the cryostat to detect the Mössbauer effect gamma ray. The calibration for the experiments was determined by the inner four lines of the ⁵⁷Co(Rh) versus iron foil measurement. The zero velocity channel was determined by a ⁹⁹Rh(Ru) versus ruthenium powder experiment.

Acknowledgements

The authors are very grateful to Professor Philip Coppens (University at Buffalo) for his constructive comments as well as helpful discussions. M. J. DeMarco is grateful to the American Chemical Society (PRF No. 34777-SF00) for financial support for this project.

References

1. E. A. Seddon and K. R. Seddon, The Chemistry of Ruthenium, Elsevier Science Publishing, Amsterdam, 1984, ch. 14 and references therein.
2. D. R. Lang, J. A. Davis, L. G. F. Lopes, A. A. Ferro, L. C. G. Vasconcellos, D. W. Franco, E. Tfouni, A. Wieraszko and M. J. Clarke, Inorg. Chem., 2000, 39, 2294–2300.
3. M. Imlau, T. Woike, R. Scheider and R. A. Rupp, Phys. Rev. Lett., 1999, 82, 2860–2863.
4. (a) M. D. Carducci, M. R. Pressprich and P. Coppens, J. Am. Chem. Soc., 1997, 119, 2669–2678; (b) P. Coppens, D. Fomitchev, M. D. Carducci and K. Culp, J. Chem. Soc., Dalton Trans., 1998, 865–872.
5. (a) C. Kim, I. Novozhilova, M. S. Goodman, K. A. Bagley and P. Coppens, Inorg. Chem., 2000, 39, 5791–5795; (b) D. V. Fomitchev, I. Novozhilova and P. Coppens, Tetrahedron, 2000, 56, 6813–6820; (c) Y. Morioka, A. Ishikawa, H. Tomizawa and E.-I. Miki, J. Chem. Soc., Dalton Trans., 2000, 781–786.
6. O. C. Kistner, S. Monaro and R. Segnan, Phys. Lett., 1963, 5, 299.
7. For some early examples see: (a) D. C. Foyt, T. H. Siddall III, C. J. Alexander and M. L. Good, Inorg. Chem., 1974, 13, 1793–1796; (b) G. Kaindl, W. Potzel, F. Wagner, U. Zahn and R. L. Mössbauer, Z. Phys., 1969, 226, 103–115; (c) W. Potzel, F. Wagner, U. Zahn, R. L. Mössbauer and J. Danon, Z. Phys., 1970, 240, 306–313; (d) C. A. Clausen III, R. A. Prados and M. L. Good, J. Am. Chem. Soc., 1970, 92, 7483–7485.
8. (a) M. J. DeMarco, H. Blackstead, J. D. Dow, M. K. Wu, D. Y. Chen, F. Z. Chien, M. Haka, S. Toorongian and J. Fridmann, Phys. Rev. B, 2000, 62, 14301–14303; (b) M. J. DeMarco, G. Cao, J. E. Crow, S. Toorongian, M. Haka and J. Fridmann, Phys. Rev. B, 2000, 62, 14297–14300.
9. (a) J. T. Veal and D. J. Hodgson, Acta Crystallogr., Sect. B., 1972, 28, 3525; (b) S. H. Simonson and M. H. Mueller, J. Inorg. Nucl. Chem., 1965, 27, 309–320.
10. R. Greatrex, N. N. Greenwood and P. J. Kaspi, Chem. Soc. A, 1971, 1873–1877.
11. P. T. Manoharan and H. B. Gray, Inorg. Chem., 1966, 5, 823–839.
12. (a) G. M. Bancroft, Coord. Chem. Rev., 1973, 11, 247–262; (b) G. M. Bancroft, Mössbauer Spectroscopy—An Introduction for Inorganic Chemists and Geochemists, McGraw-Hill, London, 1973.
13. A. Y. Nazarenko, E. V. Polshin and Y. Z. Voloshin, Mendeleev Commun., 1993, 45–47.
14. G. M. Bancroft, K. D. Butler and E. T. Libbey, J. Chem. Soc., Dalton Trans., 1972, 2643–2646.
15. J. M. Fletcher, I. L. Jenkins, F. M. Lever, F. S. Martin, A. R. Powell and R. Todd, J. Inorg. Nucl. Chem., 1955, 1, 378–401.
16. J. N. Armor, H. A. Scheidegger and H. Taube, J. Am. Chem. Soc., 1968, 90, 5928–5929.
17. B. J. Coe, T. J. Meyer and P. S. White, Inorg. Chem., 1995, 34, 593–602.
18. I. P. Evans, A. Spencer and G. Wilkinson, J. Chem. Soc., Dalton Trans., 1973, 204–209.
19. M. J. DeMarco, D. Graf, J. Rijssenbeek, R. J. Cava, D. Z. Wang, Y. Tu, Z. F. Ren, J. H. Wang, M. Haka, S. Toorongian, M. J. Leone and M. J. Naughton, Phys. Rev. B, 1999, 60, 7570–7574.
20. For maximum resonant cross section and the recoil free fraction, the values for ⁵⁷Fe are larger than for ⁹⁹Ru. The factors are multiplicative and together their effect on the FWHM linewidth is on the order of one hundred. P. Gutlich, R. Link and A. Trautein, Mössbauer Spectroscopy and Transition Metal Chemistry, Springer-Verlag, Berlin, 1978, pp. 36–39.

---