How hydrogen bonding affects ligand binding and fluxionality in transition metal complexes: a DFT study on interligand hydrogen bonds involving HF and H2O
Eric Clot*a, Odile Eisensteina and Robert H. Crabtreeb
aLSDSMS (UMR 5636), Case Courrier 14, Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersité de Montpellier 2, 34095, Montpellier cedex 5, France. E-mail: clot@lsd.univ-montp2.fr
ersité de Montpellier 2, 34095, Montpellier cedex 5, France. E-mail: clot@lsd.univ-montp2.fr
bDepartment of Chemistry, Yale Uni![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ersity, New Ha
ersity, New Ha![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) en, CT 06520-8107, USA. E-mail: robert.crabtree@yale.edu
en, CT 06520-8107, USA. E-mail: robert.crabtree@yale.edu
First published on 1st December 2000
Abstract
DFT calculations (B3PW91) predicted structures for hydrogen-bonded complexes of type Ir(H)(L)(bq–G)(PH3)2q+ (bq–H = benzo[h]quinoline-10-yl, L = empty site, FH or OH2; G = H or NH2, q = 1; L = F−, G = NH2, q = 0), which are either too unstable for X-ray crystallography study, or for which the crystal structure does not allow H atom positions reliably to be located. The work shows how the two-point binding site provided by the bq–NH2 complex is ideal for HF but not for H2O binding, thus stabilizing the former to the extent that it can be observed by NMR at low temperature. Fluxionality in the aqua complex is fully interpreted by location of the appropriate TS. One such TS is strongly stabilized by hydrogen bonding leading to rapid exchange of NH2 positions even at −80 °C. An improved ligand is suggested for stabilizing an HF complex.
Introduction
Interaction energies in chemistry go from the weak van der Waals bond (100 cm−1 for D0 in Ar·H2O)1 to the strong covalent bond (150 kcal mol−1 for C–F bond in C6F6).2 The directionality and intermediate interaction energy of the hydrogen bond allow creation of specific interactions in crystal engineering and supramolecular architecture;3–5 theoretical studies on weak hydrogen bonds have been reviewed recently.6Multifunctional ligands with reactive groups not involved in metal–ligand binding are of particular interest when they contain lone pairs unable to bind directly to the metal, but able to hydrogen bond to an adjacent ligand.7,8 If properly placed, these groups could have effects similar to those of hydrogen-bonding residues in the active site cavity of metalloenzymes which are believed to contribute to the acceleration of enzyme reactions by transition-state stabilization.9
A simple example is shown as 1 below, where G can be either H (denoted 1H) or a pendant amino group NH2 (denoted 1N) capable of hydrogen bonding to an incoming ligand L′ bearing acidic protons (HF, H2O, for example). In prior work we have shown how water binds to 1H to yield the aqua complex Ir(H)(H2O)(bq–H)(PPh3)2+2H (bq–H = benzo[h]quinolin-10-yl) that can reversibly bind H2 with loss of H2O.10,11
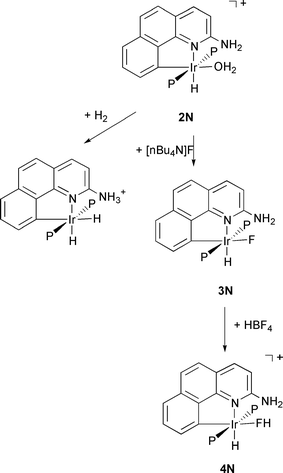
In the case of G = NH2, the aqua complex Ir(H)(H2O)(bq–NH2)(PPh3)2+2N reacts with H2 to give reversible heterolytic cleavage of H2 not seen for 2H (Scheme 1).12 Moreover, the complex 2N reacts rapidly with [nBu4N]F to give the fluoride complex 3N (Scheme 1).13,14
 | ||
| Scheme 1 | ||
Ligand substitution in metal fluoro complexes is subject to acid catalysis and the intermediacy of transient HF complexes was proposed15 but experimental support was never obtained in prior studies. Fully characterized halogenocarbon complexes of type LnM–X–R (X = halide, R = alkyl or aryl) have been known for some time,16 but the corresponding hydrogen halide complexes (R = H, X = F) have only been reported very recently.13,14,17 Two bifluoride complexes, Mo(PMe3)4(H)2(F)(FHF)18 and trans-Ru(dmpe)2(H)(FHF),19 have also been characterized very recently by X-ray crystallography. In both cases the bifluoride ligand is η1- bonded to the metal with an M–F···F angle of 134 and 130°, respectively.20 The hydrogen-bond within the coordinate bifluoride is asymmetric and less strong than in free FHF−.
The
HF complex 4N is obtained by protonation of 3N
(HBF4·Et2O) and has so far only been detected spectroscopically
and at low temperature (Scheme 1). The critical observation
was the finding of a JHF
value of 440 Hz, characteristic
of hydrogen bonded HF. The pendant group NH2 is believed
to interact with the HF ligand through hydrogen bonding
to give overall two point binding ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ia an Ir–F coordinate
bond and an N···HF hydrogen bond. With the stabilization of
an HF complex, we now have experimental support for the presence of such intermediates in acid catalysed substitution and
also a new ligand type.
ia an Ir–F coordinate
bond and an N···HF hydrogen bond. With the stabilization of
an HF complex, we now have experimental support for the presence of such intermediates in acid catalysed substitution and
also a new ligand type.
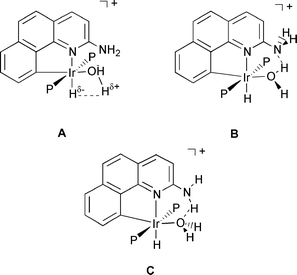
Since the HF complex decomposes with loss of HF above −30 °C, no crystal structure is available and so the metric parameters of this new ligand type were still unknown. Efforts to make stabler derivatives having failed, we turn here to DFT (B3PW91) studies to predict the static structure expected for the new ligand. Being difficult to locate with X-ray diffraction the presence of H is often inferred from IR and NMR spectroscopic observations. Theory is one of the most powerful tools available to characterize the geometry of hydrogen bonded species and an accurate determination of the hydrogen atom positions is provided by DFT calculations.21 The aqua complex 2N provides a stringent test of the DFT methodology with three types of hydrogen bonding situations in competition (Scheme 2).
 | ||
| Scheme 2 | ||
The aim of this paper is thus to explore computationally the structure and reactivity of the complexes between 1 and ligands like H2O, F− or HF. Emphasis will be put on the role of G and thus on how hydrogen bonding helps in stabilizing particular geometries and in determining reactivity. One of our goals is to use DFT calculations to analyse the trends in binding energies between the metal fragment 1 and ligands like H2O or HF as a function of pendant group G.
Computational details
All calculations have been performed within the framework of Density Functional Theory (DFT) with the GAUSSIAN 98 set of programs.22 The B3 hybrid exchange potential of Becke23 was used in conjunction with the PW91 correlation potential of Perdew and Wang.24 The relativistic Effective Core Potential (RECP) of the Stuttgart group was used for Ir with the associated (8s7p5d)/[6s5p3d] basis set augmented with an f function (α = 1.0).25 The phosphorus atoms were also treated with Stuttgart's RECPs and the associated basis set,26 augmented by a d function (α = 0.387). A 6-31G(d,p) basis set was used for the hydride, the fluoride, both atoms (C and N) linked to Ir, and for the atoms of the G group (G = H or NH2). For the remaining atoms a 6-31G basis set was used.Geometry
optimizations without any symmetry constraints
were performed on model systems where the three conjugated
rings of the bq–G (G = H or NH2) ligand were explicitly considered.
The only difference between the experimental and the calculated
molecules lies in the use of PH3 to represent the phosphine
ligands. This turns out to be a reasonable simplification
since the electronic influence of PPh3 is rather well reproduced
by PH3 according to the respective Tolman electronic
factors (2069 cm−1 for PPh3![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. estimated 2081 cm−1 for PH3).27
We will therefore not introduce an additional labeling
scheme to distinguish between experimental and theoretical
systems. This study being mostly theoretical, we will explicitly
indicate when we refer to experimental results.
s. estimated 2081 cm−1 for PH3).27
We will therefore not introduce an additional labeling
scheme to distinguish between experimental and theoretical
systems. This study being mostly theoretical, we will explicitly
indicate when we refer to experimental results.
The nature of all located extrema was checked through analytical computations of the vibrational frequencies. The binding energy ΔbindXE(L′) of the ligand L′ in the complex 1X–L′ (X = H for G = H and X = N for G = NH2) is evaluated as in eqn. (1) where Eopt(Y) is the electronic energy of system Y in its optimized geometry (binding energies are thus defined to be positive). Note that no basis set superposition error (BSSE) correction has been introduced since we focus on trends only (role of G) and BSSE is known to be small for DFT calculations with a double zeta polarisation (DZP) quality basis set.28
 | (1) |
Results and discussion
G = H: Hydrogen bond?
The
optimized geometry for complex 2H is shown in Fig. 1
along with some geometrical parameters. The agreement with
the crystal structure is acceptable since the crystallographic
determination was of only moderate quality (R
= 8.5%). The best
agreement is obtained for Ir–C (2.018 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 1.99(2) Å), Ir–P (2.318
s. 1.99(2) Å), Ir–P (2.318
![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 2.336(7) and 2.319(7) Å), and the bite angle of the bq–H ligand
(80.2
s. 2.336(7) and 2.319(7) Å), and the bite angle of the bq–H ligand
(80.2 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 80.2(9)°). The Ir–N (2.189
s. 80.2(9)°). The Ir–N (2.189 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 2.10(2) Å) and Ir–O (2.319
s. 2.10(2) Å) and Ir–O (2.319
![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 2.26(2) Å) bonds are computed too long. The Ir–H bond distance
(1.593 Å) is typical of iridum (III) complexes.
s. 2.26(2) Å) bonds are computed too long. The Ir–H bond distance
(1.593 Å) is typical of iridum (III) complexes.
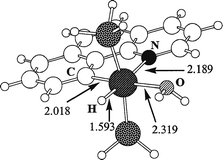 | ||
| Fig. 1 Optimized geometry for the aqua complex, 2H, with G = H. Bond distances are in Å. | ||
The calculated binding energy ΔbindHE(H2O) of the H2O ligand is 23.2 kcal mol−1. This value is rather high for an aqua complex especially with a long Ir–O bond distance (2.319 Å). This finding is in agreement with the experimental observation of tenacious binding of the aqua ligand in 2H. Even if the reagents and solvents used are dried, the aqua complex still tends to be formed from adventitious water.11
One factor that leads to the special stability of the aqua complex can be seen from the geometry of 2H (Fig. 1) where one O–H bond is aligned with the Ir–H bond (H–Ir–O–H dihedral angle: 4°). This “cis interaction” (A in Scheme 2) between polarized Mδ+ − Hδ− and Oδ− − Hδ+ bonds resembles that described by Milstein et al. for cis-[Ir(H)(OH)(PMe3)4][PF6],31 where the neutron diffraction structure32 shows a short O–H···H–Ir distance of 2.40(1) Å and a small Ir–O–H angle of 104.4(7)°. This orientation, reproduced by DFT calculations,33 was explained by a dipole–dipole interaction.34
Although
there is certainly no covalent bond between the
basic hydride and the acidic proton on H2O in complex 2H
(H···H 2.642 Å), the interaction might have been viewed as a hydrogen
bond, but, this “hydrogen bond”, if any, is certainly very weak
both from experiment (the two Hs on H2O are equivalent
by NMR even at low temperature) and from theory (the two
O–H bond distances are the same: 0.966 Å). Interestingly the
Ir–O–H angles are different. That for the O–H aligned with
Ir–H is significantly smaller (108.6 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 117.1°). The metal–hydride
bond might thus be considered as a source of weak attracting
interaction. This cis effect35 is sufficiently strong to induce
a preferential orientation for an H2
ligand in cis position with
respect to M–H: in a cis-M(H)(H2) unit, M, H and H2
are almost
always coplanar.21
s. 117.1°). The metal–hydride
bond might thus be considered as a source of weak attracting
interaction. This cis effect35 is sufficiently strong to induce
a preferential orientation for an H2
ligand in cis position with
respect to M–H: in a cis-M(H)(H2) unit, M, H and H2
are almost
always coplanar.21
![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ide infra).
ide infra).The
instability of the HF complex for G = H could then be attributed
to the absence of stabilizing interaction within the complex.
However, we showed for 2H that the Ir–H bond is a source
of stabilization (although weak) for the Xδ−
− Hδ+ bond. We therefore
looked for possible complexation of HF
to 1H and found the
ground state structure 4H (Fig. 2).
The essential feature
of the optimized structure 4H is the geometry of the HF ligand.
The Ir–F bond (2.416 Å) is
much longer than the usual
range and in particular much longer than in the bifluoride complexes (2.124(3) Å for Mo(PMe3)4(H)2(F)(FHF)18 and
2.284(5) Å for trans-Ru(dmpe)2(H)(FHF)19).36
The Ir–F–H angle
of 107.5° is smaller than the corresponding angle for Mo(PMe3)4(H)2(F)(FHF) (123.4°) indicating some attraction between
the basic hydride and the acidic proton. As expected for an attractive effect, the coordinated HF in 4H is slightly elongated
in comparison with free HF (0.930 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 0.922 Å).
s. 0.922 Å).
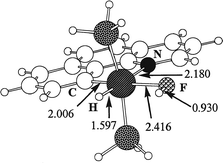 | ||
| Fig. 2 Optimized geometry for the hydrogen fluoride complex, 4H, with G = H. Bond distances are in Å. | ||
The binding energy ΔbindHE(HF) of 18.0 kcal mol−1 is rather high, a result that can not entirely be attributed to the cis effect. We have therefore tried to estimate the magnitude of the stabilizing cis attraction by Ir–H. Rotating the HF ligand by 180° around the Ir–F bond removes the cis interaction. A geometry, 4H-TS, was optimized as a transition state on the potential energy surface. The motion along the coordinate associated with the imaginary frequency corresponds to a departure of the HF ligand from the bq plane to yield back 4H. The geometry of the HF ligand in the TS confirms the absence of cis attraction (Ir–F 2.437, H–F 0.928 Å, and Ir–F–H 124.3°). The relative energy of +3.1 kcal mol−1 for 4H-TS with respect to 4H gives an estimate of the stabilizing energy associated with the cis effect which gives only a small contribution to the total binding energy (18.0 kcal mol−1).
The
coordination of HF being thermodynamically favored,
why have so few systems been characterized? In the particular
case of 4H a key point is that the binding energy of H2O is
stronger and the equilibrium (2) is shifted to the right. The
reaction energy of −5.2 kcal mol−1 is large enough for the thermal
population of 4H to be negligible (![[double less-than, compressed]](https://www.rsc.org/images/entities/char_2aa1.gif) 1%), and moreover free HF is very reactive toward glassware. The equilibrium
is then probably completely shifted to the right.
1%), and moreover free HF is very reactive toward glassware. The equilibrium
is then probably completely shifted to the right.
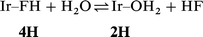 | (2) |
To isolate an HF complex it is necessary both to increase the binding energy and to protect the acidic proton from any adventitious base. The key is to design a system with a strong hydrogen-bonding capability. The basic group must not be too strong however, or the proton will transfer to the base and we will no longer have an HF complex.
G = NH2: Hydrogen bond!
The
optimized geometry for complex 3N (Fig. 3) is in very
good agreement with the crystal structure. The NH2 group is
almost planar and the nitrogen lone pair conjugates with the
bq rings as illustrated by the short C2–N2 bond (1.348 Å). The G
group and the vacant site in 1 define a “
binding cavity” where
two-point binding of L′ with Ir and G may occur.38 The NH2
hydrogens are labeled Hendo (toward the vacant site) and Hexo
(away from the vacant site). From the optimized structure
for 3N (Fig. 3) there is clearly an F···H–N hydrogen bond, in agreement
with the experimental results. The N–Hendo bond
is noticeably elongated compared to N–Hexo (1.051 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. 1.005
Å). The F···H distance of 1.560 Å is consistent with the observed J(F,H)
coupling constant of 52 Hz at 193 K. In the optimized structure
3N the two NH2 protons are inequivalent as observed
by NMR at low temperature.
s. 1.005
Å). The F···H distance of 1.560 Å is consistent with the observed J(F,H)
coupling constant of 52 Hz at 193 K. In the optimized structure
3N the two NH2 protons are inequivalent as observed
by NMR at low temperature.
 | ||
| Fig. 3 Optimized geometry for the fluoride complex, 3N, with G = NH2 and comparison with geometrical parameters for the corresponding experimental structure (PPh3).14 Bond distances are in Å and angles are in degrees. | ||
Having established the existence of an F···H–N hydrogen bond in complex 3N we now turn to the estimation of the strength of this bond. Experimentally, this is usually done by VT NMR experiments in which the two NH2 protons are different at low temperature but become equivalent at room temperature. The Gibbs energy of activation ΔG‡ for H exchange (12.4 kcal mol−1) gives an estimate of the strength of the hydrogen-bond after correction for the intrinsic rotation barrier around the C–N bond.8
This
correction procedure is easily carried out through calculations
by locating the appropriate transition states for
rotation around the C–N bond. Starting from 1N (vacant site trans
to C) the NH2 group can be rotated in two ways (Fig. 4). The structure 1N-TSendo, optimized as a transition state (i209 cm−1), contains a nitrogen lone pair pointing toward the vacant
site (endo position, Fig. 4). A second transition state 1N-TSexo
(i355.9 cm−1) has a nitrogen lone pair pointing away
from
the vacant site (exo position, Fig. 4). As expected, the interaction
between the nitrogen lone pair and the vacant site in 1N-TSendo favors this structure over the other one 1N-TSexo:
+4.3 ![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) s. +8.8 kcal mol−1. It is interesting that it costs only 4.3 kcal
mol−1 to reach a geometry (1N-TSendo) ideally suited for hydrogen
bonding interaction with an incoming ligand L′ (
s. +8.8 kcal mol−1. It is interesting that it costs only 4.3 kcal
mol−1 to reach a geometry (1N-TSendo) ideally suited for hydrogen
bonding interaction with an incoming ligand L′ (![[italic v]](https://www.rsc.org/images/entities/i_char_e0f5.gif) ide
infra).
ide
infra).
 | ||
| Fig. 4 Transition states for NH2 rotation in the complex with L = vacant site and G = NH2, 1N. See text for definition of endo and exo; energies in kcal mol−1. | ||
Two similar transition states for H exchange, 3N-TSendo (i489 cm−1) and 3N-TSexo (i501 cm−1), were located (Fig. 5). Owing to the lone pairs of the fluoride ligand, lone pair–lone pair repulsion may be present in the transition state. It is therefore not surprising to obtain an inversion of the TS order with 3N-TSendo lying at +29.9 kcal mol−1 above 3N and 3N-TSexo lying at +17.3 kcal mol−1. The latter is in fair agreement with ΔG‡ = 12.4 kcal mol−1 for H exchange at 193 K in 3N (VT NMR). If the calculated 3N-TSexo is stabilized by hydrogen bonds to CD2Cl2 solvent experiment and theory can be reconciled.
 | ||
| Fig. 5 Transition states for NH2 rotation in the complex with fluoride ligand and G = NH2, 3N. Details as in Fig. 4. | ||
The exchange mechanism for the two Hs of NH2 does not require a 360° rotation around the C–N bond. A 180° rotation through 3N-TSexo is sufficient to achieve exchange (Scheme 3). With equivalent phosphine ligands, configurations (a) and (b) are enantiomeric and thus equivalent in NMR studies in an achiral solvent.
 | ||
| Scheme 3 | ||
The difference in relative energy for 3N-TSendo and 3N-TSexo illustrates the concept of transition-state stabilization.9 The lower activation energy for 3N-TSexo arises from a conjunction of two factors: the absence of lone pair–lone pair repulsion and the presence of a hydrogen bonding interaction between F and both N–H bonds. From the relative energies of the four TS, the following semi-quantitative scheme can be derived: ΔErot + ΔElp,vs = 4.3; ΔErot = 8.8; ΔErot + ΔElp,lp + ΔEH-bond = 29.9; ΔErot + ΔEH-bond = 17.3. Here ΔErot is the intrinsic rotation barrier for NH2 , ΔElp,vs the stabilizing (negative) energy associated with lone pair–vacant site interaction in 1N-TSendo, ΔEH-bond the energy of the hydrogen bond in 3N lost in both TS (3N-TSendo and 3N-TSexo), and ΔElp,lp the lone pair–lone pair repulsion introduced in 3N-TSendo. The neglect of the weak hydrogen-bonding (2.292 Å) stabilizing term in 3N-TSexo leads to a slight overestimation of the lp–lp repulsion. We thus obtain the following values: ΔErot = 8.8, ΔElp,vs = −4.5, ΔElp,lp = 12.6 and ΔEH-bond = 8.5 kcal mol−1. The strength of the hydrogen bond in complex 3N can thus be estimated as 8.5 kcal mol−1 in agreement with estimated values in related systems.6,39
The existence of the HF complex being established, we turn to DFT calculations to predict its structure. The optimized geometry of the complex clearly exhibits a coordinated HF molecule interacting with the amino group (Fig. 6). The essential features are entirely consistent with those deduced from the spectral data but we can now also predict the key metric parameters. The H–F ligand lies in the “ binding cavity” with an F–H···N bond to G. The H–F distance of 1.042 Å is slightly longer than that of monomeric HF (0.922 Å),41 but much shorter than the F···Hendo–N distance (1.560 Å) in the neutral system 3N. The formation of an H–F bond has also resulted in a significant elongation of the Ir–F bond (from 2.123 Å in 3N to 2.262 Å in 4N). However the variation is much smaller for G = NH2 than for G = H where the Ir–F bond elongates from 2.072 Å for 3H to 2.416 Å for 4H as a result of a stronger HF bond (0.930 Å).
 | ||
| Fig. 6 Optimized geometry for the hydrogen fluoride complex, 4N, with G = NH2. Bond distances are in Å. | ||
The distance between N and the H of HF (1.43 Å) is considerably longer than in the two normal N–H covalent bonds (1.021 Å). This is entirely consistent with the description of 4N as an HF complex. The F···N distance of 2.470 Å is much shorter than the F···N distance found experimentally (X-ray) for the fluoride complex 3N (2.674 Å). The N–H–F angle of 175° is in excellent agreement with the linear arrangement usually preferred for hydrogen bonding given the constraints of the bonding site. The marked pyramidalization of N certainly increases the Lewis basicity of the lone pair involved in the hydrogen bond.
The calculated binding energy ΔbindNE(HF) of 28.2 kcal mol−1 in complex 4N is very much higher than for G = H (18.0 kcal mol−1) consistent with the presence of additional stabilization as a result of hydrogen bonding. We can qualitatively estimate the hydrogen bonding contribution. The intrinsic binding energy of HF to Ir is 15 kcal mol−1 as deduced from 4H-TS where the cis interaction with Ir–H is absent. The hydrogen bonding strength in 4N is best evaluated with 1N-TSendo as a reference (having a similar orientation of the NH2 group). The total binding energy is therefore 32.5 kcal mol−1 from which the intrinsic binding energy of HF needs to be subtracted. This yields a qualitative estimate of the hydrogen bond in 4N of 17.5 kcal mol−1. The value is doubled by comparison to 3N (8.5 kcal mol−1) in agreement with N being a better base than F and HF being a better acid than RNH2.
To elucidate the origin of such a stabilization we have carried out an Atoms in Molecules43 analysis (AIM) of the electron density for the two HF complexes 4H and 4N. The important result (Table 1) from this analysis is the existence of bond critical points for 4N for both F–H and H···N bonds. However the two bonds are not of the same type. The electron density ρb at the critical point is much higher for F–H (Table 1). The Laplacian of the density also shows that more electron density has accumulated in the vicinity of the critical point for F–H (more negative value). Finally, the electron energy density is clearly more negative for F–H than for N···H. This is a sign of increased covalent character of the bond.44 Therefore we can conclude that, in 4N, there is clearly a hydrogen bond as illustrated by the presence of two critical points. The hydrogen bond can best be described as F–H···N with a covalent bond between F and H and a donor/acceptor type of bond between H and N.
| 4H | 4N | |||||||
|---|---|---|---|---|---|---|---|---|
| Bond | ρb | ∇ρb2 | ε | Hb | ρb | ∇ρb2 | ε | Hb |
| Ir–H | 0.1549 | 0.0744 | 0.0590 | −0.0867 | 0.1607 | 0.0484 | 0.0613 | −0.0929 |
| Ir–F | 0.0355 | 0.1805 | 0.0316 | −0.00268 | 0.0541 | 0.267 | 0.240 | −0.0048 |
| F–H | 0.3574 | −2.730 | 0.0028 | −0.7660 | 0.2426 | −0.8965 | 0.0036 | −0.3344 |
| N···H | — | — | — | — | 0.1075 | −0.0107 | 0.0049 | −0.0618 |
Moreover, the AIM analysis for complex 4H does not show any critical point between the hydride and the acidic H of HF. The cis interaction is thus best described as a dipole–dipole interaction between polarized bonds. The presence of the amino group in 4N has completely reversed the geometrical preference by creating the F–H···N hydrogen bond. We have tried to optimize the complex Ir(H)(F)(bq–NH3+)(PH3) with an N–H···F hydrogen bond but the system always returned to 4N. This is consistent with N being a better hydrogen bond acceptor than F, and H–F being a better hydrogen bond donor than N–H. The case of L′ = H2O is somewhat analogous in this respect and also shows the dichotomy of hydrogen bond acceptor/hydrogen bond donor power, to a lesser extent however.
We now find the predicted ground state structure for complex 2N is best described as structure B (Scheme 2 and Fig. 7). The essential feature of the structure is the presence of an O–H···N hydrogen bond. Each O–H bond is different (O–Hendo 1.004 and O–Hexo 0.963 Å). The O–H–N angle of 159° is not optimal for efficient hydrogen bonding but is imposed by the steric constraints introduced by G = NH2. The Ir–O bond (2.246 Å) is typical for a water complex.11 Structure 2N (Fig. 7) does not strictly agree with the experimental results because the four protons of NH2 and H2O are all different. As the oxygen atom is pyramidal (Hendo–O–Hexo 110°) the seemingly equivalent protons for NH2 are in fact diastereotopic. We next searched for possible low energy pathways for proton exchange.
 | ||
| Fig. 7 Optimized geometry for the aqua complex, 2N, with G = NH2. Bond distances are in Å. | ||
The key point governing the dynamics of complex 2N is the maintenance of stabilizing interactions in the transition states. This is in fact the case for the transition state 2N-TSN that exchanges the Hs of NH2. The most striking difference between 2N and 2N-TSN is the planarity of the H2O ligand in the TS. The O–H bonds are still different (0.993 and 0.960 Å) showing some O–H···N hydrogen bonding is maintained in the transition state. As a consequence 2N-TSN is only 2.0 kcal mol−1 above 2N indicating very easy exchange.
The transition state coordinate (i416 cm−1) corresponds to the out of plane motion of Hexo. The easy exchange associated with 2N-TSN therefore keeps both protons on H2O different while making both Hs on NH2 equivalent. The very low activation energy of 2.0 kcal mol−1 is consistent with the experimental observation of only one NMR peak for NH2 even down to the lowest accessible temperature (−80 °C).
We could not locate a second transition state 2N-TSO with N–H···O rather than O–H···N hydrogen bonding. However, a geometry with the OH2 perpendicular to the bq plane and NH2 in the plane is only 7 kcal mol−1 above the ground state. So the barrier for H/H′ exchange in HOH′ must be about the same size. In conclusion the H/H′ exchange in the NH2 group is fast and one NMR peak is always seen but the H/H′ exchange in the H2O ligand is slow enough so that two peaks are seen at −80 °C. The exchange with free H2O makes a quantitative estimate of the H/H′ exchange barrier in the complex difficult to make but lineshape analysis shows it is close to 9 kcal mol−1.
 | (3) |
Thermodynamically, the HF complex is more stable than the H2O complex and is the favored species at low temperature (G = NH2). This is in full agreement with experiment where the HF complex is observed at low temperature and dissociates upon warming. The enhanced stability of the HF complex is thus caused by the N···H–F hydrogen bond.
The special topology of the binding cavity has two major consequences. The size is perfectly suited for HF hydrogen bonding (F–H–N angle of 175°), but less favorable for H2O (O–H–N angle of 159°). The thermodynamic preference for the HF complex is thus enhanced for G = NH2 both by making the HF complex more stable and making the H2O complex less stable.
By its design, the binding cavity protects the acidic proton from external reagent and enhances the kinetic stability of the complex. The key to isolating an HF complex would be to build a binding cavity with somewhat stronger hydrogen bonding capabilities that also sterically protects the HF molecule from any incoming reagent. One possibility is a binding cavity with a nitrogen lone pair pointing towards the binding site. A bq with a fused pyridine ring (see below) should be perfect in this respect. Preliminary studies of the HF complex of this system gave a binding energy of 35.2 kcal mol−1. Thus the hydrogen bond in this system is stronger than in 4N and experimental work at Yale is underway to synthesize and try to isolate and structurally characterize this HF complex.45
Conclusion
In this paper we predict the structure of a new type of complex that has proved too unstable for X-ray crystallography study and suggest a ligand system that might better stabilize it for future isolation. We have also shown by DFT calculations how hydrogen bonding can be a very powerful and sensitive tool to tune structure and reactivity in organometallic chemistry. With appropriate ligand design, it becomes possible to stabilize unusual species like HF selectively while not stabilizing the corresponding aqua complex even though it has the same structure. We find hydrogen bonding facilitates several dynamic processes. Calculations have shown how strong hydrogen bonding in one TS allows fast exchange of NH2.Acknowledgements
This work was supported by the U.S. NSF, the Université de Montpellier and the CNRS. E. C. would like to thank the RSC for a generous travel grant. R.H.C. thanks the University of Montpellier for a visiting professorship. We are grateful to Dong-Heon Lee for checking the NMR spectroscopic properties of the aqua complex 2N.References and notes
- R. C. Cohen and R. J. Saykally, J. Chem. Phys., 1993, 98, 6007 CrossRef CAS.
- B. E. Smart, Mol. Struct. Energy, 1986, 3, 141 Search PubMed.
- D. Braga, F. Grepioni and G. R. Desiraju, Chem. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1998, 98, 1375 Search PubMed.
., 1998, 98, 1375 Search PubMed. - D. Braga, F. Grepioni and G. R. Desiraju, J. Organomet. Chem., 1997, 548, 33 CrossRef CAS.
- L. Brammer, D. Zhao, F. T. Ladipo and J. Braddockwilking, Acta Crystallogr., Sect. B: Struct. Sci., 1995, 51, 632 CrossRef.
- M. J. Calhorda, Chem. Commun., 2000, 801 RSC.
- E. Peris, J. C. Lee, Jr and R. H. Crabtree, J. Chem. Soc., Chem. Commun., 1994, 2573 RSC.
- E. Peris, J. C. Lee, Jr., J. R. Rambo, O. Eisenstein and R. H. Crabtree, J. Am. Chem. Soc., 1995, 117, 3485 CrossRef CAS.
- C. Walsh, Enzymatic Reaction Mechanisms, Freeman, San Francisco, 1979. Search PubMed.
- R. H. Crabtree, M. Lavin and L. Bonneviot, J. Am. Chem. Soc., 1986, 108, 4032 CrossRef CAS.
- M. Lavin, E. M. Holt and R. H. Crabtree, Organometallics, 1989, 8, 99 CrossRef CAS.
- D.-H. Lee, B. P. Patel, E. Clot, O. Eisenstein and R. H. Crabtree, Chem. Commun., 1999, 297 RSC.
- B. P. Patel and R. H. Crabtree, J. Am. Chem. Soc., 1996, 118, 13105 CrossRef CAS.
- D.-H. Lee, H.-J Kwon, B. P. Patel, L. M. Liable-Sands, A. L. Rheingold and R. H. Crabtree, Organometallics, 1999, 18, 1615 CrossRef CAS.
- R. Kuhlman, Coord. Chem. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1997, 167, 205 Search PubMed.
., 1997, 167, 205 Search PubMed. - R. J. Kulawiec and R. H. Crabtree, Coord. Chem. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1990, 99, 89 Search PubMed.
., 1990, 99, 89 Search PubMed. - Z. Mazej, K. Borrmann, K. Lutar and B. Žemva, Inorg. Chem., 1998, 37, 5912 CrossRef CAS.
- V. J. Murphy, T. Hacall, J. Y. Chen and G. Parkin, J. Am. Chem. Soc., 1996, 118, 7428 CrossRef CAS.
- M. K. Whittlesey, R. N. Perutz, B. Greener and M. H. Moore, Chem. Commun., 1997, 187 RSC.
- During the completion of this work we became aware of the synthesis of a new bifluoride complex: D. C. Roe, W. J. Marshall, F. Davidson, P. D. Soper and V. V. Grushin, Organometallics, 2000, 19, 4575 CrossRef CAS.
- F. Maseras, A. Llédos, E. Clot and O. Eisenstein, Chem. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 2000, 100, 601 Search PubMed.
., 2000, 100, 601 Search PubMed. - M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. G. Zakrzewski, J. A. Montgomery, R. E. Stratmann, J. C. Burant, S. Dapprich, J. M. Millam, A. D. Daniels, K. N. Kudin, M. C. Strain, O. Farkas, J. Tomasi, V. Barone, M. Cossi, R. Cammi, B. Mennucci, C. Pomelli, C. Adamo, S. Clifford, J. Ochterski, G. A. Petersson, P. Y. Ayala, Q. Cui, K. Morokuma, D. K. Malick, A. D. Rabuck, K. Raghavachari, J. B. Foresman, J. Cioslowski, J. V. Ortiz, B. B. Stefanov, G. Liu, A. Liashenko, P. Piskorz, I. Komaromi, G. Gomperts, R. L. Martin, D. J. Fox, T. Keith, M. A. Al-Laham, C. Y. Peng, A. Nanayakkara, C. Gonzalez, M. Challacombe, P. M. W. Gill, B. G. Johnson, W. Chen, M. W. Wong, J. L. Andres, M. Head-Gordon, E. S. Replogle and J. A. Pople, GAUSSIAN 98, Revision A.7, Gaussian, Inc., Pittsburgh, PA, 1998..
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648 CrossRef CAS.
- J. P. Perdew and Y. Wang, Phys. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) . B, 1992, 82, 284 Search PubMed.
. B, 1992, 82, 284 Search PubMed. - D. Andrae, U. Häußermann, M. Dolg, H. Stoll and H. Preuß, Theor. Chim. Acta, 1990, 77, 123 CAS.
- A. Bergner, M. Dolg, W. Küchle, H. Stoll and H. Preuß, Mol. Phys., 1999, 30, 1431.
- C. A. Tolman, J. Am. Chem. Soc., 1970, 92, 2953 CrossRef CAS.
- A. Rosa, A. W. Ehlers, E. J. Baerends, J. G. Snijders and G. te Velde, J. Phys. Chem., 1996, 100, 5690 CrossRef CAS.
- H. Taube, Coord. Chem. Re
![[italic v]](https://www.rsc.org/images/entities/char_e0f5.gif) ., 1978, 26, 33 Search PubMed.
., 1978, 26, 33 Search PubMed. - R. H. Crabtree, P. C. Demou, D. Eden, J. M. Mihelcic, C. Parnell, J. M. Quirk and G. E. Morris, J. Am. Chem. Soc., 1982, 104, 6994 and references cited in this paper CrossRef CAS.
- D. Milstein, J. C. Calabrese and I. D. Williams, J. Am. Chem. Soc., 1986, 108, 6387 CrossRef CAS.
- R. C. Stevens, R. Bau, D. Milstein, O. Blum and T. F. Koetzle, J. Chem. Soc., Dalton Trans., 1990, 1429 RSC.
- D. Braga, F. Grepioni, E. Tedesco, M. J. Calhorda and P. E. M. Lopes, New J. Chem., 1999, 23, 129 RSC.
- J. C. Lee, Jr, A. L. Rheingold, B. Muller, P. S. Pregosin and R. H. Crabtree, J. Chem. Soc., Chem. Commun., 1994, 1021 RSC.
- L. S. Van der Sluys, J. Eckert, O. Eisenstein, J. H. Hall, J. C. Huffman, S. A. Jackson, T. F. Koetzle, G. J. Kubas, P. J. Vergamini and K. G. Caulton, J. Am. Chem. Soc., 1990, 112, 4831 CrossRef CAS.
- The long Ir–F bond length is similar to the Ag–F bond distance in Ag···FH+ (2.403 Å) computed by Chattaraj and Schleyer at the MP2/6-311 + G** level.37.
- P. K. Chattaraj and P. von Rague Schleyer, J. Am. Chem. Soc., 1994, 116, 1067 CrossRef CAS.
- K. Gruet, R. H. Crabtree, D.-H. Lee, L. M. Liable-Sands and A. L. Rheingold, Organometallics, 2000, 19, 2228 CrossRef CAS.
- R. H. Crabtree, P. E. M. Siegbahn, O. Eisenstein, A. L. Rheingold and T. F. Koetzle, Acc. Chem. Res., 1996, 29, 348 CrossRef CAS.
- F. Basolo and R. G. Pearson, Mechanism of Inorganic Reactions, Wiley, New York, 1958, p. 153. Search PubMed.
- B3PWP1/6-31G** optimal value for free HF for comparison with the calculated value in the complex. This value compares well with the experimental value of 0.9168 Å as deduced from IR spectra of HF in rare-gas matrices.42.
- M. G. Mason, W. G. von Holle and D. W. Robinson, J. Chem. Phys., 1971, 54, 3491 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules, Clarendon Press, Oxford, 1990. We have used the AIMPAC package from Bader's group available on the internet at http://www.chemistry.mcmaster.ca/aimpac. Search PubMed.
- D. Cremer and E. Kraka, Angew. Chem., Int. Ed. Engl., 1984, 23, 627 CrossRef.
- R. H. Crabtree and T. Dubé, work in progress..
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2001 |