Chemistry of vibronic coupling. Part 2. How to maximize the dynamic diagonal vibronic coupling constant for T₁ states in AB systems (A, B = H, Li, Na, K, Rb, Cs, F, Cl, Br or I)?

Abstract

The dynamic diagonal vibronic coupling constant (VCC) in several series of AB and AA molecules (A, B = H, Li, Na, K, Rb, Cs, F, Cl, Br or I) has been investigated. The electronic states considered are the singlet ground state (“ionic ” for heteronuclear AB species) and first excited singlet or triplet states (“covalent”). The VCC is thus studied for a charge transfer lowest lying triplet state. Qualitative trends in the VCC within the families of systems studied have been sought, with the aim of finding “ a chemistry of vibronic coupling”. Two interesting correlations emerge: the VCC for the charge transfer states in an AB system grows as the sum of the electronegativities of the A and B elements increases, as well as with decreasing AB bond length. A parameter f was defined as the sum of the electronegativities of the A and B elements divided by the AB bond length. This leads to a nearly monotonic correlation between computed values of VCC and f for 55 molecules originating from three distinct classes with a formal single bond: intermetallic species M¹M² (M = alkali metal), interhalogens X¹X² (X = halogen) and salt-like compounds MX. It emerges that contracted p-type orbitals making up the σ* MO (occupied by one electron in the excited state) seem to provide higher values of VCC than diffused s orbitals. The energy of the singlet–triplet gap is also correlated with the sum of the electronegativities of the A and B elements within two families of diatomics. Quantitative explanations of these two trends are still sought.

---

Introduction

The vibronic coupling constant (VCC, the molecular analogue of an electron–phonon coupling constant, EPCC, in extended systems) is a central molecular parameter of interest in the classical BCS theory of superconductivity.² The EPCC for an inter-valence (IV) charge transfer (CT) process (hereafter: IVCT) is believed to influence the critical superconducting temperature (T_c) in high-temperature cuprate and bismuthate superconductors.^3,4 While BCS theory fails in detail for the high temperature superconductors (HTSC), there exists a monotonic relationship between values of T_c and those predicted by BCS for many superconductors⁵ (see also Fig. 1 in ref. 6). Thus it is not surprising that in parallel with attempts to formulate new theories of HTSC, efforts continue to modify BCS theory so as to obtain better accord between theoretical and experimental results for T_c. We are also interested in examining vibronic coupling (VC) more closely, a traditional and understandable explanatory idea of superconductivity.

Our viewpoint is a chemist's one. We look at VCC as a parameter characteristic of a given molecular or extended system. Qualitati[italic v]e trends for the VCC in families of chemical systems should originate in a direct or indirect way from the periodic table. We try to identify such trends and to explain them in as simple a way as possible.

In the present paper we start from small molecular systems. In this way we continue our computational investigations of VCCs in the context of high-temperature superconductivity, begun in part 1 of this series.¹ We examine here in detail values of the diagonal VCC for AB, AA and BB closed-shell systems built of s- and p-block elements (A, B = H, Li, Na, K, Rb, Cs, F, Cl, Br or I). In the next paper we will also look at off-diagonal VCC for IVCT in open-shell species, such as “mixed valence” AB₂ and B₂A molecules.⁶ Subsequently we aim to obtain insight into VCC in systems containing the s, p and d block elements.⁷ We will try to see which kind of s, p and d orbital maximizes the VCC for mixed valence triatomics. Finally, we want to understand how the extension of a molecular system into a solid affects the value of the VCC.⁸ Building a bridge between the VCC in mixed-valence cuprates in the solid state and the same parameter for small molecular systems is an important goal which is not easy to reach.

Methods of calculations

The dynamic diagonal linear VCC (briefly referred to as the dynamic VCC, also denoted as h_ee) is a parameter which is defined by eqn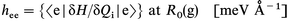. (1)

as the average value of the derivative of energy of the state e along the ith vibration normal coordinate (Q_i), calculated at the ground state (g) geometry corresponding to its (g's) minimum energy, R₀(g). h_ee is then simply the force that acts in the e state along Q_i (F_i^e). So calculated, h_ee is different from the off-diagonal linear VCC which describes the coupling of electronic states g and e through the ith normal vibration and is defined in eqn. (2).

In the present paper we want to look only at the diagonal VCC [eqn. (1)], denoted here simply as h. The diagonal VCC is often calculated for systems with a degenerate ground state, which might be subject to a first order Jahn–Teller effect.⁹ In the first paper in our series we carefully defined and interrelated the various definitions of VCCs common in the literature.

We want to explore diagonal VCCs relevant to CT states.¹⁰ Accordingly, we have chosen the S₀ → T₁ transition, which in the heteronuclear closed-shell AB molecules we investigate is usually a σ → σ* transition and has substantial CT character. The above is also true for the S₀ → S₁ transition. What holds true for the spatial part of T₁ should be roughly correct for S₁ (we will probe and confirm this in section 1, using the LiH molecule as an example).¹¹

In fact, distortion of T₁ states in diatomic molecules (towards either dissociation or just bond elongation) as studied by us in this contribution is not a textbook example of vibronic coupling. As a reviewer remarks, for such states a nomenclature of “energy gradients ” instead of vibronic coupling constants would suffice. However there are many connections between “real” vibronic coupling constants and the force acting at a certain nuclear arrangement in some PES. First, the off-diagonal vibronic coupling constant h_egⁱ equals the energy gradient in the most popular diabatic models of mixed-valence systems. Secondly, there is an important relationship between a singlet–triplet gap in AA diatomics and the “real ” vibronic instability of linear symmetric AAA triatomics.¹² Also, as we show in part 3 of this series,⁶ there is a connection between the force in T₁ states of AB diatomics and the vibronic stability parameter G in ABA triatomics.

Computational details

To calculate the diagonal VCC for a given AB molecular system, we have scanned the potential energy surface (PES) of states g ≡ S₀ and e ≡ T₁ along the stretching normal coordinate of AB molecules, using the configuration interaction for single excited states (CIS) method. The dynamic VCC was obtained from numerical differentiation of the computed PES for the excited T₁ state at the ground state (S₀) geometry. The probing step, both to find R₀ for the S₀ state, and for differentiation, was 0.025 Å. We used a 6-311++ G** basis set¹³ for H to Cl elements and the WTBS basis set¹⁴ or core potentials LANL2DZ¹⁵ for heavier elements. All computations were performed using the GAUSSIAN 94 program.¹⁶ The WTBS basis set was obtained from the web.¹⁷ All I- and Cs-containing species were calculated with use of core potentials; the K-, Rb- and Br-containing species were calculated either with the WTBS basis set or with use of core potentials. Our calculations are non-relativistic.

We want to emphasize that both the energy of the S₀ → T₁ transition and the geometry and value of the VCC for AB species were quite insensitive to the computational method and basis set used. For example, the correlation factor between values of VCC obtained by unrestricted Hartree–Fock (UHF) computation with the STO-6G** basis set and those obtained with CIS and the 6-311++ G** basis set was 0.9. We have also found in some exploratory calculations for several selected molecules that use of the configuration interaction for single and double excited states (CISD) method, UHF computations with a perturbation correction at the MP2 level (UHF/MP2), and complete active space self consistent field [CASSCF(2,4)] methods resulted in about ± 15% differences between computed values of VCC. The 0.025 Å uncertainty in determination of energy minima for the S₀ state usually led to no more than ± 5% differences. Also use of core potentials gave h_ee values similar to those obtained with the WTBS basis set for elements such as K or Br. This means that one may obtain reasonable qualitative trends for the VCC and the energy of the S₀ → T₁ transition with the simple UHF method, as well as within the core-potential approximation for heavier elements.

In most cases the ground state of a simple diatomic molecular species has the shortest bond length among all the electronic states of the molecule. Actually, there are some interesting exceptions to this rule.¹⁸ For all the systems we investigated the S₁ states (and sometimes T₁ states¹⁹) have minima that are at longer bond lengths than that of the ground state. Thus, in all cases the derivatives of the energy of the S₁ and T₁ states at R₀ are negati[italic v]e. In this paper we always present the absolute (positive) value of a dynamic VCC.

Results and discussion

The plan of this paper is as follows: in section 1 we will show in some detail how we compute and think about the diagonal VCC, with the LiH molecule as an example. In section 2 we will present computed values of the VCC for all AB molecules investigated. Finally, in section 3 we will try to summarize the results obtained, abstracting some simple qualitative rules for predicting values of the VCC. Our goal is to maximize the VCC within certain families of molecular species. This might eventually provide a basis for the design of new BCS-type superconductors.

1 LiH

The LiH molecule is the simplest diatomic heteronuclear molecule. It has widely been investigated both in theory and experiment.^20–23 In Fig. 1 we show the computed PES for the ground state (¹Σ  = S₀) and two lowest lying excited states (³Σ  = T₁ and ¹Σ  = S₁) of the LiH molecule. In a one-electron picture these three states originate from a specific configuration, a certain occupation of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) levels. The T₁ state is repulsive (dissociative), while the S₁ state has its minimum at about 1.9 Å.²⁴ The S₀ ground state has a certain degree of ionicity, with the LiH bond polarized towards H (Li⁺H⁻). The direction of polarization of the Li–H bond changes in both the T₁ and S₁ states, which are more or less “non-ionic” or even slightly polarized toward the Li atom.²⁵ Thus the S₀ → S₁ and the S₀ → T₁ electronic transitions have charge transfer character, and may serve as a simple model for such transitions in more complicated systems. The force (F) acting in the ground state at R(g₀) along the ith normal coordinate is zero (F_i^g  = 0). Thus we can write eqn. (3).

Fig. 1 The PES for the ground state (¹Σ  = S₀) and two lowest lying excited states (³Σ  = T₁ and ¹Σ  = S₁) of the LiH molecule.

This treatment allows generalization of the h_ee definition given in eqn. (1), as in eqn. (4)

The definition of h [  =  h_ee(R₀)] given in eqn. (4) is closer to the photochemist's sense of diagonal coupling constants than that given in eqn. (1). Eqn. (4) defines h_ee using a derivative of the excitation energy along a normal coordinate. In other words, the diagonal coupling constant is large if the vertical excitation energies differ much during stretching and shrinking of the AB bond from its ground state equilibrium value.

Let us now compare excitation energies and diagonal coupling constants for the T₁ and S₁ states. The computed values of E_exc are 3.10 and 4.08 eV for the S₀ → T₁ and S₀ → S₁ transition, respectively. The values of h_ee at R(g₀) computed for the S₁ and T₁ states are relatively close to each other, being about 1.15 and 1.55 eV Å⁻¹, respectively. We have observed that for most of the AB species investigated the VCC for S₁ states is about 60–70% of the value of the VCC for T₁ states, where we could calculate both.

In the next section we present results of computations of the S₀/T₁ gap, and the dynamic linear vibronic coupling constant h_ee at R(g₀) for T₁ states for a broader spectrum of AB molecules.

2.1 Other AB systems

The molecules investigated in this part of the paper belong to the following three classes: interhalogen compounds X¹X², alkali metal halides MX and intermetallic compounds M¹M². The alkali metal hydrides MH are another group, bridging MX and M¹M² species as regards chemical properties. We will hereafter call these molecules AB, AA or BB, where A is the more electropositive and B the more electronegative element. In total, these 45 heteronuclear and 10 homonuclear molecules represent a rich variety of compounds, of different chemical character. For example, the difference in Pauling electronegativities in this series varies from 0 for “ covalent” homoatomic molecules such as Cs₂ or F₂ to 3.3 for “ionic” CsF. The calculated A–B bond length varies from about 0.73 Å for H–H to about 5.05 Å for Cs₂. The redox properties of the molecules investigated also differ markedly: F₂ is known to be a strong oxidant, H₂ is quite an inert species, while CsH or CsLi are indicated by the computed energies of the HOMO and LUMO levels to be strong reductants. The calculated S₀/T₁ gap varies from near 0 eV for Cs₂ to over 11 eV for HF. The T₁ state is usually weakly attractive for interhalogen compounds, while it is repulsive for all other species studied (salts and intermetallic compounds). T₁ often has strong CT character for MX species while it has no CT component for homonuclear species. Clearly these molecules represent a great chemical variety.

We have calculated the value of the S₀/T₁ gap and the dynamic diagonal VCC [using eqn. (1)] for T₁ states all of the above molecules. Table 1 presents the calculated bond lengths (R₀) of these molecules in the S₀ ground state, the S₀ → T₁ excitation energy (E_exc) and the calculated values of the dynamic vibronic coupling constant (h/eV Å⁻¹) in the T₁ state at R₀ of the S₀ state.

Table 1 Calculated bond lengths (R/Å) of ground state geometries (top), S₀ → T₁ excitation energies (eV) (middle entry) and (bottom) calculated values of the dynamic diagonal vibronic coupling constant for the T₁ state h (eV Å⁻¹)

F2	Cs2	CsRb
1.325 Å	5.050 Å	4.775 Å
3.99 eV	0.00 eV	0.60 eV
18.82	0.24	0.00
Cl2	Rb2	RbK	CsK
2.000 Å	4.525 Å	4.325 Å	4.525 Å
3.03 eV	0.00 eV	0.06 eV	0.59 eV
7.10	0.30	0.34	0.01
Br2		K2			KNa	RbNa	CsNa
2.450 Å		4.200 Å			3.700 Å	3.900 Å	4.100 Å
1.50 eV		0.08 eV			0.28 eV	0.24 eV	0.79 eV
3.96		0.34			0.43	0.39	0.02
I2	Na2			NaLi	KLi	RbLi	CsLi
2.825 Å	3.200 Å			3.000 Å	3.500 Å	3.700 Å	3.975 Å
1.24 eV	0.43 eV			0.51 eV	0.34 eV	0.30 eV	0.68 eV
2.75	0.59			0.62	0.45	0.41	0.08
Li2			LiH	NaH	KH	RbH	CsH
2.775 Å			1.600 Å	1.925 Å	2.350 Å	2.550 Å	2.800 Å
0.84 eV			3.10 eV	2.37 eV	2.85 eV	1.68 eV	4.526 eV
0.23			1.55	1.38	0.68	0.67	0.50
H2			HF	LiF	NaF	KF	RbF	CsF
0.725 Å			0.900 Å	1.575 Å	1.950 Å	2.375 Å	2.450 Å	2.675 Å
10.21 eV			11.22 eV	8.57 eV	7.08 eV	6.55 eV	6.63 eV	6.58 eV
15.62			11.65	3.73	2.40	1.56	1.56	0.94
		ClF	HCl	LiCl	NaCl	KCl	RbCl	CsCl
		1.625 Å	1.275 Å	2.025 Å	2.425 Å	2.850 Å	3.025 Å	3.250 Å
		3.38 eV	7.57 eV	6.30 eV	3.96 eV	4.85 eV	4.88 eV	4.96 eV
		7.73	7.96	2.34	1.64	1.09	0.99	0.80
BrCl	BrF	HBr	LiBr	NaBr	KBr	RbBr	CsBr
2.225 Å	1.825 Å	1.425 Å	2.175 Å	2.55 Å	3.050 Å	3.225 Å	3.400 Å
2.33 eV	2.57 eV	6.95 eV	5.34 eV	3.64 eV	2.57 eV	2.52 eV	3.89 eV
5.63	6.42	7.45	2.41	2.68	1.20	1.05	0.84
IBr	ICl	IF	HI	LiI	NaI	KI	RbI	CsI
2.625 Å	2.375 Å	1.925 Å	1.575 Å	2.425 Å	2.750 Å	3.250 Å	3.450 Å	3.675 Å
1.47 eV	2.07 eV	2.20 eV	5.61 eV	4.69 eV	4.05 eV	3.68 eV	3.54 eV	3.51 eV
3.26	4.50	4.57	5.91	1.88	1.66	1.01	0.92	0.76

---

Though they are not at all the focus of our study, the approximate bond lengths found during CIS UHF/6-311++ G** PES scans agree reasonably well with experimental values.²⁶ In most cases the computed bond lengths are close to or larger than the experimental ones, but there are some exceptions to this. Compare for example values of R₀ for the smallest molecule, H₂ [computed (comp.) 0.725 Å, experimental (exp.) 0.742 Å], interhalogens Cl₂ (comp. 2.000, exp. 1.891 Å), ClF (comp. 1.625, exp. 1.628 Å), hydrogen halides HF (comp. 0.900, exp. 0.917 Å), HBr (comp. 1.425, exp. 1.414 Å), intermetallics Na₂ (comp. 3.200, exp. 3.079 Å), Li₂ (comp. 2.775, exp. 2.673 Å), metal hydrides LiH (comp. 1.600, exp. 1.595 Å), KH (comp. 2.350, exp. 2.244 Å), and salts KI (comp. 3.250, exp. 3.23 Å), KCl (comp. 2.850, exp. 2.94 Å).

It is difficult to compare computed values of h with experimental ones, due to the lack of experimental data for most molecules investigated.

2.2 What could one correlate h with?

It is very instructive to look at the data obtained in plots. Searching for chemical interpretation of computed values, we will plot both E_exc and h [italic v]s. a difference of Pauling electronegativities (Δ EN) of the A and B elements constituting an AB molecule. Given the energetic nature of the variables we consider, it would appear that Mulliken electronegativities should be used in the correlation. However these are not available for some of the elements we consider in this series of papers. There is also a good correlation between Mulliken and Pauling EN.

We will in addition plot h [italic v]s. E_exc. Still another classification is of great chemical utility, that focusing on cations and on anions present in an AB system.²⁷ Combining the three above types of plots with the cation/anion division, we obtain the six plots presented in Fig. 2–4. Some regularities are apparent in these figures, especially in the behavior of E_exc and h. In particular, it appears to be useful to plot E_exc and h [italic v]s. the difference of the Pauling electronegativities (Δ EN) of A and B elements. Fig. 2(a) and 2(b) show the dependence of the S₀ → T₁ excitation energy (E_exc) in AB molecules on the difference in the Pauling electronegativities (Δ EN) of the A and B elements.

Fig. 2 The S₀ → T₁ excitation energy (E_exc/eV) in AB molecules plotted [italic v]s. the difference in Pauling electronegativities (Δ EN) of A and B elements. (a) Each set of points corresponds to a given anion (e.g. F⁻) in different X¹X² and MX species. (b) Each set of points corresponds to a given cation (e.g. Cs⁺ or I⁺) in different molecules. Solid, dashed and dotted lines show linear regressions for H⁺-, Li⁺- and Cs⁺-containing species, respectively.

Fig. 3 The dynamic VCC (h/eV Å⁻¹) in AB molecules plotted [italic v]s. the difference in Pauling electronegativities (Δ EN) of A and B elements. (a) Each set of points corresponds to a given anion (e.g. F⁻) in different X¹X² and MX species. (b) Each set of points corresponds to a given cation (e.g. Cs⁺ or I⁺) in different molecules.

Fig. 4 Value of the dynamic VCC (h/eV Å⁻¹) in AB molecules plotted [italic v]s. the S₀ → T₁ excitation energy (E_exc/eV) in AB molecules. (a) Each set of points corresponds to a given anion (e.g. F⁻) in different X¹X² and MX species. (b) Each set of points corresponds to a given cation (e.g. Cs⁺ or I⁺) in different molecules. Solid, dashed and dotted lines show linear regressions for H⁺-, Li⁺- and Cs⁺-containing species, respectively.

Let us concentrate first on alkali metal halides. For these molecules the S₀ → T₁ excitation is essentially a p(X) → s(M) transition. It is then not surprising that E_exc grows with increasing EN of X (X⁻ becomes a worse electron donor) in each series of molecules investigated. However, it is quite surprising that E_exc increases with increasing EN of M. The opposite might have been expected from the increase of the HOMO/LUMO gap in MX with decreasing EN of M (M⁺ becomes a better electron acceptor).

The resolution of this seeming paradox is given by the simplest theory of donor–acceptor complexes.²⁸ One usually approximates E_exc as in eqn. (5),

where Δ_HOMO/LUMO is the HOMO/LUMO gap and the − (δe)²/R term is an electrostatic stabilization connected with the attraction of a hole in the HOMO and the electron in the LUMO in the CT state (a charge of δe is transferred upon excitation). One may expect that as a consequence of the cationic radius increasing strongly (as one moves from H to Cs), and due to increased mixing of the M and X atomic orbitals (mixing decreases in same direction), δe should increase as one moves from H to Cs. This would lead to an increase of the coulombic component of the E_exc (the CT character of LMCT increases), providing an explanation for the relationship observed in Fig. 2(b).

Values of E_exc for the compounds containing the hydride (H⁻) ion are of interest. Hydrides occupy a position between iodides (I⁻) and intermetallic species, such as “lithides ” (Li⁻). The “ positioning” of H in the periodic table has always been debated. It is usually assumed that its place is in between the alkali metals and halogens (EN_Li  = 1.0<EN_H  = 2.1<EN_I  = 2.5). Other perspectives on the position of H look to polarizabilities [α(H⁻)≈α(I⁻)], or to ionic radii [r(F⁻)<r(H⁻)<r(Cl⁻)]. The values of E_exc follow the trend indicated by the electronegativity values. Another observation deserving comment is the slope of the h [italic v]s. E_exc dependence. One sees in Fig. 4(b) that this increases strongly in the direction Cs⁺ → Li⁺ → H⁺ → X⁺ (X = halogen) [Fig. 2(b)]. Again, the position of H between alkali metals and halogens is evident.

Let us now analyse the h parameter, which is of greatest interest to us. Fig. 3(a) and 3(b) show h in AB molecules plotted [italic v]s. the difference of Pauling electronegativities (Δ EN) of A and B. One sees characteristic regularities in these plots as well. The value of h increases for a given series of salts in the direction H⁺ → Li⁺ → Cs⁺ and Li⁻ → H⁻ → I⁻ → F⁻. In this case as well, H assumes a position in the periodic table between I and Li. The only exception from this rule is the value of h for the H₂ molecule, which is between that for F₂ and that for Cl₂.

Interestingly, h is usually the greatest for the homonuclear species in a given series.²⁹ This is true both for the series of interhalogen compounds [h(F₂)>h(ClF)>h(BrF), etc.], salts [h(F₂)>h(HF)>h(LiF)>···>h(CsF)] and intermetallic compounds [h(Na₂)>h(KNa)>···>h(CsNa)]. The biggest value of h is obtained for F₂ and H₂ molecules (ca. 18.8 and 15.6 eV Å⁻¹, respectively), followed by the HF molecule (11.7 eV Å⁻¹). In general, values of h for intermetallic species are the lowest, “ salts” are intermediate, and interhalogen compounds have the highest values. We think that this is a part of a more general rule.

It is interesting to look for correlation between the h and E_exc values. Fig. 4(a) and 4(b) show a dependence of the dynamic VCC (h) in AB molecules plotted [italic v]s. the S₀ → T₁ excitation energy (E_exc). Evidently, h always increases with growing E_exc. The slope of the h [italic v]s. E_exc dependence is similar for anions, while E_exc intercepts (cut-off ordinate values at h  = 0) differ greatly. The biggest intercepts are for alkali metal fluorides (ca. 6 eV); the intercepts are smaller for iodides (ca. 3.0 eV) and interhalogen species (ca. 0 eV). Thus it is the interhalogen compounds which provide the highest values of h at relatively small values of E_exc .

Let us summarize the major tends emerging. For E_exc: (i) E_exc for the S₀ → T₁ excitation in AB molecules gets larger with increasing EN of the more electronegative element (B); (ii) E_exc for the S₀ → T₁ excitation in AB molecules grows with increasing EN of the less electropositive element (A) in the series of AB salts and interhalogens; (iii) values of E_exc for the S₀ → T₁ excitation in intermetallic compounds are usually very small (<1 eV). For h: (iv) values of h in AB molecules grow with increasing EN of the more electronegative element (B); (v) values of h in AB molecules get larger with increasing EN of the less electropositive element (A) in the series of AB salts and interhalogen compounds; (vi) values of h in the intermetallic compounds are usually very small (<4 meV Å⁻¹); (vii) values of h in AB molecules usually grow with decreasing difference in electronegativities between A and B; (viii) h always increases with increasing E_exc in a given series of molecules; (ix) values of E_exc, of h, and of the slope of the h [italic v]s. E_exc curves for H-containing species (in both its formal + 1 and − 1 oxidation state) point to a “position” of H either between Li and I or between F and Cl.

3 How to obtain the maximum value of the VCC in AB species?

In the previous section we have presented several detailed “rules” (abstracted from calculations) for the factors controlling the values of E_exc and h in the MX, M¹M² and X¹X² systems. We have observed that values of h for intermetallic species are the lowest, “ salts” show intermediate values, and interhalogen compounds have the highest values of h. Still, it seems that the salts, intermetallic compounds and interhalogen compounds form three distinct groups from the point of view of VCC values. Now we would like to build a bridge between these three quite different chemical categories, trying to maximize the diagonal VCC for T₁ states in any closed shell A–B species. Answering this question might guide us to the factors controlling VCCs for d- and f-block metals as well.

How to unify the behavior of h values for M¹M², MX and X¹X² systems in one plot? To approach this problem we note two things: (i) these three families of species are built of (s,s), (s,p) and (p,p) block elements, respectively; (ii) h grows with increasing sum of the EN of A and B as well as with decreasing AB bond length. It is then reasonable to try to plot h [italic v]s. a new parameter f, defined as a sum of A and B electronegativities divided by the AB bond length, (EN_A + EN_B)/R_AB. This way we attempt to correlate a computed molecular parameter with an empirical parameter, but one based on variables of proven utility in chemistry. The proposed correlation is shown in Fig. 5.

Fig. 5 The dynamic VCC [h(arbitrary units)] in AB molecules plotted [italic v]s. the sum of the Pauling electronegativities of A and B elements divided by the bond length of the AB molecule, f  = (EN_A + EN_B)/R_AB.

Clearly the suggested correlation between h and f exists. We find it impressive that using f we manage to unify a certain molecular parameter (here: h) for three families (X¹X², MX and M¹M²) that are so chemically different. Values of h tend to grow quite monotonically with increasing f. Although the trend is not followed too well for large values of f, it seems that f might be used to determine the value of VCC not only in a qualitative but also a semi-quantitative way, based only on well-known atomic variables. Also, might this correlation be extended for molecules containing d- and f-block elements, as well as for other systems (e.g. organic compounds etc.)? We will try to answer these questions in the following papers of this series.^6,7

Let us now try to find an explanation for the h [italic v]s. f correlation. It is helpful to recall the chemical interpretation of VCC given in the first paper of this series,¹ and here in eqn. (4). The diagonal VCC (h) is the derivative of excitation energy along the normal coordinate of a given molecular vibration, evaluated at R₀ (the minimum of the ground state). In this way, the VCC of simple AB molecules roughly measures how much the excitation energy varies upon expansion and contraction of the AB bond.

We will now use a simplified picture derived from a molecular orbital (MO) model, with orbitals frozen during the AB stretching vibration. We have chosen Li₂ and I₂ molecules as examples of the M₂ and X₂ systems. These are respectively (s,s) and (p,p) systems, according to the notation introduced in this section. The atomic radii of the elements constituting these species are quite close to each other [r(Li) = 152 pm while r(I) = 133 pm], but the character of the bonding and antibonding σ* orbitals is quite different in these molecules: the s character is stronger and p character weaker in the σ* of Li₂ than in that of I₂ . The antibonding character of the LUMO σ* orbital increases during a contraction of the AB bond, due to the increasing out-of-phase overlap of atomic orbitals (AOs) of A and B. Conversely, the antibonding character of the LUMO decreases in the course of AB bond stretching. Thus the energy of the excited state connected with the σ_bond → σ_antibond transition is higher (with respect to its energy at R₀) during contraction and lower during expansion of the AB bond. This gives rise to a non-vanishing contribution to the VCC.

Certainly, the nature of the T₁ states differs among the different families of AB molecules (even though they all are ³Σ states). T₁ states for the (p,p) systems (i.e. F₂, FCl, etc.) originate from the σ_nonbond → σ_antibond transition, which entails electron transfer from the antisymmetric lone pair combination to the σ* level. These states are not dissociative and have relatively large force constants. However, for the (s,p) systems, the T₁ states are most likely connected with the σ_bond → σ_antibond transition, which is a ligand-to-metal charge- transfer transition.³⁰ These states dissociate easily. The same is true for the (s,s) systems. As a result, the force in the T₁ state at R(S₀) (i.e. h) is much larger for (p,p) systems (the excited state formally still has a bond order of about 1/2) than for (s,p) and (s,s) ones (the bond order is now ≈0).

Given the different nature of the T₁ (Σ_u) states for the (s,s) and the (p,p) systems, the existence of the h [italic v]s. f relationship (Fig. 6) is very interesting. The h values for Li₂ and I₂ molecules are about 0.23 and 2.75, respectively.³¹ We thought that this 13-fold difference might be connected to a larger change in the p–p overlap for I₂ than in the s–s overlap for Li₂, as R is varied near the equilibrium value. However, examination of actual changes does not support this argument.

Fig. 6 Value of E_exc/eV in AB molecules plotted [italic v]s. the sum of the Pauling electronegativities (EN_A + EN_B) of A and B elements. Lines for the two groups of points have been introduced to guide the eye.

On the other hand, it has been shown by Allen that the derivative of the effective radial potential (i.e. force) acting near a given atom (from the p block of the periodic table) correlates linearly with a spectroscopically derived electronegativity value for this atom.³² We connect this to the diffuse character of s orbitals and contracted character of low-lying p orbitals. Transferring this reasoning from atoms to molecules, and its generalization for s-, d- and f-block elements, might be an attractive path to understanding our h [italic v]s. f relationship.

If the relationship found by Allen were transferable to T₁ states of AB molecules it might point to a connection between h and the position of the Fermi level of a molecule.³³ A low Fermi level corresponds to strongly bound electrons, and thus large changes in the antibonding character of the σ* orbital of I₂ as compared to that for Li₂ in the course of the stretching vibration. A more quantitative approach to relationships between all the above parameters is being explored by Ayers and Parr.³³

What type of element, s or p, should be taken in order to provide the maximum h value? As shown by our results for (s,s)-, (s,p)- and (p,p)-type species, the (p,p) combination in the interhalogen species is best for maximizing h. The highest VCC value is obtained for the F₂ molecule, a (p,p) system with quite contracted p orbitals.³⁴ The values of VCCs for (s,p)-type species (one s orbital) are usually smaller than those for (p,p)-type species. The remaining (s,s) combination (two s orbitals) yields the smallest VCC values. A single exception to this rule is the smallest molecule, H₂, which competes with interhalogen species.

Notice here that most of the known “good” superconductors are of the (p,p)- (bismuthates, fullerides or acetylides) or (p,d)-type (cuprates) in our notation. There are several superconducting hydrides known, with the highest critical temperature of about 8 K for ThH_x³⁵ [an (f,s) system in our classification]. However, predictions of superconductivity in metallic hydrogen [(s,s)-type] exist.³⁶

The quantitative approach and search for trends for VCCs within s, p and d blocks will be subject of our next papers.⁷

4 How might one correlate values of E_exc in AB species?

Encouraged by the existence of the monotonic f [italic v]s. h correlation, we will try now to unify in one plot the values of E_exc for the three families of molecules investigated. Recollect that f was defined as the sum of the ENs of A and B divided by the AB bond length and served as a parameter to be correlated with h. It is then reasonable to try for sake of consistency a correlation of E_exc with a simple sum of the electronegativities of A and B elements. This correlation is presented in Fig. 6.

It is apparent from Fig. 6 that the E_exc[italic v]s. sum of EN dependence shows much correlation but distinguishes three families: X¹X², MX and M¹M². The sum of the ENs allows a comparison of E_exc within a certain family (the E_exc[italic v]s. sum of EN dependence is monotonic for salts and for interhalogen species). Again, H₂ differs from all other molecules: it belongs in Fig. 6 neither to the interhalogen nor to the intermetallic families. The appearance of two branches of points in Fig. 6 may be understood if one recollects that the nature of the T₁ states for the (s,s) and (s,p) and for the (p,p) molecules is different (see previous section). The σ_bond → σ_antibond LMCT states for (p,p) systems, which might be compared with those for the (s,s) and for the (s,p) ones, lie well above the actual σ_nonbond → σ_antibond T₁ states.³⁷

The E_exc[italic v]s. sum of EN correlation followed independently in the two families of points in Fig. 6 seems to be promising for a semi-quantitative description of E_exc within a certain family of species. As in the case of h, no QM (quantum mechanical) computations need to be undertaken in order to predict qualitatively the value of E_exc for a molecule, given known values of E_exc for two other members of a family and the sum of the electronegativities for all three molecules. Our investigations of the singlet–triplet gap for diatomics may be important for predicting pathways and energy barriers for the prototypical atom exchange reactions in triatomic systems.^12b We will come back to this in our next paper.⁶

Conclusion

We have investigated theoretically the dynamic diagonal VCC (h) for T₁ states in the series of AB, AA and BB molecules where A, B = H, Li, Na, K, Rb, Cs, F, Cl, Br or I. The electronic state for which the VCC is calculated is the first excited triplet state (“covalent”, in contrast to the singlet ground state which is “ ionic” for heteronuclear AB species). In this way we model the VCC for a LMCT state for some species. We looked for qualitative trends in the VCC within the family of systems studied, with the purpose of finding “a chemistry of the diagonal VC”.

It appears that a very simple rule obtains: the VCC for T₁ states in MX system grows with the increasing sum of the electronegativities of A and B elements as well as with decreasing AB bond length. The largest values of dynamic VCCs are found for interhalogen species, including hydrogen halides. Salts usually have intermediate h values, between interhalogens and intermetallics. It appears that the s-block elements yield smaller VCCs than p-block elements, probably due to the more pronounced diffuseness of the orbitals of the s-block elements.

We managed to correlate h with a parameter f, defined as the sum of the electronegativities of the A and B atoms, divided by the AB bond length. This correlation unifies three families of species with formal single bonds: intermetallic species M¹M², interhalogens X¹X² and salts MX. Another monotonic correlation relates E_exc for the S₀ → T₁ transition and the sum of the electronegativities of the A and B atoms constituting an AB molecule. In this case the three families investigated in this paper generate two different families of points. This may be explained taking into account the character of the excitation for the T₁ states in the (s,s), (s,p) and (p,p) families of diatomics.

In the next papers of this series we will study the VCC through the periodic table, investigating molecules built of elements different from those in the Ia and VIIa groups.⁷ Keeping in mind the importance of the inter-valence charge-Transfer transition in HTSC materials we will look at the dynamic off-diagonal VCC for such states in simple molecular A₂B systems.

Acknowledgements

We are grateful to several reviewers for their substantive criticism. This research was conducted using the resources of the Cornell Theory Center, which receives funding from Cornell University, New York State, the National Center for Research Resources at the National Institutes of Health, the National Science Foundation, the Defense Department Modernization Program, the United States Department of Agriculture and corporate partners. This work was supported by the Cornell Center for Materials Research (CCMR), a Materials Research Science and Engineering Center of the National Science Foundation (DMR-9632275). W. G. also thanks the Kosciuszko Foundation for financial support.

References and notes

1. Part 1: W. Grochala, R. Konecny and R. Hoffmann, Chem. Phys., submitted..
2. J. Bardeen, L. N. Cooper and J. R. Schrieffer, Phys. Re[italic v]., 1957, 108, 175.
3. J. K. Burdett, Inorg. Chem., 1993, 32, 3915.
4. V. Meregalli and S. Y. Savrasov, Phys. Re[italic v]. B, 1998, 57, 14453.
5. B. Chakraverty and T. Ramakrishnan, Physica C, 1997, 282, 287–290.
6. Part 3: W. Grochala and R. Hoffmann, J. Phys. Chem. A, 2000, 104, 9740.
7. Part 4: W. Grochala and R. Hoffmann, J. Am. Chem. Soc., submitted..
8. Part 5: W. Grochala and R. Hoffmann, manuscript in preparation..
9. K. Yoshizawa, T. Kato and T. Yamabe, J. Chem. Phys., 1998, 108, 7637; K. Yoshizawa, T. Kato, M. Tachibana and T. Yamabe, J. Phys. Chem. A, 1998, 102, 10113.
10. Our interest in CT states derives from the eventual aim of applying our theory to the design of superconducting materials. For the cuprates, for instance, Cu³⁺ + O²⁻ → Cu²⁺ + O⁻ (i.e. a ligand to metal CT process) in one way or another figures in most mechanisms suggested..
11. Here the difference between the diagonal (h_ee) and off-diagonal coupling constant (h_eg) becomes evident. For all heteronuclear diatomic molecules h_ee has non-zero values for both e = S₁ and e = T₁. However, h_eg is zero for T₁ and not zero for S₁ (h_eg is zero for S₁ only for most homonuclear diatomics). This is because the S₀ → T₁ transition is spin-forbidden, which results in vanishing of the off-diagonal EVCC for T₁. Of course, one may still calculate the interesting spatial part of h_eg for the S₀ → T₁ transition. It is essential to keep the difference between diagonal and off-diagonal EVCC in mind..
12. (a) S. S. Shaik and A. Shurki, Angew. Chem., Int. Ed., 1999, 38, 586; (b) P. Maitre, P. C. Hiberty, G. Ohanessian and S. S. Shaik, J. Phys. Chem., 1990, 94, 4089.
13. (a) R. Krishnan, J. S. Binkley, R. Seeger and J. A. Pople, J. Chem. Phys., 1980, 72, 650; (b) T. Clark, J. Chandrasekhar and P. v. R. Schleyer, J. Comp. Chem., 1983, 4, 294.
14. S. Huzinaga and B. Miguel, Chem. Phys. Lett., 1990, 175, 289; S. Huzinaga and M. Klobukowski, Chem. Phys. Lett., 1993, 212, 260.
15. T. H. Dunning, Jr. and P. J. Hay, in Methods of Electronic Structure, Theory, ed. H. F. Schaefer III, Plenum Press, New York, 1977, vol. 2..
16. GAUSSIAN 94, Revision D.3, M. J. Frisch, G. W. Trucks, H. B. Schlegel, P. M. W. Gill, B. G. Johnson, M. A. Robb, J. R. Cheeseman, T. Keith, G. A. Petersson, J. A. Montgomery, K. Raghavachari, M. A. Al-Laham, V. G. Zakrzewski, J. V. Ortiz, J. B. Foresman, J. Cioslowski, B. B. Stefanov, A. Nanayakkara, M. Challacombe, C. Y. Peng, P. Y. Ayala, W. Chen, M. W. Wong, J. L. Andres, E. S. Replogle, R. Gomperts, R. L. Martin, D. J. Fox, J. S. Binkley, D. J. Defrees, J. Baker, J. P. Stewart, M. Head-Gordon, C. Gonzalez and J. A. Pople, Gaussian, Inc., Pittsburgh, PA, 1995..
17. Basis sets were obtained from the Extensible Computational Chemistry Environment Basis Set Database, Version 1.0 (http://wserv1.dl.ac.uk:800/ems1 pnl/basisform.html), as developed and distributed by the Molecular Science Computing Facility, Environmental and Molecular Sciences Laboratory, which is part of the Pacific Northwest Laboratory, Richland, Washington, and funded by the U.S. Department of Energy. The Pacific Northwest Laboratory is a multi-program laboratory operated by Battelle Memorial Institute for the U.S. Department of Energy under contract DE-AC06-76RLO 1830. Contact David Feller or Karen Schuchardt for further information..
18. K. P. Huber and G. Herzberg, Molecular Spectra and Molecular Structure, Van Nostrand Reinhold, Princeton, 1979, vol. 4..
19. T₁ is most often a repulsive state..
20. F. X. Gadea, H. Berriche, O. Roncero, P. Villarreal and G. J. Delgado Barrio, Chem. Phys., 1997, 107, 10515.
21. A. Luchow and J. B. Anderson, J. Chem. Phys., 1996, 105, 7573.
22. F. V. Lundsgaard Morten and H. Rudolph, J. Chem. Phys., 1999, 111, 6724.
23. F. Gemperle and F. X. Gadea, J. Chem. Phys., 1999, 110, 11197.
24. In fact our CIS/6-311++ G** calculations do not predict properly the dissociative behavior of LiH (the ground state does not dissociate to Li + H in our calculations). Probably the same is true for some other molecules considered in this paper. However, our interest is in modeling h in T₁ states at R₀'s of the S₀ states, at rather small interatomic distances. Our simple calculations do not provide very accurate values of R₀'s and h's, but rather show trends (important for chemists) in the behavior of h's..
25. The Mulliken charge on the Li atom is negative and relatively small in both excited states. The computed charges on Li and H atoms might be erroneous, because the Mulliken population analysis may cause substantive artifacts when used with large basis sets, and in general does not converge with the size of the basis set, as a referee correctly reminded us..
26. All experimental data are taken from: G. Herzberg, Molecular Spectra and Molecular Structure, 2nd edn, D. van Nostrand Company, Inc., Princeton, 1950, vol. 1..
27. The division into cations and anions is based on an electronegativity criterion. For example, iodine may act as the anion I⁻ as in KI or as the cation I⁺ as in IF..
28. R. Mulliken and W. B. Person, J. Am. Chem. Soc., 1969, 91, 3409.
29. When considering CCs for homonuclear molecules one has to remember that the off-diagonal coupling constant through the σ_g vibration is equal to zero (due to the spatial part of the wavefunction) for both S₀/S₁ and S₀/T₁ pairs of states..
30. There may also be low lying ³Π states of a different bonding nature, but they are not considered here (all T₁ states computed in this paper are ³Σ_u states, and not ³Π ones)..
31. Interestingly, the (s,p) system of similar dimensions, RbF [R(Rb⁺) = 152 pm, R(F⁻) = 133 pm] has h  = 1.56, in between the h values for Li₂ and I₂ molecules..
32. L. C. Allen, J. Am. Chem. Soc., 1989, 111, 9011.
33. P. W. Ayers and R. G. Parr, personal communication..
34. The F₂ molecule is an exception, in fact. It is known that the force constant in the ground state of F₂ is smaller than that for Cl₂ and does not follow the trend observed for I₂, Br₂ and Cl₂. This is attributed to repulsive interaction of lone π electron pairs, which significantly weakens the F–F bond. It might also be that h computed by us for F₂ is subject to significant error..
35. H. G. Schmidt and G. Wolf, Solid State Commun., 1975, 16, 1085.
36. Superconductivity in metallic hydrogen at 230 ± 85 K has been theoretically predicted: T. W. Barbee III, A. Garcia and M. L. Cohen, Nature (London), 1989, 340, 369. However, metallic hydrogen has not been obtained so far at pressures up to 342 GPa: C. Narayana, H. Luo, J. Orloff and A. L. Ruoff, Nature (London), 1998, 393, 46..
37. It would be very interesting to check whether the σ_bond → σ_antibond LMCT states for (p,p) systems belong to the same family in Fig. 6 as the (s,s) and (s,p) ones..

---

Footnote

† For part 1, see ref. 1.

---