Highly distorted d⁸-rhodium(+I) and d¹⁰-rhodium(−I) complexes: synthesis, reactivity, and structures in solution and solid state

Abstract

A synthesis of the new ligand 5-diphenylphosphanyl-10-methyl-5H-dibenzo[a,d]cycloheptene (^metropp^ph) was developed in order to prepare highly distorted tetra-co-ordinated rhodium(+I) complexes. The ligand ^metropp^ph contains a cycloheptatriene ring in a rigid boat conformation such that a Ph₂P and an olefinic binding site are perfectly arranged for transition metal complexation. Four equivalents of ^metropp^ph react with [Rh₂(μ-Cl)₂(cod)₂] in the presence of KPF₆ to yield almost quantitatively [Rh(+I)(^metropp^ph)₂]PF₆, which was isolated in the form of dark red-violet crystals. A crystal structure analysis reveals that the co-ordination sphere of the rhodium centre in [Rh(+I)(^metropp^ph)₂]⁺ deviates strongly from a square planar arrangement (φ  =  42°). One methyl group in [Rh(+I)(^metropp^ph)₂]⁺ can be deprotonated by KOBu^t to give the allyl complex [Rh(^allyltropp^ph)(^metropp^ph)]. This complex has a structure that may be best described as a distorted trigonal bipyramid. The boron hydride [BEt₃H]⁻ and organolithium reagents, LiR, react with [Rh(^allyltropp^ph)(^metropp^ph)] in allylic alkylation reactions to yield anionic rhodate complexes [Rh(^RCH2tropp^ph)(^metropp^ph)]⁻ (R  =  H, Me, n-Bu, Ph) that formally have a d¹⁰ valence electron configuration. The rhodate [Rh(^metropp^ph)₂]⁻ can be obtained directly by reduction of cation [Rh(^metropp^ph)₂]⁺ with alkali metals. In a sym-proportionation reaction [Rh(^metropp^ph)₂]⁺ and [Rh(^metropp^ph)₂]⁻ give the neutral d⁹-[Rh(^metropp^ph)₂] radical (K  =  1.1 × 10⁷), which is not stable but decomposes with loss of H₂ to give the allyl complex [Rh(^allyltropp^ph)(^metropp^ph)]. The structures in solution of [Rh(^metropp^ph)₂]⁺, [Rh(^allyltropp^ph)(^metropp^ph)], and [Rh(^nBuCH2tropp^ph)(^metropp^ph)]⁻ were determined by NMR techniques, which reveal that (i) they match the solid state structures and (ii) are rather similar to each other. This fact may explain the remarkable electronic flexibility of the rhodium centre, which changes reversibly its formal oxidation state from + I to 0 to − I at rather low negative potentials (ΔE⁰¹  =  − 0.882 V; ΔE⁰²  =  − 1.298 V).

---

The chemistry of rhodium and iridium complexes in formally low oxidation states, that is 0 and − I, is comparatively little studied. In early works, strongly electron withdrawing ligands L like CO¹ and fluorophosphanes² were used for the synthesis of [ML₄]⁻ anions (M  =  Rh, Ir) with a formal d¹⁰ valence electron count on the metal. Only recently, the first stable rhodium and iridium d¹⁰-complexes with chelating phosphanes were prepared. ^{3a, 3b} The synthesis of stable monomeric d⁹-[ML₄] complexes was also only recently achieved. ^{3b, 4} These 17-electron complexes may have interesting properties as catalysts for the photolytic cleavage of water.⁵

We have designed tropylidenylphosphanes (tropp)⁶ as a new ligand system to allow the synthesis of stable rhodium^4a and iridium^4b complexes in their formal oxidation states 0 and − I. These complexes were completely characterised including X-ray analyses, which allowed us to study structural changes caused by the addition or abstraction of single electrons (see also ref. 3b). Furthermore, these [M(tropp)₂]^m complexes (M  =  Rh, Ir; m  =  + 1, 0, − 1) show very low redox potentials [M⁺¹/M⁰: − 1.0 V (M  =  Rh), − 0.97 V (M  =  Ir); M⁰/M⁻¹: − 1.2 V (M  =  Rh), − 1.4 V (M  =  Ir) [italic v]s. Ag/AgCl], which make them indeed potentially interesting as redox catalysts.

The vast structural data available for tetra-co-ordinated d⁸-rhodium(+I) complexes show these to be square planar, which is also supported by molecular orbital calculations.⁷ With the aim to provoke an even more anodic shift of the reduction potentials of rhodium tropp complexes, we wanted to prepare tetra-co-ordinated cationic rhodium(+I) compounds that are significantly distorted from their square planar configuration towards a tetrahedron.⁸ We expected that the ground state of the cation would be more destabilised than that of the product by such a distortion, leading to a lowering of the reduction potential. As will be seen later, this is not observed. However, we succeeded in the preparation of a strongly distorted tetra-co-ordinated rhodium complex and the chemistry of this compound and its derivatives is reported in this paper. In particular, the synthesis of a new substituted tropp ligand and a new method to prepare d¹⁰-rhodate complexes by nucleophilic attack on an allyl moiety co-ordinated to a rhodium(+I) centre are described.

Results and discussion

Synthesis of ^metropp^ph

The introduction of a methyl group into the olefinic unit of the central seven-membered ring of tropp, which co-ordinates to the metal centre, should increase the steric congestion and hence enforce a distorted co-ordination sphere. The synthesis of this new tropp ligand is outlined in Scheme 1. Starting from the readily available dibenzosuberenone 1, 10-bromo-5H-dibenzo[a,d]cyclohepten-5-one 2 was prepared by bromination of the double bond and subsequent HBr elimination.⁹ In the next step, the ketone functionality was protected by ketalisation using glycol in the presence of para-toluenesulfonic acid (pTosOH). In contrast to the literature procedure¹⁰ this conversion gave almost quantitatively compound 3. Reaction of 3 with excess Mg turnings in THF gave the corresponding Grignard reagent, which was reacted with an excess of methyl iodide. After addition of concentrated aqueous HCl and reflux for about 12 h, 10-methyl-5H-dibenzo[a,d]cyclohepten-5-one 4 was obtained in very good yield (90%) while the known procedure gave only 37% overall yield.¹⁰ The suberenone derivative 4 was reduced by modifying the literature procedure¹⁰ and then transformed into 5-chloro-10-methyldibenzo[a,d]cycloheptene 5. The addition of diphenylphosphine in toluene, followed by an aqueous work-up under basic conditions, led cleanly to the desired 5-diphenylphosphanyl-10-methyldibenzo[a,d]cycloheptene 6 as a racemic mixure of the R and S isomers in 86% isolated yield after recrystallisation from acetonitrile. Following our simplified nomenclature,^4,6 we name this ligand ^metropp^ph where the superscript in front (me) indicates substituents bonded to the C[double bond, length half m-dash]C bond of the seven-membered ring and the superscript at the end denotes the substituents bonded to phosphorus.

Scheme 1 Synthesis of ^metropp^ph.

Synthesis of d⁸-rhodium ^metropp^ph complexes

The ^metropp^ph ligand rac-6 reacts quantitatively with the chloro-bridged binuclear rhodium cyclooctadiene (cod) complex 7 at room temperature to give an orange methylene chloride solution that contains a mixture of all possible diastereomers of the rhodium complexes 8, as indicated by the ³¹P NMR data given below (Scheme 2). The isomers cis-C₂-8 and trans-C₂-8 contain a C₂ rotation axis, cis-meso-8 a mirror plane and trans-i-8 an inversion centre as symmetry elements and therefore each isomer should give rise to one ³¹P resonance signal split into a doublet by ¹⁰³Rh–³¹P coupling.

Scheme 2 Synthesis of the cationic rhodium bis(^metropp^ph) complex 9.

Indeed, in the ³¹P NMR spectrum recorded at room temperature only two exchange broadened doublets are seen, which upon cooling to − 70 °C split into four doublets [1: δ³¹P 110.3, ¹J(¹⁰³Rh³¹P)  =  212 Hz, 50%; 2: δ³¹P 110.0, ¹J(¹⁰³Rh³¹P)  =  209 Hz, 35%; 3: δ³¹P 109.4, ¹J(¹⁰³Rh³¹P)≈207 Hz, 10%; 4: δ³¹P 109.5, ¹J(¹⁰³Rh³¹P)≈207 Hz, 50%]. In an ¹H-NOESY NMR spectrum, it is seen that e[italic v]ery isomer does exchange with every other component. Regarding the different possible configurations of 8 in Scheme 2, apart from an intermolecular process [italic v]ia the solvated complex [RhCl(^metropp^Ph)S] A (S  =  CH₂Cl₂), an intramolecular process [italic v]iaB can explain the pair-wise exchange between cis-C₂-8 and trans-C₂-8 on one hand and cis-meso-8 and trans-i-8 on the other.¹¹ All other exchanges must proceed [italic v]ia intermolecular pathways on which intermediates A or higher nuclear complexes like C, which subsequently collapse to give all possible stereoisomers, may appear. Note that when [Rh₂(μ-Cl)₂(cod)₂] 7 is added, it also exchanges with all other components although none of the mixed dimer [Rh₂(μ-Cl)₂(tropp^ph)(cod)] was directly observed. We did not assign the NMR signals to the different isomers nor determine the isomeric distribution. Crystals of 8 suitable for an X-ray analysis were not obtained. Note that in this context, the structure of [Rh₂(μ-Cl)₂(tropp^ph)₂] containing the unsubstituted tropp^ph ligand was determined earlier and the major isomer showed the two phosphorus atoms in a cis arrangement.¹² When 8 is dissolved in a co-ordinating solvent like THF or MeCN, only one broadened ³¹P resonance is observed at 103.5 ppm [¹J(¹⁰³Rh³¹P)  =  203 Hz].

Even when a large excess of rac-6 is reacted with 7 at elevated temperatures, no bis(^metropp^ph) type complexes are formed, in contrast to reactions with the non-methyl-substituted ligand tropp^ph, for which [RhCl(tropp^ph)₂] is obtained.^{4a, 12} However, when potassium hexafluorophosphate, KPF₆, is added to an acetonitrile solution of 8, the dark red-violet bis(^metropp^ph) complex 9 forms. Complex 9 is obtained in about 86% isolated yield; it is soluble in CH₂Cl₂ and acetonitrile but poorly soluble in THF. It can be crystallised by layering CH₂Cl₂ or CH₃CN solutions with n-hexane. In solution, exclusively one isomer can be detected by NMR spectroscopy. The ¹⁰³Rh–³¹P coupling constant [¹J(¹⁰³Rh³¹P)  =  192 Hz is indicative of a cis isomer whereas the trans isomer [¹J(¹⁰³Rh³¹P)  =  132 Hz] is predominant (80%) in solutions of the [Rh(tropp^ph)₂]⁺ cation.⁴

Interestingly, some of the protons of the annelated benzo groups and the phenyl substituents bonded to the phosphorus centres within each ^metropp^ph ligand show quite distinct ¹H NMR signals in comparison to the uncomplexed ligand. For the ortho phenyl protons a (δ  =  5.50) and b (δ  =  7.65) (Fig. 1) in particular, this difference is significant and amounts to 2.15 ppm. It should be noted that this large difference is observed not only for the ortho protons but also for the entire phenyl rings. Indeed, for the latter, a remarkably different shielding is observed as a consequence of the conformation and arrangement of the phenyl substituents with respect to each other and to the benzo groups of the cycloheptatriene unit. A NMR determination of the three-dimensional solution structure reveals that one phenyl ring defines a plane with the Rh–P bond vector. This brings the ortho protons a into a deshielding region (indicated by x in Fig. 1) due to the magnetic anisotropy of the rhodium nucleus. The latter is caused by the d_z²-type orbital at Rh(+I), which induces an unusually high frequency. On the other hand, the NOE between the PCH proton and the ortho protons b is remarkably weak, consistent with a dihedral angle between the corresponding phenyls of ca. ± 90° with respect to the Rh–P bond. In this conformational arrangement, the protons b are subject to a two-fold shielding anisotropy effect: (i) intraligand (y₁) due to the neighbouring benzo group of the tropylidene unit and (ii) interligand (y₂) due to a parallel arrangement of equivalent phenyl rings on each ligand in such a way that the protons of one ring lie in the shielding region of the other.

Fig. 1 Schematic representation of the cation of complex 9. a and b denote the set of different ortho-phenyl protons on each P centre. For a detailed picture of the structure see Fig. 2.

We have no evidence for the formation of penta co-ordinated [Rh(tropp)₂L]⁺ complexes (L  =  MeCN or THF) even though such species are formed with sterically less encumbered tropp-type ligands.^4c Indeed, the exclusive formation of the chiral (C₂ symmetry) R,R and S,S isomers, respectively, was established by an X-ray analysis ([italic v]ide infra). The meso isomer is not observed, probably because of even higher steric congestion, which prevents its formation. In the ¹⁰³Rh NMR spectrum of a CH₂Cl₂ solution of 9, one sharp resonance signal (triplet) at + 162 ppm is observed, which is typical for 16-electron rhodium tropp complexes.

Structure of [Rh(^metropp^ph)₂]PF₆·2CH₃CN (9)

The salt [Rh(^metropp^ph)₂]PF₆9 crystallises with two crystallographically independent pairs of enantiomers in the unit cell. All bonds and angles are equal within the limits of experimental accuracy and we discuss therefore only one of the two cations. Additionally, two acetonitrile molecules are included, which have no close contact with the rhodium centre. Further crystallographic details are given in Table 1, selected bond lengths and angles are listed in Table 2. In Fig. 2, an ORTEP 3 plot¹³ of the cation of 9 is shown.

Table 1 Crystallographic data of compounds 9 and 10

9	10
Chemical formula	C58H49F6NP3Rh	C55.5H45.40Cl1.50P2Rh
Formula weight	1069.80	942.45
Crystal system	Triclinic	Orthorhombic
Space group	P1̄	C2/c
a/Å	10.844(2)	45.90(5)
b/Å	20.697(4)	10.159(10)
c/Å	22.722(5)	19.773(19)
α/°	91.629(13)	90
β/°	91.462(13)	102.27(8)
γ/°	101.890(12)	90
U/Å^3	4985.7(17)	9009(16)
Z	4	8
T/K	293(2)	293(2)
μ/mm^−1	0.501	4.842
Reflections collected	28990	4804
Independent reflections	14653 [R(int)  =  0.0378]	4620 [R(int)  =  0.0428]
Final R indices [I>2σ(I)]
R1	0.036	0.046
wR2	0.072	0.113

---

Table 2 Selected bond lengths (Å) and angles (°) of the two crystallographically independent cations of 9

Rh1–P1	2.226(1)	Rh1b–P1c	2.212(1)
Rh1–P1a	2.260(1)	Rh1b–P1b	2.266(2)
Rh1–C5	2.337(4)	Rh1b–C5c	2.341(4)
Rh1–C4	2.362(4)	Rh1b–C4c	2.381(4)
Rh1–C5a	2.404(4)	Rh1b–C5b	2.401(4)
Rh1–C4a	2.451(4)	Rh1b–C4b	2.508(4)
P1–C17	1.818(5)	P1b–C23b	1.812(5)
P1–C23	1.819(4)	P1b–C17b	1.839(4)
P1–C1	1.878(4)	P1b–C1b	1.874(4)
C4–C5	1.372(6)	C4b–C5b	1.373(6)
P1a–C23a	1.825(5)	P1c–C23c	1.817(4)
P1a–C17a	1.830(4)	P1c–C17c	1.819(4)
P1a–C1a	1.858(4)	P1c–C1c	1.872(4)
C4a–C5a	1.380(6)	C4c–C5c	1.375(6)
P1–Rh1–P1a	94.18(4)	P1c–Rh1b–P1b	93.44(4)
P1–Rh1–C5	90.2(1)	P1c–Rh1b–C5c	90.8(1)
P1A–Rh1–C5	166.7(1)	P1b–Rh1b–C5c	169.8(1)
P1–Rh1–C4	90.1(1)	P1c–Rh1b–C4c	89.7(1)
P1a–Rh1–C4	133.3(1)	P1b–Rh1b–C4c	136.8(1)
C5–Rh1–C4	34.0(1)	C5c–Rh1b–C4c	33.8(1)
P1–Rh1–C5a	167.0(1)	P1c–Rh1b–C5b	164.1(1)
P1a–Rh1–C5a	89.7(1)	P1b–Rh1b–C5b	89.2(1)
C5–Rh1–C5a	88.8(1)	C5c–Rh1b–C5b	89.3(1)
C4–Rh1–C5a	96.2(1)	C4c–Rh1b–C5b	99.1(1)
P1–Rh1–C4a	134.5(1)	P1c–Rh1b–C4b	131.8(1)
P1a–Rh1–C4a	89.3(1)	P1b–Rh1b–C4b	89.8(1)
C5–Rh1–C4a	96.6(2)	C5c–Rh1b–C4b	94.3(2)
C4–Rh1–C4a	119.3(2)	C4c–Rh1b–C4b	119.1(1)
C5a–Rh1–C4a	33.0(1)	C5b–Rh1b–C4b	32.4(1)
C17–P1–C23	102.6(2)	C23b–P1b–C17b	104.2(2)
C17–P1–C1	102.8(2)	C23b–P1b–C1b	99.6(2)
C23–P1–C1	101.6(2)	C17b–P1b–C1b	103.3(2)
C17–P1–Rh1	125.0(1)	C23b–P1b–Rh1b	110.7(1)
C23–P1–Rh1	111.8(1)	C17b–P1b–Rh1b	125.8(1)
C1–P1–Rh1	110.3(1)	C1b–P1b–Rh1b	110.1(1)
C23a–P1a–C17a	105.4(2)	C23c–P1c–C17c	106.9(2)
C23a–P1a–C1a	101.8(2)	C23c–P1c–C1c	100.7(2)
C17a–P1a–C1a	102.6(2)	C17c–P1c–C1c	103.3(2)
C23a–P1a–Rh1	110.2(1)	C23c–P1c–Rh1b	110.7(1)
C17a–P1a–Rh1	124.6(1)	C17c–P1c–Rh1b	122.6(1)
C1a–P1a–Rh1	109.8(1)	C1c–P1c–Rh1b	110.3(1)

---

Fig. 2 Molecular structure of one of the crystallographically independent cations of 9. Hydrogen atoms are omitted for clarity. Selected bond lengths and angles are given in Table 2.

The two phosphorus centres occupy the cis positions if an idealised square planar conformation is taken into consideration. However, the co-ordination sphere of the rhodium centre is strongly distorted towards a tetrahedron. The angle φ between the two planes that run through each phosphorus centre, the rhodium centre and the midpoint of each of the metal-bound C[double bond, length half m-dash]C bonds amounts to 42°. Hence, the co-ordination is halfway between a square plane (φ  =  0°) and a tetrahedron (φ  =  90°) and is to our knowledge the second strongest deviation observed to date for tetra-co-ordinated d⁸-rhodium complexes.⁸ While the Rh–P distances [mean 2.241(1) Å; max. difference Δ: 0.054 Å] lie within the usual range (≈2.30 Å),¹⁴ the steric congestion is more clearly seen in the unusually long Rh–C distances [mean: Rh–C4: 2.426(4) Å, Δ  =  0.066 Å; Rh–C5: 2.371(4) Å, Δ  =  0.146 Å], which are about 0.24 Å longer than the usually observed bond lengths (≈2.15 Å).¹⁴ The variation of the individual Rh–P or Rh–C4/C5 bonds expressed by the difference Δ between the shortest and longest bond is also considerable.¹⁴ The co-ordinated C[double bond, length half m-dash]C bonds [mean: 1.375(6) Å] are not very elongated when compared to the free ligand.⁶ The sum of bond angles around the carbon centre C4 shows only a weak pyramidalisation (by less than 4°), indicating only a weak d → p(π) back donation from the metal centre to the C[double bond, length half m-dash]C unit.

Synthesis of the allyl complex [Rh(^allyltropp^ph)(^metropp^ph)] (10)

When potassium tert-butoxide is added to a solution of R,R-9 (S,S-9) in THF (Scheme 3) an immediate colour change from deep red to intense orange occurs and 10, 10′ are formed quantitatively.

Scheme 3 Synthesis of the allyl complex 10 and allylic alkylation giving 12a–d.

In the reaction solution, only two products are observed by ³¹P NMR in a ca. 28:1 ratio, showing each signal as a doublet of doublets [major: δ ³¹P 88.0, ¹J(¹⁰³Rh³¹P)  =  172.0 Hz, 79.0 ¹J(¹⁰³Rh³¹P)  =  159 Hz; 91.7 ¹J(¹⁰³Rh³¹P)  =  168 Hz, 81.4 ¹J(¹⁰³Rh³¹P)  =  158 Hz]. The very similar chemical shifts and coupling constants observed suggest the formation of two structurally related isomers.

Recrystallisation from CH₂Cl₂–n-hexane gave complex 10 in almost quantitative yield. The structure was determined by an X-ray analysis (Fig. 4) and we reasonably assume that this structure corresponds to the major isomer 10 (see Scheme 3) observed in solution. However, when pure re-crystallised 10 is dissolved in CH₂Cl₂, both isomers are again found in the same ratio (28:1). Because of the similarity of the ³¹P NMR data, we assign to the minor component 10′ a structure in which the intact ^metropp^ph ligand has rotated by 180° when compared to the major product. Consequently, the methyl group points towards the CH₂ terminus of the allyl moiety as shown in Scheme 3. For this isomerisation, an interesting possibility would have consisted of an intra-molecular deprotonation of the methyl substituent of one tropp ligand by the allyl group of the other. However, 2D-NOESY spectra show no cross-peaks for the corresponding protons and hence give no indication for such a phenomenon.

Most informative are the heteronuclear correlations. For the ¹⁰³Rh–¹H HMQC (heteronuclear multiple quantum coherence) NMR data of rhodium ^metropp^ph complexes, the three expected ¹⁰³Rh–¹H cross-peaks per inequivalent ligand are found for the protons of the PCH and the olefinic H and Me group. However, there is an additional cross-peak for 10, indicating the formation of a CH₂ unit with diastereotopic protons rather than an additional Me group. The low frequency ¹⁰³Rh shift (δ  =  −370) is consistent with the formulation of an η³-allyl moiety. This is further confirmed by the ¹³C, ¹H one- and multiple-bond correlations showing a tertiary C⁵H, quaternary C⁴ and secondary C¹⁶H₂ with δ  =  61.7, 103.0 and 58.1, respectively (see Fig. 3). Such values are typically encountered for η³-allyl groups.

Fig. 3 Schematic representation of 10 illustrating two- and multiple-bond correlations.

After having identified some structural features of the complex, we now turn to an analysis of the solution structure. As such, the two-bond coupling constants between ligand atoms are the most valuable tool in the determination of the configuration at the rhodium centre. In this respect, ²J(³¹P³¹P)  =  29 Hz indicates a cis arrangement of the P1 and P1a centres. Within the constraints of an assumed trigonal bipyramid, this means that either both phosphorus are equatorial or one is equatorial and the other one axial. Placing the ^allyltropp ligand with its P¹ centre in an axial position brings both allyl termini C⁵ and C¹⁶ in equatorial positions. Hence, the angle between these two carbon atoms and the P^1a nucleus of the ^metropp would have similar values. However, this is in contrast to the observed coupling constants ²J(³¹P¹³C) of 41.8 and 11.0 Hz for the CH and CH₂ carbons, respectively. Indeed, the former value indicates a transoid arrangement. Accordingly, the allyl C⁵H carbon is most probably located in an axial position trans to the P^1a centre of the ^metropp ligand. Consequently, the allyl C¹⁶H₂ and the olefinic bond are equatorial. A retention of the chirality of the ligands requires that the angle C^5a–Rh–P¹ be larger than C^4a–Rh–P¹. This is indeed reflected by the larger coupling constant values [²J(³¹P¹³C)  =  21.8 Hz] for the C^5aH carbon relative to the C^4aMe [²J(³¹P¹³C)  =  10.3 Hz].

The NOE results are fully consistent with these results, the olefinic H at C^5a is close to both anti protons H^a of the allyl moiety, whereas the syn proton H^s shows a short separation to the ortho proton of the in-plane phenyl group attached to the intact ^metropp^ph ligand. On the basis of the NMR data, with the exception of phenyl ring flips (rather than rotations), the solution structure can be assumed as being quite static, showing no indication of the dynamic behaviour often encountered in allyl and penta co-ordinated organometallic chemistry.

The allyl complexes 10,10′ do not react with water or alcohol and resists treatment with diluted acetic acid. However, when stronger acids like HO₂CCF₃, aqueous HPF₆, or HBF₄ are added, a clean re-protonation occurs and the cationic complex 9 is reformed quantitatively.

Structure of [Rh(^allyltropp^ph)(^metropp^ph)] (10)

An ORTEP 3 plot of the structure of 10 is shown in Fig. 4. Crystallographic details are given in Table 1, selected bond lengths and angles are listed in Table 3. The rhodium centre lies within a highly distorted co-ordination sphere, which we describe here as trigonal pyramidal where P1a, C5 occupy the axial positions (P1a–Rh1–C5 159.8°) and the olefinic unit C4a[double bond, length half m-dash]C5a, P1, and C16 the equatorial positions.

Fig. 4 Molecular structure of 10. Hydrogen atoms are omitted for clarity. Selected bond lengths and angles are given in Table 3.

Table 3 Selected bond lengths (Å) and angles (°) of 10

Rh1–C4	2.168(4)	P1–C23	1.839(5)
Rh1–C5a	2.203(5)	P1–C1	1.889(4)
Rh1–C5	2.208(4)	P1a–C17a	1.839(4)
Rh1–P1a	2.278(2)	P1a–C23a	1.843(5)
Rh1–C16	2.293(6)	P1a–C1a	1.879(4)
Rh1–C4a	2.295(4)	C4–C5	1.437(6)
Rh1–P1	2.341(2)	C4a–C5a	1.424(6)
P1–C17	1.823(5)
C4–Rh1–C5a	109.1(2)	C5–Rh1–P1	88.9(1)
C4–Rh1–C5	38.3(2)	P1a–Rh1–P1	101.0(1)
C5a–Rh1–C5	90.6(2)	C16–Rh1–P1	122.0(1)
C4–Rh1–P1a	123.2(1)	C4a–Rh1–P1	111.6(1)
C5a–Rh1–P1a	90.4(1)	C17–P1–C23	102.0(2)
C5–Rh1–P1a	159.8(1)	C17–P1–C1	99.4(2)
C4–Rh1–C16	37.0(2)	C23–P1–C1	100.3(2)
C5a–Rh1–C16	86.5(2)	C17–P1–Rh1	121.0(2)
C5–Rh1–C16	64.1(2)	C23–P1–Rh1	122.7(1)
P1a–Rh1–C16	95.9(1)	C1–P1–Rh1	107.3(1)
C4–Rh1–C4a	135.0(2)	C17a–P1a–C23a	100.2(2)
C5a–Rh1–C4a	36.8(2)	C17a–P1a–C1a	101.0(2)
C5–Rh1–C4a	100.9(2)	C23a–P1a–C1a	103.8(2)
P1a–Rh1–C4a	91.9(1)	C17a–P1a–Rh1	121.9(1)
C16–Rh1–C4a	122.8(2)	C23a–P1a–Rh1	119.1(2)
C4–Rh1–P1	90.1(1)	C1a–P1a–Rh1	108.2(2)
C5a–Rh1–P1	147.4(1)

---

The intersection of the plane defined by P1a, Rh1 and the midpoint of the C4a[double bond, length half m-dash]C5a unit and the P1–Rh1–C4 plane, gives an angle φ of 78°. The phosphorus rhodium distances [Rh–P1 2.341(2); Rh–P1a 2.278(2) Å] fall within the expected range, while the olefinic [Rh1–C5a 2.203(5); Rh1–C4a 2.295(4) Å] and the allylic [Rh1–C5 2.208(4); Rh1–C4 2.164(4); Rh1–C16 2.293(6) Å] bond lengths are longer than usually observed. Both the C[double bond, length half m-dash]C and the allyl group are unsymmetrically bound to the rhodium centre (Δ_Rh–C≈0.09 Å). However, the almost equal C–C bond lengths [C4–C5 1.437(6); C4–C16 1.421(6) Å] within the allyl moiety, when compared to the corresponding distances in the intact ^metropp^ph ligand [C4a–C5a 1.424(6); C4a–C16a 1.513(7) Å], clearly indicate the η³ binding mode. An alternative possibility would have been a σ(η¹),π(η²)-enyl mode in which the CH₂ group is σ-bonded and the C[double bond, length half m-dash]C unit π-bonded to the rhodium centre (see, however, ref. 15b). Also, the sum of bond angles at C4 (360°) when compared to C4a (353.3°) is in line with the η³-description of the allyl group.

In summary, it can be concluded that the solution structure of 10 and its solid state structure ([italic v]ide infra) are very closely related.

Synthesis of d¹⁰-rhodate complexes

The nucleophilic attack on co-ordinated allyl groups has been widely studied, in particular for cationic 16-electron palladium complexes, [Pd(C₃R₅)L₂]⁺.¹⁶ Little is known about the corresponding reaction of isoelectronic but neutral rhodium complexes. In recent work, it was shown that rhodium complexes of the Wilkinson type prepared in situ from [RhCl(PPh₃)₃] and P(OR)₃ may have an interesting synthetic potential as catalysts for allylic alkylation reactions.¹⁵ However, it was proposed that π(η³)-allyl intermediates are not the reactive species but rather a σ(η¹),π(η²)-enyl complex with a formal oxidation state of + III on the rhodium centre.^15b

In this context, the reaction of the rhodium(+I) complex 10 with various nucleophiles LiR 11a–d was particularly interesting (Scheme 3). Note that 10 is within formal concepts an electronically saturated 18-electron metal complex in which the η³-coordination mode of the allyl moiety is clearly established. In view of the vast literature available on the nucleophilic attack on 16-electron complexes, which are mostly cationic, this reaction seemed not that evident with the neutral 18-electron complex 10. However, in all cases the nucleophile attacks the CH₂ terminus of the co-ordinated allyl moiety and the d¹⁰-rhodate complexes 12a–d are formed. The syntheses of 12a and 12c proceeded even at room temperature within less than 5 min. The two complexes were isolated as highly oxygen- and water-sensitive deep burgundy-red micro-crystalline substances. The formation of the compounds 12b and 12d is slow and these could only be characterised by NMR spectroscopy in solution. Other nucleophiles like amides, alcoholates, or thiolates did not react. During these reactions, the formal valence electron count does not change—all complexes are 18-electron species—and the formal oxidation state of the rhodium centre is diminished from + I to − I. Consequently, the rhodate complex 12a could also be prepared from the cationic d⁸-rhodium complex 9 by two-electron reduction with elemental lithium, sodium or potassium in THF. Unfortunately, we did not succeed in growing crystals suitable for an X-ray analysis of one of these compounds.

All complexes show fairly complex NMR spectra and as an example, complex 12c was carefully investigated by various techniques. For this molecule the solution structure can be determined unambiguously as there is not a single atom related to any other by symmetry. A complete assignment of the ¹⁰³Rh, ³¹P, ¹³C, and ¹H resonances was possible on the basis of ¹⁰³Rh–¹H, ³¹P–¹H and ¹³C–¹H one- and multiple-bond correlations in combination with ¹H–¹H TOCSY and NOESY measurements. Subtle effects, such as chirality of the ligand, phenyl ring orientations and pentyl side chain conformations could all be determined. With respect to the former two points, it turns out that: (i) both ligands in 12c have the same absolute configuration and (ii) the phenyl ring orientations are as already discussed for 9. The interligand relationship is interesting because it determines the structure around the central rhodium atom. Starting from a tetrahedral situation (see A in Fig. 5), one expects to have the olefinic protons close to each other and to the ortho protons of the adjacent arene ring of the bis(benzo)cycloheptatriene. However, this is clearly not the case as can be seen from Fig. 6. In fact, the distances a₁ between the olefinic proton on the ^pentyltropp^ph ligand group and the methyl group and from the latter to the olefinic proton of the ^metropp^ph ligand, a₂, seem to be quite similar. A similar short triangulation, b₁, b₂, to the olefinic proton and one arene proton of the opposing ^metropp^ph ligand is seen for one of the diastereotopic methylene H of the CH₂ pentyl group directly linked to the central seven-membered ring. This indicates a situation (B) where the tetrahedron is strongly distorted towards a square planar arrangement. Indeed, the structure found for the Rh(+I) compound 9 fits exceptionally well with the constraints of the NOE data.

Fig. 5 Schematic representation of two possible structures of 12c in solution. (A) tetrahedral structure; (B) distorted planar structure resembling closely the one of 9. The HH distances a₁, a₂, b₁, and b₂ are indicated by dotted lines.

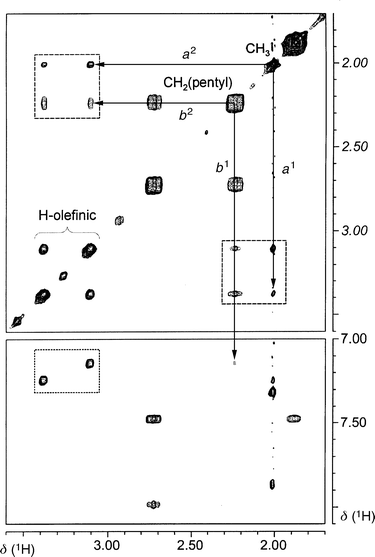Fig. 6 Contour plots of sections from the 2D NOESY spectrum (400.13 MHz, τ_mix  =  600 ms) recorded for 12c. The dotted box in the lower part shows two cross-peaks due to intra-ligand NOEs between the two olefinic protons and adjacent ortho-protons of the benzoheptene moiety. Note that cross-peaks in the opposite corners of the box stemming from the inter-ligand NOEs expected for a regular tetrahedral structure are absent. The dashed boxes in the upper part of the spectrum show cross-peaks of similar intensity from each of the two olefinic protons to the methyl and to one of the diastereotopic methylene protons of the pentyl group. These observations are in agreement with the distorted structure described in the text.

In the ¹⁰³Rh spectra of 12a, a triplet centered at δ  =  − 344 is observed. Complex 12c shows a doublet of doublets at δ  =  −325. Both chemical shifts fall within the same range as the one found for the allyl complex 10 while 16-electron rhodium tropp complexes like 9 show resonances shifted about 500 ppm to higher frequencies.

Electrochemical investigations and observation of the d⁹-rhodium tropp complex

In previous work, we have shown that the tropp^ph ligand stabilises rhodium and iridium complexes in their formally low oxidation states.⁴ In particular, the redox potentials M⁺¹/M⁰ and M⁰/M⁻¹ are considerably lowered (up to 1 V) when compared to reported systems.¹⁷ We expected that the highly tetrahedrally distorted cation d⁸-[Rh(^metropp^ph)₂]⁺ in 9 would be reduced to the corresponding d⁹ and d¹⁰ valence states at even lower potentials ([italic v]ide supra). The cyclic voltammogram of 9 in THF solution (1 × 10⁻³ M) containing 0.25 mol n-Bu₄NPF₆ as electrolyte at room temperature is shown in Fig. 7. Using a scan rate of 100 mV s⁻¹, two almost reversible redox waves at − 0.882 V (ΔE_red/ox¹  =  82 mV) and − 1.298 V (ΔE_red/ox²  =  85 mV) are recorded (potentials [italic v]s. Ag/AgCl; reference: ferrocene/ferrocenium). The first wave corresponds to the redox couple [Rh(^metropp^ph)₂]⁺(9)/[Rh(^metropp^ph)₂] (13), the second to the couple 13/[Rh(^metropp^ph)₂]⁻(12a) (Scheme 4).

Fig. 7 Cyclic voltammograms of 9 measured in THF (20 °C); scan rate: 100 mV s⁻¹; E [italic v]s. Ag/AgCl.

Scheme 4 Disproportionation and decomposition of d⁹-[Rh(^metropp^ph)₂] 13.

From the ΔE of the two redox processes, the formation constant K_f of the reaction 9 + 12a⇋2 13 was calculated to be 1.1 × 10⁷ at 298 K. Indeed, this reaction is the most convenient way to prepare 13 (see Scheme 4). However, the rhodium(0) complex 13 is not stable but decomposes cleanly—formally with loss of H₂—at room temperature in about one week, in 15 min at 70 °C, by a yet unclarified pathway to the allyl complex 10.

Despite the strong distortion of the cation [Rh(^metropp^ph)₂]⁺ in 9, the first reduction to the neutral complex 13 shifts only about 0.12 V to less negative potentials when compared to that of the sterically less encumbered cation [Rh(tropp^ph)₂]⁺, which has a square planar co-ordination sphere.^4a The second reduction appears at about the same potential as that of this latter complex (only a slight cathodic shift of about − 0.08 V is observed). These experiments clearly show that a distortion of about 40° is not sufficient to cause a significant anodic shift of the reduction potential in this type of rhodium complexes. Furthermore, the electron-donating effect of the methyl group¹⁸ may partly counterbalance the diminution of the first redox potential induced by the geometric distortion.

Conclusions

A high yield synthesis of a sterically demanding new tropylidene phosphane, ^metropp^ph, was developed. This ligand allowed the preparation of the tetra-co-ordinated cationic rhodium complex 9, which is obtained as a racemic mixture of the chiral R,R and S,S enantiomers exclusively. The cation 9 shows a deep red-violet colour in contrast to the bright red-orange colour usually observed for tetra-co-ordinated cationic d⁸-rhodium complexes. The co-ordination sphere deviates strongly from planarity with φ  =  42° being almost precisely between a square plane (φ  =  0°) and a tetrahedron (φ  =  90°). Comparable distorted structures were also determined for the neutral d⁹-[M(tropp^ph)₂] complexes (M  =  Rh, Ir) and anionic d¹⁰-[M(tropp^ph)₂]⁻ compounds, the parent cationic complex d⁸-[M(tropp^ph)₂]⁺ being planar.⁴

Unfortunately, the expected shift to less negative potentials for the reduction of the d⁸-rhodium(+I) to d⁹-rhodium(0) state is not observed. The latter complex, d⁹-[Rh(^metropp^ph)₂] 13, characterised by its deep green colour, is less stable compared to the sterically less encumbered complex d⁹-[Rh(tropp^ph)₂] and decomposes with formal loss of H₂ to the allyl complex [Rh(^allyltropp^ph)(^metropp^ph)] 10. This allyl complex may be prepared more conveniently in almost quantitative yield from cation 9 and KOBu^t. Despite the electronic saturation of 10 (18 valence electrons), nucleophilic attack by lithium organyls, LiR, cleanly afforded new anionic rhodate complexes d¹⁰-[Rh(^RCH2tropp^ph)(^metropp^ph)]⁻12a–c in which the R group has been incorporated into the former methyl group of one ^metropp^ph ligand.

The structures of 9, 10 and 12c were determined in solution by NMR techniques. All complexes are remarkably rigid; even the phenyl groups seem to be locked into specific conformations. The solid state structures of cation 9 and of the allyl complex 10 are fully confirmed in solution as well. Furthermore, it could be demonstrated that the anionic complex 12c must have a structure in solution very close to the one of cation 9, that is a structure deviating considerably from the tetrahedral one that is expected for a tetra-co-ordinated d¹⁰-metal centre. In summary, there is only relatively little structural change between 9, 10 and 12. This may explain some of their properties, such as low redox potentials or facile nucleophilic attack on the allyl moiety, reactions by which the formal oxidation state of the rhodium centre is changed. Obviously the steric constraints imposed by the tropp-type ligands make the complexes sterically rigid but the metal centres electronically flexible.

Experimental

General methods

NMR spectra were taken on a Bruker DPX Avance Series 250–400 MHz. ¹H- and ¹³C-chemical shifts are calibrated against the solvent signal (CDCl₃: ¹H-NMR: 7.27 ppm; ¹³C-NMR: 77.23 ppm; CD₂Cl₂: ¹H-NMR: 5.32 ppm; ¹³C-NMR: 54.00 ppm; THF-d8: ¹H-NMR: 3.58 ppm; ¹³C-NMR: 67.57 ppm). ³¹P chemical shifts are calibrated against 85% H₃PO₄ as external standard. ¹⁰³Rh-NMR spectra are referenced to Ξ  =  3.16 MHz, where TMS appears at exactly 100.000000 MHz. ¹⁰³Rh–¹H, ¹³C–¹H correlations were measured using standard HMQC and HMBC (heteronuclear multiple bond coherence) methods, ³¹P–¹H 2D spectra using the COSY method with ¹H detection, ¹H–¹H TOCSY with MLEV 17 mixing and the ¹H–¹H NOESY with a mixing time of 600 ms. All NMR spectra were measured at ambient temperature. Cyclic voltammograms were acquired with an EG&G potentiostat model 362. UV/Vis spectra were recorded on a Perkin Elmer UV/Vis/NIR-spectrometer Lambda 19 and mass spectra on a Finnigan MAT SSQ 7000 (EI: 70 eV). All chemicals were used as purchased from Aldrich or Fluka, solvents were purified and dried following standard procedures. 10-Bromo-5H-dibenzo[a,d]cyclohepten-5-one 2 was prepared following a literature procedure.⁹

Crystallographic analysis of 9 and 10

The data sets for the single-crystal X-ray studies were collected on a Stoe Image Plate System (9) or a fully automated Siemens-Stoe AED2 four-circle diffractometer (10). All calculations were performed using the SHELXS-86 and SHELXS-93 program suites. The specific data for the crystals and refinements are collected in Table 1.

CCDC reference number 440/204. See http://www.rsc.org/suppdata/nj/b0/b002906h/ for crystallographic files in .cif format.

Synthesis of compounds

10-Bromo-5,5-ethylenedioxy-5H-dibenzo[a,d]cycloheptene (3). To bromoketone 2⁹ (14.2 g, 50 mmol) in benzene (250 ml), ethylene glycol (50 ml) and para-toluenesulfonic acid (1.0 g) were added and the resulting mixture was heated at reflux for 3 days using a Dean–Stark apparatus. After cooling, triethylamine (10 ml) and then water (500 ml) were added. After separation of the organic phase, the aqueous phase was extracted three times with methylene chloride (100 ml). Drying over sodium sulfate and removal of the solvent provided crude 3 (16.3 g), which was subjected to sublimation at 150 °C (0.05 mbar) to yield 15.9 g (97%) of colourless needles. Mp: 172 °C (lit:¹⁰ 172–173 °C). ¹H-NMR (CDCl₃, 300 MHz): δ  =  8.03–7.97 (m, 1 H, CH_ar), 7.88–7.82 (m, 2 H, CH_ar), 7.73 (s, 1H, [double bond, length half m-dash]CH), 7.44–7.28 (m, 5 H, CH_ar), 4.27–4.15 (m, 2 H, CH₂exo), 3.83–3.70 (m, 2 H, CH₂endo). ¹³C-NMR (CDCl₃, 75.4 MHz): δ  =  139.3 (C_qar), 138.9 (C_qar), 133.7 (CH_ar), 132.7 (C_qar), 132.3 (C_qar), 130.3 (CH_ar), 129.4 (CH_ar), 128.8 (CH_ar), 128.2 (CH_ar), 127.9 (CH_ar), 127.7 (CH_ar), 124.7 ([double bond, length half m-dash]CBr), 123.8 (CH_ar), 106.0 ([double bond, length half m-dash]CH), 65.0 (CH₂endo), 64.4 (CH₂exo).

10-Methyl-5H-dibenzo[a,d]cycloheptene-5-one (4). A solution of 3 (8.5 g, 26 mmol) in dry THF (150 ml) was slowly dropped into a suspension of magnesium turnings (2.5 g, 100 mmol), activated with a small amount of iodine, in dry THF (100 ml). After complete addition, the deep red solution was held at 50 °C for 3 h. Excess magnesium was removed by filtration and the Grignard solution was treated with methyl iodide (3.1 ml, 7.1 g, 50 mmol). After overnight stirring, the reaction mixture was evaporated to dryness. The residue was taken up in THF (200 ml), filtered and diluted with 6 N aqueous hydrochloric acid (100 ml). After heating at reflux for 12 h the reaction mixture was neutralized with 20% sodium hydroxide and extracted several times with ethyl acetate. The combined organic phases were dried over sodium sulfate and evaporated to yield the crude ketone 4. After distillation, the product was obtained as a colourless oil, which crystallised upon storage at room temperature (5.2 g, 91%). Analytical data correspond to published data.¹⁰

5-Chloro-10-methyl-5H-dibenzo[a,d]cycloheptene (5). To a vigorously stirred suspension of 4 (4.4 g, 20 mmol) in methanol (200 ml), a solution of sodium borohydride (760 mg, 20 mmol) and potassium hydroxide (560 mg, 10 mmol) in water (2 ml) was added at once. After 2 h of stirring, a clear solution was obtained, which was evaporated to dryness. The residue was partitioned between water and methylene chloride, the organic phase separated, dried over sodium sulfate and concentrated. Addition of hexane precipitated the alcohol as colourless crystals (4.30 g, 19.4 mmol, 97%). After filtration and drying, the residue was taken up in dry toluene (50 ml) and treated dropwise with freshly distilled thionyl chloride (4.0 ml, 6.08 g, 51 mmol) at 0 °C. After overnight stirring, the solvent was removed in [italic v]acuo to yield a slightly brownish oil, which crystallised upon layering with a small amount of diethyl ether (5, 4.41 g, 91% from 4). Compound 5 is obtained as a mixture of exo and endo isomers. Mp: 72 °C. MS m/z: 242 (M⁺, 5%), 240 (M⁺, 8%), 205 (10-methyl-5H-dibenzo[a,d]tropylium⁺,100%). ¹H-NMR (CDCl₃, 300 MHz): δ  =  6.24 (s, 1 H, CHCl_maj), 5.60 (s, 1 H, CHCl_min), 2.59 (s, 1 H, CH_3maj), 2.53 (s, 1 H, CH_3min). ¹³C-NMR (CDCl₃, 75.4 MHz): δ  =  138.1, 137.2, 137.1, 136.6, 134.9, 132.8, 131.5, 129.9, 129.5, 129.0, 128.8, 128.6, 128.55, 128.4, 128.35, 128.3, 128.2, 127.8, 127.6, 127.55, 127.5, 127.0, 126.7, 126.4, 125.3 ([double bond, length half m-dash]CH_min), 125.2 ([double bond, length half m-dash]CH_maj), 123.3, 123.0, 67.4 (CHCl_maj), 61.1 (CHCl_min), 25.0 (CH_3maj), 24.3(CH_3min).

5-Diphenylphosphanyl-10-methyl-5H-dibenzo[a,d]cycloheptene (^metropp^ph, 6). A solution of diphenylphosphane (1.85 g, 10 mmol) in dry toluene (50 ml) was slowly transferred [italic v]ia syringe into a solution of 5 (2.4 g, 10 mmol) in dry toluene (100 ml). A white precipitate formed immediately. After 2 h of stirring, a carefully degassed 5% aqueous solution of sodium carbonate was added, the organic layer separated, dried over sodium sulfate and the solvent removed under reduced pressure leaving crude 6. After recrystallisation from acetonitrile, 6 was obtained as colourless crystals (3.35 g, 86%). Mp: 127 °C. MS m/z: 390 (M⁺, 42%), 205 (10-methyl-5H-dibenzo[a,d]tropylium⁺, 100%). ³¹P-NMR (CDCl₃, 121.5 MHz): δ  =  − 11.7. ¹H-NMR (CDCl₃, 300 MHz): δ  =  7.48–7.42 (m, 1 H, CH_ar), 7.34–6.94 (m, 17 H, CH_ar), 7.14 (s, 1 H, [double bond, length half m-dash]CH), 4.80 [d, ²J(PH)  =  6.2 Hz, CHPR₂], 2.51 (s, 3 H, CH₃). ¹³C-NMR (CDCl₃, 75.4 MHz): δ  =  139.8 [d, J(CP)  =  8.2 Hz, C_qar], 138.9 [d, J(CP)  =  8.8 Hz, C_qar], 138.5 [d, J(CP)  =  20.1 Hz, C_qar]), 138.1 [d, J(CP)  =  19.5 Hz, C_qar], 138.0 [d, J(CP)  =  5.2 Hz, C_qar], 137.1 [d, J(CP)  =  4.6 Hz, C_qar], 133.7 [d, J(CP)  =  20.4 Hz, CH_ar], 133.4 [d, J(CP)  =  19.6 Hz, CH_ar], 130.4 [d, J(CP) 5.8 Hz, CH_ar], 129.7 [d, J(CP)  =  3.4 Hz, CH_ar], 129.2 [d, J(CP)  =  3.0 Hz, CH_ar], 129.0 [d, J(CP)  =  1.8 Hz, CH_ar], 128.3 (s, CH_ar), 128.2 (s, CH_ar), 127.8 [d, J(CP)  =  2.1 Hz, CH_ar], 127.8 [d, J(CP)  =  2.1 Hz, CH_ar], 127.7 [d, J(CP)  =  1.8 Hz, CH_ar], 127.3 (s, [double bond, length half m-dash]CH), 126.8 [d, J(CP)  =  1.0 Hz, CH_ar], 126.3 [d, J(CP)  =  1.3 Hz, CH_ar], 126.4 (s, [double bond, length half m-dash]CBr), 126.2 [d, J(CP)  =  1.5 Hz, CH_ar], 56.9 [d, ¹J(PC)  =  20.1 Hz, CHPR₂], 25.0 (s, CH₃).

[Rh(^metropp^ph)₂]PF₆ (9). Phosphane 6 (850 mg, 2.25 mmol), [Rh₂(μ-Cl)₂(cod)₂] 7 (247 mg, 0.5 mmol) and potassium hexafluorophosphate (250 mg, 1.35 mmol) were mixed in dry acetonitrile (40 ml) and then heated at reflux for 20 min. An immediate colour change from orange to deep red-violet was observed. The solvent was evaporated and the residue re-dissolved in methylene chloride (25 ml). After filtration, the solution was layered carefully with toluene (50 ml) yielding complex 9 as almost black crystals (889 mg, 86%). Single crystals were obtained by storage of the reaction mixture overnight at − 24 °C. Selected physical data are given in Table 4.

Table 4 Selected physical data of ligand 6, and complexes 9, 10 (maj), 10′ (min), 12a–d. NMR data (δ, J in Hz)

	^103Rh	^31P	CH[double bond, length half m-dash]CR	CH[double bond, length half m-dash]CR	CH[double bond, length half m-dash]CR	CHPPh2	Mp/ °C	λmax/nm
6		− 11.7 (s)	127.3 (s)	126.4 (s)	25.0 (s)	56.9 [d, ^1J(PC)  =  20.1]	127
			7.14 (s)		2.51 (s)	4.80 [d, ^2J(PH)  =  6.2]
9	162 (t)	84.5 [d, ^1J(RhP)  =  192]	99.9 (m)	123.7 (m)	30.0 (s)	58.8 (m)	247–252	510
		− 142.7 [h, ^1J(PF)  =  708]	6.73 (s)		2.75 (s)	4.85 (m)	(dec.)	324
10 (maj)	−370 (dd)	88.0 [dd, ^1J(RhP1)  =  172,	61.7 [dd, ^1J(RhC)  =  7.5,	103.0 (m)	58.1 (m)	54.2 [d, ^1J(PC)  =  14.5]	265–268	329
		^2J(PP)  =  29.0]	^3J(P2C)  =  1.3]		2.97 (m, CH exo)	5.06 [d, ^2J(PH)  =  12.0]	(dec.)
			2.68 [dd, ^1J(PH)  =  8.7,		2.73 (m, CH endo)
^2J(RhH)  =  1.4]
		79.0 [dd, ^1J(RhP2)  =  159,	79.5 [dd, ^3J(P1C)  =  22.0,	64.3 [ddd, ^2J(P2C)  =	29.8 [d, ^2J(RhC)  =  4.5]	55.7 [d, ^1J(PC)  =  15.4]
		^2J(PP)  =  29.0]	^1J(RhC)  =  7.0]	41.7, ^1J(RhC)  =  10.2,	1.99 (s)	4.98 [d, ^2J(PH)  =  12.8]
			3.92 (m)	^2J(P1C)  =  6.5]
10′ (min)		91.7 [dd, ^1J(RhP1)  =  168,
^2J(PP)  =  26.1]
81.4 [dd, ^1J(RhP2)  =  158,
^2J(PP)  =  26.1]
12a	−344 (t)	87.4 [d, ^1J(RhP)  =  180	70.6 [ddd, ^2J(PalterC)  =  42.2,	48.5 [d, ^1J(RhC)  =  12.6]	30.8 (m)	57.6 [dd, ^1J(PC)  =  10.3,		502
			^1J(RhC)  =  9.1, ^2J(PipsoC) =  1.8]		1.86 (s)	^2J(RhP)  =  4.3]		377
			3.13 [d, ^2J(PH)  =  4.3]			4.44 [d, ^2J(PH)  =  9.3]		292
12b		85.8 [dd, ^1J(RhP1)  =  184,
^2J(PP)  =  7.8]
85.2 [dd, ^1J(RhP2)  =  183,
^2J(PP)  =  7.8]
12c	−325 (dd)	86.2 [dd, ^1J(RhP1)  =  182,	68.4 (m)	54.4 [d, ^1J(RhC)  =  12.5]	42.8 (m, Cα), 32.6 (s, Cγ), 30.5	57.6 [dd, ^1J(PC)  =		497
		^2J(PP)  =  7.5]	3.49 (m)		(m, Cβ), 23.9 (Cδ), 14.9 (s, Cε)	10.5, ^2J(RhP)  =  4.1]		372
					2.53 (m, CαH), 2.06 (m, CαH),	4.38 [d, ^2J(PH)  =  10.2]		284
1.65 (m, CβH), 1.39–1.12 (m,
5H, CβH, CγH2, CδH2), 0.89
					[t, 3H, ^3J  =  6.8, (CεH3)]
		85.4 [dd, ^1J(RhP2)  =  184,	69.8 (m)	48.4 [d, ^1J(RhC)  =  12.7]	30.8	57.6 [dd, ^1J(PC)  =
		^2J(PP)  =  7.5]	3.17 (m)		1.82 (s)	10.5, ^2J(RhP)  =  4.1]
4.45 [d, ^2J(PH)  =  10.0]
12d	85.6 [dd, ^1J(RhP1)  =  179,
^2J(PP)  =  7.4]
84.0 [dd, ^1J(RhP2)  =  182,
^2J(PP)  =  7.4]

---

[Rh(^allyltropp^ph) (^metropp^ph)] (10). Potassium tert-butoxide (15 mg, 135 μmol), dissolved in THF (2 ml), was added to a suspension of 9 (103 mg, 100 μmol) in THF (2 ml) providing a clear orange solution of 10. A microcrystaline orange product (85 mg, 95%) precipitated upon addition of hexane (10 ml). Single crystals were grown by layering a methylene chloride solution of 10 with hexane. Selected physical data are given in Table 4.

[M(THF)_x][Rh(^metropp^ph)₂] (12a) (M  =  Li, x  =  4; M  =  Na, K, x  =  6). A small piece of an alkali metal (Li, Na or K) was added to a suspension of 9 (70 mg, 68 μmol) in THF (2 ml). Upon stirring the colour changed from deep red-violet [italic v]ia brown to deep green and then to dark red. The alkali metal was removed by filtration and the solution layered with 5 ml hexane. The product was isolated as a deep red microcrystalline powder (65 mg, 72%). Selected NMR data are given in Table 4.

[Li(THF)₄][Rh(^metropp^ph)(^RCH2tropp^ph)] (R  =  H 12a, Me 12b, n-Bu 12c or Ph 12d). General procedure for the preparation of 12a–d by allylic alkylation is given below. To a solution of 10 (30 mg, 34 μmol) in THF (1 ml), 0.1 ml of a commercially available solution of the corresponding lithium reagent (12a: 1 M LiBEt₃H in THF; 12b: 2.5 M MeLi in diethyl ether; 12c: 1.6 M n-BuLi in hexane; 12d: 2 M Li in cyclohexane–diethyl ether 70:30) was added. In all cases, a colour change from orange to deep red occurred. Addition of hexane provided deep red powders (yields ranging from 60% to 76%), which were re-dissolved in THF-d₈ for NMR experiments. Selected NMR data are given in Table 4.

In the case of 12c a microcrystalline product was obtained directly from the reaction mixture after a few minutes.

Acknowledgements

This work was supported by the Swiss National Science Foundation. S. D. thanks the Gottlieb–Daimler and Carl–Benz Foundation for a grant.

References and notes

1. Neutral mononuclear d⁹-rhodium and iridium carbonyls can only be isolated by matrix techniques: (a) A. J. L. Hanlan and G. A. Ozin, Inorg. Chem., 1979, 18, 2091 and refs. cited therein; (b) A. B. P. Lever, G. A. Ozin, A. J. L. Hanlan, W. J. Power and H. B. Gray, Inorg. Chem., 1979, 18, 2088; (c) J. H. B. Chenier, M. Histed, J. A. Howard, H. A. Joly, H. Morris and B. Mile, Inorg. Chem., 1989, 28, 4114d¹⁰-rhodate and d¹⁰-iridate anions: (d) [Rh(CO)₄]⁻: P. Chini and S. Martinengo, Inorg. Chim. Acta, 1969, 3, 21; (e) [Ir(CO)₄]⁻: L. Malatesta, G. Caglio and M. Angoletta, Chem. Commun., 1970, 532; (f) [Rh(CO)₂(PPh₃)₂]⁻ and [Ir(CO)₃(PPh₃)]⁻: J. P. Collman, F. D. Vastine and W. R. Roper, J. Am. Chem. Soc., 1968, 90, 2282 and refs. cited therein; (g) [Rh(CO)(triphos)]⁻: G. G. Johnston and M. C. Baird, J. Organomet. Chem., 1986, 314, C51..
2. d¹⁰-M fluorophosphine complexes (M = Rh, Ir): (a) [Rh(PF₃)₄]⁻: T. Kruck, N. Derner and W. Lang, Z. Naturforsch. B, 1966, 21, 1020; (b) [Ir(PF₃)₄]⁻: M. A. Bennett and D. J. Patmore, Inorg. Chem., 1971, 10, 2387 and refs. cited therein[Rh(PF₂NMe₂)₄]⁻: D. A. Clement and J. F. Nixon, J. Chem. Soc., Dalton Trans., 1973, 195.
3. (a) [Rh(Ph₂P–(CH₂)_n–PPh₂)₂]⁻ (n = 2, 3): B. Bogdanović, W. Leitner, C. Six, U. Wilczok and K. Wittmann, Angew. Chem., 1997, 109, 518Angew. Chem., Int. Ed. Engl., 1997, 36, 500 (b) [Ir(dppf)₂]⁻ [dppf = 1,1′-bis(diphenylphosphino)ferrocene]: B. Longato, L. Riello, G. Bandoli and G. Pilloni, Inorg. Chem., 1999, 38, 2818.
4. (a) H. Schönberg, S. Boulmaâz, M. Wörle, L. Liesum, A. Schweiger and H. Grützmacher, Angew. Chem., 1998, 110, 1492Angew. Chem., Int. Ed., 1998, 37, 1423 (b) S. Boulmaâz, M. Mlakar, S. Loss, H. Schönberg, S. Deblon, M. Wörle, R. Nesper and H. Grützmacher, Chem. Commun., 1998, 2623; (c) S. Deblon, unpublished results. Further details will be provided upon request to the authors.
5. (a) S. Oishi, J. Mol. Catal., 1987, 39, 225; (b) E. Amouyal, in Homogeneous Photocatalysis, ed. M. Chanon, Wiley, New York, 1997, vol. 2, pp. 264–307.
6. J. Thomaier, S. Boulmaâz, H. Schönberg, H. Rüegger, A. Currao, H. Grützmacher, H. Hillebrecht and H. Pritzkow, New J. Chem., 1998, 21, 947.
7. E. A. Halevi and R. Knorr, Angew. Chem., 1982, 94, 307; Angew. Chem., Int. Ed. Engl., 1982, 21, 288; T. A. Albright, J.-K. Burdett, and M.-H. Whangbo, Orbital Interactions in Chemistry, Wiley, New York, 1985, p. 305.
8. The strongest deviation (49.7°) was observed by: (a) V. Di Noto, G. Valle, B. Zarli, B. Longato, G. Pilloni and B. Corain, Inorg. Chim. Acta, 1995, 233, 165We thank the authors for bringing this value to our attention. Further distorted complexes: (b) [RhCl(CO)(PBu₃^t)₂] has the structure of a flattened tetrahedron: P–Rh–P 162°, Cl–Rh–C: 150°: H. Schumann, M. Heisler and J. Pickardt, Chem. Ber., 1977, 110, 1020; (c) R. L. Harlow, S. A. Westcott, D. L. Thorn and R. T. Baker, Inorg. Chem., 1992, 31, 323, and refs. cited therein; (d) Compare also distortion angles in other bisphosphane-bisolefin complexes like [Rh(cod)(R,R-Me–BPE)]⁺ (φ = 24°), [Rh(cod)(R,R-Me–DuPhos)]⁺ (φ = 18°): M. J. Burk, J. E. Feaster, W. A. Nugent and R. L. Harlow, J. Am. Chem. Soc., 1993, 115, 10125; (e) [Ir(cod)(R,R-Me–DuPhos)]⁺ (φ = 18°): B. F. M. Kimmich, E. Somsook and C. R. Landis, J. Am. Chem. Soc., 1998, 120, 10115; (f) See also: A. Miedaner, R. C. Haltiwanger and D. DuBois, Inorg. Chem., 1991, 30, 417.
9. G. N. Walker and A. R. Engle, J. Org. Chem., 1972, 37, 4294.
10. K. C. Pich, R. Bishop, D. C. Craig and M. L. Scudder, Aust. J. Chem., 1994, 47, 837.
11. For clarity, the orientation of the methyl groups in A, B and C is not specified in Scheme 2. A comparable mechanism has been proposed for isomerisation reactions in zinc thiolates containing a Zn₂(μ-N)(μ-S) four-membered ring: H. Grützmacher, M. Steiner, H. Pritzkow, L. Zolnai, G. Huttner and A. Sebald, Chem. Ber., 1992, 125, 2199.
12. J. Thomaier, PhD Dissertation, University of Freiburg, Freiburg, Germany, 1996..
13. The figures were produced with the facilities included in the program package WINGX: L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837.
14. A. G. Orpen, L. Brammer, F. H. Allen, O. Kennard, D. G. Watson and R. Taylor, J. Chem. Soc., Dalton Trans., 1989, S1.
15. (a) P. A. Evans, J. E. Robinson and J. D. Nelson, J. Am. Chem. Soc., 1999, 121, 6761; (b) P. A. Evans and J. D. Nelson, J. Am. Chem. Soc., 1998, 120, 5581; (c) P. A. Evans and J. D. Nelson, Tetrahedron Lett., 1998, 39, 1725; (d) R. Takeuchi and N. Kitamura, New J. Chem., 1998, 22, 659.
16. For recent review on transition-metal-catalysed allylic alkylations see: B. M. Trost and D. L. Van Vranken, Chem. Re[italic v]., 1996, 96, 395.
17. (a) [RhCl(PPh₃)₃]: D. C. Olson and W. Keim, Inorg. Chem., 1969, 8, 2028; (b) L. Horner, K. Dickerhof and J. Mathias, Phosphorus Sulfur Relat. Elem., 1981, 10, 349; (c) [MCl(dppe)₂], [MX(dppe)(CO)_n], and [M(dppe)₂]⁺ (M = Rh, Ir): G. Pilloni, E. Vecchi and M. Martelli, J. Electroanal. Chem., 1973, 45, 483; (d) G. Pilloni, G. Zotti and M. Martelli, Inorg. Chim. Acta, 1975, 13, 213; (e) J. A. Sofranko, R. Eisenberg and J. A. Kampmeier, J. Am. Chem. Soc., 1979, 101, 1042; (f) J. A. Sofranko, R. Eisenberg and J. A. Kampmeier, J. Am. Chem. Soc., 1980, 102, 1163; (g) G. Pilloni, G. Zotti and M. Martelli, Inorg. Chem., 1982, 21, 1283; (h) F. Morandini, G. Pilloni, G. Consiglio and A. Mezzetti, Organometallics, 1995, 14, 3418; (i) [Rh(P(OiPr₃)₄]⁺: G. Pilloni, G. Zotti and S. Zecchin, J. Organomet. Chem., 1986, 317, 357; (j) [M(PPh₃)₃(L)]⁺: G. Zotti, S. Zecchin and G. Pilloni, J. Electroanal. Chem., 1984, 175, 241; (k) [MX(CO)(PPh₃)₂]: G. Schiavon, S. Zecchin, G. Pilloni and M. Martelli, J. Organomet. Chem., 1976, 121, 261; (l) G. Schiavon, S. Zecchin, G. Pilloni and M. Martelli, J. Inorg. Nucl. Chem., 1977, 39, 115; (m) G. Zotti, S. Zecchin and G. Pilloni, J. Organomet. Chem., 1983, 246, 61; (n) [Rh(cod)₂]⁺: J. Orsini and W. E. Geiger, J. Electroanal. Chem., 1995, 380, 83.
18. Compare, for example, [Fe(Cp)₂]/[Fe(Cp)₂]⁺ ΔE_red/ox = +450 mV and [Fe(Cp*)₂]/[Fe(Cp*)₂]⁺ ΔE_red/ox = −100 mV (Cp = cyclopentadienyl; Cp* =  pentamethylcyclopentadienyl): P. Zanello in Ferrocenes, eds. A. Togni and T. Hayashi, VCH–Wiley, Weinheim, 1995, p. 317..
19. Simulation software for cyclic voltammograms, version 3.03: M. Rudolph, D. D. Reddy and S. W. Feldberg, Anal. Chem., 1994, 66, 589, distributed by Bioanalytical Systems, Inc., West Lafayette, IN 47906, USA..

---