Doping studies of the ferromagnetic superconductor RuSr2GdCu2O8†
A. C. Mclaughlinab, V. Janowitzab, J. A. McAllisterab and J. P. Attfield*ab
aDepartment of Chemistry, University
of Cambridge, Lensfield Road, Cambridge, UK CB2 1EW
bInterdisciplinary Research Centre in
Superconductivity, University of Cambridge, Madingley Road, Cambridge, UK CB3 0HE
First published on UnassignedUnassigned3rd October 2000
Abstract
Solid solutions of the ferromagnetic superconductor Ru1 − xMxSr2GdCu2O8 have been prepared for M = Sn or Nb. Up to 7.5% Sn and 20% Nb have been incorporated into the structure, and powder diffraction and physical measurements show that substitution occurs at the Ru site. A suppression of the ferromagnetic moment in the ruthenate layers is observed upon Sn and Nb substitution and the Curie temperature drops from 136 K in the undoped material to 103 K in Ru0.8Nb0.2Sr2GdCu2O8. The onset of superconductivity increases from 19 K in the 15% Nb doped sample to 38 K in the parent compound to 50 K in the 7.5% Sn doped sample, evidencing a tuning of the superconducting transition by charge transfer. Structural changes upon M doping have been determined from powder synchrotron X-ray diffraction and, for one sample, neutron diffraction using the high flux diffractometer GEM to compensate for the high absorption of natural Gd.
Introduction
Superconductivity and ferromagnetism are important and useful properties, but they do not usually coexist in the same material. This is borne out by several re-entrant superconductors in which the onset of ferromagnetic ordering destroys the superconductivity; for example ErRh4B4 exhibits a superconducting transition at 8.7 K and orders ferromagnetically at TM = 0.93 K, with the simultaneous disappearance of the superconducting state.1 However, a coexistence of ferromagnetism and superconductivity has recently been observed in the 1212 type layered cuprate RuSr2GdCu2O8,2–10 which is a bulk superconductor below Tc = 0–46 K. The magnetic transition at TM = 136 K results from the ordering of moments in the RuO2 planes and persists through the onset of superconductivity to the lowest temperature investigated (1.9 K). A variety of physical measurements, in particular zero-field muon spin rotation experiments,6 have demonstrated that the material is isotropically uniform with no evidence of spatial separation of the superconducting and magnetic regions. The presence of ferromagnetism is confirmed by the observation of hysteresis loops in variable field measurements below TM, with remnant and saturated moments of 0.1 and 1.0 μB per Ru atom. However, only antiferromagnetic order within the RuO2 planes was detected in a recent neutron scattering experiment and the ferromagnetism is proposed to arise from a spin flop transition at high fields.8 The Gd moments align antiferromagnetically, but at much lower temperatures (TN = 2.9 K).The average crystal structure of RuSr2GdCu2O8 is tetragonal with P4/mmm space group symmetry and the structure is similar to that of other 1212-type cuprate superconductors, consisting of a layer of almost regular RuO6 octahedra connected through their apices to two layers of CuO5 square pyramids (Fig. 1). There is a bond mismatch between the in-plane Ru–O and Cu–O bonds leading to rotations of the RuO6 octahedra around c by 13° at 295 K. A slight tilting of the polyhedra which reduces the Cu–O–Ru angle to 173° is also observed.7,9 A slight canting of the moments may arise from an antisymmetric (Dzyaloshinsky–Moriya) interaction between neighbouring Ru moments, which is non-zero due to the twists and tilts of the RuO6 octahedra. This would give rise to an overall magnetic arrangement containing both ferro- and antiferromagnetic components, in keeping with the above magnetic observations.
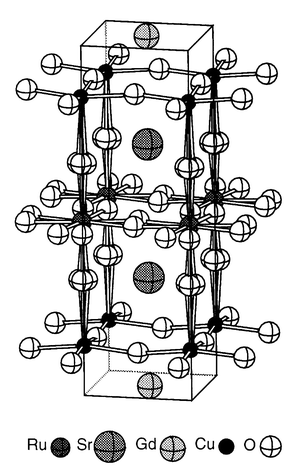 | ||
| Fig. 1 The average crystal structure of RuSr2GdCu2O8 showing the tilts and rotations of the RuO6 octahedra. | ||
RuSr2GdCu2O8 is found to be both cation and oxygen stoichiometric7 and the hole doping of the copper oxide planes necessary to induce superconductivity arises from the overlap of the Ru: t2g and the Cu: 3dx2 − y2 bands. The formula may be written as Ru5 − 2p0Sr2Gd(Cu2 + p0)2O8 to show the average Ru and Cu oxidation states. Transport measurements suggest that the copper oxide planes in RuSr2GdCu2O8 are underdoped with intrinsic hole doping level p0 = 0.076 as optimum superconductivity in the layered cuprates is generally found at p0 = 0.16. In order to investigate the charge distribution and magnetisation of RuSr2GdCu2O8 further, we have attempted to replace Ru by non-magnetic, fixed valent cations. The substitution of the larger Sn4+ ion for Ru was previously found to increase the bond mismatch between the in plane Ru–O and Cu–O bonds, and enhanced Tc but suppressed TM.11 However, firm conclusions about the origin of these effects could not be made because the samples were impure. A series of phase pure Sn-doped samples for x < 0.1 and a series of >98% pure Nb doped samples have subsequently been prepared and characterised by X-ray diffraction, room temperature thermopower measurements, SQUID magnetometry and conductivity measurements. A summary of the physical properties of these materials has been reported elsewhere.12
Experimental
Ceramic samples of nominal composition Ru1 − xMxSr2GdCu2O8 (M = Sn: x = 0, 0.025, 0.05, 0.075; M = Nb: x = 0, 0.05, 0.1, 0.15, 0.2) were prepared by the solid state reaction of stoichiometric powders of RuO2, SnO2, Nb2O5, SrCO3, Gd2O3, and CuO. These were ground and die-pressed into pellets before preliminary reaction in flowing nitrogen at 1010![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for 20 hours in order to minimise the formation of SrRuO3.
This was followed by reaction in flowing oxygen at 1050
°C for 20 hours in order to minimise the formation of SrRuO3.
This was followed by reaction in flowing oxygen at 1050![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C and
1055
°C and
1055![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C for 10 hours each. The sample was furnace cooled, reground
and repelleted between each step. The samples were annealed at 1060
°C for 10 hours each. The sample was furnace cooled, reground
and repelleted between each step. The samples were annealed at 1060![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C
under flowing oxygen for 4 days and finally slow cooled to room temperature.
X-Ray diffraction patterns demonstrated that the Ru1 − xSnxSr2GdCu2O8 solid solutions were phase pure, however there was a trace (<2%)
of SrRuO3 in the Ru1 − xNbxSr2GdCu2O8
samples. Thermogravimetric analyses under flowing H2/N2
showed the samples to have oxygen contents of 8.00 ± 0.05%,
and so they are oxygen stoichiometric within the limits of the measurements.
°C
under flowing oxygen for 4 days and finally slow cooled to room temperature.
X-Ray diffraction patterns demonstrated that the Ru1 − xSnxSr2GdCu2O8 solid solutions were phase pure, however there was a trace (<2%)
of SrRuO3 in the Ru1 − xNbxSr2GdCu2O8
samples. Thermogravimetric analyses under flowing H2/N2
showed the samples to have oxygen contents of 8.00 ± 0.05%,
and so they are oxygen stoichiometric within the limits of the measurements.Room temperature X-ray diffraction data were collected for the Ru1 − xNbxSr2GdCu2O8 solid solutions on a high resolution STOE transmission diffractometer using Cu Kα1 radiation. The counter is a moving linear position sensitive detector with a resolution of <0.06° FWHM (Full Width at Half Maximum) in 2θ. Data were collected over the range 5° < 2θ < 100°, with a step size of 0.01°. Powder synchrotron X-ray diffraction patterns of the Ru1 − xSnxSr2GdCu2O8 solid solutions (x = 0, 0.05, 0.075) were recorded on ESRF instrument BM16 at 295 K.13 A wavelength of 0.325104 Å was used and the sample was contained in a 0.5 mm diameter borosilicate glass capillary mounted on the axis of the diffractometer about which it was spun at 1 Hz to improve the powder averaging of the crystallites. Diffraction patterns were collected over the angular range 2–50° by continuously scanning the bank of nine Ge(111) analyser crystals and scintillation detectors at a rate of 1 degree per minute and recording data every 100 ms. The high-angle parts of the pattern were scanned several times to improve the statistical quality of the data in these regions. The counts from the nine detectors were then normalised, summed and rebinned to a constant step size of 0.004° for each scan.
Time-of-flight (TOF) neutron powder diffraction data were collected on the General Materials Diffractometer (GEM) of the ISIS facility at the Rutherford-Appleton Laboratory, UK for the Ru0.95Sn0.05Sr2GdCu2O8 sample. GEM has been designed as a high intensity, high-resolution neutron diffractometer for structural studies of disordered materials and crystalline powders and has an incident flight path of 17 m. A cylindrical sample was prepared to allow for the extremely high absorption cross section of Gd for thermal neutrons by coating a cylinder of adhesive tape (approximate dimensions 6.1 × 0.6 cm) with a 0.05 mm layer of Ru0.95Sn0.05Sr2GdCu2O8 powder. This cylinder was held in a vanadium can and room temperature diffraction patterns were collected over the range 1000–22000 µs in 24 h from the 20, 60, and 90° 2θ detector banks.
Magnetisations were measured on powdered samples in a Quantum Design SQUID magnetometer. The resistivities of sintered polycrystalline bars (approximate dimensions 4 × 4 × 12 mm3) were measured between 7 and 300 K using the standard four-probe ac technique. The thermoelectric powers of the same sintered bars were measured at 290 K using the method and instrument developed by Obertelli et al.,14 and were corrected for the contribution from the gold connecting leads which was measured separately using a Pb standard.
Results
The X-ray and TOF neutron powder diffraction patterns were all fitted by the Rietveld method15 using a GSAS program16 with the starting model previously reported for RuSr2GdCu2O8.7 The backgrounds were fitted using linear interpolation and the peak shapes were modelled using a pseudo-Voigt function. The oxygen sites of the RuO6 octahedra are split to model the disordered rotations and tilts of the octahedra (Table 1). Good Rietveld fits were obtained for all samples (Fig. 2).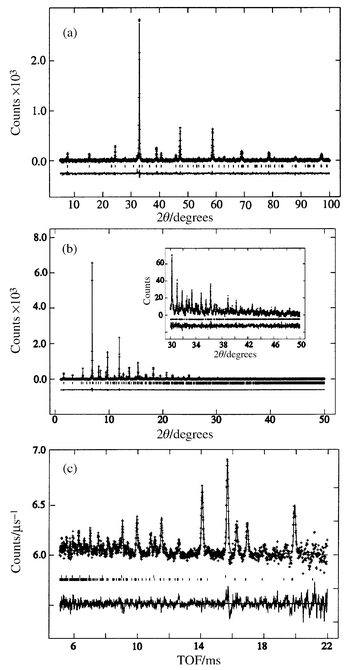 | ||
| Fig. 2 Rietveld refinement fits to (a) the Cu Kα1 X-ray diffraction pattern of Ru0.8Nb0.2Sr2GdCu2O8, (b) the synchrotron X-ray diffraction pattern of Ru0.95Sn0.05Sr2GdCu2O8 and (c) the TOF neutron diffraction pattern of Ru0.95Sn0.05Sr2GdCu2O8. | ||
| Atom | Occupancy | % Sn | % Nb | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 5 (N) | 7.5 | 0 | 5 | 10 | 15 | 20 | |||
| Ru | 1.00 | Uiso/Å2 | 0.0037(2) | 0.0039(2) | 0.0071(85) | 0.0046(2) | 0.0003(3) | 0.0034(3) | 0.0027(2) | 0.021(2) | 0.0068(5) |
| Sr | 1.00 | z | 0.30926(6) | 0.30873(7) | 0.3031(12) | 0.30877(8) | 0.3105(1) | 0.3099(1) | 0.3086(1) | 0.3084(1) | 0.3072(2) |
| Uiso/Å2 | 0.0084(1) | 0.0079(2) | 0.0071 | 0.0086(2) | 0.00030 | 0.0034 | 0.0027 | 0.0021 | 0.0068 | ||
| Gd | 1.00 | Uiso/Å2 | 0.0046(1) | 0.0045(1) | 0.0071 | 0.0046(2) | 0.00030 | 0.0034 | 0.0027 | 0.0021 | 0.0068 |
| Cu | 1.00 | z | 0.14611(9) | 0.14607(9) | 0.1511(12) | 0.1458(1) | 0.1475(2) | 0.1473(2) | 0.147(2) | 0.1463(2) | 0.1470(5) |
| Uiso/Å2 | 0.0052(2) | 0.0051(2) | 0.0071 | 0.0053(2) | 0.00030 | 0.0034 | 0.0027 | 0.0021 | 0.0068 | ||
| O(1) | 0.25 | x | 0.049(3) | 0.054(3) | 0.030(13) | 0.042(5) | 0.063(7) | 0.04(2) | 0.079(5) | 0.074(6) | 0.080(1) |
| z | 0.3332(4) | 0.3340(4) | 0.3356(16) | 0.3331(5) | 0.3318(9) | 0.3337(9) | 0.3350(8) | 0.3360(9) | 0.3360(9) | ||
| Uiso/Å2 | 0.0127(7) | 0.0120(7) | 0.0071 | 0.0155(9) | −0.012(2) | −0.012(2) | −0.012(2) | −0.015(3) | −0.011(3) | ||
| O(2) | 1.00 | z | 0.1304(3) | 0.1308(3) | 0.1239(10) | 0.1304(3) | 0.1339(6) | 0.1302(5) | 0.1335(5) | 0.1345(6) | 0.1330(9) |
| Uiso/Å2 | 0.0127(7) | 0.0120(7) | 0.0071 | 0.0155(9) | −0.012 | −0.012 | −0.012 | −0.015 | −0.011 | ||
| O(3) | 0.50 | x | 0.113(2) | 0.116(2) | 0.1183(59) | 0.120(2) | 0.133(4) | 0.138(4) | 0.137(3) | 0.148(4) | 0.1621(5) |
| Uiso/Å2 | 0.0127(7) | 0.0120(7) | 0.0071 | 0.0155(9) | −0.012 | −0.012 | −0.012 | −0.015 | −0.011 | ||
Refinement of the internal co-ordinates in the Ru1 − xNbxSr2GdCu2O8 solid solutions reveals increases in the average in-plane Ru–O (Fig. 3) and Sr–O bonds (Table 2) and an increase of the rotations of the RuO6 octahedra around c. Overall increases in the lattice parameters (Table 2) and cell volume (Fig. 4) are also observed in accordance with the substitution of the slightly larger Nb5+ for Ru4+/5+. The observation of an increase in the apical Cu–O bond distance with Nb substitution (Fig. 5) is indicative of a reduction in hole transfer from the ruthenate to the cuprate layers, in keeping with the transport properties below.
 | ||
| Fig. 3 Variation of the in-plane Ru–O bond with x in the Ru1 − xNbxSr2GdCu2O8 solid solutions. | ||
 | ||
| Fig. 4 Variation of the cell volume with x in Ru1 − xNbxSr2GdCu2O8. | ||
 | ||
| Fig. 5 Changes in the apical Cu–O bond with Nb content in the Ru1 − xNbxSr2GdCu2O8 solid solutions. | ||
| % Sn | % Nb | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 5 | 5 (N) | 7.5 | 0 | 5 | 10 | 15 | 20 | |
| Cu–O(1) × 1 | 2.174(5) | 2.186(5) | 2.14(2) | 2.176(6) | 2.13(1) | 2.16(1) | 2.19(1) | 2.21(1) | 2.21(2) |
| Cu–O(2) × 4 | 1.9284(3) | 1.9289(3) | 1.945(3) | 1.9290(4) | 1.920(1) | 1.924(1) | 1.921(1) | 1.920(1) | 1.925(1) |
| Sr–O(1) × 2 | 2.601(9) | 2.591(8) | 2.66(3) | 2.620(9) | 2.55(2) | 2.61(3) | 2.52(1) | 2.53(1) | 2.52(2) |
| Sr–O(1) × 2 | 2.864(9) | 2.881(9) | 2.82(4) | 2.847(9) | 2.89(2) | 2.83(4) | 2.94(1) | 2.93(1) | 2.96(3) |
| Sr–O(2) × 4 | 2.823(3) | 2.817(3) | 2.83(1) | 2.821(3) | 2.796(6) | 2.830(6) | 2.785(5) | 2.775(5) | 2.780(9) |
| Sr–O(3) × 2 | 2.661(4) | 2.660(4) | 2.71(2) | 2.652(4) | 2.596(9) | 2.597(9) | 2.605(7) | 2.586(8) | 2.576(15) |
| Sr–O(3) × 2 | 3.226(5) | 3.242(5) | 3.29(2) | 3.254(6) | 3.26(1) | 3.27(1) | 3.29(1) | 3.33(1) | 3.37(3) |
| Ru–O(1) × 2 | 1.939(5) | 1.933(5) | 1.91(2) | 1.940(6) | 1.96(1) | 1.94(1) | 1.93(1) | 1.91(1) | 1.91(2) |
| Ru–O(3) × 4 | 1.968(1) | 1.972(2) | 1.972(5) | 1.976(2) | 1.981(4) | 1.983(5) | 1.988(4) | 2.000(5) | 2.015(9) |
| Cu–O(1)–Ru | 169.5(1) | 168.5(7) | 174(3) | 171.0(9) | 166(2) | 170(2) | 163(1) | 164(1) | 163(3) |
| Cu–O(2)–Cu | 169.2(2) | 169.5(2) | 162(2) | 169.4(3) | 170.6(5) | 171.0(7) | 170.7(5) | 171.9(5) | 170.4(9) |
| Ru–O(3)–Ru | 154.6(4) | 153.8(4) | 153(1) | 152.9(5) | 150.9(9) | 149.7(9) | 148.9(8) | 146.6(9) | 144.1(9) |
| a/Å | 3.83955(1) | 3.84157(1) | 3.8388(6) | 3.84162(1) | 3.82765(5) | 3.82828(6) | 3.83083(4) | 3.83188(5) | 3.83840(2) |
| c/Å | 11.57239(7) | 11.58011(8) | 11.571(3) | 11.58258(7) | 11.5365(2) | 11.5356(3) | 11.5408(2) | 11.5432(2) | 11.5444(8) |
| V/Å3 | 170.602(11) | 170.895(1) | 170.51(1) | 170.936(1) | 169.020(8) | 169.062(8) | 169.364(6) | 169.492(8) | 169.69(1) |
| χ2 | 2.0 | 1.9 | 1.0 | 1.4 | 1.2 | 1.4 | 1.5 | 1.4 | 1.0 |
| RWP (%) | 8.9 | 9.0 | 0.3 | 10.5 | 2.8 | 3.0 | 2.8 | 3.0 | 6.2 |
| RP (%) | 6.4 | 6.5 | 0.3 | 7.7 | 3.6 | 3.9 | 2.8 | 3.0 | 7.9 |
A previous study showed that the substitution of Sn into RuSr2GdCu2O811 increases the a cell parameter, while c decreases leading to no overall change in the cell volume. Refinement of the cell parameters from more highly-resolved synchrotron data confirms the increase in the a cell parameter but an expansion of c and cell volume are observed (Table 2), as expected for the substitution of the larger Sn4+ ion for Ru4+/5+. The increase of the in-plane Ru–O bond and the concomitant decrease in Ru–O–Ru angle detected in the previous study are also observed, however clear trends in the Cu–O distances are not seen in these results.
An acceptable Rietveld refinement of the structure of Ru0.95Sn0.05Sr2GdCu2O8 was obtained by fitting the neutron diffraction data from the 90° bank of GEM (Fig. 2(c)). The data were corrected for Gd absorption, varying as TOF, and reflections from the vanadium can were fitted as a secondary phase. Free refinement of the atomic coordinates was possible although all of the isotropic thermal factors were constrained to be equal. The atomic positions, bond distances and angles (Tables 1 and 2) from this refinement are in good agreement with those from the synchrotron X-ray refinement of the same structure, within the usual criterion of three e.s.d.s (estimated standard deviations), and the neutron e.s.d.s on the oxygen positions and metal to oxygen distances are only 4–5 times larger than those for the synchrotron refinement. These results demonstrate that powder neutron structure determination of materials containing significant quantities of natural Gd is now possible because of the very high flux offered by diffractometers such as GEM. The future addition of backscattering detector banks should yield even better refinements from this instrument.
A reduction of the Curie temperature (TM) and a broadening of the magnetic transition is clearly observed in magnetisation data for both the Sn and Nb substituted materials (Fig. 6), collected while warming in an applied field of 1 kOe after zero-field cooling. Magnetic hysteresis loops recorded at 10 K with the field swept between ±50 kOe confirm that there is a ferromagnetically ordered component in all the samples; a typical loop is displayed in Fig. 7. The remnant moment and coercive field decrease smoothly with x for both Ru1 − xSnxSr2GdCu2O8 and Ru1 − xNbxSr2GdCu2O8 series (Table 3). Both the Ru moment μRu and the paramagnetic Gd moment μGd contribute to the overall magnetisation. The saturated Ru moment was estimated by fitting the total magnetic moment μ(H) in the range H = 25–50 kOe with the function:
 | (1) |
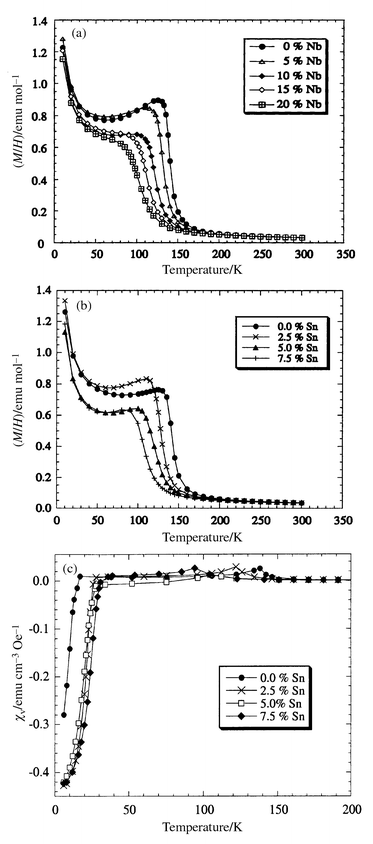 | ||
| Fig. 6 Magnetisation/field data for Ru1 − xMxSr2GdCu2O8 with (a) M = Nb and (b) M = Sn; (c) shows the volume susceptibility for M = Sn at H = 2 Oe. | ||
 | ||
| Fig. 7 Magnetic hysteresis loop for Ru0.9Nb0.1Sr2GdCu2O8 at 10 K. | ||
| p | % Nb | % Sn | Tc,onset/K | Tc,0/K | Tc,dia/K | TM/K | Hco/Oe | μR/μB | μRu/μB | S290/µV K−1 |
|---|---|---|---|---|---|---|---|---|---|---|
| 0.064(5) | 20 | — | — | — | 103(1) | 238(1) | 0.049(2) | 0.59(1) | 117(1) | |
| 0.068(5) | 15 | — | 19(1) | — | 110(1) | 295(1) | 0.075(1) | 0.73(1) | 110(3) | |
| 0.072(5) | 10 | — | 19(1) | — | 118(1) | 308(1) | 0.086(2) | 0.82(1) | 99(4) | |
| 0.076(5) | 5 | — | 29(1) | 15(1) | 127(1) | 330(1) | 0.109(1) | 0.94(1) | 90(1) | |
| 0.080(5) | 0 | — | 37(1) | 14(1) | 136(1) | 405(1) | 0.125(1) | 0.99(1) | 72(2) | |
| 0.080(5) | — | 0 | 38(1) | 23(1) | 17(1) | 136(1) | 420(1) | 0.142(1) | 1.09(1) | 92(3) |
| 0.091(5) | — | 2.5 | 45(1) | 31(1) | 28(1) | 126(1) | 370(1) | 0.114(1) | 1.00(1) | 81(3) |
| 0.101(5) | — | 5 | 46(1) | 31(1) | 29(1) | 117(1) | 340(1) | 0.096(1) | 0.84(1) | 76(2) |
| 0.112(5) | — | 7.5 | 50(1) | 36(1) | 39(1) | 103(1) | 320(1) | 0.088(2) | 0.78(1) | 70(2) |
The Meissner state is evidenced by measuring magnetisations in a field of 2 Oe, after zero-field cooling. Data were collected for the Ru1 − xSnxSr2GdCu2O8 solid solutions as shown in Fig. 6(c). The Tc's measured from the onset of diamagnetism are in good agreement with the zero-resistance values obtained from resistivity measurements (Table 2). The Curie transitions are indicated by small maxima in the susceptibilities, at the same temperatures as the transitions in the high field data in Fig. 6(a). The observation of both transitions in the same low field experiments demonstrates the coexistence of the superconductivity and magnetism.
Resistivity measurements (Fig. 8) show that all samples are metallic (dρ/dT > 0) at high temperatures although a semiconducting upturn is observed close to Tc. Superconducting transitions are observed for the Ru1 − xNbxSr2GdCu2O8 solid solutions with x = 0–0.15 but not for x = 0.2 down to 7 K. All the Ru1 − xSnxSr2GdCu2O8 samples are superconducting and the onset Tc increases from 38 K to 50 K in the 7.5% Sn sample. The Seebeck coefficient derived from the thermopower measurements increases with x in the Nb doped samples, but decreases in the Sn doped samples (Fig. 9). The Seebeck coefficients are very sensitive to the absolute hole concentrations, and the difference between the values for the x = 0 samples in the Ru1 − xSnxSr2GdCu2O8 and Ru1 − xNbxSr2GdCu2O8 series (Table 3) shows that there is a small systematic offset between the doping levels in the two series. This may arise from a small difference in average oxygen contents, below the sensitivity of the thermogravimetric analyses, as the two series were annealed separately.
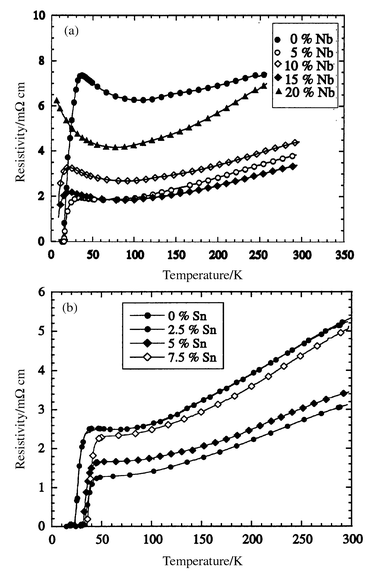 | ||
| Fig. 8 Resistivity data for Ru1 − xMxSr2GdCu2O8 with (a) M = Nb and (b) M = Sn. | ||
 | ||
| Fig. 9 Variation of the room temperature Seebeck coefficient for Ru1 − xMxSr2GdCu2O8 with (a) M = Nb and (b) M = Sn. | ||
Discussion
The crystallographic, magnetic and transport properties evidence the progressive substitution of Ru by M = Nb or Sn in the Ru1 − xMxSr2GdCu2O8 solid solutions. The substitution of diamagnetic Sn4+ or Nb5+ results in a dilution of the ferromagnetism in the Ru–O layers and the Curie temperature, remnant and saturated Ru moments, and coercive field all decrease with x as would be expected.Both Sn4+ and Nb5+ are larger than Ru, leading to a slight increase in the average (Ru,M)–O in-plane bond length upon substitution. This increases the bond mismatch between the xy plane Ru–O and Cu–O bonds resulting in greater rotation of the RuO6 octahedra around c from 15° at x = 0 to 17° in the 20% Nb sample (Table 2). The large increase of the apical Cu–O bond from 2.13 Å in the undoped sample to 2.21 Å in Ru0.8Nb0.2Sr2GdCu2O8 with a concomitant decrease in the Ru–O apical bonds evidences a reduction in the hole concentration in the CuO2 planes. Similar results are found during the reduction of YBa2Cu3O7 − δ17 as the apical C–O bond increases in length while Tc decreases.
The charge distribution in the doped materials may be written as (Ru5 − 2p0)1 − xMxqSr2Gd(Cu2 + p0 + Δp)2O8 where the extrinsic doping introduced by the substituents M of charge q is Δp = (5 − q − 2p0)x/2, assuming the intrinsic doping level p0 remains constant. Therefore substitution of Ru(5 − 2p0)+ by Nb5+ leads to the removal of holes from the CuO2 planes, so that the materials become more underdoped. This is supported by the increase in the 290 K Seebeck coefficient with x in the Ru1 − xNbxSr2GdCu2O8 solid solutions, and the decrease in Tc to 19 K in the 15% Nb sample. The opposite effect occurs upon Sn substitution; the hole concentration increases with a subsequent increase in Tc to 50 K and the Seebeck coefficient decreases. These results provide a good chemical demonstration that the doping of the cuprate planes necessary for superconductivity results from band overlap with the ruthenate states; Sn4+ and Nb5+ can only have opposite doping effects if the mean Ru oxidation state is intermediate between +4 and +5.
Tc varies quadratically with the hole concentration in cuprates18 and a fit to the data for the two Ru1 − xMxSr2GdCu2O8 series yields values of p0 = 0.08 for the intrinsic doping level and an estimated maximum Tc of 65 ± 10 K12 at the optimum p = 0.16 level. This is much lower than the highest Tc of 105 K obtained for comparable 1212 cuprates such as (Tl0.5Pb0.5)Sr2(Ca,Y)Cu2O7.19 This suppression could reflect a pairbreaking interaction with the ferromagnetic moments in the RuO2 plane, although this effect would be expected to be greater in the undoped compound in which the ferromagnetism is stronger. There is no evidence for this in the data in Fig. 10. The low Tc's in this system may instead reflect lattice strains from the bond mismatch between the cuprate and ruthenate layers. The apical Cu–O bond length of 2.16 Å in RuSr2GdCu2O8,7,11 which is shorter than that in any other cuprate, provides evidence that the geometry of the structure is not optimal for superconductivity.
 | ||
| Fig. 10 The variation of the onset superconducting critical temperature (Tc) and the Curie temperature (TM) with doping level p (lower scale) and % Nb or Sn (upper scale) in the Ru1 − xMxSr2GdCu2O8 solid solutions. | ||
Acknowledgements
We thank EPSRC for the provision of research grant GR/M59976, ESRF beam time, and a studentship for ACM; I. Pape and A. N. Fitch for help with the synchrotron X-ray diffraction experiment, P. G. Radaelli for assistance with the neutron experiment and S. Rycroft and J. R. Cooper for help with transport measurements.References
- W. A. Fertig, D. C. Johnston, L. E. Delong, R. W. McCallum and M. B. Maple, Phys. Rev. Lett., 1977, 38, 987 CrossRef CAS.
- L. Bauernfeind, W. Widder and H. F. Braun, Physica C, 1995, 254, 151 CrossRef CAS.
- K. B. Tang, Y. T. Qian, L. Yang, Y. D. Zhao and Y. H. Zhang, Physica C, 1997, 282–287, 947 CrossRef CAS.
- I. Felner, U. Asaf, S. Reich and Y. Tsabba, Physica C, 1999, 311, 163 CrossRef CAS.
- J. L. Tallon, C. Bernhard, M. E. Bowden, P. W. Gilberd, T. M. Stoto and D. J. Pringle, IEEE Trans. Appl. Supercond., 1999, 9, 1696 CrossRef.
- C. Bernhard, J. L. Tallon, C. Niedermayer, T. Blasius, A. Golnik, E. Brucher, R. K. Kremer, D. R. Noakes, C. E. Stronach and E. J. Ansaldo, Phys. Rev. B, 1999, 59, 14099 CrossRef CAS.
- A. C. Mclaughlin, W. Zhou, J. P. Attfield, A. N. Fitch and J. L. Tallon, Phys. Rev. B, 1999, 60, 7512 CrossRef CAS.
- J. W. Lynn, B. Keimer, C. Ulrich, C. Bernhard and J. L. Tallon, Phys. Rev. B, 2000, 61, 14964 CrossRef.
- A. C. Mclaughlin, J. P. Attfield and J. L. Tallon, Int. J. Inorg. Mater., 2000, 2, 95 CrossRef CAS.
- O. Chmaissam, J. D. Jorgensen, H. Shaked, P. Dollar and J. L. Tallon, Phys. Rev. B, 2000, 61, 6401 CrossRef.
- A. C. Mclaughlin and J. P. Attfield, Phys. Rev. B, 1999, 60, 14605 CrossRef CAS.
- A. C. Mclaughlin, V. Janowitz, J. A. McAllister and J. P. Attfield, Chem. Commun., 2000, 1331 RSC.
- (a) A. N. Fitch, Mater. Sci. Forum, 1996, 228–231, 219 Search PubMed; (b) J. L. Hodeau, P. Bordet, M. Anne, A. Prat, A. N. Fitch, E. Dooryhee, G. Vaughan and A. Freund, SPIE Proc., 1998, 3448, 353 Search PubMed.
- S. D. Obertelli, J. R. Cooper and J. L. Tallon, Phys. Rev. B, 1992, 46, 14928 CrossRef CAS.
- H. M. Rietveld, Acta Crystallogr., 1967, 22, 151 CrossRef CAS.
- A. C. Larson and R. B. Von Dreele, Los Alamos National Laboratory Report No. LA-UR-86-748, 1994..
- R. J. Cava, A. W. Hewat, E. A. Hewat, B. A. Batlogg, M. Marezio, K. M. Rabe, J. J. Krajewski, W. F. Peck Jr. and L. W. Rupp Jr., Physica C, 1990, 165, 419 CrossRef CAS.
- M. R. Presland, J. L. Tallon, R. G. Buckley, R. S. Liu and N. E. Flower, Physica C, 1991, 176, 95 CrossRef CAS.
- R. S. Liu, P. P. Edwards, Y. T. Huang, S. F. Wu and P. T. Wu, J. Solid State Chem., 1990, 86, 334 CrossRef CAS.
Footnote |
| † Basis of a presentation given at Materials Discussion No. 3, 26–29 September, 2000, University of Cambridge, UK. |
| This journal is © The Royal Society of Chemistry 2001 |
