Characteristics of a rf-only hexapole ion-guide interface for plasma-source time-of-flight mass spectrometry
John P.
Guzowski Jr†
and
Gary M.
Hieftje
*
Department of Chemistry, Indiana University, Bloomington, IN 47401, ,USA
First published on 11th July 2001
Abstract
A hexapole collision cell has been designed and incorporated into an orthogonal extraction plasma-source time-of-flight mass spectrometer (TOFMS). The ion-guide assembly was constructed from 20 cm long, 3.175 mm diameter stainless steel rods. The cell is positioned between the second and third vacuum stages of the mass spectrometer. The device was characterized with an inductively coupled plasma ionization source (ICP). Pressurization of the cell with a buffer gas (such as helium or hydrogen) lowers the axial energy of the ions, and produces a beam having a most probable energy of 1.3 eV and an energy spread of less than 2 eV. The signal levels were found to be strongly influenced by pressure in the cell, rf voltage applied to the rods, and operating frequency of the ion guide. Lighter ions (m/z 7) were transmitted more efficiently at higher frequencies and reduced rf voltages, while signals for heavier ions (m/z 238) were greater at lower frequencies and elevated voltages. Detection limits with the conventional static ion optics and hexapole collision cell were comparable, in the range of 0.4–2 ng ml−1 and similar when either helium or hydrogen collision gas was used. Precision for the peak height measurement was 5.4% RSD with the hexapole ion guide, slightly better than when static optics were employed (7.3% RSD). The strong signals from 40Ar+ could be reduced by four orders of magnitude through use of hydrogen as a collision gas because of efficient and selective charge-exchange reactions. Isotope ratio precision was found to be counting-statistics limited, with the best precision obtained for the isotopes of silver at 0.043% RSD (n = 7) for 10 million sequentially summed spectra. The mass resolving power (FWHM) of the spectrometer was improved through the use of the hexapole ion-guide assembly (2915) relative to that obtained with static ion optics (1510).
Introduction
Mass spectrometrists and physicists have been using various embodiments of rf-only ion transmission and containment devices for well over 20 years. Teloy and Gerlich first described the guided-beam technique to solve problems in chemical physics;1 later, Gerlich published a treatise outlining the theoretical and practical aspects of ion guides.2 Yost et al.3 described a scheme for performing low-energy dissociation in an rf-only quadrupole chamber of a tandem mass spectrometer. The subsequent development of the triple-quadrupole mass spectrometer has radically changed organic mass spectrometry. Although ion guides have been used for quite some time, most of the theoretical and practical information available pertains to the relatively simple quadrupole-based systems.4Atomic spectroscopists have begun recently to incorporate devices such as a hexapole collision cell and a quadrupole dynamic reaction cell into their plasma-source mass spectrometers in order to change the ion beam in some predictable fashion. Although similar types of hardware are employed in these systems, their purpose and function are quite different.
Tanner and Baranov5,6 have championed use of a quadrupole dynamic reaction cell (DRC) for effecting selective and specific ion–molecule chemistries. A quadrupole geometry is used in the DRC because of its special stability properties and its ability to operate conveniently as a band-pass filter. A reagent gas such as ammonia or hydrogen is admitted into the DRC for the purpose of promoting reactions that can eliminate selected spectral interferences in the atomic mass spectrum (i.e. chemical resolution). In some cases, the interfering ion is neutralized. It is possible also to shift the interferant (or the ion of interest) to another m/z where background levels are lower or isobars do not exist. Collisional dampening and focussing can also be accomplished in the DRC and some control of the reaction pathways can thus be assured. Unfortunately, not all reactions result in interference-free by-products. Gas-phase impurities, such as those resulting from pump oil and solvents, can produce a variety of product ions, increase background levels, and generate new isobars. Selective ion-molecule reactions can also be employed for the removal of troublesome isobars in atomic ion-trap mass spectrometry;7,8 furthermore, buffer gases are used to collisionally dampen ion motion in these devices.9 Houk and co-workers10 have identified some less-common buffer gases (methane, xenon and ethane) that can mitigate problematic isobars in the plasma-source quadrupole mass filter. Clearly, the reaction cell is a valuable tool that can help overcome some interferences in plasma-source (PS) mass spectrometry.
An rf-only ion guide can also be operated as a simple focussing and energy-dampening device, with the anticipated benefit of improved mass resolution and sensitivity.11 The hexapole collision cell (or ion guide, IG) described in this report has been configured to operate in this manner. The cell is pressurized with an inert gas and the ion beam's translational energy reduced through repeated collisions with buffer gas. Concurrently, an electric field inside the ion guide having cylindrical symmetry focuses the ion beam onto the device axis. The goal is to produce a collimated ion beam having a low and well-defined axis energy that is virtually independent of its initial state. Helium is the most commonly employed gas; however, hydrogen can also be used and reacts selectively with argon through well-known channels.8,12–14 The operation of an n-pole for this application is less restrictive than when it is to be used as an ion–molecule reactor; accordingly, a wider variety of trap geometries and configurations might find use. Indeed, we have also conducted experiments coupling an argon glow discharge and ICP to an octapole ion guide and found its performance to be quite similar to that of the hexapole; these data will be the subject of another study.
A hexapole collision cell has been developed and interfaced to our orthogonal extraction time-of-flight mass spectrometer. The performance of this device has been characterized with an inductively coupled plasma (ICP) ionization source. Signal levels were found to be strongly influenced by the operating frequency of the device, rf voltage applied to the rods, and buffer gas density. The argon ion signal was reduced by more than four orders of magnitude when low flow rates (∼5 ml min−1) of hydrogen were introduced into the collision cell. Similar detection limits were measured with the static optics and hexapole ion guide; moreover, comparable sensitivity was obtained with hydrogen and helium buffer gas. Precision was slightly better with the hexapole IG than with static ion optics, and resolving power was enhanced. Isotope ratio measurements for silver were found to be counting-statistics limited and similar to previously reported work with the electrostatic ion optics.15
Experimental
A hexapole ion guide (IG) was designed and constructed in-house and replaces the static ion optics in our orthogonal extraction time-of-flight mass spectrometer (TOFMS).16,17 The IG is positioned between the second and third vacuum stages of the mass spectrometer (see Fig. 1). The hexapole electrodes are constructed from 3.175 mm diameter 314 stainless steel (SS) rods, which have been polished with a 40 µm abrasive cloth. The rods are placed in parallel and symmetrically arranged around a circle having a 3.175 mm radius (also known as the ‘free’ or ‘inscribed’ radius).1,18 Circular stock is used to approximate hyperbolic rods and produces a cylindrically-symmetrical field that confines the ions to the inner portion of the guide.4 The 20 cm long rods are secured to three Macor® (Corning, Corning, NY, USA) supports that are equally spaced along the assembly's length. The rods and supports are enclosed in a SS housing (3.175 cm id) and the rods extended 3 mm beyond the front of this enclosure. A 4.0 mm thick Macor® insulating washer at the assembly exit (third vacuum stage) fills the gap between the housing and ion lens 4 (Fig. 1), creates a vacuum seal (viaO-rings), and provides a 1.0 mm stand-off between the rod ends and this ion lens. A set of 4.0 mm long Macor® spacers were used at the front (second vacuum stage) of the assembly between electrostatic lens 2 (Fig. 1) and the rods. The stand-offs create an opening around the rods, which serves to increase conduction of the cell and provides a 1.0 mm gap between the lens and hexapole array. | ||
| Fig. 1 Diagram of hexapole ion guide installed in the plasma source TOFMS. The cell is enclosed in a grounded SS housing. Lenses 1 and 2 collect and focus the ion beam. Lens 1 is a barrel optic: ions pass into the device through a 1.95 mm hole (nominal) in lens 2. Lens 3 is the hexapole rod array, and can be floated at a potential independent of Vrf and of the other lenses. Ion lens 4 serves as a conduction-limiting orifice between the second and third vacuum stages; the diameter of this orifice (nominally 1.0 or 1.58 mm) can easily be changed to study different gases. Lenses 5 and 6 are simple focussing optics: lens 6 is a barrel optic. The voltage of each lens can be independently adjusted; they are electrically isolated through the use of Macor and alumina spacers. Collision gas is metered in through a manual mass flow controller and enters the cell through a port at the front of the device. The ions are transported between the second and third vacuum stages through the IG. The hexapole directly replaces the static optics, and no further instrumental modifications were necessary. | ||
A time-varying voltage (between 0.2 and 2 V for Vrf 500 V) was observed at ion lenses 2 and 4 during initial testing of the device, a consequence of the rods not being equidistant from each lens. This minor mechanical misalignment was corrected by lapping the rods, which reduced this voltage disparity by a factor of ten. The voltage of each ion lens could be independently adjusted; the SS IG housing could also be biased although it was usually grounded. Ion lens 4 serves as both a conduction-limiting orifice and as a focussing optic. Ion lenses 2 and 4 are 5.0 mm thick, and lens 5 is 2.0 mm thick. The third-stage pressure was nominally less than 4 × 10−6 Torr during the IG experiments, comparable to that realized with static optics.19 The rear barrel optic (lens 6, Fig. 1) retains circular symmetry of the ion beam; however, it might be desirable to transform this into one having planar symmetry through use of a slit. Compensation for spatial distribution of the ion beam is most effective if its width is small relative to that of the extraction zone.15,19 Myers et al.16 have examined the effect of beam shape on TOF resolution and sensitivity. We are currently investigating alternative designs for the rear optic. Typical instrumental parameters are presented in Table 1.
| Ion guide— |
| Frequency/MHz: 3.0 |
| Rod voltage (0-to-peak): 130 |
| Collision gas flow rate/ml min−1: 30–50 |
| Collision gas: helium, hydrogen |
| Front barrel optic voltage, lens 1/−V: 600 |
| Front IG plate voltage, lens 2/−V: 50 |
| Hexapole rod bias, lens 3/+V: 5 |
| Rear IG plate voltage, lens 4/−V: 40 |
| Rear central IG optic voltage, lens 5/−V: 15 |
| Rear barrel optic voltage, lens 6/−V: 225 |
| Time-of-flight mass spectrometer— |
| Repeller frequency/kHz: 12 |
| Repeller voltage/+V: 650 |
| Repeller plate bias/+V: 0 |
| XY steering-plate voltage/−V: 2010 |
| Deflection steering-plate voltage/−V: 2010 |
| Flight-tube potential/−V: 2000 |
| Detector voltage/−V: 4900 |
| Inductively coupled plasma— |
| Forward power/kW: 1.15 |
| Reflected power/W: <5 |
| Nebulizer flow rate (argon)/L min−1: 1.1 |
| Outer flow rate (argon)/L min−1: 16.0 |
| Intermediate flow rate (argon)/L min−1: 1.8 |
| Sample solution uptake rate/ml min−1: 1.1 |
Buffer gas was admitted to the cell through a port at the front of the IG housing, close to where ions enter the device. A diaphragm-type mass flow controller (Brooks Model 8744A, Hatfield, PA, USA) was employed to meter the buffer gas. Flow through this controller was calibrated with a soap-bubble flow meter (1–100 ml min−1) and a wet test meter (>100 ml min−1); flow rates were independently verified by calibration against an electronic flow meter (1159A, MKS, Burlington, MA, USA). Two different buffer gases were tested, and a separate calibration curve was generated for each one. It was not possible to incorporate a pressure measurement device in the collision cell due to the compact design of the IG assembly and limited space in the vacuum chamber.
The rf generator was constructed in-house and is based on a design by Jones et al.20 The dc float (or bias) potential for the rods was supplied by a Hewlett-Packard 6267B power supply; the same voltage was applied to all rods (Mathieu stability parameter a = 0) although provisions exist for other voltage combinations (a ≠ 0).4 Typically, the dc bias voltage ranged from −20 to +20 V. The rf generator output was coupled to the IG assembly via 50 Ω cables and insulated electrical vacuum feed-through connectors (Insulator Seal Inc., Hayward, CA). Similar length electrical connections between the IG and rf generator were used for each channel in order to minimize imbalances in the oscillator circuit. The generator could be varied over a frequency range of approximately 1.6–8.5 MHz, although this could be changed by using other tank coils.20 The oscillator frequency was measured with a Hewlett-Packard 5315A universal counter (Palo Alto, CA, USA). The generator output voltage was adjustable from 20 to 500 V zero-to-peak (40–1000 V peak-to-peak) and has the form of Vrf cos ωt; voltage applied to adjacent rods in the hexapole array is equal in magnitude but 180° out of phase. A Universal Voltronics (Kisco, NY, USA) direct current (dc) power supply provides voltage to the oscillator, which then is converted into the radiofrequency output (Vrf). All references to Vrf in this manuscript are for the 0-to-peak values. The oscillator would not resonate at voltages lower than about 20 V.
The voltage output from the two generator channels (Vrf) was balanced prior to its use with the ion guide. Imbalances are troublesome because they can result in non-zero values for the Mathieu stability parameter a, and they can also create a time-varying voltage at the lenses closest to the rods, thereby generating time-varying fringing fields. The outputs were balanced by empirically optimizing the feedback capacitors in the rf oscillator circuit (see Fig. 1 in ref. 20: 33 pf capacitors located between the vacuum tubes and tank coil) while monitoring the rf generator output on an analog oscilloscope. The rf voltage was stepped down for this measurement by means of a matched pair of 1∶100 oscilloscope probes. Initially, a moderate imbalance was found between the two channels (∼10 V for a Vrf of 500 V), likely a consequence of parasitic capacitances introduced into the circuit during its construction. Furthermore, the rf generator employs a symmetrical oscillator design and variability between electronic components having the same nominal values can exist, contributing to this voltage disparity.
The inductively coupled plasma (ICP) was operated under conventional conditions of gas flow rates and power21–23 listed in Table 1. A Scott double-pass (chilled to 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C) spray chamber and Meinhard pneumatic nebulizer were used for sample introduction. The sampler and skimmer orifices were 1.1 mm and 1.0 mm, respectively. A separate roughing pump was installed on each of the two turbo-molecular pumps (second and third vacuum stages) in order to accommodate the extra gas load, which might originate from use of the collision cell. Previously,17,19 a single roughing pump was used for both turbo-molecular pumps. Analyte solutions were serially diluted with 5% nitric acid from 1000 µg ml−1
(ppm) stock solutions. Precision was better than 7%
RSD, except where noted. Ultra-pure helium and hydrogen gases were purchased from Air Products (Allentown, PA, USA) and used without further purification.
°C) spray chamber and Meinhard pneumatic nebulizer were used for sample introduction. The sampler and skimmer orifices were 1.1 mm and 1.0 mm, respectively. A separate roughing pump was installed on each of the two turbo-molecular pumps (second and third vacuum stages) in order to accommodate the extra gas load, which might originate from use of the collision cell. Previously,17,19 a single roughing pump was used for both turbo-molecular pumps. Analyte solutions were serially diluted with 5% nitric acid from 1000 µg ml−1
(ppm) stock solutions. Precision was better than 7%
RSD, except where noted. Ultra-pure helium and hydrogen gases were purchased from Air Products (Allentown, PA, USA) and used without further purification.
The mass resolution data were collected on a 500 MHz Tektronix digital oscilloscope (TDS520, Beaverton, OR, USA). Detection limit and background count data were collected on an EG&G 9308 picosecond time analyzer (Oak Ridge, TN, USA). Typically, 105 successive mass spectra were summed. At least three replicate measurements (back-to-back) were performed at each experimental set point unless otherwise noted. Several experiments were designed to investigate the relationship between rf frequency and Vrf; a Tennelec quad constant-fraction discriminator (TC454, Oxford Nuclear Instruments, Gaithersburg, MD, USA) was operated in the gated mode such that the count rate at a single m/z (flight-time, 50 ns wide gate) could be measured for various voltages and frequencies. The average value for the peak height or peak area was used to prepare all plots. Data were manually processed and plotted in Kaleidagraph (Synergy Software, Reading, PA, USA).
Results and discussion
The theoretical and experimental implementation of guided-beam methods has been described in a variety of journals over the last few years, including some related to plasma-source mass spectrometry (PSMS).1,6–8,24–30 A number of ion-guide geometries have been described, from the simple quadrupole design31 to the more complex dodecapole.2,32 Our investigations into the use of ion guides initially began with an argon glow discharge coupled to an octapole collision cell that was installed in our right-angle TOFMS.19 However, it was subsequently discovered that a hexapole provided better sensitivity and our focus shifted to this configuration. The hexapole geometry has shown promising results in earlier ICP-MS studies12,29,33 and thus provided us with a point of reference for the present work. It is our intention eventually to evaluate the performance of the octapole and quadrupole designs and compare the figures of merit for all three.The inscribed (or ‘free’) radius of the ion guide is related to the rod diameter by:2,18
 | (1) |
Ion motion in quadrupolar fields has been extensively studied both experimentally and theoretically, for use as a mass filter as well as for rf-only containment and reaction devices.4-6,31,34 Work on higher-order systems is considerably more limited, and debate exists in the literature concerning the best way to model ion movement in these fields; the equations of motion are more complex than in a simple quadrupole because the x-y (transverse) movement cannot be mathematically decoupled. There are even differences amongst the equations used to describe the Mathieu stability parameters.2,4,5,24,36 We have elected to follow the conventions of Tanner and Baranov37 and Dawson4 when reporting values for the stability parameter q:
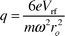 | (2) |
Ideally, the acceptance of the ion guide should be matched with the emittance of the ionization source for best sensitivity and transmissivity;4,42–44 the generous inscribed radius of the current device (3.175 mm) obviated the need to exhaustively optimize these parameters for our initial investigation.
Effect of collision-gas flow rate on signal
The collision gas flow rate strongly influences a number of important parameters: signal levels, mass resolution, background continuum, and energy characteristics of the ions sampled for mass analysis. Let us first investigate the effect of gas flow rate on ion signal levels.The influence of helium flow rate into the cell on normalized analytical signals is depicted in Fig. 2A; three replicates were collected at each set point (f = 3.05 MHz, Vrf = 125 V). The signal at each m/z is seen initially to increase beyond a flow rate of about 5 ml min−1, but to change little over the range from 20 to 40 ml min−1. The signals then decline to a vanishingly small level above 55 ml min−1, likely a result of scattering losses in the system.34 A marginal mass dependence is noted for the gas flow rates; lead optimizes at a slightly higher flow than does cobalt. For these experiments, the third stage conduction-limiting orifice in lens 4 was reduced from 1.58 mm to 1.0 mm in order to probe a range of flow rates. Helium flows in excess of 50 ml min−1 caused the third stage pressure to rise above 8 × 10−6 Torr when the 1.0 mm orifice was in place. These findings were even more pronounced when hydrogen was used as a collision gas. Atomic signal levels in a commercial plasma-source mass spectrometer fitted with a hexapole collision cell have responded similarly to changes in the buffer gas flow rate.12
 | ||
| Fig. 2 Effect of buffer gas introduced into the hexapole collision cell on the normalized ICP-TOFMS signal. The orifice diameter in optic 4 was 1.0 mm, f = 3.05 MHz, Vrf was 125 V, and the rod-offset potential was +2.0 V. The displayed flow rates correspond approximately to pressures in the range of 0.5–20 × 10−3 Torr. A, Helium; B, hydrogen. | ||
Other researchers have also reported a strong correlation between the buffer gas density and mass spectrometric signal; these effects have been attributed to collisional focusing (or dampening) of the ion beam onto the optical axis of the ion guide.5,12,31,45 The optimal pressures within the cell have been reported to be in the range of 8–12 × 10−3 Torr,31,46 although higher pressures have also been used.41,45 It was not possible here to directly measure the pressure in the hexapole collision cell. Moreover, the cell's open architecture likely creates a pressure gradient within the device, which additionally complicates measurement of the collision gas density.
The ion guide initially was operated as a sealed unit, in which gases could escape only through the front and rear orifices. It was possible to measure the pressure in this earlier device by replacing lens 2 (cf.Fig. 1) with an adapter for a Pirani gauge that had a 1.95 mm orifice to simulate gas loading. The pressure was found to be in the range from 0.1 to 15 × 10−3 Torr for buffer gas flows of 0.5–30 ml min−1 (slightly lower flow rates than those used with the open cell). Performance of the closed cell was similar to that of the open architecture in all respects except that the mass spectrometric signal and ion beam currents were unstable and precision was poor (>30% RSD). Plasma gas from the ICP likely entered the cell and compromised the ion-guide's performance by diluting the buffer gas with plasma gas. Argon is less desirable than helium as a collision agent because of its greater mass, potentially increasing scattering losses especially for low mass species.47 Performance of the hexapole ion guide was improved by replacing the solid Macor washer at the cell entrance with stand-offs of similar thickness; this design was used throughout the rest of our experiments.
Helium is used commonly as a collision gas in rf-only devices, although other gases such as hydrogen and ammonia have been employed to effect specific ion–molecule reactions.5,7,8,10,48,49 The hydrogen molecule has several energy states that are closely aligned with those of 40Ar+; therefore, argon ions can be effectively neutralized through a series of charge and proton transfer reactions that yield H2+, H3+ and Ar0.7,8 These reactions are reported to be extremely selective and much faster for Ar+ than for other atomic ions. After reacting, argon neutrals can be pumped away and hydrogen ions will be unstable under ordinary operating conditions (f = 3 MHz, Vrf = 125).8
The effect of hydrogen flow rate on the normalized analyte signal is depicted in Fig. 2B; each point is the average of three replicate measurements. The argon deflection circuitry21 was not employed in these experiments so that the true argon ion signal levels could be tracked. Accordingly, detector gain was lowered to avoid blinding the microchannel plates, which otherwise would reduce their sensitivity for ions arriving at longer flight times.19 The normalized signals in Fig. 2B are not flat over a broad range of gas flow rates, unlike those depicted in Fig. 2A. Instead, the span of optimal hydrogen flow rates was much narrower and the signal exhibits a stronger mass dependence. The optimal flow rate for focussing of the incoming beam by hydrogen was about one half that for helium. Comparable signal levels are obtained for the two buffer gases when the same analyte solution was introduced into the ICP. The mass of the hydrogen molecule is one half that of the helium atom; however, they have approximately the same collisional cross sections, σ (helium = 0.263 nm2, hydrogen = 0.287 nm2),47 suggesting that the mass of the buffer gas particle is an important factor in the cooling process. Tanner and Baranov5 have reported recently that the ion–buffer gas mass ratio critically affects how quickly and efficiently ions are lowered to the collision-gas temperature. Additionally, the hydrogen molecule can disperse energy through additional degrees of freedom not available to helium, which also could explain why signal levels optimize at different flow rates for these gases.
The argon ion signal drops sharply at very low hydrogen flow rates; the signal is reduced by more than four orders of magnitude for a H2 flow rate of only 5 ml min−1. Presumably, this reduction reflects neutralization of argon ion by charge transfer.8,10,14 Lowering the 40Ar+ signal level has several instrumental and spectroscopic benefits.12 The argon deflection pulse is no longer required,19 which simplifies instrumental operation and tuning, and lessens perturbations in the field-free region that can negatively impact an ion's trajectory. The formation of polyatomic argides and therefore spectroscopic interferences should also be reduced if the argon ion population is diminished.5,10,50 Mixtures of hydrogen and helium might be useful in simultaneously reducing the argon ion signal and collisionally dampening the beam. Encouraging results demonstrating the use of mixed gases have recently been published for a hexapole collision/reaction cell.12
Effect of rf voltage on analyte signal levels
The rf voltage is another parameter that can affect an ion's stability in the collision cell. The normalized analyte signal over a range of rf voltages is illustrated in Fig. 3. Each point on the graph is the average of three replicate measurements. The helium flow was 30 ml min−1 and f = 3.01 MHz. The q values for these ions were all less than 0.25, except for lithium (q = 0.91). However, the lithium signal was more than one and a half orders of magnitude lower than that of other constituents (for equal analyte concentrations, µg ml−1). The signals rise in concert with Vrf (which corresponds to increasing values of q, see eqn. 2), reach an apex, and then decline as the ions become unstable. The signals are seen to retain about 50% of their maximum count rate over a Vrf span of 75–100 V. The bulk ion beam current measured at lens 4 responded similarly to changes in Vrf (data not shown). There exists no single Vrf at which all ions are transmitted with the same efficiency (for a constant frequency), although it is possible to transmit a range of m/z values (18–238) at one common set point. Comparable results were obtained at different IG frequencies (f = 1.65, 5.01 MHz); however, these frequencies correspond to different m/z transmission windows.4 The results of Fig. 3 closely mimic those reported by Xu and co-workers29 for a hexapole ion guide coupled to an arc discharge; the transmitted ion beam current and corresponding mass spectrometric signal respond strongly to the rf voltage. | ||
| Fig. 3 Normalized ICP-TOFMS signal as a function of rf voltage applied to the rods, at a constant frequency of 3.01 MHz and a rod-offset potential of +2.0 V. The helium buffer gas flow rate was 30 ml min−1. The orifice diameter in optic 4 was 1.0 mm. | ||
The magnitude of the rf voltage applied to the ion-guide assembly also influences the TOFMS resolving power; this relationship is presented in Fig. 4 for 107Ag+. Each datum in Fig. 4 is the average of two replicate measurements. The spectrometer was tuned for the largest signal so data could be obtained over a broad dynamic range. Resolution is found to be strongly influenced by the rod voltage and is greatest when q = 0.17 (Vrf = 105, f = 3.01 MHz, m/z = 107); this voltage also corresponds to the highest signal level. The TOF resolving power changes by more than two-fold over the range of voltages tested (25–210); similar correlations were also found for cobalt and lead. Energy dampening is most effective when q values are small (<0.3) because ion energy is virtually unaffected by the rf field (adiabatic approximation).2,38 Collisional focussing concurrently drives the ions towards the optical axis, which is where the rf field is lowest and least likely to alter the ion beam's KE distribution.1,2
 | ||
| Fig. 4 Mass resolving power of the TOFMS as a function of rf voltage applied to the rods, measured for silver at a constant frequency (f = 3.01 MHz), buffer gas flow rate of 30 ml min−1 and rod offset potential of +2.0 V. | ||
Mass resolution in TOFMS is strongly influenced by the spatial and energy distribution of the ion beam.11,15,19,41 The hexapole collision cell produces a spatially compact beam that has well-defined energy characteristics, which simplifies transport into the extraction region and improves mass resolving power.
Signal versus ion-guide frequency
Frequency is another important factor that governs the stability of an ion in the collision cell (see eqn. 2). A simple way to map out regions of stability for specific m/z values is to sweep the rf generator across a range of frequencies (while holding Vrf constant) and measure the signal level at each set point. The normalized ICP-TOFMS signals for lead, argon and lithium are presented as a function of frequency in Fig. 5; other ions (165Ho+, 63Cu+, 107Ag+) exhibited similar behavior but have been omitted for clarity. Each point in Fig. 5 is the average value of three observations. In general the signals increase with frequency, reach a plateau, and then decline. Ion transmission occurs over a broad range of frequencies (ca. 2–3 MHz) for each species while retaining at least 50% of the peak signal level. The 7Li+ signal appears to optimize over a slightly broader frequency range than do other ion signals. The complete response curve for lead cannot be viewed because the tank coil limits the frequency range. At the apex of the analyte response curves presented in Fig. 5, the q values are: lead = 0.29, argon = 0.20, lithium = 0.56. | ||
| Fig. 5 Normalized ICP-TOFMS signal as a function of the rf generator frequency at a constant Vrf of 125 V and a rod offset potential of +2.0 V. The helium buffer gas flow rate was 30 ml min−1. The orifice diameter in optic 4 was 1.0 mm. | ||
The optimal rf frequency for transmission of a specific m/z (constant q) is quadradically related to Vrf (see eqn. 2); experimentally, this relationship is depicted in Fig. 6 for 63Cu+. Output from the detector preamplifier was presented to a gated CFD and the rf voltage producing the highest count rate at each discrete frequency (17 levels) was recorded: two measurements were made at each level. The signal level was not uniform across this frequency range (cf.Figs. 3 and 5). An excellent correlation was found to exist between the square root of Vrf and frequency (f = 2.1 × 105V0.5rf, R > 0.99); similar correlations were also noted for iron and lead.
 | ||
| Fig. 6 The rf voltage producing the greatest signal level for copper was measured at various generator frequencies. The detector preamplifier output was sent to a constant fraction discriminator and universal frequency counter. Helium buffer gas flow rate was 30 ml min−1, and a rod offset potential +2.0 V employed. | ||
It appears unlikely that a single frequency can be used to transmit all atomic species with equal efficiency. Instead, light analytes are best transmitted at higher frequencies (and low Vrf), while heavier species are transmitted more efficiently at reduced rf frequencies (and elevated Vrf).4 Similar results have been reported by Tanner and Baranov,5 who mapped the m/z 56 signal strength as a function of q in their DRC.
Ion transmission and selection in the quadrupole mass filter is accomplished by scanning simultaneously the rf voltage (q) and dc difference potential (a).51 Mass selection also can be accomplished by scanning the operating frequency52 although this mode of operation is less common. Qualitatively, the same results are noted for the hexapole IG; ion stability and transmission are related to both the frequency (f) and voltage (Vrf). Moreover, the IG's low and high mass cut-off will be determined by the ion stability parameters, which in turn are defined by Vrf, ω, and the dc difference potential. Similar results have been reported for the analysis of biomolecules using an octapole collision cell interfaced to a quadrupole ion trap.30 Tanner and Baranov5,37 found it possible to operate their DRC as a limited band-pass device by selecting the appropriate values of rf frequency, voltage, and difference potential applied to the rods. Transmission efficiency in an rf-only containment device can be improved potentially by scanning Vrf in concert with that of a quadrupole mass filter located downstream of the ion guide.5
Field distortions are known to impact on performance characteristics of quadrupole mass filters4 and they also could be problematic for rf-only devices. Several types of distortions have been identified: fringing fields, geometrical faults such as those related to misaligned rods, higher-order harmonics mixed in with the rf voltage, and local imperfections such as contamination of rod surfaces. The rf generator used in these experiments does produce some higher-order harmonics (data not shown), and it is unclear to what extent these might negatively influence its operation.4,32,39 Efforts are currently under way to identify and eliminate these potentially harmful overtones. Rf-only devices have been reported to be less susceptible to mechanical misalignments than quadrupole mass filters2,4 and these are not expected to significantly impair performance of the IG used in these experiments.
Effects related to the focussing optics
The analyte signal also depends strongly upon the ability of the focussing optics to get ions into and out of the hexapole. An electrostatic barrel optic (lens 1, Fig. 1) is positioned directly behind the grounded skimmer and is used to collect ions and partially collimate the beam.21 The ion beam then impinges upon electrostatic optic 2 (cf.Fig. 1), which passes ions into the hexapole through a 1.95 mm orifice. Larger diameters for the lens 2 orifice were qualitatively found to increase background counts (2–5×), presumably a consequence of Ar0 entering the cell.The normalized ICP-TOFMS ion signal level for several m/z values as a function of the front barrel optic voltage is presented in Fig. 7A; each datum is the average of three replicate observations. The ion-guide frequency was set to 3.01 MHz, Vrf to 125 V, and the rod bias was +2 V. The voltage for lens 2 was held constant during these studies at −50 V. A wide range of m/z appears to be uniformly transmitted over a span of lens voltages from −400 to −800 V dc; the optimal values are about two times lower than those used with static optics.19 The analyte signal responds similarly to changes in the front plate voltage (see Fig. 7B) and useful analyte signals arise over a range of settings from −10 to −600 V dc; lens 1 was held at −400 V for this study. Results for 165Ho+ (three replicates) in Fig. 7B are representative of those for other elements such as cobalt and lead. The ions experience a decelerating field as they pass through lens 2 and enter the collision cell, which reduces their velocity. The number of rf cycles that an ion spends in the fringing field of a quadrupole mass filter is known to influence the analyzer's sensitivity;4 this number of cycles can be controlled in the IG by the combined effects of lens potentials and buffer gas pressure.
 | ||
| Fig. 7 Normalized ICP-TOFMS signals as a function of the voltage applied to the focussing optics with other potentials held constant. Ion guide operated at a frequency of 3.01 MHz, Vrf of 125, buffer gas flow rate (helium) 30 ml min−1. A: Front barrel optic (lens 1, Fig. 1), lens 2 held at −50 V, rod offset was +2.0 V. B: Front plate (lens 2, Fig. 1), barrel optic held at −400 V, rod offset +2.0 V. C: Offset potential of the hexapole rod assembly (lens 3, Fig. 1), barrel optic voltage −400, front plate voltage −50 V. | ||
The dc float (or bias) potential of the ion-guide rods also affects ion focusing through the device. The normalized signal as a function of bias potential is depicted in Fig. 7C for several m/z values. The front barrel optic (lens 1) and plate (lens 2) voltages were set to −400 and −50 V, respectively, each point being the average of three replicate measurements. The heavier ions appear to be more strongly influenced by the bias potential at lower settings; however, all ions optimize at about the same voltage (+11 V) and simultaneously decline beyond this value. Overall, signal levels drop by about 50% over the bias range of +10 to +20 V. It is also possible to focus ions through the device with negative float potentials; however, the voltage range providing acceptable transmission is considerably more limited (0 to −5 V). Feldmann and co-workers12 report that analyte signal levels in a commercial hexapole-PSMS are strongly impacted by the hexapole bias potential, consistent with results in Fig. 7C. Moreover, Feldman12 used the hexapole rod bias as an energy barrier whereby low-energy polyatomic species formed in the collision cell were prevented from entering the mass analyzer, which can simplify the mass spectrum and discriminate against harmful isobars.
The optimal XY steering-plate potential was found to correlate (R > 0.99) with the rear barrel optic voltage (lens 6, Fig. 1) and reflects how beam velocity can be modified by this potential (data not shown). The voltage supplied to lens 6 was kept as low as possible to minimize its influence on the ion-beam energy. Furthermore, the optimal set points for the rear optics did not vary by more than 20% from values listed in Table 1.
The transmission of the hexapole collision cell was estimated by monitoring the beam currents collected at various ion lenses.29,31 The ion beam current impinging upon ion lens 2 (see Fig. 1) was found to be 0.9 µA at typical operating voltages (−150 V). The rf voltage was removed from the IG and a total current of 19.1 nA was collected at the six rods. Thus, only a small fraction of ion flux present at lens 2 enters the rod assembly (19.1 nA/900 nA or 2.1%). The current was then measured at lens 4 and found to be 15.5 nA while it was held −300 V; rf was applied to the hexapole rods during this latter test and adjusted for optimal argon ion transmission (f = 3.05 MHz, Vrf = 66). Moreover, optics 5 and 6 were back-biased at +100 V to discourage ions from passing through the 1.58 mm orifice in optic 4.45 Ion transmission down the rods was calculated to be 81% (15.5 nA/19.1 nA). Xu29 reports that almost 90% of the ion beam current extracted from a low-pressure helium arc discharge can be transmitted through a hexapole ion guide; similar measurement techniques were used in their study as in the present one.
The ion current passing through the orifice in lens 4 was also measured. As mentioned above, the total current impinging upon the lens was found to be 15.5 nA. When the back biases (+100 V, lenses 5,6) were removed, the ion current at lens 4 dropped to 7.5 nA, indicating that 8.0 nA had passed through the 1.58 mm diameter hole, or 51.6% (8.0 nA/15.5 nA). Presumably, if the rear orifice were enlarged by 1.94-fold (100/51.6), sensitivity could be enhanced by passing a larger fraction of the beam current into the mass analyzer.45 Transmission efficiency through the conduction-limiting orifice might be improved by using an rf-only quadrupole to generate a more compact ion beam;6 alternatively, the same result might be obtained by using smaller diameter rods for the hexapole (see eqn. 1). The IG assembly also could be housed in a separate vacuum chamber having a dedicated set of pumps, which would permit the use of a larger orifice and higher gas flow rates. These options are currently under investigation in our laboratory.
The ion beam current is more efficiently transported through the hexapole IG than through the static optics; however, a direct comparison of these two systems should be viewed with caution because of their obvious differences. The beam current passing through the conduction-limiting orifice of the static optics21 was 900 nA but only 7.1 nA of this reached the extraction zone, suggesting an overall transport efficiency of 0.8% (7.1 nA/900 nA) through this lens stack. The IG performs much better; about 42% of the current collected at the rods enters the extraction region (8.0 nA/19.1 nA). Yet, sensitivity for the two ion optical systems is similar, which would appear to contradict these results. The answer appears to lie in the need for conduction-limiting orifices (lenses 2 and 4, Fig. 1) at the ends of the collision cell. As was indicated above, only about 2% of the impinging ion current passes through lens 2; 50% of the remainder is intercepted by lens 4, giving the entire IG assembly roughly the same transmission as the static optics. Clearly, performance will be improved if a better way can be found to focus the incoming beam through the entrance aperture in lens 2. Ion funnels53,54 and other devices might prove effective.
Eliminating the vertical steering-plate bias
One limitation of the orthogonally extracted TOFMS is a mass-dependent steering-plate bias15,55 that originates from the sampling of an atmospheric pressure ionization source. As a result of the supersonic expansion, all ions and neutrals are transported at the same velocity (v), so ions acquire a mass (m) dependent kinetic energy (KE = ½mv2).22,56 Consequently, a common steering-plate voltage cannot be used to direct all of the ions through the flight-tube with equal efficiency; this disparity is illustrated in Fig. 8A for an ICP ion source and traditional static ion optical arrangement. The average value from three replicate measurements was used for each datum in Figs. 8A and B. The optimal voltages differ by approximately 70 V (7Li+ to 238U+); similar results have been noted by other researchers.55,57 This mass-dependent bias complicates tuning the spectrometer over a wide mass range and can compromise sensitivity.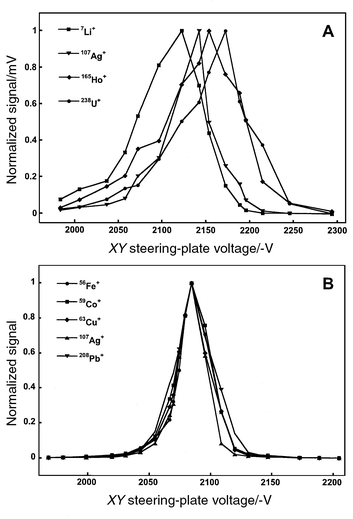 | ||
| Fig. 8 Normalized ICP-TOFMS signal as a function of the XY (vertical) steering-plate potential for different ion-lens configurations. A: Static ion optics. The disparity of these tuning voltages is due to the mass-dependent energy imparted to ions during supersonic expansion of the beam. B: Hexapole ion guide with helium buffer gas (30 ml min−1), f = 3.01 MHz, Vrf = 125 V. The mass-dependence noted in Fig. 8A has been eliminated because the axial energy of the ion beam has been reduced as a result of multiple collisions with buffer gas. | ||
Rf-only collision cells have been used to modify the energy characteristics for a variety of ionization sources.1,29,41,58 The axial energy of the ions is dampened through multiple interactions with the buffer gas. Thermalization implies that all ions acquire the same mean kinetic energy; the steering-plate bias can therefore be eliminated as depicted in Fig. 8B. This modification overcomes one of the primary limitations of the orthogonal extraction geometry for TOFMS. The voltage span (FWHM) displayed in Fig. 8B also suggests that the energy distribution of the beam is smaller than that for the static optics (cf.Fig. 8A).
Energy properties of the ion beam
Resolution and sensitivity can be limited by the ability to efficiently focus, direct, and transport the ion beam into a TOFMS. The task becomes more difficult as the average energy and energy distribution of the ion beam increases.59 Obviously, it would be desirable to have an ion transport mechanism whose operation is independent of the ionization source and which always produces a beam of ions having the same energy profile. A collision cell can be used to accomplish this goal; energy dampening and collisional focussing in the hexapole can be used to control the energy characteristics of the ion beam that is presented to the mass analyzer.The ICP produces an ion beam with a potentially broad energy spread (upwards of 10 eV) and a mean kinetic energy of 5–30 eV;22,23 the exact values vary from day-to-day and are strongly influenced by experimental variables. The supersonic expansion also contributes to the axial energy of the ions, up to ∼5 eV for 238U+.22,56 The energy of the ICP ion beam in the present experiments was measured with the static optics in place and the most probable energy (MPE) was found to be 8 eV with an energy spread of 6 eV full width at half maximum (FWHM).
The technique used to measure the ion-beam energy has been documented elsewhere17 and is similar to that used in other studies.60,61 Accordingly, only a brief description will be provided here. Beam energy was measured by applying a stopping voltage to a grid affixed to the front of a Faraday cup located outside the TOF extraction region. A programmable power supply incrementally and automatically increased the stopping voltage (in 0.1 V steps) and the ion-beam current measured at each step. A Gaussian curve was mathematically fitted to the first derivative of the ion-beam current versus stopping voltage; the most probable energy and energy distribution of the beam were obtained from the equation of fit. The precision of this measurement was 5% RSD and χ2 used to evaluate the quality of fit to the data.
The energy characteristics of an ion beam passing through a pressurized hexapole collision cell are quite different than for one that is transported by static optics. In a collision cell, the translational energy of the ion beam can be significantly reduced after a sufficient number of collisions occur between the ions and bath gas atoms.2,5,31,47 The efficiency of this process depends upon the collisional cross sections (σ) and mass ratio of ions and atoms,5 collision-gas thickness (CGT),46 and the collisional partners numbers of degrees of freedom. The effect of collision-gas flow rate on the axial energy of an ICP ion beam is depicted in Fig. 9. Very low gas flows (<5 ml min−1) do not appreciably affect the beam energy but dampening effects are pronounced at flow rates exceeding ca. 30 ml min−1. The energy of the beam is noted to increase slightly with flow rates between 3 and 8 ml min−1. This rise could be related to frictional heating of the ions as they enter the cell; this behavior will be discussed in more detail later. Ultimately, at a He flow of 50 ml min−1, the energy was reduced by more than seven fold to less than 1.0 eV. Higher collision-gas flow rates (>55 ml min−1) were not tested due to ion-scattering losses and a consequent reduction of ion-beam current by more than 100-fold. Mass spectral signals were also very low at these elevated flows, as seen in Fig. 2A. Energy dampening has been observed for biomolecular ions electrosprayed into a quadrupole collision cell coupled to an orthogonal-extraction TOFMS,11,41 which improved instrumental sensitivity and mass resolution.
 | ||
| Fig. 9 Changing the axial energy of the ICP ion beam by passing it through a hexapole IG pressurized with helium buffer gas (50 ml min−1). The beam energy (principally 40Ar+) was measured by applying a stopping potential to a grid affixed to the front of a Faraday cup. The ion guide was operated at 3.01 MHz and Vrf of 125 V. The orifice diameter in lens 4 was 1.0 mm. | ||
The energy distribution of the argon ion beam is also reduced through pressurization of the collision cell with a buffer gas. Fig. 10 illustrates a typical stopping-potential curve measured at the Faraday cup; helium flow was 40 ml min−1, f = 3.01 MHz and Vrf set to 65 V. The beam current was reduced by more than 90% over a stopping voltage of 1.5 eV, which suggests an energy spread of 1.9 eV (FWHM). Lower energies were obtained at higher helium flow rates (<1.3 eV); however, the beam current and mass spectrometric signals were too low to be of practical utility. Similar modifications in ion-beam energies have been reported for hexapole ion guides coupled with an arc discharge29 and electrospray ionization source.41
 | ||
| Fig. 10 Energy distribution for the ICP hexapole ion beam. The energy drops by more than 90% over a span of 1.5 eV; this corresponds to an energy spread of 1.9 eV (FWHM). The IG was operated at a frequency of 3.01 MHz, 65 V Vrf, and +2.0 V as a rod offset. The orifice diameter in lens 4 was 1.0 mm. | ||
The energy distribution of the ion beam does not decline linearly with an increase in buffer gas density; instead, it actually broadens at low flow rates (below 12 ml min−1, see Fig. 11). At gas flows exceeding 40 ml min−1, the energy spread drops to 1.9 eV. Baranov and Tanner6 have recently modeled the behavior of ions in a high-pressure quadrupole reaction cell. They report that ions experience a net increase in radial and centrifugal energy immediately following their movement into the high-pressure region of the reaction cell and then quickly lose this energy through additional collisions with bath gas. This behavior is consistent with data displayed in Fig. 11, although energy is monitored not as a function of time but rather as the bath-gas number density. For low gas flow rates (corresponding to the initial entry of ions into the cell) the neutral atom-number density is too low to significantly reduce the ion-beam energy. At intermediate pressures (or a short residence time in the IG) the limited number of collisions heat up the ions but are too few to efficiently cool the beam. At even higher flow rates (or a long time in the cell), energy is dissipated through many collisions and the distribution lowered to near-thermal levels. This description of the cooling process explains why the MPE rises slightly at low gas flow rates (cf.Fig. 9) and then drops as the helium flux increases. Ions injected into a high-pressure drift tube are noted to exhibit similar behavior; initial heating of the beam followed by rapid quenching of the energy.62
 | ||
| Fig. 11 Energy spread (FWHM) of the ICP ion beam at various helium buffer gas flow rates. The ion guide was operated at 3.01 MHz, 125 V Vrf, and a +2.0 V rod bias. | ||
Instrumental figures of merit
Detection limits were measured with the hexapole ion-guide system in place, each collision gas (He, H2) was separately tested. For comparison, the detection limits were measured also with the electrostatic optics in place: these are included in order to account for changes in detector sensitivity and other variables (nebulizer, torch, sampler/skimmer) that might compromise a fair comparison. Results are summarized in Table 2. Measurements were all made at the same f (3.02 MHz) and Vrf (125 V) with the exception of those for lithium, which were obtained at f = 5.0 MHz, Vrf = 26 V (see Figs. 3 and 5). The detection limits for the IG system are similar to those of the static optics and within a factor of ten for all elements tested. Detection limits were calculated according to:63 | (3) |
| Analyte | He buffer gas | H2 buffer gas | Static optics | |||||
|---|---|---|---|---|---|---|---|---|
| 1.0 mmb | 1.58 mmb | 1.0 mmb | ||||||
| ppbc | cpsc | ppb | cps | ppb | cps | ppb | cps | |
| a Detection limits (µg L−1) calculated at 3σ, minimum of five replicates. Blank signals were measured off-peak at a m/z adjacent to the analyte. b Diameter of the third-stage conduction-limiting orifice. c Concentration units: µg L−1; sensitivity: cps ppb−1 in the ion beam. d Lithium measured at 5.0 MHz, Vrf = 26, all others at 3.02 MHz, and Vrf = 125. | ||||||||
| 7Lid | 1.1 | 85 | 0.4 | 211 | 1.1 | 78 | 0.4 | 197 |
| 59Co | 1.2 | 79 | 0.5 | 181 | 1.9 | 72 | 0.5 | 185 |
| 64Zn | 2.7 | 66 | 1.2 | 155 | 2.9 | 65 | 3.7 | 64 |
| 107Ag | 2.0 | 70 | 0.7 | 193 | 2.2 | 70 | 3.1 | 68 |
| 114Cd | 2.9 | 62 | 1.1 | 152 | 6.0 | 48 | 7.1 | 57 |
| 165Ho | 3.3 | 58 | 1.2 | 168 | 6.9 | 45 | 3.3 | 74 |
| 208Pb | 6.2 | 45 | 2.0 | 146 | 4.3 | 52 | 6.4 | 53 |
| 238U | 8.2 | 36 | 3.5 | 95 | 4.2 | 56 | 5.2 | 47 |
The transmission efficiency of the ion guide was shown above to be a function of both the rf voltage and frequency (cf.Figs. 3, 5). Table 3 suggests the improvements that could be realized by tailoring the operating conditions for specific m/z values. In this case, signals were monitored on the analog oscilloscope and adjusted for greatest intensity, then detection limits were measured by means of ion counting (100 k sequentially summed spectra, three replicates). Dramatic changes in detection limits (greater than 100-fold) were observed when the signal level was optimized for a particular mass-to-charge ratio, as compared with that of a generic global optimization. Moreover, employing a computer controlled power supply (Vrf) and frequency generator (f) should further improve detection limits because it would then be possible to accurately and precisely define the optimal set points (q) for each analyte.
| Frequency (Vrf)b | 59Co+ | 165Ho+ | 208Pb+ | 238U+ |
|---|---|---|---|---|
| a Peak height measured for the primary isotope of the element in a 100 ppb solution, prepared in 5% HNO3, helium buffer gas, 1.0 mm conduction-limiting orifice in lens 4, detection limits calculated at 3σ, minimum of five replicates. Blank signals were measured off-peak at a m/z adjacent to the analyte. b Frequency reported in MHz, rf voltage is 0-to-peak. | ||||
| 1.48 (117 V) | 27.0 | 1.7 | 1.8 | 0.9 |
| 3.09 (132 V) | 2.1 | 11.3 | 13 | 6.0 |
| 4.08 (108 V) | 0.8 | 243 | 390 | 325 |
The detection limits reported in Table 3 are several orders of magnitude worse than some of the best values being reported for commercial plasma-source mass spectrometers.34,50 These disappointingly low values appear to originate from our use of in-house built accessories (samplers, skimmers, nebulizers, torches) as both ion optical systems exhibit comparable sensitivity. Nonetheless, this study documents the relative changes that can be reasonably expected when a rf-only hexapole collision cell is used in place of conventional static optics.
Previous work65 has demonstrated that background counts in this TOF instrument result from charge exchange with neutral species that subsequently initiate detector events. The continuum background is on the order of 1000–6000 counts per second (measured over a 50 ns window, 100 k summed spectra) with the static ion optical arrangement. Energy discrimination (ED)65 was developed as a method to lower the background and thereby improve the signal-to-noise ratio; with this technique the background counts are reduced to 10–15 cps over the same 50 ns window.65 The collision cell also serves to reduce the background continuum, presumably by serving as an efficient ion-neutral separator; analyte ions are well separated from neutral plasma gas species and selectively transferred into the TOF.29Fig. 12 shows detector background counts as a function of helium flow rate into the collision cell; the number of counts drops rapidly as the helium flow rate exceeds 8 ml min−1. At each flow rate in Fig. 12, the total number of ion hits across a 50 ns window were counted for 100 k successively summed spectra. The IG was configured for optimal argon ion transmission for this experiment (f = 3.05 MHz, Vrf = 66). Because helium comprises the majority of gas that enters the system and has a high ionization potential, charge exchange with 40Ar+ is unlikely. Of course, charge exchange with hydrogen could lower background counts even if its partial pressure were low (cf.Fig. 2B). Hydrogen is often found in the buffer gas as an impurity (ppm levels) and H2 could even be formed in the plasma through reduction of water. Unfortunately, background counts measured with the collision cell in place are of the same magnitude as when ED is employed with the static optics; thus, no net gain in the signal-to-noise ratio is realized for comparable signal levels. However, ED has been shown to slightly compromise the performance of TOF and its removal should improve mass resolution.65
 | ||
| Fig. 12 Lowering of the background continuum with the hexapole IG as the He buffer gas flow rate increases, f = 3.05 MHz, Vrf = 66 V. The lens 4 orifice diameter was 1.0 mm. The y-axis represents total number of noise counts collected over a 50 ns window for 100 k successively summed spectra. The average number of counts measured for the static optics is 1000–6000 under similar conditions. | ||
The isotope ratio precision for this instrument was earlier shown to be limited by counting statistics.15 The isotope ratio for silver (107Ag+/109Ag+, 3 µg ml−1) was measured with the IG in place and again precision was found to be limited by counting statistics; the best precision obtained was 0.046% RSD (n = 7) for 10 million sequentially summed spectra. A large orifice diameter (1.58 mm) was used in lens 4 to maximize ion throughput; approximately 8.5 million ions were collected for each silver isotope. The isotope ratio precision for a sequence of 50 million summed spectra was actually worse (0.11% RSD), primarily because of signal fluctuations and a general decline over this lengthy collection period (6 replicates, total of 5.5 h). Signal losses were related to changes in the optimal steering-plate voltages and plasma positioning; unfortunately, instrumental drift can negatively impact reproducibility as the data-collection period increases. Bandura and Tanner66 report an external isotope ratio precision for silver (40 ng ml−1, 105 min analysis time) of 0.023% RSD using a commercial DRC ICP-MS. Feldman and coworkers50 used an ICP quadrupole MS with an rf-only hexapole collision cell to measure the isotope ratios of 206Pb+/208Pb+ and found precision to be 0.0862% RSD for ten replicate measurements. Feldman's instrument employed a Daly cup with optical detection, which precludes a direct comparison to ion-counting data but demonstrates attainable precision.
A useful improvement in the mass resolving power (t/2Δt at FWHM) was realized with the hexapole ion-guide assembly in place. Resolution data were collected on the digital oscilloscope, with 10 averages collected for the isotopes of silver. Five replicates were collected at each set point; the average value of these measurements is reported in Table 4. Data were collected with hydrogen and helium buffer gases. Additionally, two different conduction orifice diameters for lens 4 (1.0 and 1.58 mm) were evaluated. The best resolving power was found with helium buffer gas (2915) and the small orifice. Apparently, the reduced orifice size serves to restrict the angular and radial acceptance of the lenses that subsequently transport the ion beam into the TOF;67 moreover, ions are sampled closer to the center of the ion-guide axis where perturbations to their motion are minimized by the low rf field. This filtering process was not as effective when the larger orifice was employed so a lower mass resolving power (2320) was obtained. Importantly, this improved resolving power approaches that specified for some commercial “high-resolution” ICP mass spectrometers (R = 3000).
| Ion optics | Buffer gas | Orifice diametera | Resolving powerb |
|---|---|---|---|
| a Orifice in lens 4 (see Fig. 1), units of millimetres. b Measured as t/2Δt, 10 averages collected on the digital oscilloscope, analyte concentration 10 ppm. c Not applicable. | |||
| Static | —c | —c | 1510 |
| Hexapole | Helium | 1.0 | 2915 |
| Hexapole | Helium | 1.58 | 2320 |
| Hexapole | Hydrogen | 1.0 | 2260 |
Conclusions
A hexapole collision cell has been developed and incorporated into an orthogonal PS-TOFMS; an ICP was used in these characterization studies. The ion beam could be effectively cooled using helium as a buffer gas, with both translational energy and energy distribution of the argon ion beam being significantly reduced. Hydrogen also works well as a collision gas, and can be used to reduce the argon ion signal via charge exchange reactions. The analyte signals were found to be strongly influenced by rf voltage, frequency, and collision gas flow into the cell. It was not possible to transmit all atomic species (1–238 u) through the IG with equal efficiency under a single set of experimental conditions. Detection limits for the hexapole IG and static ion optics were found to be comparable. In addition, similar detection limits were found with both helium and hydrogen buffer gases. Mass resolving power was nearly doubled with the hexapole IG as compared to operation with static optics; both buffer (H2, He) gases can be used to effect this improvement. Isotope ratio precision for silver was found to be counting-statistics limited.Acknowledgements
Funding was provided in part by the Department of Energy through grant #DE-FG02-98ER14890, ICI Technologies and by Merck Research Laboratories. JPG would like to thank Eli Lilly & Co. and the Department of Education for Fellowship support. Andrew Alexander of the Electronic Instrument Services group (IUB) constructed the rf generator. Mechanical Instrument Services group (IUB) fabricated the IG assembly. JPG would also like to thank Scott Tanner (PE-Sciex) for helpful comments and discussions. William Wetzel (Hieftje Group) assisted with collection of data for Figs. 2A and B.References
- E. Teloy and D. Gerlich, Chem. Phys., 1974, 4, 417 CrossRef CAS.
- D. Gerlich, in Advanced Chemical Physics, eds. C. Y. Ng and M. Baer, 1992, vol. 82, p. 1 Search PubMed.
- R. A. Yost, C. G. Enke, D. C. McGilvery and J. D. Morrison, Int. J. Mass Spectrom. Ion Processes, 1979, 30, 127 CrossRef CAS.
- P. H. Dawson, Quadrupole Mass Spectrometry and its Applications, American Institute of Physics, Woodbury, NY, 1995 Search PubMed.
- S. D. Tanner and V. I. Baranov, J. Am. Soc. Mass Spectrom., 1999, 10, 1083 CrossRef.
- V. I. Baranov and S. D. Tanner, J. Anal. At. Spectrom., 1999, 14, 1133 RSC.
- G. C. Eiden, C. J. Barinaga and D. W. Koppenaal, J. Anal. At. Spectrom., 1996, 11, 317 RSC.
- G. C. Eiden, C. J. Barinaga and D. W. Koppenaal, Rapid Commun. Mass Spectrom., 1997, 11, 37 CrossRef CAS.
- R. E. March, J. Am. Soc. Mass Spectrom., 1997, 32, 351 CrossRef CAS.
- J. T. Rowan and R. S. Houk, Appl. Spectrosc., 1989, 43, 976 Search PubMed.
- I. V. Chernushevich, W. Ens and K. G. Standing, Anal. Chem., 1999, 452A–461A CAS.
- I. Feldmann, N. Jakubowski and D. Stuewer, Fresenius' J. Anal. Chem., 1999, 365, 415 CrossRef CAS.
- C.-L. Liao, R. Xu, G. D. Flesch, M. Baer and C. Y. Ng, J. Chem. Phys., 1990, 93, 4818 CrossRef CAS.
- C.-L. Liao, R. Xu, S. Nourbakhsh, G. D. Flesch, M. Baer and C. Y. Ng, J. Chem. Phys., 1990, 93, 4832 CrossRef CAS.
- P. P. Mahoney, S. J. Ray and G. M. Hieftje, Appl. Spectrosc., 1997, 51, 16A Search PubMed.
- D. P. Myers, G. Li, P. P. Mahoney and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1995, 6, 400 CrossRef.
- J. P. Guzowski, J. A. C. Broekaert, S. J. Ray and G. M. J. Hieftje, J. Anal. At. Spectrom., 1999, 14, 1121 RSC.
- Y. Huang, S. Guan, H. S. Kim and A. G. Marshall, Int. J. Mass Spectrom. Ion Processes, 1996, 152, 121 CrossRef CAS.
- D. P. Myers, G. Li, P. Yang and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1994, 5, 1008 CrossRef CAS.
- R. M. Jones, D. Gerlich and S. L. Anderson, Rev. Sci. Instrum., 1997, 68, 3357 CrossRef CAS.
- D. P. Myers, G. Li, P. P. Mahoney and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1995, 6, 411 CrossRef.
- K. E. Jarvis, A. L. Gray and R. S. Houk, Handbook of Inductively Coupled Plasma Mass Spectrometry, Chapman and Hall, New York, NY, 1992, 30–31 Search PubMed.
- A. Montaser, Inductively Coupled Plasma Mass Spectrometry, Wiley-VCH, New York, NY, 1998 Search PubMed.
- I. Szabo, Int. J. Mass Spectrom. Ion Processes, 1986, 73, 197 CrossRef CAS.
- P. Tosi, G. Fontana, S. Longano and D. Bassi, Int. J. Mass Spectrom. Ion Processes, 1989, 93, 95 CrossRef CAS.
- C. Hagg and I. Szabo, Int. J. Mass Spectrom. Ion Processes, 1986, 73, 277 CrossRef.
- C. Hagg and I. Szabo, Int. J. Mass Spectrom. Ion Processes, 1986, 73, 295 CrossRef.
- C. Hagg and I. Szabo, Int. J. Mass Spectrom. Ion Processes, 1986, 73, 237 CrossRef.
- H. J. Xu, M. Wada, J. Tanaka, H. Kawakami and I. Katayama, Nucl. Instrum. Methods Phys. Res., Sect. A, 1993, 333, 274 Search PubMed.
- R. D. Voyksner and Heewon Lee, Rapid Commun. Mass Spectrom., 1999, 13, 1427 CrossRef CAS.
- D. J. Douglas and J. B. French, J. Am. Soc. Mass Spectrom., 1992, 3, 398 CrossRef CAS.
- A. J. Boerboom and C. E. Ouwerkerk in Advances in Mass Spectrometry, Part B, ed. J. F. Todd, John Wiley, New York, NY, 1985, pp. 843–844 Search PubMed.
- C. M. Whitehouse and E. Gulcicek, “Multipole Ion for Mass Spectrometry” WO 95/23018, United States of America, 1995.
- V. Baranov and S.D Tanner in Plasma Source Mass Spectrometry, ed. G. Holland and S. D. Tanner, Royal Society of Chemistry, Cambridge, 1999, pp. 34–45 Search PubMed.
- K. M. Ervin, PhD Thesis, University of California, Berkeley, 1986.
- S. C. Davis and B. Wright, Rapid Commun. Mass Spectrom., 1990, 4, 186 CAS.
- S. D. Tanner and V. I. Baranov, At. Spectrosc., 1999, 20, 45 Search PubMed.
- A. Dodonov, V. Kozlovsky, A. Loboda, V. Raznikov, I. Sulimenkov, A. Tolmachev, A. Kraft and H. Wollnik, Rapid Commun. Mass Spectrom., 1997, 11, 1649 CrossRef CAS.
- D. B. Gordon and M. D. Woods, Int. J. Mass Spectrom. Ion Processes, 1995, 148, 31–44 CrossRef CAS.
- C. M. Lock and E. Dyer, Rapid Commun. Mass Spectrom., 1999, 13, 432–448 CrossRef CAS.
- A. N. Krutchinsky, I. V. Chernushevich, V. L. Sicer, W. Ens and K. G. Standing, J. Am. Soc. Mass Spectrom., 1998, 9, 569 CrossRef CAS.
- P. H. Dawson in Advances in Mass Spectrometry, Volume 7B, Heyden & Son, Reading, UK, 1978, pp. 905–912 Search PubMed.
- N. V. Konenkov, Int. J. Mass Spectrom. Ion Processes, 1993, 123, 101 CrossRef CAS.
- J. F. Hennequin and R. L. Inglebert, Int. J. Ion Process Mass Spectrom., 1978, 26, 131 Search PubMed.
- D. J. Douglas and J. B. French, United States Patent 4,963,736, 1990.
- M. Morris, P. Thibault and R. K. Boyd, J. Am. Soc. Mass Spectrom., 1994, 5, 1042–1063 CrossRef CAS.
- P. W. Atkins, Physical Chemistry, W.H. Freeman and Company, New York, NY, 1994 Search PubMed.
- P. H. Dawson and D. J. Douglas in Tandem Mass Spectrometry, ed. F. W. McLafferty, John Wiley & Sons, New York, NY, 1983, 125–195 Search PubMed.
- S. A. McLuckey, G. J. Van Berkel, D. E. Goeringer and G. L. Glish, Anal. Chem., 1994, 66, 689A CAS.
- I. Feldmann, N. Jakubowski, C. Thomas and D. Stuewer, Fresenius' J. Anal. Chem., 1999, 365, 422 CrossRef CAS.
- P. E. Miller and M. B. Denton, J. Chem. Ed., 1986, 63, 617 Search PubMed.
- B. Landais, C. Beaugrand, L. Capron-Dukan, M. Sablier, G. Simonneau and C. Rolando, Rapid Commun. Mass Spectrom., 1998, 12, 302 CrossRef CAS.
- T. Kim, A. V. Tolmachev, R. Harkewicz, D. C. Prior, G. Anderson, H. R. Udseth, T. H. Bailey, S. Rakov, J. H. Futrell and R. SmithAnal. Chem. 2000, in the press Search PubMed.
- S. A. Shaffer, D. C. Prior, G. A. Anderson, H. R. Udseth and R. D. Smith, Anal. Chem., 1998, 70, 4111 CrossRef CAS.
- M. Guilhaus, J. Mass Spectrom., 1995, 30, 1519 CAS.
- D. P. Myers and G. M. Hieftje, Microchem. J., 1993, 48, 259 CrossRef CAS.
- D. P. Myers, M. J. Heintz, P. P. Mahoney, G. Li and G. M. Hieftje, Appl. Spectrosc., 1994, 48, 1337 Search PubMed.
- A. V. Tolmachev, I. V. Chernushevich, A. F. Dodonov and K. G. Standing, Nucl. Instrum. Meth. Phys. Res. B, 1997, 124, 112 Search PubMed.
- R. Cotter, in Time of Flight Mass Spectrometry; ed. R. Cotter, American Chemical Society, Washington, DC, 1994, 16–48 Search PubMed.
- J. E. Fulford and D. J. Douglas, Appl. Spectrosc., 1986, 40, 971 Search PubMed.
- J. A. Simpson, Rev. Sci. Instrum., 1961, 32, 1283 CAS.
- S. J. Valentine, J. G. Anderson, A. D. Ellington and D. E. Clemmer, J. Phys. Chem. B, 1997, 101, 3891 CrossRef.
- G. L. Long and J. D. Winefordner, Anal. Chem., 1983, 55, 712A–719A CrossRef CAS.
- A. M. Leach, M. Heisterkamp, F. C. Adams and G. M. Hieftje, J. Anal. At. Spectrom., 2000, 15, 151 RSC.
- P. P. Mahoney, S. J. Ray, G. Li and G. M. Hieftje, J. Am. Soc. Mass Spectrom., 1997, 8, 125 CrossRef CAS.
- D. R. Bandura and S. D. Tanner, At. Spectrosc., 1999, 20, 69 Search PubMed.
- J. Smolanoff, A. Lapicki and S. L. Anderson, Rev. Sci. Instrum., 1995, 66, 3706 CrossRef CAS.
Footnote |
| † Present address: DuPont Pharmaceuticals, Experimental Station, Wilmington DE 19880, USA. |
| This journal is © The Royal Society of Chemistry 2001 |
