Templating and structural engineering in organic–inorganic perovskites

Abstract

Hybrid perovskites provide the possibility of integrating useful organic and inorganic characteristics within a single crystalline molecular-scale composite, enabling unique electronic, magnetic and optical properties. The ability to understand and control the organic and inorganic structural attributes of these hybrids is important for being able to engineer the physical characteristics, both for fundamental studies as well as potential applications. Recently, a number of new and interesting perovskite structures have been reported and a better understanding has begun to emerge with respect to crystal design considerations. This contribution will review several of these new developments and will provide a more general discussion of structural engineering within this diverse family of compounds.

---

David B. Mitzi

David Mitzi was born in Red Bank, NJ in 1963. He received a B.S.E. in Electrical Engineering from Princeton University in 1985 and a Ph.D. in Applied Physics from Stanford University in 1990. In 1990 he joined the I.B.M. T. J. Watson Research Center and has since been examining crystal structure–property relationships in a variety of materials with interesting electronic and/or optical properties. Most recently, his focus has been on a family of perovskite-based organic–inorganic hybrids, with the goal of creating useful materials for transistor and light-emitting device applications.

---

1 Introduction

Organic compounds offer a number of useful properties, including structural diversity, plastic mechanical properties, ease of processing, and efficient luminescence. Inorganic materials have a distinct set of advantages, including good electrical mobility, band gap tunability (enabling the design of metals, semiconductors, and insulators), mechanical and thermal stability, and interesting magnetic or dielectric transitions. Organic–inorganic hybrids offer an important opportunity to combine useful properties from these two chemical realms within a single molecular scale composite. Numerous natural examples, including mollusk sea shells, tooth enamel, and bone, have evolved over millions of years into highly organized combinations of inorganic and organic phases, leading to composites with superior strength, fracture toughness and durability compared with either of the components independently.¹ More recent examples of man-made organic–inorganic systems include sol–gel derived silicates,² surface derivatized quantum dot structures,³ and sequentially deposited organic–inorganic superlattices.⁴ Each of these hybrids consists of at least one amorphous component (either organic or inorganic). Fully crystalline materials have the advantage that they can structurally be characterized using techniques such as X-ray or neutron diffraction, making it possible to correlate crystal structure features with specific materials properties. The ability to examine the structural properties across an entire family of compounds also enables a better understanding of and the ability to control these structural features and therefore create more functional materials.

The organic–inorganic perovskites are one of the most extensively studied crystalline families of hybrids,⁵ consisting of a wide range of inorganic anions (each comprised of an extended network of corner-sharing metal halide octahedra), alternating with a variety of different organic cations. In addition to structural flexibility, interesting and potentially useful magnetic, electrical and optical properties arise in the perovskites as a result of the unusual structural and electronic attributes. By independently controlling the energy levels of the organic and inorganic components of the hybrids, for example, self-assembling quantum well structures can be designed and synthesized. In contrast to the analogous structures created using molecular beam epitaxy (MBE), these systems have atomically smooth interfaces and single crystals of the structures can readily be grown. The interesting properties of these natural quantum well structures include a semiconductor–metal transition and large electrical mobility in the tin(II) halide-based hybrids,^6–8 and novel optical properties, arising from exciton states associated with the inorganic sheets in the germanium(II), tin(II), and lead(II) halide-based systems.^9–12 Many of the first row divalent transition metal halide hybrids are also ideal model systems for the study of lower-dimensional magnetism.^13–15

The hybrid perovskites self-assemble from ambient-temperature solutions and are generally stable up to the decomposition point (typically >250 °C). In a few cases the hybrids melt before decomposing and crystals can be grown from the melt.¹⁰ Intimate mixtures of the starting metal halide and organic salts will sometimes undergo solid-state reaction even at room temperature.⁵ In addition, the structures will generally form from the vapor phase using, for example, two-source thermal evaporation ¹⁶ or single source thermal ablation.¹⁷ The substantial stability for the hybrids and propensity to self-assemble from the solid, liquid, or vapor phase derives from the specific range of chemical interactions found in these systems—from relatively weak van der Waals interactions among the organic components, to hydrogen bonding interactions between the organic and inorganic components (as well as among the organic molecules), and stronger ionic and covalent interactions within the metal halide sheets.

The tendency to self-assemble from either the solution or vapor phase also enables a number of useful thin film deposition techniques for the hybrids, including spin coating, stamping, ink-jet printing and thermal evaporation.^5,18 While the relatively mature discipline of organic electronics has attracted attention as a result of the possibility of forming devices that can cheaply be processed on flexible substrates,^19,20 the emerging field of organic–inorganic hybrid electronics ¹⁸ offers many of the same processing advantages, with the added benefits (e.g. high mobility, thermal stability) of an inorganic framework. Recently, an organic–inorganic field-effect transistor (OIFET), based on a spin-coated tin(II) iodide-based perovskite channel layer, has been demonstrated,²¹ with a field-effect mobility of 0.6 cm² V⁻¹ s⁻¹ (comparable to amorphous silicon). A bright green electroluminescent device has also been reported,²² employing as the light-emitting layer a thermally ablated film of a perovskite based on lead(II) chloride layers and the oligothiophene derivative 5,5′′′-bis(aminoethyl)-2,2′ : 5′,2′′∶5′′,2′′′-quaterthiophene (AEQT).

The ability to rationally design materials for use in fundamental studies or applications is a key motivation in the field of solid-state chemistry. Given the complexity and range of interactions within most real solids, accurately predicting structures using computational techniques is generally not practical. Nevertheless, through the characterization of a sufficient number of compounds within a particular structural class, empirical rules can often be generated to aid in the design and control of the structures. Since the first mention of organic–inorganic perovskites over 100 years ago,²³ hundreds of related structures have been reported and some understanding and guidelines for the construction of the hybrids can now be deduced. It is the aim of this Perspective to summarize some of the recent structural developments within the hybrid perovskite field, as well as to outline some of the considerations that direct structure formation within this interesting class of materials.

2 Basic perovskite structures

The cubic AMX₃ perovskite structure (Fig. 1) consists of an extended three-dimensional (3-D) network of corner-sharing MX₆ octahedra, where M is generally a divalent metal and X a halide. The larger A cations fill the 12-fold coordinated holes among the octahedra. A typical example is provided by (CH₃NH₃)SnI₃, which has the cubic lattice constant a = 6.2397(5) Å.⁸ Analogous lead(II)-based perovskites have also been formed and characterized.²⁴ For the 3-D perovskites the size of the organic A cation is limited by the size of the 3-D hole into which it must fit. For a perfectly packed perovskite structure the geometrically imposed condition for the A, M, and X ions to be in close contact is (R_A + R_X) = t(√2)(R_M + R_X), where R_A, R_M, and R_X are the ionic radii for the corresponding ions and the tolerance factor must satisfy t ≈ 1. Empirically it is found that 0.8 ≤ t ≤ 0.9 for most cubic perovskites, although there is a slightly expanded range for distorted structures.²⁵ Using t = 1 and essentially the largest values for R_M and R_X (e.g.R_Pb = 1.19, R_I = 2.20 Å),²⁶ the limit on R_A is found to be approximately 2.6 Å. Consequently, only small organic cations (i.e. those consisting of three or less C–C or C–N bonds) are expected to fit into the structure. Recently, the methylammonium cation has been replaced by the larger formamidinium cation.²⁷ The fully substituted (NH₂CH[double bond, length half m-dash]NH₂)SnI₃ system has a cubic lattice at room temperature with a = 6.316(1) Å, approximately 1.2% larger than that for the methylammonium analog.

Fig. 1 (a) Ball and stick model of the basic AMX₃ perovskite unit cell and (b) polyhedral representation of how the structure extends in three dimensions.

Lower-dimensional perovskites are defined as structures that can conceptually be derived from specific cuts or slices of the 3-D perovskite structure. The simplest layered perovskite consists of MX₄²⁻ layers of corner-sharing metal halide octahedra, alternating with organic cation bilayers (for monofunctional cations) or monolayers (for bifunctional cations) (Fig. 2). The inorganic layers are derived from the 3-D parent compound by taking single 〈100〉-oriented layers from the AMX₃ structure. Note that, in contrast to the 3-D perovskites, the layered two-dimensional (2-D) systems can accommodate much larger and more complex organic cations, since the cage into which the organic cation must fit is no longer confined in three dimensions. Several guidelines can be established for selecting suitable organic cations for incorporation within the layered perovskite framework.⁵ First, the organic molecule must contain one or more terminal cation groups that can ionically interact with and effectively hydrogen bond to the extended inorganic anion, without the rest of the organic molecule sterically interfering with the halides of the inorganic sheets. For most known layered perovskites the organic molecule (R) is terminated with one or two protonated primary amines, yielding the general formulas (RNH₃)₂MX₄ or (NH₃RNH₃)MX₄.

Fig. 2 Schematic representation of single-layer 〈100〉-oriented perovskites with (a) monoammonium (RNH₃⁺) or (b) diammonium (⁺NH₃RNH₃⁺) organic cations.

The choice of hydrogen bonding scheme is important for determining the orientation and conformation of the organic molecule within the layered hybrid structure. In principle, the ammonium head(s) of the organic cations can hydrogen bond to any of the eight halides (i.e. four bridging/four terminal) within the holes formed by the corner-sharing MX₆ octahedra (Fig. 3). In practice, due to the geometric constraints of the ammonium group and the organic tail, the N–H ⋯ X interactions generally form either to two bridging halides and one terminal halide (bridging halide configuration) or to two terminal halides and one bridging halide (terminal halide configuration). Note that some MX₄²⁻ frameworks are more flexible than others. In the copper(II) halide systems, for example, the Jahn–Teller distortion of the CuX₆ octahedra enables a larger degree of flexibility in the hydrogen bonding between the organic cation and the inorganic sheets.

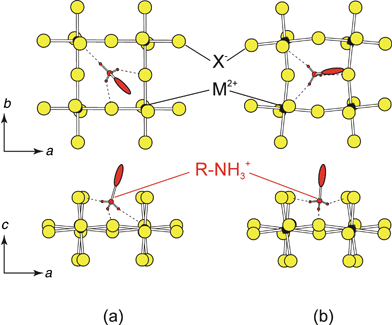Fig. 3 Two hydrogen-bonding schemes typically observed in the (RNH₃)₂MX₄ and (NH₃RNH₃)MX₄ type structures: (a) the bridging halide configuration and (b) the terminal halide configuration.⁵

The second structural criterion for layered systems involves the size and shape of the organic molecule. While the organic molecule in the layered structure is no longer three-dimensionally constrained to the relatively small interstices within the AMX₃ perovskite structure, the molecule must still fit within the “footprint” provided by the 2-D inorganic framework. The projection down the long axis of the organic cation (or the “cross sectional area” of the molecule) must approximately fit into an area defined by the terminal halides from four adjacent corner-sharing octahedra. One edge of the square is approximately twice the average bridging interatomic M–X distance. As an example, the copper(II) chloride framework provides an area of approximately 27 Ų, whereas the larger lead(II) iodide framework yields a square covering approximately 40 Ų. If the “cross sectional area” of the organic molecule is much smaller than the area provided by the inorganic framework, the structure can accommodate by allowing the organic molecules to tilt or interdigitate. On the other hand, if the molecular cross-sectional area is too large, the perovskite structure may not be able to accommodate the steric interactions among nearest-neighbor organic moieties and a different structural type may result.

In contrast to the width of the organic cation, the length of the molecule (which should extend nominally away from the perovskite sheets) can take on a wide range of values, since the distance between perovskite sheets can vary. Consequently, long and narrow molecules are favored over molecules with a large cross-sectional area. In fact, many of the reported layered perovskites contain minimally branched aliphatic ammonium cations or aromatic cations with a narrow structural profile. Note that, besides the size and shape of the organic molecule, interactions between the organic R groups can either stabilize or destabilize the perovskite structure. These interactions may include hydrogen bonding, aromatic–aromatic or van der Waals interactions. While many of these interactions are weak, in more complex organic moieties with multiple functional groups the effects of the interactions along the length of the organic molecule are additive and can therefore play a more important structure-directing role.

The nature of the coupling between the organic and inorganic components of the perovskite structures suggests that the inorganic framework can play an important templating role with respect to the ordering and conformation of the organic component. Likewise, the organic cations should also have a templating influence on the inorganic framework. Recently, several examples have appeared of organic–inorganic hybrid systems in which one component controls the structure and properties of the other component or directs the overall structural characteristics of the material. The following examples also highlight the structural guidelines discussed above.

3 Controlling the organic layer structure

3.1 Simple organic cations

Most layered organic–inorganic perovskites contain relatively simple organic layers, consisting of aliphatic or single ring aromatic cations. One interesting family, (C₆H₅C₂H₄NH₃)₂MX₄ (e.g. M = Cu, Pb or Sn; X = Cl, Br or I), is based on the phenethylammonium cation. The basic structural unit of (C₆H₅C₂H₄NH₃)₂CuX₄ (X = Cl or Br) (Fig. 4), for example, consists of well ordered layers of corner-sharing CuX₆ octahedra, with a layer of phenethylammonium cations capping each inorganic sheet on both sides.²⁸ The ammonium group on each organic cation hydrogen bonds to halogens in the perovskite layer. The full 3-D structure is then created by stacking the neutral organic-sheathed (C₆H₅C₂H₄NH₃)₂CuX₄ units along the c axis. Weak (e.g. van der Waals) interactions between the phenyl groups of successive (C₆H₅C₂H₄NH₃)₂CuX₄ layers hold the structure together, with no interleaving among the phenethylammonium cations from adjacent layers.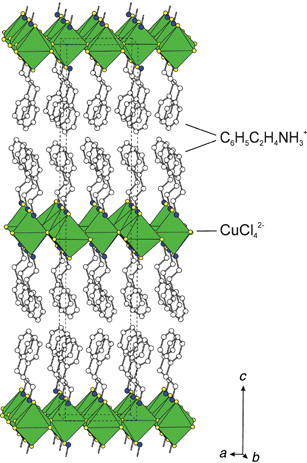

Fig. 4 Polyhedral representation of the (C₆H₅C₂H₄NH₃)₂CuX₄ (X = Cl) structure,²⁸ viewed approximately down the b axis. The dashed lines indicate the unit cell outline. The same structure is observed with X = Br.

The unit cell for (C₆H₅C₂H₄NH₃)₂PbCl₄, though similar, is not isostructural with the cell reported for (C₆H₅C₂H₄NH₃)₂CuX₄ (X = Cl or Br).²⁹ Each of the triclinic unit cell dimensions within the plane of the perovskite sheets [a = 11.1463(3) and b = 11.2181(3) Å] is approximately twice the simple cubic perovskite lattice parameter, a_p [the 3-D perovskite CH₃NH₃PbCl₃, for example,³⁰ has a_p = 5.657(2) Å]. The 2a_p × 2a_p superstructure is uncommon among the known layered perovskites.⁵ More typically, the organic–inorganic perovskite structures adopt a (√2)a_p × (√2)a_p superstructure. In (C₃H₇NH₃)₂PbCl₄, for example, which has the phenethylammonium cation replaced by a propylammonium cation, the orthorhombic lattice constants are a = 7.815(1), b = 7.954(1), and c = 25.034(3) Å.³¹ In (C₆H₅C₂H₄NH₃)₂CuCl₄ the orthorhombic lattice constants are a = 7.328(1), b = 7.295(1), and c = 38.618(5) Å.²⁸

A view perpendicular to the perovskite sheets in the (C₆H₅C₂H₄NH₃)₂MCl₄ (M = Cu or Pb) structures (Fig. 5) highlights some factors that give rise to the different superstructures. In (C₆H₅C₂H₄NH₃)₂CuCl₄ the antiferrodistortive arrangement of the long semicoordinate Cu–Cl bonds in the plane of the perovskite sheets (resulting from Jahn–Teller distortion of the CuCl₆ octahedra) enables a strong interaction between the ammonium tail of the phenethylammonium cation and two bridging chlorides (i.e. the cations adopt the bridging halide hydrogen bonding configuration). Each phenethylammonium cation sits nominally in a square defined by four nearest neighbor Cu atoms and the Cu–Cl–Cu linkages between them. If the CuCl₆ octahedra were perfect and not tilted or rotated relative to each other, and neglecting the conformation and ordering of the organic cation, the unit cell dimensions within the perovskite sheet would be defined by this a_p × a_p square. In the actual structure (Fig. 5a) tilting of the octahedra apices away from the perovskite sheet perpendicular, as well as ordering of the organic cations, gives rise to the observed (√2)a_p × (√2)a_p superstructure.

Fig. 5 Single layer from the (C₆H₅C₂H₄NH₃)₂MCl₄ structures, viewed perpendicular to the perovskite sheets, for (a) M = Cu and (b) M = Pb.²⁹ The dashed lines indicate where the unit cell intersects each perovskite layer, with the axes of the M = Cu structure rotated by 45° with respect to those of the M = Pb structure to achieve the same orientation relative to an ideal perovskite sheet. For the M = Cu structure the filled (black) bonds represent short Cu–Cl bonds, while the open (white) bonds represent elongated Cu–Cl semicoordinate bonds. The M = Pb structure contains four independent phenethylammonium cations (labelled PE1–PE4).

In the analogous lead(II) chloride structure there is less flexibility within the inorganic framework and the phenethylammonium cations adopt the terminal halide hydrogen bonding configuration. The square defined by the four nearest-neighbor Pb atoms and the associated Pb–Cl–Pb linkages is substantially distorted by rotations of the PbCl₆ octahedra in the ab plane (Fig. 5b). For the square at the center of the unit cell (around PE2) the square edges are pinched in along the b axis and pushed out along the a axis. The nearest-neighbor squares along both the a and b directions (around PE3 and PE4) each have the opposite distortion (i.e. they are pinched in along the a axis and push out along the b axis). The repeat distance of this alternating distortion along each axis is two squares, thereby providing for the 2a_p × 2a_p superstructure. The substantial difference between the phenethylammonium positional and orientational ordering in the M = Cu and Pb structures highlights the important templating influence provided for the organic cations by the metal halide sheets.

For (C₆H₅C₂H₄NH₃)₂PbCl₄ all of the carbons in the phenyl ring, along with the first ethylammonium carbon attached to the ring, essentially lie in a plane (Fig. 6a). However, the terminal ethylammonium carbon and nitrogen atoms are not in the same plane. When viewed from the side (i.e. parallel to the plane of the phenyl group) the molecules adopt an unusual J-shaped conformation. In contrast, the phenethylammonium cations in C₆H₅C₂H₄NH₂·HCl and (C₆H₅C₂H₄NH₃)₂CuX₄ (X = Cl or Br) adopt a more typical conformation (Fig. 6b), with a single independent phenethylammonium cation in the unit cell and the ethylammonium fragment curving downward rather than to the right or left.^28,32 The resulting trans conformation for the ethylammonium fragment [N(1)–C(1)–C(2)–C(3)] is expected to be the most stable configuration for the free molecule.³³ Apparently, in the lead(II) chloride-based perovskite, the specific hydrogen bonding interactions and the constraints imposed by the distorted perovskite framework stabilize the “J”-shaped conformation. The inorganic framework can therefore be used to template not only the orientation, but also the conformation of the organic molecules within the layered perovskite structures.

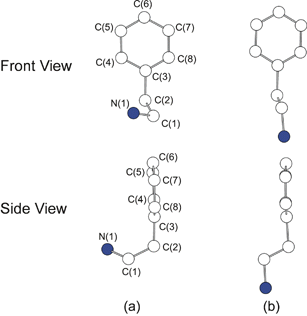Fig. 6 Conformations for the phenethylammonium cation in (a) (C₆H₅C₂H₄NH₃)₂PbCl₄ and (b) (C₆H₅C₂H₄NH₃)₂CuCl₄.²⁹ Upper panels represent the front view and lower panels the side view for each cation.

Note that, while (C₆H₅C₂H₄NH₃)₂CuBr₄ forms a typical layered perovskite structure (Fig. 4), closely related bis[methyl(2-phenethyl)ammonium] tetrabromocuprate, (C₆H₅C₂H₄NH₂CH₃)₂CuBr₄, forms a distinct structure with isolated CuBr₄²⁻ anions (intermediate in geometry between square planar and tetrahedral), despite the similar 2∶1 ratio between the organic cation and the metal halide components.³⁴ The organic cation in the latter hybrid is similar to the phenethylammonium cation, except that there is an additional methyl attached to the ammonium tethering group. This methyl group impedes the hydrogen bonding required to stabilize a layered perovskite structure, therefore leading to an alternative structure with isolated CuBr₄²⁻ units. The more open inorganic framework enables hydrogen bonding to the halides, without the methyl group sterically interfering with the hypothetical inorganic sheets of a layered perovskite structure.

3.2 Dye molecules

While most of the perovskites studied to date contain relatively simple organic cations, in principle more complex organic molecules can also be incorporated, subject to the chemical and structural constraints described in section 2. An oligothiophene derivative, 5,5′′′-bis(2-aminoethyl)-2,2′∶5′,2′′∶5′′,2′′′-quaterthiophene (AEQT), has recently been designed and incorporated between the MX₄²⁻ (M = Sn or Pb; X = Cl, Br or I) perovskite sheets (Fig. 7).³⁵ The AEQT cation has the appropriate tethering group (i.e. ethylammonium) and rigid, narrow profile ideally suited for incorporation within the layered perovskite framework.

Fig. 7 Crystal structure of (H₂AEQT)PbBr₄, viewed down the b axis.³⁵ The compound crystallizes in a monoclinic subcell (C2/c space group), with the lattice constants a = 39.741(2), b = 5.8420(3), c = 11.5734(6) Å, and β = 92.360(1)°.

An interesting general feature of oligomer-containing organic–inorganic perovskites is the fact that, as for the phenethylammonium-based systems, the orientation and conformation of the oligomer cations can be controlled or templated as a result of the inorganic framework. This templating can have important implications with regard to the optical and electrical properties of the organic layers. In organic thin-film transistors (OTFTs), for example, the mobility of the channel layer is critically affected by the degree and type of molecular ordering within the oligomer layer.^36,37 By analogy, in hybrids containing layers of organic molecules with extended π systems (e.g. oligothiophene, oligophenylenes), templating should affect the electrical transport properties of the organic layer. The AEQT-containing organic–inorganic perovskite systems demonstrate that the inorganic sheets can be used to template the formation of single crystalline layers of relatively complex organic cations, potentially therefore providing a pathway to higher mobility oligomer layers than currently achievable in simple organic thin films.

In the (H₂AEQT)MX₄ compounds each quaterthiophene oligomer is ordered between the metal halide sheets in a herringbone arrangement with respect to neighboring quaterthiophenes.³⁵ The conformation of the protonated 5,5′′′-bis(2-aminoethyl)-2,2′∶5′,2′′∶5′′,2′′′-quaterthiophene molecule in (H₂AEQT)PbBr₄ is shown in Fig. 8. Each quaterthiophene oligomer can fully be described by two independent thiophene rings T₁{S(1), C(3), C(4), C(5), C(6)} and T₂{S(2), C(7), C(8), C(9), C(10)}. The other half of the quaterthiophene oligomer is generated by symmetry, yielding the rings T₁′{S(1)′, C(3)′, C(4)′, C(5)′, C(6)′} and T₂′{S(2)′, C(7)′, C(8)′, C(9)′, C(10)′}. The backbone conformation among the four rings is syn-anti-syn. Each thiophene ring is essentially planar, with all non-hydrogen atoms falling within 0.01(1) Å of the least squares best plane. The dihedral angle between the planes defined by the thiophene rings T₁ and T₂ (or T₁′ and T₂′) is 9.0(2)°. This angle is accomplished by a combination of a tilting of the connecting C(6)–C(7) [C(6)′–C(7)′] bond, out of the plane of the central two thiophene rings (T₂ and T₂′), as well as by a rotation about this bond axis.

Fig. 8 Top (a) and side (b) view of the doubly protonated 5,5′′′-bis(2-aminoethyl)-2,2′∶5′,2′′∶5′′,2′′′-quaterthiophene (AEQT) molecule in (H₂AEQT)PbBr₄.³⁵ The AEQT conformation in other examined (H₂AEQT)MX₄ structures is essentially identical to that found in the lead(II) bromide analog.

The syn-anti-syn geometry is somewhat uncommon among the oligothiophenes. Generally, as a result of steric interactions, the all-anti (or all-trans) geometry can be regarded as the lowest energy configuration.³⁸ In the solid state the all-anti conformation is adopted for α-quaterthiophene,³⁹ as well as for the compounds 5,5′′′-bis[(2,2,5,5-tetramethyl-1-aza-2,5-disila-1-cyclopentyl)methyl]-2,2′∶5′,2′′∶5′′,2′′′-quaterthiophene and 5,5′′′-bis[N,N-bis(trimethylsilyl)aminomethyl]-2,2′∶5′,2′′∶5′′,2′′′-quaterthiophene, which each have bulky terminal groups attached to the quaterthiophene moiety.⁴⁰ However, 5,5′′′-bis[(2,2,5,5-tetramethyl-1-aza-2,5-disila-1-cyclopentyl)ethyl]-2,2′∶ 5′,2′′∶5′′,2′′′-quaterthiophene has recently been shown ⁴⁰ to adopt a nearly planar (dihedral angle of 5.0° between least-squares best planes containing adjacent thiophene rings) syn-anti-syn conformer, similar to that observed in (H₂AEQT)PbBr₄. In each of these cases the specific environment for the quaterthiophene moiety, as modified by the tethering groups and the interaction with the extended inorganic anions (for the perovskite), leads to the shift in conformation from all-anti to syn-anti-syn.

Other chromophore-containing perovskites have also recently been considered, including the compounds (RNH₃)₂PbCl₄ (R = 2-phenylethyl, 2-naphthylmethyl, or 2-anthrylmethyl).^41,42 This is a particularly interesting series because, for R = 2-phenylethyl, the singlet and triplet states of the organic cation are higher in energy than the exciton state of the inorganic sheets, and therefore emission from the inorganic exciton is observed in the photoluminescence spectrum. For R = 2-naphthylmethyl the inorganic exciton state apparently falls between the organic singlet and triplet states, and phosphorescence from the organic molecules dominates the emission spectrum. Finally, for R = 2-anthrylmethyl, the inorganic exciton state is higher in energy than both the organic singlet and triplet states, and chromophore singlet emission is dominant. Similar tunability with respect to the relative energy level positions for the hybrid organic and inorganic components has been reported in (H₂AEQT)PbX₄ (X = Cl, Br or I).³⁵ The ability to incorporate dye molecules within the layered perovskites therefore has a profound effect on the optical properties, as well as the structural attributes, of the hybrids.

3.3 Polymerization

Another interesting example of templating involves solid-state polymerization within the organic layer of perovskite structures.^43,44 For this class of perovskites, more reactive R groups (such as diene or diyne groups) are employed within the organic layers of the (RNH₃)₂MX₄ structures. Generally the goal is for the suitably designed perovskite to undergo “topochemical polymerization”, i.e. a diffusionless solid state transformation of a crystal containing a monomer to one containing the corresponding polymer, in such a way that the center of gravity positions and symmetry of the monomers are constrained to be similar to those found in the base units of the polymer.⁴⁵ In this type of process the reaction proceeds by a specific rotation of the monomer on each lattice site, in a manner determined by the packing properties of the molecules in the crystal structure. If polymerization can proceed with a sufficiently small change in the position and orientation of the monomers, then a single crystal containing the monomer may be transformed into a single crystal containing the polymer species.

In one example the hydrochloride salt of 6-amino-2,4-trans,trans-hexadienoic acid, within a cadmium(II) chloride perovskite framework, polymerizes under ultraviolet (UV) or γ irradiation. The polymerization occurs through a 1,4 addition mechanism, leading to a well ordered polymer layer (Fig. 9).⁴³ The exclusive formation of the 1,4-trans polymer in the cadmium(II) compound results from the layered structure, which limits the photoreactivity to two dimensions, and from the appropriate distances between monomer units, which favor the 1,4-addition process but are too large for the competing (2 + 2) cycloaddition of the butadiene units.⁴³ The same photoreactive organic cation in a copper chloride perovskite framework does not undergo polymerization. The structural differences in the inorganic framework, induced by the Jahn–Teller distortion of the copper(II) chloride octahedra, lead to an unfavorable (with respect to the polymerization process) configuration of the monomer within the organic layer. Consequently, as for the simple phenethylammonium and oligomer-containing metal(II) halides, the inorganic framework can be used to control the ordering of photosensitive organic molecules. However, in this case, the control over ordering also determines whether or not a potentially reactive monomer-containing system is susceptible to polymerization.

Fig. 9 Crystal structure of the polymerized product formed by subjecting (HO₂CCH[double bond, length half m-dash]CHCH[double bond, length half m-dash]CHCH₂NH₃)₂CdCl₄ to UV or γ irradiation.⁴³ Polymerization yields ordered 1,4-disubstituted trans-polybutadiene [–CH(CO₂H)CH[double bond, length half m-dash]CHCH(CH₂NH₂)–]_∞. Hydrogen bonding between CO₂H groups on adjacent layers is shown by dashed lines and helps to stabilize the structure.

4 Controlling the inorganic framework

4.1 Metal-deficient perovskite layers

While great flexibility has been demonstrated with regard to substitutions within the organic layers of hybrid perovskites, the flexibility of the inorganic framework has generally been limited by the need to incorporate divalent metals. This valency constraint derives from the requirement for charge neutrality among the organic cations and the metal halide anion layers. In the single layer perovskites, (NH₃RNH₃)MX₄ [(RNH₃)₂MX₄], for example, the MX₄²⁻ perovskite sheets counterbalance the NH₃RNH₃²⁺ [RNH₃⁺] layers. With a halide as the X anion, the metal (M) is generally expected to be a divalent cation that can adopt an octahedral coordination (e.g. Cu²⁺, Mn²⁺, Co²⁺, Cd²⁺, Ge²⁺, Sn²⁺, Pb²⁺ or Eu²⁺).⁵ Recently, however, trivalent-metal-based (H₂AEQT)M_2/3I₄ (M = Bi³⁺ or Sb³⁺) systems have also been reported.⁴⁶ The trivalent-metal structures are essentially identical with those reported for the analogous divalent-metal (H₂AEQT)PbX₄ (X = Br or I) systems (Fig. 7) with, however, one-third of the metal sites vacant.

The formation of single layers of corner-sharing metal halide octahedra is unusual in bismuth(III) and antimony(III) hybrid chemistry. As for conventional perovskite frameworks, bismuth(III) and antimony(III) halide lattices generally consist of distorted MX₆ octahedra. These octahedra form discrete or extended inorganic networks of corner-, edge-, or face-sharing octahedra, leading to an extensive family of metal(III) halogeno anions (e.g. MX₄⁻, MX₅²⁻, MX₆³⁻, M₂X₉³⁻, M₂X₁₁⁵⁻, M₃X₁₂³⁻, M₄X₁₈⁶⁻, M₅X₁₈³⁻, M₆X₂₂⁴⁻, and M₈X₃₀⁶⁻).⁴⁷ Within these networks the metal(III) sites are essentially fully occupied. The (H₂AEQT)M_2/3I₄ (M = Bi³⁺ or Sb³⁺) systems are the first members of a proposed more general metal-deficient family of hybrids consisting of (Mⁿ⁺)_2/nV_(n−2)/nX₄²⁻ sheets, where the vacancies, V, are usually left out of the formula and the metal cation valence, n, is greater than 2.⁴⁶ The metal sites within the (Mⁿ⁺)_2/nV_(n−2)/nX₄²⁻ network are essentially arranged in a two-dimensional square lattice and each site is occupied with probability p = 2/n (assuming a random distribution of vacancies among the metal sites). Numerical calculations for an infinite two-dimensional square lattice predict a percolation threshold at p_c = 0.59.⁴⁸ Consequently, the trivalent (n = 3) systems are notable because they are the only members of the metal-deficient layered perovskite family in which clusters of connected corner-sharing metal halide octahedra are predicted to extend entirely across each infinite inorganic sheet (e.g. for n = 4, p = 0.5 is less than the percolation threshold).

Each metal cation vacancy creates a local concentration of negative charge. The creation of a substantial number of randomly positioned vacancies within the perovskite sheets should therefore be energetically unfavorable, unless some other aspect of the system can help to offset the energy deficit. Attempts to stabilize the metal-deficient perovskites using bismuth(III) iodide and various long, relatively flexible organic diammonium cations (e.g. diprotonated alkyldiamines) led to the formation of a distinct class of hybrids containing chains of corner-sharing bismuth iodide octahedra with fully occupied metal sites,⁴⁹ rather than the metal-deficient layered perovskites. Note that, in combination with many divalent metal halides, these same organic cations readily form the layered perovskite structure.⁵ It is therefore interesting to consider the potential role played by the (H₂AEQT)²⁺ organic cation layer in stabilizing the metal-deficient perovskites layers.

The conformation and ordering of the 5,5′′′-bis(aminoethyl)-2,2′∶5′,2′′∶5′′,2′′′-quaterthiophene molecule in (H₂AEQT)M_2/3I₄ is very similar to that observed in the lead(II) analogs (Section 3.2). Viewing down the length of the quaterthiophene molecules, the oligomers adopt a herringbone arrangement, similar to that found in purely organic crystals and films of most oligothiophenes (Fig. 10).^50–53 In fact, the AEQT layer structure in the perovskites, viewed down the long axis of the quaterthiophene moiety (Fig. 10a), can virtually be superimposed on a layer from α-quaterthiophene viewed similarly (Fig. 10b), despite the very different environment in which the quaterthiophene moiety is held (i.e. the inorganic framework) and the different molecular conformation (i.e.syn-anti-synversus all-anti). This similarity in structure suggests a particular stability to these 2-D oligothiophene layers.

Fig. 10 (a) View down the long molecular axis of one layer of AEQT cations in the (H₂AEQT)Bi_2/3I₄ structure.⁴⁶ For clarity, only the quaterthiophene component of the AEQT molecule is drawn, demonstrating the herringbone arrangement of the quaterthiophene units in the structure. In (b) a similar view for one layer of quaterthiophene molecules in crystalline α-quaterthiophene is shown for comparison.³⁹ Reproduced with permission from Inorg. Chem., 2001, in press. Copyright 2001 Am. Chem. Soc.⁴⁶

The herringbone arrangement of the quaterthiophene moieties is common among other aromatic organic molecules (e.g. naphthalene,⁵⁴ anthracene,⁵⁵ biphenyl,⁵⁶ quaterphenyl ⁵⁷) and can be explained in terms of edge-to-face (tilted-T) aromatic interactions.^51,58–62 These interactions arise as a result of electrostatic and London dispersion effects (i.e. van der Waals interactions) ^59,60 and, for typical aromatic–aromatic encounters, have an interaction energy of approximately −2 kcal mol⁻¹,⁶⁰ similar in magnitude to that of a weak hydrogen bond. However, for more complex organic molecules, which consist of a rigid network of multiple aromatic components, the effects of these interactions can add up and therefore have a more substantial structure-directing influence on the resulting system. In fact, edge-to-face aromatic interactions are now known to play an important role in protein folding ⁶¹ and molecular recognition.⁶²

For the rigid quaterthiophene moiety (e.g. AEQT) the effect of the edge-to-face interactions is similarly expected to be important during compound formation. The unusual metal-deficient inorganic layers are likely to be templated by preferential formation of the two-dimensional layers of AEQT, stabilized by the edge-to-face interactions among the rod-like molecules. Given this proposed structure-directing mechanism, it is likely that other organic cations may also be used to stabilize the higher-valence, metal-deficient perovskite frameworks. In addition to various length oligothiophene derivatives, analogous oligophenylene derivatives are likely to be suitable. Other organic cations based on the oligocene (e.g. naphthalene, anthracene, tetracene) series might also be appropriate to consider, since these relatively narrow, rigid molecules are subject to substantial edge-to-face interactions. Analysis of hybrids containing these alternative organic cations, as well as other related systems, will help to elucidate the templating mechanism that is suggested by the (H₂AEQT)M_2/3I₄ (M = Bi³⁺ or Sb³⁺) structures. In particular, it will be interesting to see whether the length of the oligomers or the choice of mono- versus di-ammonium derivatives has any impact on the stability of the metal-deficient layers. It is also important to see whether higher valence (>3+) metal halide frameworks can be incorporated within the metal-deficient perovskite framework.

4.2 Thickness of perovskite sheets

The 3-D perovskites discussed in section 2 are stabilized by mixing 1∶1 ratios of metal halides with organic cation salts, where the organic cation must be small enough to fit in the holes within the 3-D inorganic network of corner-sharing metal halide octahedra. In contrast, the single-layered 2-D perovskites form from mixtures of metal halide and generally longer or more complex organic salts. An interesting situation arises when mixtures of short and long organic cations are employed. In principle, several possibilities might be expected. The mixed-cation reaction might macroscopically segregate into a phase containing the small organic cation and another containing the longer cation. Alternatively, the organic cations might locally segregate onto separate layers of a more complex hybrid structure, thereby creating intergrowths of the 3-D perovskite and the single-layered perovskite structures (Fig. 11).

Fig. 11 Family of intergrowth compounds formed from the parent AMX₃ (3-D) and (RNH₃)₂MX₄ (2-D) perovskites. The 〈100〉-oriented layered perovskite series, (RNH₃)₂A_n−1M_nX_3n + 1, can also conceptually be derived by (a) taking n layers from along the 〈100〉 direction of the 3-D perovskite structure and (b) alternating these layers with bilayers of organic cations.

When growing crystals of the materials from solution the outcome of mixing long- and short-chain organic cations depends on the relative solubility of the two organic ions and the metal halide under consideration. Given sufficiently compatible solubility characteristics for the two organic components, intergrowth structures can be stabilized. In addition, changing the relative ratios of the two organic cations and the metal halide salt in the starting solution influences the number of perovskite sheets between the organic layers. In the family (RNH₃)₂(CH₃NH₃)_n−1M_nX_3n + 1, for example, n perovskite layers alternate with the RNH₃ bilayers. For R = C₄H₉ (butyl), M = Sn²⁺, and X = I⁻, the n = 1,2,3,4, and 5 compounds have all been stabilized in single-phase form.⁶ The n = ∞ compound corresponds to the 3-D perovskite (CH₃NH₃)SnI₃. Similar layered families have been reported with tin(II) replaced by lead(II), iodide with bromide, and the butylammonium cation by nonylammonium or phenethylammonium.¹²

The effective dimensionality of the extended inorganic anion (as controlled by n) has a significant impact on the physical properties. For the tin(II) compounds (C₄H₉NH₃)₂(CH₃NH₃)_n−1Sn_nI_3n + 1 a semiconductor–metal transition is observed as a function of increasing n.⁶ The n = 1 compound is a fairly large band gap semiconductor, with a room temperature resistivity of approximately 10⁵ Ω cm. With increasing n the resistivity of the materials rapidly decreases, with a transition to metallic behavior for n ≥ 3. The n → ∞ end-member, (CH₃NH₃)SnI₃, is a low-carrier density p-type metal with a room-temperature Hall mobility (pressed pellet sample) of approximately 50 cm² V⁻¹ s⁻¹ and a carrier density of approximately 10¹⁹ cm⁻³.⁸ The transition in electrical properties from semiconducting to metallic also correlates with a reduction in the degree of structural distortion of the SnI₆ octahedra within the perovskite sheets.⁶ In addition to the unusually high conductivity in the tin(II) iodides, both the tin(II) and lead(II) halide organic–inorganic perovskites exhibit enhanced exciton binding energies due to a dielectric confinement effect (with an associated intense luminescence peak in the visible spectral range at room temperature),^9,63 non-linear optical properties with the potential for third harmonic generation,¹² and electroluminescence.⁶⁴ Examination of the optical properties as a function of decreasing thickness of the perovskite sheets in the family (C₆H₅C₂H₄NH₃)₂(CH₃NH₃)_n−1Pb_nI_3n + 1 demonstrates a substantial increase in the band gap, the lowest exciton energy, and the exciton binding energy, as a result of quantum confinement or dimensionality effects.⁶⁵ In essence, then, mixtures of appropriately chosen organic cations can be used to vary the thickness of the perovskite sheets and therefore the physical character of the hybrids.

4.3 Orientation of perovskite sheets

In addition to controlling the dimensionality of the inorganic sheets, the choice of organic cation(s) can also influence the crystallographic orientation of the inorganic framework. The multilayered structures schematically depicted in Fig. 11 consist of n 〈100〉-oriented layers from the 3-D perovskite structure, alternating with organic bilayers. Other layering schemes are also possible within the hybrids, as has previously been demonstrated with the strictly inorganic oxide- and halide-based perovskites.^66–68 The series [NH₂C(I)[double bond, length half m-dash]NH₂]₂(CH₃NH₃)_mSn_mI_3m + 2, for example, has recently been reported,⁷ consisting of m 〈110〉-oriented perovskite sheets separated by iodoformamidinium layers (Fig. 12). Lattice parameters for the observed family members approximately follow the rule a = a_p, b = (√2)a_p, and c = K + ma_p/(√2), where a_p is the lattice parameter for the cubic 3-D perovskite CH₃NH₃SnI₃ and K ≈ 5.98(5) Å. The monoclinic angle, β, is also found to decrease with increasing “m”, from 92.96(1) (m = 2) to 91.83(1)° (4).⁷ Note that in contrast to the 〈100〉-oriented perovskites, where the in-plane lattice parameters are approximately a_p × a_p (most commonly with a 2a_p × 2a_p or (√2)a_p × (√2)a_p supercell), for the 〈110〉-oriented compounds the new slice of the 3-D perovskite structure results in the distinct in-plane a_p × (√2)a_p dimensions. A similar family of 〈110〉-oriented layered perovskites also forms with lead(II) iodide replacing tin(II) iodide.

Fig. 12 Schematic representation of the 〈110〉-oriented family of layered hybrid perovskites, A′₂A_mM_mX_3m + 2. The layered perovskite framework is derived from the 3-D perovskite parent compound by (a) taking m layers from along the 〈110〉 direction of the 3-D structure and (b) alternately stacking these layers with organic cations. Note that the specific choice of organic cations, A′, can determine whether the 〈100〉- or 〈110〉-oriented perovskite family will form. One member of the 〈110〉-oriented family ⁷ has A′ = NH₂C(I)[double bond, length half m-dash]NH₂⁺, A = CH₃NH₃⁺, M = Sn²⁺, and X = I⁻.

While the cation stoichiometries of the 〈100〉- and 〈110〉-oriented families are slightly different for a given perovskite sheet thickness (n, m), the same family of oriented structures crystallizes from solution over a wide range of organic cation : metal halide ratios, as long as the types of organic cations remain the same. In fact, the 〈110〉-oriented structures have never been observed to form from solutions containing only alkylammonium halides and tin(II) [or lead(II)] iodide, without the presence of the iodoformamidinium cation (or some other similar structure-directing species). Apparently, the specific molecular features of the iodoformamidinium cation favor the 〈110〉-oriented rather than the 〈100〉-oriented framework. These features include the fact that the iodine on the iodoformamidinium cation completes a 12-fold coordination sphere around the methylammonium cations within the perovskite sheets. Also, the iodoformamidinium cations form hydrogen bonded “chains” down the channels provided by the 〈110〉-oriented perovskite surface (Fig. 13). The selectivity of certain organic cations toward the formation of specific orientations of the layered perovskite framework therefore provides a useful opportunity to control this crystallographic orientation.

Fig. 13 Crystal structure of the m = 2 〈110〉-oriented perovskite, [NH₂C(I)[double bond, length half m-dash]NH₂]₂(CH₃NH₃)₂Sn₂I₈, which adopts a monoclinic (P2₁/m) cell with a = 6.2649(4), b = 8.6624(5), c = 14.787(2) Å, and β = 92.960(8)°.⁷ The iodoformamidinium iodine atom is disordered over two symmetry equivalent sites. For clarity, only one of the two sites is shown occupied.

The m = 2 〈110〉-oriented perovskite framework (Fig. 13) is composed of an extended two-dimensional network of corner-sharing metal halide octahedra. For m > 2, as for the 〈100〉-oriented layered perovskite family with increasing n, the inorganic framework becomes progressively more three-dimensional. For the tin(II) compounds this increase in effective dimensionality is reflected in the electrical transport properties, as the materials become progressively more conducting with increasing m.⁷ For m = 1, the 2-D extended perovskite framework breaks down into layers of one-dimensional (1-D) chains of corner-sharing metal halide octahedra (Fig. 12).⁶⁹ The reduction of effective dimensionality in the m = 1 system is reflected in the optical absorption spectrum for the material, which is shifted to higher energy relative to the two-dimensional (m > 1) systems.⁷⁰ The [NH₂C(I)[double bond, length half m-dash]NH₂]₂(CH₃NH₃)_mSn_mI_3m + 2 family (which can be generalized to other metal halides) therefore enables the effective dimensionality of the inorganic framework to be varied from 1- to 2- to 3-D, all within a single structural family.

The idealized m = 1 structure from the [NH₂C(I)[double bond, length half m-dash]NH₂]₂(CH₃NH₃)_mSn_mI_3m + 2 family (Fig. 12) has methylammonium cations separating the SnI₅³⁻ chains, in what is left of the perovskite sheets. While there has been some evidence that this compound can be crystallized from solution, higher quality crystals have been grown when the methylammonium cation is replaced by the larger formamidinium or iodoformamidinium cations.^69,71 The 1-D systems can then be expressed, [NH₂C(I)[double bond, length half m-dash]NH₂]₂ASnI₅, with A = NH₂C(I)[double bond, length half m-dash]NH₂⁺ or NH₂CH[double bond, length half m-dash]NH₂⁺ (similar materials have been made with Pb replacing Sn). Both materials share very similar gross structural features (Fig. 14). However, the distinct unit cells and especially the characteristic colors (orange-yellow for A = iodoformamidinium versus dark red for A = formamidinium) hint at differences in local tin(II) coordination in the two structures.

Fig. 14 Comparison of two m = 1 structures, [NH₂C(I)[double bond, length half m-dash]NH₂]₂ASnI₅, viewed down the a axis (i.e. parallel to the SnI₅³⁻ chains).⁷¹ The A = iodoformamidinium structure (a) crystallizes in a monoclinic (P2₁/c) cell with a = 6.4394(4), b = 20.069(2), c = 18.722(1) Å, and β = 92.822(6)°. The corresponding material with A = formamidinium (b) adopts a triclinic cell with the lattice constants a = 6.3635(3), b = 8.8737(5), c = 10.8782(6) Å, α = 111.616(5), β = 92.938(4), and γ = 95.358(4)°. In (c) the SnI₅³⁻ chain structure for the A = iodoformamidinium compound is shown extending along the a axis. The shorter Sn–I bonds are drawn as filled (or black), whereas the longer 3.484(1) Å Sn–I bonds are drawn as narrower and unfilled.

For A = iodoformamidinium the tin(II) ion is surrounded by six iodides in a highly distorted octahedral arrangement, with bond lengths ranging from 2.957(1) to 3.484(1) Å.⁶⁹ The longest and shortest Sn–I bonds alternate down the length of the SnI₅³⁻ chain, thereby disrupting the continuity of the extended anion. The Sn–I(1)–Sn angle of 177.30(5)° indicates that the inorganic chain is close to being linear along the a axis. The four terminal Sn–I bonds, perpendicular to the chain direction, are intermediate in length [3.110(2), 3.097(2), 3.267(2), 3.330(2) Å]. For A = formamidinium the tin(II) ions are coordinated by six more equidistant iodides.⁷¹ In this case the Sn–I bond lengths alternate between 3.210(6) and 3.154(6) Å down the length of the chain, resulting in a chain with substantially better connectivity than for the A = iodoformamidinium system. The chains are also closer to being perfectly linear, as indicated by the 179.4° Sn–I(1)–Sn bond angle. Perpendicular to the chain the four terminal Sn–I bond lengths are 3.153(8), 3.178(8), 3.140(8) and 3.159(7) Å. The average Sn–I bond length for the A = formamidinium system, 3.166 Å, is substantially shorter than for the A = iodoformamidinium system, which has an average interatomic distance of 3.202 Å. The shorter average Sn–I bond length and reduced SnI₆ octahedron distortion correspond to a smaller band gap for the compound. The choice of “A” cation can therefore be used to tailor the detailed chain structure and band gap of the 1-D inorganic frameworks.

Recently, the compound [CH₃SC([double bond, length half m-dash]NH₂)NH₂]₃PbI₅ has also been reported,⁷² demonstrating that the m = 1 framework can accommodate other organic cations besides the iodoformamidinium cation. In contrast to [NH₂C(I)[double bond, length half m-dash]NH₂]₃PbI₅, however, the inorganic chains are highly disrupted, with alternating 3.037(2) and 3.882(2) Å bridging Pb–I bonds down the length of the chain. The PbI₆ octahedra are sufficiently distorted that an alternate description in terms of isolated PbI₅ square pyramids is perhaps more appropriate. The inorganic framework in this compound might therefore be considered intermediate between an extended 1-D and an isolated zero-dimensional (0-D) system. The analogous chloride-based compound, [CH₃SC([double bond, length half m-dash]NH₂)NH₂]PbCl₅·[CH₃SC([double bond, length half m-dash]NH₂)NH₂]Cl, has a very similar structure, with however an additional organic salt layer between each layer of inorganic chains.⁷²

Other orientations of perovskite sheets besides the 〈100〉- and 〈110〉-oriented varieties have also been reported, but are less common. One possibility is the 〈111〉-oriented layered perovskite family, A′₂A_q−1M_qX_3q + 3, where A′ and A are organic cations (Fig. 15). For ideal 〈111〉-oriented slabs, each MX₆ octahedron on the outer surface of a slab contributes three halides to the terminating surface (i.e. an octahedron face). In contrast, for 〈100〉-oriented slabs (Fig. 11), the terminating surface contains one halide from each octahedron (an octahedron corner), and for 〈110〉-oriented systems (Fig. 12), each octahedron contributes two halides to the terminating surface (i.e. an octahedron edge). Although not generally recognized as such, several q = 2 examples of this family include (CH₃NH₃)₃Bi₂Br₉, [NH₂(CH₃)₂]₃Sb₂Cl₉, and [NH(CH₃)₃]₃Sb₂Cl₉.^73–75 In each of these systems A′ and A can be the same organic cation since the molecules are relatively small. Note also that in the q = 2 examples, in order to accommodate the A₃M₂X₉ stoichiometry, the metal cation must be trivalent. In fact, in contrast to the 〈100〉-oriented and 〈110〉-oriented families, A′₂A_n−1M_nX_3n + 1 and A′₂A_nM_nX_3n+2, if A′ and A are monovalent cations the A′₂A_q−1M_qX_3q + 3 series requires a different average metal valence for each q. So far, the 〈111〉-oriented systems have only been stabilized with relatively simple organic cations. An interesting area of future research involves stabilizing higher-order members of this family, as well as incorporating more complex, perhaps functional molecules.

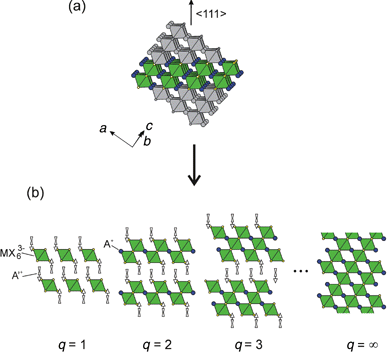Fig. 15 Schematic representation of the 〈111〉-oriented family of layered hybrid perovskites, A′₂A_q−1M_qX_3q + 3. The layered perovskite framework is derived from the 3-D perovskite parent compound by (a) taking q layers from along the 〈111〉 direction of the 3-D structure and (b) alternately stacking these layers with organic cations.

Note that for the 〈111〉-oriented family the q = 1 member actually consists of layers of isolated metal halide octahedra, and can therefore be loosely considered a 0-D perovskite structure (Fig. 15). This is in contrast to the 〈100〉-oriented family, where the n = 1 materials correspond to layered systems, and the 〈110〉-oriented family, where the m = 1 materials are chain-like 1-D compounds. An interesting example is shown in Fig. 16, where the tilt direction of each successive layer of isolated SnCl₆²⁻ octahedra alternates along the c axis.⁷⁶ With the inclusion of the 0-D perovskite-related systems, it is therefore possible to control the effective dimensionality of the inorganic framework over the range 0-D to 3-D by controlling the thickness as well as the orientation of the perovskite layers.

Fig. 16 Crystal structure of the q = 1 〈111〉-oriented system [(CH₃)₂NH₂]SnCl₆, viewed approximately down the a axis.⁷⁶ The structure adopts an orthorhombic (Pmnn) unit cell with the lattice parameters a = 7.220(1), b = 7.340(2), c = 14.446(3) Å.

5 Conclusion

Organic–inorganic perovskites combine, on a molecular level, an extended inorganic framework with a network of organic molecules. Distinct properties and functionality can be associated with the organic and inorganic structural components independently, as well as with the interaction and interface between the two components. In order to fully realize the potential offered by perovskite systems, it is important to understand and have the ability to control the structural character of both components of the hybrids. Given the steric and ionic constraints imposed by the inorganic framework, several guidelines have been outlined for designing organic cations to fit within the structure. First, the molecule must contain tethering cationic end groups (generally protonated amines), which are able to effectively hydrogen bond to the anionic metal halide framework. The molecules must also have a relatively narrow cross sectional area so that neighboring molecules within the organic layer do not sterically interfere. Finally, the organic cations may contain functional groups that either stabilize or destabilize the arrangement imposed by the inorganic framework. Given these constraints on molecular size, shape and functionalization, the perovskite organic cations are generally protonated aliphatic or simple aromatic primary amines. Recently, however, more complex oligomeric cations have also been incorporated, including an example from the NH₃(CH₂)_mT_n(CH₂)_mNH₃²⁺ family, where T_n represents an oligothiophene chain consisting of n thiophenes.^35,46 In these oligothiophene-based structures the edge-to-face aromatic–aromatic interactions and the rod-like character of the molecules help to stabilize a layered perovskite structure.

The inorganic frameworks can template the conformation and orientation of relatively simple organic cations (e.g. phenethylammonium), as well as more complex and functional dye or oligomeric molecules. For the quaterthiophene-based cation, AEQT, the inorganic framework helps to stabilize the syn-anti-syn conformation, rather than the more common all-anti conformation observed in α-quaterthiophene.³⁵ The templating arises from hydrogen bonding interactions between the cationic head group of the organic cation and the metal halide framework, as well as from steric constraints imposed by the inorganic arrays into which the organic cation must fit. The inorganic framework can also be used as an atomic scale “work bench” on which to perform photochemistry on reactive organic molecules. One example of this is provided by the topochemical photopolymerization of organic butadiene-based cations constrained to certain configurations within layered perovskite structures.^43,44 In these systems the inorganic framework can be used to control whether or not the molecules are held in an appropriate configuration for the 1,4 addition reaction to occur upon UV exposure.

The inorganic frameworks of the hybrid perovskites consist of 0-, 1-, 2-, or 3-D networks of corner-sharing metal halide octahedra, separated by organic cations. Just as the inorganic framework can template the organic molecule, the organic component of the structure also can template the inorganic framework. One example of this is found in the metal-deficient single-layer 〈100〉-oriented perovskites, based on 2-D (Mⁿ⁺)_2/nV_(n-2)/nX₄²⁻ sheets, where V is a vacancy (usually left out of the formula) and the metal cation valence, n, is greater than 2.⁴⁶ While, in general, these structures are difficult to stabilize, through the appropriate choice of a particularly stable organic cation bilayer (e.g. a rigid, rod-like oligomer layer with substantial edge-to-face interactions works well), the metal-deficient layered structures can be formed. The ability to incorporate non-divalent metal halide layers within the organic–inorganic perovskite framework widens the range of possible inorganic frameworks to explore, hopefully enabling new and useful (e.g. semiconducting, ferroelectric, optical, magnetic) properties to be uncovered.

The most common organic–inorganic perovskites consist of the single 〈100〉-oriented sheets. By mixing appropriately chosen short and long organic cations within the reaction, multilayer perovskite structures can also be stabilized, as the organic cations segregate onto separate layers of the hybrid structure. By controlling the number of perovskite sheets between the organic cation bilayers, the effective dimensionality of the inorganic framework can therefore be tailored. Furthermore, while the 〈100〉-oriented family of hybrid perovskites are most common, other orientations of the parent 3-D perovskite structure can also be stabilized within the lower-dimensional perovskite family (e.g. 〈110〉- and 〈111〉-oriented systems). The different inorganic frameworks can be templated by the appropriate choice of organic cation (e.g. iodoformamidinium cations for the 〈110〉-oriented family), as well as by properly selecting the valence of the metal cation.

Finally, different organic cations substituted into a perovskite family can have an important impact on the local coordination of the metal halide octahedra and therefore on the physical properties. One example of this is the [NH₂C(I)[double bond, length half m-dash]NH₂]₂ASnI₅ family, with A = NH₂C(I)[double bond, length half m-dash]NH₂⁺ or NH₂CH[double bond, length half m-dash]NH₂⁺.^69,71 Both materials share very similar SnI₅³⁻ chain-like structures. However, the A = iodoformamidinium system provides substantially more distortion to the tin(II) iodide octahedra and consequently a larger band gap relative to the A = formamidinium system. Presumably this control over coordination is provided by differences in hydrogen bonding between the two species within the solid, as well as by the very different steric constraints imposed by the two related cations. Other examples of structural control are provided in the (RNH₃)₂MX₄ family, where for a given metal halide framework, MX₄²⁻, different R groups result in a different degree of distortion of the MX₆ octahedra making up the framework.

Though the hybrid perovskites have been known for more than 100 years,²³ the recent developments discussed above have enabled a wider appreciation of the structural issues within this diverse family. While much still remains to be learned, the process of designing and synthesizing new organic–inorganic perovskites has begun to be transformed from a hit-or-miss proposition to a field in which the term “structural engineering” is more appropriate. A particularly important aspect to future hybrid perovskite research involves developing techniques to more effectively model these and related systems, so that structures and properties can reliably be predicted. As the field continues to mature, it is expected that many interesting new materials will be developed, potentially providing important opportunities for fundamental studies, as well as for the development of organic–inorganic hybrid microelectronic technologies.¹⁸

References

1. J. D. Currey, J. Mater. Educ., 1987, 9, 119.
2. C. Sanchez, F. Ribot and B. Lebeau, J. Mater. Chem., 1999, 9, 35.
3. C. B. Murray, C. R. Kagan and M. G. Bawendi, Science, 1995, 270, 1335.
4. J. Takada, Jpn. J. Appl. Phys., 1995, 34, 3864.
5. D. B. Mitzi, Prog. Inorg. Chem., 1999, 48, 1.
6. D. B. Mitzi, C. A. Feild, W. T. A. Harrison and A. M. Guloy, Nature (London), 1994, 369, 467.
7. D. B. Mitzi, S. Wang, C. A. Feild, C. A. Chess and A. M. Guloy, Science, 1995, 267, 1473.
8. D. B. Mitzi, C. A. Feild, Z. Schlesinger and R. B. Laibowitz, J. Solid State Chem., 1995, 114, 159.
9. T. Ishihara, J. Takahashi and T. Goto, Solid State Commun., 1989, 69, 933.
10. D. B. Mitzi, Chem. Mater., 1996, 8, 791.
11. G. C. Papavassiliou and I. B. Koutselas, Synth. Met., 1995, 71, 1713.
12. J. Calabrese, N. L. Jones, R. L. Harlow, N. Herron, D. L. Thorn and Y. Wang, J. Am. Chem. Soc., 1991, 113, 2328.
13. L. J. de Jongh and A. R. Miedema, Adv. Phys., 1974, 23, 1.
14. R. Willett, H. Place and M. Middleton, J. Am. Chem. Soc., 1988, 110, 8639.
15. G. V. Rubenacker, D. N. Haines, J. E. Drumheller and K. Emerson, J. Magn. Magn. Mater., 1984, 43, 238.
16. M. Era, T. Hattori, T. Taira and T. Tsutsui, Chem. Mater., 1997, 9, 8.
17. D. B. Mitzi, M. T. Prikas and K. Chondroudis, Chem. Mater., 1999, 11, 542.
18. D. B. Mitzi , K. Chondroudis and C. R. Kagan , IBM J. Res. Dev., in press..
19. F. Garnier, R. Hajlaoui, A. Yassar and P. Srivastava, Science, 1994, 265, 1684.
20. G. Gustafsson, Y. Cao, G. M. Treacy, F. Klavetter, N. Colaneri and A. J. Heeger, Nature (London), 1992, 357, 477.
21. C. R. Kagan, D. B. Mitzi and C. D. Dimitrakopoulos, Science, 1999, 286, 945.
22. K. Chondroudis and D. B. Mitzi, Chem. Mater., 1999, 11, 3028.
23. H. Topsöe, Z. Kristallogr., 1884, 8, 246.
24. A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373.
25. F. S. Galasso , Structure, Properties and Preparation of Perovskite-Type Compounds, Pergamon, New York, 1969..
26. R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751.
27. D. B. Mitzi and K. Liang, J. Solid State Chem., 1997, 134, 376.
28. R. D. Willett, Acta Crystallogr., Sect. C, 1990, 46, 565.
29. D. B. Mitzi, J. Solid State Chem., 1999, 145, 694.
30. O. Knop, R. E. Wasylishen, M. A. White, T. S. Cameron and M. J. M. Van Oort, Can. J. Chem., 1990, 68, 412.
31. A. Meresse and A. Daoud, Acta Crystallogr., Sect. C, 1989, 45, 194.
32. P. G. Tsoucaris, Acta Crystallogr., 1961, 14, 909; E. Horn, E. R. T. Tiekink, G. P. Jones, B. P. Naiola and L. G. Paleg, Acta Crystallogr., Sect. C, 1990, 46, 1575.
33. T. Ueda, M. Oma, K. Shimizu, H. Ohki and T. Okuda, Z. Naturforsch., Teil A, 1997, 52, 502.
34. H. Place and R. D. Willett, Acta Crystallogr., Sect. C, 1988, 44, 34.
35. D. B. Mitzi, K. Chondroudis and C. R. Kagan, Inorg. Chem., 1999, 38, 6246.
36. B. Servet, G. Horowitz, S. Ries, O. Lagorsse, P. Alnot, A. Yassar, F. Deloffre, P. Srivastava, R. Hajlaoui, P. Lang and F. Garnier, Chem. Mater., 1994, 6, 1809.
37. F. Garnier, A. Yassar, R. Hajlaoui, G. Horowitz, F. Deloffre, B. Servet, S. Ries and P. Alnot, J. Am. Chem. Soc., 1993, 115, 8716.
38. V. Barone, F. Lelj, N. Russo and M. Toscano, J. Chem. Soc., Perkin Trans. 2, 1986, 907.
39. T. Siegrist, C. Kloc, R. A. Laudise, H. E. Katz and R. C. Haddon, Adv. Mater., 1998, 10, 379.
40. H. Muguruma, K. Kobiro and S. Hotta, Chem. Mater., 1998, 10, 1459.
41. M. Era, K. Maeda and T. Tsutsui, Chem. Lett., 1997, 1235.
42. M. Braun, W. Tuffentsammer, H. Wachtel and H. C. Wolf, Chem. Phys. Lett., 1999, 303, 157.
43. B. Tieke and G. Chapuis, Mol. Cryst. Liq. Cryst., 1986, 137, 101; B. Tieke and G. Chapuis, J. Polym. Sci. Polym. Chem. Ed., 1984, 22, 2895.
44. P. Day and R. D. Ledsham, Mol. Cryst. Liq. Cryst., 1982, 86, 163.
45. G. Wegner, Pure Appl. Chem., 1977, 49, 443.
46. D. B. Mitzi , Inorg. Chem., submitted. .
47. G. A. Fisher and N. C. Norman, Adv. Inorg. Chem., 1994, 41, 233.
48. D. Stauffer, Phys. Rep., 1979, 54, 1.
49. D. B. Mitzi and P. Brock , Inorg. Chem., submitted. .
50. L. Antolini, G. Horowitz, F. Kouki and F. Garnier, Adv. Mater., 1998, 10, 382.
51. T. M. Barclay, A. W. Cordes, C. D. MacKinnon, R. T. Oakley and R. W. Reed, Chem. Mater., 1997, 9, 981.
52. S. Hotta and K. Waragai, Adv. Mater., 1993, 5, 896.
53. W. Porzio, S. Destri, M. Mascherpa and S. Brückner, Acta Polymer, 1993, 44, 266.
54. C. P. Brock and J. D. Dunitz, Acta Crystallogr., Sect. B, 1982, 38, 2218.
55. C. P. Brock and J. D. Dunitz, Acta Crystallogr., Sect. B, 1990, 46, 795.
56. A. Hargreaves and S. Rizvi, Acta Crystallogr., 1962, 15, 365.
57. Y. Delugeard, J. Desuche and J. L. Baudour, Acta Crystallogr., Sect. B, 1976, 32, 702.
58. C. A. Hunter and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5525.
59. S. Paliwal, S. Geib and C. S. Wilcox, J. Am. Chem. Soc., 1994, 116, 4497.
60. W. L. Jorgensen and D. L. Severance, J. Am. Chem. Soc., 1990, 112, 4768.
61. S. K. Burley and G. A. Petsko, Science, 1985, 229, 23.
62. C. Seel and F. Vögtle, Angew. Chem., Int. Ed. Engl., 1992, 31, 528.
63. X. Hong, T. Ishihara and A. V. Nurmikko, Phys. Rev. B, 1992, 45, 6961.
64. X. Hong, T. Ishihara and A. V. Nurmikko, Solid State Commun., 1992, 84, 657.
65. T. Ishihara , J. Luminesc., 1994, 60 and 61, 269..
66. M. Nanot, F. Queyroux, J.-C. Gilles, A. Carpy and J. Galy, J. Solid State Chem., 1974, 11, 272.
67. E. T. Keve, S. C. Abrahams and J. L. Bernstein, J. Chem. Phys., 1969, 51, 4928.
68. H. G. v. Schnering and P. Bleckmann, Naturwissenschaften, 1968, 55, 342.
69. S. Wang, D. B. Mitzi, C. A. Feild and A. Guloy, J. Am. Chem. Soc., 1995, 117, 5297.
70. I. B. Koutselas, D. B. Mitzi, G. C. Papavassiliou, G. J. Papaioannou and H. Krautscheid, Synth. Met., 1997, 86, 2171.
71. D. B. Mitzi, K. Liang and S. Wang, Inorg. Chem., 1998, 37, 321.
72. G. A. Mousdis, V. Gionis, G. C. Papavassiliou, C. P. Raptopoulou and A. Terzis, J. Mater. Chem., 1998, 8, 2259.
73. H. Ishihara, K. Watanabe, A. Iwata, K. Yamada, Y. Kinoshita, T. Okuda, V. G. Krishnan, S. Dou and A. Weiss, Z. Naturforsch., Teil A, 1992, 47, 65.
74. J. Zaleski and A. Pietraszko, Acta Crystallogr., Sect. B, 1996, 52, 287.
75. A. Kallel and J. W. Bats, Acta Crystallogr., Sect. C, 1985, 41, 1022.
76. M. H. Ben Ghozlen, A. Daoud and J. W. Bats, Acta Crystallogr., Sect. B, 1981, 37, 1415.

---