Matching of molecular and supramolecular symmetry. An exercise in crystal engineering

---

Abstract

With the aim of understanding the transfer of molecular threefold symmetry into supramolecular systems, the crystal structures of 2,4,6-tris(5-chloro-3-pyridyloxy)-1,3,5-triazine, 1,3,5-tris(3-methylphenyl)benzene and 1,3,5-tripyrrolylbenzene are described. In all three cases, C₃ molecular symmetry is carried over into hexagonal crystal packing. This is rationalized in terms of the supramolecular or void symmetry and the relevant intermolecular interactions.

---

One of the goals of crystal engineering is to obtain crystals that have or lack a particular symmetry element. In this context, it is useful to consider relationships between molecular and supramolecular symmetry under three categories: (1) the symmetry of the molecule is lowered in the crystal; (2) the crystal symmetry is higher than the molecular symmetry; (3) the molecular and crystal symmetries are matched. The first of these categories is very common but not so useful in crystal design,¹ being merely a restatement of Kitaigorodskii's close-packing principle.² A common example in the second category is when carboxylic groups with 1-symmetry are hydrogen bonded as dimers with 1̄-symmetry. But, such symmetry increase has not been explored systematically. The third category listed above, symmetry matching, is very useful in crystal engineering. However, structural chemists and crystal engineers are used to thinking of the close-packing principle as being of near-universal applicability, and, therefore, such studies of symmetry carry-over of higher-fold symmetry elements have generally not been pursued.

Here, we discuss the packing features of three diverse molecules, 1–3, with threefold symmetry that crystallize in space groups with 3-axes. In all of these three C₃ molecules – 2,4,6-tris(5-chloro-3-pyridyloxy)-1,3,5-triazine³1, 1,3,5-tris(3-methylphenyl)benzene⁴2 and 1,3,5-tripyrrolylbenzene⁵3 – the symmetry of the molecule coincides with a crystal symmetry element.

Triazine 1 when crystallized from 1∶1 hexane–EtOAc adopts the centrosymmetric space group R3̄ (no. 148) (Table 1). The asymmetric unit contains 1/3 molecule. The C_3i-symmetric Piedfort Unit⁷ (C_3i-PU) formed by an assembly of two stacked molecules of 1 may be identified (Fig. 1). The two molecules in the C_3i-PU are related by a 3̄-axis and are held together by weak intermolecular interactions,⁸ π⋯π, C–H⋯O and C–H⋯N (Table 2). The C_3i-PUs are stacked along [0 0 1] in a staggered manner to produce a columnar structure, which in turn is stabilized by short N⋯Cl interactions (3.18 Å, 148.5°). The PU stacks are themselves related by 3₁-axes being connected with C–H⋯N hydrogen bonds (Fig. 2). This helical arrangement is finally stabilized by C–H⋯Cl interactions. Both the formation of the C_3i-PUs via π⋯π stacking and the interconnection of the PUs via C–H⋯N hydrogen bonds are important in preserving the supramolecular threefold symmetry in 1.

Fig. 1 Stacking of triazine 1 molecules to form a C_3i-Piedfort Unit. Molecules at different levels are shaded differently. C–H⋯O and C–H⋯N interactions are shown as dashed lines.

Fig. 2 C–H⋯N (pyridine) hydrogen bonds (dashed lines) connect Piedfort Units in a threefold helical arrangement in the crystal structure of 1. Notice the synthon (void) symmetry. Click image or 2.htm to access a 3D representation.

Table 1 Summary of crystal data for 1–3^a,b,c

Parameter	1	2	3
a All data were collected at T⊕=⊕120 K using a MADNES-Messerschmidt and Pflugrath diffractometer with MoKα radiation (λ⊕=⊕0.71073 Å). b Full-matrix, least squares refinement on F^2 using SHELXL-97.^6 c Click b104431c.txt for full crystallographic data (CCDC 164454–164456).
Empirical formula	C18H9N6O3Cl3	C27H24	C18H15N3
M	463.66	348.46	273.33
Crystal system	Hexagonal	Hexagonal	Hexagonal
Space group	R3̄	P63	R3̄c
a/Å	21.189(3)	12.3060(17)	19.420(3)
b/Å	21.189(3)	12.3060(17)	19.420(3)
c/Å	7.1030(14)	7.5710(15)	6.6760(13)
V/Å^3	2761.8(8)	992.9(8)	2180.4(6)
Z	6	2	6
D c/Mg m^−3	1.673	1.166	1.166
F(000)	1404	372	864
μ/mm^−1	0.535	0.066	0.076
θ Range for data collection/°	3.08–28.55	3.63–27.48	3.30–27.48
Index ranges	−27⊕≤⊕h⊕≤⊕26; −23⊕≤⊕k⊕≤⊕25; −9⊕≤⊕l⊕≤⊕8	0⊕≤⊕h⊕≤⊕15; −13⊕≤⊕k⊕≤⊕0; 0⊕≤⊕l⊕≤⊕9	0⊕≤⊕h⊕≤⊕25; −21⊕≤⊕k⊕≤⊕0; −8⊕≤⊕l⊕≤⊕8
Reflections collected	4168	818	1020
Unique reflections	1456	818	543
R 1	0.0425	0.0613	0.0547
wR 2	0.1060	0.1631	0.1396

---

Table 2 Geometrical parameters of interactions in the crystal structure of triazine 1

Interaction^a	D/Å	d/Å	θ/°
a C–H bonds are neutron normalized to 1.08 Å. b π is the centroid of the aromatic ring.
ortho-C–H⋯O	3.309	2.73	112.8
ortho-C–H⋯N	3.556	2.58	149.6
para-C–H⋯N	3.663	2.61	163.4
para-C–H⋯Cl	3.871	3.09	129.3
π⋯π^b	3.345

---

The next compound of interest is 2. This hydrocarbon crystallizes in the non-centrosymmetric space group P6₃ (no. 173) (Table 1). The asymmetric unit contains 1/3 molecule. The 6₃-related molecules are connected by C–H⋯π interactions (2.94 Å, 3.914 Å, 150.1°) involving the CH₃ groups as donors⁹ (Fig. 3). Further stabilization is provided by C(phenyl)–H⋯π interactions (2.78 Å, 3.791 Å, 154.3°). Additionally, adjacent CH₃ groups of threefold-related molecules form a hydrophobic core (methyl pool) that effectively defines the supramolecular void in this packing. All these interactions are combined to generate the hexagonal network structure.

Fig. 3 Stereoview of the crystal structure of hydrocarbon 2. Molecules shaded differently are located on 3-axes and are connected to 6₃-related molecules by C–H⋯π interactions. Notice the methyl-rich hydrophobic core enclosing a void with C₃ symmetry. Click image or 3.htm to access a 3D representation.

When heterocycle 3 is crystallized from chlorobenzene, it crystallizes in the centrosymmetric hexagonal space group R3̄c (no. 167) (Table 1).† The asymmetric unit contains 1/6 molecule. Molecules are stacked at a distance of 3.34 Å and, remarkably, with no offset (Fig. 4). The π–π stacking interactions are very significant. They arise from the electron-deficient nature of the aromatic rings¹⁰ and could be major determinants in the generation of a hexagonal crystal structure, in that there is no offset. The reader should note that the existence of any lateral offset would necessarily break the hexagonal symmetry.

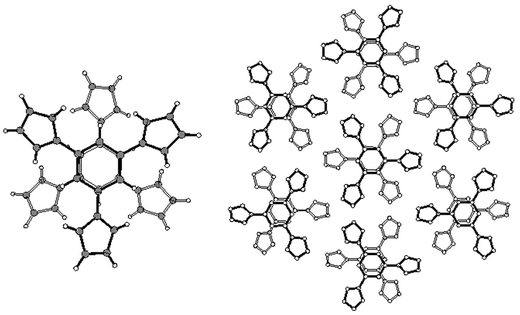Fig. 4 Dimer (left) and complete structure (right) of heterocycle 3. H atoms are removed in the right view for clarity. Notice how the absence of lateral offset in π–π stacking is compatible with supramolecular hexagonal symmetry.

Finally, it should be noted that for none of the compounds studied here is the full molecular symmetry transferred into the crystal. For example, in the tripyrrolyl derivative 3, there is the possibility that the molecule could crystallize with Z′⊕=⊕1/12 with the molecule being planar. In the observed structure, Z′⊕=⊕1/6 and the heterocyclic rings are inclined at an angle of 31° to the plane of the central phenyl ring. This is not surprising. The ubiquity and near-universality of the close-packing principle is such that even partial retention of molecular symmetry in the crystal is noteworthy.

This study shows that matching of molecular and supramolecular symmetry is achieved when the symmetry of the molecule matches the symmetry of the intermolecular voids, in other words the supramolecular synthon¹¹ symmetry. Synthon symmetry follows from the nature, number and relative positioning of intermolecular interactions; by no means need these be connected to the molecular symmetry, at least in a general sense. For example, closely related analogues of compounds 1–3 crystallize in low symmetry, close-packed structures.¹²

These difficulties do not apply for the most part in substituted tetraphenylmethanes where there is a facile symmetry carry-over between molecules and crystals. In these compounds, S₄ molecular symmetry relates to tetragonal crystal symmetry because of the characteristic tetraphenyl embrace,¹³ which encloses a tetrahedral void. Even the space groups of these compounds may be roughly predicted to be either P4̄2₁c or I4̄.¹⁴ In trigonal molecules, such symmetry carry-over is more difficult because there is no clear classification of the pertinent supramolecular synthons in terms of their symmetry properties. The present work attempts to identify some synthons that connect C₃ molecular symmetry and hexagonal crystal packing. The next step would be to identify more molecules that crystallize with these synthons, thus establishing robustness.

Acknowledgements

We thank Dr Ashwini Nangia (Hyderabad) for discussions and Professor Joseph Zyss (Cachan) for measuring the β value of compound 3. P. K. T. thanks the CSIR for fellowship support; K. C. and S. K. thank RSIC-Mumbai for recording spectral data; A. K. K. and H. L. C. acknowledge financial support from grant CA-10925 of the National Institute of Health; G. R. D. acknowledges financial support from CSIR project 01(1570)/99/EMR-II.

References

1. G. R. Desiraju, Crystal Engineering: The Design of Organic Solids, Elsevier, Amsterdam, 1989.
2. A. I. Kitaigorodskii, Molecular Crystals and Molecules, Academic Press, New York, 1973.
3. F. C. Schaefer, J. T. Thurston and J. R. Dudley, J. Am. Chem. Soc., 1951, 73, 2990.
4. S. Kotha, K. Chakraborty and E. Brahmachary, Synlett., 1999, 1621.
5. H. A. M. Biemans, C. Zhang, P. Smith, H. Kooijman, W. J. J. Smeets, A. L. Spek and E. W. Meijer, J. Org. Chem., 1996, 61, 9012.
6. G. M. Sheldrick, SHELXL-97, Program for Refinement of Crystal Structures, University of Göttingen, Germany, 1997.
7. A. S. Jessiman, D. D. MacNicol, P. R. Mallinson and I. Vallance, J. Chem. Soc., Chem. Commun., 1990, 1619.
8. G. R. Desiraju and T. Steiner, The Weak Hydrogen Bond in Structural Chemistry and Biology, Oxford University Press, Oxford, 1999.
9. V. R. Thalladi, R. Boese, S. Brasselet, I. Ledoux, J. Zyss, R. K. R. Jetti and G. R. Desiraju, Chem. Commun., 1999, 1639.
10. F. Cozzi, M. Cinquini, R. Annunziata, T. Dwyer and J. S. Siegel, J. Am. Chem. Soc., 1992, 114, 5729.
11. G. R. Desiraju, Angew Chem., Int. Ed. Engl., 1995, 34, 2311.
12. P. K. Thallapally, K. Chakraborty, H. L. Carrell, S. Kotha and G. R. Desiraju, Tetrahedron, 2000, 56, 6721.
13. I. Dance and M. Scudder, Chem. Eur. J., 1996, 2, 481.
14. M. A. Lloyd and C. P. Brock, Acta Crystallogr., Sect. B, 1997, 53, 780.

---

Footnote

† The nonlinear hyperpolarisability (β) of 3 measured at 1.064 µm in CHCl₃ is (1.9⊕±⊕0.4)⊕×⊕10⁻³⁰ esu.

---