Spectroscopy and magnetism of polymeric Ln(CCl3COO)3·2 H2O and their heteronuclear Ln2Cu(CCl3COO)8 ·6 H2O analogues (Ln=Sm, Gd)
Janina Legendziewicz*a, Małgorzata Borzechowskaa, Graźyna Oczkoa and Gerd Meyerb
aFaculty of Chemistry, University of Wrocław, 14 Joliot Curie str, Wrocław, Poland. E-mail: jl@wchuwr.chem.uni.wroc.pl
bInstitut für Anorganische Chemie, Universität zu Köln, Greinstrasse 6, D-50939, Köln, Germany
First published on UnassignedUnassigned4th January 2000
Abstract
In order to study the exchange interactions between f- and d-electron ions two series of compounds, heteronuclear Ln2Cu(CCl3COO)8· 6 H2O (1, Sm; 2, Gd) and polymeric Ln(CCl3COO)3·2 H2O (3, Sm; 4, Gd) trichloroacetates, were synthesised. Polymeric trichloroacetates 3 and 4 are isomorphous with erbium chloroacetate, whose structure contains dimeric units linked by carboxyl bridges and water molecules into endless chains. Heteronuclear 1 and 2 are isomorphous with Nd2Cu(CCl3COO)8·6 H2O reported by us previously. Absorption spectra of single crystals of 1–4 for two orientations of the crystals down to 4 K were investigated. Magnetic susceptibility measurements in the range 300–1.8 K were carried out. Optical and magnetic properties are related to the X-ray data. Electron transition probabilities were calculated and the effect of coupled ion pairs in the polymeric structure on the optical and magnetic properties was analysed. Changes in magnetic properties in relation to the mononuclear systems are discussed.
In the last few years many studies have been devoted to polynuclear and heteronuclear dimeric and polymeric systems. Binucleating ligands may provide unusual structural features and/or magnetic, optical and catalytic properties and allow the preparation of sophisticated molecular optical and magnetic devices, etc.1–9 For the same reasons, heteronuclear copper lanthanide compounds have been widely studied and also because of their potential applications in superconducting ceramics. In addition, it is well known that lanthanide(III) ions show peculiar physical and chemical properties that make them essential components in the preparation of many new materials. The main features of these materials can be influenced by structural parameters, the anisotropy of the ground state of 4f ions and by the nature and intensity of the exchange and other interactions involving rare earths and d-electron ions. In these systems two paramagnetic metal centres can interact either ferromagnetically or antiferromagnetically through the bridging group.
With the aim of shedding light on this field we synthesised two series of polynuclear (3,4) and heteronuclear (1,2) trichloroacetates. The correlation of their optical and magnetic properties to the X-ray data is the subject of this report.
Experimental
Polynuclear single crystals of Ln(CCl3COO)3·2H2O (Ln=Sm, 3; Gd, 4) and their heteronuclear analogues Ln2Cu(CCl3COO)8·6 H2O (Ln=Sm, 1, Gd, 2) were synthesised according to the procedure described previously.10,11 Samples 1–4 were checked by single crystal X-ray diffraction and the cell constants were determined. Polynuclear trichloroacetates 3 and 4 are isomorphous with the erbium complex.12 Heteronuclear Cu:Ln 1 and 2 have a similar structure to that previously reported for the Cu:Nd crystal.10Absorption spectra between 250 and 1600 nm for two orientations (a and b) of single crystals of compounds 1–4 were recorded in the 293–4 K temperature range using a Cary–Varian 5 spectrophotometer equipped with a helium (Oxford) cryostat. Intensities of the f–f and d–d transitions were calculated and converted into oscillator strength values and further applied for calculation of the Judd–Ofelt parameters (τλ). Raman spectra reported in ref. 13 were used in the vibronic components analysis. Magnetic susceptibility measurements were carried out with a SQUID magnetometer down to 1.7 K in both the low-field and high-field regimes. The data were corrected for diamagnetic contributions using Pascal's constants.
Results and discussion
X-Ray structure characteristics
As all the effects detected in the spectra (intensity, splitting, broadening) depend strongly on the structure of the system under investigation, essential X-ray structural data are given here. The crystal structure of Nd2Cu(CCl3COO)8·6 H2O reported by us earlier10 (and isomorphous with both crystals 1 and 2 investigated here) consists of heteronuclear chains composed of dimers of Nd(1)O9 and Nd(2)O8 polyhedra, linked through three bidentate and one chelating bridging (tridentate type) carboxylate groups of the trichloroacetate molecules. Thus, a noncentrosymmetric dimeric unit is formed, further connected by planar CuO4 squares. Two water molecules (OW1, OW2) add to the strongly distorted octahedron and link together the Cu(II) and Nd(IIIIII) ions, as do the carboxylic bridges. In this manner endless chains are formed, as shown in Fig. 1. Intrachain M–M distances are as follows: Nd1–Nd2=4.38 Å; Cu1–Nd1=4.155 Å; Cu1–Nd2=4.137 Å. The interchain separations are 9.472 Å (Nd2–Nd1) and 8.680 Å (Cu1A–Cu2B). Magnetic properties are affected by the chain structure and may depend strongly on the dimensionality of polymeric systems.![Part of the one-dimensional [Nd2Cu(CCl3COO)8(H2O)4] chain in the crystal structure of Nd2Cu(CCl3COO)8·6 H2O.10](/image/article/2000/NJ/a905956c/a905956c-f1.gif) | ||
| Fig. 1 Part of the one-dimensional [Nd2Cu(CCl3COO)8(H2O)4] chain in the crystal structure of Nd2Cu(CCl3COO)8·6 H2O.10 | ||
The structure of Ln(CCl3COO)3·2 H2O is an example of a one-dimensional polymer, composed of two different centosymmetric dimeric subunits bridged by carboxyl units and water molecules.12
Spectroscopic results
The absorption spectrum of a Gd(CCl3COO)3 ·2 H2O single crystal in the range 270–314 nm is presented in Fig. 2. Rather broad, unsplit bands were detected and the splitting of these bands does not change with a decrease in temperature to 4 K. Only two transitions from the 8S7/2 level to the 6PJ multiplet were detected (6P7/2 and 6P5/2, the weakest, 6P3/2, was not observed). The 8S7/2→6IJ transitions at higher energy also do not split cleanly. Such behaviour can indicate disorder in the structure or effects of the ion–ion interaction in the undiluted single crystal, leading to a broadening of the lines. This is so in our case, a fully concentrated single crystal of the gadolinium compound. Although the positions of the f–f absorption lines are weakly dependent on the material type, the absorption lineshape and the Stark splitting differ from material to material. A relatively small splitting is caused by the crystal field (CF) effect. The 8S7/2 ground state has a very small Stark splitting15 (of the order of 0.1 cm−1) so that the absorption spectra reflect directly the splitting of the excited states.15–17
 | ||
| Fig. 2 Absorption spectra of a Gd(CCl3COO)3 ·2 H2O crystal at 293 K (d=0.1355 cm; I: slit=0.1 nm, II: slit=0.2 nm) and 4.2 K (d=0.117 cm; slit=0.2 nm). | ||
Comparison of the splitting of the 6P multiplets with those in other systems indicates a CF effect for Gd3+ in the discussed crystal 4 (7/2, 72 cm−1; 5/2, 64 cm−1), comparable to those reported for the GdAl3(BO3)4 single crystal (7/2, 96 cm−1; 5/2, 62 cm−1; 3/2, 18 cm−1)18 and larger than in Gd:LaCl3 (7/2, 50 cm−1; 5/2, 37 cm−1; 3/2, 18 cm−1).19 Intensity analysis of the f–f transitions in the observed spectral range is collected in Table 1, for one orientation of both the polynuclear and heteronuclear gadolinium trichloroacetate crystals. In the heteronuclear crystal, oscillator strength values indicate only a small increase in the intensities of the 8S7/2→6P7/2 , 6I7/2 transitions in comparison to those in crystal 4. Since the splitting of the 8S7/2 level is very small, the decrease in temperature does not reflect the CF effect. Thus, the observed subtle changes in the intensities reflect the vibronic coupling and cooperative effects.
| Gd(CCl3COO)3 ·2 H2O | Gd2Cu(CCl3COO)8·6 H2O | ||||||
|---|---|---|---|---|---|---|---|
| λ/nm | 293 K | 4.2 K | 293 K | ||||
| 8S7/2→6P7/2 | 313–309 | 9.10 | 9.67 | 11.99 | |||
| 8S7/2→6P5/2 | 306.5–305 | 3.67 | 5.53 | 7.42 | |||
| 8S7/2→6I7/2 | 280–278 | 9.79 | 11.70 | 13.96 | |||
| 8S7/2→6I9/2,6I17/2 | 278–275 | 69.55 | 71.31 | 77.49 | |||
| 8S7/2→6I11/2,6I13/2, 6I15/2 | 275–270 | 153.72 | 158.71 | 162.49 | |||
| 8S7/2→6D9/2 | 253.5–252 | 13.08 | |||||
| Cu(CCl3COO)2·3 H2O | Gd2Cu(CCl3COO)8·6 H2O | ||||||
| λ/nm | 293 K | λ/nm | 293 K | 4.2 K | |||
| orientation | a | b | a | b | b | ||
| d–d Cu | 500–1400 | 218.68 | 269.76 | 400–1300 | 407.77 | 456.66 | 410.28 |
A comparison of the f–f transition intensities in the single crystals under investigation with those reported by Carnall et al.14 in water solution (HClO4) reveals slightly lower intensities in the single crystal spectra. We have calculated the oscillator strength values for two orientations of the crystals (axes a and b). It is necessary to calculate the third orientation of the crystal (axis c) to obtain the mean values, which can be compared to those in solution. Since the calculated changes in intensities for two orientations are not high they should not change much, even after correction for the third orientation.
The fitting procedure for the coordination polyhedra of the Ln3+ ions in the crystal structures leads to C2v symmetry for the lanthanide centres, both for the polynuclear trichloroacetates and for one Nd ion position in their heteronuclear analogue. Hence, the symmetry of the metal ion in water solutions, C3h,14,20,21 is higher than in the trichloroacetate single crystals.
A comparison of the f–f transition probabilities of crystals 2 and 4 shows a smooth variation of the oscillator strengths. This confirms that the metal centres in both types of crystals have similar environments.
Let us now focus on another aspect of the spectroscopic results, the intensities of the d–d transition in the heteronuclear Gd:Cu system and the monomeric Cu(CCl3COO)2·3 H2O crystal (Fig. 3). Both the intensities and energies of the d–d band are significantly different. Strong distortion of the octahedral symmetry is manifested by an increase of the d–d band intensity in the heteronuclear Gd:Cu crystal. Also, the energy of the split band of 2 at 4 K is shifted to higher values. This effect is accompanied by a shift of the charge transfer (CT) Cu2+ band to higher energies (≈280 nm). The energy of this band remains in resonance with the 6I multiplets of the Gd3+ ions.
 | ||
| Fig. 3 (I) Absorption spectra of a Gd2Cu(CCl3COO)8·6 H2O crystal at 293 K (orientations a and b; d=0.0475 cm; o: in paraffin oil) and at 4.2 K (orientation b; d=0.067 cm). (II) Absorption spectra of a Cu(CCl3COO)2·3 H2O crystal at 293 K (orientations a and b; d=0.031 cm). | ||
 | ||
| Fig. 4 Absorption spectrum of a Sm2Cu(CCl3COO)8·6 H2O crystal at 293 K. The insert shows the expanded spectrum between 320 and 540 nm. | ||
 | ||
| Fig. 5 Absorption spectra of a Sm2Cu(CCl3COO)8·6 H2O crystal at 4.2 K. Spectra (a) and (b) show expanded regions of the full spectrum in (c). | ||
 | ||
| Fig. 6 Absorption spectrum of a Sm(CCl3COO)3 ·2 H2O crystal at 293 K. | ||
| Sm2Cu(CCl3COO)8·6 H2O | Sm(CCl3COO)3 ·2 H2O | ||||
|---|---|---|---|---|---|
| λ/nm | 293 K | 4.2 K | 293 K | 4.2 K | |
| a The τλ·109 parameters: τ2=6.80±3.20; τ4=13.12±1.02; τ6=8.94±0.95, for Sm2Cu(CCl3COO)8·6 H2O. | |||||
| 6H5/2→6F1/2, 6H15/2 | 1786–1538 | 58.4 | 58.30 | 46.55 | 45.10 |
| 6H5/2→6F3/2 | 1538–1471 | 161.72 | 236.42 | 158.72 | 21.36 |
| 6H5/2→6F5/2 | 1471–1316 | 366.69 | 422.74 | 344.04 | — |
| 6H5/2→6F7/2 | 1316–1163 | 383.98 | 415.46 | 289.18 | — |
| 6H5/2→6F9/2 | 1136–1020 | 235.14 | 352.47 | 239.58 | — |
| 6H5/2→6F11/2 | 980–909 | 21.75 | 42.49 | 30.56 | — |
| 6H5/2→4G7/2 | 505–493 | 4.10 | 14.94 | 6.84 | 5.55 |
| 6H5/2→4I9/2, 4M15/2, 4I11/12 | 493–469 | 142.95 | 287.59 | 162.04 | 195.10 |
| 6H5/2→4I13/2 | 469–455 | 71.34 | 97.10 | 76.58 | 62.77 |
| 6H5/2→4F5/2 | 455–450 | 2.56 | 5.27 | 1.58 | 3.06 |
| 6H5/2→4M17/2, 4G9/2, 4I15/2 | 450–427 | 35.2 | 67.92 | 35.87 | 46.65 |
| 6H5/2→4L13/2 | 427–405 | 80.71 | 137.26 | 75.65 | 91.76 |
| 6H5/2→4F7/2, 6P3/2, 4K11/2, 4M21/2 | 405–392 | 466.21 | 382.89 | 427.04 | 406.07 |
| 6H5/2→4L15/2, 4G11/2 | 392–382 | 34.76 | 113.51 | 36.43 | 39.58 |
| 6H5/2→4D1/2, 6P7/2, 4L17/2, 4K13/2, 4F9/2 | 379–368 | 237.10 | 425.53 | 247.04 | 240.47 |
| 6H5/2→4D3/2, (4D, 6P)5/2 | 368–356 | 129.31 | 283.40 | 127.84 | 136.50 |
| 6H5/2→4H7/2 | 356–350 | 5.90 | — | 3.57 | — |
| 6H5/2→4K15/2, 4H9/2, 4D7/2, | 350–336 | 130.03 | 346.30 | 175.14 | 176.22 |
| (4K, 4L)17/2, 4L19/2, 4H11/2 | |||||
| d–d Cu | 500–1200 | 665.71 | 667.28 | ||
Since the first excited state lies at relatively low energy, it can be partially populated at room temperature. We have estimated this population to be 1.3%. Therefore, the population of this term must affect both the spectroscopic and magnetic properties of the systems under investigation. In fact, with a decrease in temperature, the intensities of almost all transitions increase, similarly to the europium single crystal spectra. These results are in contrast to those for the other lanthanide trichloroacetates for which a decrease of intensities is observed at low temperatures.11,13
Magnetic properties
 | (1) |
with T being the temperature, g the Zeeman factor and λ the spin-orbit coupling parameter. When considering the magnetic properties of lanthanide compounds one must remember the CF effect and the possible thermal population of the higher states for some ions (Sm and Eu).
In the polynuclear and heteronuclear systems ferromagnetic and antiferromagnetic ordering can be expected at low temperature. In fact, for 4f1 through 4f6 configurations of Ln(III) ions the angular and spin momenta can lead to antiparallel ordering in the 2S+1LJ free ion ground state. Parallel alignment of the Ln(III) and Cu(II) spin momenta can lead to an antiparallel alignment of the angular momenta and to an overall antiferromagnetic interaction. On the other hand, for 4f8 through 4f13 configurations angular and spin momenta are parallel in the ground state (J=L+S) and a parallel alignment of the Ln(III) and Cu(II) spin momenta may lead to parallel ordering of the magnetic moments, that is to a ferromagnetic interaction. In this case also, the CF effect complicates the situation.
In our earlier reports we have discussed the spectroscopic and magnetic data of two series of Ln and Ln:Cu trichloroacetates (Ln=Nd, Pr). Here we present results for the gadolinium and samarium polynuclear and heteronuclear analogues. In the first system, Gd(CCl3COO)3·2 H2O (4), a simple model can be analysed. Since the Gd3+ ion has a 8S7/2 ground state, which is almost unsplit (0.1 cm−1) and is located ≈32000 cm−1 below the first excited state, the magnetic moment is given by the spin momenta only. The second term of eqn. (1) is negligible and the magnetic susceptibility obeys the Curie law: χM·T=21Nβ2/k. However, our results are not consistent with the free ion approximation nor the reasoning and results reported for dimeric gadolinium systems by Kahn and coworkers.30 This is understandable because, in contrast to the earlier data reported by Kahn and coworkers,30,31 for both types of gadolinium chloroacetates, Gd2Cu(CCl3COO)8·6 H2O (2) and Gd(CCl3COO)3·2 H2O (4), polymeric chains are formed with dimeric subunits, which are further linked to each other by the Cu ion, or in 4, by carboxyl groups and water molecules. They differ also from other heteronuclear systems investigated by Kahn et al.32
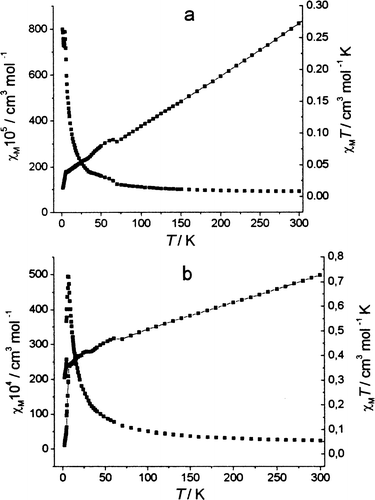
χM and χM· T vs. T for the gadolinium systems 2 and 4 are plotted in Fig. 7. For the polynuclear system 4 χM ·T exhibits what looks like antiferromagnetic ordering at low temperature. At very low temperatures the dramatic decrease in χM·T could also be a result of a very small splitting of the 8S7/2 multiplet at zero field or additional splitting of the ground state multiplet promoted by a Gd(III)–Gd(III) inter action. On the other hand, for the heteronuclear system Gd:Cu ferromagnetic ordering can be considered, but in this case also the relation of χM·T is not comparable to the previously reported results, most probably for the same reason as in the polymeric single crystals of compound 4 since the heteronuclear chain is composed also of Gd–Gd dimer units (see Fig. 1). Similar results and relations of χM·T for Cu:Gd heteronuclear compounds were reported by Benelli and co-workers.33,34 in drastically different heteronuclear chelates.
 | ||
| Fig. 7 Experimental (■) magnetic susceptibility χM and (–■–) χM·T calculated per molecule in the complex plotted vs. temperature. (a) Gd (CCl3COO)3 ·2 H2O, (b) Gd2Cu(CCl3COO)8·6 H2O. | ||
 | ||
| Fig. 8 Experimental (■) magnetic susceptibility χ (–■–) and χ·T calculated per molecule in the complex plotted vs. temperature. (a) Sm(CCl3COO)3 ·2 H2O, (b) Sm2Cu(CCl3COO)8·6 H2O. | ||
| T/K | χM·103/cm3 mol−1 | μeff/μB |
|---|---|---|
| 1.73 | 20.61 | 0.53 |
| 2.75 | 21.57 | 0.68 |
| 3.50 | 22.85 | 0.80 |
| 4.25 | 25.66 | 0.93 |
| 5.44 | 43.60 | 1.38 |
| 6.41 | 49.44 | 1.59 |
| 7.97 | 44.89 | 1.69 |
| 9.09 | 40.20 | 1.71 |
| 10.50 | 35.22 | 1.72 |
| 20.06 | 19.90 | 1.78 |
| 52.94 | 8.68 | 1.91 |
| 100.19 | 5.05 | 2.01 |
| 160.31 | 3.58 | 2.14 |
| 220.31 | 2.89 | 2.26 |
| 300.27 | 2.42 | 2.41 |
Using the free ion approximation, Kahn and colleagues31 derived the relation of χM for the Sm3+ ion in monomeric systems, in which χM can be given by the following equation for the six states arising from the 6H ground state multiplet:
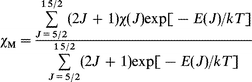 | (2) |
where χ(J) is given by eqn. (1) and E(J)=λ[J(J+1)−35/4]/2. Kahn et al. obtained excellent theory–experiment agreement. At low temperatures χMT reaches the value of 0.89 cm3 mol−1 K predicted by theory. Our results for the heteronuclear 1 system show completely different behaviour for χM and χMT vs. temperature (Fig. 8, Table 3) in comparison to the monomeric systems reported by Kahn et al.31
EPR investigations (300–4 K) of the heteronuclear Ln:Cu trichloroacetates show Ln: Cu interactions larger than for Ln: Ln systems.35,36 In addition, in the Pr:Cu trichloroacetates Cu:Cu interactions appear through the dimeric unit of the lanthanide ions. This was explained by a superexchange interaction involving the s and d orbitals of the Pr3+ ion.35–37
Summary
Two types of single crystals, heteronuclear Sm2Cu(CCl3COO)8·6H2O (1) and Gd2Cu(CCl3COO)8 ·6H2O (2) and homonuclear Sm(CCl3COO)3·2H2O (3) and Gd(CCl3COO)3·2H2O (4) trichloroacetates were obtained. Their optical and magnetic properties were investigated in the 1.7–293 K range.Their optical properties indicate marked differences in the structures of these two types of single crystals, with transformation of centro- to noncentrosymmetric lanthanide dimeric subunits.
The f–f transition probabilities were analysed and the Judd–Ofelt parameters calculated with a relatively small error.
Vibronic components were evaluated and assigned on the basis of IR spectra.
The magnetic moments of 1 and 3 decrease with temperature. This can be due to the crystal field effect and antiferromagnetic interactions of pairs of ions in compounds 1 and 3. Magnetic susceptibilities increase with decreasing temperature and ferromagnetic ordering seems to occur in compound 2.
References
- O. Kahn, Struct. Bonding (Berlin), 1987, 68, 89 Search PubMed.
- G. M. Villacorta and S. J. Lippard, Inorg. Chem., 1987, 26, 3672 CrossRef CAS.
- J. M. Lehn, Angew. Chem., Int. Ed. Engl., 1988, 27, 89 CrossRef.
- J. Legendziewicz, in Excited States of Transition Elements, World Scientific Publishing Co. Pte. Ltd., Singapore, 1992, pp. 149–179. Search PubMed.
- G. Blasse, Chem. Mater., 1989, 1, 294 CrossRef CAS.
- R. Reisfeld and C. Jørgensen, Laser and Excited States of Rare Earth, Springer, Berlin, 1977. Search PubMed.
- J. Legendziewicz, Acta Phys. Pol., 1996, 90, 127 Search PubMed.
- J. P. Costes, F. Dahan, A. Dupuis and J. P. Laurent, Inorg. Chem., 1977, 36, 3429 CrossRef CAS.
- J. P. Costes, F. Dahan, A. Dupuis and J. P. Laurent, Chem. Eur. J., 1998, 9, 1617.
- I. Kutlu, G. Meyer, G. Oczko and J. Legendziewicz, Eur. J. Solid State Inorg. Chem., 1997, 34, 231 CAS.
- J. Legendziewicz, G. Oczko and G. Meyer, Polyhedron, 1991, 10, 1921 CrossRef CAS.
- T. Imai and A. Ouchi, Bull. Chem. Soc. Jpn., 1987, 60, 408 CAS.
- J. Legendziewicz, G. Oczko, W. Strek and J. Hanuza, Eur. J. Solid State Inorg. Chem., 1995, 32, 95 CAS.
- W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4443 CrossRef CAS.
- G. H. Dieke, Spectra and Energy Levels of Rare Earth Ions in Crystals, Interscience Publishers, New York, 1968, p. 250. Search PubMed.
- L. Couture, J. Lumin., 1979, 18/19, 891 CrossRef.
- M. J. Weber, in Laser Spectroscopy of Solids, ed. W. M. Yen and P.M. Selzer, Springer-Verlag, Berlin, 1986, ch. 6. p. 189. Search PubMed.
- T. Tsuboi and S. Augusto, J. Phys. Conden. Matter, 1998, 10, 2787 Search PubMed.
- R. L. Schwiesow and H. M. Crosswhite, J. Opt. Soc. Am., 1969, 59, 592 Search PubMed.
- W. T. Carnall, P. R. Fields and K. Rajnak, J. Chem. Phys., 1968, 49, 4412 and 4424. Search PubMed.
- R. D. Peacock, Struct. Bonding (Berlin), 1975, 22, 83 Search PubMed.
- M. Malinowski, R. Wolski, Z. Srukacz, T. Łukasiewicz and N. Z. Łuczyński, J. Appl. Spectrosc., 1995, 62, 49 CAS.
- M. S. Magno and G. H. Dieke, J. Chem. Phys., 1962, 37, 2354 CrossRef CAS.
- H. Gobrecht, Ann. Physik, 1938, 31, 755 Search PubMed.
- W. T. Carnall, D. M. Gruen and R. L. McBeth, J. Phys. Chem., 1962, 2159 CAS.
- B. R. Judd, Phys. Rev., 1962, 127, 750 CrossRef CAS.
- G. Oczko, J. Legendziewicz, J. Mrozinski and G. Meyer, J. Alloys Compd., 1998, 275–277, 219 CrossRef CAS.
- J. Legendziewicz, M. Borzechowska, G. Oczko and J. Mrozinski, Spectrochim. Acta Part A, 1998, 54, 2197 Search PubMed.
- R. L. Carlin, Magnetochemistry, Springer Verlag, Berlin, 1986. Search PubMed.
- A. Panagiotopolus, T. F. Zafiropoulos, S. P. Perlepes, E. Bakalbasis, J. Masson–Ramade, O. Kahn, A. Terzis and C. Raptopoulu, Inorg. Chem., 1995, 34, 4918 CrossRef.
- M. Andruh, E. Bakalbassis, O. Kahn, J. C. Trombe and P. Porcher, Inorg. Chem., 1993, 32, 1616 CrossRef CAS.
- O. Kahn, O. Guillou, R. L. Oushoorn, M. Drillon and P. Rabu, New J. Chem., 1995, 19, 655 Search PubMed.
- C. Benelli, A. Caneschi, D. Gatteschi and L. Pardi, Mater. Chem. Phys., 1992, 31, 17 CrossRef CAS.
- C. Benelii, T. Guerriero, S. Tanburini and P. A. Vigato, Mater. Chem. Phys., 1992, 31, 137 CrossRef.
- Y. Yablokov, V. Voronkova, J. Legendziewicz, G. Oczko and M. Borzechowska, Appl. Magn. Reson., in press. Search PubMed.
- J. Legendziewicz, J. Alloys Compd., in press. Search PubMed.
- V. K. Voronkova, Y. V. Yablokov, J. Legendziewicz, G. Oczko, M. Borzechowska, Solid State Phys., 1999, 41, 41 (in Russian). Search PubMed.
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2000 |
