Novel uses of lasers in atomic spectroscopy†. Plenary Lecture
J. D.
Winefordner
*,
I. B.
Gornushkin
,
D.
Pappas
,
O. I.
Matveev
and
B. W.
Smith
Department of Chemistry, University of Florida, Gainesville, FL 32611, USA
First published on 29th June 2000
Abstract
This paper reviews several novel uses of lasers in atomic spectroscopy. A tutorial discussion is given of the basic processes involving the interaction of laser radiation with atoms and the measurement approaches. Laser microprobes, especially laser induced breakdown spectroscopy and laser ablation-inductively coupled plasma-optical emission or mass spectrometry are reviewed thoroughly with respect to principles, instrumentation and applications. Laser excited atomic fluorescence and atomic absorption spectrometry with diode lasers are considered primarily with respect to recent publications. Laser-enhanced ionization, resonance ionization and resonance ionization imaging are also thoroughly reviewed with respect to recent publications. Diagnostical measurements of plasmas and atom reservoirs are discussed. The principles of six laser based atomic absorption methods are given and the methods are compared with respect to detection limits. Finally, future uses of lasers in atomic spectroscopy and a comparison of the characteristics of various atomic methods for trace elements are given.
It has been 20 years since the monograph by Omenetto1 and 14 years since the monograph by Peipmeier.2 During this time, numerous books and review articles have appeared. Several other pertinent books3–12 and a major review13 on laser analytical atomic spectroscopy will be mentioned here. This paper will review major recent advances in lasers in analytical atomic spectroscopy. We will particularly elaborate on several novel uses of lasers. The analytical methodologies involving lasers to be considered are atomic absorption spectrometry, atomic emission spectrometry [particularly laser induced breakdown spectroscopy (LIBS)], atomic fluorescence spectrometry and atomic ionization spectrometry (see Table 1 for a summary of the laser-based methods). In addition, we will emphasize the use of laser ionization and fluorescence for imaging both atomic and molecular processes. We will probably not mention some work by other scientists who consider their work to be on the cutting edge; for such omissions, we apologize. We will especially focus on those laser-based analytical methods which have been developed and used in several laboratories involved in the detection of trace and ultra-trace elements in various solid, liquid and gaseous sample matrices with special emphasis on those methods also developed and used in the authors' laboratories.
| Absorption | Lasers used as primary sources for atomic and molecular absorption measurements. Lasers are nowadays mainly diode lasers but dye lasers and solid state tunable lasers (e.g., OPO) have been used. Absorbing species are generally located outside (e.g., flames, plasmas, furnaces) the laser cavity but also can be present inside the cavity (intracavity absorption) |
| Emission | Lasers tightly focused on a solid, liquid or a gas (the target) to create a plasma from which atoms and molecules emit. In the case of solids, ablation occurs prior to creation of the discharge |
| Fluorescence | Lasers used as excitation sources (primarily pulsed dye and solid state lasers) to pump atoms into selected excited states from which radiative de-excitation (fluorescence) is measured. Atoms are normally produced outside the laser cavity (e.g., flames, furnaces, plasmas, glow discharge); also atoms can be produced inside the cavity (intracavity fluorescence). Fluorescence can also be excited in atoms produced by ablation and/or the resulting plasma |
| Ionization | Lasers (generally two or more laser wavelengths) are used to pump atoms into highly excited levels from which collisional ionization [laser enhanced ionization (LEI)] occurs or by selective photoionization of the highly excited atoms [resonance ionization spectroscopy (RIS) or resonance ionization mass spectrometry (RIMS)]. The charges formed are measured (e.g., in flames, LEI or at low pressure, RIS) or the ions are measured by time-of-flight mass spectrometry (RIMS) |
| Photothermal | Lasers (pulsed) are used to pump atoms into excited states which deactivate by means of collisional processes producing heat and refractive index changes. The heat is measured by photoacoustic methods and the refractive index change measured by thermal lensing, photothermal deflection, photothermal refraction, or photothermal diffraction. Except for mercury, photothermal spectroscopy is rarely used for atomic studies |
One of the major reasons for the excitement of using lasers in analytical atomic spectrometry is the possibility of detecting and even measuring single atoms. Alkemade14,15 was the first to discuss the efficiency of detection and the conditions necessary to detect single atoms. Winefordner and co-workers16–18 expanded on the Alkemade approach in order to apply it to the efficiency of both measurement and detection. The latter groups developed theoretical expressions for the efficiency of detection and measurement and for the detection limits for a number of atomic methods, including several laser-based techniques. No attempt will be made here to review the above papers or to expand the concepts to cover all the laser-based methods. However, the reader is referred to the paper by Omenetto et al.,19 who discuss the concepts of absolute (number of grams) and relative (concentrations) detection limits in laser-based analysis. For example, a laser-based method might have an absolute detection limit of 1 ag. If the amount of sample actually interrogated by the laser is only 1 ng, then the relative detection limit is 1 ng mL−1, which is still excellent but not as impressive as 1 ag. On the other hand,19 if sample amount is not limited, then a CW technique such as ICP-MS should be used where a detection limit of 0.1 pg mL−1 is possible in some cases; if a 5 mL sample solution is required, then the absolute detection limit is 0.5 pg. However, if one uses a 5 g sample and dilutes it 100-fold for analysis, then the effective detection limit becomes 50 pg, which is still excellent but not as impressive as the 0.5 pg in this case.
We will also not discuss here the characteristics and operation of laser systems. The reader is referred to previous publications.1–12 Despite the excellent characteristics and capabilities of lasers, such as selective detection of single atoms14–18 or ions,20 laser systems, for the most part, are still complex to operate and expensive to acquire. It seems clear that the use of lasers in routine applications will generally be limited to a few selected applications where certain elements must be determined with a high degree of selectivity and with exceedingly low detection limits. The major exceptions to this are LIBS and atomic absorption spectrometry with diode lasers. Certainly, with the development of compact, turn-key operation and inexpensive all solid state lasers, which will eventually replace gas lasers and liquid dye lasers, more routine applications of lasers in analytical atomic spectrometry will arise.
Nevertheless, with the exception of LIBS, all laser-based atomic methods are single element methods and so cannot compete well with multi-element methods, such as ICP-MS and ICP-OES, assuming the detection power of the latter two methods is sufficient for the specific application. Fortunately, semiconductor diode lasers should soon be available for the violet–blue region. There is little doubt that solid state lasers are the future of analytical laser spectroscopy.
In Fig. 1, the principles of the laser analytical atomic spectrometry methods discussed in this review are briefly summarized. In Fig. 2, simplified experimental arrangements are given for the various laser-based methods. In Table 2, the most common means of producing atoms and ions in laser based methods are summarized.
 | ||
| Fig. 1 Principles of several laser excited atomic spectrometric methods: LEAFS (laser excited fluorescence spectrometry); LEIS (laser enhanced ionization spectrometry); LIBS (laser induced breakdown spectrometry); RIS (resonance ionization spectrometry); RIMS (resonance ionization mass spectrometry); LAAS (laser atomic absorption spectrometry); and LIMS (laser ionization mass spectrometry). | ||
 | ||
| Fig. 2 Experimental basis of laser atomic (and ionic) analytical spectrometric (non-imaging) methods. | ||
| Flames, plasmas—nebulization of solutions or introduce from a GC, HPLC, CZE, SCFC, HG, FIA system, etc. |
| Laser ablation/vaporizaton/atomization/ionization |
| Particle (atoms or ions) bombardment of solids |
| Hydride generation plus heat |
| Electrothermal atomization (ETA) |
As stated above, only representative papers and applications will appear in the list of references. This review is meant to be more tutorial than exhaustive, especially since the review has originated from a lecture. Again, apologies are made to authors who have published papers based on novel research. An Appendix with definitions of acronyms is also given.
Laser microprobes
Among laser microprobe techniques nowadays, the most popular sampling–detection combinations are laser ablation coupled with optical emission spectrometry (LA-OES), which is also called laser induced breakdown spectroscopy (LIBS), laser ablation coupled with inductively coupled plasma optical emission spectrometry (LA-ICP-OES) and laser ablation coupled with inductively coupled plasma mass spectrometry (LA-ICP-MS). General information on nearly all methods utilizing laser ablation can be found in comprehensive reviews by Radziemski,21 Russo,22 Darke and Tyson23 and, most recently, Rusak et al.24,25In this paper, we will focus mainly on the three techniques mentioned above based on the literature of the past two years, 1998 and 1999. Special attention will be paid to studies where fundamentals of laser ablation have been investigated, along with work on the use and practical applications of LA-based techniques.
Fundamentals and diagnostics of LA
Cabalín and Laserna26 studied the effect of laser wavelength on the ablation threshold for metals with different thermal properties (from Zn to W). Three harmonics (1064, 532 and 266 nm) from a 5 ns pulse width Nd∶YAG laser were used. The fluence threshold (J cm−2) was shown to be the lowest for longer wavelengths of 1064 and 532 nm, whereas the energy threshold was the lowest for the shortest wavelength of 266 nm. This result agreed with the fact that cascade-like growth of the electron number density due to inverse bremsstrahlung is considerably more favorable in the IR than in the UV region (λ2 dependence), although the laser coupling is more effective at lower wavelengths. Fluence threshold correlated reasonably well with thermal properties such as melting and boiling points at all three wavelengths used, whereas surface reflectivity was found to be an irrelevant parameter. Another experimental confirmation of more efficient coupling of the IR with laser-induced plasma was found when a pulsed CO2 laser (10.6 µm, 300 MW cm−2) was used for ablation of a Ti target;27 emission from Ti(IV) ions was observed. In contrast, an excimer laser (308 nm, 500 MW cm−2), which was used for ablation of the same target, produced the maximum ionization state of only Ti(III).28 Therefore, the plasma induced by the UV laser had a lower initial electron temperature than that induced by the infrared CO2 laser.
 | ||
| Fig. 3 (a) Observed values of damage threshold at 1053 nm as a function of the laser pulse width. Solid lines are τ1/2 fits to long pulse results. (b) Calculated evolution of free electron density for a 100 fs, 1053 nm pulse (dashed curve) of peak intensity 11.7 TW cm−2 in fused silica. Multi-photon ionization (dotted curve) starts the avalanche; solid curve is total electron density including impact ionization. (From ref. 31.) | ||
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–15
000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K) for the time window of 0.35–1.4 µs were obtained from Stark-broadened lineshapes and from a multi-line graphical Saha–Boltzmann approach, respectively. Changing the ambient gas, the laser energy, particulate levels and humidity levels produced little variation in the temperature and electron density of the laser spark, as was expected on the basis of the LSRW model.
000 K) for the time window of 0.35–1.4 µs were obtained from Stark-broadened lineshapes and from a multi-line graphical Saha–Boltzmann approach, respectively. Changing the ambient gas, the laser energy, particulate levels and humidity levels produced little variation in the temperature and electron density of the laser spark, as was expected on the basis of the LSRW model.
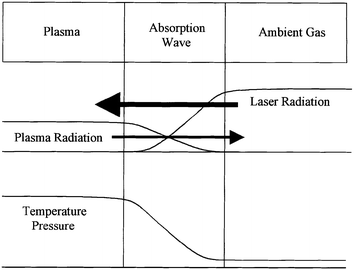 | ||
| Fig. 4 Plasma heating by radiation wave. (From ref. 38.) | ||
 | ||
| Fig. 5 Schematic diagram of discontinuities within a shock wave and a refractive index distribution, t ≈ 70 ns after pulse beginning. Shock front: steep rise of the refractive index (RI) = high neutral particle density. Ionization front: steep decrease of the RI = high electron density. Contact front: rise of the RI = transition from ambient gas to material vapor. Plasma core front: dense material plasma. (From ref. 45.) | ||
A Michelson interferometer was used by Schittenhelm and co-workers45,46 to image a refractive index distribution in the laser plume. The plasma was created by a KrF laser on a Cu target, and a time resolution of 500 ps was achieved by using a dye laser pumped by an N2 laser.45 The images, taken within the first 100 ns, showed a high refractive index at the shock wave front and a steep decrease toward the target closely behind the shock front (see Fig. 5). In this region, the refractive index had a lower value than in vacuum owing to a high concentration of free electrons. Two-wavelength interferometry allowed the same workers to calculate the numerical values of electron number densities.46 Variation of the ambient gas caused a drastic change in the electron density, although the efficiency of ablation (the ablation rate) remained the same. In an argon atmosphere, formation of a laser-supported detonation wave, instead of a shock wave, arose for energy fluences greater than 20–25 J cm−2.
Laser microprobe analysis
 | ||
| Fig. 6 Experimental arrangement for LA-OES (or LIBS) with an échelle spectrometer. More typically, a monochromator is used in place of the échelle spectrometer. | ||
Chaléard et al.47 quantified optical emission signals and corrected for matrix effects assuming emission lines to be a function of two parameters: the vaporized mass and the plasma excitation temperature. The ablated mass was accounted for using an acoustic signal and the excitation temperature was measured by the two-line method. It was demonstrated that normalization of the net emission intensity by both the acoustic signal and the temperature allowed for a multi-matrix calibration curve with a satisfactory level of precision. Examples included single slope calibration curves for Cu in brass, aluminum and steel matrices, for Mn in steel, aluminum and nickel matrices and for Cu in Zn, Al–Cu and Al–Zn alloys. Panne et al.48,49 proposed a calibration approach for analysis of major constituents (Si, Al, Ca) in glass and glass melts, where line intensity ratios, Mg/Si, Mg/Ca and Mg/Al, were normalized to electron temperatures. The plasma temperatures were computed using the Boltzmann plot method. The normalization resulted in linear calibration plots and improved precision and accuracy.
Numerous experimental optimizations have been undertaken to achieve better analytical performance. Aguilera et al.50 studied the effect of focusing distance and laser pulse energy on accuracy and limit of detection of atmospheric LIBS. A 64 ppm LOD and 4% RSD were obtained for Ni in steel when the 250 mJ Nd∶YAG laser was focused 12 mm below the sample surface. The plasma shielding effect was also discussed. Castle et al.51 studied factors influencing the precision in LA-OES measurements using a pure Cu target. It was demonstrated that such quantities as sample translation velocity, laser pulse stability, detector gate delay and number of accumulated spectra strongly affected the precision, whereas surface roughness had a minimal effect. The best precision obtained was 0.03%.
In almost all optical spectrometers, the price for high spectral resolution is a narrow spectral working window. With regard to LIBS, however, both of these quantities are very important: the simultaneous measurement of a complete optical spectrum with high resolution can dramatically improve the precision, accuracy and detection limits of LA-OES measurements. Therefore, the application of an échelle spectrometer, combined with a gated ICCD, is of special interest. The operation principle of échelle spectrometer was well described by Lindblom52 and a practical LIBS system with an échelle spectrometer (Fig. 6) was demonstrated by Bauer et al.53 The system was applied to the analysis of Al-based samples. Linear single-shot calibration plots were obtained for six elements with limits of detection of the order of 1–10 µg g−1. Additionally, the plasma temperature was easily determined from a Boltzmann plot. The plasma temperature could further be used for normalization of analyte line intensities.
 | ||
| Fig. 7 Schematic diagram of a laser ablation system used in LA-ICP-OES and LA-ICP-MS. (From ref. 63.) | ||
Accuracy remains a major figure of merit in all techniques involving LIBS. Nölte et al.54 studied the influence of simultaneous internal standardization and background correction on signal repeatability in LA-ICP-OES. LA-ICP-MS and LA-ICP-OES were compared for homogeneity of the main components (Ba, Al and Si) in glass. Single shots were fired at the glass sample and Si was used as an internal standard. For ICP-MS, which is a fast sequential technique, the RSDs were >2%, whereas for ICP-OES, with simultaneous measurements, the RSDs were <1%, allowing evaluation of the homogeneity of the sample. Motelica-Heino et al.55 found that the response factor in LA-ICP-OES was strongly dependent on the chemical form of the analyte, on the bulk composition of the matrix and on the ablation wavelength. Different salts of Mg, Al and Fe were used separately and spiked with SiO2 or CaCO3. In contrast, there was no influence of the grain size or binding pressure of pressed pellets. The importance of internal standardization was also emphasized. Gagean and Mermet56 analyzed brasses using LA-ICP-OES. A XeCl laser and four harmonics of an Nd∶YAG laser were used for ablation. A Zn enhancement was observed which could be suppressed using high fluence UV ablation. No simple relationship between the signal and the concentration was observed for Cu. This was attributed to specific structural features of brass. Russo and co-workers contributed a series of papers57–61 where they also used ICP-OES and brass samples to study mass ablation rate, ablated mass composition and the effects of ambient gas and laser wavelength. Two Nd∶YAG lasers and an excimer laser with pulse widths ranging from 35 ps and 30 ns and wavelengths ranging from 266 to 1064 nm were used for ablation. It was shown that the laser pulse width, fluence and wavelength and the ambient atmosphere strongly influenced the mass removal. The Zn-to-Cu ratio was found to be almost constant and close to the stoichiometric value at high laser fluences and short laser pulses (picoseconds). The most efficient ablation was obtained with short laser pulses operating in the UV region in an He atmosphere. A non-thermal ablation mechanism, involving the interaction between space charges and ionized species at the sample surface, was proposed to describe ablation with the picosecond laser. Plasma shielding was suggested as a possible mechanism for the gas effect on laser sampling. Rings et al.62 used LA-ICP-OES to study the spatial distribution of elements in amorphous solids, Si–B–N–C and Ba–Si–Al–O–C. This was important in order to reveal exact structure and understand physical and chemical properties of this type of material. Homogeneity was evaluated and the concentration of the main components were determined with a resolution of 50 µm. Good reproducibility was obtained using one element for internal standardization (0.3–0.7% RSD for Si and Al with Ba as internal standard and ∼1.5% for B with Si as internal standard).
Here, we review some of the advances in LA-ICP-MS during 1998–99. Alexander et al.64 confirmed once again that UV ablation yielded good precision (5–10% RSD) and minimal fractionation and matrix effect, whereas for visible or IR ablation these parameters were much worse. They found that the majority of the UV-ablated material was present as particles 0.1–1.0 µm in diameter, which were ideally suited for transport and complete digestion in the ICP. Mass spectra, normalized to particle counts, yielded perfectly linear calibration plots in the range 1.5–1500 ppm for Mg and Sr in nuclear waste simulants. Elemental fractionation during laser sampling for ICP-MS was studied by Eggins et al.,65 who ablated a glass sample with a KrF laser and studied the ablation pit morphology. Examination of pit morphology revealed the importance of sequential condensation of refractory and then volatile phases from the cooling plasma. Figg et al.66 used 532 nm ablation in glass and reported the preliminary results on whether fractionation occurred during the ablation process or in the ICP. Two parameters, important for elemental fractionation, were monitored: laser irradiance and particle size. Three types of MS responses were observed and, correspondingly, three groups of elements were identified showing no fractionation, ablation fractionation or ICP fractionation. Schroeder et al.67 also analyzed glasses using LA-ICP-MS with a 266 nm laser ablation system. Limits of detection in the ppt range were obtained for Ag, La, Eu, Tl and Th; the 206Pb/207Pb isotope ratio was measured with external reproducibility better than 3%. It was shown that shorter laser pulses (3 and 8 ns pulses were studied) yielded better signal stability. Jeffries et al.68 compared 266 and 213 nm (quintupled Nd∶YAG) ablation lasers for LA-ICP-MS analysis of a NIST glass standard. A 213 nm laser produced a higher volume of transportable particulate, flatter and higher intensity signals and a lesser degree of elemental fractionation as compared with a conventional 266 nm laser. Wolf and co-workers69 investigated the feasibility of LA-ICP-MS for analysis of industrial polymers. For filled polymer films, the concentrations of 10 elements of interest obtained by LA-ICP-MS compared well (within ±30%) with the results obtained by solution ICP-OES (Fig. 8). It was emphasized that in the case of ICP-OES, complete digestion and analysis took 1–2 d, whereas in the case of LA-ICP-MS, the sample preparation was eliminated and analysis took only 5 min.
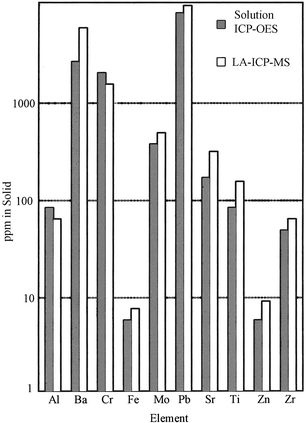 | ||
| Fig. 8 Comparison of LA-ICP-MS results with solution ICP-OES results for 10 elements in filled polymer film. (From ref. 69.) | ||
The unique versatility of laser ablation as a microscopic sampling tool was demonstrated by Neilsen et al.,70 who used LA-ICP-MS in combination with gel electrophoresis for speciation of metal binding serum proteins. Such a development is consistent with, and complementary to, the use of laser desorption mass spectrometry for the characterization of proteins separated by gel electrophoresis. Pooled human serum spiked with Co was used as a test sample; metal protein distribution in electrophoresis gels was mapped and quantified. Reference gels for quantitative analysis were prepared from pure water containing increasing amounts of Co. Günter et al.71 applied LA-ICP-MS with a 193 nm ablation laser for multi-element analysis of microscopic (5–50 µm in diameter) fluid inclusions in minerals. The calibration procedure was based on direct ablation of standard solutions through a plastic film; 23Na was used as internal standard. Quantitative data for 19 elements in the concentration range 0.5 µg g−1–300 mg g−1 in natural fluid inclusions were obtained with a typical accuracy between 5 and 20%.
Calibration methodology and accuracy remain major problems in LA-ICP-MS. The most common quantification method so far is external calibration using matrix-matched standards. However, a general need exists for analysis which does not require solid calibration standards, as it is difficult and time consuming to prepare such materials. In contrast, solution-based calibration is a well established procedure for ICP-MS and deserves to be applied in a combination with LA. A number of attempts were undertaken to use liquid standards in LA-ICP-MS. Leach et al.72 used solution standards to calibrate the response of LA-ICP-MS. The dried aerosols from solution standards were introduced by flow injection on top of a baseline of ions from the solid produced by LA (Fig. 9). Because the standards and samples were introduced to the plasma simultaneously, the method was believed to compensate for matrix effects caused by the major components of the solid. Indeed, trace elements in SRM steel were determined with only ∼8% deviation from certified values, one of the best results reported in the literature. Two complications of using this method must be mentioned, however. First, laser ablation and nebulizer transport rates had to be measured prior to analysis and second, no elemental fractionation had to be assumed in the nebulization, desolvation or laser ablation processes. Falk et al.73 used LA-ICP-MS for the determination of trace elements in copper reference samples. Liquid standards were introduced into the ICP without a desolvation step and a tail of a mass peak of the matrix element (Cu) was used for internal standardization. The value of this peak corresponded to an MS signal from the solution containing 250 mg L−1 of Cu. Such a solution, spiked with increasing amounts of elements of interest, was used for calibration. Deviations from certified values were within ±20%. Shuttleworth and Kremser74 used LA-ICP-sector field mass spectrometry and obtained impressively low detection limits (at the ppt level) and excellent precision (<10%) for a large number of elements in glass. Therefore, coupling LA-ICP with sector field MS provided an alternative to commonly used LA-ICP-quadrupole MS systems when ultimate detection limis are required.
![Plot of count rate vs. time for flow injection additions of 25, 50 and 100 ppb Co solution standards during continuous laser ablation of NIST 1263a. The shoulder under the peaks corresponds to [Co]solid = 0.048 wt.%. (From ref. 72.)](/image/article/2000/JA/a910219l/a910219l-f9.gif) | ||
| Fig. 9 Plot of count rate vs. time for flow injection additions of 25, 50 and 100 ppb Co solution standards during continuous laser ablation of NIST 1263a. The shoulder under the peaks corresponds to [Co]solid = 0.048 wt.%. (From ref. 72.) | ||
Van Vaeck et al.75 compared laser microprobe mass spectrometry (TOF-LMMS and FT-LMMS, ablation at 266 nm) and static secondary ion mass spectrometry (S-SIMS) for the speciation of inorganic compounds such as MoO3 and Na2SO4. Generally, the SIMS technique is based on the interaction of primary ions in the keV range with the surface components of solids. The surface becomes a source of secondary ions which are accelerated by an electrostatic field and detected by MS. S-SIMS uses a low primary ion current density so that each molecular microenvironment is hit by only one primary ion. It was demonstrated that mass spectra from LMMS allowed the direct identification of an analyte, whereas S-SIMS required the use of reference spectra for such identification. On the other hand, S-SIMS allowed the analysis of molecular monolayers, which was virtually impossible with LMMS. Norman et al.76 compared trace element data obtained by LA-ICP-MS, solution ICP-MS, electron microprobe analysis and proton microprobe analysis for a variety of silicate glasses and minerals. Microprobe spot diameters on an analyte surface were 30–50 µm for 266 nm photos in LA-ICP-MS, ≤10 µm for electrons and 30 µm for protons in electron and proton microprobe analysis, respectively. For LA-ICP-MS, relative element sensitivities were calibrated against a NIST glass standard and 44Ca was measured as an internal standard. Results obtained for the various microbeam and solution methods agreed well (typically within 10%) for concentrations ranging over several orders of magnitude. This study therefore demonstrated that matrix effects for the LA-ICP-MS analysis of silicates was not a serious problem. Becker and co-workers77 analyzed GaAs by (i) solid state MS methods including spark source MS (SSMS), LA-ICP-MS, radiofrequency glow discharge MS (rf GDMS) and SIMS and (ii) solution-based methods including ICP-MS and ICP-AES. A synthetic solid GaAs standard doped with elements of interest was used for analysis of GaAs by solid-state methods and a digested aqueous solution of the same standard was used for analysis by ICP-MS and ICP-AES. The results of the determination of dopants by different methods were in reasonably good agreement, typically within a factor of 2. Major advantages of solid-state methods were the low contamination risk and less time consuming preparation steps. A comparison of different techniques in terms of their figures of merits was given.
Applications
| Atom | Method | Molecule support | Wavelength/nm | Gas diluting | Detection limit |
|---|---|---|---|---|---|
| a Ionic lines. | |||||
| Sulfur | LIBS | Steel | 180.73 | Air | 70 ppm |
| ICP-OES | (NH4)2SO4 (aq) | 182.03 | He | 1.7 ppm | |
| (C6H5)2S2 | 921.29 | Ar | 100 ppm | ||
| CuSO4 | 180.73 | Ar | 24 ppb | ||
| MIP-OES | H2S | 921.29 | He | 30 ppb | |
| H2S | 180.73 | He | 0.4 ppb | ||
| Phosphorus | LIBS | PH3 | 604.3a | He | 3 ppm |
| DIMP | 604.3a | Air | 690 ppm | ||
| ICP-OES | (NH4+, H2PO2−) (aq) | 213.62 | He | 80 ppb | |
| NaH2PO4 (aq) | 177.5 | Ar | 8 ppb | ||
| MIP-OES | KH2PO4 (aq) | 213.62 | He | 4.5 ppb | |
| Chlorine | LIBS | NaCl (aq) | 837.59 | Air | 8 ppm |
| CCl4 | 837.59 | Air | 1.5 ppm | ||
| MIP-OES | NaCl (aq) | 479.45a | He | 120 ppb | |
| 481.0a | 350 ppb | ||||
| Fluorine | LIBS | CCl2F2 | 685.60 | Air | 38 ppm |
| ICP-OES | C2ClF5 | 683.43 | Ar | Qualitative detection | |
| 685.60 | |||||
Chin et al.84 used LA-ICP-MS for the direct analysis of airborne particulate matter collected on a membrane filter. More than 20 major, minor and trace elements were determined. The optimum ablation efficiency was achieved using a single shot laser (1064 nm, 160 mJ) operated in the free-running mode with a 6.5 mm defocus distance from the filter surface. Hahn85 used LIBS for sizing and elemental analysis of aerosol particles directly in the air. A particle stream was generated by a commercial ICP nebulizer in the laboratory and the air inlet stream of a gas-turbine cogeneration facility has also been used. A novel two-part calibration scheme was developed which established the LIBS system response to (i) a known mass concentration (µg m−3) and (ii) and a known discrete particle mass. The characteristic plasma volume (2.5 × 10−4 cm3) was then determined, and the overall procedure allowed the quantitative analysis of the mass and elemental compositions of individual, sub-micrometer to micrometer-sized aerosol particles. Casini et al.86 and Lazzani et al.87 used time resolved LIBS for the quantification of pollutants (Hg) in air.
 | ||
| Fig. 10 Schematic diagram of the microscopic LIB instrument. (From ref. 95.) | ||
Niki et al.99 measured simple LA-OES spectra to determine the isotopic ratio of boron, which is used as a neutron absorber in atomic power plants. An Nd∶YAG laser was used for ablation and a scanning monochromator with a PMT detector for collection of spectral data. The ratio was evaluated from the relative intensities of a BO molecular band which consisted of three prominent peaks. The peaks were attributed to either the 11BO emission band or a 11BO–10BO emission band combination. The observed spectra were matched with those simulated by a computer and the relative abundances of boron isotopes could be estimated within a 5% limit of uncertainty.
Laser excited atomic fluorescence
Recent advances in laser excited atomic fluorescence spectrometry (LEAFS) continue to be very modest. In comparison with other elemental analysis techniques, such as AAS and ICP, the main attractions of LEAFS are its great sensitivity and extremely large linear dynamic range. The limitations, however, remain the same and include the only single element capability, the high cost of tunable laser systems and the absence of an ideal atom reservoir, free from matrix interferences. The first limitation can be partly overcome by using rapidly scanned diode lasers or optical-parametric oscillators (OPO), but diode lasers work mainly in the IR-VIS region, whereas most useful atomic transitions lie in the UV region, and the OPO-based lasers are still expensive and difficult to use. Significant revitalization of LEAFS should occur when cheap commercial diode lasers covering the entire UV-VIS spectral range become available.Meanwhile, LEAFS is still used successfully when high sensitivity analysis or spectroscopic measurements are the goals. Recent reviews by Hou et al.100 and Hill et al.101 cover LEAFS instrumentation and applications up to 1997. Here, we will focus on some achievements in LEAFS during 1998 and 1999. Although LEAFS relates to the detection of atoms, we will also consider some examples when laser induced fluorescence was used for detection of simple molecules.
Analytical applications
Electrothermal atomizers remain the most popular atom cells in LEAFS. Among them, graphite tube furnaces, initially designed for AAS, are mostly used and, according to the literature of last 2 years, were the only ones, except laser plasma, applied in combination with LEAFS. A short survey of atomizers used in LEAFS can be found in the review by Hou et al.;100 applications of LEAFS coupled with laser plasmas are described in the laser microprobe section of this paper. For clarity of discussion, a schematic diagram of a typical LEAF spectrometer with an electrothermal atomizer is shown in Fig. 11. | ||
| Fig. 11 Schematic diagram of ETA-LEAFS experimental set-up. | ||
A series of papers were published by Aucélio et al.102–104 on the use of ETA-LEAFS for trace analysis. A dye laser pumped by a high repetition rate copper vapor laser (∼10 kHz) was used as an excitation source. The high duty cycle of the copper vapor laser provided a high probe efficiency for the atomized material. Indium in blood, urine, urban dust, and soil was determined at concentrations between 20 ng g−1 and 1 µg g−1. A comparison was made between wall and platform atomization, in favor of platform atomization; the effect of several chemical modifiers on signal stability and magnitude was studied with the best results obtained for HNO3. A precision of 4.1% was achieved for concentrations of indium in aqueous solution as low as 10 ng mL−1. Lead in blood was determined by using filter furnace ETA.103 The filter furnace was a commercial tube furnace with a porous graphite insert. The sample was deposited between the tube wall and the filter. During atomization, the sample vapor diffused to the furnace center, where it interacted with the laser. A unique calibration curve was obtained for both aqueous and blood standards that allowed the analysis of blood using only aqueous standards. The filter furnace, however, did not perform well when used for ultratrace determination of platinum in environmental and biological samples.104 In this case, wall atomization provided better signal-to-noise ratio and lower ashing temperature. Platinum was determined in urine, blood, autocatalyst and soil in the concentration range 120 ng g−1–44 µg g−1. An absolute detection limit of 50 fg was obtained; a precision of 4.5% was demonstrated for 10 µL aqueous samples with 10 ng mL−1 of Pt.
The examples above show that the atomizer and operating parameters are extremely specific with respect to the matrix to be analyzed and the analyte to be detected. In the three studies cited,102–104 for example, the optimum blood analysis was provided by using three different atomization approaches: platform atomization for In,102 filter furnace atomization for Pb103 and wall atomization for Pt.104
Swart et al. used ETA-LEAFS for the determination of Se, As and Sb in aqueous solutions105 and Se in serum.106 Production of far-UV (<200 nm) radiation necessary for excitation of As and Se atoms was accomplished by stimulated Raman shifting of the output of a frequency-doubled dye laser operating near 230 nm. For Se, fluorescence was excited from the ground state at 196 nm and from the excited state at 206 nm. The absolute limits of detection were 200 fg (ground-state LIF) and 150 fg (excited-state LIF) for Se, 200 fg for As and 10 fg for Sb. These LODs compared favorably with results reported previously for ETA-LEAFS, ETA-AAS and ICP-MS methods. It was emphasized that despite the similar LODs obtained for ETA-LEAFS and ICP-MS techniques, the selectivity of ETA-LEAFS is inherently higher, which is beneficial when samples of complex composition are to be analyzed. Indeed, the direct determination of Se in serum was carried out by using a simple aqueous dilution of the serum samples and a Pd–Mg chemical modifier to reduce pre-atomization losses of the analyte.7 The fluorescence of Se was excited at 196 nm and aqueous calibration was found to be adequate for the determination of Se in the serum matrix. The analysis of 128 serum samples yielded values of ∼90 ± 20 ng g−1.
Zhou et al.107 demonstrated the possibility of relatively rapid sequential multi-element ETA-LEAFS analysis using an OPO-based laser as an excitation source. Five elements, Cd, Co, Pb, Mn and Tl, were determined in a river sediment standard in the concentration range 1–560 mg g−1 using aqueous calibration. The laser could be slow scanned between exictation wavelengths (228–304 nm range) in 15 min. This allowed each element to be determined sequentially with the analysis time determined primarily by the slow heating cycle of the furnace rather than the laser wavelength tuning. Detection limits in the multi-element mode were 545, 111, 28, 445 and 24 fg for Cd, Co, Pb, Mn and Tl, respectively. The total analysis time, including sample preparation procedure, was 12 h.
Wan-yun et al.108 used ETA-LEAFS for the determination of gold in geogas. The samples were 5 L gas extracts extracted from the soil on a polyurethane foam. For analysis, the foam was ashed and dissolved in pure aqua regia. Aqueous AuCl3 solutions were used for calibration. The concentrations of gold in the 82 geogas samples were determined in the range 0.002–0.182 ng mL−1. The detection limit of Au was 0.005 ng mL−1.
Several researchers109–111 have recently reported the determination of nitric oxide (NO) by laser induced fluorescence (LIF). The detection of NO is of particular interest because this molecule is a major combustion-generated pollutant. The two-photon LIF technique for the detection of NO in a gas cell or in a propane–air flame was demonstrated by Reeves et al.109 Two ∼453 nm photons from a pulsed dye laser were absorbed by the NO molecule to yield fluorescence in the range 200–300 nm. A linear dependence of the fluorescence signal on concentration was obtained for a gas cell when the concentration of NO in N2 varied between 300 and 2000 ppm. The same linear dependence, except for the region between 0 and 75 ppm of NO, was observed for the propane–air flame, in which NO was introduced in increasing concentrations. In the region 0–75 ppm, the fluorescence signal did not change, which was attributed to the ability of the flame to maintain, to a certain extent, an equilibrium concentration of NO. Schulz et al.110 performed quantitative measurements of NO in high pressure flames (methane–air, heptane–air) by exciting molecular fluorescence at 248 nm. Calibration was effected by doping flames with increasing amounts of NO. The collisional processes that influenced quantification were assessed and corrected for. It was also found that the range of small dopant levels (below 200 ppm) should not be taken into account. Cooper et al.111 used laser-saturated, laser-induced and planar laser-induced fluorescence to measure the concentration and the spatial distribution of NO in a high pressure flame (lean direct-injection spray flame) which was analogous to gas-turbine combustors. Molecular fluorescence was excited at 226 nm and detected at 236 nm. Concentrations of NO were measured at different axial burner heights (5–20 mm) and ranged between ∼5 × 1014 and 0 cm−3 for radial distances of 0–30 mm.
Chérigier et al.112 used two-photon LEAFS for spatially resolved measurements of atomic hydrogen in a radiofrequency capacitively coupled discharge. The discharge was operated in pure hydrogen at pressures between 25 and 85 Pa. Doppler-free, two-photon excitation at 205 nm (to n = 3) resulted in fluorescence at 656 nm (Balmer α). Absolute density calibration was carried out with the aid of a flow tube reactor and titration with NO2. Maps of absolute atomic hydrogen densities within the discharge were obtained under various discharge conditions. The method was very sensitive with a detection limit of about 2 × 1018 m−3.
A summary of some recent applications of LEAFS is given in Table 4.
| Element | Matrix | Methodology | Precision (%) | LOD | Ref. |
|---|---|---|---|---|---|
| In | Blood, urine, urban dust, soil | Cu-vapor laser, platform ETA | 4.1 | 1 fg | 3 |
| Pb | Blood | Cu-vapor laser, filter furnace ETA | 6 | — | 4 |
| Pt | Urine, blood, autocatalyst, soil | Cu-vapor laser, ETA | 4.5 | 50 fg | 5 |
| Se | Aqueous solutions | Pulsed dye laser, harmonic generation, ETA | 3 | 150, 200 fg | 6 |
| As | 18 | 200 fg | |||
| Sb | — | 10 fg | 7 | ||
| Se | Serum | ETA | 7 | ||
| Cd | River sediment | OPO-based laser, sequential multi-element analysis, ETA | 5 | 545 fg | 8 |
| Co | 6 | 111 fg | |||
| Pb | 3 | 28 fg | |||
| Mn | 5 | 445 fg | |||
| Tl | 8 | 24 fg | |||
| Au | Geogas | ETA | 30 | 5 fg mL−1 | 9 |
| NO | Air–fuel gas mixtures | Flames | ppm | 10–12 | |
| H | Low pressure hydrogen | Rf discharge | 15 | 2 × 1018 m−3 | 13 |
Diagnostics
Laser excited atomic fluorescence has great potential for spectroscopic diagnostics, allowing sensitive and non-perturbing detection of low concentrations of atoms and molecules. Many important spectroscopic quantities, such as transition lifetimes and linewidths, collisional coefficients and quenching rates, have been measured using this method. In this section, we briefly review some recent diagnostic applications of LEAFS.In the previously cited work by Chérigier et al.,112 hydrogen was replaced with xenon in the discharge chamber (no discharge was run) in order to correct for geometric distortion effects. Two-photon excitation at 206 nm promoted Xe atoms to the Rydberg state 15p[21/2] (J = 2), from which fluorescence at 582 nm was observed. Measuring the relative shift with respect to well known value of the hydrogen resonance, the absolute value of the Rydberg state was found (E = 96948.2 cm−1). Also, the natural lifetime of the excited state and self-quenching coefficient were determined from the time and pressure dependences of the fluorescence signal.
Song et al.113 used time-resolved LEAFS for the determination of radiative lifetimes of praseodymium transitions. Fourteen new lifetimes of Pr I low-lying states were measured by using thermal atomic beam and a single-step laser fluorescence excitation. The lifetimes were calculated from decaying portions of fluorescence signals. Zhang et al.114 measured quenching cross-sections for the LIF of atomic arsenic. The quenching counter partners for As were H2, CO, CH4 and N2, which were mixed with arsenic atom vapor in a specially designed cell. The fluorescence was excited at 197 nm and monitored at 249 nm. The quenching constants were calculated from the slopes of Stern–Volmer plots of fluorescence intensities vs. quencher concentrations. The quenching cross-section for ethylene was much larger than that for other quenching species. This was attributed to the resonance energy transfer between the excited state of As and the energetically close excited states of ethylene. Storm and Cappelli115 used laser excited fluorescence of hydrogen Balmer-α (Hα) as a diagnostic for measuring velocity, temperature and electron density within the nozzle of an arc-jet thruster. A narrow band CW laser was scanned across the Hα transition at different locations in the jet stream. Axial velocities were determined from the Doppler shift of the Hα line center relative to a stationary reference, whereas translational temperatures and electron number densities were determined from a lineshape analysis of the Hα transition.
Laser enhanced ionization, resonance ionization, resonance ionization imaging
The stepwise ionization of atomic vapors is recognized as a technique that can achieve detection limits at the parts per trillion level owing to the selectivity of the multi-wavelength ionization process. In laser-enhanced ionization spectroscopy (LEIS) and resonance ionization spectroscopy (RIS), electrons are excited to electronic states that approach or surpass the ionization continuum. The difference between laser-enhanced ionization and resonance ionization lies in the mechanism of the final ionization step. In LEIS, the final ionization step occurs via collisional excitation, whereas in RIS the final step occurs when the atom absorbs a photon to ionize the atom (see Fig. 12). Laser-enhanced ionization is in fact a subdivision of resonance ionization spectroscopy, and is usually applied to dense gases or flames. The need for two or more photons to produce an ion–electron pair makes laser ionization a selective and sensitive technique. In recent years, LEIS and RIS have been applied to trace analysis, flame diagnostics and the detection of photons. LEIS and RIS will be discussed in terms of principles and applications from a variety of published work. The resonance detection of photons and resonance ionization imaging detection, a relatively new technique, will be reviewed with a focus on work published in the authors' laboratory. | ||
| Fig. 12 Energy level diagrams and wavelength transitions for LEIS and RIS. In LEIS, the final step of ionization is provided by collisional excitation (a), whereas in RIS the final ionization step is provided by a quantum of light (b). | ||
A typical instrument for LEIS or RIS is shown in Fig. 13. Two or more dye lasers are pumped by either a frequency doubled or tripled Nd∶YAG or excimer laser. The output of each dye laser is tuned to an atomic transition of the element of interest. Typically, the output of the first dye laser is frequency doubled to reach UV transitions of most metals. The laser beams are directed into the sample cell, which can be a flame, a sealed quartz or glass cell, an electrothermal atomizer or a variety of other atom reservoirs. Two electrodes are used to collect electrons formed in the laser intersection volume and the current is amplified and processed into a signal.
 | ||
| Fig. 13 Experimental set-up and energy level diagram for a typical LEIS/RIS system. SHG = second harmonic generator. | ||
Applications of LEIS and RIS
The earliest applications of LEIS and RIS were for trace determinations of metals in flame. Detection of ultra-trace levels of metals in biological, environmental and geological samples continues to be an important application of laser ionization. The instrumentation of LEIS and RIS has not changed significantly since the introduction of the technique, but some improvements have been reported. Improvements in laser-pumped dye lasers116 and counting electronics have increased the sensitivity of the technique and the signal-to-noise ratio (S/N). Novel advances in laser ionization spectroscopy, discussed below, deal with the coupling of the sensitivity and selectivity of LEIS and RIS with separation apparatus and mass analyzers. One particular advance in LEIS is the addition of an electrothermal atomizer as an atom source in trace analysis. In the trace determination of lead in blood, Riter et al.117 coupled a graphite furnace atomizer with a small acetylene–air flame. A detection limit of 890 fg was reported. The capability for temperature programming using ETA allows samples with matrices that cause interferences in flames to be analyzed indirectly. The addition of flow-injection analysis (FIA) to LEIS methods has also been reported.118 The FIA system separated the lead species and passed the eluate into a flame for LEIS analysis. Using a two-step excitation scheme, a detection limit of 3.2 ± 0.1 ppt was achieved. An identical LEIS experiment without FIA preconcentration and separation yielded a detection limit of 9 ppt.Signal detection in LEIS or RIS usually relies on the measurement of electrons formed in the laser illumination region. Electrodes in the sample cell can cause interferences, such as cooling of the atomic vapor and contamination from metals embedded in the electrodes, and require the use of high-precision preamplifiers and electrical filters. An alternative method of detecting charge pairs is the measurement of emission from a buffer gas.119,120 The electrons formed during mercury ionization excite neon atoms, causing them to relax radiatively. The detector, a photomultiplier tube with a glass filter, is a simple device and can be used when sample cell geometries and conditions preclude the use of electrodes. A pulsed electric field was applied to two planar electrodes outside the sample cell, eliminating the need for complex cell design. Atoms in sealed vapor cells, reactors and harsh environments can be studied by measuring the emission of a buffer gas excited by electrons formed via LEIS or RIS. A buffer gas is also useful when the measurement of an electric current is desired,121 as the buffer gas can increase the signal by avalanche amplification. Because an electron is generated via photoionization and accelerated toward an electrode, the electron can collide and ionize buffer gas atoms. Amplification factors of 106 are attained in this manner. The detection limit for mercury atoms using avalanche amplification has been estimated to be approximately 15 atoms per laser pulse. Laser ionization has been used for a variety of techniques involving trace analysis and high-resolution spectroscopy. In a recent report by Bushaw and Cannon,122 the sensitivity and high resolution of RIS were combined with low-cost diode lasers and a low-resolution quadrupole mass filter to determine 90Sr in solid Sr samples. The detection of 90Sr in nuclear waste is important owing to its high toxicity to humans and its resemblance to calcium with respect to mineral uptake in bones. Resonance ionization spectroscopy has shown clear advantages over traditional ionization methods for atomic mass spectrometry as isobaric interferences, such as 90Zr, are reduced. This technique was shown to be both spectroscopically and mass selective, as tuning the lasers produced ions of different strontium isotopes. The selective ionization of nickel to separate radioactive isotopes has also been reported.123
In addition to trace analysis, RIS and LEIS have been used as diagnostic tools. The spectroscopy of mercury Rydberg states has been reported by Clevenger et al.124 Both collisional and photoionization processes affect the signals measured while exciting Rydberg states. Using time resolved techniques and by adjusting the buffer gas pressure, the collisional ionization effect was minimized. In a second study,125 the Rydberg states of mercury were measured via laser-enhanced ionization. The effects of Stark shifting and buffer gas broadening/shifting were observed for higher electric fields and gas pressures, respectively. Fig. 14 shows the Rydberg spectrum of mercury atoms as a third laser was scanned across Rydberg states. High-resolution spectroscopic studies of Ce and Lu have also been reported.126,127
 | ||
| Fig. 14 LEIS Rydberg spectrum of Hg. The insets (1) and (2) show the Rydberg states close to the ionization potential. | ||
Laser enhanced ionization has been used to perform flame diagnostics. The temperature profile of a flame was measured by Ke and Lin.128 A flame was moved through the interaction region of two laser beams, yielding a spatial resolution of approximately 1 mm. Al and Ga atoms were used as temperature probes, and Boltzmann temperatures were obtained for each by scanning the fine structure of the atoms to measure population ratios. In this manner, the temperature profile was obtained along the 10 cm burner axis and also along the height on the flame. Sodium diffusion coefficients,129 photoionization cross-sections of Rb130 and actinide ionization potentials131 have also been measured by LEIS and RIS spectroscopy.
Detection of resonant photons in RIS
While conventional RIS and LEIS use lasers to excite the transitions used in an ionization scheme, a metal vapor can also be used as a detector of resonance photons. Fig. 15 shows a schematic diagram for the detection of photons by resonance ionization. The first electronic transition is the wavelength of interest, while the subsequent electronic transitions are excited by tunable dye lasers. The detection of single photons of 253.7 nm by a mercury resonance ionization detector (RID) was reported.132 Mercury was chosen as an active element because the number density of the vapor is high at room temperature. The 5 mW mercury lamp was located 2 m from the detector cell and was not focused or spatially isolated. The ionization scheme for mercury, and several other elements, is given in Table 5. After mercury atoms had absorbed the 253.7 nm radiation from a mercury lamp, the excited mercury atoms were ionized with the 435.8 and 489.0 nm output from two pulsed dye lasers. The maximum S/N was 104 and the detection limit was 0.5 photon. | ||
| Fig. 15 Experimental set-up used for the resonance ionization detection of single photons. | ||
| Element | λ 1/nm | λ 2/nm | λ 3/nma | Ref. |
|---|---|---|---|---|
| a CI = collisional ionization. | ||||
| Cr | 427.387 | 427.287 | CI | 142 |
| Pb | 283.3 | 509.0 | CI | 117 |
| Th | 580.575 | 623 | 566 | 131 |
| Np | 311.903 | 541 | — | 131 |
| Pu | 649.072 | 629.751 | 579 | 131 |
| Am | 640.677 | 584.596 | 578 | 131 |
| Cm | 655.643 | 640.742 | 573 | 131 |
| Cf | 572.764 | 625.215 | 581 | 131 |
| Hg | 253.652 | 313.184 | 626 | 140 |
| Ni | 305.082 | 611.106 | 748.219 | 123 |
| Sr | 689.45 | 688.02 | 488.0 | 122 |
| Cs | 852.113 | 621.310 | 1064 | 143 |
The technique can also be applied to the detection of photons from sources other than metal vapor discharge lamps. The detection of Rayleigh or Raman scatter, and also Doppler-shifted photons, is possible. It has been shown133 that the number of electrons produced in an RID by the absorption of resonant photons can be expressed by the following equation:
 | (1) |
Resonance ionization imaging detection (RIID)
For the last few years, research in the authors' laboratory has been focused on developing resonance ionization imaging detectors (RIID) and resonance fluorescence imaging monochromators (RFIM) in an effort to produce wavelength-selective images with high sensitivity. The RIID and RFIM have characteristics that make them an attractive alternative to many conventional imaging systems. The quantum efficiency, q, of a resonance ionization detector can be expressed by | (2) |
In order to demonstrate the capability of the RIID to produce an image, an RFIM cell containing mercury vapor was illuminated by two lasers tuned to the electronic transitions of mercury having wavelengths 253.7 and 435.8 nm, respectively.135 The laser system was comprised of an excimer XeCl laser pumping at 308 nm and two dye lasers. The light from the first dye laser—the laser producing the 253.7 nm beam—passed through a mask with the letters "UF" (see Fig. 16). The second excitation step (see Fig. 17 for the complete scheme of ionization and fluorescence) was provided by a second dye laser and delivered to the cell by a circle-to-line fiber optic bundle and entered the cell from the left in Fig. 18. The fluorescence from the 73S1 → 63P02 transition was observed when both dye lasers were tuned to the two successive mercury transitions. The green 546.1 nm image of the mask formed in the Hg vapor was clearly visible to the eye and captured on photographic film (Fig. 18).
 | ||
| Fig. 16 Schematic diagram of RFIM experiment. MA = mask; M = mirror; BE = beam expander; L = lens. | ||
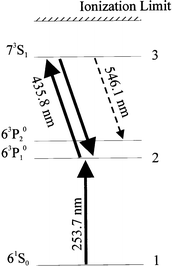 | ||
| Fig. 17 Partial energy level diagram for Hg. | ||
 | ||
| Fig. 18 Image of 546.1 nm fluorescence from Hg RFIM. | ||
Resonance ionization imaging is a variation on resonant fluorescence imaging described above. An early demonstration of the device showed the ability of the RIID to generate position sensitive images, and also verify the wavelength selectivity of the technique.136 The resonance ionization of Hg atoms occurred at a single point in space and the resulting electrons were accelerated toward a luminescent screen. Two laser beams having wavelengths of 253.7 and 435.8 nm were directed into an evacuated cylindrical cell containing saturated Hg vapor (nsat ≈ 4 × 1013 atoms cm−3) at ambient temperature. The 435.8 nm beam was transformed into a planar beam 2 mm thick and 16–18 mm wide. The planar beam was directed close to the surface of the input window as shown in Fig. 19. The quartz input window of the cell was located 7.0 cm from the luminescent screen. The grounded stainless steel flange, ring electrode and current conducting luminescent screen were connected to a variable high voltage dc power supply. The 235.7 nm beam entered the cell at an angle of ∼15° and had a diameter of 4–5 mm on the surface of the window and 7–9 mm on the surface of the screen. The luminescent screen was covered by a thin layer of ZnS∶Cu phosphor which was sensitive to both high energy electrons and UV quanta from λ1. When the laser was tuned to the 61S0 → 63P01 → 73S1 mercury transitions, two clearly visible and distinguishable position sensitive luminescent images were produced as a result of Hg resonance ionization and the UV laser when it struck the luminescent screen directly. The electron beam image intensity and its appearance as a function of wavelength are shown in Fig. 20. The diameter of the electron beam image was 4–5 mm, corresponding to the diameter of the λ1 beam when it entered the area illuminated by the second laser to produce ions. At the pressures and temperatures used, the cross-section for electron scatter by mercury atoms is so small that the probability of elastic collisions between accelerated electrons and Hg atoms is virtually negligible at this vapor density and under these experimental conditions.
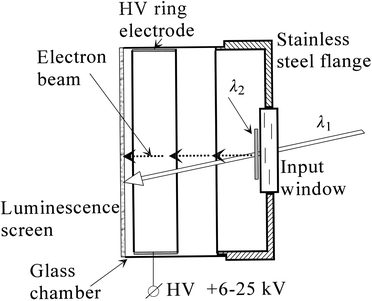 | ||
| Fig. 19 Diagram of RIID cell. | ||
 | ||
| Fig. 20 RIID image intensity vs. wavelength offset. The 435.8 nm beam was scanned, showing the degradation in image quality and intensity as the laser is detuned from the mercury absorption line. | ||
The system described above had certain limitations which made it unsuitable for high resolution and sensitive imaging. The phosphor on the screen suffered from parasitic luminescence from stray UV laser radiation and also from UV radiation from the surroundings. This created a significant amount of noise on the screen which could overshadow weaker images. The image was also distorted from the accumulation of charge on dielectric surfaces. In addition, the luminescent screen did not provide a high level of signal amplification, and the images were faint and the S/N was degraded. The distortion of the image was compounded by the fact that the large distance between the window and the screen caused an additional decrease in spatial resolution.
An improvement in RIID design is the incorporation of a microchannel plate (MCP).137 The MCP can decrease the influence of the aforementioned obstacles and produce true 2D images with excellent S/N and resolution. A microchannel plate is relatively insensitive to UV radiation and can amplify a signal 104–107-fold. The RIID cell used a Hamamatsu F2221-11P microchannel plate (see Fig. 21). The 235.7 nm laser was expanded to illuminate a cross-shaped mask and the subsequent transmission was focused on to the input window of the RIID. The planar 435.8 nm beam was directed to the front surface of the input window. When the lasers were tuned to the 61S0 → 63P01 → 73S1 mercury transitions, a distinguishable luminescent image of the mask was produced by the ions generated due to resonance ionization. The intensity and characteristics of the image formed were studied as a function of the high voltage applied to the MCP screen. The intensity of the image was voltage dependent, as can be seen in Fig. 22. The lower right corner of the images in Fig. 22 shows an artificial image of the camera tripod reflected from the screen of the monitor.
 | ||
| Fig. 21 A microchannel plate RIID. | ||
 | ||
| Fig. 22 MCP RIID images vs. voltage applied to MCP (note: the artifact in lower right corner is due to reflection from the monitor screen). PE = image due to photoelectric effect; RI = image due to resonance ionization. | ||
The two pictures in Fig. 22 denoted "PE" are due to the photoelectric effect of the screen when λ2 was blocked. These images are an indication of the noise level because they result from the photoelectric effect when λ1 struck the surface of the MCP. By reinstating λ2 at 3.55 kV, the image intensity increased 30–40-fold. With an ionization efficiency of only 10−4–10−5, an S/N of 105–106 was achieved. It should be mentioned that an active element with a higher work function than the resonant quanta would have a lower photoelectric effect and therefore a higher S/N.
Although this system had much improved S/N and eliminated the problem of parasitic luminescence, it suffered from the accumulation of surface charge on the input window. This created a distorted image after increased exposure time. A solution to this problem was to coat the input window with a thin layer of conductive material whose photoelectric work function (Φp) is greater than the energy of a λ1 photon (hν253.7 nm = 4.88 eV). This would eliminate charge build-up and the resulting image distortion. The chosen material for this experiment was platinum (Φp = 5.65 eV).138 The effectiveness of the platinum coating as a charge removal system was evaluated using a laser beam shaped by a mask. Fig. 23 shows the experimental schematic and the image of the mask taken immediately and after 20 min. The images in Fig. 23 show no visible distortion after an exposure time of 20 min with the most intense λ1 beam. An image of a mesh was taken using the RIID to study the resolution of the detector. Fig. 24 shows the image of the mesh and the experimental schematic. Fig. 25 also shows the limit of spatial resolution, an image of the metal mesh at 1∶1 magnification. From the intensity distribution of this image, according to Rayleigh criteria, the spatial resolution is estimated to be better than 120 µm, which in this case corresponds to the distance between the peaks of the intensity distribution. The spatial resolution can be improved, however, by increasing the atomic vapor density, but it is ultimately dependent on the resolution elements of the microchannel plate and CCD detector.
 | ||
| Fig. 23 Experimental set-up of RIID and images taken at 0 and 20 min exposure time. There is no visible sign of image degradation due to the charge removal effects of the Pt-coated window. | ||
 | ||
| Fig. 24 Spatial resolution of the RIID. A 120 µm period mesh was illuminated by 253.7 nm resonant quanta. The RIID image and plot of intensity vs. distance are shown below. | ||
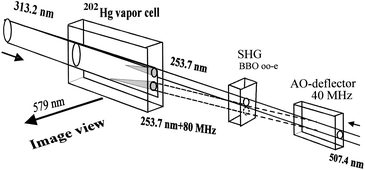 | ||
| Fig. 25 Experimental set-up for differential imaging. An acousto-optic deflector combined with an SHG generate two beams separated spectrally by 80 MHz. | ||
The spectral resolution of an RFIM was demonstrated by Podishivalov et al.139 Using an acousto-optic deflector (AOD) to generate two beams of 253.7 nm light with a frequency difference of 80 MHz, spectrally resolved fluorescence traces were observed (Fig. 25). The difference in absorption lengths of the two traces (see Fig. 26) yielded different absorption coefficients and allowed the two signals to be distinguished from each other. The two beams were spectrally distinct because the absorption lengths were different for each frequency. A spectral resolution of at least 80 MHz can be achieved with an RFIM detector despite the fact that the Hg Doppler broadened linewidth of the active element can be of the order of 1 GHz.
 | ||
| Fig. 26 Absorption traces for 253.7 nm photons vs. frequency offset. | ||
The excitation schemes for mercury mentioned above all used the 61S0 → 63P01 → 73S1 transitions to produce ionization or fluorescence with an efficiency of 10% at best. The addition of a third dye laser to promote the atoms to a Rydberg state improves the ionization efficiency, but requires a powerful pump laser and also an additional dye laser. The use of a three-photon, two dye laser scheme to increase the ionization efficiency to nearly 100% has been reported.140 The first transition was identical with the first step in previous experiments (253.7 nm). Instead of using the 435.8 nm beam for the second step, the Hg atoms were excited into one of three 6D states by laser radiation at 313 nm. The 313 nm radiation was generated from a dye laser emitting at 626 nm, frequency doubled by a BBO crystal. The third step came from the same laser but using the first harmonic at 626 nm to transfer the Hg atoms from a 6D state to the Hg ionization continuum. The essence of this scheme is that for the second excitation step (313 nm), the second harmonic was used, and the remainder of the unconverted radiation from the fundamental harmonic (626 nm) was used for the third excitation step (see Fig. 27). The clear advantage of this ionization scheme is the high efficiency obtained and the fact that only two dye lasers are used to produce three quanta.
 | ||
| Fig. 27 Two ionization schemes for mercury, showing the two-laser, three-photon scheme for efficient ionization of Hg atoms. | ||
Comparison of the RIID with other imaging and non-imaging spectral devices
A discussion of the RIID would be incomplete without a comparison of the RIID with other spectral instruments. There is some difficulty, however, in directly comparing many instrumental methods owing to the difference in the instruments' function. The luminosity-resolving power product, however, is a universal comparison of the spectral efficiency and throughput of a system. Briefly, the luminosity, L, of the RIID can be expressed as L = AΩ, where A is the input area of the detector and Ω is the solid angle of acceptance. The resolving power, R, is the average wavelength of two narrow spectral lines divided by the spectral resolution of the detector: | (3) |
Table 8 lists the LR products for several spectral devices such as prism spectrometers, Fabry–Perot interferometers, and heterodyne detectors. For heterodyne detection, it can be seen that even with a resolving power of 109, an increase in pixel number, computer speed and local oscillator power of the order of 109 cm2 sr would be necessary to match the LR product of the RIID with a similar resolving power. The resolving power of the RIID can be calculated to be 109 cm2 sr, which gives an LR product of 1010 cm2 sr for a naturally broadened line and 108 cm2 sr for a Doppler broadened line. The next-largest LR product, that of an acousto-optic tunable filter or a Fabry–Perot interferometer, is 105 times smaller than the Doppler-broadened RIID.
| Spectral device | LR product/cm2 sr |
|---|---|
| Prism spectrometer | 0.03 |
| Littrow grating spectrometer | 1.7 |
| Fabry–Perot interferometer | 630 |
| Michelson interferometer | 315 |
| Acousto-optic tunable filter | 636 |
| Heterodyne detection | 1.4 × 10−8 |
| RIID (Doppler broadening) | 7.8 × 107 |
| RIID (natural broadening) | 5.2 × 1010 |
Potential applications of the RIID
Table 9 lists a summary of several applications of the RIID. The ultra-narrow bandwidth and sensitivity of the detector make it amenable to many communications, military, biomedical and industrial applications. Brief discussions of the applications of the RIID are given below, with particular attention paid to some applications currently studied in the authors' laboratory.| Communications (satellite, underwater, etc.) |
| Ultrasonic field measurements for non-destructive materials testing |
| Detection of moving objects (LIDAR, velocimetry) |
| Aero- and hydrodynamic flow field imaging (i.e., blood flow) |
| Raman and fluorescence imaging |
| Photoacoustic spectroscopy in biomedicine, environmental remote sensing, chemical/materials industries |
| Reflectance or transmission-mode microscopy using low-power lasers |
| Imaging of vibrations and oscillations |
| Doppler ultrasound for tissue motion measurements |
| Single cell/bacterium fluorescence microscopy |
The resolution of optical imaging microscopy is limited by the wavelength of light used to illuminate the sample. Near-field techniques are not limited by the wavelength used but require sample rastering and suffer from low signals. Using an RIID with helium as the active element, a spatial resolution of the order of 25–30 nm should be attained.134 The 50–59 nm transition of helium can be reached by gas discharge lamps and, in the future, a vacuum UV laser. One disadvantage of such an RIID would be that the absorption efficiency of the detector would decrease if the discharge lamp had significant broadening of its spectral lines. Despite this drawback, the RIID can provide true imaging without the need to scan the sample. Coupling the RIID to a confocal imaging system can produce direct three-dimensional images with a spatial resolution unattainable by conventional optical microscopy.
The narrowband, differential imaging capabilities of the RIID allow researchers to image small frequency shifts in the MHz regime. The detection of frequency-shifted light from ultrasonic fields, moving objects and fluids, Raman scatter and photoacoustic fields is possible. In ultrasonic field imaging, a laser (or piezoelectric transducer) modulated at frequency ω creates ultrasonic fields in a sample (see Fig. 28). The RIID probe laser, operating at a frequency shift ω from the center of the absorption line at ν1, is frequency shifted by the value of ω into the absorption region of the RIID, forming an image. The principle is similar for photoacoustic spectroscopy and Doppler velocimetry. In the case of photoacoustic spectroscopy, the modulated laser is scanned across the infrared spectrum, generating ultrasonic fields in the sample which shift the probe laser light into the detection bandwidth of the RIID. In the case of Raman or Rayleigh scatter, the probe laser scatters off the surface of the target and is collected by objectives into the RIID. For Rayleigh scattered light, the probe laser will be tuned to ν1, whereas in Raman spectroscopy the laser will be tuned to a frequency of ν1 + ΔνR, where ΔνR is the frequency of the Raman shift of interest.
 | ||
| Fig. 28 Detection schematic for photoacoustic spectroscopy, ultrasonic field detection and Raman spectroscopy. | ||
The RIID can also be applied to the imaging of moving objects. In LIDAR or Doppler velocimetry, the probe laser is frequency shifted into the RIID bandwidth by the Doppler shifting of light by a moving object (Fig. 29). The high sensitivity of the RIID can detect a small number of photons, making long-range target imaging, such as LIDAR or missile/aircraft tracking, possible. The differential imaging of fluid dynamics is also possible. Blood flow and tissue movement could be monitored by scanning the probe laser across a range of Doppler-shifted frequencies.
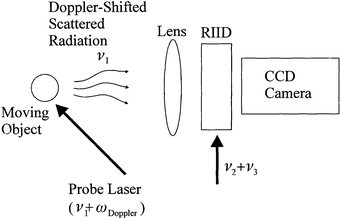 | ||
| Fig. 29 Detection of Doppler-shifted light for velocimetry, blood flow and moving object detection. | ||
The RIID and RFIM have been shown to be efficient, selective, ultra-narrowband detectors. The spatial resolution is currently in the 100 µm range, and the spectral resolution is 80 MHz. The resolution will increase as newer designs are employed and studied. The RIID can be applied to the detection of Doppler-shifted, Raman and other frequency-shifted light and also light due to Rayleigh scatter. Applications to the communication, medical and materials evaluation field are numerous, and as the technology improves, so will the detection capabilities of the RIID. Using an RIID, one can achieve true multi-point imaging of large surface areas with low limits of detection, high S/N and ultra-high spectral resolution.
Diagnostics of plasmas/atom reservoirs by laser spectroscopy
Although the diagnostics of plasmas and atom reservoirs are not strictly analytical spectroscopy, the topic is still of great importance in the understanding of atomization, excitation and ionization processes in such systems. Certainly, laser diagnostics of plasmas/atom reservoirs were immediately recognized as being superior to the analytical potential of lasers. The capability of spatial and temporal measurements of most parameters listed in Table 10 is especially important. The reader is referred to a number of the previously mentioned references1–10 and also several more recent references144–146 for a more thorough discussion of the principles and applications of diagnostic measurements. Laser diagnostics in plasmas, flames, glow discharges and other atom (ion) reservoirs have been used to measure the physical parameters listed in Table 10. Because the diagnostics of plasmas and atom reservoirs have been given in several other sections of this paper (laser microprobes, laser excited atomic fluorescence and laser ionization spectrometry), only a few selected papers with especially interesting approaches to plasma diagnostics will be mentioned here.| Temperature |
| Electron number density |
| Atom number density |
| Ion number density |
| Ion mobility and velocities |
| Flame and plasma gas velocity |
| Atomization efficiency |
| Ionization efficiency |
| Lifetimes of levels |
| Collisional rate constants |
| Fluorescence quantum efficiencies |
| Charge transfer and Penning ionization in plasmas |
| Matrix effects— |
| Easily ionized elements |
| Dissociation of molecular species |
| Imaging of atomic and molecular populations in flames and plasmas |
| Recombination rates |
Hirata et al.147,148 measured two-dimensional images of radiative and metastable atoms in a low pressure 13.56 MHz argon ICP. They used both line emission and diode laser absorption as well as Langmuir probe measurements to obtain radial profiles of the number densities of the Ar 3p5 state for a variety of pressures (1.5–300 mTorr) and plasma powers (20–400 W). These workers also compared the Ar ICP with the Ar CCP (capacitively coupled plasma) and found similar profiles and number densities.
Hermann et al.149,150 performed temporal and spatial resolved plasma diagnostics during UV excimer laser ablation of a Ti target in a low pressure N2 atmosphere. Spectral lines emitted in the first 200 ns were measured and compared with line profiles calculated for a plasma in local thermodynamic equilibrium. The laser fluence and nitrogen pressure were set to values typically applied to pulsed laser deposition of thin films. The emission spectrum under these conditions was dominated by continuum emission and carbon ion lines during the first 200 ns, whereas molecular bands of C2 and CN radicals were observed at later times after the vapor had expanded through the ambient gas. Emission spectra of C2, CN and N2+ were recorded as functions of time for various distances from the target. Kinetic information and gas phase reactions allowed a better understanding of the deposition of carbon nitride thin films.
Puretsky and Geohegan151 used LIF imaging and absorption spectroscopy to study laser desorbed planes from organic crystals commonly used as MALDI (matrix assisted laser desorption/ionization) matrices. These plasma diagnostic techniques and also ion probe measurements were used to determine desorbed product number densities, fractional ionization and velocity distributions of the ejected species typically encountered as the main desorption products in the MALDI analysis of biomolecules. Pulse UV (193 and 248 nm) absorption from 3-hydroxypicolinic acid showed very different absorption cross-sections at these two wavelengths. In both cases, LIF revealed a fast, low intensity component and a slower, more intense component.
Gornushkin et al.152 used resonance shadowgraphs to image laser produced plasmas. They produced shadowgraphs of lead and tin plasmas and post-plasma plumes obtained by igniting plasmas on the surface of pure lead or pure tin and illuminating the plasmas with a strong Pb (283.3 nm) or Sn (286.3 nm) transition. They visualized the UV photodecomposition of Pb2 and Sn2 or large clusters of lead and tin present in the atmosphere. The shock wave produced by laser ablation was clearly observed. Moreno et al.153 also used high resolution shadowgraphs to map the evolution of a plasma in a microcapillary by means of a compact 46.9 nm laser. These images were the first plasma diagnostical data obtained using a table-top, soft X-ray laser. Iwase et al.154 used a Schleiren method to study shock wave phenomena in laser produced plasmas and Mach–Zehnder interferometry to determine electron number density. Siano et al.155 generated excimer laser induced plasmas during the ablation of alumina, silicon, and steel in air and used a shadowgraph technique called refractive fringe diagnostics which required a very simple uncritical experimental system. The electron number density distribution obtained was compared with that obtained by spatial and temporal emission spectroscopy.
Lowe et al.156 characterized the reactive gas phase in the vicinity of the substrate during diamond deposition in a flat, pre-mixed, acetylene–oxygen–argon flame by means of LIF. Optimum conditions for deposition of diamond films were found for O2 to C2H2 ratios of 1.3 and 1.4 and distances between substrate and burner of 8, 9 and 10 mm. Gas temperatures and OH radical number densities were measured by LIF. The hydrogen atom number densities were measured using three-photon excitation and fluorescence detection. Molecular beam mass spectrometry was used to determine bulk number densities of stable species and hydrocarbon intermediates (CH3, C3H3, C4H3 and CxH2, where x = 4, 6 and 8). The multiple carbon containing radical species played an active role in diamond chemical vapor deposition (CVD), not previously discussed. Diamond formation seemed to be controlled by a counterbalance between OH and the hydrocarbon intermediates at a position in the flame where sufficient H atoms and CH3 radicals were present to support diamond film growth.
Atomic absorption spectrometry with diode lasers
Until tunable diode lasers became available, there were no inexpensive tunable lasers available for analytical atomic absorption spectrometry (AAS). All other tunable laser systems (dye lasers and solid state tunable lasers, e.g., OPOs, other than diode lasers) were expensive and difficult to use. Prior to the use of diode lasers, the only lasers used in commercial and/or everyday analytical systems were fixed wavelength gas lasers for Raman spectrometry and Nd∶YAG lasers for LIBS.Although diode lasers are tunable over restricted spectral ranges (a few nanometers), they do allow tuning to atomic (and molecular) transitions.157–159 Diode lasers typically have linewidths of the order of 20 MHz, which is about 30 times less than the atomic absorption linewidths observed for room temperature atomic reservoirs at low pressure and about 100 times less than the linewidths of atoms in atmospheric flames and furnaces. Therefore, diode lasers provide a nearly ideal line source for AAS since the peak absorption will be maximum and the linear dynamic ranges of calibration curves can be increased greatly by detection of absorption in the wings of the absorption line where optically thin conditions exist. In addition, diode lasers are extremely stable and a monochromator is not needed as a spectral isolation device as with hollow cathode lamp AAS, i.e., there are no unwanted lines from either the cathode material or the inert gas, which exist when using hollow cathode lamps.
Other advantages of diode lasers157,158 include the opportunity for isotope selective analysis where the isotopic line shifts are sufficient to allow spectral separation. Sufficiently large isotopic shifts only exist for light (e.g., Li) and heavy (e.g., U) elements when using one-step excitation. If two-step excitation by a narrow band diode laser is used, then isotopic selectivity can be as great as 104–106.
Commercially available single mode diode lasers yield up to 100 mW in the 670–870 nm range and 5–30 mW in the 630–670 nm range.157,158 Second harmonic generation (SHG) in non-linear crystals can provide 0.1 µW in the 335–410 nm region and up to 1–3 µW in the 410–430 nm region. Greater conversion efficiencies are possible resulting in powers as high as 1 mW in several isolated cases. On the other hand, deep blue diode lasers are being developed, e.g., InGaN diode lasers have achieved 50 mW of power and about 1000 h of use.160,161 In addition, sum frequency generation (SFG) can be used to provide tunable laser sources in the UV region and powers in the 10–100 nW range should be possible in the near future.160,161 It is interesting that both Hg and Pb transitions at 365 and 283 nm, respectively, have been reached by frequency doubling and sum frequency mixing of two semiconductor lasers.162,163
Under optimum experimental conditions and under the source shot noise limit, the minimum absorption which can be measured with diode lasers in the mW range is in the 10−6–10−8 absorbance range.157 Another major advantage of diode lasers is the possibility of modulation at GHz frequencies. In addition, wavelength modulation of diode lasers with detection of absorption at the second harmonic (2-f) of the modulation frequency greatly reduces flicker noise in the baseline, producing improved detection limits.157,158
Because of the spatial coherence of diode lasers, it is possible to generate a narrow beam at a large distance for atomic absorption measurements in a long cell with a small inner diameter (∼1 mm). Also, the use of collimated beams allows spatial filtering to minimize stray light and emission from the atomizer.157,158
Zybin et al.157 have reviewed the analytical applications of diode lasers in atomic spectroscopy.
Wavelength modulation diode laser atomic absorption spectrometry (WM-DL-AAS), has achieved a minimum peak absorbance below 10−5 absorbance units for a 50–100 µW diode laser. By the addition of modulation (wavelength modulation of the diode laser and modulation of the absorption process) to WM-DL-AAS, it has been possible to achieve a minimum absorbance below 10−6 absorbance units for the 837.60 nm line of Cl. These values should be compared with a minimum absorbance of ∼10−3 for HCL-AAS. With SHG of the diode laser, it has been possible to reach the shot noise limit of 10−4 absorbance units with diode lasers. When using the fundamental output of diode lasers, the shot noise limited absorbance is 10−7–10−8, which has not yet been achieved due to the presence of other noise sources.
Niemax and co-workers157,158 used DLAAS for the detection of selected elements in species separated by GC or LC. Detection limits in the range 0.1–1 ng s−1 have been achieved for elements such as Cl. Speciation is also possible by combination of chromatographic separation with DLAAS detection.
Niemax and co-workers157,158 also used WM-DLAAS for the detection of Li, Rb and Pb isotopes. Axner and co-workers164–168 performed an extensive theoretical and experimental investigation on the 2-f wavelength modulation technique applied to the detection of rubidium atoms in atmospheric pressure atomizers. The influence of hyperfine structure and isotope shift as well as the temperature dependence of the 2-f wavelength modulated signal were studied.
Extremely high element and isotopic selectivity can be obtained by combining resonance multi-step photoionization followed by mass spectrometric analysis (RIMS). Wendt and co-workers169 have shown that the RIMS selectivity can be as high as 1016, which should allow isotopic selective detection of rare radionuclide isotopes in real samples without complex and lengthy radiochemical separations. Diode lasers have also been used for the first resonance transition of La using three-step RIMS170 and the double-resonance excitation of Sr isotopes by two diode lasers followed by ionization with the 488 nm Ar+ laser line.171 Up to now, the applications of RIMS to real samples has been limited by the need for two or three dye lasers. Diode lasers could replace one or more of the dye lasers, simplifying the method.
Several interesting recent studies should be highlighted. Peterson and Oh172 measured CH radial distributions in ethylene–air and methane–air flames using WM-DLAAS. Tunable 426 nm radiation was generated by SHG of 852 nm distributed Bragg reflection diode lasers. Absorbances down to 5 × 10−5 were measured using WM-DLAAS. Both line of sight absorption and spatially resolved LIF with a single excitation beam were demonstrated.
Zybin et al.173 showed that calibration curve linearity can be increased up to an absorbance of 1.7 even in the presence of background absorbances as high as 1.4. Raab et al.174 described a diode laser spectrometer at 493 nm for the spectroscopy of single trapped Ba+ ions. Frequency doubling of a 100 mW diode laser at 986 nm resulted in up to 60 mW at 493 nm with a bandwidth of less than 60 kHz. The fluorescence excitation spectrum of a single Ba+ ion exhibited well-resolved dark resonances confirming the versatility of the system for quantum optical experiments.
An interesting aspect of AAS which occurs if the absorption line is broadened only by natural broadening should be mentioned. Hannaford175 in 1994 demonstrated the surprising independence of the peak absorption coefficient on the absorption oscillator strength, fabs. This is mentioned since the absorption source would have to have a spectral line half-width less than the natural broadened absorption line. Of the tunable lasers available, diode lasers would be suitable for an application where the atoms are cooled sufficiently that all broadening sources except for natural broadening are minimized. The peak absorption coefficient becomes dependent on the absorption oscillator strength only through additional broadening processes, such as Doppler and collisional broadening. From the classical theory of optical dispersion and for the case of pure natural broadening of the absorption line, the absorption cross-section, σ0, is given by
 | (4) |
![[small lambda, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cc.gif) 0 = λ0/2π, where λ0 is the absorption wavelength (cm). Note that σ0 is independent of fabs as is the peak absorption coefficient k0 [k0 = σ0n0, where n0 is the absorber number density (cm−3)]. If Doppler broadening and/or collisional broadening become dominant, which is the usual case in atomic absorption spectroscopy, then σ0 and k0 depend directly upon fabs and also upon the half-widths of the Doppler broadened and collisional broadened absorption lines. Finally, it should be stressed that no matter what the broadening source is, the area under the absorption line,
0 = λ0/2π, where λ0 is the absorption wavelength (cm). Note that σ0 is independent of fabs as is the peak absorption coefficient k0 [k0 = σ0n0, where n0 is the absorber number density (cm−3)]. If Doppler broadening and/or collisional broadening become dominant, which is the usual case in atomic absorption spectroscopy, then σ0 and k0 depend directly upon fabs and also upon the half-widths of the Doppler broadened and collisional broadened absorption lines. Finally, it should be stressed that no matter what the broadening source is, the area under the absorption line,  or
or  , is a constant provided that the number density of absorbers, n0, is a constant. Therefore, a spectral line which has a natural width of say 10−4 Å will have a peak absorption 100 times larger than an absorption line which has a collisional width of 10−2 Å. Despite the interesting conclusions, we can only obtain naturally broadened absorption lines by extensive cooling and stopping of atoms, which are not simple, inexpensive or even possible with many of the atomic absorption atomizers.
, is a constant provided that the number density of absorbers, n0, is a constant. Therefore, a spectral line which has a natural width of say 10−4 Å will have a peak absorption 100 times larger than an absorption line which has a collisional width of 10−2 Å. Despite the interesting conclusions, we can only obtain naturally broadened absorption lines by extensive cooling and stopping of atoms, which are not simple, inexpensive or even possible with many of the atomic absorption atomizers.
Theoretical comparison of analytical atomic absorption spectrometric methods
In this section, we compare several absorption spectroscopic methods based on S/N and LOD. Although the comparison is primarily for AAS, it also applies to narrow line excitation molecular absorption spectroscopy. The absorbing species can therefore be atoms (or molecules) in a gas, and molecules in liquids or solids. The absorption signal, in general, is not influenced by either quenching processes or high concentrations of charged species (e.g., in a plasma cell). Although diode lasers have found considerable use in atomic and molecular absorption spectrometry, no specific discussion of these will be given here; the reader is referred to the separate section on atomic absorption spectrometry with diode lasers. Diode lasers have also found extensive use in molecular absorption spectroscopy for monitoring atmospheric pollutants, including CO, NOx, SO2 and polycyclic aromatic hydrocarbons. Readers are referred to several excellent reviews on analytical absorption spectroscopy.176–182The absorption methods to be compared reflect recent advances in the use of laser-based methodologies and are based on the following: (1) single pass absorption; (2) multi-pass absorption; (3) cavity enhanced absorption; (4) cavity ring down; (5) intracavity absorption; and (6) single pass absorption with cavity enhanced frequency modulation optical heterodyne detection. The principles of operation of these six types of absorption methods are given in Fig. 30. The LOD is defined according to IUPAC as the analyte concentration of amount giving S/N = 3, where S/N is given in terms of fraction absorbed (fraction absorbed corresponds to absorbance provided that A ≲ 0.01).
 | ||
| Fig. 30 Schematic diagram of the six laser-pulsed absorption spectroscopic methods: single pass absorption spectroscopy (SPAS); multipass absorption spectroscopy (MPAS); cavity enhanced absorption spectroscopy (CEAS); cavity ring down spectroscopy (CRDS); intracavity absorption spectroscopy (ICAS); and frequency modulation optical heterodyne absorption spectroscopy (FMOHAS). | ||
For each of the six absorption methods, it will be assumed that the absorption lines are Lorentz broadened (collisional broadening for most practical atomic absorption cells). For inhomogeneously broadened lines (Doppler broadening), the S/N expressions will be different and will not be given here. This restricts the direct applicability of our approach to atom reservoirs or techniques where Doppler broadening can be made negligible. The source in all absorption methods will be a narrowband laser (diode laser). Even though laser radiation shot noise can be suppressed (2–3-fold) by using squeezed light,183 optimum instrumentation to realize the benefits of squeezed light are still too complicated and expensive and the gain of a factor of 2–3 is not sufficient to justify the broad use of this technique. From literature information on the laser noise power spectrum, it is clear that the S/N becomes quantum shot noise limited when the source is modulated at high frequencies (≥1 MHz).184 By modulation at such frequencies, low frequency (1/f) noise can be essentially eliminated.185 Therefore, for the theoretical comparison of the six absorption methods, the limiting noise10 will be assumed to be source quantum shot noise, which is given for the six methods by
 | (5) |
In order to obtain the largest possible absorption signal (fraction absorbed), we will assume for all six methods that the intensity of the laser source equals the saturation intensity, defined as
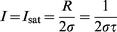 | (6) |
The S/N expressions for the six absorption methods are taken from a future paper by Matveev et al.185 It is important to stress that the statistical fluctuations of the number of atoms in the laser beam are not considered.14 As a result, whenever the predicted LOD reaches a small number of atoms, the expressions for the limiting noise should be modified.186,187
1. Single pass absorption spectroscopy (SPAS)
The S/N in this case is given186 by | (7) |
 | (8) |
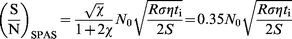 | (9) |
An estimate of the LOD can be obtained from eqn. (9) for Hg if S = 0.1 cm2, η = 0.3, t = 10 s, 1/R = 0.2 ns and σ = 2 × 10−14 cm2 for Hg in the atmosphere, 1/R = 118 ns and σ = 6 × 10−13 cm2 for Hg in a vacuum and 1/R = 118 ns and σ = 4.4 × 10−10 cm2 for Hg cooled by laser radiation. The resulting detection limits are N0L = 220, 980 and 38 atoms for the three cases. The laser powers to saturate the Hg transition for the three cases are 9800, 0.55 and 0.00074 W, respectively. Hence excellent LODs can be obtained by SPAS with simple and inexpensive equipment.
2. Multipass absorption spectroscopy (MPAS)
Here the laser beam is passed through the atoms G times by means of mirrors or 90° prisms. The S/N in this case is given186 by | (10) |
3. Cavity enhanced absorption spectroscopy (CEAS)
In this approach, the absorbing medium is placed within a cavity containing two plane mirrors with a high coefficient of reflection, ρ (close to unity). For the sake of simplicity, it is assumed that the absorption line is at the minimum of cavity transparency and is several times smaller than the cavity free spectral range. Because the laser beam in the cavity makes many passes,188,189 the absorption signal is increased by 2/(1 − ρ + αn) where αn is the non-selective absorption fraction of laser light in the absorbing medium and ρ is the reflectivity of the mirrors. The signal is, however, also decreased by the factor (1 − ρ)(1 − αn)/2. Therefore, for a laser power close to the saturation level, the noise will be proportional to [1/2(1 − ρ)(1 − αn)1/2 and so the S/N is given186 for CEAS by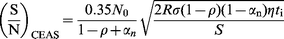 | (11) |
4. Cavity ring down spectroscopy (CRDS)
As in the previous case, here the absorbing medium is placed between highly reflective plane mirrors.190–198 After injecting a short laser pulse along the optical axis or after interrupting CW generation, the laser intensity versus time is measured for a given absorption wavelength. The pulse decay time, τCR is given186 by | (12) |
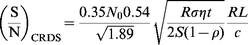 | (13) |
 , which is only a factor of three if ρ = 0.99.
, which is only a factor of three if ρ = 0.99.
5. Intracavity absorption spectroscopy (ICAS)
The idea of ICAS was proposed almost 30 years ago200 and is very similar to CRDS. In order to eliminate the effect of the exponentially decaying laser pulse in ICAS, the signal is amplified by a laser active medium and, in principle, the signal can be accumulated for a long period of time. References to ICAS can be found in a book201 and a review.202 Since the ICAS signal is amplified, there is no need to use highly reflective mirrors. Optical parametric oscillators28 can be used in wavelength regions where no appropriate laser action medium exists.The S/N in ICAS is given by186
 | (14) |
6. Frequency modulation optical heterodyne absorption spectroscopy (FMOHAS)
This approach was proposed by Bjorklund204 in 1980. The basic idea is to use three equidistant lines produced by a single frequency laser which is frequency modulated at frequency Ω. The resulting laser spectrum has a central line carrier and two sideband lines located ±Ω from the carrier.If the index of modulation of the optical frequency modulator M ≪ 1 and background non-selective absorption losses αn ≪ 1 and if Ω > Δνabs, the absorption linewidth, then the S/N is given by
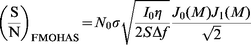 | (15) |
 | (16) |
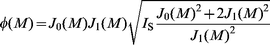 | (17) |
 | (18) |
Concluding remarks
As long as the shot noise limitation is maintained and the other assumptions given are valid, the six absorption methods give near single atom detection. In fact, of the six methods, all give similar S/Ns and LODs except for ICAS, which is several orders of magnitude better. Unfortunately, as the measurement time is increased in any of the methods but especially ICAS, the LODs deteriorate rapidly because of the onset of flicker noise. Nevertheless, it is interesting that Sierks et al.205 predicted the detection of single atoms by ICAS.Since our discussion is restricted to atomic absorption analysis, it is also interesting to compare the six laser-based atomic absorption methods with the classical non-laser method, i.e., conventional hollow cathode lamp (HCL) furnace AAS. For the source shot noise limited case, the S/N is given by10
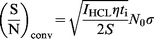 | (19) |
Conclusion
In Tables 11 and 12, comparisons of the characteristics of several methods for the detection and determination of trace elements in solids and in solutions, respectively, are given. These tables should aid readers in applying the methods to real samples. However, the characteristics of a given method for a given analyte and a given sample may differ from the general ones given in Tables 11 and 12.| Method | Sample typea/environmentb | Energy/power input | LOD/ng g−1 | RSD (%) | Multi-element | Destructivitye | Elemental selectivityf | Matrix effect | Depth/lateral resolution |
|---|---|---|---|---|---|---|---|---|---|
| a S (B) = solids, bulk method; S (S) = solids, surface method; L = liquids; Su = suspensions; P = particulates; A = aerosols. b Atm = atmospheric pressure; LP = low pressure; VLP = very low pressure required for sampling (not for detection). c Quadrupole MS. d Sector MS. e Amount of sample destroyed as given in parentheses. f I, isotopic selectivity in addition to element selectivity. | |||||||||
| Furnace AAS | S (B), L, Su/Atm | 1–5 kW | 10−1–103 | 2–5 | No | Yes (mg) | Good | Moderate | None |
| GD-OES | S (S)/LP | 0.1–1 kW | 10−1–103 | 1–5 | Yes | Yes (ng) | Moderate | Moderate | 10–50 nm/few mm |
| GD-MS | S (S)/LP | 0.1–1 kW | 10−1–10 | 1–5 | Yes | Yes (ng) | Good (I)d | Moderate | 10–50 nm/few mm |
| Furnace LEAFS | S (B), L, Su/Atm | 1–5 kW | 10−4–1 | 3–6 | No | Yes (mg) | Excellent | Moderate | None |
| GD-LEAFS | S (S)P/LP | 0.1–1 kW | 10−1–102 | 1–5 | No | Yes (ng) | Excellent | Moderate | 10–50 nm/few mm |
| RIMS | S (S), P, L, Su/Atm | 0.1–1 kW | 10−3–102 | 3–6 | No | Yes (mg) | Excellent (I) | Small | None |
| LIMS | S (S), P/LP | 106–1014 W cm−2 UV-IR | 1–102 | 5–10 | Yes | Yes (ng) | Excellent (I) | Moderate | 0.1 µm/1–100 µm |
| LIBS (LA-OES) | S (S), P, L, Su/G, A/Atm | 106–1014 W cm−2 UV-IR | 103–105 | 5–10 | Yes | Yes (ng–µg) | Moderate | Moderate | 0.1 µm/1–100 µm |
| LA-ICP-OES | S (S), P/Atm | 106–1012 W cm−2 UV-IR | 102–104 | 1–10 | Yes | Yes (ng–µg) | Moderate | Moderate | 0.1 µm/1–100 µm |
| LA-ICP-MS | S (S), P/Atm | 106–1012 W cm−2 UV-IR | 10–102, 10−2–10−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) d d |
1–10 | Yes | Yes (ng–µg) | Excellent (I)c | Moderate | 0.1 µm/1–100 µm |
| SIMS | S (S)/VLP | 3–15 keV ions | 1–102 | 1–10 | Yes | Yes (ng) | Excellent (I) | Large | 0.1 µm/0.1–100 µm |
| XPS | S (S)/VLP | 15 keV electrons | 102 | 1–10 | Yes | No | Good | Moderate | 30 Å/1–10 µm |
| XRF | S (S)/Atm | keV X-Rays | 1–10 | 1–10 | Yes | No | Good | Moderate | 1 µm/100 µm |
| PIXE | S (S), L, P/VLP | 3 MeV protons | 1–102 | 1–10 | Yes | No | Good | Moderate | 5 µm/5–100 µm |
| Method | Pressure/gas | LOD/ng mL−1 | RSD (%) | Sample volume/mL | Multi-element | Range of analysis | Elemental selectivity | Isotopic selectivity | Matrix effects |
|---|---|---|---|---|---|---|---|---|---|
| Flame AAS | Atmospheric/C2H2 | 1–104 | 1 | 1–10 | No | Metals | Good | No | Large |
| Furnace AAS | Atmospheric/Ar | 10−2–102 | 5 | 10−3–10−1 | No | Metals | Good | No | Moderate |
| ICP-OES | Atmospheric/Ar | 10−1–102 | 1 | 1–10 | Yes | Most | Moderate | No | Moderate |
| ICP-MS | Atmospheric/Ar | 10−4–1 | 1 | 1–10 | Yes | Most | Good | Yes | Moderate |
| Furnace LEAFS | Atmospheric/Ar | 10−5–10 | 5 | 10−3–10−1 | No | Metals | Excellent | No | Moderate |
| ICP-LEAFS | Atmospheric/Ar | 10−2–1 | 1 | 1–10 | No | Metals | Excellent | No | Moderate |
| Flame LEI | Atmospheric/C2H2 | 10−4–102 | 1 | 1–10 | No | Metals | Good | No | Large |
| Furnace RIMS | Vacuum | 10−4–10 | 5 | 10−3–1 | No | Most | Excellent | Yes | Small |
In the idealized comparison of laser-based absorption methods, since it is based upon the assumption that shot noise is reached and is the limiting noise of the technique, it is nevertheless clear that absorption methods, both direct and indirect, based on the use of lasers, deserve to be revisited. It is fair to say that, since the advent of lasers (especially pulsed lasers) in analytical spectroscopy, the absorption technique has somewhat fallen into oblivion in favor of the fluorescence and ionization methods, which have taken advantage of the high power achieved with laser sources. With the advent of diode lasers, whose linewidths are very narrow compared with the absorption linewidth, and the practical feasibility of cooling an atomic system so that natural broadening is indeed reached, an ideal direct absorption measurement is clearly approached. The peculiar features of working with the concept of a radiation cavity, containing the absorption analyte, have led to the analytical development of techniques such as cavity-enhanced, intracavity and cavity ring down absorption methods, which are now gaining increasing popularity and a much improved understanding of their underlying analytical features.
The application of diode lasers is now well established in several fields of spectroscopy, for both fundamental and analytical studies and for both atomic and molecular species. This field is therefore expected to grow at a steady rate. Reliable diode lasers operating in the blue region of the spectrum are, however, still under development. Nevertheless, efficient frequency doubling and mixing techniques are now used to reach UV transitions. Atomic absorption measurements with UV diode lasers will then become routine, with all the obvious advantages that these lasers have when compared with hollow cathode sources. It seems fair to stress here that reaching the UV and even the vacuum UV region with lasers for specific applications has never been a problem if one considers the large variety of non-linear techniques used (frequency doubling, tripling and mixing in crystals and atomic vapors). The real breakthrough will be to make low wavelength radiation available with a source which is no more complicated to operate than a conventional lamp.
Microchip lasers are now commercially available. These all-solid-state lasers possess some of the ideal features of an optimum source for several analytical techniques, e.g., molecular fluorescence and laser induced plasma emission. Their use in laser induced plasma emission seems to be very promising, in view of the remarkable peak power obtained with limited pulse energies, and consequently of the capability of reaching breakdown on metals and on many other absorptive samples. The high repetition frequency (typically 8–15 kHz) allows analytical data to be obtained practically in real time. Their use is then expected to increase as well as the areas of the applicability, especially in the field of environmental sensing (e.g., aerosols and bioaerosol particles in the atmosphere).
It is difficult to foresee a decrease in the number of papers dealing with the diagnostic aspects and analytical application of laser induced plasma spectroscopy. As it could have indeed been anticipated, commercial availability is now a fact. It seems fair to anticipate that no revolutionary developments are to be expected in this field, but rather many evolutionary developments both in the process of miniaturizing the set-up, by making the systems portable and easy of use (remote sensing), and in enlarging the range of applications.
Resonance ionization imaging detectors have many more potential applications than those currently explored. Research is therefore expected to grow constantly in several fields (e.g., combustion diagnostics and bio-medicine), albeit not strictly related to chemical analysis.
The current trend in analytical spectroscopy continues to be focused on the development and optimization of a single technique (e.g., absorption, emission) rather than on the combination of many techniques in a single instrument. This is due on the one hand to the availability of compact and reliable laser sources combined with an increasing number of applications, and on the other hand to the still high cost of an all-solid-state, state-of-the-art, multi-purpose laser spectrometer.
A final consideration seems to be in order here. After having reviewed many well established and/or very promising techniques based on absorption, emission, fluorescence and ionization, the authors would like to stress that, despite the proven capability of these laser-based techniques to detect single atoms and molecules, one could seldom take advantage of these impressive characteristics in the real analytical world, where all techniques, for an analyte concentration below a given level, will become blank limited. It is therefore surprising that the attractive feature of laser-based methods of being potential candidates for "absolute analysis" has not yet received systematic attention, in contrast to the use of conventional atomic absorption with hollow cathode sources. Laser induced fluorescence, and especially laser induced ionization, can be challenged to this purpose. Moreover, diode laser atomic absorption and laser induced plasma emission are both capable, in principle, of performing analysis without the need for standards. Perhaps now is the right time to revitalize this attractive line of research.
Appendix 1: Definitions of acronyms
| AAS | Atomic absorption spectrometry |
| AES | Atomic emission spectrometry |
| AFS | Atomic fluorescence spectrometry |
| AIS | Atomic ionization spectrometry |
| AOD | Acousto-optic deflector |
| APS | Atomic photothermal spectrometry |
| CCD | Charge coupled device |
| CEAS | Cavity enhanced absorption spectroscopy |
| CRDS | Cavity ring down spectroscopy |
| CZE (CE) | Capillary zone electrophoresis (capillary electrophoresis) |
| DL | Diode laser |
| ETA | Electrothermal atomization |
| ETV | Electrothermal vaporization (production of particles and atoms) |
| FIA | Flow injection analysis |
| FMOHAS | Frequency modulation optical heterodyne absorption spectroscopy |
| FT-LMMS | Fourier transform laser microprobe mass spectrometry |
| GC | Gas chromatography |
| GD | Glow discharge |
| HCL | Hollow cathode lamp |
| HG | Hydride generator |
| HPLC | High performance liquid chromatography |
| ICAS | Intracavity absorption spectroscopy |
| ICCD | Intensified charge coupled device |
| ICP | Inductively coupled plasma |
| ICP-MS | ICP mass spectrometry |
| ICP-OES | ICP optical emission spectrometry |
| IUPAC | International Union of Pure and Applied Chemistry |
| LAAS | Laser atomic absorption spectrometry |
| LA-OES | Laser ablation optical emission spectrometry (also called LIBS) |
| LA-ICP-MS | Laser ablation inductively coupled plasma mass spectrometry |
| LA-ICP-OES | Laser ablation inductively coupled plasma optical emission spectrometry |
| LEAFS | Laser excited atomic (ionic) fluorescence spectrometry |
| LEIS | Laser enhanced ionization spectrometry |
| LIBS | Laser induced breakdown spectroscopy |
| LIFS | Laser induced fluorescence spectrometry |
| LMMS | Laser microprobe mass spectrometry |
| LOD | Limit of detection |
| LR | Luminosity-resolving power product |
| LSRW | Laser supported reduction wave (model) |
| LTE | Local thermodynamic equilibrium |
| MPAS | Multi-pass absorption spectroscopy |
| MCP | Microchannel plate |
| MP | Microwave plasma |
| MS | Mass spectrometry |
| OES | Optical emission spectrometry |
| RFIM | Resonance fluorescence imaging monochromator |
| RID | Resonance ionization detector |
| RIID | Resonance ionization imaging detector |
| RIMS | Resonance ionization mass spectrometry |
| RIS | Resonance ionization spectrometry |
| RSD | Relative standard deviation |
| SIMS | Secondary ion mass spectrometry |
| S/B | Signal-to-background ratio |
| S/N | Signal-to-noise ratio |
| SPAS | Single pass absorption spectroscopy |
| TOF-LMMS | Time-of-flight laser microprobe mass spectrometry |
Acknowledgements
Many of the research topics discussed in this paper were supported by DOE-DE-F602-99ER 14960 and by the Engineering Research Center (ERC) for Particle Science and Technology, NSF EEL-94-02989 and the industrial partners of the ERC.References
- Analytical Laser Spectroscopy, in Chemical Analysis, ed. N. Omenetto, Wiley-Interscience, New York, vol. 50, 1979. Search PubMed.
- Analytical Applications of Lasers, in Chemical Analysis, ed. E. H. Piepmeier, Wiley-Interscience, New York, vol. 87, 1986. Search PubMed.
- Laser Analytical Spectrochemistry, ed. V. S. Letokhov, Adam Hilger, Bristol, 1985. Search PubMed.
- M. A. Bolshov, Ullmann's Encyclopedia of Industrial Chemistry, vol. B5, Urban and Schwartzenburg, Munchen, Germany, 1994, p. 653. Search PubMed.
- Laser Induced Plasmas and Applications, ed. L. J. Radziemski and D. A. Cremers, Marcel Dekker, New York, 1989. Search PubMed.
- Modern Techniques in Raman Spectroscopy, ed. J. J. Laserna, John Wiley, New York, 1996. Search PubMed.
- Laser Enhanced Ionization Spectrometry, ed. J. C. Travis and G. C. Turk, in Chemical Analysis, Wiley-Interscience, New York, vol. 136, 1996. Search PubMed.
- D. M. Lubman, Lasers and Mass Spectrometry, Oxford University Press, New York, 1990. Search PubMed.
- W. Demtröder, Laser Spectroscopy, Springer, Berlin, 2nd edn., 1996. Search PubMed.
- V. S. Letokhov, Laser Photoionization Spectroscopy, Academic Press, Orlando, FL, 1987. Search PubMed.
- G. S. Hurst and M. G. Payne, Principles and Applications of Resonance Ionization Spectroscopy, IOP Publishing, Adam Hilger, Bristol, 1988. Search PubMed.
- Applied Laser Spectroscopy: Techniques, Instrumentation and Applications, ed. D. L. Andrews, VCH, New York, 1992. Search PubMed.
- N. Omenetto, J. Anal. At. Spectrom., 1998, 13, 385 RSC.
- C. Th. J. Alkemade, Appl. Spectrosc., 1981, 35, 1 Search PubMed.
- C. Th. J. Alkemade, in Analytical Applications of Lasers, ed. E. H. Piepmeier, Wiley-Interscience, New York, 1986, ch 4. Search PubMed.
- J. D. Winefordner, G. A. Petrucci, C. L. Stevenson and B. W. Smith, J. Anal. At., Spectrom., 1994, 9, 131 RSC.
- C. L. Stevenson and J. D. Winefordner, Spectrochim. Acta, Part B, 1993, 48, 757 CrossRef.
- C. L. Stevenson and J. D. Winefordner, Appl. Spectrosc., 1992, 46, 407 Search PubMed.
- N. Omenetto, G. A. Petrucci, P. Cavalli and J. D. Winefordner, Fresenius' J. Anal. Chem., 1996, 355, 878 CAS.
- D. J. Wineland, W. M. Itano and I. C. Berquist, Opt. Lett., 1987, 12, 389 Search PubMed.
- L. J. Radziemski, Microchem. J., 1994, 50, 218 CrossRef CAS.
- R. E. Russo, Appl. Spectrosc., 1995, 49(9), 14A Search PubMed.
- S. A. Darke and J. F. Tyson, J. Anal. At. Spectrom., 1993, 8, 145 RSC.
- D. A. Rusak, B. C. Castle, B. W. Smith and J. D. Winefordner, Crit. Rev. Anal. Chem., 1997, 27(4), 257 Search PubMed.
- D. A. Rusak, B. C. Castle, B. W. Smith and J. D. Winefordner, Trends Anal. Chem., 1998, 17, 453 CrossRef CAS.
- L. M. Cabalín and J. J. Laserna, Spectrochim. Acta, Part B, 1998, 53, 723 CrossRef.
- J. Hermann, C. Boulmer-Leborgne, I. N. Mihailescu and B. Debreuil, J. Appl. Phys., 1993, 73, 1091 CrossRef CAS.
- J. Hermann, C. Boulmer-Leborgne and D. Hong, J. Appl. Phys., 1998, 83, 691 CrossRef CAS.
- M. D. Perry, B. C. Stuart, P. S. Banks, M. D. Feit, V. Yanovsky and A. M. Rubenchik, J. Appl. Phys., 1999, 85, 6803 CrossRef CAS.
- A.-C. Tien, S. Backus, H. Kapteyn, M. Murnane and G. Mourou, Phys. Rev. Lett., 1999, 82, 3883 CrossRef CAS.
- B. C. Stuart, M. D. Feit, A. M. Rubenchik, B. W. Shore and M. D. Perry, Phys. Rev. Lett., 1995, 74, 2248 CrossRef CAS.
- D. Du, X. Liu, G. Korn, J. Squier and G. Mourou, Appl. Phys. Lett., 1994, 64, 3071 CrossRef.
- M. Lenzner, J. Krüger, S. Sartania, Z. Cheng, Ch. Spielmann, G. Mourou, W. Kautek and F. Krausz, Phys. Rev. Lett., 1998, 80, 4076 CrossRef CAS.
- L. St-Onge, M. Sabsabi and P. Cielo, Spectrochim. Acta, Part B, 1998, 53, 407 CrossRef.
- J. G. Lunney and R. Jordan, Appl. Surf. Sci., 1998, 127–129, 941 CrossRef CAS.
- J. Hermann, C. Vivien, A. P. Carricato and C. Boulmer-Leborgne, Appl. Surf. Sci., 1998, 127–129, 645 CrossRef CAS.
- G. Callies, H. Schittenhelm, P. Berger and H. Hügel, Appl. Surf. Sci., 1998, 127–129, 134 CrossRef CAS.
- Ş. Yalçin, D. R. Crosley, G. P. Smith and G. W. Faris, Appl. Phys. B, 1999, 68, 121 CrossRef.
- L. A. Doyle, G. W. Martin, A. Al-Khateeb, I. Weaver, D. Riley, M. J. Lamb, T. Morrow and C. L. S. Lewis, Appl. Surf. Sci., 1998, 127–129, 716 CrossRef CAS.
- I. B. Gornushkin, L. A. King, B. W. Smith, N. Omenetto and J. W. Winefordner, Spectrochim. Acta, Part B, 1999, 54, 1771. Search PubMed.
- I. Weaver, G. W. Martin, W. G. Graham, T. Morrow and C. L. S. Lewis, Rev. Sci. Instrum., 1999, 70, 1801 CrossRef CAS.
- M. P. Nelson, W. C. Bell, M. L. McLester and M. L. Myrick, Appl. Spectrosc., 1998, 52, 179 Search PubMed.
- B. A. Bushaw and M. L. Alexander, Appl. Surf. Sci., 1998, 127–129, 935 CrossRef CAS.
- G. W. Martin, L. A. Doyle, A. Al-Khateeb, I. Weaver, D. Riley, M. J. Lamb, T. Morrow and C. L. S. Lewis, Appl. Surf. Sci., 1998, 127–129, 710 CrossRef CAS.
- H. Schittenhelm, G. Callies, P. Berger and H. Hügel, Appl. Surf. Sci., 1997, 109–110, 493 CrossRef.
- H. Schittenhelm, G. Callies, P. Berger and H. Hügel, Appl. Surf. Sci., 1998, 127–129, 922 CrossRef CAS.
- C. Chaléard, P. Mauchien, N. Andre, J. Uebbing, J. L. Lacour and C. Geertsen, J. Anal. At. Spectrom., 1997, 12, 183 RSC.
- U. Panne, C. Haisch, M. Clara and R. Niessner, Spectrochim. Acta, Part B, 1998, 53, 1957 CrossRef.
- U. Panne, C. Haisch, M. Clara and R. Niessner, Spectrochim. Acta, Part B, 1998, 53, 1969 CrossRef.
- J. A. Aguilera, C. Aragón and F. Peñalba, Appl. Surf. Sci., 1998, 127–129, 309 CrossRef CAS.
- B. C. Castle, K. Talabardon, B. W. Smith and J. D. Winefordner, Appl. Spectrosc., 1998, 52, 649 Search PubMed.
- P. Lindblom, Anal. Chim. Acta, 1999, 380, 353 CrossRef CAS.
- H. E. Bauer, F. Leis and K. Niemax, Spectrochim. Acta, Part B, 1998, 53, 1815 CrossRef.
- J. Nölte, F. Scheffler, S. Mann and M. Paul, J. Anal. At. Spectrom., 1999, 14, 597 RSC.
- M. Motelica-Heino, O. F. X. Donard and J. M. Mermet, J. Anal. At. Spectrom., 1999, 14, 675 RSC.
- M. Gagean and J. M. Mermet, Spectrochim. Acta, Part B, 1998, 53, 581 CrossRef.
- O. V. Borisov, X. L. Mao, A. C. Ciocan and R. E. Russo, Appl. Surf. Sci., 1998, 127–129, 315 CrossRef CAS.
- X. L. Mao, A. C. Ciocan, O. V. Borisov and R. E. Russo, Appl. Surf. Sci., 1998, 127–129, 262 CrossRef CAS.
- X. L. Mao, O. V. Borisov and R. E. Russo, Spectrochim. Acta, Part B, 1998, 53, 731 CrossRef.
- W. T. Chan, A. P. K. Leung, X. L. Mao and R. E. Russo, Appl. Surf. Sci., 1998, 127–129, 269 CrossRef CAS.
- A. P. K. Leung, W. T. Chan, X. L. Mao and R. E. Russo, Anal. Chem., 1998, 70, 4709 CrossRef CAS.
- S. Rings, R. Sievers and M. Jansen, Fresenius' J. Anal. Chem., 1999, 363, 165 CrossRef CAS.
- D. Günter, S. E. Jackson and H. P. Longerich, Spectrochim. Acta, Part B, 1999, 54, 381 CrossRef.
- M. L. Alexander, M. R. Smith, J. S. Hartman, A. Mendoza and D. W. Koppenaal, Appl. Surf. Sci., 1998, 127–129, 255 CrossRef CAS.
- S. M. Eggins, L. P. J. Kinsley and J. M. G. Shelley, Appl. Surf. Sci., 1998, 127–129, 278 CrossRef CAS.
- D. J. Figg, J. B. Cross and C. Brink, Appl. Surf. Sci., 1998, 127–129, 287 CrossRef CAS.
- E. Schroeder, M. Hamester and M. Kaiser, Appl. Surf. Sci., 1998, 127–129, 292 CrossRef CAS.
- T. E. Jeffries, S. E. Jackson and H. P. Longerich, J. Anal. At. Spectrom., 1998, 13, 935 RSC.
- R. E. Wolf, C. Thomas and A. Bohlke, Appl. Surf. Sci., 1998, 127–129, 299 CrossRef CAS.
- J. L. Nielsen, A. Abildtrup, J. Christensen, P. Watson, A. Cox and C. W. McLeod, Spectrochim. Acta, Part B, 1998, 53, 339 CrossRef.
- D. Günter, A. Audétat, R. Frischknecht and C. A. Heirich, J. Anal. At. Spectrom., 1998, 13, 263 RSC.
- J. J. Leach, L. A. Allen, D. B. Aeschliman and R. S. Houk, Anal. Chem., 1999, 71, 440 CrossRef CAS.
- H. F. Falk, B. Hattendorf, K. Krengel-Rothensee, N. Wieberneit and D. L. Dannen, Fresenius' J. Anal. Chem., 1998, 362, 468 CrossRef CAS.
- S. Shuttleworth and D. T. Kremser, J. Anal. At. Spectrom., 1998, 13, 697 RSC.
- L. Van Vaeck, A. Adriaens and F. Adams, Spectrochim. Acta, Part B, 1998, 53, 367 CrossRef.
- M. D. Norman, W. L. Griffin, N. J. Pearson, M. O. Garcia and S. Y. O'Reilly, J. Anal. At. Spectrom., 1998, 13, 477 RSC.
- J. S. Becker, R. S. Soman, T. Becker, V. K. Panday and H.-J. Dietze, J. Anal. At. Spectrom., 1998, 13, 983 RSC.
- M. Milán, P. Lucena, L. M. Cabalín and J. J. Laserna, Appl. Spectrosc., 1998, 52, 444 Search PubMed.
- D. Romero and J. J. Laserna, J. Anal. At. Spectrom., 1998, 13, 557 RSC.
- J. M. Vadillo, C. C. García, S. Palanco and J. J. Laserna, J. Anal. At. Spectrom., 1998, 13, 793 RSC.
- J. M. Vadillo, I. Vadillo, F. Carrasco and J. J. Laserna, Fresenius' J. Anal. Chem., 1998, 371, 119 CrossRef CAS.
- B. Wanner, C. Moor, R. Richner, R. Brönnimann and B. Magyar, Spectrochim. Acta, Part B, 1999, 54, 289 CrossRef.
- L. Dudragne, P. Adam and J. Amouroux, Appl. Spectrosc., 1998, 52, 1321 Search PubMed.
- C.-J. Chin, C.-F. Wang and S.-L. Jeng, J. Anal. At. Spectrom., 1999, 14, 663 RSC.
- D. W. Hahn, Appl. Phys. Lett., 1998, 72, 2960 CrossRef CAS.
- M. Casini, M. A. Harith, V. Patteschi, D. P. Singh and M. Vaselli, Laser Particle Beams, 1991, 9, 633 Search PubMed.
- C. Lazzani, M. DeRosa, S. Rastelli, A. Ciucci, V. Patteschi and A. Salvetti, Laser Particle Beams, 1994, 12, 525 Search PubMed.
- L. M. Berman and P. J. Wolf, Appl. Spectrosc., 1998, 52, 438 Search PubMed.
- N. H. Cheung, C. W. Ng, W. F. Ho and E. S. Yeung, Appl. Surf. Sci., 1998, 127–129, 274 CrossRef CAS.
- M. Saito, S. Izumida, K. Onishi and J. Akazawa, J. Appl. Phys., 1999, 85, 6353 CrossRef CAS.
- S. Izumida, K. Onishi and M. Saito, Jpn. J. Appl. Phys., 1998, 37, 2039 CrossRef CAS.
- J. Noack, D. X. Hammer, G. D. Noojin, B. A. Rockwell and A. Vogel, J. Appl. Phys., 1998, 83, 7488 CrossRef CAS.
- A. Vogel, J. Noack, K. Nahen, D. Theisen, S. Busch, U. Parlitz, D. X. Hammer, G. D. Noojin, B. A. Rockwell and R. Birngruber, Appl. Phys. B, 1999, 68, 271 CrossRef.
- R. Sattmann, I. Mönch, H. Krause, R. Noll, S. Couris, A. Hatziapostolou, A. Mavromanolakis, C. Fotakis, E. Larrauri and R. Miguel, Appl. Spectrosc., 1998, 52, 456 Search PubMed.
- I. B. Gornushkin, B. W. Smith, H. Nasajpour and J. D. Winefordner, Anal. Chem., 1999, 71, 5157. Search PubMed.
- W. Devos, C. Moor and P. Lienemann, J. Anal. At. Spectrom., 1999, 14, 621 RSC.
- B. W. Smith, I. B. Gornushkin, L. A. King and J. D. Winefordner, Spectrochim. Acta, Part B, 1998, 53, 1131 CrossRef.
- B. W. Smith, A. Quentmeier, M. Bolshov and K. Niemax, Spectrochim. Acta, Part B, 1999, 54, 943 CrossRef.
- H. Niki, T. Yasuda and I. Kitazima, J. Nucl. Sci. Technol., 1998, 35, 34 Search PubMed.
- X. Hou, P. Stchur, K. X. Yang and R. G. Michel, Trends Anal. Chem., 1998, 17, 532 CrossRef CAS.
- S. J. Hill, J. B. Dawson, W. J. Price, I. L. Shuttler, C. M. M. Smith and J. F. Tyson, J. Anal. At. Spectrom., 1998, 13, 131R RSC.
- R. Q. Aucélio, B. W. Smith and J. D. Winefordner, Appl. Spectrosc., 1998, 52, 1457 Search PubMed.
- R. Q. Aucélio, B. W. Smith and J. D. Winefordner, Anal. Sci., 1999, 15, 321 Search PubMed.
- R. Q. Aucélio, V. N. Rubin, B. W. Smith and J. D. Winefordner, J. Anal. At. Spectrom., 1998, 13, 49 RSC.
- D. J. Swart, M. Ezer, H. L. Pacquette and J. B. Simeonsson, Anal. Chem., 1998, 70, 1324 CrossRef CAS.
- D. J. Swart and J. B. Simeonsson, J. Anal. At. Spectrom., 1999, 14, 929 RSC.
- J. X. Zhou, X. Hou, K. X. Yang and R. G. Michel, J. Anal. At. Spectrom., 1998, 13, 41 RSC.
- W. Y. Ma, M. Xue, J. Zhang and D. Y. Chen, Spectrochim. Acta, Part B, 1998, 53, 1421 CrossRef.
- M. Reeves, M. Musculus and P. Farrell, Appl. Opt., 1998, 37, 6627 Search PubMed.
- C. Schulz, V. Sick, U. E. Meier, J. Heinze and W. Stricker, Appl. Opt., 1999, 38, 1434 Search PubMed.
- C. S. Cooper, R. V. Ravikrishna and N. M. Laurendeau, Appl. Opt., 1998, 37, 4823 Search PubMed.
- L. Chérigier, U. Czarnetzki, D. Luggenhölscher, V. Schulz-von der Gathen and H. F. Döbele, J. Appl. Phys., 1999, 85, 696 CrossRef CAS.
- M. Song, Y. P. Li, W. X. Peng, Z. K. Jiang, C. Guo and Y. N. Yu, Eur. Phys. J. D, 1998, 2, 115 CrossRef CAS.
- Y. Zhang, Y. Yoon, P. B. Kelly and I. M. Kennedy, Appl. Opt., 1998, 37, 7132 Search PubMed.
- P. V. Storm and M. A. Cappelli, Appl. Opt., 1998, 37, 486 Search PubMed.
- N. Erdmann, V. Sebastian, V. N. Fedoseyev, M. Hannawald, G. Huber, T. Kautzch, K. L. Kratz, V. I. Mishin, M. Nunnemann, G. Passler and N. Trautmann, Appl. Phys. B, 1998, 66, 431 CrossRef.
- K. L. Riter, O. I. Matveev, B. W. Smith and J. D. Winefordner, Anal. Chim. Acta, 1996, 333, 187 CrossRef CAS.
- C. Ke and K. C. Lin, Anal. Chem., 1999, 71, 1561 CrossRef CAS.
- O. I. Matveev, L. S. Mordoh, W. L. Clevenger, B. W. Smith and J. D. Winefordner, Appl. Spectrosc., 1997, 51, 798 Search PubMed.
- O. I. Matveev, W. L. Clevenger, L. S. Mordoh, B. W. Smith and J. D. Winefordner, RIS Conf. Proc., 1996, 171 Search PubMed.
- W. L. Clevenger, O. I. Matveev, S. Cabredo, N. Omenetto, B. W. Smith and J. D. Winefordner, Anal. Chem., 1997, 69, 2232 CrossRef CAS.
- B. A. Bushaw and B. D. Cannon, Spectrochim. Acta, Part B, 1997, 52, 1839 CrossRef.
- A. Jokinen, A.-H. Evensen, E. Kugler, J. Lettry, H. Ravn, P. Van Duppen, N. Erdmann, Y. Jading, S. Kohler, K.-L. Kratz, N. Trautmann, A. Wohr, V. N. Fedoseyev, V. I. Mishnin and V. Tikhonov, Nucl. Instrum. Methods Phys. Res. B, 1997, 126, 95 Search PubMed.
- W. L. Clevenger, L. S. Mordoh, O. I. Matveev, N. Omenetto, B. W. Smith and J. D. Winefordner, Spectrochim. Acta, Part B, 1997, 52, 295 CrossRef.
- W. L. Clevenger, O. I. Matveev, N. Omenetto, B. W. Smith and J. D. Winefordner, Spectrochim. Acta, Part B, 1997, 52, 1139 CrossRef.
- E. P. Vidolova-Angelova, T. B. Krustev, D. A. Angelov and S. Mincheva, J. Phys. B, 1997, 30, 667 Search PubMed.
- Y. Ogawa and O. Kujirai, J. Phys. Soc. Jpn., 1999, 68, 428 Search PubMed.
- C. Ke and K. C. Lin, Appl. Spectrosc., 1998, 52, 187 Search PubMed.
- P. Barker and H. Rubinsztein-Dunlop, Spectrochim. Acta, Part B, 1997, 52, 459 CrossRef.
- C. Gabbanini, S. Gozzini and A. Lucchesini, Opt. Commun., 1997, 141, 25 CrossRef CAS.
- S. Kohler, R. Beißenberger, K. Eberhardt, N. Erdmann, G. Herrmann, G. Huber, J. V. Kratz, M. Nunemann, G. Passler, P. M. Rao, J. Riegel, N. Trautmann and K. Wendt, Spectrochim. Acta, Part B, 1997, 52, 717 CrossRef.
- O. I. Matveev, B. W. Smith, N. Omenetto and J. D. Winefordner, Spectrochim. Acta, Part B, 1996, 51, 563 CrossRef.
- B. W. Smith, N. Omenetto and J. D. Winefordner, Spectrochim. Acta, Part B, 1989, Special Suppl., 101. Search PubMed.
- O. I. Matveev, B. W. Smith and J. D. Winefordner, Appl. Opt., 1997, 36, 8833 Search PubMed.
- O. I. Matveev, B. W. Smith and J. D. Winefordner, Opt. Lett., 1998, 23, 304 Search PubMed.
- O. I. Matveev, B. W. Smith and J. D. Winefordner, Appl. Phys. Lett., 1998, 72, 1673 CrossRef CAS.
- O. I. Matveev, B. W. Smith and J. D. Winefordner, Opt. Commun., 1998, 156, 259 CrossRef CAS.
- A. A. Podishivalov, W. L. Clevenger, O. I. Matveev, B. W. Smith and J. D. Winefordner, Appl. Spectrosc., 2000, 54, 175. Search PubMed.
- A. A. Podishivalov, M. R. Shepard, O. I. Matveev, B. W. Smith and J. D. Winefordner, J. Appl. Phys. Lett., 1999, 86, 5337. Search PubMed.
- A. A. Podishivalov, O. I. Matveev, B. W. Smith and J. D. Winefordner, Spectrochim. Acta, Part B, 1999, 54, 1795. Search PubMed.
- O. I. Matveev, B. W. Smith, N. Omenetto and J. D. Winefordner, Appl. Spectrosc., 1999, 53, 1341. Search PubMed.
- D. M. Paquet, J. F. Gravel, P. Nobert and D. Boudreau, Spectrochim. Acta, Part B, 1998, 53, 1907 CrossRef.
- E. B. Saloman, Spectrochim. Acta, Part B, 1991, 46, 319 CrossRef.
- T. G. M. Freegarde and G. Hancock, J. Phys. IV, 1997, 7, 15 Search PubMed.
- U. Czarnetzki, J. Phys. IV, 1997, 7, 175 Search PubMed.
- J. Uhlenbusch, Fusion Technol., 1998, 33, 345 Search PubMed.
- M. Tadokoro, H. Hirata, N. Nakano, Z. Llj. Petrovic and T. Makabe, Phys. Rev. E, 1998, 58, 7823 CrossRef CAS.
- H. Hirata, M. Tadokoro, N. Nakano, Z. Llj. Petrovic and T. Makabe, IEEE Trans. Plasma Sci., 1999, 27, 50 CrossRef CAS.
- J. Hermann, C. Boulmer-Leborgne and D. Hong, J. Appl. Phys., 1998, 83, 691 CrossRef CAS.
- C. Vivien, J. Hermann, A. Perrone, C. Boulmer-Leborgne and A. Luches, J. Appl. Phys., 1998, 31, 1263 CrossRef CAS.
- A. A. Puretsky and D. B. Geohegan, Appl. Surf. Sci., 1998, 129, 248 CrossRef.
- I. B. Gornushkin, M. Clara, B. W. Smith, J. D. Winefordner, U. Panne and R. Niesnner, Spectrochim. Acta, Part B, 1997, 52, 1617 CrossRef.
- C. H. Moreno, M. C. Marceni, W. Shlyaptsev and J. J. Rocca, IEEE Trans. Plasma Sci., 1999, 27, 6 CrossRef CAS.
- U. Iwase, W. Suss, D. H. H. Hoffmann, M. Roth, C. Stockl, M. Giessel, W. Seelig and R. Bock, Phys. Scr., 1998, 58, 634 Search PubMed.
- S. Siano, G. Pacini, R. Pini and S. Salimbeni, Opt. Commun., 1998, 154, 319 CrossRef CAS.
- A. G. Lowe, A. T. Hartlieb, J. Brand, B. Atakan and K. Kohse-Hoinghaus, Combust. Flame, 1999, 118, 37 CrossRef CAS.
- A. Zybin, C. Schnürer-Patschan, M. A. Bolshov and K. Niemax, Trends Anal. Chem., 1998, 17, 513 CrossRef CAS.
- J. Franzke, A. Schnell and K. Niemax, Spectrochim. Acta Rev., 1993, 15, 379 Search PubMed.
- T. Imasaka, Talanta, 1999, 48, 305 CrossRef CAS.
- S. Nakamura, M. Senoh, S. Nagahama, N. Iwasa, T. Yamada, T. Matsushita, Y. Sugimoto and H. Kiyoku, Jpn. J. Appl. Phys., 1997, 36, L1059 CrossRef.
- S. Nakamura, M. Senoh, S. Nagahama, N. Iwasa, H. Matsushita, H. Kiyoku, Y. Sugimoto, T. Kozaki, H. Umemoto, M. Sano and K. Chocko, Appl. Phys. Lett., 1998, 72, 211 CrossRef CAS.
- J. Franzke, Spectrochim. Acta, Part B, 1998, 53, 1595 CrossRef.
- J. Franzke, R. W. Fox and L. Hollberg, Spectrochim. Acta, Part B, 1998, 53, 1951 CrossRef.
- J. Gustafsson, D. Rojas and O. Axner, Spectrochim. Acta, Part B, 1997, 52, 1937 CrossRef.
- J. Gustafsson and O. Axner, Spectrochim. Acta, Part B, 1998, 53, 1895 CrossRef.
- D. Rojas, R. Ljung and O. Axner, Spectrochim. Acta, Part B, 1997, 52, 1663 CrossRef.
- N. Hadgu, J. Gustafsson, W. Frech and O. Axner, Spectrochim. Acta, Part B, 1998, 53, 923 CrossRef.
- J. Gustafsson and O. Axner, Spectrochim. Acta, Part B, 1998, 53, 1827 CrossRef.
- K. Wendt, K. Blaum, B. A. Bushaw, F. Juston, W. Nörtershauser, N. Trautman and B. Wiche, Fresenius' J. Anal. Chem., 1997, 359, 361 CrossRef CAS.
- R. Shaw, J. Young and D. Smith, Anal. Chem., 1989, 61, 695 CrossRef CAS.
- B. Bushaw and B. Cannon, Spectrochim. Acta, Part B, 1997, 52, 1839 CrossRef.
- K. A. Peterson and D. B. Oh, Opt. Lett., 1999, 24, 667 Search PubMed.
- A. V. Zybin, V. V. Liger and Y. A. Kuritsyn, Spectrochim. Acta, Part B, 1999, 54, 613 CrossRef.
- C. Raab, J. Bolle, H. Oberst, J. Eschner, F. Schmidt-Kaler and R. Blatt, Appl. Phys. B, 1998, 67, 683 CrossRef.
- P. Hannaford, Spectrochim. Acta, Part B, 1994, 49, 1581 CrossRef.
- K. Niemax, H. Groll and C. Schurer-Patshen, Spectrochim. Acta Rev., 1993, 15, 349 Search PubMed.
- T. Imasaka, Spectrochim. Acta Rev., 1993, 15, 329 Search PubMed.
- K. Niemax, A. Zybin, C. Schurer-Patschan and H. Groll, Anal. Chem., 1996, 68, 351A CAS.
- J. J. Scherer, J. B. Paul, A. O'Keefe and R. J. Saykally, Chem. Rev., 1997, 97, 25 CrossRef CAS.
- J. Ye, L.-S. Ma and J. L. Hall, J. Opt. Soc. Am., 1998, 15, 6 Search PubMed.
- R. E. Sturgeon, J. Anal. At. Spectrom., 1998, 13, 351 RSC.
- Squeezed and Nonclassical Light, ed. P. Tombesi and E. R. Pike, Plenum Press, New York, 1989. Search PubMed.
- E. S. Polzik, J. Carri and H. J. Kimble, Appl. Phys. B, 1992, 55, 279.
- V. Liger, A. Zybin, Y. Kuritsyn and K. Niemax, Spectrochim. Acta, Part B, 1997, 52, 1125 CrossRef.
- O. I. Matveev, N. Omenetto, B. W. Smith and J. D. Winefordner, unpublished data, University of Florida, Gainesville, FL, USA, 2000..
- A. Kastler, Appl. Opt., 1962, 1, 17 Search PubMed.
- J. D. Winefordner, G. A. Petrucci, C. L. Stevenson and B. W. Smith, J. Anal. At. Spectrom., 1994, 9, 131 RSC.
- L.-S. Ma and J. L. Hall, IEEE J. Quantum Electron., 1990, 26, 2006 CrossRef CAS.
- R. T. Jongma, G. H. Boogarts, I. Holleman and G. Meijer, Rev. Sci. Instrum., 1995, 66, 2821 CrossRef CAS.
- J. T. Hodges, J. P. Looney and R. D. van Zee, Appl. Opt., 1996, 35, 4112 Search PubMed.
- P. Zalicki and R. Zare, J. Chem. Phys., 1995, 102, 2708 CrossRef CAS.
- A. O'Keefe, Chem. Phys. Lett., 1998, 293, 331 CrossRef CAS.
- M. D. Levenson, B. A. Paldus, T. G. Spence, C. C. Harb, J. S. Harris, Jr. and R. N. Zare, Chem. Phys. Lett., 1998, 298, 1998.
- K. J. Schulz and W. R. Simpson, Chem. Phys. Lett., 1998, 297, 523 CrossRef CAS.
- E. Engeln, G. Berden, R. Peeters and G. Meijer, Rev. Sci. Instrum., 1998, 69, 3763 CrossRef CAS.
- R. D. van Zee, J. T. Hodgas and J. P. Looney, Appl. Opt., 1999, 38, 3951 Search PubMed.
- E. R. Crosson, P. Haar, G. A. Marcus and H. A. Schwettman, Rev. Sci. Instrum., 1999, 70, 4 CrossRef CAS.
- Mercury Analyzer RA-915+, Lumex, St. Petersburg, 1999. Search PubMed.
- A. F. Suchkov, Preprint 126, Physical Institute of USSR Academy of Science, Moscow, 1970. Search PubMed.
- C. F. Luk'yanenko, M. M. Makagon and L. N. Sinitsa, Intracavity Laser Spectroscopy, Nauka, Novosibirsk, 1985. Search PubMed.
- V. M. Baev, T. Latz and P. E. Toschek, Appl. Phys. B, in the press. Search PubMed.
- K.-J. Boller and T. Schroder, J. Opt. Soc. Am. B, 1993, 10, 1778 Search PubMed.
- J. Sierks, T. Latz, V. M. Baev and P. E. Toschek, Phys. Rev., 1998, 57, 2186 Search PubMed.
- G. C. Bjorklund, Opt. Lett., 1980, 5, 15 Search PubMed.
- J. Sierks, T. Latz, V. M. Baer and P. E. Toschek, paper presented at EQEC 96, European Electronics Conference, Hamburg, September 1996.
Footnote |
| † Presented at the 2000 Winter Conference on Plasma Spectrochemistry, Fort Lauderdale, FL, USA, January 10–15, 2000. |
| This journal is © The Royal Society of Chemistry 2000 |
