Cathodic dissolution in the electrocoagulation process using aluminium electrodes
Thibaut
Picard
*a,
Geneviève
Cathalifaud-Feuillade
a,
Michel
Mazet
a and
Colette
Vandensteendam
b
aLaboratoire des Sciences de L'Eau et l'Environnement, Parc d'Ester Technopôle, 87068, Limoges, France. E-mail: tpicard@ensil.unilim.fr
bLaboratoire de Chimie des Plasmas, Faculté des Sciences, av. Albert Thomas, 87060, Limoges, France
First published on 1st February 2000
Abstract
All the authors working with aluminium electrodes in the electrocoagulation process have shown that a dissolution occurs at the cathode. This result cannot be explained by the electrochemical process in which only the anodes should be dissolved. The most probable reaction is a chemical attack by hydroxyl ions (generated during water reduction) on the aluminium cathode but nobody has proved it in the framework of the electrocoagulation process. So we are interested in determining what kind of reactions occurs at the cathode. For that, we have elaborated a batch pilot apparatus divided into two compartments, allowing measurement of gas formation taking place only in one compartment. The gases measurements were performed by mass spectrometry with helium as carrier gas. To validate our experimental protocol, the first experiments have been done with a stainless steel cathode: in this case, the results have indicated that the amount of created hydrogen is in good agreement with the values calculated using the second Faraday's law. The experiments realised with an aluminium cathode have shown that the hydrogen formation, in these conditions, was higher than those observed with the stainless steel cathode. All our investigations enable us to propose that with an aluminium cathode, hydrogen formation can be separated into two phenomena. The first one is due to an electrochemical reaction (water reduction), and the second one arises from a chemical reaction explaining the dissolution observed at the cathode.
Introduction
Nowadays, to clarify an effluent containing organic and colloidal matter, a physicochemical process commonly called coagulation–flocculation is used in most cases. However, an alternative technique, which seems to be very efficient, has appeared in the last decade:1–6 electrocoagulation. This process consists in generating, in the effluent to be treated, some metallic ions by using the principle of soluble anodes (iron or aluminium). The major reactions likely to take place with aluminium electrodes are described as follows:at the anode, aluminium oxidation
 | (i) |
The aluminium ions can then react with the water:
 | (ii) |
at the cathode, water reduction:
 | (iii) |
Then, the flocs formed can be removed by settling6–8 or flotation.9–12 All the authors4,5,13–15 working with aluminium electrodes have observed that aluminium cathodes are dissolved and this phenomenon cannot be explained by the electrochemical process. Generally, the cathodes are supposed to be attacked by hydroxyl ions generated during water reduction (iii). The reaction written as follows:
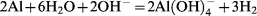 | (iv) |
For this purpose, we have compared the experimental amount of hydrogen created at the cathode with the theoretical amount calculated using the second Faraday's law:
Experimental procedures
All solutions were prepared with ultrapure water produced by a Millipore Helix system, with a resistivity higher than 15 MΩ cm, a concentration of TOC (total organic carbon) lower than 10 µg L−1, and a pH ranging between 5.5 and 6.0. All the products used were of analytical quality. The experiments were carried out at ambient temperature (20 ± 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) °C). As has been shown in previous studies,8,18,19 in the absence of halide ions it is very difficult to dissolve aluminium anodes because of the passivation of the electrodes. Moreover, in all industrial electrocoagulation units, there is always an addition of sodium chloride in order to limit the formation of the passivation layer and to increase the conductivity (so as to decrease the energy consumption). Therefore, our experiments were carried out with solutions containing sodium chloride. As our investigations concern a supposed chemical reaction, we used concentrated sodium chloride solutions (0.6 mol L−1) to limit the temperature variations (due to the Joule effect) which could be responsible for kinetic modifications for the reaction studied as described by Arrhenius law.
°C). As has been shown in previous studies,8,18,19 in the absence of halide ions it is very difficult to dissolve aluminium anodes because of the passivation of the electrodes. Moreover, in all industrial electrocoagulation units, there is always an addition of sodium chloride in order to limit the formation of the passivation layer and to increase the conductivity (so as to decrease the energy consumption). Therefore, our experiments were carried out with solutions containing sodium chloride. As our investigations concern a supposed chemical reaction, we used concentrated sodium chloride solutions (0.6 mol L−1) to limit the temperature variations (due to the Joule effect) which could be responsible for kinetic modifications for the reaction studied as described by Arrhenius law.
Batch electrocoagulation pilot cell and electrodes material
The electrodes are made of 5754 aluminium alloy, the composition of which (AFNOR NF EN 573-1) indicates that this alloy contains silicion (<0.40%), iron (<0.40%), copper (<0.10%), magnesium (from 2.6 to 3.6%), manganese (<0.50%), chromium (<0.30%), with aluminium constituting the remainder. We have retained this alloy because of its substantial use in industrial electrocoagulation units. To validate our experimental protocol concerning the gas measurements, we first used electrodes made of stainless steel (type 316). The batch electrocoagulation pilot apparatus, constructed following the work of Dobolyi20 (Fig. 1), consists of a Plexiglass electrolysis cell composed of two compartments each having a volume of 300 mL. | ||
| Fig. 1 Batch electrocoagulation pilot apparatus. | ||
Two vertical aluminium electrodes can be placed in parallel: the electrodes have a 3 mm thickness with an active surface (one face) of 45 cm2, their total surface being 128 cm2. In their lower part, a central opening (1 cm high, 3 cm broad) enables the provision of a stir per bar used for an agitation of solutions in each compartment. The gap between the electrodes is fixed at 21 mm. Between the two electrodes, a fibreglass filter (diameter 4.7 mm, porosity 1.2 µm) is inserted in the Plexiglas wall to avoid the migration of gases between the two compartments: the sealing of this diaphragm is ensured by positioning an O-ring. Both electrodes are connected to a dc generator supplying 10 A at 65 V. An airtight cover includes the electrical connections and two openings in each compartment, allowing a gaseous sweep used for the continuous analysis of generated gases.
Measurements of hydrogen
Measurements concerning the hydrogen formation were carried out by a mass spectrometer (Fisons Instruments, Gaslab 300). During an experiment, only hydrogen formed in one of the compartments was analysed . The gas (helium U) flow rate used is measured by an analogic mass debimeter. The mass spectrometer is connected to the output of the compartment by a bleed on the exit pipe using a capillary and the acquisition time varies from five to ten s.Before experiments, a calibration was carried out with a standard mixture containing 8.56% of hydrogen in helium. In our case, the recorded partial pressures of fragments of mass 2 and 4 were related to the volume composition of the standard. During an experiment, if a known amount of helium (0.9 L min−1) is flowed through the studied compartment, the ratio of the partial pressures of fragments 2 and 4 leads to the volume ratio H2∶He at the exit of the compartment. The helium flow rate being known with a good precision, the amount of hydrogen formed per time unit can be calculated. Because of its very low solubility in water, dissolved hydrogen has been neglected. Therefore, the following experimental protocol was used: 250 mL of solution were introduced in each compartment, the diaphragm and the electrodes were fitted and the solution stirred, after which increasing current intensities (from 1 A to 10 A) were imposed. Each intensity value was held until stabilisation of the mass spectrometer response occurred, then the current was switched off. When hydrogen was formed by a purely electrochemical reaction when the current was turned off, the mass spectrometer values merged with the base line. On the other hand, when a chemical reaction occurred, the values measured after the current was stopped indicated that the chemical reaction was proceeding. In both cases we began with an intensity of 1 A, and after stabilisation the current was turned off before increasing gradually the intensity value up to 10 A. The analysis of the results then allowed us to determine the average amount of gas formed per unit of time during the response stabilisation.
For all experiments, we used an aluminium anode: according to the experiments, the cathode was made of stainless steel or aluminium. The theoretical amount of hydrogen resulting from reaction (iii) was calculated according to the time of experiment and the current intensity using the second Faraday's law. The values obtained were compared with the experimental results of mass spectrometry measurements for a cathode of stainless steel and of aluminium.
Results and discussion
First, a stainless steel cathode was used to validate our experimental protocol because in this case the only reaction which could take place (under our conditions) was water reduction [reaction (iii)]. The observed amount of hydrogen created with this stainless steel cathode was compared with the theoretical amount calculated using the second Faraday's law. As explained previously, for measurements we have used concentrated sodium chloride solutions (0.6 mol L−1) and imposed current intensities between 1 and 10 A. An example of the results obtained for one experiment is presented Fig. 2.![Hydrogen formation for different current intensities (stainless steel cathode, [NaCl] = 0.6 mol L−1).](/image/article/2000/EM/a908248d/a908248d-f2.gif) | ||
| Fig. 2 Hydrogen formation for different current intensities (stainless steel cathode, [NaCl] = 0.6 mol L−1). | ||
We can see that, initially, the curve merges with the abscissa axis. Then, a 1 A current is imposed and we measure immediately the hydrogen formation (plate); when the current is switched off there is no more hydrogen formation. The same phenomenon can be observed for all the imposed intensities: the curve always merges with the abscissa axis. So, it has been proved that with a stainless steel cathode the hydrogen formation is due only to an electrochemical reaction.
Fig. 3 presents the comparison between the experimental amount of hydrogen created with a stainless steel cathode (average of six experiments) and Faraday's law. We note a perfect correlation between the obtained experimental results and the theory: therefore, we can consider that our experimental protocol is suitable.
 | ||
| Fig. 3 Experimental hydrogen formation versus current intensity for a stainless steel cathode correlated with Faraday's law. | ||
Next, we carried out the same experiments with an aluminium cathode. Fig. 4 presents an example of the results obtained.
![Hydrogen formation for different current intensities (aluminium cathode, [NaCl] = 0.6 mol L−1).](/image/article/2000/EM/a908248d/a908248d-f4.gif) | ||
| Fig. 4 Hydrogen formation for different current intensities (aluminium cathode, [NaCl] = 0.6 mol L−1). | ||
When comparing Figs. 2 and 4, we notice two major differences. First, for the same intensities, the amount of hydrogen created is higher with an aluminium cathode than with the stainless steel cathode. So, the total amount of hydrogen formed with an aluminium cathode is greater than that calculated using the second Faraday's law, as explained by,15–17 proving that hydrogen formation under our conditions is not solely due to an electrochemical reaction. Secondly, when the current is switched off, the curve does not merge with the abscissa axis but remains above it: the stabilised response observed in this case corresponds to a chemical reaction described by equation (iv).
According to these observations, it can be concluded that hydrogen formation in these conditions is due to two reactions: one is electrochemical [reaction (iii)] and the other is purely chemical because it occurs without current [reaction (iv)]. We have therefore defined each contribution to hydrogen formation with an aluminium cathode as follows:
| Intensity/A | Theoretical H2 formed calculated by Faraday's law/L min−1 | H2 (total) stainless steel cathode/L min−1 | H2 (total) aluminium cathode/L min−1 | H2 (electro.) aluminium cathode/L min−1 | H2 (chem.) aluminium cathode/L min−1 |
|---|---|---|---|---|---|
| 1 | 0.0070 | 0.0073 | 0.0123 | 0.0073 | 0.0050 |
| 2 | 0.0139 | 0.0142 | 0.0205 | 0.0140 | 0.0065 |
| 3 | 0.0209 | 0.0204 | 0.0316 | 0.0207 | 0.0109 |
| 5 | 0.0348 | 0.0338 | 0.0515 | 0.0343 | 0.0172 |
| 7 | 0.0488 | 0.0478 | 0.0775 | 0.0488 | 0.0287 |
| 8.5 | 0.0592 | 0.0589 | 0.0932 | 0.0582 | 0.0350 |
| 10 | 0.0697 | 0.0696 | 0.1208 | 0.0692 | 0.0517 |
The remaining problem is to know if the aluminium ions coming from this chemical reaction have the same efficiency as those coming from the anode and if they can react with the pollutants one wishes to remove.
Acknowledgements
The authors thank the Regional Council of the Limousin who sponsored our research concerning the electrocoagulation process.References
- R. Määtä and D. Tabakov, Aqua Fen., 1987, 17, 239 Search PubMed.
- B. Fleet, Solid/Liquid Separation: Waste Management and Productivity Enhancement, ed. H. S. Muralidhara, 1989, pp. 479–496. Search PubMed.
- J. Koren and U. Syversen, Filtr. Sep., 1995, 2, 153 CrossRef.
- M. J. Matteson, R. L. Dobson, R. W. Glenn, N. S. Kukunoor, W. H. Waits and E. J. Clayfield, Colloids Surf. A, 1995, 104, 101 CrossRef CAS.
- N. Mameri, A. Yeddou, H. Lounici, D. Belhocine, H. Grib and D. Bariou, Water Res., 1998, 32, 1604 CrossRef CAS.
- S. H. Lin, C. T. Shyu and M. C. Sun, Water Res., 1998, 32, 1059 CrossRef CAS.
- V. Y. Baklan, G. V. Radygin, S. N. Gonopol'skii, N. A. Shuster, A. I. Rukitskii, F. V. Markodei, V. F. Khitrich and T. I. Ponomarenko, Sov. J. Water Chem. Technol., 1994, 16, 334 Search PubMed.
- J. Szynkarczuk, J. Kan, T. A. Hassan and J. C. Donini, Clays Clay Miner., 1994, 42, 667 Search PubMed.
- D. Averisyan, A. S. Tarkhanyan and L. N. Safaryan, Sov. J. Water Chem. Technol., 1984, 6, 84 Search PubMed.
- I. A. Zolotukhin, Sov. J. Water Chem. Technol., 1989, 11, 147 Search PubMed.
- A. Y. Hosny, Filtr. Sep., 1992, 9, 419 CrossRef.
- M. F. Pouet and A. Grasmick, Water Sci. Technol., 1995, 31, 275 CrossRef CAS.
- E. A. Vik, D. A. Carlson, A. S. Eikum and E. T. Gjessing, Water Res., 1984, 18, 1355 CrossRef CAS.
- C. Radovan, I. Vlaicu, G. A. Ciorba and M. Adam-Stoia, Proc. Electrochem. Soc., 1998, 97, 427 Search PubMed.
- V. I. Przhegorlinskii, A. I. Ivanishvili and V. D. Grebenyuk, Sov. J. Water Chem. Technol., 1987, 9, 181 Search PubMed.
- L. Antropov, Electrochimie Théorique, Mir, Moscow, Russia, 1981. Search PubMed.
- J. C. Donini, J. Kan, J. Szynkarczuk, T. A. Hassan and K. L. Kar, Can. J. Chem. Eng., 1994, 72, 1007 Search PubMed.
- T. Picard G. Cathalifaud M. Mazet, Environ. Technol., submitted for publication. Search PubMed.
- J. Jiaqian, Water Treat., 1988, 3, 344 Search PubMed.
- E. Dobolyi, Water Res., 1978, 12, 1113 CrossRef CAS.
- D. Landolt, Traité des Matériaux: Corrosion et Chimie de Surface des Métaux, Presse Polytechniques et Universitaires Romandes, 1993. Search PubMed.
- C. Vargel, Corrosion de l'Aluminium, Dunod, 1999. Search PubMed.
| This journal is © The Royal Society of Chemistry 2000 |


