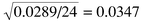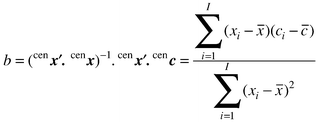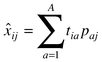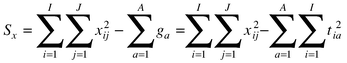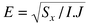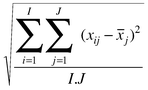Introduction to multivariate calibration in analytical chemistry

Contents

• 1 Introduction
  • 1.1 Overview
  • 1.2 Case study 1
  • 1.3  Case study 2

• 2  Calibration methods
  • 2.1  Univariate calibration
  • 2.2  Multiple linear regression
  • 2.3  Principal components regression
  • 2.4  Partial least squares
  • 2.5  Multiway methods

• 3  Model validation
  • 3.1  Autoprediction
  • 3.2  Cross-validation
  • 3.3  Independent test sets
  • 3.4  Experimental designs

• 4  Conclusions and discussion

• Acknowledgements

• Appendices
  • A1 Vectors and matrices
  • A2 Algorithms

• References

Richard G. Brereton

Richard Brereton performed his undergraduate, postgraduate and postdoctoral studies in the University of Cambridge, and moved to Bristol in 1983, where he is now a Reader. He has published 169 articles, 85 of which are refereed papers, and his work has been cited over 1100 times. He has presented over 50 public invited lectures. He is currently chemometrics columnist for the webzine the Alchemist. He is author of one text, and editor of three others. His interests encompass multivariate curve resolution, calibration, experimental design and pattern recognition, primarily in the area of coupled chromatography, as applied to a wide variety of problems including pharmaceutical impurity monitoring, rapid reaction kinetics, food and biological chemistry.

---

1 Introduction

1.1 Overview

Multivariate calibration has historically been a major cornerstone of chemometrics as applied to analytical chemistry. However, there are a large number of diverse schools of thought. To some, most of chemometrics involves multivariate calibration. Certain Scandinavian and North American groups have based much of their development over the past two decades primarily on applications of the partial least squares (PLS) algorithm. At the same time, the classic text by Massart and co-workers¹ does not mention PLS, and multivariate calibration is viewed by some only as one of a large battery of approaches to the interpretation of analytical data. In Scandinavia, many use PLS for almost all regression problems (whether appropriate or otherwise) whereas related methods such as multiple linear regression (MLR) are more widely used by mainstream statisticians.

There has developed a mystique surrounding PLS, a technique with its own terminology, conferences and establishment. Although originally developed within the area of economics, most of its prominent proponents are chemists. There are a number of commercial packages on the market-place that perform PLS calibration and result in a variety of diagnostic statistics. It is, though, important to understand that a major historic (and economic) driving force was near infrared spectroscopy (NIR), primarily in the food industry and in process analytical chemistry. Each type of spectroscopy and chromatography has its own features and problems, so much software was developed to tackle specific situations which may not necessarily be very applicable to other techniques such as chromatography or NMR or MS. In many statistical circles NIR and chemometrics are almost inseparably intertwined. However, other more modern techniques are emerging even in process analysis, so it is not at all certain that the heavy investment on the use of PLS in NIR will be so beneficial in the future. Despite this, chemometric approaches to calibration have very wide potential applicability throughout all areas of quantitative analytical chemistry.

There are very many circumstances in which multivariate calibration methods are appropriate. The difficulty is that to develop a very robust set of data analytical techniques for a particular situation takes a large investment in resources and time, so the applications of multivariate calibration in some areas of science are much less well established than in others. It is important to distinguish the methodology that has built up around a small number of spectroscopic methods such as NIR, from the general principles applicable throughout analytical chemistry. This article will concentrate on the latter. There are probably several hundred favourite diagnostics available to the professional user of PLS e.g. in NIR spectroscopy, yet each one has been developed with a specific technique or problem in mind, and are not necessarily generally applicable to all calibration problems. The untrained user may become confused by these statistics; indeed he or she may have access to only one specific piece of software and assume that the methods incorporated into that package are fairly general or well known, and may even inappropriately apply diagnostics that are not relevant to a particular application.

There are a whole series of problems in analytical chemistry for which multivariate calibration is appropriate, but each is very different in nature.

1. The simplest is calibration of the concentration of a single compound using a spectroscopic or chromatographic method, an example being determining the concentration of chlorophyll by EAS (electronic absorption spectroscopy).² Instead of using one wavelength (as is conventional for the determination of molar absorptivity or extinction coefficients), multivariate calibration involves using all or several of the wavelengths.

2. A more complex situation is a multi-component mixture where all pure standards are available, such as a mixture of four pharmaceuticals.³ It is possible to control the concentration of the reference compounds, so that a number of carefully designed mixtures can be produced in the laboratory. Sometimes the aim is to see whether a spectrum of a mixture can be employed to determine individual concentrations, and, if so, how reliably. The aim may be to replace a slow and expensive chromatographic method by a rapid spectroscopic approach. Another rather different aim might be impurity monitoring,⁴ how well the concentration of a small impurity may be determined, for example, buried within a large chromatographic peak.

3. A different approach is required if only the concentration of a portion of the components is known in a mixture, for example, the polyaromatic hydrocarbons within coal tar pitch volatiles.⁵ In the natural samples there may be tens or hundreds of unknowns, but only a few can be quantified and calibrated. The unknown interferents cannot necessarily be determined and it is not possible to design a set of samples in the laboratory containing all the potential components in real samples. Multivariate calibration is effective provided that the range of samples used to develop the model is sufficiently representative of all future samples in the field. If it is not, the predictions from multivariate calibration could be dangerously inaccurate. In order to protect against samples not belonging to the original dataset, a number of approaches for determination of outliers have been developed.

4. A final case is where the aim of calibration is not so much to determine the concentration of a particular compound but a group of compounds, for example protein in wheat.⁶ The criteria here become fairly statistical and the methods will only work if a sufficiently large and adequate set of samples are available. However, in food chemistry if the supplier of a product comes from a known source that is unlikely to change, it is often adequate to set up a calibration model on this training set.

There are many pitfalls in the use of calibration models, perhaps the most serious being variability in instrument performance over time. Each instrument has different characteristics and on each day and even hour the response can vary. How serious this is for the stability of the calibration model needs to be assessed before investing a large effort. Sometimes it is necessary to reform the calibration model on a regular basis, by running a standard set of samples, possibly on a daily or weekly basis. In other cases multivariate calibration gives only a rough prediction, but if the quality of a product or the concentration of a pollutant appears to exceed a certain limit, then other more detailed approaches can be used to investigate the sample. For example, on-line calibration in NIR can be used for screening a manufactured sample, and any dubious batches investigated in more detail using chromatography.

There are many excellent articles and books on multivariate calibration which provide greater details about the algorithms.^7–14 This article will compare the basic methods, illustrated by case studies, and will also discuss more recent developments such as multiway calibration and experimental design of the training set. There are numerous software packages available, including Piroutte,¹⁵ Unscrambler,¹⁶ SIMCA¹⁷ and Matlab Toolkit¹⁸ depending on the user’s experience. However, many of these packages contain a large number of statistics that may not necessarily be relevant to a particular problem, and sometimes force the user into a particular mode of thought. For the more computer based chemometricians, using Matlab for developing applications allows a greater degree of flexibility. It is important to recognise that the basic algorithms for multivariate calibration are, in fact, extremely simple, and can easily be implemented in most environments, such as Excel, Visual Basic or C.

1.2 Case study 1

The first and main case study for this application is of the electronic absorption spectra (EAS) of ten polyaromatic hydrocarbons (PAHs). Table 1 is of the concentrations of these PAHs in 25 spectra (dataset A) recorded at 1 nm intervals between 220 and 350 nm, forming a matrix which is often presented as having 25 rows (individual spectra) and 131 columns (individual wavelengths). The spectra are available as Electronic Supplementary Information (ESI Table S1†). The aim is to determine the concentration of an individual PAH in the mixture spectra.

Table 1 Concentrations of polyarenes in dataset A for case study 1^a

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
a Abbreviations for PAHs: Py = pyrene; Ace = acenaphthene; Anth = anthracene; Acy = acenaphthylene; Chry = chrysene; Benz = benzanthracene; Fluora = fluoranthene; Fluore = fluorene; Nap = naphthalene; Phen = phenanthrene.
1	0.456	0.120	0.168	0.120	0.336	1.620	0.120	0.600	0.120	0.564
2	0.456	0.040	0.280	0.200	0.448	2.700	0.120	0.400	0.160	0.752
3	0.152	0.200	0.280	0.160	0.560	1.620	0.080	0.800	0.160	0.118
4	0.760	0.200	0.224	0.200	0.336	1.080	0.160	0.800	0.040	0.752
5	0.760	0.160	0.280	0.120	0.224	2.160	0.160	0.200	0.160	0.564
6	0.608	0.200	0.168	0.080	0.448	2.160	0.040	0.800	0.120	0.940
7	0.760	0.120	0.112	0.160	0.448	0.540	0.160	0.600	0.200	0.118
8	0.456	0.080	0.224	0.160	0.112	2.160	0.120	1.000	0.040	0.118
9	0.304	0.160	0.224	0.040	0.448	1.620	0.200	0.200	0.040	0.376
10	0.608	0.160	0.056	0.160	0.336	2.700	0.040	0.200	0.080	0.118
11	0.608	0.040	0.224	0.120	0.560	0.540	0.040	0.400	0.040	0.564
12	0.152	0.160	0.168	0.200	0.112	0.540	0.080	0.200	0.120	0.752
13	0.608	0.120	0.280	0.040	0.112	1.080	0.040	0.600	0.160	0.376
14	0.456	0.200	0.056	0.040	0.224	0.540	0.120	0.800	0.080	0.376
15	0.760	0.040	0.056	0.080	0.112	1.620	0.160	0.400	0.080	0.940
16	0.152	0.040	0.112	0.040	0.336	2.160	0.080	0.400	0.200	0.376
17	0.152	0.080	0.056	0.120	0.448	1.080	0.080	1.000	0.080	0.564
18	0.304	0.040	0.168	0.160	0.224	1.080	0.200	0.400	0.120	0.118
19	0.152	0.120	0.224	0.080	0.224	2.700	0.080	0.600	0.040	0.940
20	0.456	0.160	0.112	0.080	0.560	1.080	0.120	0.200	0.200	0.940
21	0.608	0.080	0.112	0.200	0.224	1.620	0.040	1.000	0.200	0.752
22	0.304	0.080	0.280	0.080	0.336	0.540	0.200	1.000	0.160	0.940
23	0.304	0.200	0.112	0.120	0.112	2.700	0.200	0.800	0.200	0.564
24	0.760	0.080	0.168	0.040	0.560	2.700	0.160	1.000	0.120	0.376
25	0.304	0.120	0.056	0.200	0.560	2.160	0.200	0.600	0.080	0.752

---

A second dataset consisting of another 25 spectra, whose concentrations are given in Table 2, will also be employed where necessary (dataset B). The full data are available as Electronic Supplementary Information (ESI Table S2†). Most calibration will be performed on dataset A.

Table 2 Concentration of the polyarenes in the dataset B for case study 1

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
1	0.456	0.120	0.168	0.120	0.336	1.620	0.120	0.600	0.120	0.564
2	0.456	0.040	0.224	0.160	0.560	2.160	0.120	1.000	0.040	0.188
3	0.152	0.160	0.224	0.200	0.448	1.620	0.200	0.200	0.040	0.376
4	0.608	0.160	0.280	0.160	0.336	2.700	0.040	0.200	0.080	0.188
5	0.608	0.200	0.224	0.120	0.560	0.540	0.040	0.400	0.040	0.564
6	0.760	0.160	0.168	0.200	0.112	0.540	0.080	0.200	0.120	0.376
7	0.608	0.120	0.280	0.040	0.112	1.080	0.040	0.600	0.080	0.940
8	0.456	0.200	0.056	0.040	0.224	0.540	0.120	0.400	0.200	0.940
9	0.760	0.040	0.056	0.080	0.112	1.620	0.080	1.000	0.200	0.752
10	0.152	0.040	0.112	0.040	0.336	1.080	0.200	1.000	0.160	0.940
11	0.152	0.080	0.056	0.120	0.224	2.700	0.200	0.800	0.200	0.564
12	0.304	0.040	0.168	0.080	0.560	2.700	0.160	1.000	0.120	0.752
13	0.152	0.120	0.112	0.200	0.560	2.160	0.200	0.600	0.160	0.376
14	0.456	0.080	0.280	0.200	0.448	2.700	0.120	0.800	0.080	0.376
15	0.304	0.200	0.280	0.160	0.560	1.620	0.160	0.400	0.080	0.188
16	0.760	0.200	0.224	0.200	0.336	2.160	0.080	0.400	0.040	0.376
17	0.760	0.160	0.280	0.120	0.448	1.080	0.080	0.200	0.080	0.564
18	0.608	0.200	0.168	0.160	0.224	1.080	0.040	0.400	0.120	0.188
19	0.760	0.120	0.224	0.080	0.224	0.540	0.080	0.600	0.040	0.752
20	0.456	0.160	0.112	0.080	0.112	1.080	0.120	0.200	0.160	0.752
21	0.608	0.080	0.112	0.040	0.224	1.620	0.040	0.800	0.160	0.940
22	0.304	0.080	0.056	0.080	0.336	0.540	0.160	0.800	0.200	0.752
23	0.304	0.040	0.112	0.120	0.112	2.160	0.160	1.000	0.160	0.564
24	0.152	0.080	0.168	0.040	0.448	2.160	0.200	0.800	0.120	0.940
25	0.304	0.120	0.056	0.160	0.448	2.700	0.160	0.600	0.200	0.188

---

1.3  Case study 2

The second case study is of two-way diode array detector (DAD) HPLC data of a small embedded peak, that of 3-hydroxypyridine, buried within a major peak (2-hydroxypyridine). The concentration of the embedded peak varies between 1 and 5% of the 2-hydroxypyridine, and a series of 14 chromatograms (including replicates) are recorded whose concentrations are given in Table 3.

Table 3 Concentrations of 3-hydroxypyridine in the chromatograms of case study 2

Sample	Conc./mM
1	0.0158
2	0.0158
3	0.0315
4	0.0315
5	0.0315
6	0.0473
7	0.0473
8	0.0473
9	0.0473
10	0.0631
11	0.0631
12	0.0631
13	0.0789
14	0.0789

---

The chromatogram was sampled every 1 s, and a 40 s portion of each chromatogram was selected to contain the peak cluster, and aligned to the major peak maximum. Fifty-one wavelengths between 230 and 350 nm (sampled at 2.4 nm intervals) were recorded. Hence a dataset of dimensions 14 × 40 × 51 was obtained, the aim being to use multimode calibration to determine the concentration of the minor component. Further experimental details are reported elsewhere.⁴

The dataset is available in ESI Table S3†. It is arranged so that each column corresponds to a wavelength and there are 14 successive blocks, each of 40 rows (corresponding to successive points in time). Horizontal lines are used to divide each block for clarity. The chromatograms have been aligned.

2  Calibration methods

We will illustrate the methods of Sections 2.1–2.4 with dataset A of case study 1, and the methods of Section 2.5 with case study 2.

2.1  Univariate calibration

2.1.1  Classical calibration. There is a huge literature on univariate calibration.^19–23 One of the simplest problems is to determine the concentration of a single compound using the response of a single detector, for example a single spectroscopic wavelength or a chromatographic peak area.

Mathematically a series of experiments can be performed to give

x ≈ c.s

where, in the simplest case, x is a vector consisting of absorbances at one wavelength for a number of samples (or the response), and c is of the corresponding concentrations. Both vectors have length I, equal to the number of samples. The scalar s relates these parameters and is determined by the experiments.

A simple method for solving this equation is as follows:

c′ .x ≈ c′.c .s

so

(c′.c)⁻¹.c′. x ≈ (c′.c)⁻¹. (c′.c).s

or
where the ′ is the transpose as described in Appendix A1.

Many conventional texts use summations rather than matrices for determination of regression equations, but both approaches are equivalent. In Fig. 1, the absorbance of the spectra of case study 1A at 336 nm is plotted against the concentration of pyrene (Table 1). The graph is approximately linear, and provides a best fit slope calculated by

so that x̂ = 0.291 ĉ. Note the hat (^) symbol which indicates a prediction. The results are presented in Table 4.

Fig. 1 Absorption at 336 nm against concentration of pyrene.

Table 4 Results of regression of the concentration of pyrene (mg L⁻¹) against the intensity of absorbance at 336 nm

Concentration	Absorbance	Predicted absorbance	Residual
0.456	0.161	0.133	0.028
0.456	0.176	0.133	0.043
0.152	0.102	0.044	0.058
0.760	0.184	0.221	−0.037
0.760	0.231	0.221	0.010
0.608	0.171	0.176	−0.006
0.760	0.183	0.221	−0.039
0.456	0.160	0.133	0.027
0.304	0.126	0.088	0.038
0.608	0.186	0.177	0.009
0.608	0.146	0.177	−0.031
0.152	0.064	0.044	0.020
0.608	0.139	0.177	−0.038
0.456	0.110	0.133	−0.023
0.760	0.202	0.221	−0.019
0.152	0.087	0.044	0.043
0.152	0.076	0.044	0.032
0.304	0.104	0.088	0.016
0.152	0.120	0.044	0.076
0.456	0.125	0.133	−0.008
0.608	0.173	0.177	−0.004
0.304	0.092	0.088	0.004
0.304	0.135	0.088	0.046
0.760	0.212	0.221	−0.009
0.304	0.142	0.088	0.054

---

The quality of prediction can be determined by the residuals (or errors) i.e. the difference between the observed and predicted, i.e.x − x̂; the less this is the better. Generally the root mean error is calculated,

where d is called the degrees of freedom. In the case of univariate calibration this equals the number of observations (N) minus the number of parameters in the model (P) or in this case, 25 − 1 = 24, so that
This error can be represented as a percentage of the mean E_% = 100 (E/x̄) = 24.1% in this case. It is always useful to check the original graph (Fig. 1) just to be sure, which appears a reasonable answer. Note that classical calibration is slightly illogical in analytical chemistry. The aim of calibration is to determine concentrations from spectral intensities, and not vice versa yet the calibration equation in this section involves fitting a model to determine a peak height from a known concentration.

For a new or unknown sample, the concentration can be estimated (approximately) by using the inverse of the slope or

ĉ = 3.44 x

The spectrum of pure pyrene is given in Fig. 2, superimposed over the spectra of the other compounds in the mixture. It can be seen that the wavelength chosen largely represents pyrene, so a reasonable model can be obtained by univariate methods. For most of the other compounds in the mixtures this is not possible, so a much poorer fit to the data would be obtained.

Fig. 2 Spectrum of pyrene superimposed over the spectra of the other pure PAHs.

2.1.2  Inverse calibration. Although classical calibration is widely used, it is not always the most appropriate approach in analytical chemistry, for two main reasons. First, the ultimate aim is usually to predict the concentration (or factor) from the spectrum or chromatogram (response) rather than vice versa. There is a great deal of technical discussion of the philosophy behind different calibration methods, but in other areas of chemistry the reverse may be true, for example, can a response (e.g. a synthetic yield) be predicted from the values of the independent factors (e.g. temperature and pH)? The second relates to error distributions. The errors in the response are often due to instrumental performance. Over the years, instruments have become more reliable. The independent variable (often concentration) is usually determined by weighings, dilutions and so on, and is often the largest source of error. The quality of volumetric flasks, syringes and so on has not improved dramatically over the years. Classical calibration fits a model so that all errors are in the response [Fig. 3(a)], whereas with improved instrumental performance, a more appropriate assumption is that errors are primarily in the measurement of concentration [Fig. 3(b)].

Fig. 3 Errors in (a) Classical and (b) Inverse calibration.

Calibration can be performed by the inverse method where

c ≈ x.b

or
giving for this example, ĉ= 3.262 x. Note that b is only approximately the inverse of s (see above), because each model makes different assumptions about error distributions. However, for good data, both models should provide fairly similar predictions, if not there could be some other factor that influences the data, such as an intercept, non-linearities, outliers or unexpected noise distributions. For heteroscedastic noise distributions²⁴ there are a variety of enhancements to linear calibration. However, these are rarely taken into consideration when extending the principles to the multivariate calibration.

Most chemometricians prefer inverse methods, but most traditional analytical chemistry texts introduce the classical approach to calibration. It is important to recognise that there are substantial differences in terminology in the literature, the most common problem being the distinction between ‘x’ and ‘y’ variables. In many areas of analytical chemistry, concentration is denoted by ‘x’, the response (such as a spectroscopic peak height) by ‘y’. However, most workers in the area of multivariate calibration have first been introduced to regression methods via spectroscopy or chromatography whereby the experimental data matrix is denoted as ‘X’, and the concentrations or predicted variables by ‘y’. In this paper we indicate the experimentally observed responses by ‘x’ such as spectroscopic absorbances of chromatographic peak areas, but do not use ‘y’ in order to avoid confusion.

2.1.3  Including the intercept. In many situations it is appropriate to include extra terms in the calibration model. Most commonly an intercept (or baseline) term is included to give an inverse model of the form

c ≈ b₀+ b₁x

which can be expressed in matrix/vector notation by

c ≈ X . b

for inverse calibration where c is a column vector of concentrations and b is a column vector consisting of two numbers, the first equal to b₀ (the intercept) and the second to b₁ (the slope). X is now a matrix of two columns, the first of which is a column of 1’s, the second the spectroscopic readings, as presented in Table 5.

Table 5 X matrix for example of Section 2.1.3

1	0.456
1	0.456
1	0.152
1	0.760
1	0.760
1	0.608
1	0.760
1	0.456
1	0.304
1	0.608
1	0.608
1	0.152
1	0.608
1	0.456
1	0.760
1	0.152
1	0.152
1	0.304
1	0.152
1	0.456
1	0.608
1	0.304
1	0.304
1	0.760
1	0.304

---

Exactly the same principles can be employed for calculating the coefficients as in Section 2.1.2, but in this case b is a vector rather than scalar, and X is a matrix rather than a vector so that

b = (X′.X)⁻¹.X′ . c

or

ĉ = −0.178 + 4.391 x

Note that the coefficients are different from those of Section 2.1.2. One reason is that there are still a number of interferents, from the other PAHs, in the spectrum at 336 nm, and these are modelled partly by the intercept term. The models of Sections 2.1.1 and 2.1.2 force the best fit straight line to pass through the origin. A better fit can be obtained if this condition is not required.

The predicted concentrations are easy to obtain, the easiest approach involving the use of matrix-based methods, so that

ĉ = X.b

the root mean square error being given by
representing an E_% of 23.3%. Notice that, strictly speaking, the error term is divided by 23 (number of degrees of freedom rather than 25) to reflect the two parameters used in the model.

An alternative, and common, method for including the intercept is to mean centre both the x and the c variables to fit the equation

c − c̄ = (x − x̄)b

or

^cenc = ^cenx b

or
It is easy to show algebraically that the value of b is identical with b₁ obtained for the uncentred data (=4.391 in this example), but includes the intercept, whereas the old value of b₀ is given by (c̄ −b₁x̄), so the two methods are related. It is common to centre both sets of variables for this reason, the calculations being mathematically simpler than including an intercept term. Note that the concentrations must be centred at the same time as the response, and the predictions are of the concentrations minus their mean.

It should be pointed out that the predictions for both methods described in this section differ from those obtained for the uncentred data. It is also useful to realise that it is also possible to use an intercept in models obtained using classical calibration; the details have been omitted in this section for brevity.

2.2  Multiple linear regression

2.2.1  Multidetector advantage. Multiple linear regression (MLR) is an extension when more than one detector response is employed. There are two principal reasons for this. The first is that there may be more than one component in a mixture. Under such circumstances it is advisable to employ more than one response (the exception being if the concentrations of some of the components are known to be correlated). For N components, at least N wavelengths must be used. The second is that each detector contains some information. Some individual wavelengths in a spectrum may be influenced by noise or unknown interferents. Using, for example, 100 wavelengths averages out the information, and will often provide a better result than relying on a single wavelength.

2.2.2  Multiwavelength equations. In certain applications, equations can be developed that are used to predict the concentrations of compounds by monitoring at a finite number of wavelengths. A classical area is in pigment analysis by electronic absorption spectroscopy, especially in the area of chlorophyll chemistry.²⁵ In order to determine the concentration of four pigments in a mixture, investigators recommend monitoring at four different wavelengths, and use an equation that links absorbance at each wavelength to concentration.

In case study 1, only certain compounds absorb above 330 nm, the main ones being pyrene, fluoranthene, acenaphthylene and benzanthracene (note that the small absorbance due to a fifth component may be regarded as an interferent, although including this in the model will, of course, result in better predictions). It is possible to choose four wavelengths, preferably ones in which the absorbance ratios of these four compounds differ. In Fig. 4, the wavelengths 331, 335, 341 and 349 nm are indicated, and chosen for calibration.

Fig. 4 Spectra of pyrene, fluoranthene, acenaphthalene and benzo[a])anthracene between 330 and 350 nm with 331, 335, 341 and 349 nm indicated.

Calibration equations can be obtained, as follows, using inverse methods. First, select the absorbances of the 25 spectra at these four wavelengths to give an X matrix with four columns and 25 rows. Second, obtain the corresponding C matrix consisting of the relevant concentrations (Table 6). The aim is to find coefficients B relating X and C by

C ≈ X . B

where B is a 4 × 4 matrix, each column representing a compound and each row a wavelength. This equation can be solved using regression methods of Section 2.1.2, changing vectors and scalars to matrices, so that

B = (X′.X)⁻¹.X′ .C

giving the matrix in Table 6. These could be expressed in equation form if required, for example, the first column of B suggests that

estimated [pyrene] = −1.827 A₃₃₁ + 7.512 A₃₃₅ −6.094 A₃₄₁ + 2.355 A₃₄₉

In UV/VIS spectroscopy of pigments, for example, these type of equations are very common.

Table 6 Matrices X, C, B and Ĉ for Section 2.2.2

C				X
331	335	341	349	Py	Ace	Benz	Fluora
0.138	0.165	0.102	0.058	0.456	0.120	1.620	0.120
0.154	0.178	0.133	0.078	0.456	0.040	2.700	0.120
0.093	0.102	0.087	0.053	0.152	0.200	1.620	0.080
0.152	0.191	0.093	0.046	0.760	0.200	1.080	0.160
0.191	0.239	0.131	0.073	0.760	0.160	2.160	0.160
0.148	0.178	0.105	0.056	0.608	0.200	2.160	0.040
0.149	0.193	0.074	0.029	0.760	0.120	0.540	0.160
0.137	0.164	0.105	0.057	0.456	0.080	2.160	0.120
0.107	0.129	0.093	0.057	0.304	0.160	1.620	0.200
0.168	0.193	0.124	0.067	0.608	0.160	2.700	0.040
0.119	0.154	0.058	0.021	0.608	0.040	0.540	0.040
0.06	0.065	0.049	0.028	0.152	0.160	0.540	0.080
0.112	0.144	0.067	0.033	0.608	0.120	1.080	0.040
0.093	0.114	0.056	0.034	0.456	0.200	0.540	0.120
0.169	0.211	0.1	0.052	0.760	0.040	1.620	0.160
0.082	0.087	0.081	0.054	0.152	0.040	2.160	0.080
0.071	0.077	0.059	0.037	0.152	0.080	1.080	0.080
0.084	0.106	0.066	0.037	0.304	0.040	1.080	0.200
0.113	0.119	0.115	0.078	0.152	0.120	2.700	0.080
0.106	0.13	0.073	0.042	0.456	0.160	1.080	0.120
0.151	0.182	0.091	0.043	0.608	0.080	1.620	0.040
0.08	0.095	0.056	0.035	0.304	0.080	0.540	0.200
0.128	0.138	0.114	0.071	0.304	0.200	2.700	0.200
0.177	0.219	0.132	0.078	0.760	0.080	2.700	0.160
0.133	0.147	0.109	0.066	0.304	0.120	2.160	0.200

---

B
Py	Ace	Benz	Fluora
331	−1.827	5.950	−0.591		−1.741
335	7.512	−3.105	−11.209		2.785
341	−6.094	−4.061	48.280		−6.409
349	2.355	3.972	−19.343		9.734

---

		Ĉ
Py	Ace	Benz	Fluora
0.502	0.125	1.872	0.130
0.429	0.133	2.826	0.134
0.191	0.094	1.977	0.080
0.699	0.116	1.370	0.119
0.820	0.152	2.121	0.204
0.559	0.124	1.904	0.110
0.795	0.102	0.760	0.086
0.476	0.106	2.048	0.100
0.341	0.085	1.878	0.132
0.545	0.163	2.428	0.102
0.635	0.078	0.598	0.054
0.146	0.067	1.060	0.035
0.547	0.078	0.916	0.098
0.425	0.107	0.713	0.128
0.789	0.151	1.357	0.159
0.137	0.103	1.843	0.106
0.176	0.091	1.228	0.073
0.328	0.050	1.233	0.086
0.170	0.146	2.643	0.157
0.437	0.097	1.192	0.118
0.638	0.135	1.433	0.079
0.309	0.093	0.915	0.107
0.275	0.152	2.508	0.122
0.701	0.147	2.305	0.215
0.352	0.154	2.260	0.122

---

An estimated concentration matrix can be obtained by

Ĉ = X . B

as indicated in Table 6. For pyrene, the root mean square error of prediction is given by
(note that the divisor is 21 not 25 as four degrees of freedom are lost because there are four compounds in the model), equal to 0.042 or 9.34%, of the average concentration of pyrene, a significant improvement over the univariate model. Even further improvement could be obtained by including the intercept (usually performed by centring the data) and including the concentrations of more compounds.

It is possible also to employ classical methods. For the single detector, single wavelength model of Section 2.1.1

ĉ = x/s

where s is a scalar, and xand care vectors corresponding to the concentrations and absorbances for each of the N samples. Where there are several components in the mixture, this becomes

Ĉ = X̂.S′.(S.S′)⁻¹

and the trick is to estimate S which can be done in one of two ways:(a) by knowledge of the true spectra; and(b) by regression since C . S ≈ X, so Ŝ = (C′.C)⁻¹C′.X.  Note that

B ≈ Ŝ′. (Ŝ.Ŝ′)⁻¹

However, as in univariate calibration, the coefficients obtained using both approaches may not be exactly equal, both methods making different assumptions about error distributions.

Such equations make assumptions that the main analytes are all known, and work well only if this is true. Applying to mixtures where there are unknown interferents can result in serious estimation errors.

2.2.3  Multivariate approaches. The methods of Section 2.2.2 could be extended to all ten PAHs in the dataset of case study 1, and with appropriate choice of ten wavelengths may give reasonable estimates of concentrations. However, all the original wavelengths contain some information and there is no reason why most of the spectrum cannot be employed.

There is a fairly confusing literature on the use of multiple linear regression for calibration in chemometrics, primarily because many workers present their arguments in a very formalised manner. However, the choice and applicability of method depends on three main factors:(1) the number of compounds in the mixture (ten in this case) or responses to be estimated; (2) the number of experiments (25 in this case) often spectra or chromatograms; and (3) the number of detectors (131 wavelengths in this case).

In order to have a sensible model, the number of compounds must be less than or equal to the smaller of the number of experiments or number of detectors. In certain specialised cases this limitation can be infringed if it is known that there are correlations between the concentrations of different compounds. This may happen, for example, in environmental chemistry where there could be tens or hundreds of compounds in a sample, but the presence of one (e.g. a homologous series) suggests the presence of another, so, in practice there are only a few independent factors or groups of compounds. Also, correlations can be built into the design of a training set as discussed in Section 3.4. In most real-world situations there definitely will be correlations in complex multicomponent mixtures. However, the methods described below are for the case where the number of compounds is smaller than the number of experiments or number of detectors, for reasons described above.

The X data matrix is ideally related to the concentration and spectral matrices by

X = C . S

where X is a 25 × 131 matrix, C a 25 × 10 matrix and S a 10 × 131 matrix in the example discussed here. In calibration it is assumed that a series of experiments are performed in which C is known (e.g. a set of mixtures of compounds with known concentrations are recorded spectroscopically). An estimate of S can then be obtained by

Ŝ = (C′.C)⁻¹.C.X

and then the concentrations can be predicted

Ĉ = (X.Ŝ.′(Ŝ.Ŝ′)⁻¹

Unless the number of wavelengths or experiments are exactly equal to the number of compounds, the prediction will not exactly model the data. This approach works because the matrices (C′.C) and (Ŝ.Ŝ′) are square matrices whose dimensions equal the number of compounds in the mixture (10 × 10) and have inverses, provided that the experiments have been suitably designed and the concentrations of the compounds are not correlated. The predicted concentrations, using this approach, are given in Table 7, together with the percentage root mean square prediction error: note there are only 15 degrees of freedom (=25 experiments − 10 compounds). Had the data been centred the number of degrees of freedom would be reduced further. The predicted concentrations are acceptable for most compounds apart from acenaphthylene. The predicted spectra are presented in Fig. 5, and are not nearly so clear. In fact it would be remarkable that for such a complex mixture it is possible to reconstruct ten spectra well, given that there is a great deal of overlap. Pyrene, which is indicated in bold, exhibits most of the main peak maxima of the known pure data (compare with Fig. 1). Often, other knowledge of the system is required to produce better reconstructions of individual spectra. The reason why concentration predictions work significantly better than spectral reconstruction is that, for most compounds, there are characteristic regions of the spectrum where there are prominent features. These parts of the spectra for individual compounds will be predicted well, and will disproportionately influence the effectiveness of the method for determining concentrations.

Table 7 Predicted values of concentrations using multiple linear regression as indicated in Section 2.3.1

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
1	0.485	0.110	0.178	0.154	0.374	1.653	0.157	0.536	0.107	0.511
2	0.411	0.028	0.325	0.133	0.495	2.726	0.152	0.373	0.137	0.620
3	0.178	0.158	0.274	0.220	0.546	1.668	0.057	0.860	0.164	0.205
4	0.699	0.177	0.241	0.150	0.362	1.107	0.124	0.730	0.031	0.690
5	0.819	0.140	0.287	0.158	0.223	2.121	0.172	0.239	0.191	0.516
6	0.596	0.224	0.157	0.052	0.426	2.202	0.057	0.927	0.132	1.025
7	0.782	0.146	0.126	0.128	0.484	0.467	0.186	0.474	0.157	0.141
8	0.447	0.098	0.202	0.249	0.032	2.192	0.160	1.260	0.099	0.304
9	0.328	0.165	0.237	0.018	0.453	1.593	0.208	0.087	0.001	0.341
10	0.586	0.232	0.044	0.094	0.355	2.681	0.089	0.114	0.072	0.223
11	0.623	0.057	0.207	0.111	0.581	0.475	0.052	0.369	0.027	0.611
12	0.141	0.167	0.185	0.157	0.103	0.531	0.112	0.279	0.119	0.715
13	0.596	0.095	0.239	0.123	0.063	1.127	-0.058	0.631	0.176	0.494
14	0.453	0.211	0.081	0.013	0.259	0.542	0.165	0.753	0.105	0.262
15	0.781	0.036	0.048	0.112	0.103	1.659	0.181	0.425	0.077	0.964
16	0.129	0.065	0.112	0.016	0.347	2.166	0.113	0.378	0.228	0.353
17	0.168	0.114	0.070	0.066	0.474	1.031	0.137	0.876	0.065	0.496
18	0.287	0.079	0.148	0.108	0.217	1.101	0.189	0.332	0.136	0.245
19	0.181	0.141	0.229	0.054	0.264	2.615	0.071	0.373	0.011	0.876
20	0.424	0.154	0.095	0.147	0.494	1.115	0.105	0.349	0.241	1.022
21	0.648	0.045	0.121	0.220	0.221	1.596	-0.008	0.903	0.181	0.710
22	0.293	0.124	0.271	0.048	0.344	0.533	0.235	1.019	0.160	0.986
23	0.289	0.191	0.110	0.085	0.143	2.653	0.187	0.769	0.154	0.592
24	0.738	0.042	0.192	0.006	0.554	2.704	0.129	1.063	0.111	0.316
25	0.327	0.057	0.010	0.355	0.487	2.216	0.081	0.791	0.131	0.893
E%	7.88	32.86	15.61	59.93	13.43	3.23	46.24	23.21	29.41	16.52

---

Fig. 5 Spectra as predicted by MLR.

MLR predicts concentrations well in this case because all significant compounds are included in the model, and so the data are almost completely modelled. If we knew of only a few compounds, there would be much poorer predictions. Consider the situation in which only pyrene, acenaphthene and anthracene are known. The C matrix now has only three columns, and the predicted concentrations are given in Table 8. The errors are, as expected, much larger than those of Table 7. The absorbances of the remaining seven compounds are mixed up with those of the three modelled components. This problem could be overcome if some characteristic wavelengths or regions of the spectrum at which the selected compounds absorb most strongly (see Section 2.2.2) are identified, or if the experiments were designed so that there are correlations in the data, or even by a number of methods for weighted regression, but the need to model all significant absorbants is a major limitation of MLR.

Table 8 Predictions by MLR when only three compounds are known

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth
1	0.542	0.145	0.155
2	0.401	0.182	0.333
3	0.226	0.269	0.128
4	0.759	0.015	0.229
5	0.750	0.104	0.209
6	0.483	0.168	0.283
7	0.874	0.053	0.000
8	0.468	0.251	0.084
9	0.335	0.130	0.212
10	0.479	0.366	−0.054
11	0.743	−0.082	0.232
12	0.213	0.013	0.227
13	0.458	−0.004	0.208
14	0.432	0.090	0.053
15	0.823	0.013	0.188
16	0.021	0.262	0.148
17	0.258	0.160	0.125
18	0.333	0.116	0.101
19	0.091	0.190	0.345
20	0.503	0.082	0.221
21	0.653	0.098	0.137
22	0.368	−0.071	0.425
23	0.190	0.324	0.140
24	0.616	0.228	0.175
25	0.562	0.306	0.054
E%	28.01	115.74	61.89

---

The approach described above is related to classical calibration, but it is also possible to envisage an inverse calibration model since

Ĉ = X . B

However, unlike in Section 2.2.2, there are now more wavelengths than samples or components in the mixture. The matrix B would be given by

B = (X′.X)⁻¹.X′ .C

as above. A problem with this approach is that the matrix (X′X) is now a large matrix, with 131 rows and 131 columns, compared with the matrices used above which have ten rows and ten columns only. If there are only ten components in a mixture, the matrix X′X only has ten degrees of freedom and may not have an inverse because there will be strong correlations between wavelengths. In practice because of noise and unknown interferents an inverse can often be computed, but is not very meaningful. The determinant of the matrix X′X will be very small, and factors such as noise will influence the answer. This use of the inverse of X′X is only practicable if: (1) the number of experiments and wavelengths are at least equal to the number of components in the mixture and (2) the number of experiments is at least equal to the number of wavelengths.

Condition 2 either requires a large number of extra experiments or a reduction to 25 wavelengths. There have been a number of algorithms that have been developed to reduce the wavelengths to the most significant ones, so enabling inverse models to be used, but there is no real advantage over classical models unless very specific information is available about error distributions.

2.3  Principal components regression

MLR-based methods have the disadvantage that all significant components must be known. PCA (principal components analysis)-based methods do not require details of all components, although it is necessary to make a sensible estimate of how many significant components characterise a mixture, but not necessarily their chemical identities.

2.3.1  Principal components analysis. There are innumerable excellent descriptions of the mathematical basis of PCA^26–30 and this article will provide only a general overview. It is important, first, not to be confused between algorithms which are a means to an end, and the end in itself. There are several PCA algorithms of which NIPALS (described in Appendix A2.1) and SVD are two of the most common. If correctly applied, they will both lead to the same answer (within computer precision), the best approach depending on factors such as computing power and the number of components to be calculated.

PCA decomposes an X matrix into two smaller matrices, one of scores (T) and the other of loadings (P) as follows

X = T . P

as illustrated symbolically in Fig. 6.

Fig. 6 Principles of PCA.

The scores matrix has the following properties: 1. The number of rows equals the number of rows in the original data matrix, usually the number of samples. 2. The number of columns equals the number of significant factors in the data, and can be any number from 1 upwards. Ideally it equals the number of compounds in the original dataset but noise and spectral similarity combine to distort this number. Each column corresponds to a principal component. 3. The sum of squares of the elements of each column of the scores matrix relates to a number called the eigenvalue, and is often given as a definition of the eigenvalue. The larger the eigenvalue the more significant the component. The principal components are calculated in order of significance.

The loadings matrix has the following properties: 1. The number of columns equals the number of columns in the original data matrix, usually the number of detectors, or wavelengths in this case study. 2. The number of rows equals the number of significant factors in the data. Each row corresponds to a principal component. 3. The sum of squares of the elements of each column equals 1.

Hence each principal component, a, is characterised by: (1) a scores vector t_a being the ath column of T, (2) a loadings vector p_a being the ath row of P; and (3) an eigenvalue g_a which may be defined by

The sum of eigenvalues over all significant components should equal approximately the sum of squares of the original data, and will never be more than this number.

Principal components (PCs) are often presented geometrically. Spectra can be represented as points in J -dimensional space where each of the J -axes represents the intensity at each wavelength. Hence in case study 1, each spectrum an be represented by a point in 131-dimensional space The dataset can be represented by 25 such points, and the pattern formed in this new space indicates information about the data.

The first PC can be defined as the best fit straight line in this multi-dimensional space. The scores represent the distance along this line, and the loadings the direction (angle) of the straight line. If there is only one compound in a series of spectra, all the spectra will fall approximately on the straight line, since the intensity of each spectrum will relate directly to concentration. This distance is the score of the PC. If there are two components, ideally two PCs will be calculated, and representing the axes of a plane. For ten compounds, ideally ten PCs are calculated to give a ten-dimensional subspace of the original 131 dimensional space (in this case).

Another important property of PCs is often loosely called orthogonality. Numerically this means that

and
or t_a. t_b = 0 and p_a. p_b = 0 for two components a and b using vector notation. Some authors state that principal components are uncorrelated. Strictly speaking this property depends on data preprocessing, and is only true if the variables have been centred (down each column) prior to PCA. We will, however, use the terminology ‘orthogonality’ to refer to these properties below.

PCA can be used to reduce the number of original variables to a few reduced variables or PCs, by keeping only the largest or most significant PCs; methods for selecting how many components to keep are discussed in Section 3. In case study 1 an ideal situation would be to reduce the 131 wavelengths to ten PCs. There are a variety of methods of data preprocessing or scaling (such as centring and standardisation) that are sometimes used,²⁰ but below we use the raw data directly. The scores of the first ten PCs are given in Table 9 . Using ten PCs implies that up to ten distinct compounds are in the mixture, but, unlike in MLR it is not necessary to know the concentrations of all these components in advance, only those of the calibrants. This property, of course, allows chemometric techniques to be employed in situations where only one or two compounds are of interest, for example measuring the concentration of chlorophyll in pigment extracts of plants, or the concentration of a nutrient in a food sample. There may be a dozen or more chemical components in the mixture, most of which are unknown or of no interest. Hence it is desired only to calibrate against the known compound.

Table 9 Scores for ten PCs for the dataset of case study 1

Spectrum	PC1	PC2	PC3	PC4	PC5	PC6	PC7	PC8	PC9	PC10
1	6.066	0.032	0.098	−0.002	0.048	0.037	0.011	0.003	0.033	−0.003
2	8.040	−0.155	−0.481	−0.001	0.069	0.007	−0.051	0.016	0.077	−0.005
3	6.261	−0.064	0.261	−0.212	−0.373	0.086	−0.080	0.043	0.025	−0.015
4	5.877	0.606	0.119	0.061	0.117	0.120	−0.007	−0.012	−0.031	−0.026
5	6.928	0.072	0.012	0.399	0.164	0.009	−0.009	0.069	0.037	0.016
6	7.587	0.101	−0.188	−0.075	−0.042	−0.044	−0.017	−0.026	−0.096	0.009
7	4.320	0.373	0.667	−0.148	0.214	0.002	0.023	0.073	0.008	0.010
8	6.491	−0.290	0.302	0.296	−0.161	0.026	0.035	−0.023	0.024	−0.080
9	5.651	−0.117	−0.295	−0.145	0.182	0.166	0.018	0.014	0.020	0.013
10	6.657	−0.979	0.360	0.053	0.157	0.090	−0.005	0.022	−0.060	0.041
11	4.442	0.845	0.051	−0.209	0.226	0.055	−0.072	−0.037	0.005	0.015
12	3.612	0.542	−0.083	0.213	−0.265	0.092	0.045	0.020	0.000	0.021
13	4.144	0.493	0.005	0.354	−0.119	−0.077	−0.100	0.042	−0.039	−0.003
14	3.657	0.163	0.287	−0.152	0.014	0.000	0.071	0.057	−0.051	−0.021
15	5.666	0.200	−0.042	0.294	0.356	−0.089	0.079	−0.078	0.013	0.009
16	5.566	−0.582	−0.277	−0.158	−0.129	−0.146	0.009	0.059	0.028	0.036
17	4.775	0.039	0.067	−0.412	−0.087	0.001	0.042	−0.026	−0.009	−0.022
18	4.174	−0.034	0.069	0.035	−0.011	0.000	0.049	0.040	0.047	0.007
19	7.023	−0.269	−0.691	0.090	−0.057	0.104	−0.027	−0.046	−0.036	0.008
20	5.735	0.458	0.073	−0.105	−0.130	−0.083	0.021	−0.001	−0.002	0.078
21	5.620	0.277	0.297	0.190	−0.071	−0.118	−0.059	−0.019	−0.012	−0.011
22	5.266	0.999	−0.461	−0.158	−0.137	−0.048	0.081	0.013	0.004	−0.026
23	7.060	−0.677	−0.117	0.115	−0.143	−0.025	0.076	0.011	−0.037	−0.009
24	7.805	−0.411	−0.118	−0.289	0.293	−0.129	−0.056	0.007	−0.005	−0.055
25	7.332	−0.243	0.523	−0.076	−0.193	−0.009	−0.005	−0.138	0.045	0.028

---

2.3.2  Regression techniques. Principal components are sometimes called abstract factors, and are primarily mathematical entities. In multivariate calibration the aim is to convert these to compound concentrations. PCR uses regression (sometimes called transformation or rotation) to convert PC scores onto concentrations. This process is often loosely called factor analysis, although terminology differs according to author and discipline.

If c_n is a vector containing the known concentration of compound n in the spectra (25 in this instance), then the PC scores can be related as follows:

c_n ≈ T . r_n

where r_n is a column vector whose length equals the number of PCs calculated, sometimes called a rotation or transformation vector. Ideally the length of r_n should be equal to the number of compounds in the mixture (= 10). The vector for pyrene is presented in Table 10 and can be obtained by using the pseudo-inverse of T_,

r_n = (T′. T)⁻¹. T′. c_n

In practice, the number of compounds in a series of mixtures is not always known in advance. In a complex naturally occurring mixture it may often be impossible to determine how many significant compounds are present, and even if this is known the number of significant principal components is often much less than the true number of compounds present due to spectral similarity, noise, correlations in concentrations and so on. Hence the number of columns in T can vary. The predictions as more PCs are employed will be closer to the true values.

Table 10 Rotation vector for pyrene

0.209

0.309

0.291

0.830

−0.517

−0.395

0.878

−1.229

−0.363

---

There are a number of methods for determining how good the predictions are. Most use the calibration of predictions of concentration, on the c (or according to some authors y) block of data. These methods have been briefly introduced in the context of MLR, but when performing PCR there are a large number of methods for calculating errors, so we will expand on the techniques in this section.

The simplest method is to determine the sum of square of residuals between the true and predicted concentrations

where
for compound n using a principal components. The larger this error, the worse the prediction, and the error reduces as more components are calculated.

Often the error is reported as a root mean square error

Notice that, strictly, the error should be divided by I −a rather than I (for uncentred data) to account for the loss of degrees of freedom as successive components are calculated. Some investigators, do, however use simply the number of spectra and neglect to adjust for the number of PCs. Provided that I is considerably larger than a this adjustment is not very important.

This error can also be reported as a percentage,

E_% = 100 E/c̄_n

where c̄_n is the mean concentration. It is also possible to report errors in terms of quality of modelling of spectra (or chromatograms), often called the x block error.

The quality of modelling of the spectra using PCA (the x variance) can likewise be calculated as follows:

where
However, this error also can be expressed in terms of eigenvalues or scores, so that
for A principal components.

These can be converted to root mean square errors as above,

Notice that it is normal to divide by I.J (=40 × 51 = 2040) in this case rather than adjusting for the degrees of freedom because I.J is a comparatively large number; however, it is necessary to check each author and software package very carefully before reporting results.

The percentage root mean square error may be defined by (for uncentred data)

E_% = 100 E/x̄

Note that if x is centred, the divisor is usually defined by

where x̄_j is the average of all the measurements for the samples for variable j: obviously there are several other ways of defining this error; again each investigator has his or her own favourites.

Note that the x block error depends only on how many PCs have been used in the model, but the error in the c block depends also on the specific compound, there being a different percentage error for each compound in the mixture. For 0 PCs, the estimates of the PCs and concentrations are simply 0 (or the mean if the data have been centred). The graphs of errors for both the concentration estimates of pyrene and spectra as increasing numbers of PCs are calculated are given in Fig. 7. Although the x error graph declines steeply, which might falsely suggest only a small number of PCs are required for the model, the c error graph exhibits a much gentler decline. Some chemometricians prefer to plot the graph of ‘variances’; these are the mean square error if the data have been centred, and these graphs are presented either as percentage variance remaining (or explained by each PC) or, for the x block, by eigenvalues. Fig. 8 shows how the prediction for pyrene for dataset A of case study 1 improves with increasing PCs.

Fig. 7 Error for PCR estimates of pyrene as increasing number of components are employed.

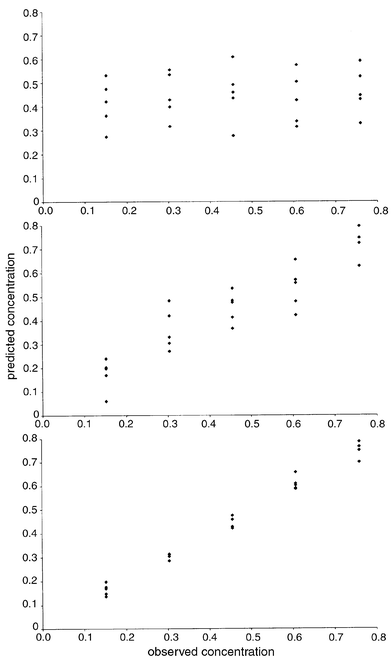Fig. 8 Predicted concentrations for pyrene using PCR as one, five and ten principal components are calculated.

If the concentration of some or all the compounds are known PCR can be extended simply by replacing the vector c_k with a matrix C, each column corresponding to a compound in the mixture, so that

C ≈ T . R

so that

R = (T′. T)⁻¹. T′. C

The number of PCs must be at least equal to the number of compounds of interest in the mixture. If the number of PCs and number of significant compounds in the mixture are equal, so that, in this example, T and C are 25 × 10 matrices, then R is a square matrix and

X= T.P = T.R.R.⁻¹.P = Ĉ.Ŝ

hence, by calculating R⁻¹.P it is possible to determine the estimated spectrum of each individual component without knowing this information in advance, and by calculating T.R concentration estimates can be obtained Table 11. provides the concentration estimates using PCR with ten significant components. The percentage mean square error of prediction (equalling the square root sum of squares of the errors of prediction divided by 15—the number of degrees of freedom which equals 25 — 10 to account for the number of components in the model, and not by 25) for all ten compounds is also presented, and, on the whole, is slightly better than that using MLR.

Table 11 Predictions of concentrations using PCR and ten significant components as discussed in Section 2.3.2

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
1	0.475	0.108	0.185	0.150	0.374	1.644	0.156	0.532	0.110	0.494
2	0.422	0.054	0.322	0.132	0.465	2.712	0.161	0.473	0.146	0.631
3	0.170	0.175	0.274	0.191	0.559	1.657	0.081	0.824	0.153	0.207
4	0.700	0.178	0.244	0.160	0.346	1.114	0.126	0.788	0.050	0.678
5	0.803	0.131	0.283	0.163	0.214	2.132	0.163	0.279	0.188	0.537
6	0.601	0.201	0.162	0.085	0.424	2.214	0.073	0.951	0.139	1.003
7	0.786	0.144	0.115	0.140	0.466	0.482	0.150	0.520	0.158	0.185
8	0.428	0.118	0.193	0.195	0.066	2.160	0.167	1.103	0.078	0.319
9	0.311	0.122	0.202	0.107	0.410	1.654	0.148	0.190	0.034	0.467
10	0.590	0.213	0.047	0.120	0.332	2.701	0.079	0.219	0.087	0.222
11	0.610	0.077	0.191	0.109	0.571	0.488	0.072	0.393	0.046	0.671
12	0.147	0.158	0.203	0.139	0.110	0.523	0.107	0.288	0.108	0.654
13	0.587	0.116	0.240	0.086	0.099	1.120	−0.011	0.537	0.160	0.490
14	0.459	0.165	0.077	0.075	0.239	0.565	0.119	0.793	0.114	0.269
15	0.765	0.030	0.055	0.094	0.118	1.653	0.179	0.373	0.072	0.934
16	0.136	0.058	0.102	0.037	0.351	2.146	0.103	0.320	0.223	0.389
17	0.176	0.102	0.075	0.087	0.465	1.021	0.126	0.883	0.072	0.468
18	0.285	0.075	0.132	0.111	0.218	1.106	0.151	0.294	0.129	0.301
19	0.198	0.141	0.229	0.084	0.253	2.626	0.072	0.415	0.034	0.878
20	0.421	0.142	0.114	0.122	0.513	1.108	0.120	0.327	0.221	0.960
21	0.657	0.094	0.159	0.130	0.267	1.541	0.061	0.804	0.158	0.582
22	0.313	0.109	0.253	0.088	0.331	0.541	0.187	1.008	0.158	1.032
23	0.312	0.171	0.109	0.103	0.141	2.661	0.148	0.771	0.142	0.582
24	0.750	0.049	0.170	0.052	0.528	2.723	0.118	1.115	0.126	0.385
25	0.304	0.094	0.045	0.224	0.556	2.181	0.140	0.626	0.090	0.776
E%	7.61	29.52	18.39	42.46	9.52	3.18	38.75	20.15	25.12	19.36

---

2.4  Partial least squares

PLS is often regarded as the major regression technique for multivariate data. In fact in many cases it is applied inappropriately and is not justified by the data. In areas outside mainstream analytical chemistry such as QSAR, or even biometrics and psychometrics, PLS certainly is an invaluable tool, because the underlying factors have little or no physical meaning so a linearly additive model in which each underlying factor can be interpreted chemically is not expected. In spectroscopy or chromatography we usually expect linear additivity, and this is especially the case in analytical chemistry calibration. Nevertheless, PLS can be a useful tool when there is partial knowledge of the data, an excellent example being the measurement of protein in wheat by NIR spectroscopy.^6,7 Under such conditions, the model will be obtained from a series of wheat samples, and PLS will try to use typical features in this dataset to establish a relationship with the known amount of protein. Unlike MLR it does not require an exact model of all components in the data. PLS models can be very robust provided that future samples contain similar features to the original data, but predictions are essentially statistical. An example might be the determination of vitamin C in orange juices using spectroscopy: a very reliable PLS model could be obtained using orange juices from a particular region of Spain, but what if some Brazilian orange juice is included? There is no guarantee that the model will perform well on the new data, as there may be different spectral features. The originators of PLS are well aware of the shortcomings as well as the successes of the method, but it is important for the analytical chemist to be very alert to potential pitfalls.

One important practical aspect of PLS is that it takes into account errors both in the concentration estimates and spectra. A method such as PCR will assume that the concentration estimates are error free. Much traditional statistics rest on this assumption, that all errors are in the dependent variables (spectra). If in medicine it is decided to determine the concentration of a compound in the urine of patients as a function of age, it is assumed that age can be estimated exactly, the statistical variation being in the concentration of a compound and the nature of the urine sample. Yet in chemistry there are often significant errors in sample preparation, for example, accuracy of weighings and dilutions and so the independent variable (c) in itself also contains errors. With modern spectrometers, these are sometimes larger than spectroscopic errors. One way of overcoming this difficulty is to try to minimise the covariance between both types of variables, namely the x (spectroscopic) and c (concentration) variables.

2.4.1  PLS1 method. The most widespread approach is often called PLS1. Although there are several algorithms, the main ones being due to Wold¹⁴ and Martens,³¹ the overall principles are straightforward. Instead of modelling exclusively the x variables, two sets of models are obtained, of the form

X = T.P + E

c = T.q + f

where q is analogous to a loadings vector, although is not normalised. These matrices are represented in Fig. 9. Hence the product of T and P approximates to the spectral data and the product of T and q  to the true concentrations. An important feature of PLS is that it is possible to obtain a scores matrix that is common to both the concentrations (c) and measurements (x). The sum of squares of the scores of each successive component is often called an eigenvalue, note that the PLS eigenvalues will not be the same as the PCA eigenvalues, and depend both on the x and c blocks.

Fig. 9 Principles of PLS1.

There are a number of alternative ways of presenting the PLS regression equations in the literature, all, in practice, equivalent. In the models above, there are three arrays T, P and q and a conventional analogy to PCA sets P as a matrix, each of whose rows has a sum of squares equal to 1. From this the magnitude of T follows, which determines q. Some packages calculate a vector proportional to q, which is also normalised, in analogy to a loadings vector. In such a situation, the second equation becomes a product of three arrays, the first one proportional to T, the second one a diagonal matrix consisting of scaling factors, and the third one a normalised vector proportional to q. It is also possible to convert both equations to products of three arrays, but the models used in this paper have the simplicity of a single scores matrix, with the disadvantage of a vector q that is not normalised.

For a dataset consisting of 25 spectra observed at 131 wavelengths, for which eight PLS components are calculated, there will be: a T matrix of dimensions 25 × 8; a P matrix of dimensions 8 × 131; an E matrix of dimensions 25 × 131; a q vector of dimensions 8 × 1 and an f vector of dimensions 25 × 1.

Each successive PLS component approximates both the concentration and spectral data better. For each component, there will be a: spectral scores vector t; spectral loadings vector p and concentration loadings scalar q.

The approximation to the concentration as successive PLS components are calculated is simply the sum of t.q for each successive component. This approach is possible in PLS1 because each successive component is orthogonal.

In case study 1, there are ten compounds, so it is possible to perform PLS1 separately on each of the ten compounds. In each case it is possible compute several PLS components, if 15 were calculated for each compound, there will be 150 PLS components in total.

In most implementations of PLS it is conventional to centre both the x and c data, by subtracting the mean of each column before analysis. In fact, there is no general scientific need to do this. Many spectroscopists and chromatographers perform PCA uncentred; however, many early applications of PLS (e.g. outside chemistry) were of such a nature that centring the data was appropriate. Much of the history of PLS in analytical chemistry relates to applications in NIR spectroscopy, where there are specific spectroscopic problems, such as due to baselines, which, in turn would favour centring. However, as generally applied to analytical chemistry, uncentred PLS is perfectly acceptable. Below, though, we review the most widespread implementation for the sake of compatibility with the most common computational implementations of the method.

For a given compound, the remaining percentage error in the x matrix for A PLS components can be expressed in a variety of ways (see Section 2.3). Note that there are slight differences according to authors that take into account the number of degrees of freedom left in the model. The predicted measurements simply involve calculating X̂ = T.P and adding on the column averages where appropriate, and error indicators in the x block can be expressed identically with those for PCA and can be calculated, see Section 2.3.2. The only difference is that each compound generates a separate scores matrix, unlike PCR where there is a single scores matrix for all compounds in the mixture.

The concentration is predicted by

or, in matrix terms

c_n = T_n q_n+ c̄_n

where c̄_n is a vector of the average concentration. Hence the scores of each PLS component are proportional to the contribution of the component to the concentration estimate. The method of the concentration estimation for two PLS components and pyrene is presented in Table 12.

Table 12 Calculation of concentration using two PLS components for pyrene and case study 1, dataset A. Note that the concentration estimated is mean-centred

Component 1 scores	q = 0.0607; conc. est. (ti1q)	Component 2 scores	q = 0.318; conc. est. (ti2q)	Centred conc. est. (ti1q + ti2q)
0.333	0.020	0.127	0.040	0.060
1.999	0.121	−0.301	−0.096	0.026
0.147	0.009	−0.352	−0.112	−0.103
0.570	0.035	0.775	0.246	0.281
1.504	0.091	0.529	0.168	0.259
1.743	0.106	0.011	0.004	0.109
−0.881	−0.053	0.869	0.276	0.223
0.679	0.041	−0.020	−0.006	0.035
−0.428	−0.026	−0.370	−0.118	−0.144
0.659	0.040	−0.389	−0.124	−0.084
−0.894	−0.054	0.759	0.241	0.187
−2.335	−0.142	−0.091	−0.029	−0.171
−1.511	−0.092	0.277	0.088	−0.004
−2.159	−0.131	0.021	0.007	−0.124
0.305	0.019	0.605	0.192	0.211
−1.028	−0.062	−1.109	−0.352	−0.415
−1.364	−0.083	−0.402	−0.128	−0.211
−1.813	−0.110	−0.242	−0.077	−0.187
0.601	0.037	−0.833	−0.265	−0.228
0.032	0.002	0.247	0.079	0.080
0.130	0.008	0.484	0.154	0.162
−0.544	−0.033	0.184	0.058	0.025
0.728	0.044	−0.765	−0.243	−0.199
1.933	0.117	−0.124	−0.039	0.078
1.592	0.097	0.110	0.035	0.132

---

The mean square error in the concentration estimate can be computed just as in PCR, although the value of ĉ_in will differ. It is also possible to provide a number of equivalent equations for this error using t and q which are left to the reader. In the case of the concentration estimates, it is usual to adjust the sum of squares according to the number of PLS components, because this number is often similar in magnitude to the number of objects in the dataset; for example, there are 25 spectra in case study 1, but we might want to look at the error when ten PLS components are calculated. These error terms will also be discussed in Section 3.1. Note an interesting difference between the conventional equations for errors in the x and c data blocks: in the former the mean is subtracted from the overall sum of squares since the data are usually mean-centred prior to PLS, whereas for the latter the raw data are usually used as the mean concentration is generally added back on to the data so predictions are expressed in the original concentration units.

These calculations are illustrated for pyrene. Table 13 is of the first 15 eigenvalues for PLS1 using pyrene as the calibrant. The total sum of squares of the mean centred spectra is 50.522, hence the first two eigenvalues account for 100x(38.578+6.269)/50.522 = 88.77% of the overall sum of squares, giving a root mean square error after two PLS components have been calculated of

Table 13 First 15 eigenvalues using PLS1 for pyrene and case study 1

 6.269

 2.563

 1.697

 0.624

 0.536

 0.081

 0.048

 0.0146

 0.0261

 0.0247

 0.0159

 0.0094

 0.0026

 0.0056

---

Table 14 is of the concentration predictions using two components. The sum of squares of the errors is 0.376. Dividing this by 22 and taking the square root leads to a root mean square error of 0.131 mg L⁻¹. The average concentration of pyrene is 0.456 mg L⁻¹. Hence the percentage root mean square error is 28.81%.

Table 14 Concentration predictions (in mg L⁻¹) for pyrene together with associated errors after two PLS components have been computed. Note that the mean has now been added back to the data

Prediction	Error
0.516	0.060
0.482	0.026
0.353	0.201
0.737	−0.023
0.715	−0.045
0.565	−0.043
0.679	−0.081
0.491	0.035
0.312	0.008
0.372	−0.236
0.643	0.035
0.285	0.133
0.452	−0.156
0.332	−0.124
0.667	−0.093
0.041	−0.111
0.245	0.093
0.269	−0.035
0.228	0.076
0.536	0.080
0.618	0.010
0.481	0.177
0.257	−0.047
0.534	−0.226
0.588	0.284

---

It is important to recognise that the percentage error of prediction in concentration may be different to the percentage error of prediction of the original spectra.

The root mean square percentage errors for modelling both spectra and concentrations of pyrene are presented in Fig. 10. Often these are plotted using a logarithmic scale for clarity. Fourteen components are required to obtain an error of prediction of concentration of less than 1%, whereas only 21 are needed to reach this for the spectral data. It is important to notice that there is not a sharp cut-off at ten components. If the number of compounds in the mixture spectra are unknown, it would not be at all obvious how complex the mixture is. Below we will discuss methods for determining the optimum number of components. The prediction error for pyrene using PLS1 and ten significant components, in this case, is considerably better than that using PCR, 3.40% as opposed to 7.61%. However, these raw errors are not always very useful indicators.

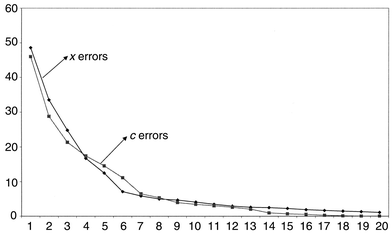Fig. 10 Root mean square errors for prediction of spectra and concentration of pyrene using PLS1 as successive number of components are employed.

Fig. 11 represents the same data for acenaphthylene. Whereas the x block modelling error is fairly similar to that of pyrene, the concentration is modelled much less well, a consequence of the substantial spectral overlap and lack of significant features.

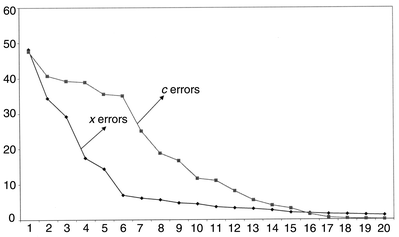Fig. 11 Root mean square errors for prediction of spectra and concentration of acenaphthylene using PLS1 as successive number of components are employed.

The errors using ten PLS components are summarised in Table 15, and are better than PCR in this case. There is, however, an important philosophical consideration about what is a better prediction; although the measured c or concentration variables are obtained with greater accuracy, it is essential to recognise that there could be errors, in turn, in these concentration measurements, so PLS could simply be predicting poorer concentration estimates more accurately because the algorithm takes into account the c as well as x values. There is no easy answer.

Table 15 Prediction of concentrations for the ten PAHs, using PLS1, and ten PLS components

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
1	0.438	0.133	0.158	0.123	0.340	1.636	0.118	0.614	0.116	0.601
2	0.462	0.043	0.282	0.210	0.447	2.709	0.116	0.382	0.153	0.749
3	0.155	0.195	0.280	0.162	0.559	1.623	0.083	0.813	0.160	0.187
4	0.729	0.183	0.219	0.195	0.336	1.108	0.115	0.781	0.042	0.761
5	0.788	0.170	0.279	0.114	0.222	2.119	0.165	0.182	0.169	0.548
6	0.608	0.211	0.175	0.059	0.452	2.168	0.055	0.811	0.116	0.931
7	0.760	0.113	0.119	0.168	0.439	0.552	0.176	0.620	0.197	0.174
8	0.471	0.086	0.229	0.174	0.114	2.124	0.129	0.985	0.038	0.180
9	0.305	0.158	0.230	0.033	0.449	1.611	0.194	0.180	0.022	0.370
10	0.605	0.169	0.050	0.159	0.334	2.732	0.053	0.200	0.084	0.210
11	0.625	0.028	0.228	0.130	0.575	0.512	0.051	0.402	0.037	0.548
12	0.155	0.156	0.179	0.189	0.099	0.539	0.095	0.289	0.119	0.736
13	0.591	0.115	0.275	0.045	0.122	1.094	0.030	0.560	0.151	0.388
14	0.471	0.203	0.060	0.051	0.232	0.526	0.125	0.779	0.084	0.351
15	0.755	0.038	0.057	0.081	0.113	1.630	0.155	0.415	0.073	0.938
16	0.148	0.026	0.114	0.038	0.340	2.167	0.058	0.399	0.193	0.364
17	0.157	0.094	0.050	0.115	0.447	1.047	0.072	0.973	0.081	0.573
18	0.296	0.058	0.157	0.139	0.218	1.100	0.191	0.381	0.140	0.220
19	0.151	0.118	0.221	0.088	0.219	2.695	0.088	0.613	0.056	0.936
20	0.460	0.159	0.115	0.101	0.552	1.075	0.123	0.194	0.192	0.935
21	0.609	0.080	0.111	0.188	0.216	1.615	0.041	1.015	0.203	0.762
22	0.305	0.092	0.272	0.079	0.336	0.563	0.211	0.980	0.169	0.962
23	0.303	0.179	0.117	0.134	0.122	2.693	0.205	0.794	0.188	0.550
24	0.756	0.076	0.170	0.036	0.551	2.691	0.166	1.049	0.130	0.378
25	0.297	0.118	0.053	0.189	0.566	2.171	0.183	0.589	0.083	0.750
E%	3.403	10.950	4.496	11.638	2.675	1.582	14.857	5.821	9.328	3.643

---

2.4.2  PLS2 method. An extension to PLS1 was suggested some 15 years ago, often called PLS2. In fact there is little conceptual difference, except that the latter allows the use of a concentration matrix, C rather than concentration vectors for each individual compound in a mixture, and the algorithm (see Appendix A2.2) is iterative. The equations above are altered slightly in that Q becomes a matrix not a vector. The number of columns in C and Q are equal to the number of compounds of interest. PLS1 requires one compound to be modelled at a time, whereas in PLS2 all known compounds can be included in the model.

It is a simple extension to predict all the concentrations simultaneously, the PLS2 predictions, together with root mean square errors being given in Table 16. Note that there is now only one set of scores and loadings for the x (spectroscopic) dataset, and one set of eigenvalues common to all ten compounds. However, the concentration estimates are different when using PLS2 to PLS1. In this way PLS differs from PCR where it does not matter if each variable is modelled separately or all together. The reasons are rather complex but relate to the fact that for PCR the principal components are calculated independently of how many concentration variables are used in the regression; however, the PLS components are influenced by the concentration variable.

Table 16 Prediction of concentration for the ten PAHs using PLS2, and ten PLS components

Polyarene conc./mg L^−1
Spectrum	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
1	0.477	0.111	0.175	0.145	0.367	1.660	0.149	0.563	0.097	0.520
2	0.434	0.071	0.313	0.116	0.475	2.701	0.156	0.402	0.139	0.647
3	0.172	0.177	0.278	0.184	0.564	1.650	0.084	0.797	0.149	0.187
4	0.701	0.185	0.231	0.159	0.344	1.121	0.119	0.767	0.046	0.715
5	0.813	0.146	0.281	0.144	0.230	2.111	0.163	0.170	0.179	0.522
6	0.602	0.214	0.156	0.085	0.435	2.189	0.073	0.840	0.149	1.011
7	0.785	0.138	0.119	0.133	0.464	0.486	0.152	0.541	0.145	0.160
8	0.423	0.113	0.210	0.197	0.077	2.151	0.179	1.066	0.095	0.271
9	0.310	0.115	0.216	0.109	0.413	1.648	0.155	0.201	0.040	0.430
10	0.590	0.213	0.044	0.125	0.332	2.700	0.076	0.214	0.088	0.236
11	0.603	0.061	0.207	0.121	0.570	0.490	0.079	0.440	0.058	0.635
12	0.151	0.158	0.197	0.142	0.105	0.531	0.101	0.329	0.108	0.683
13	0.583	0.101	0.256	0.099	0.096	1.120	−0.004	0.599	0.173	0.462
14	0.463	0.168	0.071	0.079	0.236	0.568	0.115	0.813	0.118	0.301
15	0.762	0.026	0.056	0.102	0.111	1.660	0.180	0.419	0.078	0.944
16	0.135	0.044	0.113	0.039	0.350	2.160	0.103	0.383	0.218	0.362
17	0.175	0.099	0.068	0.096	0.452	1.040	0.120	0.963	0.074	0.510
18	0.282	0.058	0.149	0.114	0.213	1.114	0.159	0.376	0.129	0.255
19	0.187	0.128	0.223	0.097	0.233	2.655	0.067	0.531	0.029	0.907
20	0.429	0.154	0.110	0.113	0.527	1.088	0.117	0.226	0.218	0.961
21	0.653	0.090	0.142	0.135	0.245	1.577	0.048	0.919	0.143	0.642
22	0.311	0.109	0.258	0.082	0.337	0.533	0.193	0.966	0.156	1.004
23	0.309	0.172	0.109	0.104	0.139	2.656	0.151	0.765	0.141	0.577
24	0.749	0.052	0.170	0.051	0.529	2.719	0.121	1.100	0.132	0.385
25	0.301	0.095	0.046	0.228	0.557	2.174	0.143	0.606	0.098	0.776
E%	7.398	26.813	12.068	42.827	7.495	2.711	36.921	10.768	30.415	13.640

---

In some cases PLS2 is helpful, especially since it is easier to perform computationally. Instead of obtaining ten independent models, one for each PAH, in this example, we can analyse all the data in one go. However, in many situations PLS2 concentration estimates are, in fact, worse than PLS1 estimates, so a good strategy might be to perform PLS2 as a first step, which could provide further information such as which wavelengths are significant and which concentrations can be determined with a high degree of confidence, and then perform PLS1 individually for the most appropriate compounds.

2.5  Multiway methods

Two way data such as DAD-HPLC, LC-MS and LC-NMR are increasingly common in analytical chemistry, especially with the growth of coupled chromatography. Conventionally either a univariate parameter (e.g. a peak area at a given wavelength) (methods of Section 2.1) or a chromatographic elution profile at a single wavelength (methods of Sections 2.2–2.4) is used for calibration, allowing the use of standard regression techniques described above. However, additional information has been recorded for each sample, often involving both an elution profile and a spectrum. A series of two way chromatograms are available, and can be organised into a three-way array often visualised as a box. Each level of the box consists of a single chromatogram. Sometimes these three-way arrays are called “tensors” but tensors often have special properties in physics which are unnecessarily complex and confusing to the chemometrician. We will refer to tensors only where it helps understand the existing methods.

Enhancements of the standard methods for multivariate calibration are required. Although it is possible to use methods such as three- way MLR, most chemometricians have concentrated on developing approaches based on PLS, which we will be restricted to below. The data will be illustrated using case study 2.

2.5.1  Unfolded calibration. One of the simplest methods is to create a single, long, data matrix from the original three way tensor. In case study 2, we take 14 samples each recorded at 40 elution times and 51 wavelengths, arranged as a 14 × 40 × 51 tensor. It is possible to change the shape so that each individual time/wavelength combination is a single variable, for example, the intensity at 242.4 nm and 9 s is represented by a single vector of length 14. This new matrix now contains 40 × 51 = 2040 variables and is the unfolded form of the original data matrix. This operation is illustrated in Fig. 12 .

Fig. 12 Unfolding a data matrix.

It is now a simple task to perform PLS (or indeed any other multivariate approach), as discussed above. The 2040 variables are centred and the prediction of the concentration of 3-hydroxypyridine when three PLS components are employed is given in Fig. 13. The error of prediction of the concentration of 3-hydroxypyridine is presented in Fig. 14 for increasing number of components. Notice that several graphs could be produced of the effectiveness of the model, ranging from the eigenvalues (related to the x variables), to the percentage prediction error in the concentration variables, and the percentage of the chromatographic data modelled by each successive component. It is interesting that three PLS components appear to be required to give a good model, even though there are only two compounds in this region of the chromatogram (the major one and the impurity). There could be other factors such as noise that are modelled by these PLS components.

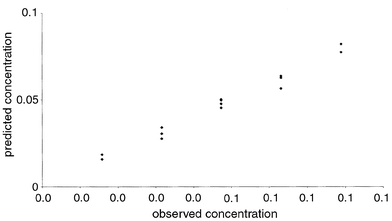Fig. 13 Predicted versus true concentrations of 3-hydroxypyridine (case study 2), using 3 PLS components and an unfolded data matrix as discussed in Section 2.5.1.

Fig. 14 Error in response of the first 10 PLS components for the data discussed in Section 2.5.1.

It is possible to improve the method by scaling the data, but it is important to be very careful to think about the consequences of the various methods employed. It is sometimes possible to scale first the two way data and then unfold. However, a final centring should normally be performed on the unfolded matrix. In addition, variable selection can have a significant influence on the effectiveness of unfolded PLS models, since not all the 2040 variables are going to be particularly relevant or informative.

2.5.2 Trilinear PLS1. Some of the most interesting theoretical developments in chemometrics over the past few years have been in so-called ‘multiway’ or ‘multimode’ data analysis.^32–35 Many such methods have been available for some years, especially in the area of psychometrics, and a few do have relevance to analytical chemistry. It is important, though, not to get too carried away with the excitement of these novel theoretical approaches. Only limited data are of sufficient quality and completeness for the application of genuine multiway methods, two main sources, in analytical chemistry calibration, being coupled chromatography and fluorescence excitation–emission spectroscopy. We will restrict the discussion in this paper to trilinear PLS1, involving a three-way x block and a single c variable. If there are several known calibrants, the simplest approach is to perform trilinear PLS1 individually on each variable.

Centring can be complex for three-way data, and there is no inherent reason to do this, therefore, for simplicity, in this section no centring is used, so raw concentrations and chromatographic/spectroscopic measurements are employed.

The experimental data of case study 2 can be considered to be arranged in the form of a cube, with three dimensions, I for the number of samples, and J and K for the measurements. For case study 2, there are: I = 14 samples; J = 40 sampling times in HPLC and K = 51 wavelengths.

Trilinear PLS1 attempts to model both the x and c blocks simultaneously. In this review we will illustrate the use with the algorithm of Appendix A2.4, based on methods proposed by de Jong³⁶ and Bro.³³

Superficially, trilinear PLS1 has many of the same objectives as normal PLS1, and the method is often represented diagrammatically as in Fig. 15, replacing ‘squares’ or matrices by ‘boxes’ or tensors, and replacing, where necessary, the dot product (‘.’) by something called a tensor product (‘⊗’). In fact, as we shall see, this is an oversimplification, and is not an entirely accurate description of the method.

Fig. 15 Principles of three way PLS.

In trilinear PLS1, for each component it is possible to determine: a scores vector (t), of length I or 14 in this example; a weight vector, which has analogy to a loadings vector (^jp) of length J or 40 in this example, referring to one of the dimensions (e.g. time), whose sum of squares equals 1, and another weight vector, which has analogy to a loadings vector (^kp) of length K or 51 in this example, referring to the other one of the dimensions (e.g. wavelength) whose sum of squares also equals 1.

Superficially these vectors are related to scores and loadings in normal PLS, but in practice they are different, a key reason being that these vectors are not orthogonal in trilinear PLS1, influencing the additivity of successive components. In this paper, we keep the notation scores and loadings, simply for the purpose of compatibility with the rest of this article.

In addition, a vector q is determined after each new component, by

q = (T′.T)⁻¹.T′. c

so that

ĉ = T.q

or

c = T.q + f

where T is the scores matrix, whose columns consist of the individual scores vectors for each component and has dimensions I × A or 14 × 3 in this example, if three PLS components are computed, and q is a column vector of dimensions A × 1 or 3 × 1.

A key difference from bilinear PLS1 is that the elements of q have to be recalculated afresh as new components are computed, whereas for two-way PLS, the first element of q, is the same no matter how many components are calculated. This limitation is a consequence of non-orthogonality of components in the algorithms conventionally applied. Therefore, the concentration estimates are best expressed in matrix terms and not so easily as summations.

The x block residuals after each component are computed conventionally by

^resid,ax_ijk = ^{resid,a −1}x − t_i^j p_j^k p_k

where ^resid,ax_ijk is the residual after a components have been calculated, which would lead to a model
Sometimes these equations are written as tensor products, but there are a large number of ways of multiplying tensors together, so this notation can be confusing.

However, tensors are simply methods for rearranging the data, and it is often conceptually more convenient to deal directly with vectors and matrices, just as in Section 2.5.1 by unfolding the data. This procedure can be called matricisation.

In mathematical terms we can state that

where ^unfoldedp_ais simply a row vector of length J.K. Where trilinear PLS1 differs from unfolded PLS described in Section 2.5.1, is that a matrix P_a of dimensions J ×K can be obtained for each PLS component and is given by

P_a = ^jp_a .^kp _a

and P_a is unfolded to give ^unfoldedp_a .

Fig. 16 represents this procedure, avoiding tensor multiplication, using conventional matrices and vectors together with unfolding. A key problem with the common implementation of trilinear PLS1 is that, since the scores and loadings of successive components are not orthogonal, the methods for determining residuals in simply an approximation. Hence the x block residuals do not have a direct physical meaning. It also means that there are no obvious analogies to eigenvalues. This means that it is not easy to determine the size of the components or the modelling power using the x scores and loadings, but, nevertheless, the concentration (or c block) is modelled well. Since the prime aim of calibration is to predict concentrations rather than spectra or chromatograms, trilinear PLS1 is adequate, provided that care is taken to interpret the output.

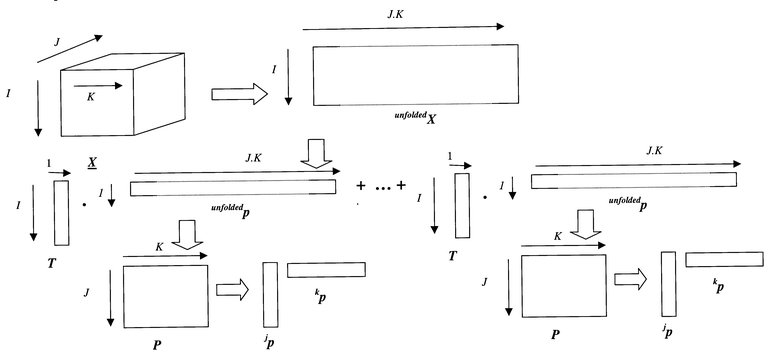Fig. 16 Three way calibration using unfolded matrix notation as discussed in Section 2.5.2.

In order to understand this method further, a small simulated example is given in Table 17, consisting of a 4 × 5 × 6 array, originating from three compounds, whose concentrations are also presented. No noise is added, so that there should be an exact model after three PLS components. Trilinear PLS1 is performed on the first compound. The main results for the first compound are given in Table 18. It can be seen that three components provide an exact model of the concentration, but there is still an apparent residual error in the x matrix, representing 2.51% of the overall sum of squares of the data (=4.03 × 10⁷): this error has no real physical or statistical meaning, except that it is small. Despite this, it is essential to recognise that the concentration has been modelled well, so for the purpose of calibration the algorithm has performed well.

Table 17 Simulated example for Section 2.5.2

(a) X data
390	421	871	940	610	525
635	357	952	710	910	380
300	334	694	700	460	390
65	125	234	238	102	134
835	308	1003	630	1180	325
488	433	971	870	722	479
1015	633	1682	928	1382	484
564	538	1234	804	772	434
269	317	708	364	342	194
1041	380	1253	734	1460	375
186	276	540	546	288	306
420	396	930	498	552	264
328	396	860	552	440	300
228	264	594	294	288	156
222	120	330	216	312	114
205	231	479	481	314	268
400	282	713	427	548	226
240	264	576	424	336	232
120	150	327	189	156	102
385	153	482	298	542	154
(b) c data (three components)
1	9	10
7	11	8
6	2	6
3	4	5

---

Table 18 Results of performing trilinear PLS1 (uncentred) on data of Table 17, and using only the first compound in the model

t	^jp	^kp	q	ĉ	RMS concentration residuals	RMS of x “residuals”
Component 1	3135.35	0.398	0.339	0.00140	4.38	20.79	2.35E+06
4427.31	0.601	0.253	6.19
2194.17	0.461	0.624	3.07
1930.02	0.250	0.405	2.70
0.452	0.470
0.216
Component 2	−757.35	−0.252	0.381	0.00177	1.65	1.33	1.41E+06
−313.41	0.211	0.259	0.00513	6.21
511.73	0.392	0.692	6.50
−45.268	0.549	0.243	3.18
−0.661	0.485
0.119
Component 3	−480.37	−0.875	−0.070	0.00201	1	0.00	1.01E+06
−107.11	−0.073	0.263	0.00508	7
−335.17	−0.467	0.302	0.00305	6
−215.76	−0.087	0.789	3
0.058	0.004
0.461

---

The application will be illustrated by the example of case study 2. The values of t, ^jp, ^kp and q for each successive component, are given in Table 19. The data are not centred. The predicted concentrations, formed by multiplying T and q, are given in Table 20. The first component contributes very little to the concentration estimate, most concentration estimates being extremely close to the average. This is because the impurity is in a small proportion and the data are uncentred, so the first component reflects primarily the overall chromatogram. At least three components are required for a sensible estimate of concentration.

Table 19 Result of performing three-way PLS on the data of case study 2, uncentred and first three components

t1	t2	t3	^jp1	^jp2	^jp3	^kp1	^kp2	^kp3	q1	q2	q3
9.424	−0.450	−0.195	0.000	0.001	0.001	0.180	0.164	−0.152	0.00491	0.00012	−0.00064
9.459	−0.047	0.086	0.000	0.002	0.003	0.095	0.109	−0.113	0.05116	0.09439
9.643	−0.211	−0.100	0.000	0.005	0.008	0.039	0.075	−0.091	−0.21409
9.762	−0.164	−0.047	0.001	0.014	0.023	0.018	0.066	−0.088
9.475	−0.095	−0.015	0.002	0.033	0.052	0.013	0.069	−0.095
9.557	−0.299	−0.237	0.003	0.065	0.102	0.013	0.075	−0.104
9.677	0.388	0.233	0.005	0.110	0.170	0.015	0.080	−0.111
9.713	−0.037	−0.041	0.007	0.162	0.243	0.018	0.082	−0.112
9.891	0.105	0.051	0.009	0.206	0.306	0.022	0.081	−0.108
9.692	0.078	−0.040	0.009	0.233	0.341	0.028	0.077	−0.099
9.555	0.045	−0.036	0.010	0.238	0.343	0.035	0.073	−0.090
9.877	0.050	−0.061	0.009	0.224	0.317	0.043	0.072	−0.085
9.922	0.339	0.053	0.009	0.200	0.270	0.053	0.076	−0.086
9.758	−0.050	−0.202	0.010	0.178	0.210	0.065	0.087	−0.096
0.016	0.172	0.134	0.079	0.103	−0.112
0.033	0.194	0.039	0.094	0.123	−0.133
0.065	0.244	−0.071	0.112	0.145	−0.158
0.118	0.303	−0.176	0.131	0.169	−0.183
0.187	0.336	−0.244	0.150	0.192	−0.207
0.259	0.310	−0.247	0.171	0.213	−0.229
0.320	0.222	−0.189	0.191	0.232	−0.247
0.357	0.100	−0.096	0.212	0.247	−0.259
0.366	−0.019	−0.003	0.230	0.257	−0.264
0.351	−0.109	0.069	0.247	0.261	−0.261
0.321	−0.161	0.114	0.261	0.258	−0.251
0.284	−0.181	0.136	0.271	0.251	−0.236
0.245	−0.178	0.141	0.276	0.241	−0.218
0.208	−0.162	0.135	0.276	0.228	−0.199
0.175	−0.142	0.124	0.271	0.214	−0.180
0.146	−0.120	0.110	0.261	0.200	−0.165
0.123	−0.100	0.095	0.244	0.187	−0.154
0.103	−0.083	0.081	0.222	0.173	−0.145
0.087	−0.069	0.068	0.195	0.158	−0.137
0.074	−0.057	0.057	0.167	0.143	−0.128
0.064	−0.047	0.049	0.140	0.128	−0.119
0.055	−0.039	0.041	0.111	0.111	−0.108
0.048	−0.032	0.035	0.080	0.092	−0.095
0.042	−0.027	0.031	0.052	0.073	−0.082
0.037	−0.022	0.026	0.030	0.056	−0.068
0.033	−0.019	0.023	0.015	0.043	−0.056
0.007	0.034	−0.046
0.004	0.026	−0.037
0.002	0.020	−0.029
0.001	0.015	−0.021
0.001	0.011	−0.015
0.001	0.007	−0.010
0.000	0.005	−0.007
0.000	0.003	−0.004
0.000	0.002	−0.003
0.000	0.001	−0.002
0.000	0.001	−0.001

---

Table 20 Predicted concentrations using three-way PLS for case study 2, uncentred data

One component	Two components	Three components
0.046	0.024	0.018
0.046	0.045	0.016
0.047	0.038	0.033
0.048	0.041	0.029
0.047	0.043	0.031
0.047	0.033	0.049
0.048	0.069	0.049
0.048	0.047	0.046
0.049	0.055	0.048
0.048	0.053	0.062
0.047	0.050	0.056
0.049	0.052	0.064
0.049	0.067	0.082
0.048	0.047	0.079
Error (%)	42.267	35.981	5.534

---

The residual sum of squares from the x block might, at first glance, suggest a very different story and are presented in Table 21. Note that the first component accounts for by far the largest sum of squares, but the concentration is modelled very poorly using only one component, hence the x residuals do not provide very good information about the number of PLS components required to model the data adequately. It is important, also to be careful when interpreting these numbers as they are not true eigenvalues, unlike for bilinear PLS1.

Table 21 Residual sum of squares of the x values for the example of Section 2.5.2 as successive components are calculated

0 components	1311.218
1 component	1.265
2 components	0.601
3 components	0.377

---

A beauty of multimode methods is that the dimensions of c (or indeed X) can be changed, for example, a matrix C can be employed consisting of several different compounds, exactly as in PLS2, or even, a tensor. It is possible to define the number of dimensions in both the x and c blocks, for example, a three way x block and a two way c block may consist of a series of two-way chromatograms each containing several compounds. However, unless one has a good grip of the theory or there is a real need from the nature of the data, it is best to reduce the problem to one of trilinear PLS1: for example a concentration matrix C can be treated as several concentration vectors, in the same way that a calibration problem that might appear to need PLS2 can be reduced to several calculations using PLS1.

Whereas there has been a huge interest in multimode calibration in the theoretical chemometrics literature, there are important limitations to the applicability of such techniques. Good, very high order, data are rare in analytical chemistry. Even three-way calibration, such as in DAD-HPLC, has to be used cautiously as there are frequent experimental difficulties with exact alignments of chromatograms in addition to interpretation of the numerical results. However, there have been some significant successes in areas such as sensory research and psychometrics.

3  Model validation

Unquestionably one of the most important aspects of all calibration methods is model validation. Numerous questions need to be answered. 1. How many significant components are needed to characterise a dataset? 2. How well is an unknown predicted? 3. How representative are the data used to produce a model?

It is possible to obtain as close a fit as desired using more and more PLS or PCA components, until the raw data are fitted exactly; however, the later components are unlikely to be physically meaningful. There is a large literature on how to decide what model to adopt which requires an appreciation of model validation, experimental design and how to measure errors. Most methods aim to guide the experimenter as to how many significant components to retain. The methods are illustrated below with reference to PLS1 for brevity, but similar principles apply to all calibration methods, including those obtained using MLR, PCR, PLS2 and trilinear PLS1.

3.1  Autoprediction

The simplest approach to determining the number of significant components is by measuring the autoprediction error. This is also called the root mean square error of calibration. Usually (but not exclusively) the error is calculated on the concentration data matrix (c), and we will restrict the discussion below to errors in concentration: importantly, similar equations can be obtained for the x data.

As more components are calculated, the residual error reduces. There are two ways of calculating this error,

where a PLS components have been calculated and the data have been centred or
Note that these errors can easily be converted to a percentage variance or mean square error as described in Sections 2.3 and 2.4.

The value of ²E_cal will always decline in value as more components are calculated, whereas that of ¹E_cal has the possibility of increasing slightly in size although, in most well behaved cases, will also reduce with number of components. If the ¹E_cal does increase against component number it is indicative that there may be problems with the data. The two autopredictive errors for acenaphthylene, case study 1 and dataset A are presented in Fig. 17, using PLS1.

Fig. 17 ²E_cal (bottom line) and ¹E_cal (top line) against component number for acenaphthylene, as discussion in Section 3.1, plotted on a logarithmic scale for clarity.

The autopredictive error can be used to determine how many PLS components to use in the model, in a number of ways.

1. A standard cut-off percentage error can be used, for example, 1%. Once the error has reduced to this cut-off, ignore later PLS (or PCA) components.

2. Sometimes an independent measure of the noise level is possible. Once the error has declined to the noise level, ignore later PLS (or PCA) components.

3. Occasionally the error can reach a plateau. Take the PLS components up to this plateau.

By plotting the eigenvalues (or errors in modelling the x block), it is also possible to determine prediction errors for the x data block. However, the main aim of calibration is to predict concentrations rather than spectra, so this information, whereas useful, is less frequently employed in calibration.

Many chemometricians do not like autoprediction as it is always possible to fit data perfectly simply by increasing the number of terms (or components) in the model. There is, though, a difference between statistical and chemical thinking. A chemist might know (or have a good intuitive feel) for parameters such as noise levels, and, therefore, in some circumstances be able to interpret the autopredictive errors successfully.

3.2  Cross-validation

An important chemometric tool is called cross-validation. The basis of the method is that the predictive ability of a model formed on part of a dataset can be tested out by how well it predicts the remainder of the data.

It is possible to determine a model using I − 1 (=24) samples leaving out one sample (i). How well does this model fit the original data? Below we describe the method when the data are centred, the most common approach.

The following steps are used:

1. Centre both the I − 1 (=24 in this example) concentrations and spectra but remember to calculate the means c̄_i and x̄_i, involving removing sample i and subtracting these means from the original data.

2. Perform PLS to give a loadings matrix P for the x data and a loadings vector q for the c data. Note that the loadings will differ according to which sample is removed from the analysis.

Predicting the concentration of an unknown sample is fairly straightforward.

1. Call the spectrum of sample i x_i(a row vector).

2. Subtract the mean of the I − 1 samples from this to give x_i−x̄_i where x̄_i is the mean spectrum excluding sample i.

3. Calculate t_i = (x_i −x̄_i).p where p are the loadings obtained from the PLS model using I − 1 samples excluding sample i.

4. Then calculate ^cvĉ_i = t_i.q + c̄_i which is the estimated concentration of sample i using the model based on the remaining (I − 1) (=24 samples), remembering to add on the mean of these samples again.

Most methods of cross-validation then repeat the calculation leaving another spectrum out, and so on, until the entire procedure has been repeated I (= 25) times over. The root mean square of these errors is then calculated, as follows

Notice that unlike the autoprediction error this term is always divided by I because each sample in the original dataset represents a degree of freedom, however many PLS or PCA components have been calculated and however the data have been preprocessed.

For acenaphthylene using PLS1, the cross-validated error is presented in Fig. 18. An immediate difference between autoprediction and cross-validation is evident. In the former case the data will always be better modelled as more components are employed in the calculation, so the error will always reduce (with occasional rare exceptions in the case of ¹E_cal). However, cross-validated errors normally reach a minimum as the correct number of components are found and then increase afterwards. This is because later components really represent noise and not systematic information in the data.

Fig. 18 E_cv for acenaphthylene using PLS1 as described in Section 3.2.

Cross-validation has two main purposes.

1. It can be employed as a method for determining how many components characterise the data. From Fig. 18, it appears that nine components are necessary to obtain an optimum model for acenaphthylene. This number will rarely equal the number of chemicals in the mixture, as spectral similarities will often reduce this, whereas impurities and noise may increase it.

2. It can be employed as a fairly realistic error estimate for predictive ability. The minimum cross-validated prediction error for acenaphthylene of 0.040 mg L⁻¹ equals 33.69%. This compares with an autopredictive error of 0.014 mg L⁻¹ or 11.64% using ten components and PLS1 which is a very over-optimistic estimate.

Many refinements to cross-validation have been proposed in the literature. It is possible to perform cross-validation on the x block to determine the optimum number of components instead of the c block. There are several alternative approaches to cross- validation, a common one involving leaving larger proportions of the data out (e.g. one tenth) at a time, valuable for very large datasets. Some statisticians also propose methods involving removing individual measurements rather than individual objects or spectra, but such approaches are less used in analytical chemistry. The ‘leave one sample out at a time’ method is a popular, easily implemented, and widespread approach. There tends to be a significant divide between statisticians who may use a number of different sophisticated methods for cross-validation and analytical chemists who are generally satisfied with a straightforward approach.

3.3  Independent test sets

A significant weakness of cross-validation, is that it depends on the design and scope of the original dataset used to form the model. This dataset is often called a ‘training’ set. Consider a situation in which a series of mixture spectra are recorded, but it happens that the concentrations of two compounds are correlated, so that the concentration of compound A is high when compound B likewise is high, and vice versa. A calibration model can be obtained from analytical data, which predicts both concentrations well. Even cross-validation might suggest the model is good. However, if asked to predict a spectrum where compound A is in a high concentration and compound B in a low concentration it is likely to give very poor results, as it has not been trained to cope with this new situation. Cross-validation is very useful for removing the influence of internal factors such as instrumental noise or dilution errors but cannot help very much if there are correlations in the concentration of compounds in the training set.

In some cases there will inevitably be correlations in the concentration data, because it is not easy to find samples without this. An example is in many forms of environmental monitoring. Several compounds often arise from a single source. For example, PAHs are well known pollutants, so if one or two PAHs are present in high concentrations it is a fair bet that others will be too. There may be some correlations, for example, in the occurrence of compounds of different molecular weights if a homologous series occurs, e.g. as the by-product of a biological pathway, there may be an optimum chain length which is most abundant in samples from a certain source. It would be hard to find field samples in which the concentrations of all compounds vary randomly. Consider, for example, setting up a model of PAHs coming from rivers close to several specific sources of pollution. The model may behave well on this training set, but can it be safely used to predict the concentrations of PAHs in an unknown sample from a very different source? Another serious problem occurs in process control. Consider trying to set up a calibration model using NIR to determine the concentration of chemicals in a manufacturing process. If the factory is behaving well, the predictions may be good, but it is precisely to detect problems in the process that the calibration model is effective: is it possible to rely on the predictions if data have a completely different structure?

Instead of validating the predictions internally, it is possible to test the predictions against an independent data set, often called a ‘test’ set. Computationally the procedure is similar to cross-validation. For example, a model is obtained using I samples, and then the predictions are calculated using an independent test set of L samples, to give

The value of ĉ_l is determined in exactly the same way as per cross-validation (Section 3.2), but the calibration model is obtained only once, from the training set.

In case study 1, we can use the data arising from Table 1 (dataset A) for the training set (see above), but test the predictions using the spectra obtained from concentrations in Table 2 (dataset B). In this case, each dataset has the same number of samples, but this is not at all a requirement. The graph of E_test for acenaphthylene is presented in Fig. 19 and shows similar trends to that of E_cv although the increase in error when a large number of components are calculated is not so extreme. The minimum error is 35.78%, only slightly higher than for cross-validation. Normally the minimum test set error is higher than that for cross-validation, but if the structure of the test set is encompassed in the training set, these two errors will be very similar.

Fig. 19 E_testfor acynaphthylene, using PLS1 as described in Section 3.3.

If, however, we use dataset B as the training set and dataset A as the test set, a very different story emerges as shown in Fig. 20 for acenaphthylene. The autopredictive and cross-validation errors are very similar to those obtained for dataset A: the value of ¹E_cal using ten PLS components is 8.71%, compared with 11.34% and the minimum value of E_cv is 27.93% compared with 33.69%. However, the test set behaves differently and exhibits a minimum error of 49.12%, well in excess of the cross-validation error. Furthermore, E_test is always higher than E_cvexcept when a very large number of components have been calculated. When the model of dataset A is used to predict dataset B, it is found that there is not such a significant difference between the two types of errors.

Fig. 20 Autopredictive, cross−validation and test errors for dataset B (acynaphthylene) and PLS1.

Hence dataset A is a good test set because it not only predicts itself well but also dataset B, but the reverse is not true. This suggests that dataset A encompasses the features of dataset B, but not the reverse. The reason for this apparent dichotomy will be discussed in greater detail in Section 3.4, and it is important to recognise that cross-validation can sometimes give a misleading and over-optimistic answer. However, this depends in part on the practical aim of the analysis. If, for example, data of the form of A are unlikely ever to occur, it is safe to use the model obtained from B for future predictions. For example, if it is desired to determine the amount of vitamin C in orange juices from a specific region of Spain, it might be sufficient to develop a calibration method only on these juices. It could be expensive and time-consuming to find a more representative calibration set. Is it really necessary or practicable to develop a method to measure vitamin C in all conceivable orange juices or foodstuffs? The answer is no, so, in some circumstances, living within the limitations of the original dataset is entirely acceptable. If at some future date extra orange juice from a new region is to be analysed, the first step is to set up a dataset from this new source of information as a test set and so determine whether the new data fit into the structure of the existing database or whether the calibration method must be developed afresh. It is, though, very important to recognise the limitations of calibration models especially if they are to be applied to situations that are wider than those represented by the initial training sets.

There are a number of variations on the theme of test sets, one being simply to take a few samples from a large training set and assign them to a test set, for example, take five out of the 25 samples from case study 1 (dataset A) and assign them to a test set, using the remaining 20 samples for the training set. Alternatively, datasets A and B could be combined, and 40 out of the 50 used for determining the model, the remaining ten for independent testing.

3.4  Experimental designs

One of the major problems arises in designing an adequate training set. In some cases it is not possible to control this easily (for example when sampling in the field) but in other situations, such as preparing mixtures in the laboratory, good design is possible.

Many brush aside the design of training sets, often using empirical or random approaches. Some chemometricians recommend huge training sets of several thousand samples so as to get a representative distribution, especially if there are known to be half a dozen or more significant components in a mixture. In large industrial calibration models such a procedure is often considered important for robust predictions. This approach, though, is expensive in time and resources, and rarely possible in routine laboratory studies. More seriously, many instrumental calibration models are unstable, so calibration on Monday might vary significantly from calibration on Tuesday, hence if calibrations are to be repeated at regular intervals, the number of spectra in the training set must be limited. Finally very ambitious calibrations can take months or even years to develop, by which time instruments and often the detection methods are replaced. It is always important to consider resources available and balance how robust a model is required, and how frequently the measurement system will change.

For the most effective calibration models, it is best to determine carefully the nature of the training set using rational experimental design prior to investing time in experimentation. Provided that the spectra are linearly additive, and there are no serious baseline problems or interactions, there are standard designs that can be employed to obtain training sets. In fact, the majority of chemometric techniques for regression and calibration assume linear additivity. In the case where this may not be so, either the experimental conditions can be modified (for example if the concentration of a compound is too high so the absorbance does not obey the Beer–Lambert law the solution is simply diluted) or various approaches for multilinear modelling are required.

In calibration it is normal to use several concentration levels to form a model. Hence two-level designs³⁷ (often presented as fractional factorials) are inadequate and typically four or five concentration levels are required for each compound. Chemometric techniques are most useful for multicomponent mixtures. Consider an experiment carried out in a mixture of methanol and acetone. What happens if the concentrations of acetone and methanol in a training set are completely correlated? If the concentration of acetone increases so does that of methanol, and similarly with a decrease. Such an experimental arrangement is shown in Fig. 21. A more satisfactory design is given in Fig. 22, in which the two concentrations are completely uncorrelated or orthogonal. In the former design there is no way of knowing whether a change in spectral characteristic results from change in concentration of acetone or of methanol. If this feature is consciously built into the training set and expected in all future samples, there is no problem, but if a future sample arises with a high acetone and low methanol concentration, calibration software will give a wrong answer for the concentration of each component. This is potentially very serious especially when the result of chemometric analysis of spectral data is used to make decisions, such as the quality of a batch of pharmaceuticals, based on the concentration of each constituent as predicted by computational analysis of spectra. In the absence of any certain knowledge (for example that in all conceivable future samples the concentrations of acetone and methanol will be correlated), it is safest to design the training set so that the concentrations of as many compounds as possible in a calibration set are orthogonal. Note that this type of orthogonality is different from the orthogonality or similarity between the spectra of each compound. Many users of chemometric calibration have a background in spectroscopy rather than experimental design and confuse these two concepts.

Fig. 21 Two factor, correlated, design.

Fig. 22 Two factor, uncorrelated, design.

A guideline to designing a series of multicomponent mixtures for calibration is described below: more details are available elsewhere.^38,39

1. Determine how many components in the mixture (=k) and the maximum and minimum concentration of each component. Remember that, if studied by spectroscopy, the overall absorbance when each component is at a maximum should be within the Beer–Lambert limit (about 1.2 A for safety).

2. Decide how many concentration levels are required for each compound (=l), typically four or five. Mutually orthogonal designs are only possible if the number of concentration levels is a prime number or a power of a prime number, meaning that they are possible for 3, 4, 5, 7, 8 and 9 levels but not 6 or 10 levels.

3. Decide on how many mixtures to produce. Designs exist involving N = ml^p mixtures, where l equals the number of concentration levels, p is an integer at least equal to 2, and m an integer at least equal to 1. Setting both m and p at their minimum values, at least 25 experiments are required to study a mixture (of more than one component) at five concentration levels.

4. The maximum number of mutually orthogonal compound concentrations in a mixture design where m = 1 is four for a three-level design, five for a four-level design and 12 for a five- level design. We will discuss how to extend the number of mutually orthogonal concentrations below. Hence choose the design and number of levels with the number of compounds of interest in mind.

The method for setting up a calibration design will be illustrated by a five-level, eight compound, 25 experiment, mixture, to give the design in Table 22.

Table 22 Construction of an orthogonal calibration design for eight compounds and 25 levels

---

1. The first step is to number the levels, typically from −2 (lowest) to +2 (highest), corresponding to coded concentrations, e.g. the 0.7–1.1 mM; note that the coding of the concentrations can be different for each compound in a mixture.

2. Next, choose a repeater level, recommended to be the middle level, 0. For between 7 and 12 factors, and a five-level design, it is essential that this is 0. The first experiment is at this level for all factors.

3. Third, select a cyclical permuter for the remaining (l − 1) levels. This relates each of the four levels as will be illustrated below; only certain cyclic generators can be used namely −2→−1→2→1→−2 and −2→1→2→−1→−2 which have the property that factors j and j + l + 1 are orthogonal. For less than seven factors, the nature of this generator is not relevant, so long as it includes all four levels. One such permuter is illustrated in Fig. 23, used in the example below.

Fig. 23 A possible permuter

4. Finally, select a difference vector; this consists of l − 1 numbers from 0 to l − 2, arranged in a particular sequence. Only a very restricted set of such vectors are acceptable of which [0 2 3 1] is an example. The use of the difference vector will be described below.

5. Then generate the first column of the design consisting of l² (= 25) levels in this case, each level corresponding to the concentration of the first compound in the mixture in each of 25 experiments.

(a) The first experiment is at the repeater level for each factor.

(b) The l − 1 (=4) experiments 2, 8, 14 and 20 are at the repeater level. In general the experiments 2, 2 + l + 1, 2 + 2 (l + 1) up to 2 + (l − 1) × (l + 1) are at this level. These divide the columns into ‘blocks’ of five (= l) experiments.

(c) Now determine the levels for the first block, from experiments 3 to 7 (or in general terms experiments 3 to 2 + l). Experiment 3 can be at any level apart from the repeater. In the example below, we use level −2. The key to the conditions for the next four experiments is the difference vector. The conditions for the 4th experiment are obtained from the difference vector and cyclic generator. The difference vector [0 2 3 1] implies that the second experiment of the block is 0 cyclical differences away from the 3rd experiment or −2 using the cyclic permuter of Fig. 23. The next number in the difference vector is 2, making the 5th experiment at level 2 which is two cyclic differences from −2 . Continuing, the 6th experiment is three cyclic differences from the 5tht experiment or at level −1, and the final experiment of the block is at level 2.

(d) For the second block (experiments 9–13), simply shift the first block by one cyclic difference using the permuter of Fig. 23 and continue until the last (or fourth) block is generated.

6. Then generate the next column of the design as follows:

(a) The concentration of the second compound for the first experiment is always at the repeater level.

(b) The concentration for the second experiment is at the same level as the third experiment of the previous column, up to the 24th [ or (l² − 1)th] experiment.

(c) The final experiment is at the same level as the second experiment for the previous compound.

7. Finally, generate successive columns using step 6 above.

The development of the design is illustrated in Table 22. Such designs can also be denoted l-level partial factorial designs. Note that a full five-level factorial design for eight compounds would require 5⁸ or 390625 experiments, so there has been a dramatic reduction in the number of experiments required.

There are a number of important features to note about the design in Table 22. 1. In each column there are an equal number of −2, −1, 0, +1 and +2 levels. 2. Each column is orthogonal to every other column, that is the correlation coefficient is 0. 3. A graph of the levels of any two factors against each other is given in Fig. 24(a) for each combination of factors except factors 1 and 7, and 2 and 8, which graph is given in Fig. 24(b). It can be seen that in most cases the levels of any two factors are distributed exactly as they would be for a full factorial design, which would require almost half a million experiments. The nature of the difference vector is crucial to this important property. Some compromise is required between factors differing by l + 1 (or 6) columns, such as factors 1 and 7. This is unavoidable unless more experiments are performed.

Fig. 24 Graph of levels of (a) factor 2 versus 1 and (b) factor 7 versus 1 for the data of Table 20.

It is possible to expand the number of factors using a simple trick of matrix algebra. If a matrix A is orthogonal, then the matrix

is also orthogonal. Therefore, new matrices can be generated from the original orthogonal designs, to expand the number of compounds in the mixture.

Any design can be checked for orthogonality, simply by determining the correlation coefficients between the concentrations of the various compounds. If the correlations are 0, then the design is a good one, and will result in a training set that spans the possible mixture space fairly evenly, whereas if there are correlations, the training set is less representative. Table 23 presents the correlations for datasets A and B of case study 1. It can be seen that the first is orthogonal, whereas the second contains correlations. This structure allows us to interpret the results of Section 3.3. The model from the well designed dataset A both predicts itself well and also predicts dataset B. However, although dataset B is well predicted using itself as a model (cross-validation) it does not provide such good predictions for the more representative dataset A.

Table 23 Correlations between concentrations for case study 1 and (a) dataset A and (b) dataset B

(a)
	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
Py	1.00
Ace	0.00	1.00
Anth	0.00	0.00	1.00
Acy	0.00	0.00	0.00	1.00
Chry	0.00	0.00	0.00	0.00	1.00
Benz	0.00	0.00	0.00	0.00	0.00	1.00
Fluora	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Fluore	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Nap	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00
Phen	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	1.00

---

(b)
	Py	Ace	Anth	Acy	Chry	Benz	Fluora	Fluore	Nap	Phen
Py	1
Ace	0.34	1
Anth	0.34	0.34	1
Acy	0.04	0.34	0.34	1
Chry	−0.38	0.04	0.34	0.34	1
Benz	−0.38	−0.38	0.04	0.34	0.34	1
Fluora	−0.9	−0.38	−0.38	0.04	0.34	0.34	1
Fluore	−0.34	−0.9	−0.38	−0.38	0.04	0.34	0.34	1
Nap	−0.34	−0.34	−0.9	−0.38	−0.38	0.04	0.34	0.34	1
Phen	−0.04	−0.34	−0.34	−0.9	−0.38	−0.38	0.04	0.34	0.34	1

---

It is always important to consider the issues of design and orthogonality of training sets, as this provides clear guidance as to when the model is likely to perform adequately, and so the scope of the calibration.

4 Conclusions and discussion

There are many topics omitted from this review, some of which are listed below.

Data preprocessing is important in multivariate calibration. Indeed, the relationship between even basic procedures such as centring the columns is not always clear, most investigators following conventional methods, that have been developed for some popular application but are not always appropriately transferable. Variable selection and standardisation can have a significant influence on the performance of calibration models.

Non-linearities occur in some forms of spectroscopy, especially when the absorbance is high, and greater effort has been made to enhance the basic PLS method to include squared and other terms. However, the analytical chemist will probably prefer to improve the experimental method of acquiring data. Non-linear calibration is most valuable in other areas of chemistry, such as QSAR, where a purely additive linear model is not necessarily expected.

Outlier detection is of concern in certain areas of science. The aim is to spot samples that do not appear to conform to the structure of the training set used to determine the calibration model. If outlying samples are treated in the normal way, inaccurate concentrations may be predicted; this is a consequence of experimental design of the training set. In the case of field samples, it is not always possible to produce training sets with orthogonal designs, so only samples with a similar structure will result in sensible predictions.

Multiway methods can be extended far beyond trilinear PLS1, and there are many cases in chemistry where such approaches are appropriate. However, in the case of calibration of analytical signals to determine concentrations, trilinear PLS1 is adequate in the majority of situations.

Users of a specific software package can often be overwhelmed by statistical output, but it is important to recognise that certain types of diagnostics are only really useful for particular problems. The huge influence that NIR had on the first applications of multivariate calibration has meant that several software packages are oriented heavily to the user of NIR instruments. Although a major success story in the history of chemometrics, it is for the analytical chemist to judge whether NIR will play a huge role in the future, or whether there are fertile new grounds for the detailed development of multivariate calibration methods throughout quantitative analytical chemistry.

It is important to understand the overall principles of the methods rather than rely too much on any individual piece of software or application. In fact the algorithms are straightforward and can be easily implemented computationally. For any individual instrumental technique, be it HPLC, or electrochemistry, or electronic absorption spectroscopy, and any specific application, such as process control or environmental monitoring, specific extensions are needed, and different workers from different scientific environments often assume that their own elaborations are generally transportable. This is often not the case, but a basic understanding of the methods reported in this paper provides a generic starting point for analytical calibration.

Acknowledgements

Steve Wilkes is thanked for obtaining case study 1 experimentally, and Kostas Zissis for case study 2. Les Erskine is thanked for producing Excel add-ins and validating the calculations, and Rasmus Bro for valuable comments on multiway calibration.

Appendices

A1 Vectors and matrices

A1.1 Notation and definitions. A single number is often called a scalar, and denoted in italics, e.g. x.

A vector consists of a row or column of numbers and is denoted as bold lower case italics e.g.x. For example x = (7 8 11 −5) is a row vector and y = a column vector.

A matrix is a two dimensional array of numbers and is denoted as bold upper case italics e.g.X. For example X = is a matrix.

The dimensions of a matrix are normally presented with the number of rows first and the number of columns second, and vectors can be represented as matrices with one dimension equal to 1, so that x above has dimensions 1 × 4 and X has dimensions 2 × 3.

A square matrix is one where the number of columns equals the number of rows. For example is a square matrix.

An identity matrix is a square matrix whose elements are equal to 1 in the diagonal and 0 elsewhere, and is often called I. For example I = is an identity matrix.

The individual elements of a matrix are often referenced as scalars, with subscripts referring to the row and column; hence, in the matrix above, y₂₁ = 6 which is the element in row 2 and column 1.

A1.2 Matrix operations.. Transposing a matrix involves swapping the columns and rows around, and is denoted by a right-hand-side superscript. For example, if Z = then

Matrix and vector multiplication using the ‘dot’ product is denoted by the symbol ‘.’ between matrices. It is only possible to multiply two matrices together if the number of columns of the first matrix equal the number of rows of the second matrix. The number of rows of the product will equal the number of rows of the first matrix, and the number of columns equal the number of columns of the second matrix. Hence a 3 × 2 matrix when multiplied by a 2 × 4 matrix will give a 3 × 4 matrix.

Multiplication of matrices is not commutative, that is A.B ≠ B.A even if the second product is allowable. Matrix multiplication can be expressed as summations. For arrays with more than two dimensions (e.g. tensors), conventional symbolism can be awkward and it is probably easier to think in terms of summations.

If matrix A has dimensions I × J and matrix B has dimensions J × K then the product C of dimensions I × K has elements defined by

When several matrices are multiplied together it is normal to take any two neighbouring matrices, multiply them together and then multiply this product with another neighbouring matrix. It does not matter in what order this is done, hence A.B.C = (A.B).C = A.(B.C).

Most square matrices have inverses, defined by the matrix which when multiplied with the original matrix gives the identity matrix, and is represented by a ⁻¹ as a right-hand-side superscript, so that D.D⁻¹ = I. Note that some square matrices do not have inverses: this is caused by there being correlations in the columns or rows of the original matrix.

An interesting property that chemometricians sometimes use is that the product of the transpose of a column vector with itself equals the sum of square of elements of the vector, so that x′.x = Σx².

A2 Algorithms

There are many different descriptions of the various algorithms in the literature. This appendix describes one algorithm for each of four regression methods.

A2.1 Principal components analysis. NIPALS is a common, iterative, algorithm.

Initialisation

1. Take a matrix Zand if required preprocess (e.g. mean-centre or standardise) to give the matrix X which is used for PCA.

The next principal component

2. Take a column of this matrix (often the column with greatest sum of squares) as the first guess of the scores first principal component, call it ^initialt̂.

Iteration for each principal component

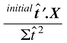3. Calculate ^unicormp̂ = Comment: ideally t.p = X,  so, pre-multiplying each side by t′ we would have  t′.t. p = ∑t²p ≈ t′X for an exact fit, leading to the   approximation above.

4. Normalise the guess of the loadings, so

Comment: this forces the sum of squares of the loadings to   equal one.

5. Now calculate a new guess of the scores^newt̂ = X.p̂′  Comment: ideally t.p = X,  so, post-multiplying each side by p we would have  t. p = X.p′.p = X since p is normalised, so its sum of   squares equals 1.

Check for convergence

6. Check if this new guess differs from the first guess, a simple approach is to look at the size of the sum of square difference in the old and new scores, i.e. Σ(^initialt −^newt)². If this is small the PC has been extracted, set the PC scores and loadings for the current PC to t̂ and p̂. Otherwise return to step 3, substituting the initial scores by the new scores.

Compute the component and calculate residuals

7. Subtract the effect of the new PC from the data matrix to get a residual data matrix  ^residX = X − t.p.

Further PCs

8. If it is desired to compute further PCs, substitute the residual data matrix for X and go to step 2.

A2.2 PLS1. There are several implementations, the one below is non-iterative.

Initialisation

1. Take a matrix Z and if required preprocess (e.g. mean-centre or standardise) to give the matrix X which is used for PLS.

2. Take the concentration vector k and preprocess it to give the vector c which is used for PLS. Note that if the data matrix Z is centred down the columns, the concentration vector must also be centred. Generally, centring is the only form of preprocessing useful for PLS1. Start with an estimate of ĉ that is a vector of 0s (equal to the mean concentration if the vector is already centred).

The next PLS component

3. Calculate the vector h = X′.c  Comment: sometimes a weighting vector s is employed, the aim being to obtain X from c or the concentrations from the observed data. For a one component mixture, ideally,

X = c. s

or

X′ .X . s′ = X′ . c. s . s′

giving

X′ .X . s′ = X′ . c. s . s′

h = X′ .X . s′ (s . s′)⁻¹ = X′ . c. (s . s′) (s . s′)⁻¹ = X′.c  The equation can also be expressed by a summation

4. Calculate the scores which are simply given by

5. Calculate the x loadings by

Comment: note that these are normalised again.

6. Calculate the c loading (a scalar) by

Comment: note this calculation is identical in nature with the x loadings except that X is replaced by c.

Compute the component and calculate residuals

7. Subtract the effect of the new PC from the data matrix to get a residual data matrix

^residX = X − t.p

8. Determine the new concentration estimate by

^newĉ = ^initialĉ + t.q

and sum the contribution of all components calculated to give an estimated ĉ. Note that the initial concentration estimate is 0 (or the mean) before the first component has been computed. Calculate

^residc = ^truec − ĉ

where ^truec contains, like all values of c, preprocessing (such as centring).

Further PLS components

9. If further components are required, replace both X and c by the residuals and return to step 3.

A2.3 PLS2. This is a straightforward, iterative, extension of PLS1. Only small variations are required. Instead of c being a vector it is now a matrix C and instead of q being a scalar it is now a vector q.

Initialisation

1. Take a matrix Z and if required preprocess (e.g. mean-centre or standardise) to give the matrix X which is used for PLS.

2. Take the concentration matrix K and preprocess it to give the matrix C which is used for PLS. Note that if the data matrix is centred down the columns, the concentration vector must also be centred. Generally, centring is the only form of preprocessing useful for PLS2. Start with an estimate of Ĉ that is a matrix of 0s (equal to the mean concentration if the matrix is already centred).

3. An extra step is required to identify a vector u which can be a guess (as in PCA), but it can be chosen as one of the columns in the initial preprocessed concentration matrix, C.

The next PLS component

4. Calculate the vector

h = X′.u

5. Calculate the guessed scores by

6. Calculate the guessed x loadings by

7. Calculate the c loadings (a vector rather than scalar in PLS2) by

8. If this is the first iteration, remember the scores, and call them ^initialt, then produce a new vector u by

and return to step 4.

Check for convergence

9. If this is the second time round compare the new and old scores vectors, for example, by looking at the size of the sum of square difference in the old and new scores, i.e. Σ(^initialt − ^newt)². If this is small the PC has been adequately modelled, set the PC scores and both types of loadings for the current component to t̂, and p̂, and q̂. Otherwise calculate a new value of u as in step 8 and return to step 4.

Compute the component and calculate residuals

10. Subtract the effect of the new PC from the data matrix to get a residual data matrix

^residX = X − t.p

11. Determine the new concentration estimate by

^newĈ = Ĉ + t.q

and sum the contribution of all components calculated to give an estimated ĉ. Calculate

^residC = ^trueC − Ĉ

Further PLS components

12. If further components are required, replace both X and C by the residuals and return to step 4.

A2.4 Tri-linear PLS1. The algorithm below is based closely on PLS1 and is suitable when there is only one column in the c vector.

Initialisation

1. Take a three way tensor Z and if required preprocess (e.g. mean-centre or standardise) to give the tensor X which is used for PLS. Perform all preprocessing on this tensor. The tensor has dimensions I × J × K. 2. Preprocess the concentrations if appropriate to give a vector c.

The next PLS component

3. From the original tensor, create a new matrix H with dimensions J × K which is the sum of each of the I matrices for each of the samples multiplied by the concentration of the analyte for the relevant sample i.e.

H = X₁ c₁ + X₂ c₂ + …. X_Ic_I

or, as a summation
Comment: this is analogous to the vector h in PLS1, given by
4. Perform PCA on H to obtain the scores and loadings, ^gt and ^gp for the first PC of H. Note that only the first PC is retained, and for each PLS component a fresh H matrix is obtained. 5. Calculate the two x loadings for the current PC of the overall dataset by normalising the scores and loadings of Hi.e
Comment: in most cases ^hp will already be normalised, so the second step is not needed. 6. Calculate the overall scores by
Comment: this is sometimes expressed in the form of tensor multiplication, but this is not always an easy concept. However, there are strong analogies to PLS1, since
because the two loadings vectors are normalised, hence their sum of squares equals 1.Therefore, analogous to step 4 of PLS1
where the symbol ⊗ is sometimes used to indicate tensor multiplication. 7. Calculate the c loadings vector

q= (T′.T)⁻¹.T′.c

where T is the scores matrix, each column consisting of one component (a vector for the first PLS component).Comment: in PLS1 each element of the c loadings can be calculated independently. This is not possible with PLS2, as the scores are not orthogonal, so the loadings vector needs to be recalculated after each component.

Compute the component and calculate residuals

8. Subtract the effect of the new PC from the original data matrix to get a residual data matrix (for each sample i)

^residX _i = X_i − t_i.^j p.^k p

9. Determine the new concentration estimates by

ĉ = T.q

Calculate

^residc = ^truec − ĉ

Further PLS components

10. If further components are required, replace both X and c by the residuals and return to step 3.

References

1. D. L. Massart, B. G. M. Vandeginste, S. N. Deming, Y. Michotte and L. Kaufman, Chemometrics: A Textbook, Elsevier, Amsterdam, 1988..
2. P. W. Araujo, D. A. Cirovic and R. G. Brereton, Analyst, 1996, 121, 581.
3. C. Demir and R. G. Brereton, Analyst, 1998, 123, 181.
4. K. D. Zissis, R. G. Brereton, S. Dunkerley and R. E. A. Escott, Anal. Chim. Acta, 1999, 384, 71.
5. D. A. Cirovic, R. G. Brereton, P. T. Walsh, J. Ellwood and E. Scobbie, Analyst, 1996, 121, 575.
6. B. G. Osborne and T. Fearn, Near Infrared Spectroscopy in Food Analysis, Longman, London, 1986..
7. H. Martens and T. Næs, Multivariate Calibration, Wiley, Chichester, 1989..
8. P. Geladi and B. R. Kowalski, Anal. Chim. Acta, 1986, 185, 1.
9. S. Wold, H. Martens and H. Wold, Proc. Conf. Matrix Pencils, Lecture Notes in Mathematics, Springer-Verlag, Heidelberg, 1983, p. 286..
10. A. Høskuldsson, J. Chemom, 1988, 2, 211.
11. R. Manne, Chemom. Intell. Lab. Syst., 1987, 2, 187.
12. P. J. Brown, J. R. Stat. Soc., Ser. B, 1982, 44, 287.
13. K. R. Beebe, R. J. Pell and M. B. Seasholtz, Chemometrics: A Practical Guide, Wiley, New York, 1998..
14. S. Wold, C. Albano, W. J. Dunn III, K. Esbensen, S. Hellberg, E. Johansson and M. Sjøstrøm, in Food Research and Data Analysis, ed. H. Martens and H. Russworm, Applied Science Publishers, London, 1983, p. 147..
15. http://www.infometrix.com/..
16. http://www.camo.no/..
17. http://www.umetrics.com/..
18. http://www.eigenvector.com/..
19. M. Thompson, D. W. Brown, T. Fearn, M. J. Gardner, E. J. Greenhow, R. Howarth, J. N. Miller, E. J. Newman, B. D. Ripley, K. J. Swan, A. Williams, R. Wood and J. J. Wilson, Analyst, 1994, 119, 2363.
20. J. N. Miller, Analyst, 1991, 116, 3.
21. J. N. Miller and J. C. Miller, Statistics for Analytical Chemistry, Ellis Horwood, Chichester, 1988..
22. C. Eisenhart, Ann. Math. Stat., 1939, 10, 162.
23. R. N. Draper and H. Smith, Applied Regression Analysis, Wiley, New York, 2nd edn., 1981..
24. D. L. Massart, B. G. M. Vandeginste, L. M. C. Buydens, S. de Jong, P. J. Lewi and J. Smeyers-Verbeke, Handbook of Chemometrics and Qualimetrics, Part A, Elsevier, Amsterdam, 1997..
25. R. J. Porra, in Chlorophyll, ed. H. Scheer, CRC Press, Boca Raton, FL, 1991, p. 31..
26. R. G. Brereton, Multivariate Pattern Recognition in Chemometrics, Illustrated by Case Studies, Elsevier, Amsterdam, 1992..
27. R. G. Brereton, Chemometrics: Applications of Mathematics and Statistics to Laboratory Systems, Ellis Horwood, Chichester, 1993..
28. S. Wold, K. Esbensen and P. Geladi, Chemom. Intell. Lab. Syst., 1987, 2, 37.
29. K. V. Mardia, J. T. Kent and J. Bibby, Multivariate Analysis, Academic Press, London, 1979..
30. R. G. Brereton, Analyst, 1995, 120, 2313.
31. H. Martens and T. Næs, in Near-infrared Technology in Agricultural and Food Industries, ed. P. C. Williams and K. Norris, American Association of Cereal Chemists, St. Paul, MN, 1987, p. 57..
32. A. K. Smilde, P. Geladi and R. Bro, Multiway Analysis in Chemistry, Wiley, Chichester, 2000..
33. R. Bro, J. Chemom., 1996, 10, 47.
34. P. Geladi, Chemom. Intell. Lab. Syst., 1989, 7, 11.
35. S. Wold, P. Geladi, K. Esbensen and J. Öhman, J. Chemom., 1987, 1, 41.
36. S. de Jong, J. Chemom., 1998, 12, 77.
37. S. N. Deming, S. L. Morgan, Experimental Design: A Chemometric Approach, Elsevier, Amsterdam, 2nd edn., 1993..
38. R. G. Brereton, Analyst, 1997, 122, 1521.
39. J. Aybar Munoz and R. G. Brereton, Chemom. Intell. Lab. Syst., 1998, 43, 89.

---

Footnote

† Electronic Supplementary Information available. See http://www.rsc.org/suppdata/an/b0/b003805i/

---