Statistical ensemble inequivalence for flexible polymers under confinement in various geometries
Abstract
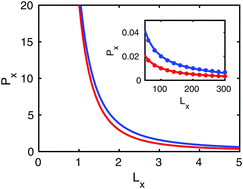
The problem of statistical ensemble inequivalence for single polymers has been the subject of intense research. In a recent publication, we show that even though the force–extension relation of a free Gaussian chain exhibits ensemble equivalence, confinement to half-space due to tethering to a planar substrate induces significant inequivalence [S. Dutta and P. Benetatos, Soft Matter, 2018, 14, 6857–6866]. In the present article, we extend that work to the conformational response to confining forces distributed over surfaces. We analyze in both the Helmholtz and the Gibbs ensemble the pressure–volume equation of state of a chain in rectangular, spherical, and cylindrical confinement. We especially consider the case of a directed polymer in a cylinder. We also analyze the case of a tethered chain inside a rectangular box, a sphere, and outside a sphere. In general, confinement causes significant ensemble inequivalence. Remarkably, we recover ensemble equivalence in the limit of squashing confinement. We trace the ensemble inequivalence to the persistence of strong fluctuations. Our work may be useful in the interpretation of single molecule experiments and caging phenomena.


 Please wait while we load your content...
Please wait while we load your content...