Towards a statistical mechanical theory of active fluids
Abstract
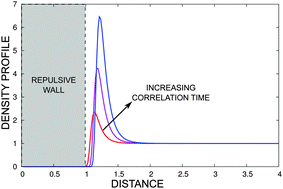
We present a stochastic description of a model of N mutually interacting active particles in the presence of external fields and characterize its steady state behavior in the absence of currents. To reproduce the effects of the experimentally observed persistence of the trajectories of the active particles we consider a Gaussian force having a non-vanishing correlation time τ, whose finiteness is a measure of the activity of the system. With these ingredients we show that it is possible to develop a statistical mechanical approach similar to the one employed in the study of equilibrium liquids and to obtain the explicit form of the many-particle distribution function by means of the multidimensional unified colored noise approximation. Such a distribution plays a role analogous to the Gibbs distribution in equilibrium statistical mechanics and provides complete information about the microscopic state of the system. From here we develop a method to determine the one- and two-particle distribution functions in the spirit of the Born–Green–Yvon (BGY) equations of equilibrium statistical mechanics. The resulting equations which contain extra-correlations induced by the activity allow us to determine the stationary density profiles in the presence of external fields, the pair correlations and the pressure of active fluids. In the low density regime we obtained the effective pair potential ϕ(r) acting between two isolated particles separated by a distance, r, showing the existence of an effective attraction between them induced by activity. Based on these results, in the second half of the paper we propose a mean field theory as an approach simpler than the BGY hierarchy and use it to derive a van der Waals expression of the equation of state.

 Please wait while we load your content...
Please wait while we load your content...