Cluster and reentrant anomalies of nearly Gaussian core particles
Abstract
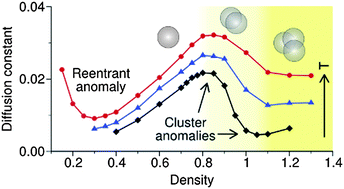
We study through integral equation theory and numerical simulations the structure and dynamics of fluids composed of ultrasoft, nearly Gaussian particles. Namely, we explore the fluid phase diagram of a model in which particles interact via the generalized exponential potential u(r) = εexp[−(r/σ)n], with a softness exponent n slightly larger than 2. In addition to the well-known anomaly associated with reentrant melting, the structure and dynamics of the fluid display two additional anomalies, which are visible in the isothermal variation of the structure factor and diffusivity. These features are correlated with the appearance of dimers in the fluid phase and with the subsequent modification of the cluster structure upon compression. We corroborate these results through an analysis of the local minima of the potential energy surface, in which clusters appear as much tighter conglomerates of particles. We find that reentrant melting and clustering coexist for softness exponents ranging from 2+ up to values relevant for the description of amphiphilic dendrimers, i.e., n = 3.
- This article is part of the themed collection: Emerging Investigators

 Please wait while we load your content...
Please wait while we load your content...