Mathematical methods on atomic force microscope cantilever systems
Abstract
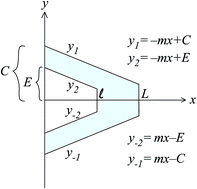
The ever increasing demand to analyse substrates means that an improved theoretical understanding is necessary for atomic force microscope cantilevers. In this study, we utilize fundamental mathematical modelling, comprising the Lennard-Jones potential and techniques involving the calculus of variations, to obtain the energy equations arising from the probe and the substrate, leading to the deflection equations of the cantilever. Here we assume a silicon tip and the substrate surface is assumed to be a graphene sheet. Based on an energy calculation, the most stable system occurs where the probe is 0.206 nm away from the substrate, and this value exists independently of the size and tilt angle of the probe. For the deflection of the cantilever, we apply the calculus of variations to the separate domains, considering derivatives up to third order at the connection point. The deflection behaviour of a V shaped plate depends primarily on its length, and the spring constants of various cantilevers are calibrated from the deflection equations. In comparison to the zeroth order method of previous studies, our method predicts a 30–50% difference in the value of their spring constants. Moreover, we observe the bending behaviour of cantilever systems by considering the energy between the probe and the substrate together with the bending energy in the cantilever, and we find that the maximum bending distance at the tip is in the range between 0.09 nm and 0.2 nm.

 Please wait while we load your content...
Please wait while we load your content...