Quantum level structures at a Fermi resonance with angular momentum: classical periodic orbits, catastrophe maps and quantum monodromy

Abstract

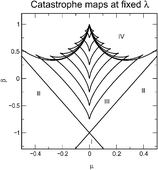
The Xiao–Kellman catastrophe map, for the classification of classical periodic orbits of the standard 2 : 1 Fermi resonance Hamiltonian is extended to species with finite vibrational angular momentum. The influence of the classical periodic orbit structure on different organizations of the quantum mechanical eigenvalues, in the four regions of the map, is strikingly demonstrated. The quantum eigenvalue lattices in angular momentum and energy space show dislocations attributable to a topological effect, termed quantum monodromy. Analogues with quantum monodromy in quasi-linear molecules and LiCN/LiNC isomerisation are demonstrated.