Structured randomness: jamming of soft discs and pins

Abstract

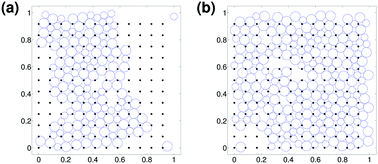
Simulations are used to find the zero temperature jamming threshold, ϕ_j, for soft, bidisperse disks in the presence of small fixed particles, or “pins”, arranged in a lattice. The presence of pins leads, as one expects, to a decrease in ϕ_j. Structural properties of the system near the jamming threshold are calculated as a function of the pin density. While the correlation length exponent remains ν = 1/2 at low pin densities, the system is mechanically stable with more bonds, yet fewer contacts than the Maxwell criterion implies in the absence of pins. In addition, as pin density increases, novel bond orientational order and long-range spatial order appear, which are correlated with the square symmetry of the pin lattice.