Emergent topological phenomena in active polymeric fluids

Abstract

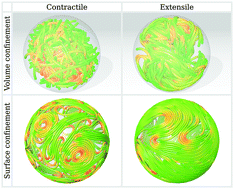
Polymeric fluids show a wealth of topological phenomena, from entanglement and reptation at microscales to orientational ordering and defect production at macroscales, which can be explained by statistical-mechanical theories. In the presence of activity, the latter must be augmented by forces that cause spontaneous chain motion and fluid flow. Here, using such augmented Langevin equations, we study active polymeric solutions and melts composed of chains of hydrodynamically interacting stresslets. In a spherical volume, contractile chains are unstable and self-knot into entangled melts at both low and high densities. Extensile chains in the same geometry form an unentangled reptating state at low densities and an entangled, coherently moving, non-reptating state at high densities. On a spherical surface, contractile chains show transitions, with increasing areal density, between isotropic, orientationally ordered and micro-phase separated states. Extensile chains in the same geometry show a transition between isotropic and nematic states. In both cases, defects in orientationally ordered states are produced athermally and without conserving topological charge. Our work reproduces the phenomenology of several recent experiments, highlights the importance of hydrodynamic interactions in active polymer fluids, and suggests non-equilibrium kinetic routes to topological structures that are otherwise difficult to obtain in equilibrium.