Droplet-train induced spatiotemporal swelling regimes in elastomers

Abstract

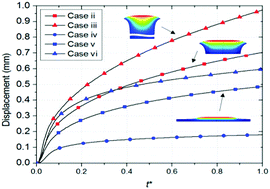
In this work, we perform a combined experimental and numerical analysis of elastomer swelling dynamics upon impingement of a train of solvent droplets. We use time scale analysis to identify spatiotemporal regimes resulting in distinct boundary conditions that occur based on relative values of the absorption timescale and the droplet train period. We recognize that when either timescale is significantly larger than the other, two cases of quasi-uniform swelling occur. In contrast, when the two timescales are comparable, a variety of temporary geometrical features due to localized swelling are observed. We show that the swelling feature and its temporal evolution depends upon geometric scaling of polymer thickness and width relative to the droplet size. Based on this scaling, we identify six cases of localized swelling and experimentally demonstrate the swelling features for two cases representing limits of thickness and width. A finite element model of local swelling is developed and validated with experimental results for these two cases. The model is subsequently used to explore the swelling behavior in the rest of the identified cases. We show that depending upon the lateral dimension of the sample, swelling can locally exhibit mushroom, mesa, and cap like shapes. These deformations are magnified during the droplet-train impact but dissipate during post-train polymer equilibration. Our results also show that while swelling shape is a function of lateral dimensions of the sample, the extent of swelling increases with the elastomer sample thickness.