Colloidal diffusion over a quenched two-dimensional random potential

Abstract

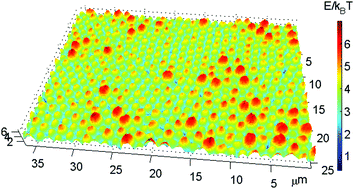
A two-layer colloidal system is developed for the study of diffusion over a quenched two-dimensional random potential. A mixture of bidisperse silica spheres is used to form a randomly packed colloidal monolayer on the bottom substrate. The corrugated surface of the bottom colloidal monolayer provides a gravitational potential field for the dilute diffusing particles in the top layer. The population probability histogram P(x,y) of the diffusing particles is obtained to fully characterize the random potential landscape U(x,y) via the Boltzmann distribution. The dynamical properties of the top diffusing particles, such as their mean square displacement (MSD), histogram of the escape time, and long-time self-diffusion coefficient, are simultaneously measured from the particle trajectories. A quantitative relationship between the long-time diffusion coefficient and the random potential is obtained, which is in good agreement with the theoretical prediction. The measured MSD reveals a wide region of subdiffusion resulting from the structural disorders. The crossover from subdiffusion to normal diffusion is explained by the Lorentz model for tracer diffusion through a heterogeneous space filled with a set of randomly distributed obstacles.