Curvature-induced microswarming†
Abstract
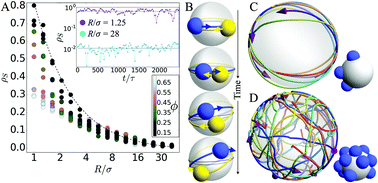
Like meridian lines on a globe, two lines on a Gaussian-curved surface cannot be simultaneously straight and parallel everywhere. We find that this inescapable property of Gaussian curvature has important consequences for the clustering and swarming behavior of active matter. Focusing on the case of self-propelled particles confined to the surface of a sphere, we find that for high curvature, particles converge to a common orbit to form symmetry-breaking microswarms. We prove that this microswarm flocking behavior is distinct from other known examples in that it is a result of the curvature, and not incorporated through Vicsek-like alignment rules or collision-induced torques. Additionally, we find that clustering can be either enhanced or hindered as a consequence of both the microswarming behavior and curvature-induced changes to the shape of a cluster's boundary. Furthermore, we demonstrate how surfaces of non-constant curvature lead to behaviors that are not explained by the simple averaging of the total curvature. These observations demonstrate a promising method for engineering the emergent behavior of active matter via the geometry of the environment.

 Please wait while we load your content...
Please wait while we load your content...