Geometry and mechanics of thin growing bilayers†
Abstract
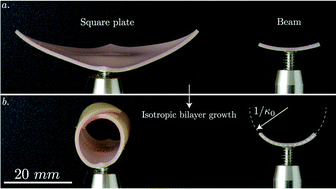
We investigate how thin sheets of arbitrary shapes morph under the isotropic in-plane expansion of their top surface, which may represent several stimuli such as nonuniform heating, local swelling and differential growth. Inspired by geometry, an analytical model is presented that rationalizes how the shape of the disk influences morphing, from the initial spherical bending to the final isometric limit. We introduce a new measure of slenderness that describes a sheet in terms of both thickness and plate shape. We find that the mean curvature of the isometric state is three fourths the natural curvature, which we verify by numerics and experiments. We finally investigate the emergence of a preferred direction of bending in the isometric state, guided by numerical analyses. The scalability of our model suggests that it is suitable to describe the morphing of sheets spanning several orders of magnitude.

 Please wait while we load your content...
Please wait while we load your content...