Capillary and winding transitions in a confined cholesteric liquid crystal

Abstract

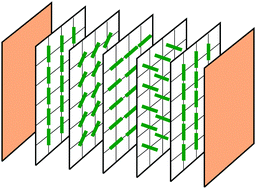
We consider a Lebwohl–Lasher model of chiral particles confined in a planar cell (slit pore) under different boundary conditions, and solve it using mean-field theory. The phase behaviour of the system with respect to temperature and pore width is studied. Two phenomena are observed: (i) an isotropic–cholesteric transition, which exhibits an oscillatory structure with respect to pore width, and (ii) an infinite set of winding transitions caused by commensuration effects between cholesteric pitch and pore width. The latter transitions have been predicted and analysed by other authors for cholesterics confined in a fixed pore and subjected to an external field promoting the uniaxial nematic phase; here we induce winding transitions solely from geometry by changing the pore width at zero external field (a setup recently explored in atomic-force microscopy experiments). In contrast with previous studies, we obtain the phase diagram in the temperature vs. pore width plane, including the isotropic–cholesteric transition, the winding transitions and their complex relationship. In particular, the structure of winding transitions terminates at the capillary isotropic–cholesteric transition via triple points where the confined isotropic phase coexists with two cholesterics with different helix indices. For symmetric and asymmetric monostable plate anchorings the phase diagrams are qualitatively similar.