A dynamic Cassie–Baxter model†
Abstract
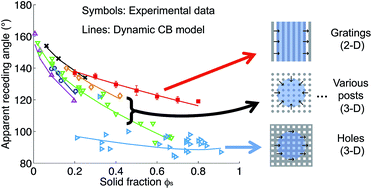
Contact-angle hysteresis of a liquid suspended on surface microstructures, namely in a Cassie–Baxter state, is determined mainly by the receding contact line although not fully understood. Existing modified Cassie–Baxter models predict some but not most experimental data in the literature. Noting that most models were based on the two-dimensional (2-D) principle whereas the experiments were under three-dimensional (3-D) conditions, here we develop a 2-D experiment. While 3-D experiments measure the receding contact lines averaged over space and time, 2-D experiments eliminate the spatial averaging and can further eliminate the temporal averaging by high-speed visualization. The resulting details of the contact line motion lead us to propose a 2-D model, which incorporates the contact-line friction. The new 2-D model matches the 2-D experimental results excellently while all existing models show significant deviation. By introducing a line solid fraction term, the 2-D model is further generalized to a 3-D model, which successfully predicts a wide range of 3-D data in the literature regardless of their distinct microstructures and receding modes.

 Please wait while we load your content...
Please wait while we load your content...